Oxidation of Thin Titanium Films: Determination of the Chemical Composition of the Oxide and the Oxygen Diffusion Factor
Abstract
1. Introduction
2. Experimental
3. Results and Discussion
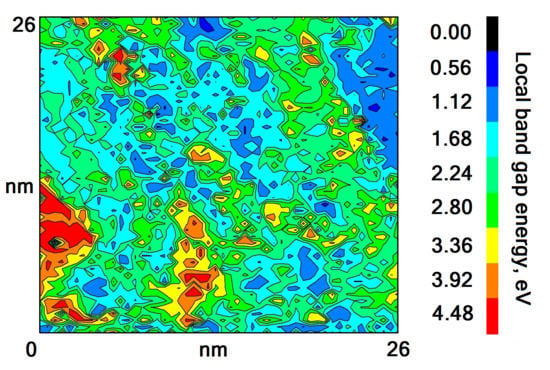
4. Determination of the Oxide Chemical Composition
5. Determination of the Oxygen Diffusion Factor in Titanium
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Freund, H.-J. Model Systems in Heterogeneous Catalysis: Selectivity Studies at the Atomic Level. Top. Catal. 2008, 48, 137–144. [Google Scholar] [CrossRef][Green Version]
- Freund, H.-J. The Surface Science of Catalysis and More, Using Ultrathin Oxide Films as Templates: A Perspective. J. Am. Chem. Soc. 2016, 138, 8985–8996. [Google Scholar] [CrossRef] [PubMed]
- Ern, V.; Switendick, A.C. Electronic Band Structure of TiC, TiN, and TiO. Phys. Rev. 1965, 137, A1927. [Google Scholar] [CrossRef]
- Henrich, V.E.; Cox, P.A. (Eds.) The Surface Science of Metal Oxides; Cambridge University Press: Cambridge, UK, 1996; p. 464. [Google Scholar]
- Reyers-Coronado, D.; Rodríguez-Gattorno, G.; Espinosa-Pesqueira, M.E.; Cab, C.; de Coss, R.; Oskam, G. Phase-pure TiO2 Nanoparticles: Anatase, Brookite and Rutile. Nanotecnology 2008, 19, 145605. [Google Scholar] [CrossRef]
- Hanson, D.M.; Stockbauer, R.; Madey, T.E. Photon-Stimulated Desorption and Other Spectroscopic Studies of the Interaction of Oxygen With a Titanium (001) Surface. Phys. Rev. B. 1981, 24, 5513–5521. [Google Scholar] [CrossRef]
- Bertel, E.; Stockbauer, R.; Madey, T.E. Electron Emission and Ion Desorption Spectroscopy of Clean and Oxidized Ti(0001). Surf. Sci. 1984, 141, 355–387. [Google Scholar] [CrossRef]
- Takano, A.; Ueda, K. A Study of the Oxygen Adsorption Process on a Titanium Single Crystal Surface by Electron Stimulated Desorption. Surf. Sci. 1991, 242, 450–453. [Google Scholar] [CrossRef]
- Ocal, C.; Ferrer, S. A New CO Adsorption State on Thermally Treated PtTiO2 Model Catalysts. Surf. Sci. 1986, 178, 850–855. [Google Scholar] [CrossRef]
- Dawson, P.H. Sims Studies of the Adsorption of O2, CO and CO2 on Titanium Using Low Primary Energies. Surf. Sci. 1977, 65, 41–62. [Google Scholar] [CrossRef]
- Brugniau, D.; Argile, C.; Barthes-Labrousse, M.-G.; Rhead, G.E. Oxygen Adsorption on Polycrystalline Titanium: Characterization of the First Stages and Coadsorption with Lead. Surf. Sci. 1984, 141, 639–653. [Google Scholar] [CrossRef]
- Azoulay, A.; Shamir, N.; Fromm, E.; Mintz, M.H. The Initial Interactions of Oxygen with Polycrystalline Titanium Surfaces. Surf. Sci. 1997, 370, 1–16. [Google Scholar] [CrossRef]
- Lu, G.; Bernasek, S.L.; Schwartz, J. Oxidation of a Polycrystalline Titanium Surface by Oxygen and Water. Surf. Sci. 2000, 458, 80–90. [Google Scholar] [CrossRef]
- Brearley, W.; Surplice, N.A. Changes in the Work Function of Titanium Films Owing to the Chemisorption of N2, O2, CO and CO2. Surf. Sci. 1977, 64, 372–374. [Google Scholar] [CrossRef]
- Platau, A.; Johansson, L.I.; Hagström, A.L.; Karlsson, S.-E.; Hagström, S.B.M. Oxidation of Cerium and Titanium Studied by Photoelectron Spectroscopy. Surf. Sci. 1977, 63, 153–161. [Google Scholar] [CrossRef]
- Martin, M.; Mader, W.; Fromm, E. Oxidation of Iron, Aluminium and Titanium Films in the Temperature Range 50–200 °C. Thin Solid Film. 1994, 250, 61–66. [Google Scholar] [CrossRef]
- Vaquila, I.; Passeggi, M.C.G.; Ferrón, J. Oxidation Process in Titanium Thin Films. Phys. Rev. B 1997, 55, 13925–13931. [Google Scholar] [CrossRef]
- Oh, W.S.; Xu, C.; Kim, D.Y.; Goodman, D.W. Preparation and Characterization of Epitaxial Titanium Oxide Films on Mo(100). J. Vac. Sci. Technol. A 1997, 15, 1710–1716. [Google Scholar] [CrossRef]
- Guo, O.; Oh, W.S.; Goodman, D.W. Titanium Oxide Films Grown on Mo(110). Surf. Sci. 1999, 437, 49–60. [Google Scholar] [CrossRef]
- Strong, R.L.; Erskine, J.L. Investigation of Underlayer Formation by Oxygen on Al(111) and Ti(0001). J. Vac. Sci. Technol. A 1985, 3, 1428–1431. [Google Scholar] [CrossRef]
- Jonker, B.T.; Morar, J.F.; Park, R.L. Surface States and Oxygen Chemisorption on Ti(0001). Phys. Rev. B 1981, 24, 2951–2957. [Google Scholar] [CrossRef]
- Aduru, S.; Rabalais, J.W. Initial Stage of Titanium Oxidation Studied by Direct Recoil Spectrometry. Langmuir 1987, 3, 543–547. [Google Scholar] [CrossRef]
- Eastman, D.E. Photoemission energy level measurements of sorbed gases on titanium. Solid State Commun. 1972, 10, 933–935. [Google Scholar] [CrossRef]
- Shih, H.D.; Jona, F. Low-Energy Electron Diffraction and Auger Electron Spectroscopy Study of the Oxidation of Ti {0001} at Room Temperature. Appl. Phys. 1977, 12, 311–315. [Google Scholar] [CrossRef]
- Porte, L.; Demosthenous, M.; Duc, T.M. Étude esca de l’interaction oxygène-titane. J. Less Common Met. 1977, 56, 183–191. [Google Scholar] [CrossRef]
- Corneille, J.S.; He, J.-W.; Goodman, D.W. Preparation and Characterization of Ultra-Thin Iron Oxide Films on a Mo(100) surface. Surf. Sci. 1995, 338, 211–224. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Hopkins, B.E. (Eds.) Oxidation of Metals and Alloys, 2nd ed.; Butterworths: London, UK, 1967; p. 319. [Google Scholar]
- Sedona, F.; Rizzi, G.A.; Agnoli, S.; Llabre’s i Xamena, F.X.; Papageorgiou, A.; Ostermann, D.; Sambi, M.; Finetti, P.; Schierbaum, K.; Granozzi, G. Ultrathin TiOx Films on Pt(111): A LEED, XPS, and STM Investigation. J. Phys. Chem. B 2005, 109, 24411. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, C.; Liu, X.; Lin, Y.; Gao, G.; Ma, C.; Yin, Y.; Li, X. Structure and Transport Properties of Titanium Oxide (Ti2O, TiO1+δ, and Ti3O5) Thin Films. J. Alloys Compd. 2019, 786, 607–613. [Google Scholar] [CrossRef]
- Choudhary, B.; Dey, M.; Choudhary, A. Defect Generation, d-d Transition, and Band Gap Reduction in Cu-Doped TiO2 Nanoparticles. Int. Nano Lett. 2013, 3, 25. [Google Scholar] [CrossRef]
- Xu, M.; Zhong, X.; Lv, J.; Cui, W.; Shi, J.; Kanchana, V.; Vaitheeswaran, G.; Hao, J.; Wang, Y.; Li, Y. Ti-Fraction-Induced Electronic and Magnetic Transformations in Titanium Oxide Films. J. Chem. Phys. 2019, 150, 154704. [Google Scholar] [CrossRef]
- Mathews, N.R.; Morales, E.R.; Corte’s-Jacome, M.A.; Toledo Antonio, J.A. TiO2 Thin Films—Influence of Annealing Temperature on Structural, Optical and Photocatalytic properties. Solar Energy 2009, 83, 1499. [Google Scholar] [CrossRef]
- Chae, S.Y.; Park, M.K.; Lee, S.K.; Kim, T.Y.; Kim, S.K.; Lee, W.I. Preparation of Size-Controlled TiO2 Nanoparticles and Derivation of Optically Transparent Photocatalytic Films. Chem. Mater. 2003, 15, 3326–3331. [Google Scholar] [CrossRef]
- Güntherodt, H.-J.; Wiesendanger, R. Principles, Scanning Tunneling Microscopy I. General. Applications to Clean and Absorbate-Covered Surfaces; Guntherodt, H.-J., Wiesendanger, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; p. 280. [Google Scholar]
- Binnig, G.; Rohrer, H.; Gerber, C.; Weibel, E. Tunneling Through a Controllable Vacuum Gap. Appl. Phys. Lett. 1982, 40, 178–180. [Google Scholar] [CrossRef]
- Meyer, E.; Hug, H.J.; Bennewitz, R. (Eds.) Scanning Probe Microscopy; Springer: Berlin/Heidelberg, Germany, 2004; p. 210. [Google Scholar]
- Hamers, R.J.; Wang, Y. Atomically-Resolved Studies of the Chemistry and Bonding at Silicon Surfaces. Chem. Rev. 1996, 96, 1261–1290. [Google Scholar] [CrossRef]
- Hamers, R.J.; Tromp, R.M.; Demuth, J.E. Surface Electronic Structure of Si (111)-(7 × 7) Resolved in Real Space. Phys. Rev. Lett. 1986, 56, 1972–1975. [Google Scholar] [CrossRef]
- Naitabdi, A.; Ono, L.K.; Cuenya, B.R. Local Investigation of the Electronic Properties of Size-Selected Au Nanoparticles by Scanning Tunneling Spectroscopy. Appl. Phys. Lett. 2006, 89, 043101. [Google Scholar] [CrossRef]
- Bartholomew, R.F.; Frankl, D.R. Electrical Properties of Some Titanium Oxides. Phys. Rev. 1969, 187, 828–833. [Google Scholar] [CrossRef]
- Abbate, M.; Potze, R.; Sawatzky, G.A.; Schlenker, C.; Teehan, D.; Turner, T.S. The Electronic Structure of Ti4O7 Studied by Resonant Photoemission. Solid State Commun. 1995, 94, 465–469. [Google Scholar] [CrossRef]
- Leonov, I.; Yaresko, A.N.; Antonov, V.N.; Schwingenschlögl, U.; Eyert, V.; Anisimov, V.I. Charge Order and Spin-Singlet Pair Formation in Ti4O7. J. Phys. Condens. Matter 2006, 18, 10955–10964. [Google Scholar] [CrossRef]
- Gatin, A.K.; Grishin, M.V.; Kirsankin, A.A.; Kozhushner, M.A.; Posvyanskii, V.S.; Kharitonov, V.A.; Shub, B.R. Measurement of Local Thickness of Oxide Layer and its Electronic Characteristics by Scanning Tunneling Microscopy. Nanotechnol. Russ. 2013, 8, 627–630. [Google Scholar] [CrossRef]
- Morikawa, T.; Asahi, R.; Ohwaki, T.; Aoki, K.; Taga, Y. Band-Gap Narrowing of Titanium Dioxide by Nitrogen Doping. Jpn. J. Appl. Phys. 2001, 40, L561–L563. [Google Scholar] [CrossRef]
- Birks, J.B. (Ed.) Modern Dielectric Materials; Heywood: London, UK, 1960; p. 253. [Google Scholar]
- Mashimo, T.; Bagum, R.; Ogata, Y.; Tokuda, M.; Okube, M.; Sugiyama, K.; Kinemuchi, Y.; Isobe, H.; Yoshiasa, A. Structure of Single-Crystal Rutile (TiO2) Prepared by High-Temperature Ultracentrifugation. Cryst. Growth Des. 2017, 17, 1460–1464. [Google Scholar] [CrossRef]
- Treacy, J.P.W.; Hussain, H.; Torrelles, X.; Grinter, D.C.; Cabailh, G.; Bikondoa, O.; Nicklin, C.; Selcuk, S.; Selloni, A.; Lindsay, R.; et al. Geometric Structure of Anatase TiO2(101). Phys. Rev. B 2017, 95, 075416. [Google Scholar] [CrossRef]
- Bredikhin, V.I.; Burenina, V.N.; Mamayev, Y.A.; Yashin, S.N. Spectral and relaxation properties of the photoconductivity of thin TiO2 films Produced by the sol-gel technique. Phys. Sci. Int. J. 2013, 3, 642. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; p. 414. [Google Scholar]
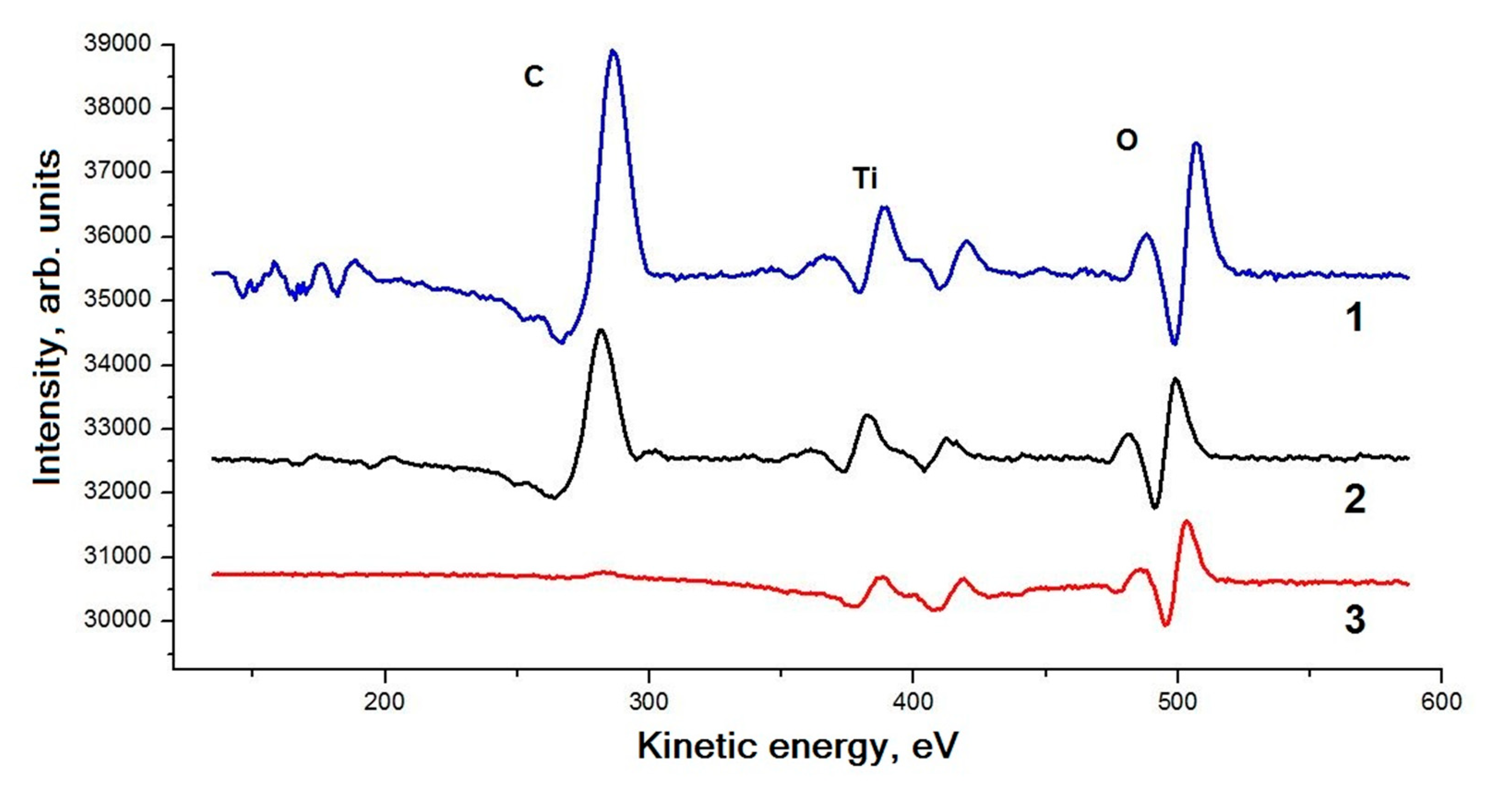
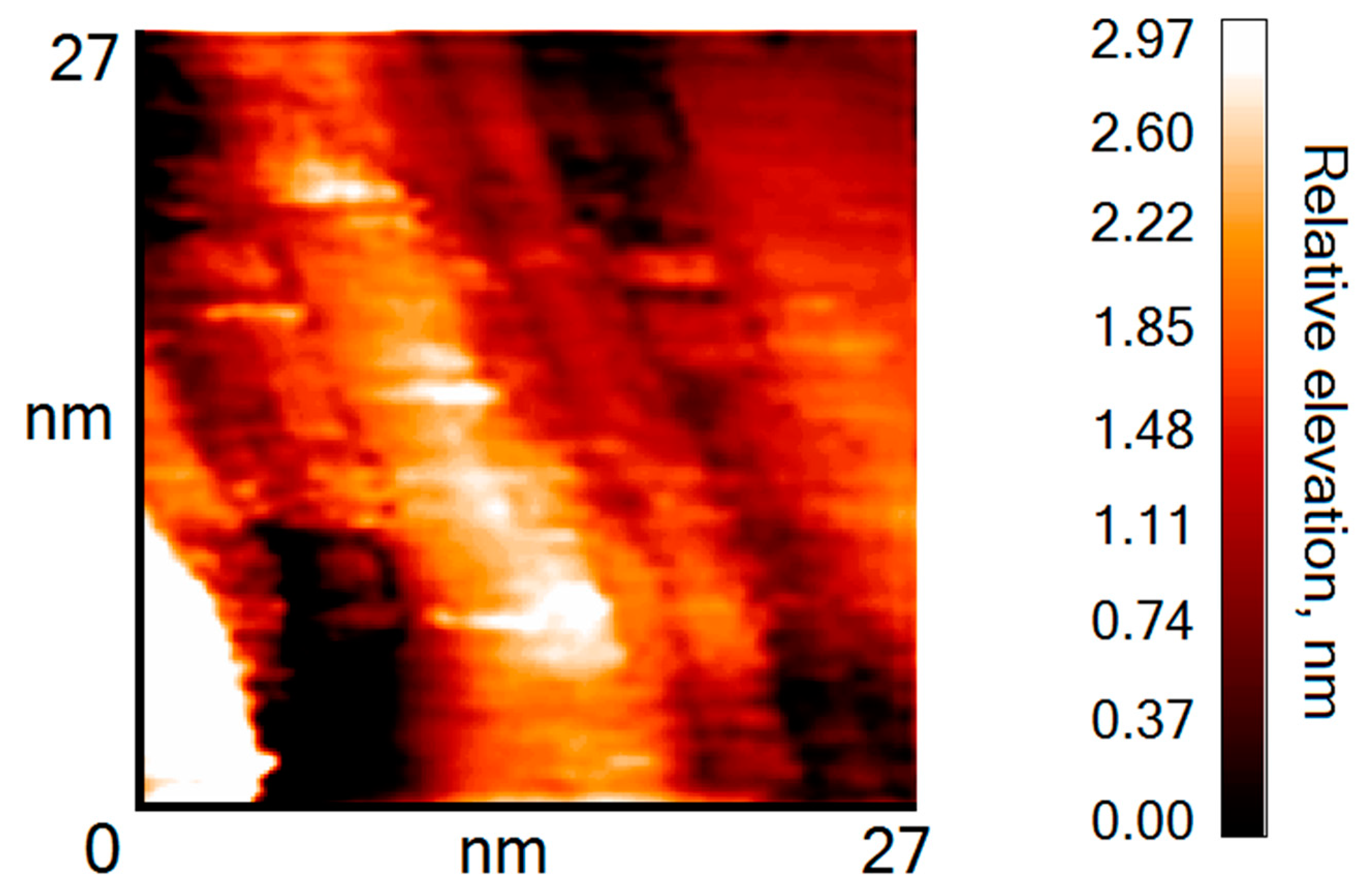
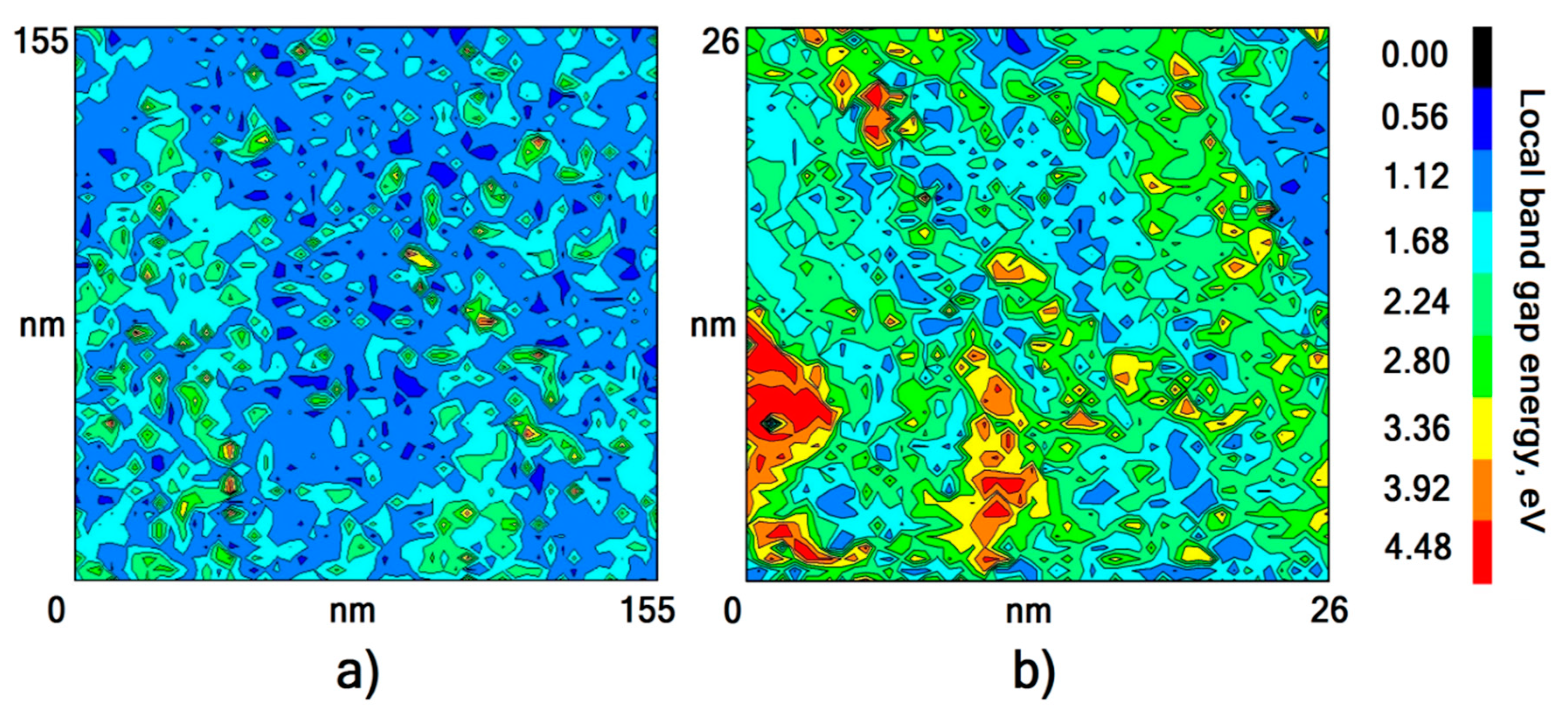
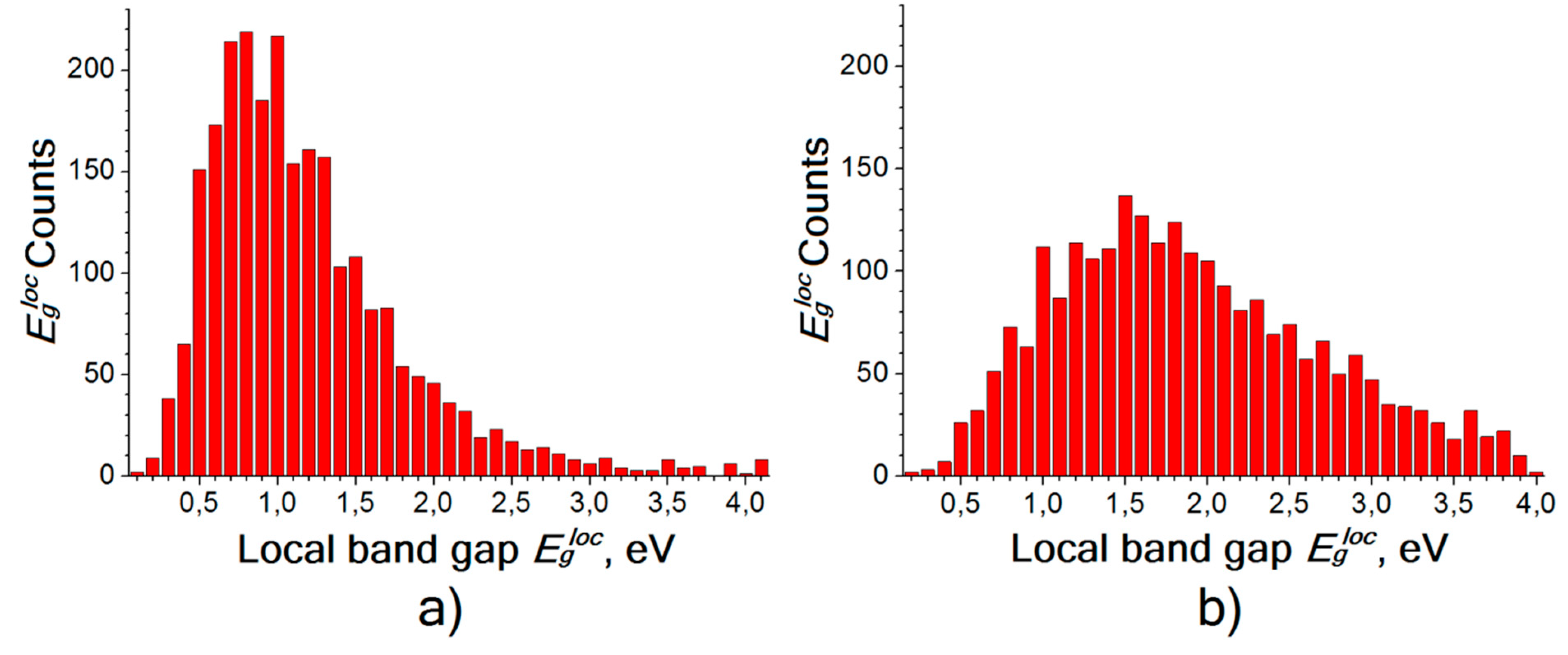
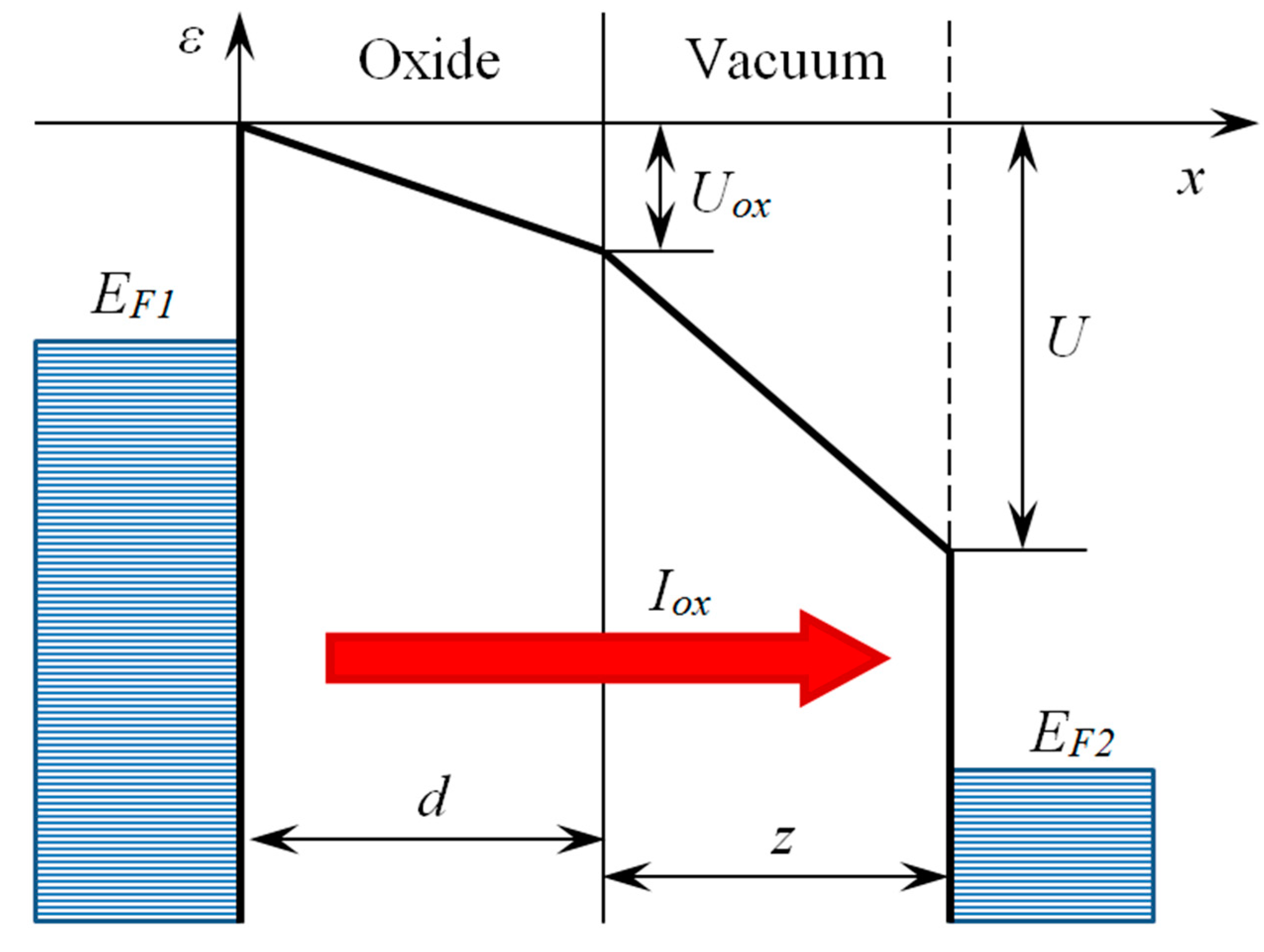
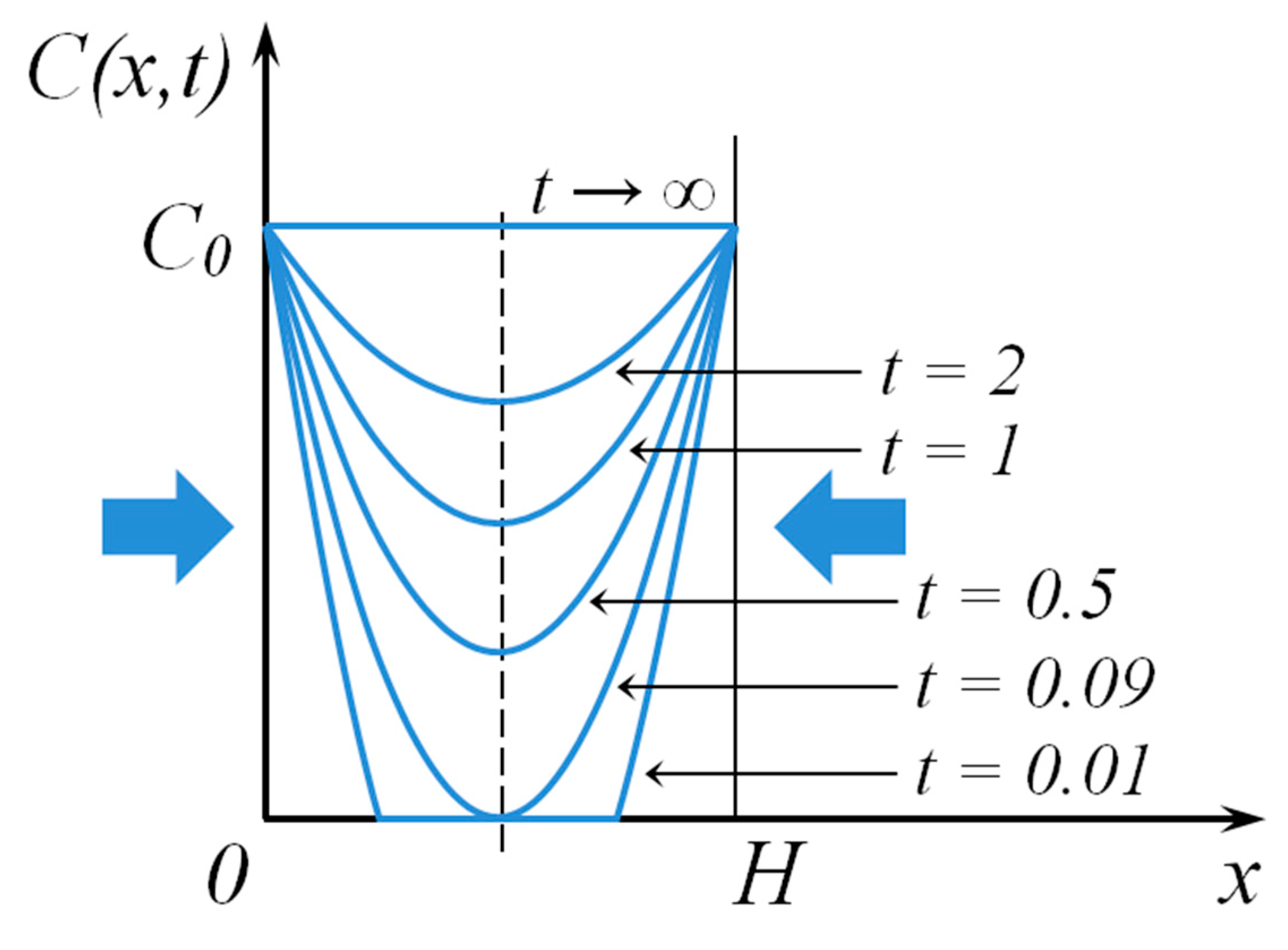
| Sample, Nos | T, K | t, h | Eg, eV |
|---|---|---|---|
| 1 | 300 | 720 | 0.8 |
| 2 | 770 | 4 | 0.8 |
| 3 | 770 | 13 | 1.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarvadii, S.Y.; Gatin, A.K.; Kharitonov, V.A.; Dokhlikova, N.V.; Ozerin, S.A.; Grishin, M.V.; Shub, B.R. Oxidation of Thin Titanium Films: Determination of the Chemical Composition of the Oxide and the Oxygen Diffusion Factor. Crystals 2020, 10, 117. https://doi.org/10.3390/cryst10020117
Sarvadii SY, Gatin AK, Kharitonov VA, Dokhlikova NV, Ozerin SA, Grishin MV, Shub BR. Oxidation of Thin Titanium Films: Determination of the Chemical Composition of the Oxide and the Oxygen Diffusion Factor. Crystals. 2020; 10(2):117. https://doi.org/10.3390/cryst10020117
Chicago/Turabian StyleSarvadii, Sergey Y., Andrey K. Gatin, Vasiliy A. Kharitonov, Nadezhda V. Dokhlikova, Sergey A. Ozerin, Maxim V. Grishin, and Boris R. Shub. 2020. "Oxidation of Thin Titanium Films: Determination of the Chemical Composition of the Oxide and the Oxygen Diffusion Factor" Crystals 10, no. 2: 117. https://doi.org/10.3390/cryst10020117
APA StyleSarvadii, S. Y., Gatin, A. K., Kharitonov, V. A., Dokhlikova, N. V., Ozerin, S. A., Grishin, M. V., & Shub, B. R. (2020). Oxidation of Thin Titanium Films: Determination of the Chemical Composition of the Oxide and the Oxygen Diffusion Factor. Crystals, 10(2), 117. https://doi.org/10.3390/cryst10020117