Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys
Abstract
1. Introduction
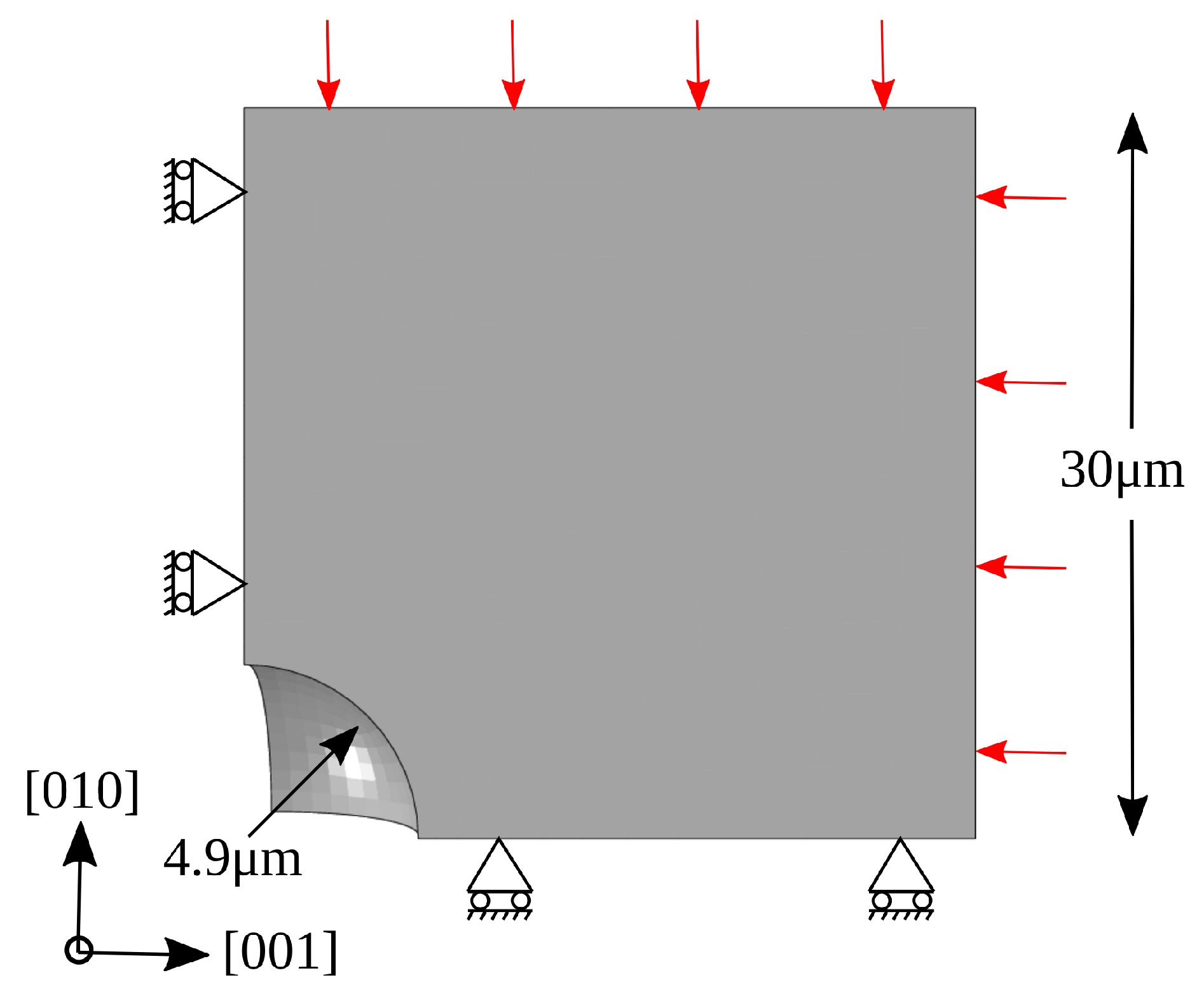
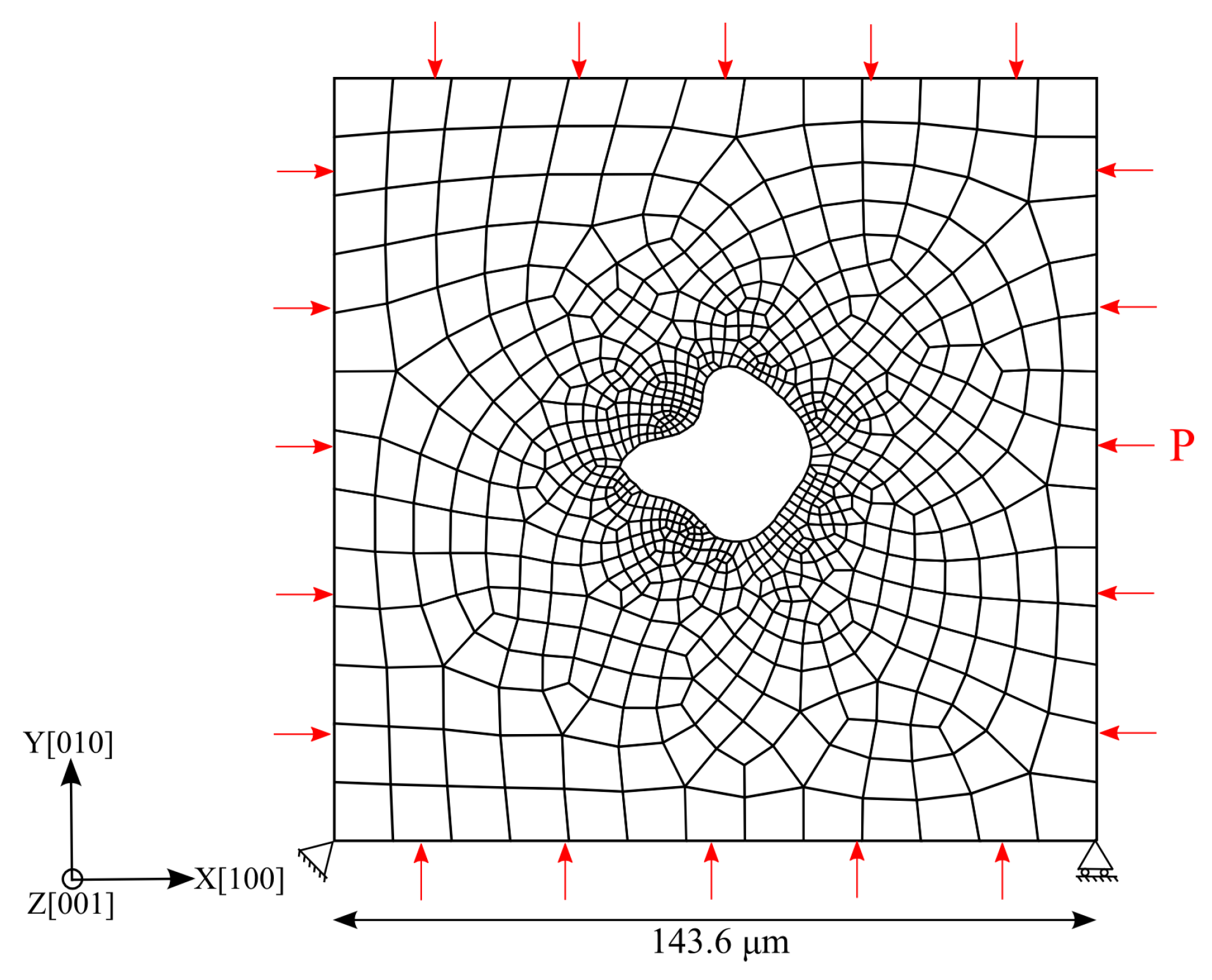
2. Micromechanical Modeling
2.1. Crystal Plasticity Model
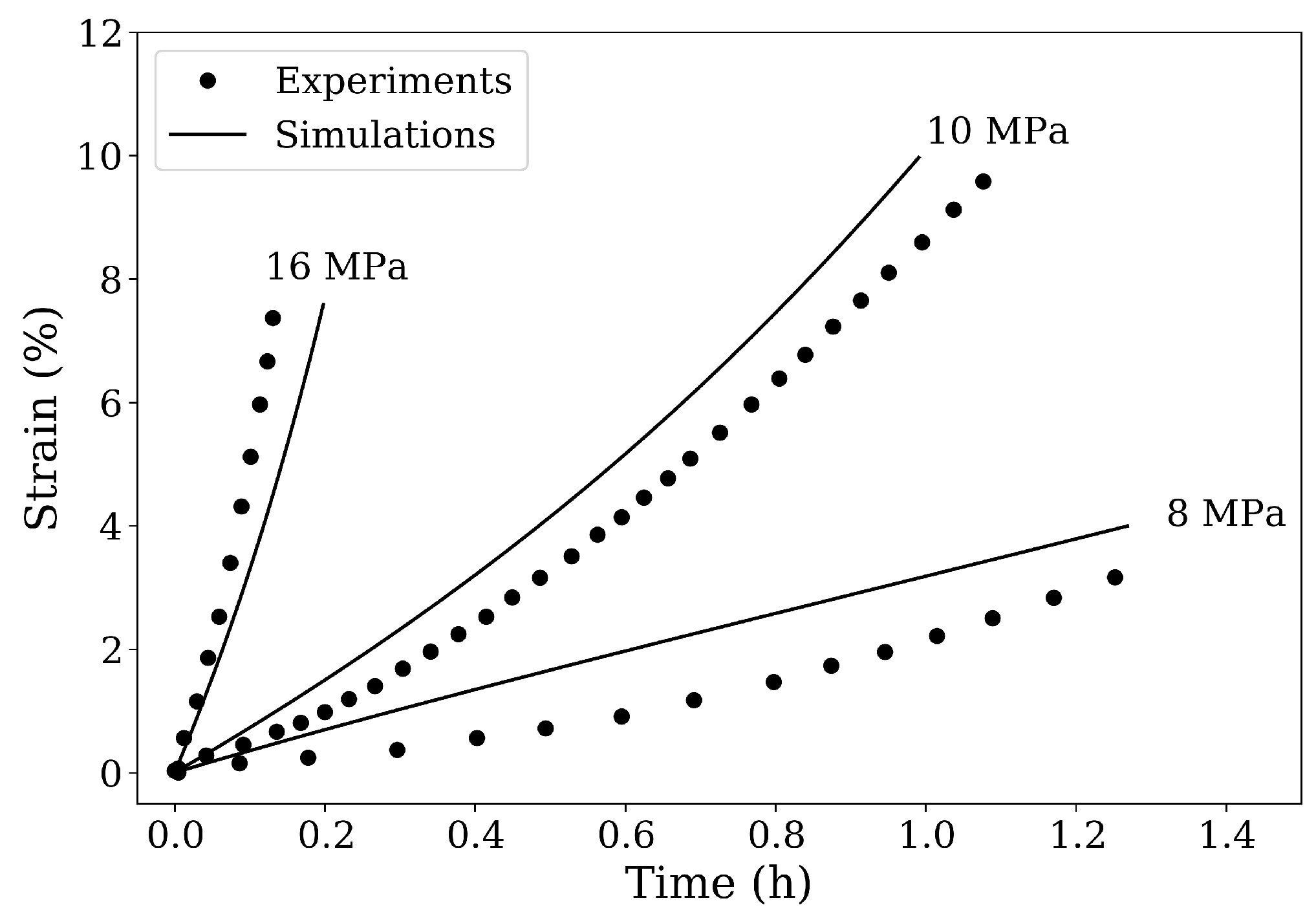
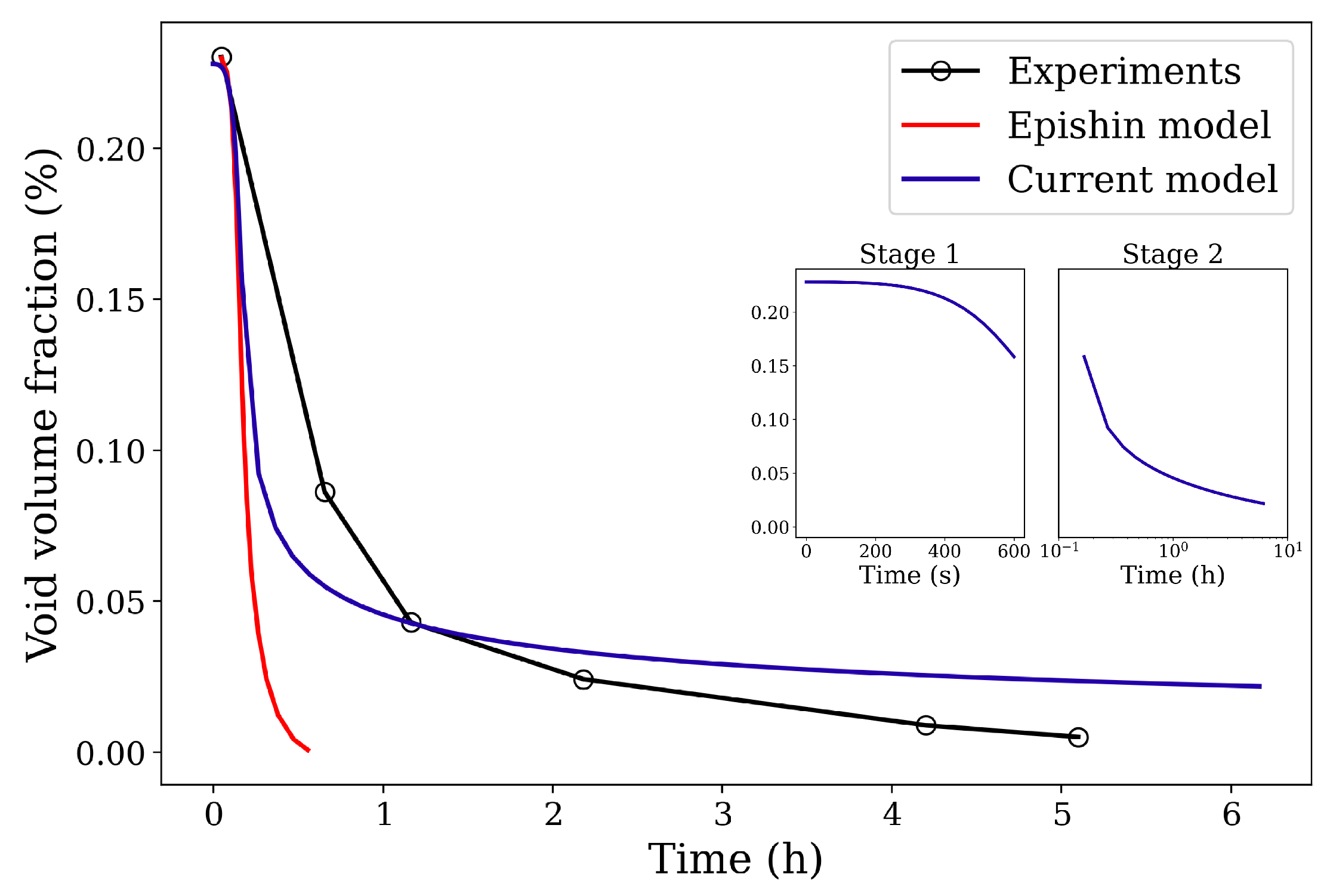
2.2. Model Calibration
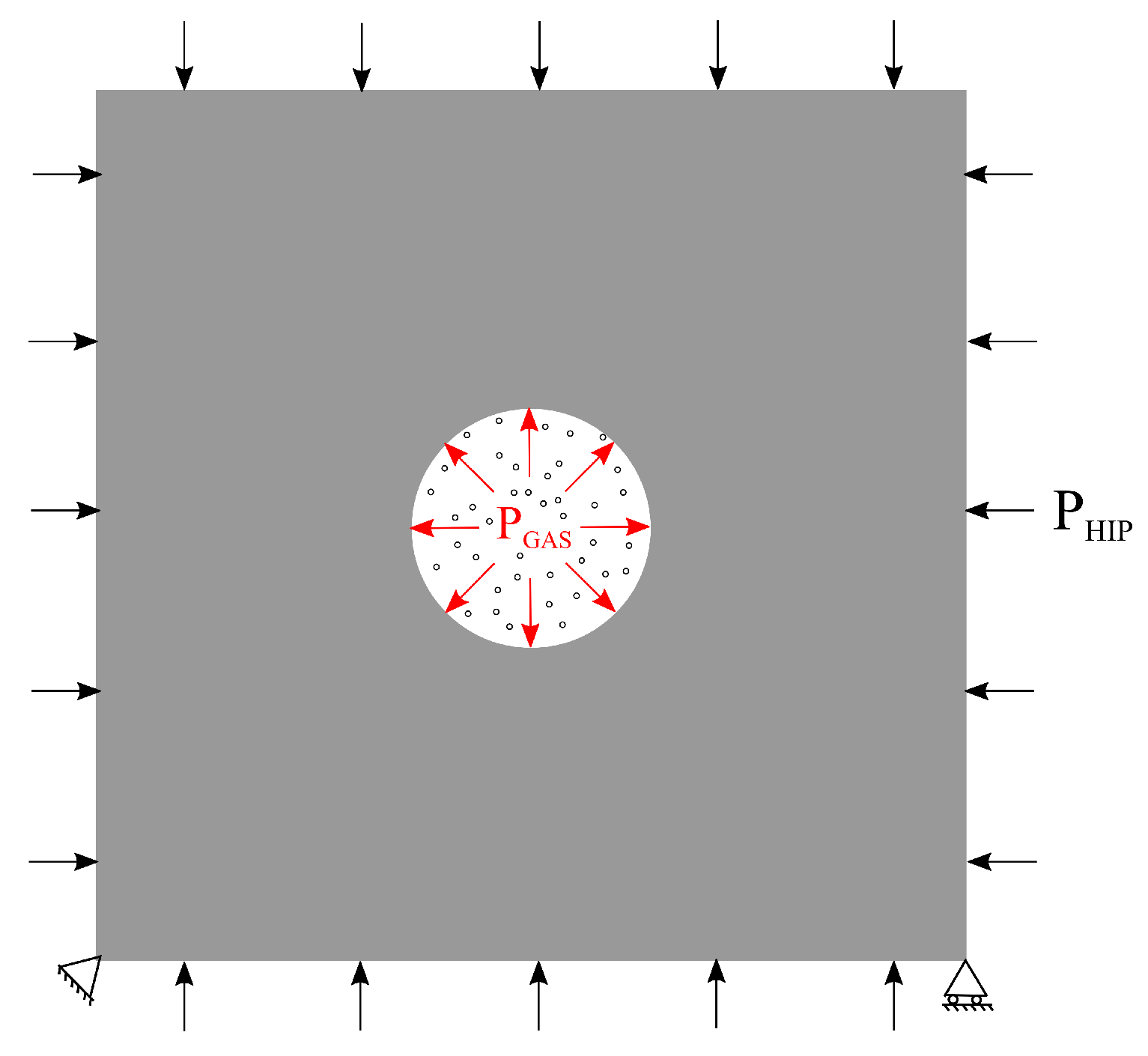
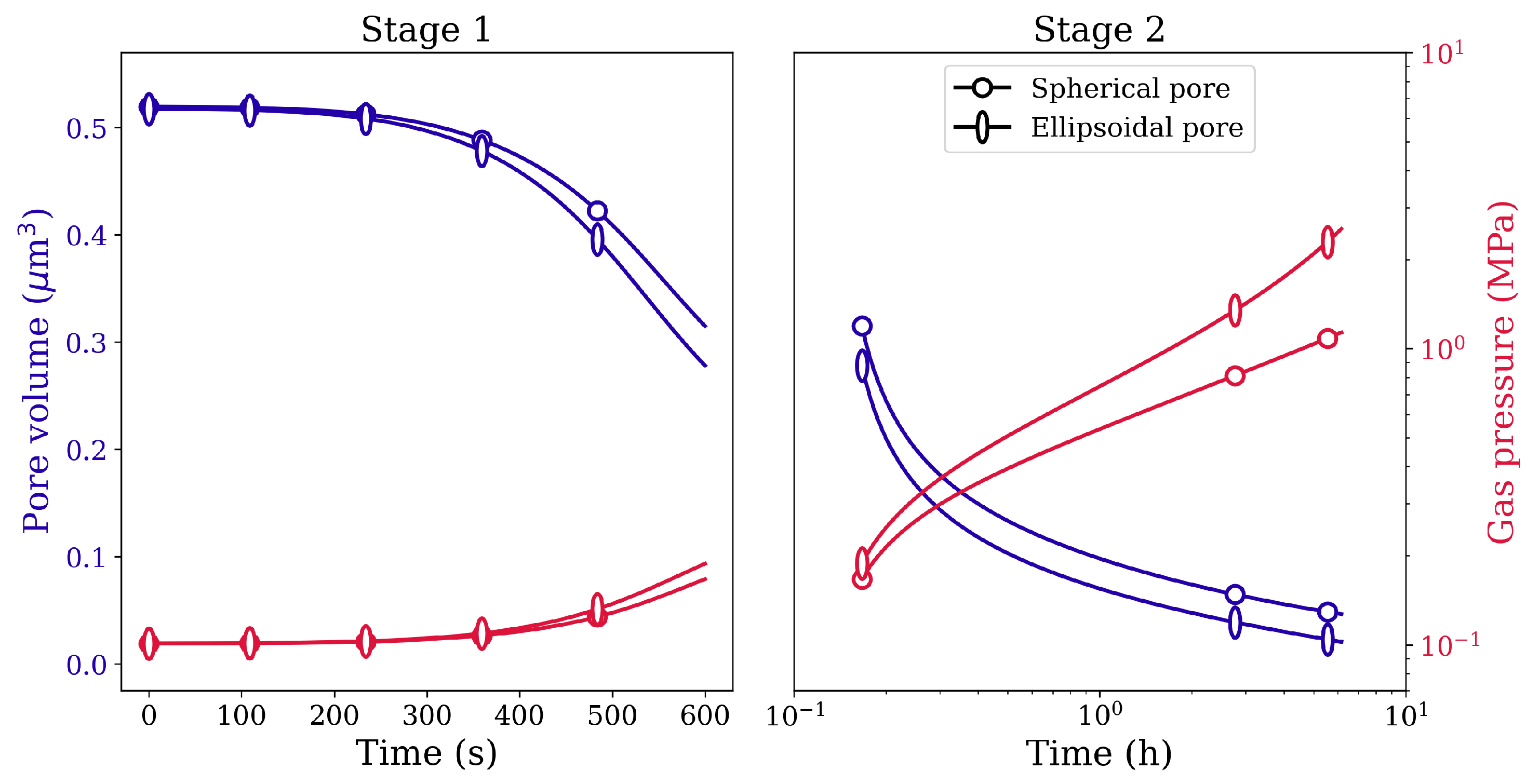
2.3. Modeling Gas inside Pores
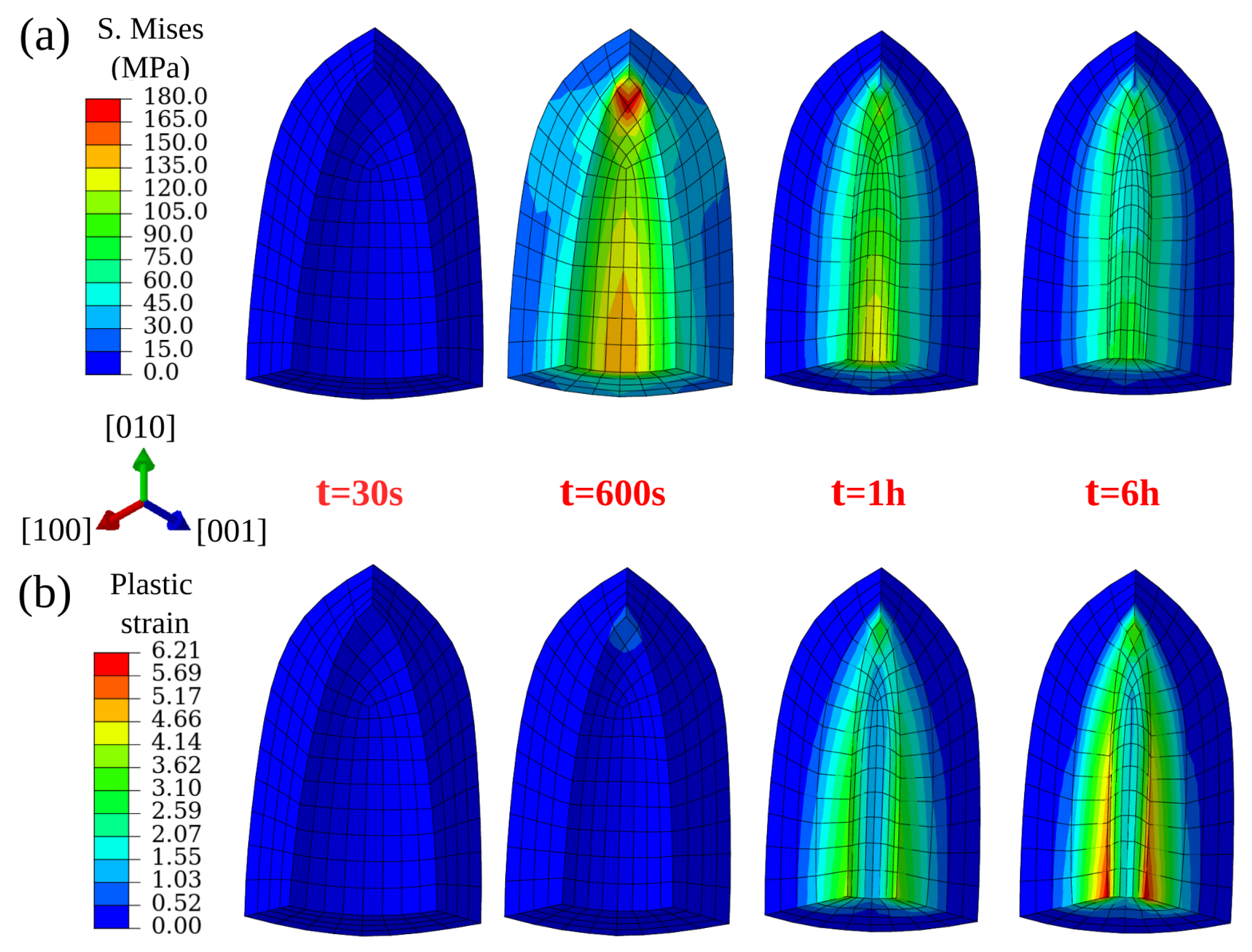
3. Numerical Study and Results
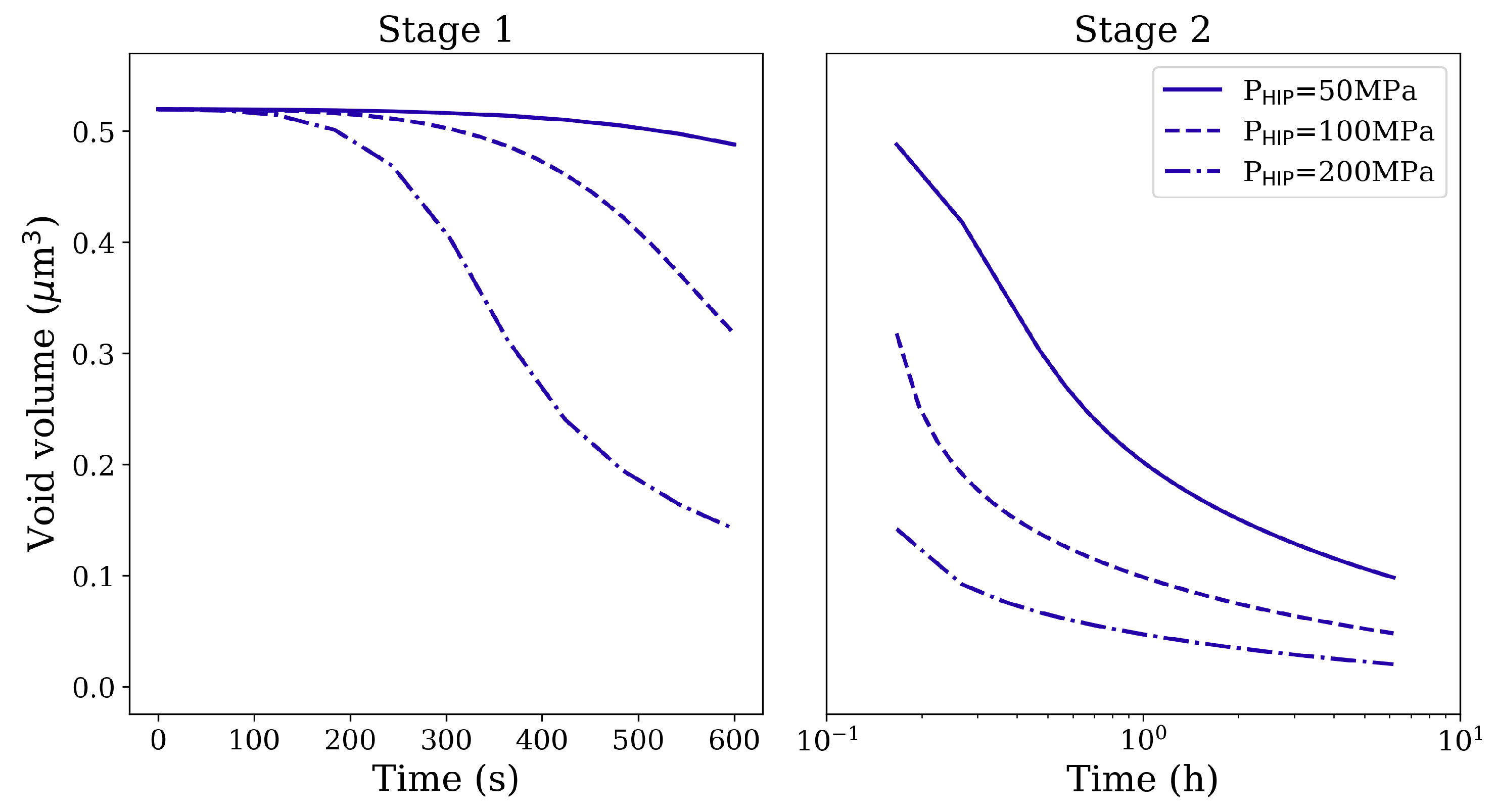
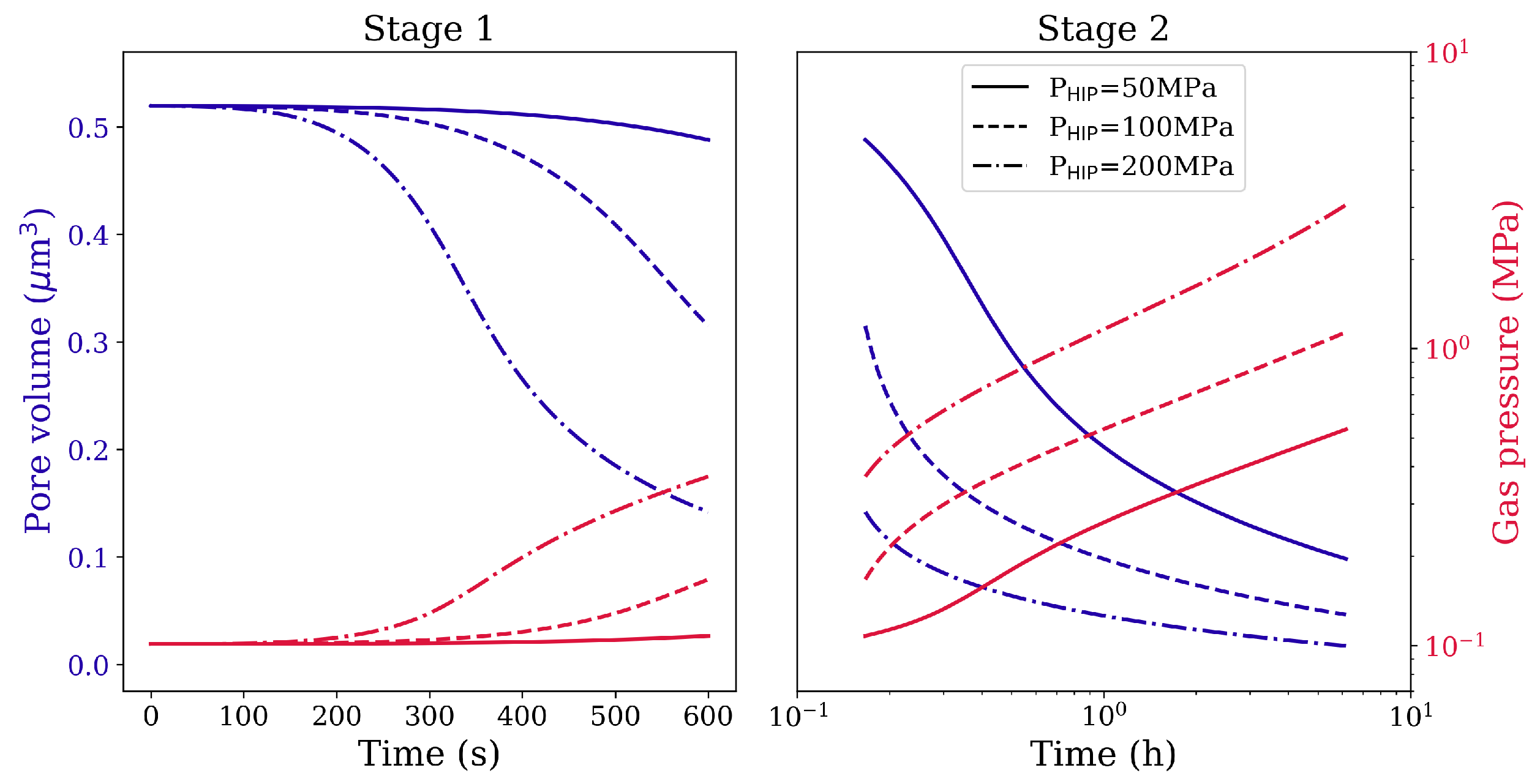
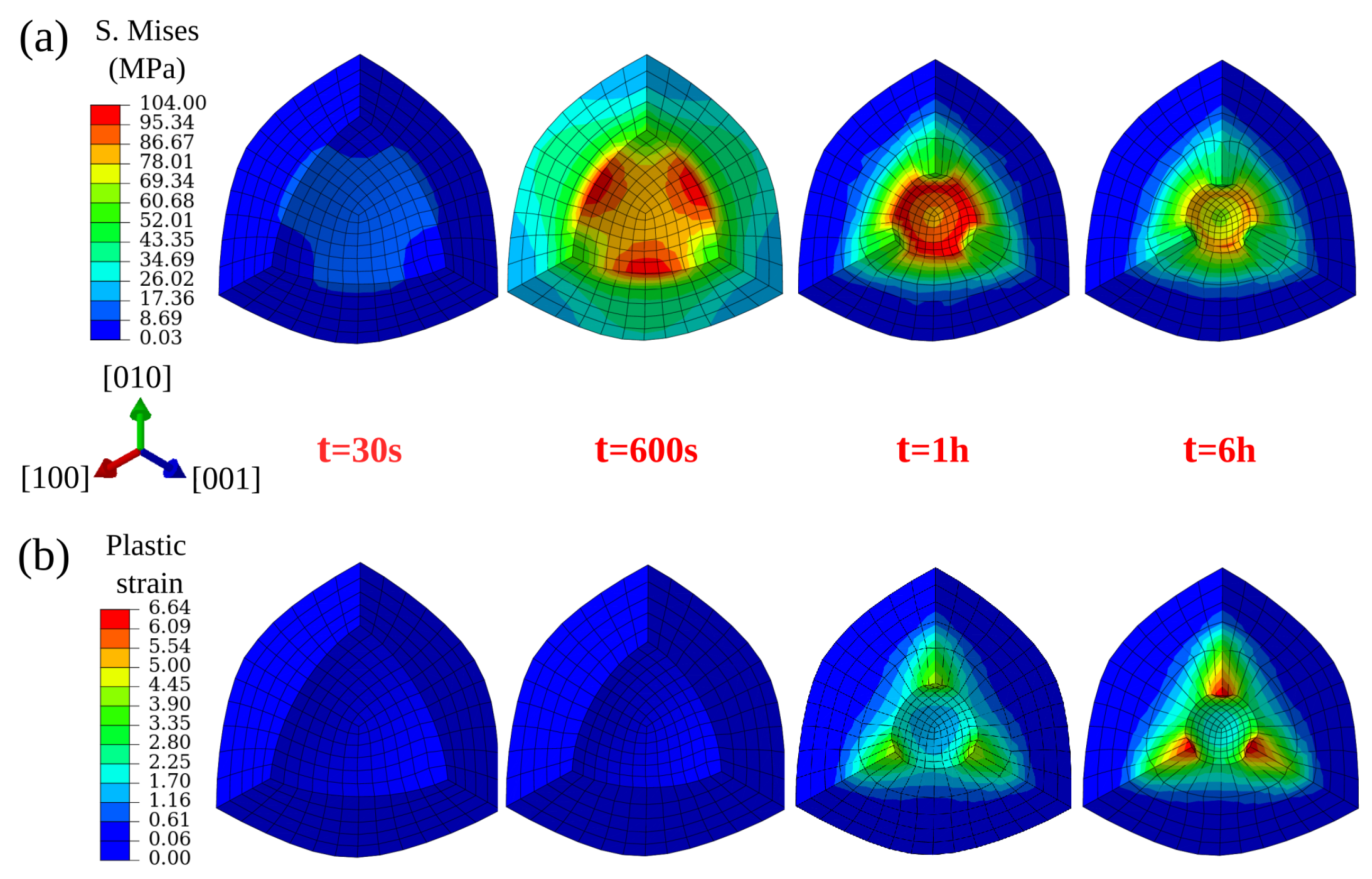
3.1. Influence of HIP Processing Conditions
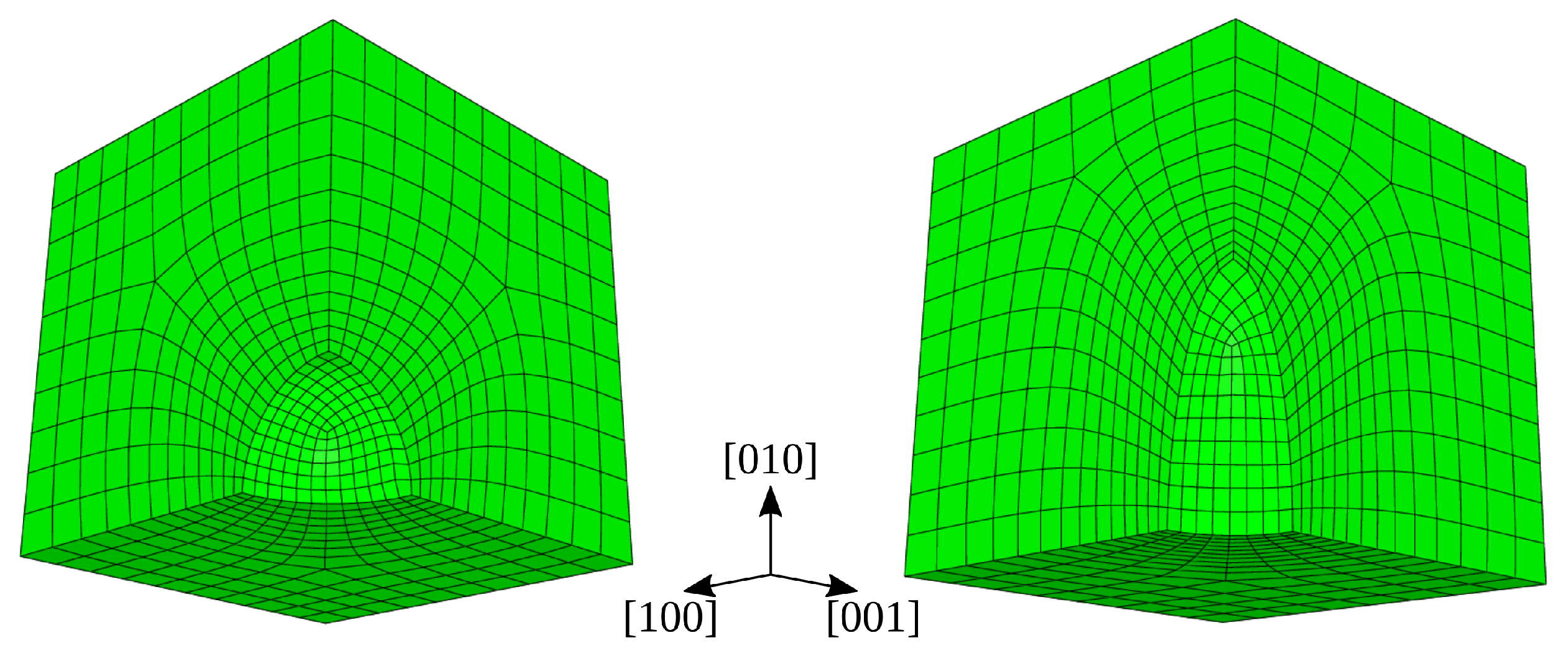
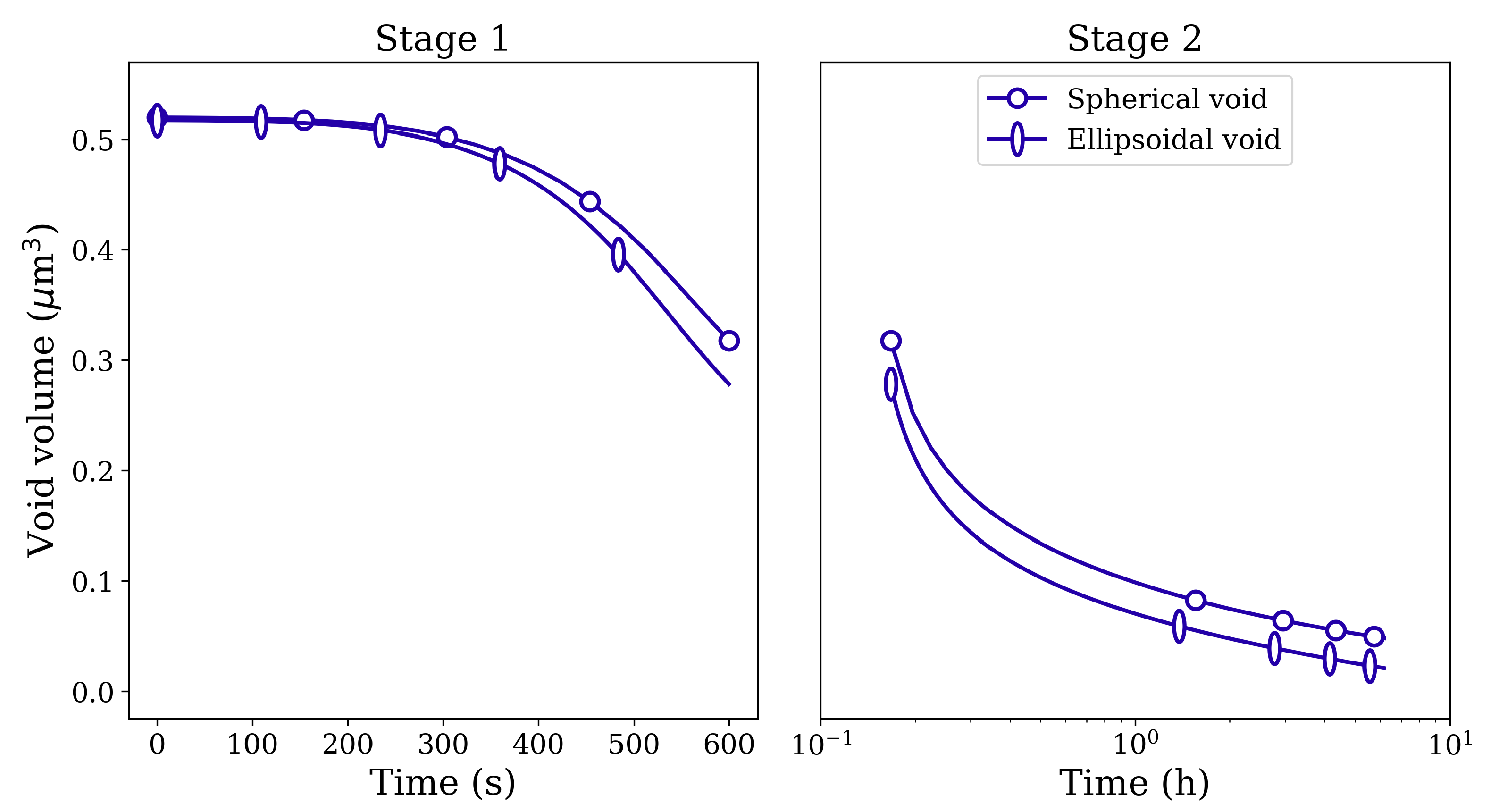
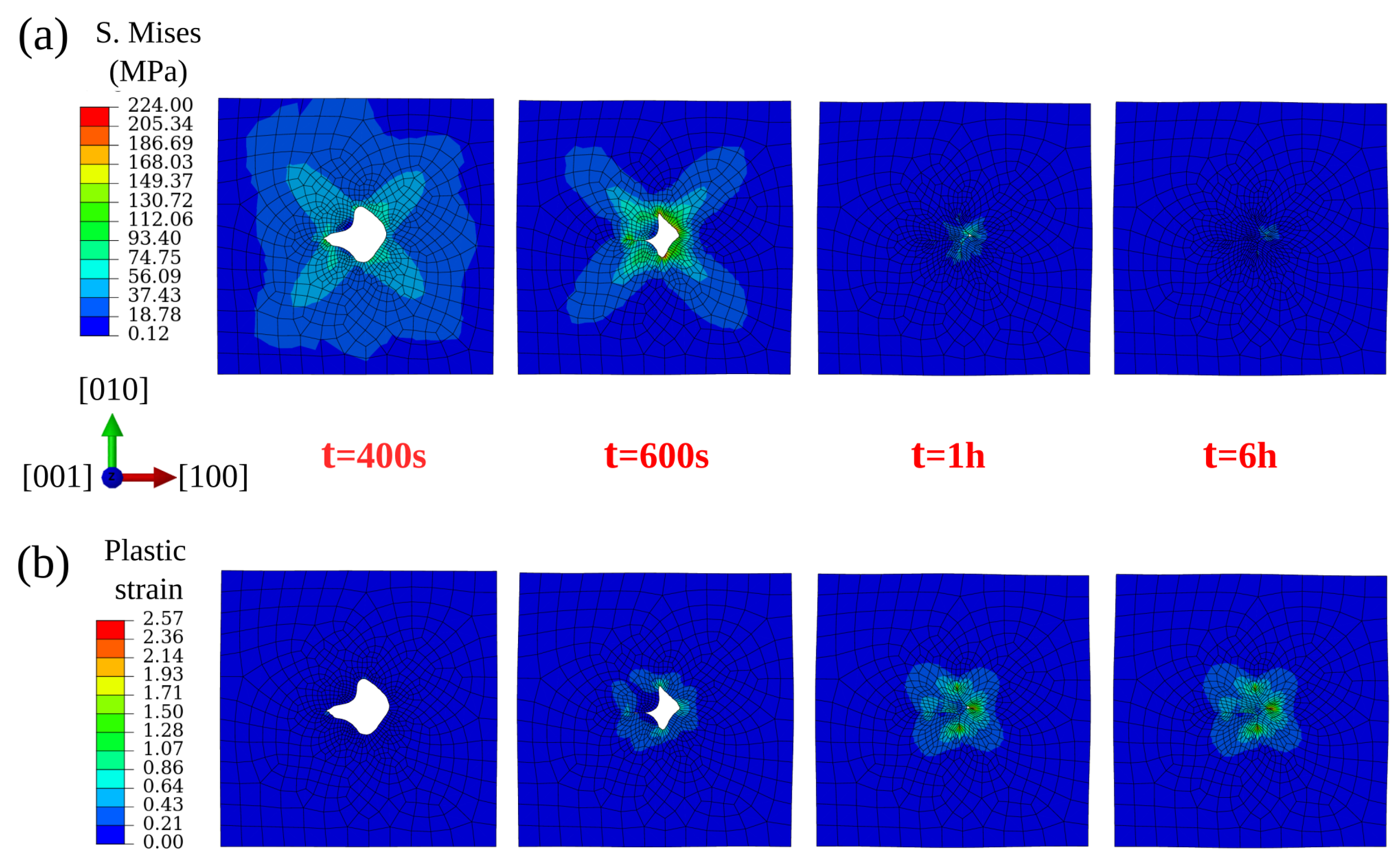
3.2. Influence of Pore Shape
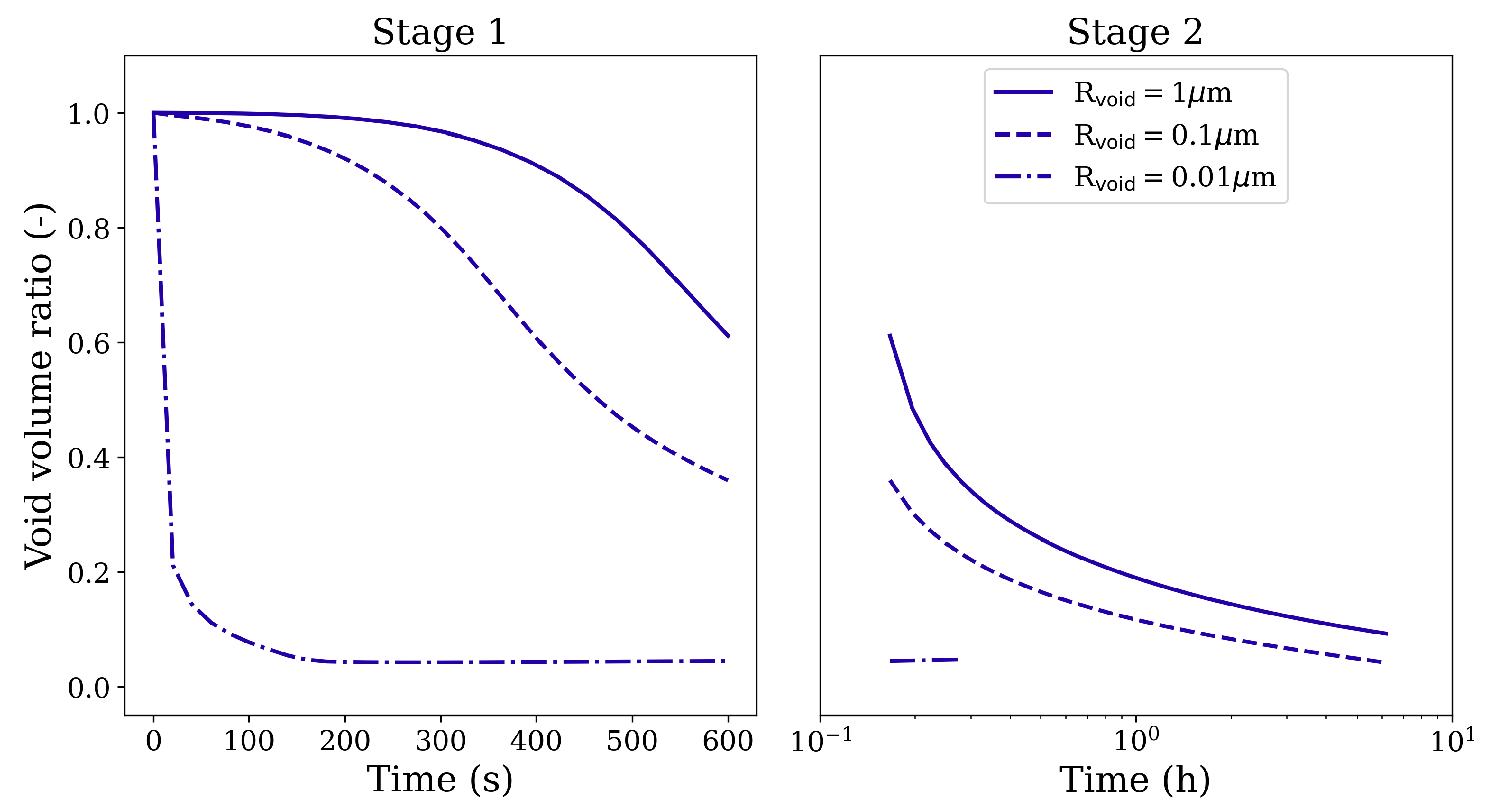
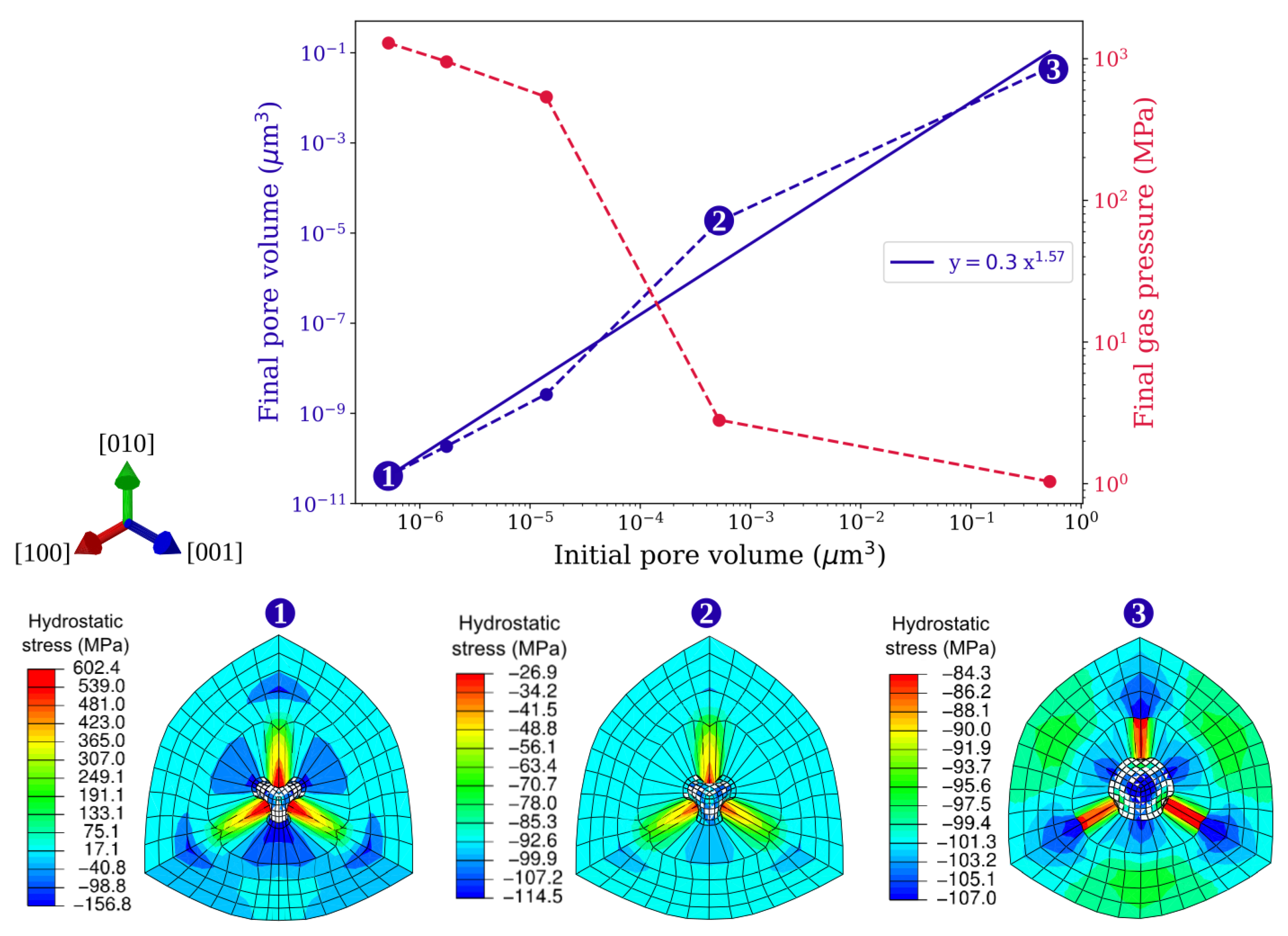
3.3. Influence of Pore Size
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HIP | Hot isostatic pressing |
| AM | Additive manufacturing |
| CP | Crystal plasticity |
References
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Bokstein, B.; Epishin, A.; Link, T.; Esin, V.; Rodin, A.; Svetlov, I. Model for the porosity growth in single-crystal nickel-base superalloys during homogenization. Scr. Mater. 2007, 57, 801–804. [Google Scholar] [CrossRef]
- Link, T.; Zabler, S.; Epishin, A.; Haibel, A.; Bansal, M.; Thibault, X. Synchrotron tomography of porosity in single-crystal nickel-base superalloys. Mater. Sci. Eng. A 2006, 425, 47–54. [Google Scholar] [CrossRef]
- Atkinson, H.; Davies, S. Fundamental aspects of hot isostatic pressing: An overview. Metall. Mater. Trans. A 2000, 31, 2981–3000. [Google Scholar] [CrossRef]
- Mälzer, G.; Hayes, R.; Mack, T.; Eggeler, G. Miniature Specimen Assessment of Creep of the Single-Crystal Superalloy LEK 94 in the 1000 Temperature Range. Metall. Mater. Trans. A 2007, 38, 314–327. [Google Scholar] [CrossRef]
- Wangyao, P.; Lothongkum, G.; Krongtong, V.; Homkrajai, W.; Chuankrerkkul, N. Microstructural Restoration by HIP and Heat Treatment Processes in Cast Nickel Based Superalloy, IN-738. Chiang Mai J. Sci. 2009, 36, 287–295. [Google Scholar]
- Bor, H.; Hsu, C.; Wei, C. Influence of hot isostatic pressing on the fracture transitions in the fine grain MAR-M247 superalloys. Mater. Chem. Phys. 2004, 84, 284–290. [Google Scholar] [CrossRef]
- Kim, M.; Chang, S.; Won, J. Effect of HIP process on the micro-structural evolution of a nickel-based superalloy. Mater. Sci. Eng. A 2006, 441, 126–134. [Google Scholar] [CrossRef]
- Appa Rao, G.; Sankaranarayana, M.; Balasubramaniam, S. Hot Isostatic Pressing Technology for Defence and Space Applications. Def. Sci. J. 2012, 62, 73–80. [Google Scholar]
- Whitesell, H.; Overfelt, R. Influence of solidification variables on the microstructure, macrosegregation, and porosity of directionally solidified Mar-M247. Mater. Sci. Eng. A 2001, 318, 264–276. [Google Scholar] [CrossRef]
- Gu, D.D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Zhao, H.; Léonard, F.; Derguti, F.; Todd, I.; Prangnell, P. XCT analysis of the influence of melt strategies on defect population in Ti–6Al–4V components manufactured by Selective Electron Beam Melting. Mater. Charact. 2015, 102, 47–61. [Google Scholar] [CrossRef]
- Kasperovich, G.; Haubrich, J.; Gussone, J.; Requena, G. Correlation between porosity and processing parameters in TiAl6V4 produced by selective laser melting. Mater. Des. 2016, 105, 160–170. [Google Scholar] [CrossRef]
- Blackwell, P. The mechanical and microstructural characteristics of laser-deposited IN718. J. Mater. Process. Technol. 2005, 170, 240–246. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Elwany, A.; Bian, L. Effects of building orientation and heat treatment on fatigue behavior of selective laser melted 17-4 PH stainless steel. Int. J. Fatigue 2017, 94, 218–235. [Google Scholar] [CrossRef]
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Withers, P.J.; Todd, I.; Prangnell, P.B. The effectiveness of hot isostatic pressing for closing porosity in titanium parts manufactured by selective electron beam melting. Metall. Mater. Trans. A 2016, 47, 1939–1946. [Google Scholar] [CrossRef]
- Beretta, S.; Romano, S. A comparison of fatigue strength sensitivity to defects for materials manufactured by AM or traditional processes. Int. J. Fatigue 2017, 94, 178–191. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N. Additive manufacturing of fatigue resistant materials: Challenges and opportunities. Int. J. Fatigue 2017, 98, 14–31. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Withers, P.; Todd, I.; Prangnell, P. Porosity regrowth during heat treatment of hot isostatically pressed additively manufactured titanium components. Scr. Mater. 2016, 122, 72–76. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Link, T.; Feldmann, T.; Svetlov, I. Pore annihilation in a single-crystal nickel-base superalloy during hot isostatic pressing: Experiment and modelling. Mater. Sci. Eng. A 2013, 586, 342–349. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Nolze, G.; Schriever, S.; Feldmann, T.; Ijaz, M.F.; Viguier, B.; Poquillon, D.; Le Bouar, Y.; Ruffini, A. Creep of single crystals of nickel-based superalloys at ultra-high homologous temperature. Metall. Mater. Trans. A 2018, 49, 3973–3987. [Google Scholar] [CrossRef]
- Ashby, M.F. Mechanisms of deformation and fracture. Adv. Appl. Mech. 1983, 23, 117–177. [Google Scholar]
- ABAQUS. Analysis User’s Manual, Version 6.14. 2017. Available online: http://130.149.89.49:2080/v6.14/books/usb/default.htm (accessed on 16 December 2020).
- Lee, E. Elastic-plastic deformation at finite strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- MacEwan, J.R.; MacEwan, J.U.; Yaffe, L. Self-diffusion in polycrystalline Nickel. Can. J. Chem. 1959, 37, 1623–1628. [Google Scholar] [CrossRef]
- Stevens, R.A.; Flewitt, P.E.J. Hot isostatic pressing to remove porosity & creep damage. Mater. Des. 1982, 3, 461–469. [Google Scholar]
- Epishin, A.; Svetlov, I. Evolution of pore morphology in single-crystals of nickel-base superalloys. Inorg. Mater. Appl. Res. 2016, 7, 45–52. [Google Scholar] [CrossRef]
- Björck, A. Numerical Methods for Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Shao, S.; Mahtabi, M.J.; Shamsaei, N.; Thompson, S.M. Solubility of argon in laser additive manufactured α-titanium under hot isostatic pressing condition. Comput. Mater. Sci 2017, 131, 209–219. [Google Scholar] [CrossRef]
- Boom, R.; Kamperman, A.A.; Dankert, O.; Van Veen, A. Argon solubility in liquid steel. Metall. Mater. Trans. B 2000, 31, 913–919. [Google Scholar] [CrossRef]
| Parameter | Value | Unit |
|---|---|---|
| G | 69.4 | GPa |
| b | 0.254 | nm |
| 3.36 × 10 [26] | ||
| 292 [26] | ||
| A | 1.2 × 10 | - |
| 3.0 | - | |
| 0.05 | - | |
| 40 | MPa | |
| 600 | MPa | |
| 60 | MPa | |
| 60 | MPa | |
| 2.0 | - |
| (kg mol) | R (JKmol) | (MPa) | (MPa) | (K) |
|---|---|---|---|---|
| 0.039948 | 8.314 | 0 | 0.101 | 1728.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prasad, M.R.G.; Gao, S.; Vajragupta, N.; Hartmaier, A. Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys. Crystals 2020, 10, 1147. https://doi.org/10.3390/cryst10121147
Prasad MRG, Gao S, Vajragupta N, Hartmaier A. Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys. Crystals. 2020; 10(12):1147. https://doi.org/10.3390/cryst10121147
Chicago/Turabian StylePrasad, Mahesh R. G., Siwen Gao, Napat Vajragupta, and Alexander Hartmaier. 2020. "Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys" Crystals 10, no. 12: 1147. https://doi.org/10.3390/cryst10121147
APA StylePrasad, M. R. G., Gao, S., Vajragupta, N., & Hartmaier, A. (2020). Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys. Crystals, 10(12), 1147. https://doi.org/10.3390/cryst10121147






