Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation
Abstract
1. Introduction
2. γ’ Rafting Behavior in Superalloys
2.1. Types of Rafting
2.2. Kinetics of Rafting
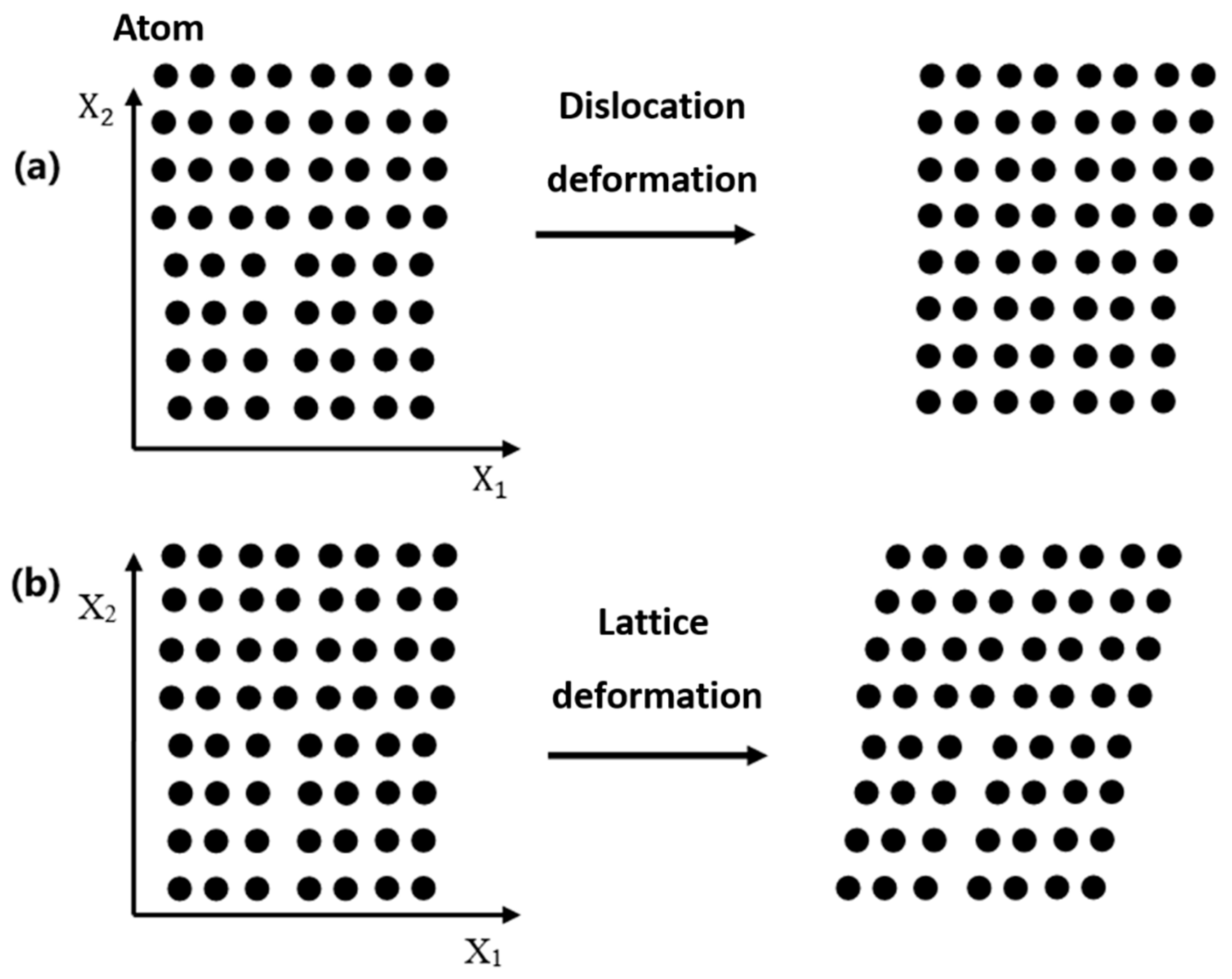
3. Crystal Plasticity Models
3.1. Crystal Plasticity Theory
3.2. Phenomenological Constitutive Models
3.3. Physics-Based Constitutive Models
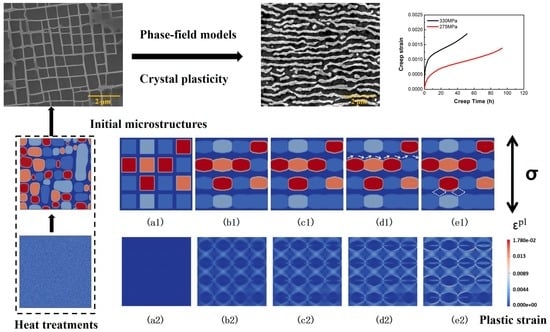
4. Phase-Field Models
4.1. Phase-Field Method
4.2. Ni-Al Binary System
4.3. Multiphase-Field Model
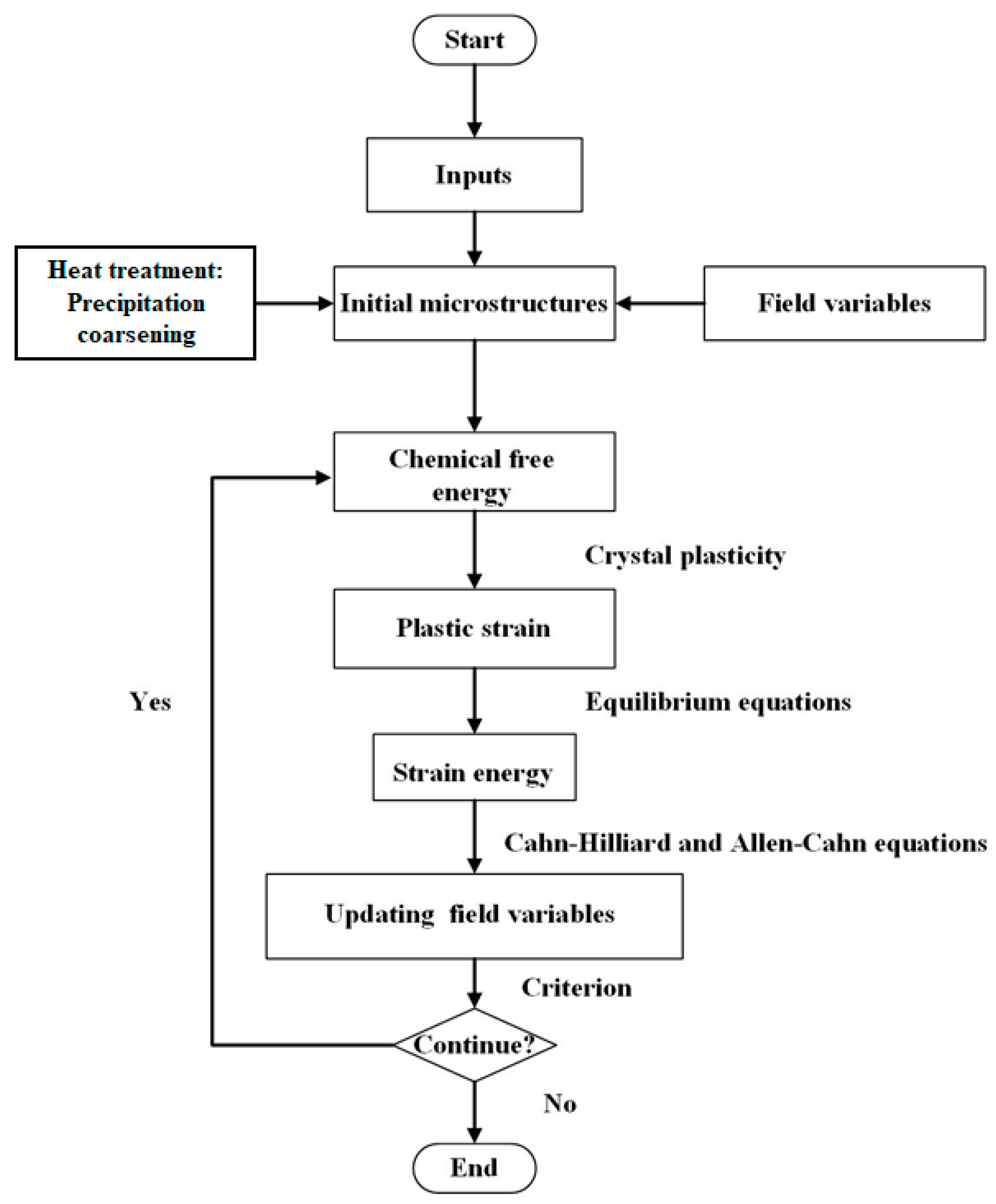
5. Application of Crystal Plasticity and Phase-Field Method in the Rafting Analysis
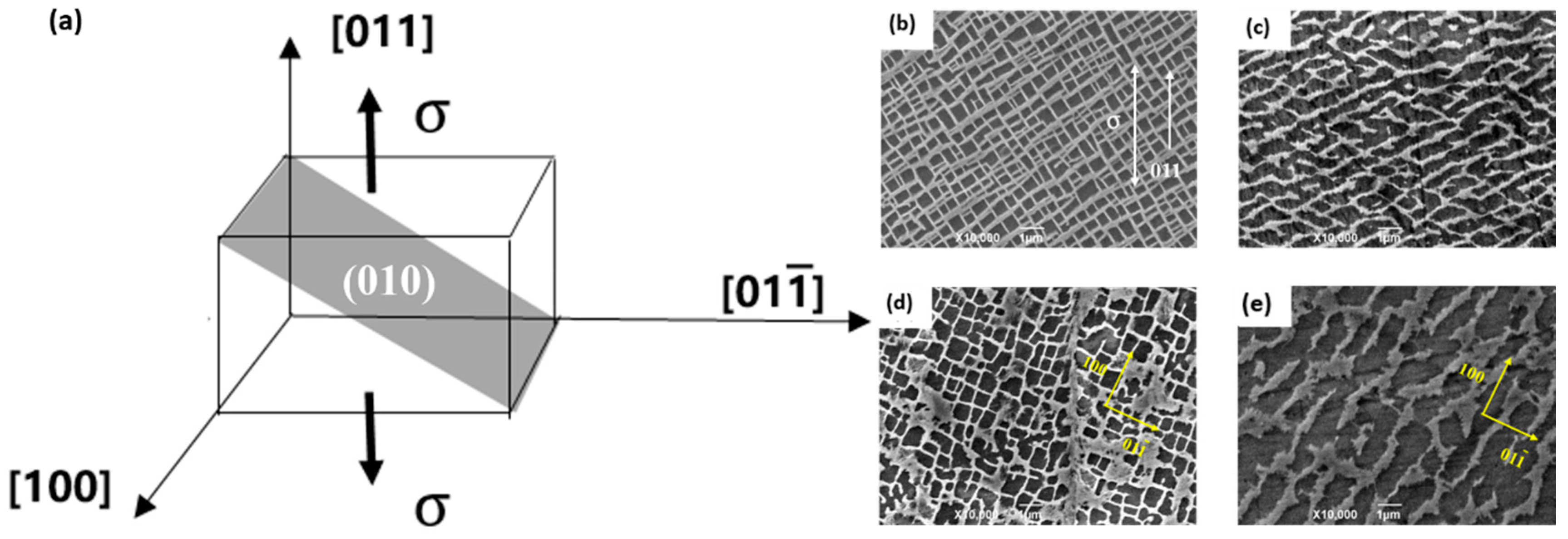
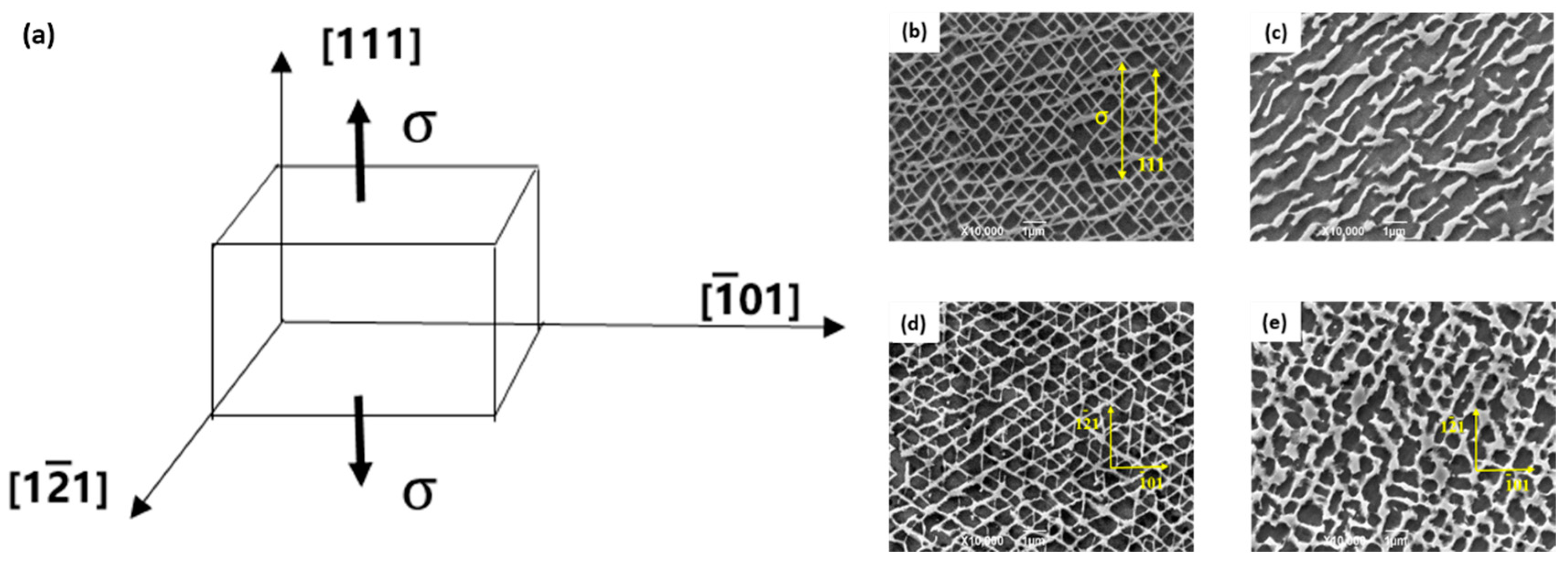
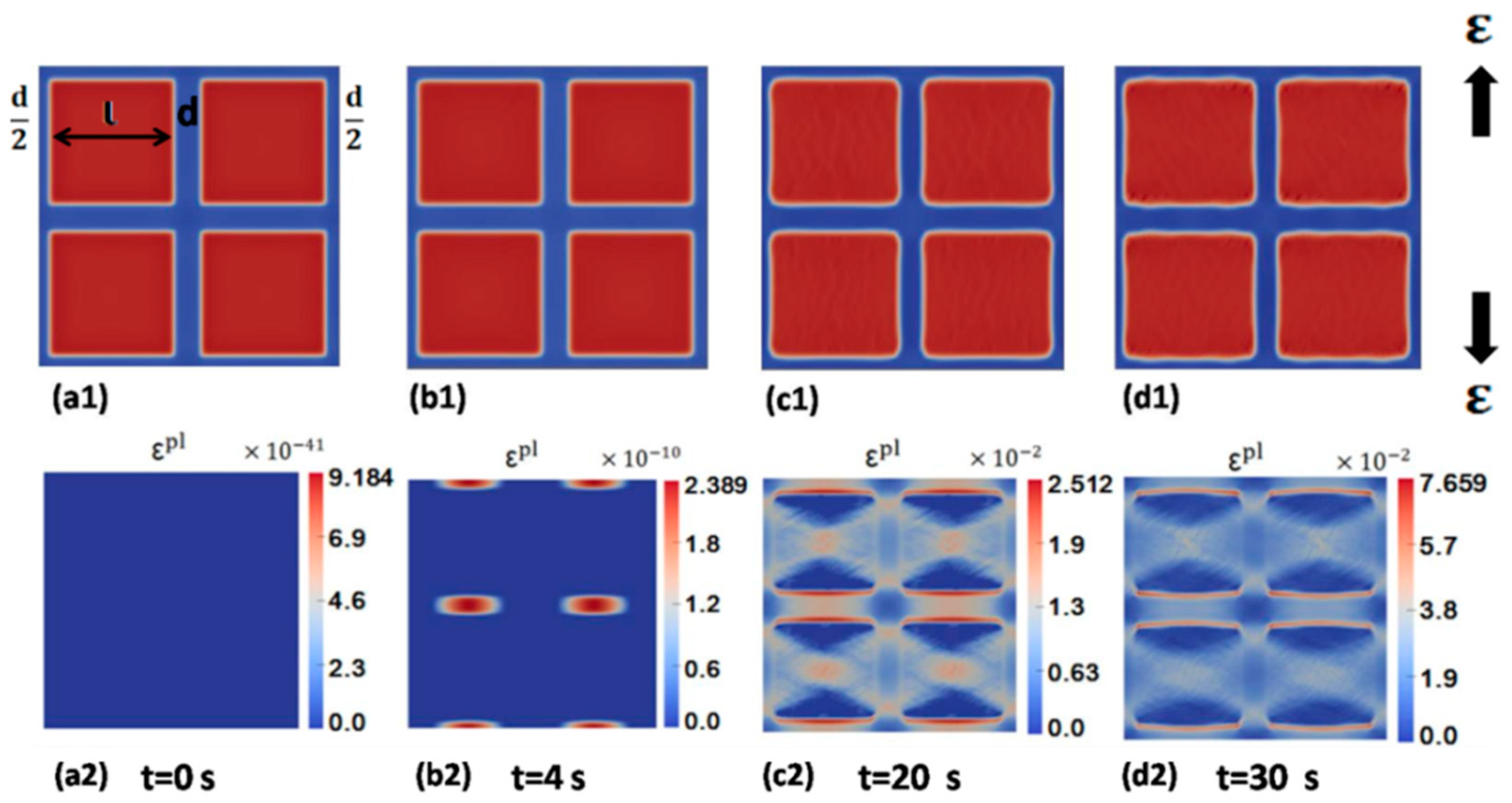
5.1. Uniaxial Tension
5.2. Creep Deformation
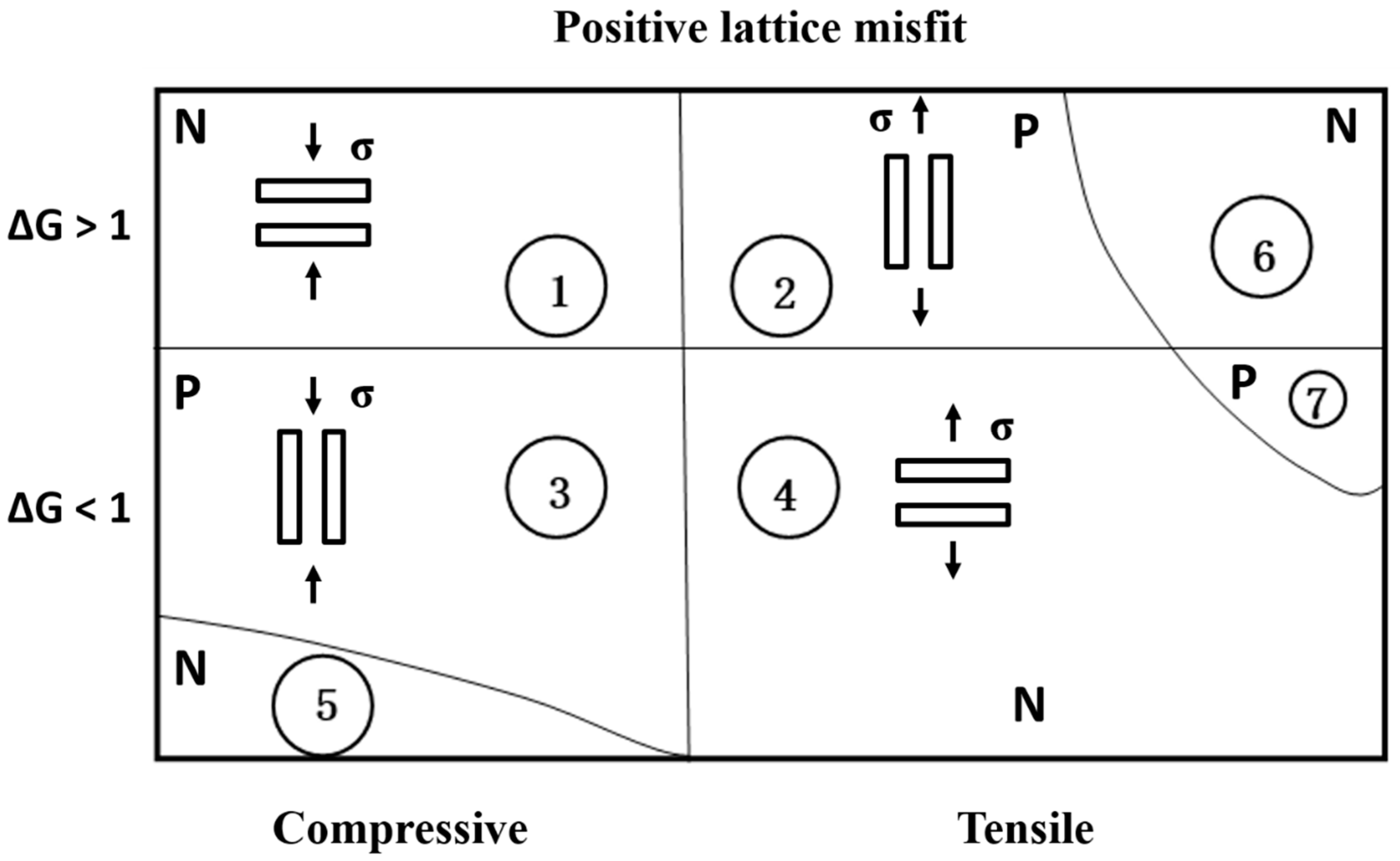
5.2.1. N-Type/P-Type Rafting
5.2.2. Complex Types of Rafting
5.2.3. Collapse and Topological Inversion
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Murakumo, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Creep behaviour of Ni-base single-crystal superalloys with various γ’ volume fraction. Acta Mater. 2004, 52, 3737–3744. [Google Scholar] [CrossRef]
- Yue, Q.; Liu, L.; Yang, W.; He, C.; Sun, D.; Huang, T.; Zhang, J.; Fu, H. Stress dependence of the creep behaviors and mechanisms of a third-generation Ni-based single crystal superalloy. J. Mater. Sci. Technol. 2019, 35, 752–763. [Google Scholar] [CrossRef]
- Xia, W.; Zhao, X.; Yue, L.; Zhang, Z. A review of composition evolution in Ni-based single crystal superalloys. J. Mater. Sci. Technol. 2020, 44, 76–95. [Google Scholar] [CrossRef]
- Pearson, D.; Lemkey, F.; Kear, B. Stress Coarsening of γ’ and its Influence on Creep Properties of a Single Crystal Superalloy. In Proceedings of the 4th International Symposium on Superallos, Champion, PA, USA, 21–25 September 1980; pp. 513–520. [Google Scholar]
- Henderson, P.J.; Mclean, M. Microstructural contributions to friction stress and recovery kinetics during creep of the nickel-base superalloy IN738LC. Acta Metall. 1983, 31, 1203–1219. [Google Scholar] [CrossRef]
- Pollock, T.M.; Argon, A.S. Directional coarsening in nickel-base single crystals with high volume fractions of coherent precipitates. Acta Metall. Mater. 1994, 42, 1859–1874. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, W.; Wen, Z.; Tong, W.; Zhang, Y.; Yue, Z.; He, P. Creep residual life prediction of a nickel-based single crystal superalloy based on microstructure evolution. Mater. Sci. Eng. A 2019, 756, 108–118. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, X.; Yue, Z.; Sun, S. Visco-plasticity phase-field simulation of the mechanical property and rafting behavior in nickel-based superalloys. Intermetallics 2020, 125, 106884. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Portella, P.D.; Bruckner, U. Evolution of the γ/γ’ microstructure during high-temperature creep of a nickel-base superalloy. Acta Mater. 2000, 48, 4169–4177. [Google Scholar] [CrossRef]
- Wu, W.P.; Li, S.Y.; Li, Y.L. An anisotropic elastic–plastic model for predicting the rafting behavior in Ni-based single crystal superalloys. Mech. Mater. 2019, 132, 9–17. [Google Scholar] [CrossRef]
- Fratzl, P.; Paris, O. Strain-induced morphologies during homogeneous phase separation in alloys. Phase Transit. 1999, 67, 707–724. [Google Scholar] [CrossRef]
- Gaubert, A.; le Bouar, Y.; Finel, A. Coupling phase field and viscoplasticity to study rafting in Ni-based superalloys. Philos. Mag. 2010, 90, 375–404. [Google Scholar] [CrossRef]
- Boussinot, G.; le Bouar, Y.; Finel, A. Phase-field simulations with inhomogeneous elasticity: Comparison with an atomic-scale method and application to superalloys. Acta Mater. 2010, 58, 4170–4181. [Google Scholar] [CrossRef]
- Kundin, J.; Mushongera, L.; Goehler, T.; Emmerich, H. Phase-field modeling of the γ’-coarsening behavior in Ni-based superalloys. Acta Mater. 2012, 60, 3758–3772. [Google Scholar] [CrossRef]
- Cottura, M.; le Bouar, Y.; Appolaire, B.; Finel, A. Rôle of elastic inhomogeneity in the development of cuboidal microstructures in Ni-based superalloys. Acta Mater. 2015, 94, 15–25. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.; Wang, Y.Z. Large-scale three-dimensional phase field simulation of γ’-rafting and creep deformation. Philos. Mag. 2010, 90, 405–436. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, L.; Tong, J. Discrete dislocation dynamics modelling of mechanical deformation of nickel-based single crystal superalloys. Int. J. Plast. 2012, 28, 141–158. [Google Scholar] [CrossRef]
- Wu, R.; Zaiser, M.; Sandfeld, S. A continuum approach to combined γ/γ’ evolution and dislocation plasticity in Nickel-based superalloys. Int. J. Plast. 2017, 95, 142–162. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, J.; Wei, H.; Gui, W.M.; Su, H.J.; Jin, T.; Liu, L. A phase-field model for creep behavior in nickel-base single-crystal superalloy: Coupled with creep damage. Scr. Mater. 2018, 147, 16–20. [Google Scholar] [CrossRef]
- Tsukada, Y.; Koyama, T.; Kubota, F.; Murata, Y.; Kondo, Y. Phase-field simulation of rafting kinetics in a nickel-based single crystal superalloy. Intermetallics 2017, 85, 187–196. [Google Scholar] [CrossRef]
- Jokisaari, A.M.; Naghavi, S.S.; Wolverton, C.; Voorhees, P.W.; Heinonen, O.G. Predicting the morphologies of γʹ precipitates in cobalt-based superalloys. Acta Mater. 2017, 141, 273–284. [Google Scholar] [CrossRef]
- Wang, C.; Ali, M.A.; Gao, S.; Goerler, J.V.; Steinbach, I. Combined phase-field crystal plasticity simulation of P- and N-type rafting in Co-based superalloys. Acta Mater. 2019, 175, 21–34. [Google Scholar] [CrossRef]
- Tsao, T.K.; Yeh, A.C.; Kuo, C.M.; Kakehi, K.; Murakami, H.; Yeh, J.W.; Jian, S.R. The High Temperature Tensile and Creep Behaviors of High Entropy Superalloy. Sci. Rep. 2017, 7, 12658. [Google Scholar] [CrossRef] [PubMed]
- Sauza, D.J.; Dunand, D.C.; Seidman, D.N. Microstructural evolution and high-temperature strength of a γ(fcc)/γ’(L12) Co–Al–W–Ti–B superalloy. Acta Mater. 2019, 174, 427–438. [Google Scholar] [CrossRef]
- Schmidt, I.; Gross, D. Directional coarsening in Ni–base superalloys: Analytical results for an elasticity–based model. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 3085–3106. [Google Scholar] [CrossRef]
- Gururajan, M.P.; Abinandanan, T.A. Phase field study of precipitate rafting under a uniaxial stress. Acta Mater. 2007, 55, 5015–5026. [Google Scholar] [CrossRef]
- Ott, M.; Mughrabi, H. Dependence of the high-temperature low-cycle fatigue behaviour of the monocrystalline nickel-base superalloys CMSX-4 and CMSX-6 on the γ/γ’-morphology. Mater. Sci. Eng. A 1999, 272, 24–30. [Google Scholar] [CrossRef]
- Mughrabi, H.; Tetzlaff, U. Microstructure and High-Temperature Strength of Monocrystalline Nickel-Base Superalloys. Adv. Eng. Mater. 2000, 2, 319–326. [Google Scholar] [CrossRef]
- Shui, L.; Jin, T.; Tian, S.; Hu, Z. Influence of precipitate morphology on tensile creep of a single crystal nickel-base superalloy. Mater. Sci. Eng. A 2007, 454, 461–466. [Google Scholar] [CrossRef]
- Tian, S.G.; Wang, M.G.; Yu, H.C.; Yu, X.F.; Li, T.; Qian, B.J. Influence of element Re on lattice misfits and stress rupture properties of single crystal nickel-based superalloys. Mater. Sci. Eng. A 2010, 527, 4458–4465. [Google Scholar]
- Mughrabi, H. The importance of sign and magnitude of γ/γ’ lattice misfit in superalloys—With special reference to the new γ’-hardened cobalt-base superalloys. Acta Mater. 2014, 81, 21–29. [Google Scholar] [CrossRef]
- Yu, J.; Sun, Y.; Sun, X.; Jin, T.; Hu, Z. Anisotropy of high cycle fatigue behavior of a Ni-base single crystal superalloy. Mater. Sci. Eng. A 2013, 566, 90–95. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, D.; Li, S.; Yue, Z.; Gao, J. Anisotropic creep damage and fracture mechanism of nickel-base single crystal superalloy under multiaxial stress. J. Alloys Compd. 2017, 692, 301–312. [Google Scholar] [CrossRef]
- Fan, Y.N.; Shi, H.J.; Qiu, W.H. Constitutive modeling of creep behavior in single crystal superalloys: Effects of rafting at high temperatures. Mater. Sci. Eng. A 2015, 644, 225–233. [Google Scholar] [CrossRef]
- Han, G.M.; Yu, J.J.; Hu, Z.Q.; Sun, X.F. Creep property and microstructure evolution of a nickel-base single crystal superalloy in orientation. Mater. Charact. 2013, 86, 177–184. [Google Scholar] [CrossRef]
- Yu, H.C.; Su, Y.; Tian, N.; Tian, S.G.; Li, Y.; Yu, X.F.; Yu, L.L. Microstructure evolution and creep behavior of a oriented single crystal nickel-based superalloy during tensile creep. Mater. Sci. Eng. A 2013, 565, 292–300. [Google Scholar] [CrossRef]
- Chatterjee, D.; Hazari, N.; Das, N.; Mitra, R. Microstructure and creep behavior of DMS4-type nickel based superalloy single crystals with orientations near <001> and <011>. Mater. Sci. Eng. A 2010, 528, 604–613. [Google Scholar] [CrossRef]
- Tian, S.; Su, Y.; Yu, L.; Yu, H.; Zhang, S.; Qian, B. Microstructure evolution of a orientation single crystal nickel-base superalloy during tensile creep. Appl. Phys. A 2011, 104, 643–647. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Zhang, G.; Zheng, W.; Qi, D.; Du, K.; Zhang, J.; Lou, L. Creep deformation related to γ’ phase cutting at high temperature of a oriented nickel-base single crystal superalloy. Mater. Sci. Eng. A 2019, 763, 138162. [Google Scholar] [CrossRef]
- Kamaraj, M. Rafting in single crystal nickel-base superalloys—An overview. Sadhana 2003, 28, 115–128. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Yang, C.; Xu, Q.Y. Numerical simulation of microstructure evolution in Ni-based superalloys during P-type rafting using multiphase-field model and crystal plasticity. Comput. Mater. Sci. 2020, 172, 109331. [Google Scholar] [CrossRef]
- Mushongera, L.T.; Fleck, M.; Kundin, J.; Wang, Y.; Emmerich, H. Effect of Re on directional γ’-coarsening in commercial single crystal Ni-base superalloys: A phase field study. Acta Mater. 2015, 93, 60–72. [Google Scholar] [CrossRef]
- Tian, S.G.; Zhang, S.; Liang, F.S.; Li, A.A.; Li, J.J. Microstructure evolution and analysis of a single crystal nickel-based superalloy during compressive creep. Mater. Sci. Eng. A 2011, 528, 4988–4993. [Google Scholar] [CrossRef]
- Fedelich, B.; Künecke, G.; Epishin, A.; Link, T.; Portella, P. Constitutive modelling of creep degradation due to rafting in single-crystalline Ni-base superalloys. Mater. Sci. Eng. A 2009, 510, 273–277. [Google Scholar] [CrossRef]
- Tinga, T.; Brekelmans, W.; Geers, M. Directional coarsening in nickel-base superalloys and its effect on the mechanical properties. Comput. Mater. Sci. 2009, 47, 471–481. [Google Scholar] [CrossRef]
- Caron, P.; Ramusat, C.; Diologent, F. Influence of the γ’ fraction on the γ/γ’ topological inversion during high temperature creep of single crystal superalloys. In Proceedings of the 11th International Symposium on Superalloys: SUPERALLOYS 2008, Seven Springs, PA, USA, 14–18 September 2008; pp. 159–167. [Google Scholar]
- Bergonnier, S.; Hild, F.; Roux, S. Local anisotropy analysis for non-smooth images. Pattern Recognit. 2007, 40, 544–556. [Google Scholar] [CrossRef][Green Version]
- Caccuri, V.; Desmorat, R.; Cormier, J. Tensorial nature of γ’-rafting evolution in nickel-based single crystal superalloys. Acta Mater. 2018, 158, 138–154. [Google Scholar] [CrossRef]
- Nguyen, L.; Shi, R.P.; Wang, Y.Z.; de Graef, M. Quantification of rafting of γ’ precipitates in Ni-based superalloys. Acta Mater. 2016, 103, 322–333. [Google Scholar] [CrossRef]
- Desmorat, R.; Mattiello, A.; Cormier, J. A tensorial thermodynamic framework to account for the γ’ rafting in nickel-based single crystal superalloys. Int. J. Plast. 2017, 95, 43–81. [Google Scholar] [CrossRef]
- Tinga, T.; Brekelmans, W.A.M.; Geers, M.G.D. Incorporating strain gradient effects in a multiscale constitutive framework for nickel-base superalloys. Philos. Mag. 2008, 88, 3793–3825. [Google Scholar] [CrossRef]
- Henderson, P.; Berglin, L.; Jansson, C. On rafting in a single crystal nickel-base superalloy after high and low temperature creep. Scr. Mater. 1998, 40, 229–234. [Google Scholar] [CrossRef]
- Matan, N.; Cox, D.; Rae, C.; Reed, R. On the kinetics of rafting in CMSX-4 superalloy single crystals. Acta Mater. 1999, 47, 2031–2045. [Google Scholar] [CrossRef]
- Taylor, C.F.E.G.I. The Distortion of an Aluminum Crystal during a Tensile Test. Proc. R. Soc. 1923, 102, 634–667. [Google Scholar]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Chowdhury, H.; Naumenko, K.; Altenbach, H. Aspects of power law flow rules in crystal plasticity with glide-climb driven hardening and recovery. Int. J. Mech. Sci. 2018, 146, 486–496. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation Mechanism Maps: The Plasticity and Creep of Metals and Ceramics; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Kamaraj, M.; Radhakrishnan, V. First Report on the Deformation Mechanism Mapping of First and Second Generation Ni-Based Single Crystal Super Alloys. Trans. Indian Inst. Metals 2017, 70, 2485–2496. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Bassani, J.L.; Wu, T.Y. Latent hardening in single crystals. II. Analytical characterization and predictions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 435, 21–41. [Google Scholar]
- Wang, X.M.; Hui, Y.Z.; Hou, Y.Y.; Yu, Z.Y.; Li, L.; Yue, Z.F.; Deng, C.H. Direct investigation on high temperature tensile and creep behavior at different regions of directional solidified cast turbine blades. Mech. Mater. 2019, 136, 103068. [Google Scholar] [CrossRef]
- Me’ric, L.; Poubanne, P.; Cailletaud, G. Single crystal modeling for structural calculations: Part 1—Model presentation. J. Eng. Mater. Technol. 1991, 113, 162–170. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Flewitt, P.; Smith, D.; Cocks, A.; Zhang, S. Quantifying internal stress and internal resistance associated with thermal ageing and creep in a polycrystalline material. Acta Mater. 2014, 67, 207–219. [Google Scholar] [CrossRef]
- Hoppe, R.; Appel, F. Origin and magnitude of internal stresses in TiAl alloys. In Gamma Titanium Aluminide Alloys 2014: A Collection of Research on Innovation and Commercialization of Gamma Alloy Technology; Wiley: Hoboken, NJ, USA, 2014; pp. 159–168. [Google Scholar]
- Kumar, A.V.; Yang, C. Study of work hardening models for single crystals using three dimensional finite element analysis. Int. J. Plast. 1999, 15, 737–754. [Google Scholar] [CrossRef]
- Cottura, M.; Appolaire, B.; Finel, A.; le Bouar, Y. Coupling the Phase Field Method for diffusive transformations with dislocation density-based crystal plasticity: Application to Ni-based superalloys. J. Mech. Phys. Solids 2016, 94, 473–489. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M.; Becker, R.; Bulatov, V.V. On the evolution of crystallographic dislocation density in non-homogeneously deforming crystals. J. Mech. Phys. Solids 2004, 52, 1213–1246. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M. Modeling the evolution of crystallographic dislocation density in crystal plasticity. J. Mech. Phys. Solids 2002, 50, 1979–2009. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling—Theory, experiments, and simulations. Acta Mater. 2006, 54, 2181–2194. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations. Acta Mater. 2006, 54, 2169–2179. [Google Scholar] [CrossRef]
- Fleck, N.; Muller, G.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Evers, L.; Brekelmans, W.; Geers, M. Non-local crystal plasticity model with intrinsic SSD and GND effects. J. Mech. Phys. Solids 2004, 52, 2379–2401. [Google Scholar] [CrossRef]
- Devincre, B.; Kubin, L.; Hoc, T. Physical analyses of crystal plasticity by DD simulations. Scr. Mater. 2006, 54, 741–746. [Google Scholar] [CrossRef]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Van der Waals, J.D. Thermodynamische Theorie der Kapillaritat unter voraussetzung stetiger Dichteanderung. Z. Phys. Chem. 1894, 13, 657–725. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Wang, Y.; Banerjee, D.; Su, C.; Khachaturyan, A. Field kinetic model and computer simulation of precipitation of L12 ordered intermetallics from fcc solid solution. Acta Mater. 1998, 46, 2983–3001. [Google Scholar] [CrossRef]
- Harikrishnan, R.; le Graverend, J.B. A creep-damage phase-field model: Predicting topological inversion in Ni-based single crystal superalloys. Mater. Des. 2018, 160, 405–416. [Google Scholar] [CrossRef]
- Amin, W.; Ali, M.A.; Vajragupta, N.; Hartmaier, A. Studying grain boundary strengthening by dislocation-based strain gradient crystal plasticity coupled with a multi-phase-field model. Materials 2019, 12, 2977. [Google Scholar] [CrossRef]
- Wang, J.C.; Osawa, M.; Yokokawa, T.; Harada, H.; Enomoto, M. Modeling the microstructural evolution of Ni-base superalloys by phase field method combined with CALPHAD and CVM. Comput. Mater. Sci. 2007, 39, 871–879. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.; Wheeler, A.; Murray, B.; Coriell, S.; Braun, R.; McFadden, G. Thermodynamically-consistent phase-field models for solidification. Phys. D Nonlinear Phenom. 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Tsukada, Y.; Murata, Y.; Koyama, T.; Morinaga, M. Phase-field simulation on the formation and collapse processes of the rafted structure in Ni-based superalloys. Mater. Trans. 2008, 49, 484–488. [Google Scholar] [CrossRef]
- Schleifer, F.; Holzinger, M.; Lin, Y.Y.; Glatzel, U.; Fleck, M. Phase-field modeling of γ/γ″ microstructure formation in Ni-based superalloys with high γ″ volume fraction. Intermetallics 2020, 120, 106745. [Google Scholar] [CrossRef]
- Gurtin, M.E. A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations. J. Mech. Phys. Solids 2002, 50, 5–32. [Google Scholar] [CrossRef]
- Steinbach, I.; Apel, M. Multi phase field model for solid state transformation with elastic strain. Phys. D Nonlinear Phenom. 2006, 217, 153–160. [Google Scholar] [CrossRef]
- Cottura, M.; le Bouar, Y.; Finel, A.; Appolaire, B.; Ammar, K.; Forest, S. A phase field model incorporating strain gradient viscoplasticity: Application to rafting in Ni-base superalloys. J. Mech. Phys. Solids 2012, 60, 1243–1256. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.J.; Wang, Y. Contributions from elastic inhomogeneity and from plasticity to γ’ rafting in single-crystal Ni–Al. Acta Mater. 2008, 56, 6156–6173. [Google Scholar] [CrossRef]
- Touratier, F.; Andrieu, E.; Poquillon, D.; Viguier, B. Rafting microstructure during creep of the MC2 nickel-based superalloy at very high temperature. Mater. Sci. Eng. A 2009, 510, 244–249. [Google Scholar] [CrossRef]
- Gaubert, A.; Jouiad, M.; Cormier, J.; le Bouar, Y.; Ghighi, J. Three-dimensional imaging and phase-field simulations of the microstructure evolution during creep tests of <011>-oriented Ni-based superalloys. Acta Mater. 2015, 84, 237–255. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, J.; Wei, H.; Zhao, Y.; Gui, W.; Su, H.; Jin, T.; Liu, L. Study of γ’ rafting under different stress states—A phase-field simulation considering viscoplasticity. J. Alloy. Compd. 2018, 769, 453–462. [Google Scholar] [CrossRef]
- Ali, M.A.; Amin, W.; Shchyglo, O.; Steinbach, I. 45-degree rafting in Ni-based superalloys: A combined phase-field and strain gradient crystal plasticity study. Int. J. Plast. 2020, 128, 102659. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, X.; Yue, Z. The effect of stress state on rafting mechanism and cyclic creep behavior of Ni-base superalloy. Mech. Mater. 2020, 149, 103563. [Google Scholar] [CrossRef]
- Goerler, J.V.; Lopez-Galilea, I.; Roncery, L.M.; Shchyglo, O.; Theisen, W.; Steinbach, I. Topological phase inversion after long-term thermal exposure of nickel-base superalloys: Experiment and phase-field simulation. Acta Mater. 2017, 124, 151–158. [Google Scholar] [CrossRef]


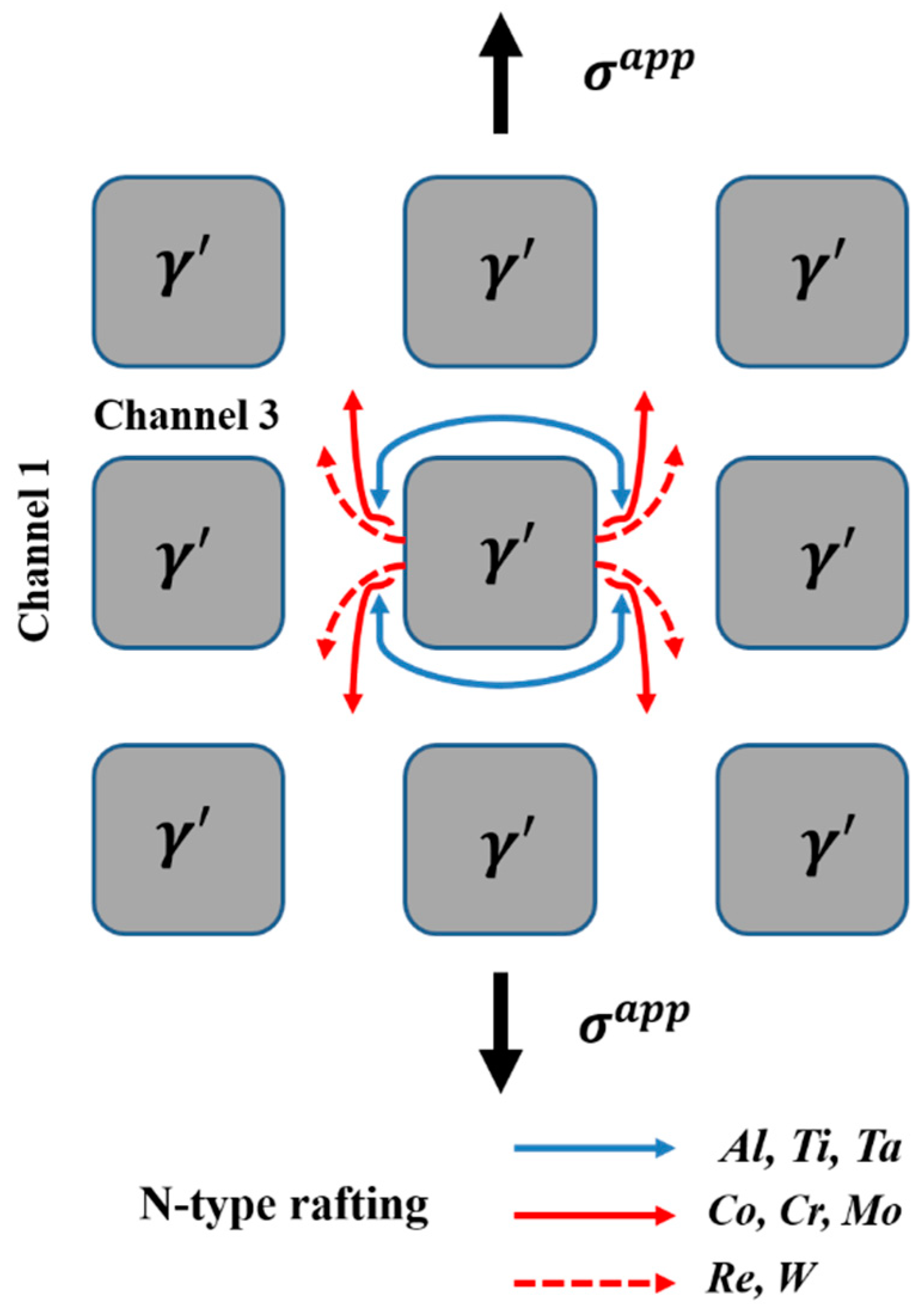

| Loading Diagram | Tension along <001> | Tension along <110> | Tension along <111> |
|---|---|---|---|
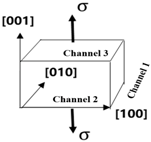 | 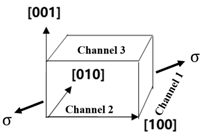 |  | |
| Channel 1 | |||
| Channel 2 | |||
| Channel 3 |
| Model | Pros and Cons | Application in the Rafting Analysis |
|---|---|---|
| Phenomenological constitutive models | Pros: Be cost-effective in determining material parameters and applicable in engineering calculations. Cons: Fail to capture the orientation dependence of the mechanical behavior of single crystals; difficult to experimentally verify the hardening rule used in the constitutive models. | Rafting with creep damage [8,19] |
| Physics-based constitutive models | Pros: Be able to model the microstructure evolution and include the contribution of dislocations. Cons: Fail to explicitly capture the motion of dislocations. | Coupling between rafting and crystal plasticity with dislocation densities [67] |
| Discrete dislocation dynamics models | Pros: Explicitly describe the dislocation distribution during microstructural evolution. Cons: Require sufficiently fine grid spacing and great computational cost in simulation. | Distribution of plastic strain in γ-channels and its effect on rafting [16] |
| Continuum dislocation dynamics models | Pros: Consider average distribution of dislocations and need less computational cost. Cons: Difficult to be compared with phenomenological constitutive models in engineering calculations. | Effect of initial dislocation density on rafting [18] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Wang, X.; Yang, F.; Yue, Z.; Li, J.C.M. Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals 2020, 10, 1095. https://doi.org/10.3390/cryst10121095
Yu Z, Wang X, Yang F, Yue Z, Li JCM. Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals. 2020; 10(12):1095. https://doi.org/10.3390/cryst10121095
Chicago/Turabian StyleYu, Zhiyuan, Xinmei Wang, Fuqian Yang, Zhufeng Yue, and James C. M. Li. 2020. "Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation" Crystals 10, no. 12: 1095. https://doi.org/10.3390/cryst10121095
APA StyleYu, Z., Wang, X., Yang, F., Yue, Z., & Li, J. C. M. (2020). Review of γ’ Rafting Behavior in Nickel-Based Superalloys: Crystal Plasticity and Phase-Field Simulation. Crystals, 10(12), 1095. https://doi.org/10.3390/cryst10121095