Stability-Ranking of Crystalline Ice Polymorphs Using Density-Functional Theory
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Abascal, J.L.F.; Sanz, E.; García Fernández, R.; Vega, C. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 2005, 122, 234511. [Google Scholar] [CrossRef] [PubMed]
- Salzmann, C.G. Advances in the experimental exploration of water’s phase diagram. J. Chem. Phys. 2019, 150, 060901. [Google Scholar] [CrossRef] [PubMed]
- Poirier, J.P. Rheology of ices: A key to the tectonics of the ice moons of Jupiter and Saturn. Nature 1982, 299, 683. [Google Scholar] [CrossRef]
- Futera, Z.; English, N.J. Pressure dependence of structural properties of ice VII: An ab initio molecular-dynamics study. J. Chem. Phys. 2018, 148, 204505. [Google Scholar] [CrossRef]
- Tammann, G. Ueber die Grenzen des festen Zustandes IV. Ann. Phys. 1900, 2, 1. [Google Scholar] [CrossRef]
- Bridgman, P.W. Water, in the Liquid and Five Solid Froms, under Pressure. Proc. Am. Acad. Arts Sci. 1912, 47, 441–558. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Hallbrucker, A.; Mayer, E.; Finney, J.L. The preparation and structures of hydrogen ordered phases of ice. Science 2006, 311, 1758–1761. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Mayer, E.; Finney, J.L. Ice XV: A new thermodynamically stable phase of ice. Phys. Rev. Lett. 2009, 103, 105701. [Google Scholar] [CrossRef]
- Falenty, A.; Hansen, T.C.; Kuhs, W.F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 2014, 516, 231. [Google Scholar] [CrossRef] [PubMed]
- Del Rosso, L.; Celli, M.; Ulivi, L. New porous water ice metastable at atmospheric pressure obtained by emptying a hydrogen-filled ice. Nat. Commun. 2016, 7, 13394. [Google Scholar] [CrossRef] [PubMed]
- Millot, M.; Coppari, F.; Rygg, J.R.; Barrios, A.C.; Hamel, S.; Swift, D.C.; Eggert, J.H. Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 2019, 569, 251. [Google Scholar] [CrossRef] [PubMed]
- Gillan, M.J.; Alfè, D.; Michaelides, A. Perspective: How good is DFT for water? J. Chem. Phys. 2016, 144, 130901. [Google Scholar] [CrossRef] [PubMed]
- Jenniskens, P.; Blake, D.F. Structural transitions in amorphous water ice and astrophysical implications. Science 1994, 265, 753–756. [Google Scholar] [CrossRef] [PubMed]
- Burnham, C.J.; English, N.J. Crystal Structure Prediction via Basin-Hopping Global Optimization Employing Tiny Periodic Simulation Cells, with Application to Water-Ice. J. Chem. Thoery Comput. 2019, 15, 3889–3900. [Google Scholar] [CrossRef]
- Oganov, A.R. Crystal structure prediction: reflections on present status and challenges. Faraday Discuss. 2018, 211, 643–660. [Google Scholar] [CrossRef]
- Desiraju, G.R. Supramolecular synthons in crystal engineering-a new organic synthesis. Angew. Chem. Int. Ed. 1995, 34, 2311–2327. [Google Scholar] [CrossRef]
- Desiraju, G.R. Crystal engineering: From molecule to crystal. J. Am. Chem. Soc. 2013, 135, 9952–9967. [Google Scholar] [CrossRef]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R. Report on the sixth blind test of organic crystal structure prediction methods. Acta Cryst. B 2016, 72, 439–459. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef]
- Stone, A. The Theory of Intermolecular Forces; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Stöhr, M.; Van Voorhis, T. Tkatchenko, A. Theory and practice of modeling van der Waals interactions in electronic-structure calculations. Chem. Soc. Rev. 2019, 48, 4118–4154. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; Di Stasio, R.A., Jr.; Car, R.; Scheffler, M. Accurate and efficient method for many-body van der Waals interactions. Phys. Rev. Lett. 2012, 108, 236402. [Google Scholar] [CrossRef] [PubMed]
- Steinmann, S.N.; Corminboeuf, C. A generalized-gradient approximation exchange hole model for dispersion coefficients. J. Chem. Phys. 2011, 134, 044117. [Google Scholar] [CrossRef] [PubMed]
- Steinmann, S.N.; Corminboeuf, C. Comprehensive benchmarking of a density-dependent dispersion correction. J. Chem. Theory Comput. 2011, 7, 3567–3577. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Burnham, C.J. Ice Structure Database. Available online: https://github.com/christianjburnham/ice_structures (accessed on 15 January 2020).
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Civalleri, B.; Roetti, C.; Saunders, V.R.; Zicovich-Wilson, C.M. CRYSTAL: A computational tool for the ab initio study of the electronic properties of crystals. Z. Kristallogr. Cryst. Mater. 2005, 220, 571–573. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.; Bush, I. CRYSTAL09 User’s Manual. University of Torino: Torino, Italy. Available online: http://www.crystal.unito.it (accessed on 15 January 2020).
- Pisani, C.; Busso, M.; Capecchi, G.; Casassa, S.; Dovesi, R.; Maschio, L.; Zicovich-Wilson, C.; Schütz, M. Local-MP2 electron correlation method for nonconducting crystals. J. Chem. Phys. 2005, 122, 094113. [Google Scholar] [CrossRef] [PubMed]
- Pisani, C.; Maschio, L.; Casassa, S.; Halo, M.; Schütz, M.; Usvyat, D. Periodic local MP2 method for the study of electronic correlation in crystals: Theory and preliminary applications. J. Comput. Chem. 2008, 29, 2113–2124. [Google Scholar] [CrossRef] [PubMed]
- Chaplin, M. Water Structure and Science. 2019. Available online: www1.lsbu.ac.uk/water (accessed on 15 January 2020).
- Londono, J.D.; Kuhs, W.F.; Finney, J.L. Neutron diffraction studies of ices III and IX on under-pressure and recovered samples. J. Chem. Phys. 1993, 98, 4878–4888. [Google Scholar] [CrossRef]
- Guo, Q.; Ghaani, M.R.; Nandi, P.K.; English, N.J. Pressure-Induced Densification of Ice Ih under Triaxial Mechanical Compression: Dissociation versus Retention of Crystallinity for Intermediate States in Atomistic and Coarse-Grained Water Models. J. Phys. Chem. Lett. 2018, 9, 5267–5274. [Google Scholar] [CrossRef] [PubMed]
- English, N.J.; Carroll, D.G. Prediction of Henry’s Law constants by a Quantitative Structure Property Relationship and neural networks. J. Chem. Inf. Comp. Sci. 2001, 41, 1150–1161. [Google Scholar] [CrossRef]
- English, N.J.; Lauricella, M.; Meloni, S. Massively-parallel molecular dynamics simulation of clathrate hydrate precursors at planar water-methane interfaces: insights into heterogeneous nucleation. J. Chem. Phys. 2014, 140, 204714. [Google Scholar] [CrossRef]
- Reddy, S.K.; Straight, S.C.; Bajaj, P.; Huy Pham, C.; Riera, M.; Moberg, D.R.; Morales, M.A.; Knight, C.; Götz, A.W.; Paesani, F. On the accuracy of the MB-pol many-body potelsntial for water: Interaction energies, vibrational frequencies, and classical thermodynamic and dynamical properties from clusters to liquid water and ice. J. Chem. Phys. 2016, 145, 194504. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.V.; Wu, X. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831. [Google Scholar] [CrossRef]
- Bartók, A.P.; Yates, J.R. Regularized SCAN functional. J. Chem. Phys. 2019, 150, 161101. [Google Scholar] [CrossRef]
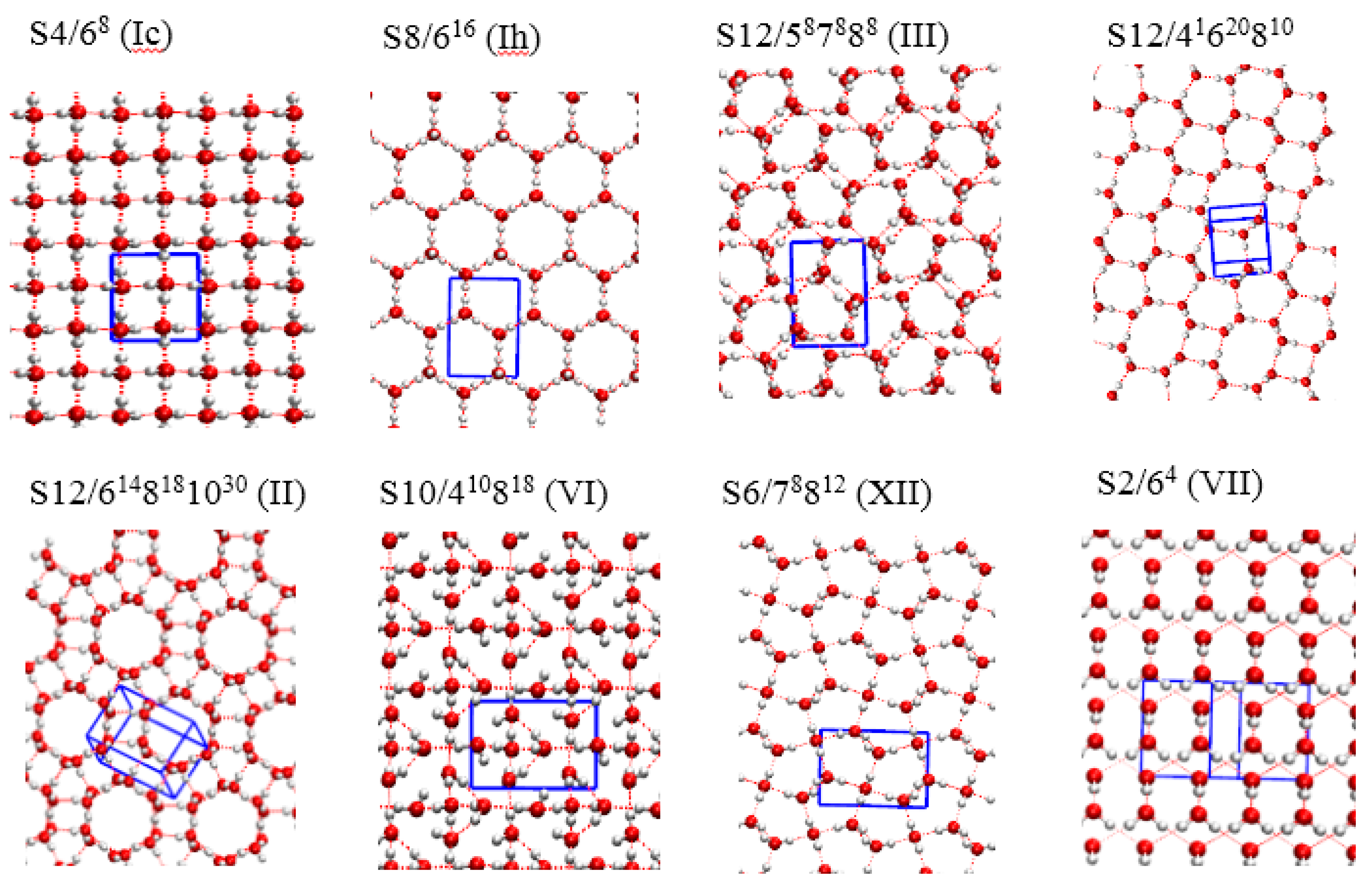
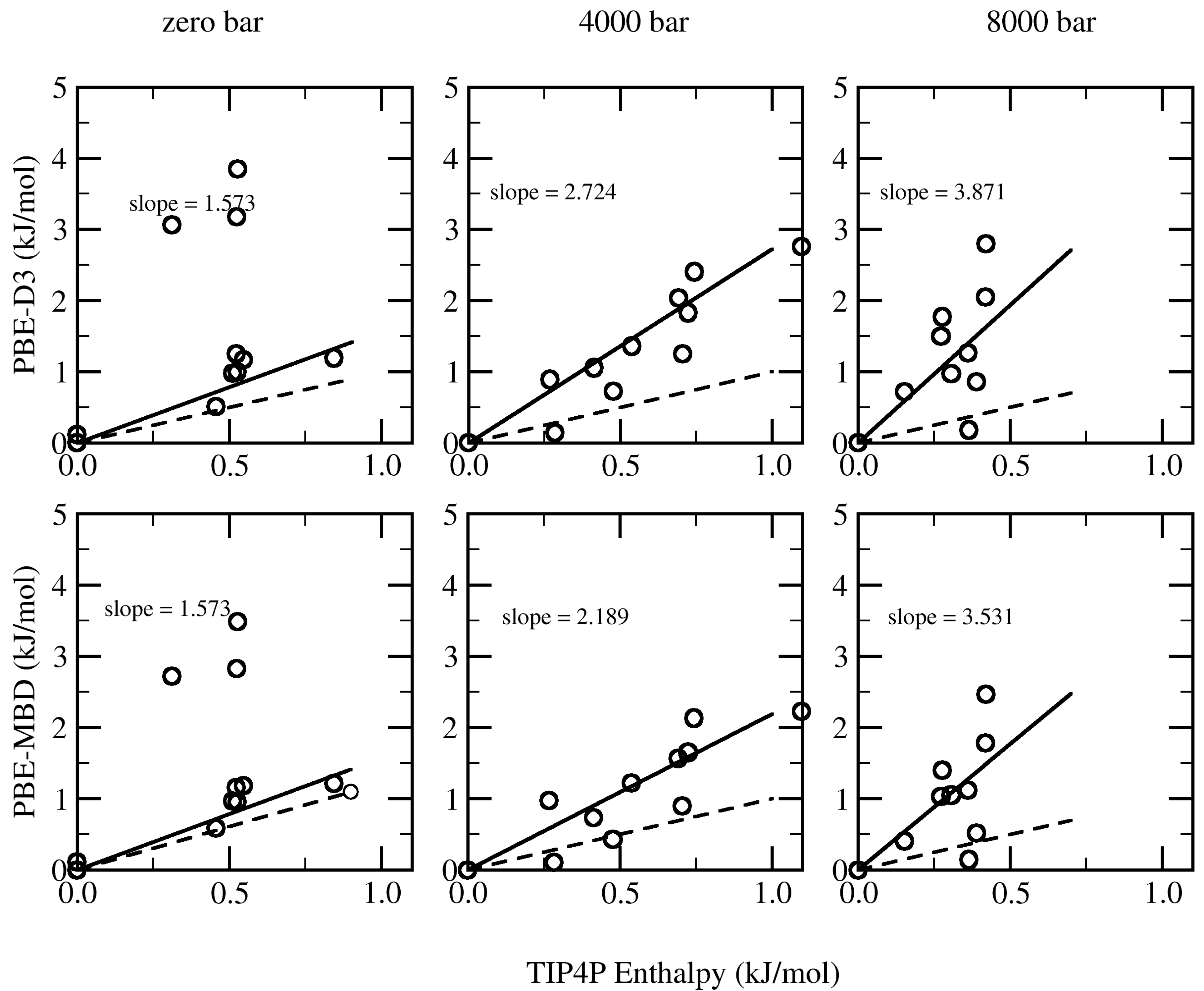
| Structure | TIP4P | PBE-D3 | PBE-MBD | PBE-dDsC |
|---|---|---|---|---|
| S8/616 (ice Ih) | 0.000 | 0.000 | 0.000 | 0.000 |
| S4/68 (ice Ic) | 0.000 | 0.113 | 0.129 | −0.152 |
| S12/587888 (ice III) | 0.311 | 3.064 | 2.778 | 1.212 |
| S12/41620810 | 0.457 | 0.508 | 0.525 | 0.656 |
| S14/526227286 | 0.511 | 0.975 | 0.967 | 0.908 |
| S14/62884 | 0.523 | 1.248 | 1.225 | 1.111 |
| S12/58627486 | 0.524 | 3.178 | 2.856 | 1.192 |
| S12/58647888 | 0.526 | 0.998 | 1.011 | 1.182 |
| S12/4254647886 | 0.527 | 3.851 | 3.640 | 2.245 |
| S12/5261678 | 0.547 | 1.166 | 1.127 | 1.018 |
| … | … | … | … | … |
| S6/5686 | 0.844 | 1.196 | 1.195 | 1.619 |
| Structure | TIP4P | PBE-D3 | PBE-MBD | PBE-dDsC |
|---|---|---|---|---|
| S12/587888 (ice III) | 0.000 | 0.000 | 0.000 | 0.000 |
| S12/4254647886 | 0.268 | 0.891 | 0.974 | 1.016 |
| S12/58627486 | 0.284 | 0.139 | 0.108 | 0.053 |
| S12/42688221030 | 0.414 | 1.056 | 0.733 | 0.089 |
| S12/6148181030 (ice II) | 0.477 | 0.725 | 0.431 | −0.023 |
| S12/5666748894 | 0.538 | 1.361 | 1.221 | 1.040 |
| S6/78812 | 0.692 | 2.037 | 1.561 | −0.502 |
| S14/44566486941024 | 0.706 | 1.250 | 0.898 | −0.018 |
| S14/57617981096101 | 0.724 | 1.830 | 1.649 | 0.947 |
| S10/546274816 | 0.744 | 2.406 | 2.131 | 1.113 |
| … | … | … | … | … |
| S10/410818 (ice VI) | 1.097 | 2.760 | 2.221 | 0.802 |
| Structure | TIP4P | PBE-D3 | PBE-MBD | PBE-dDsC |
|---|---|---|---|---|
| S12/587888 (ice III) | 0.000 | 0.000 | 0.000 | 0.000 |
| S12/42688221030 | 0.153 | 0.717 | 0.405 | −0.206 |
| S6/78812 (ice XII) | 0.272 | 1.497 | 1.030 | −1.005 |
| S14/61071682098 | 0.277 | 1.773 | 1.400 | 0.133 |
| S12/4254647886 | 0.306 | 0.973 | 1.053 | 1.065 |
| S12/5666748894 | 0.361 | 1.263 | 1.121 | 0.739 |
| S12/58627486 | 0.364 | 0.182 | 0.147 | 0.106 |
| S14/44566486941024 | 0.390 | 0.857 | 0.515 | 0.020 |
| S10/546274816 | 0.419 | 2.046 | 1.780 | 0.759 |
| S8/427482094 | 0.421 | 2.794 | 2.462 | 1.016 |
| … | … | … | … | … |
| S2/64 (ice VII) | 5.842 | 7.807 | 7.163 | 1.851 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samanta, P.K.; Burnham, C.J.; English, N.J. Stability-Ranking of Crystalline Ice Polymorphs Using Density-Functional Theory. Crystals 2020, 10, 40. https://doi.org/10.3390/cryst10010040
Samanta PK, Burnham CJ, English NJ. Stability-Ranking of Crystalline Ice Polymorphs Using Density-Functional Theory. Crystals. 2020; 10(1):40. https://doi.org/10.3390/cryst10010040
Chicago/Turabian StyleSamanta, Pralok K., Christian J. Burnham, and Niall J. English. 2020. "Stability-Ranking of Crystalline Ice Polymorphs Using Density-Functional Theory" Crystals 10, no. 1: 40. https://doi.org/10.3390/cryst10010040
APA StyleSamanta, P. K., Burnham, C. J., & English, N. J. (2020). Stability-Ranking of Crystalline Ice Polymorphs Using Density-Functional Theory. Crystals, 10(1), 40. https://doi.org/10.3390/cryst10010040






