Exploring Promising Catalysts for Chemical Hydrogen Storage in Ammonia Borane: A Density Functional Theory Study
Abstract
:1. Introduction
2. Computational Details
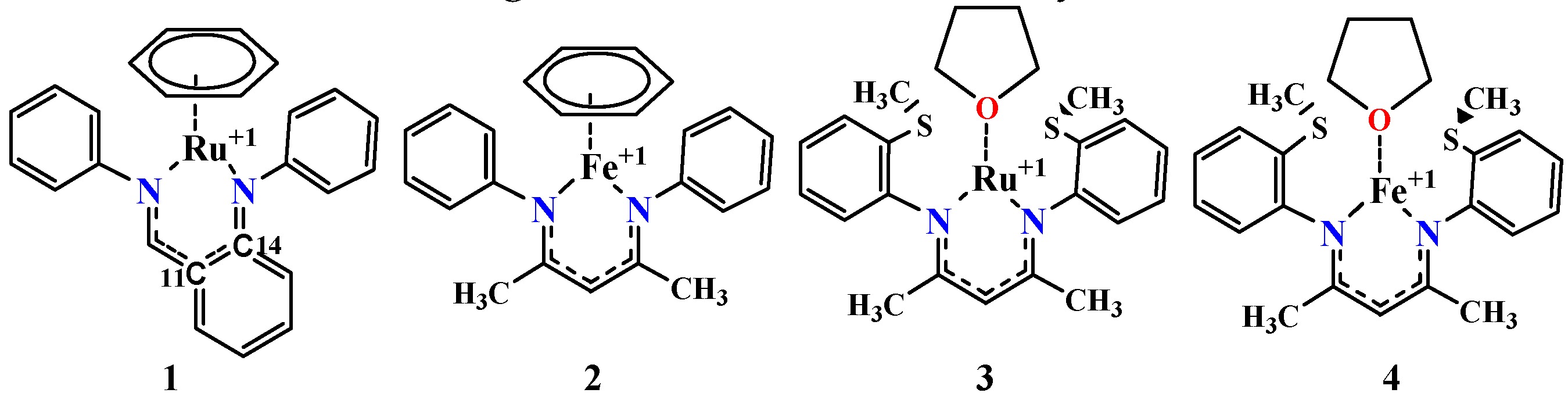
3. Results and Discussion
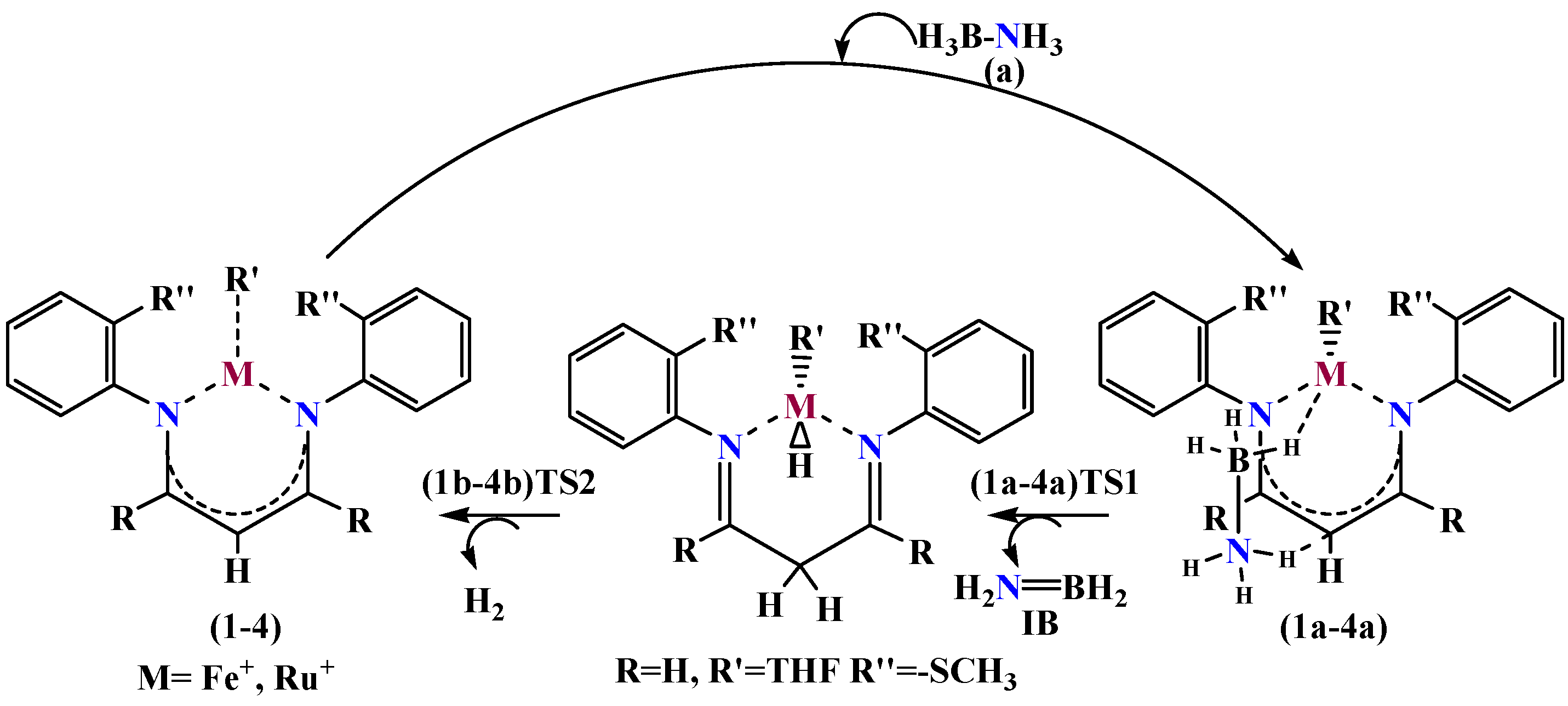
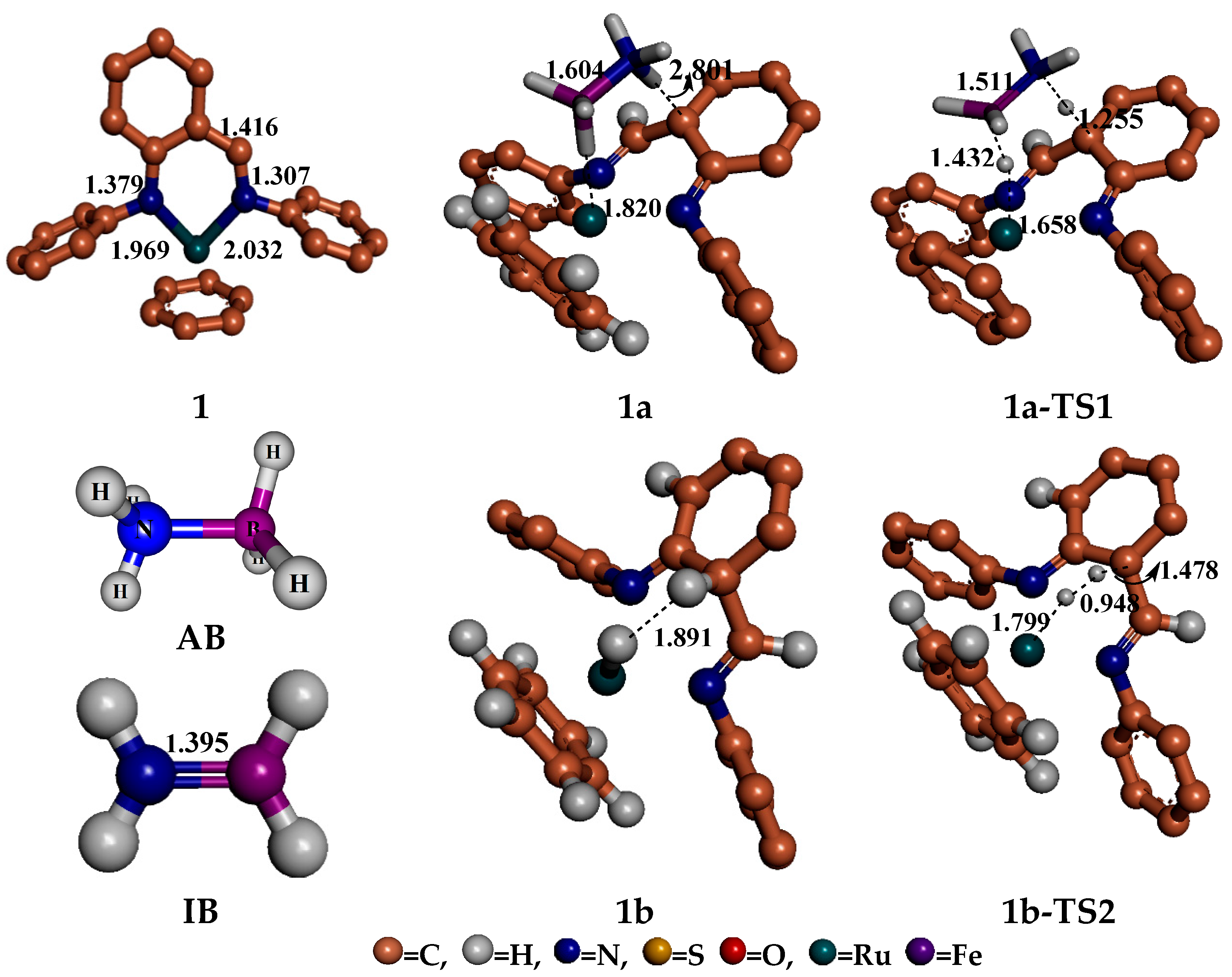
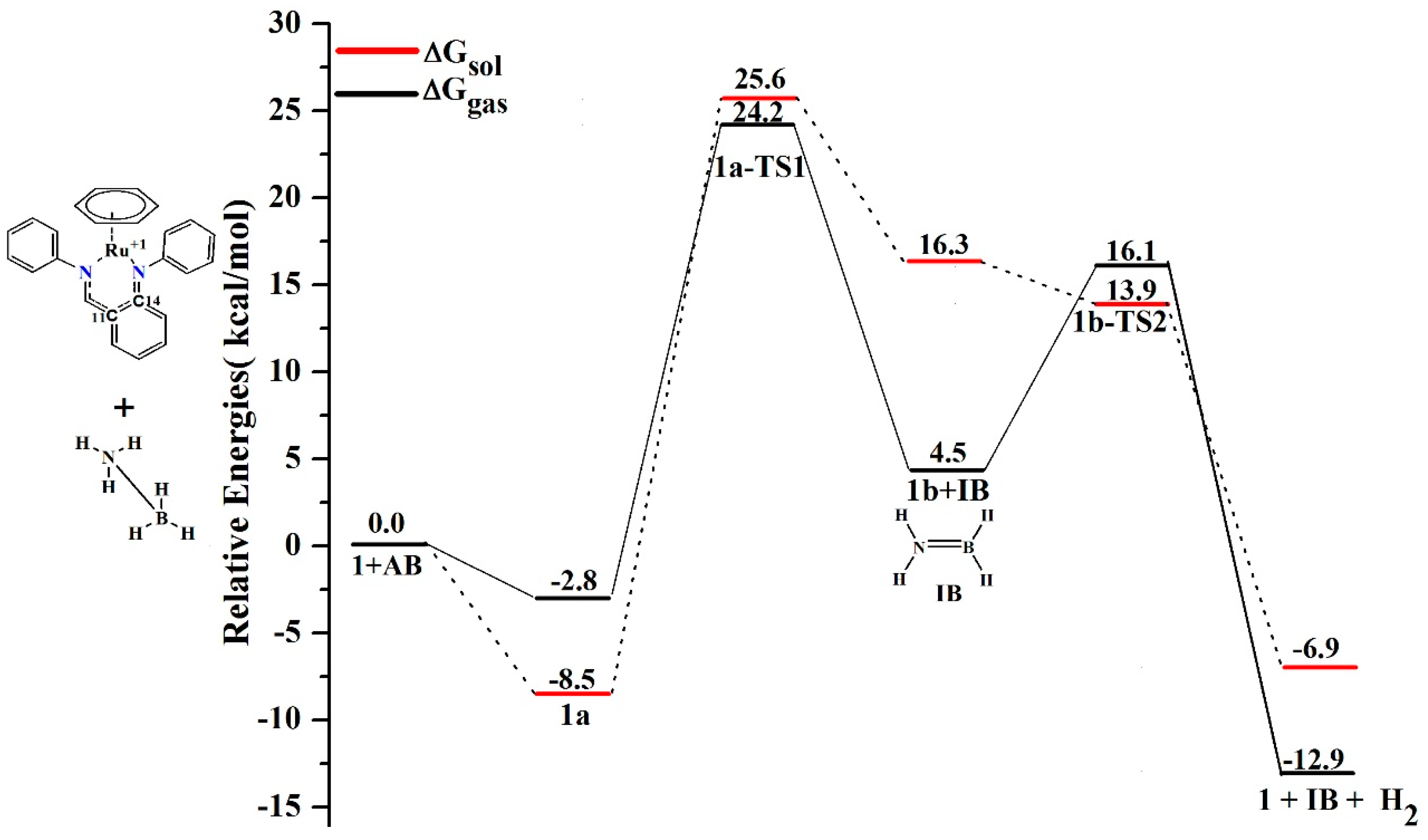
4. Mechanism for Catalyst “1” Addition to Ammonia Borane
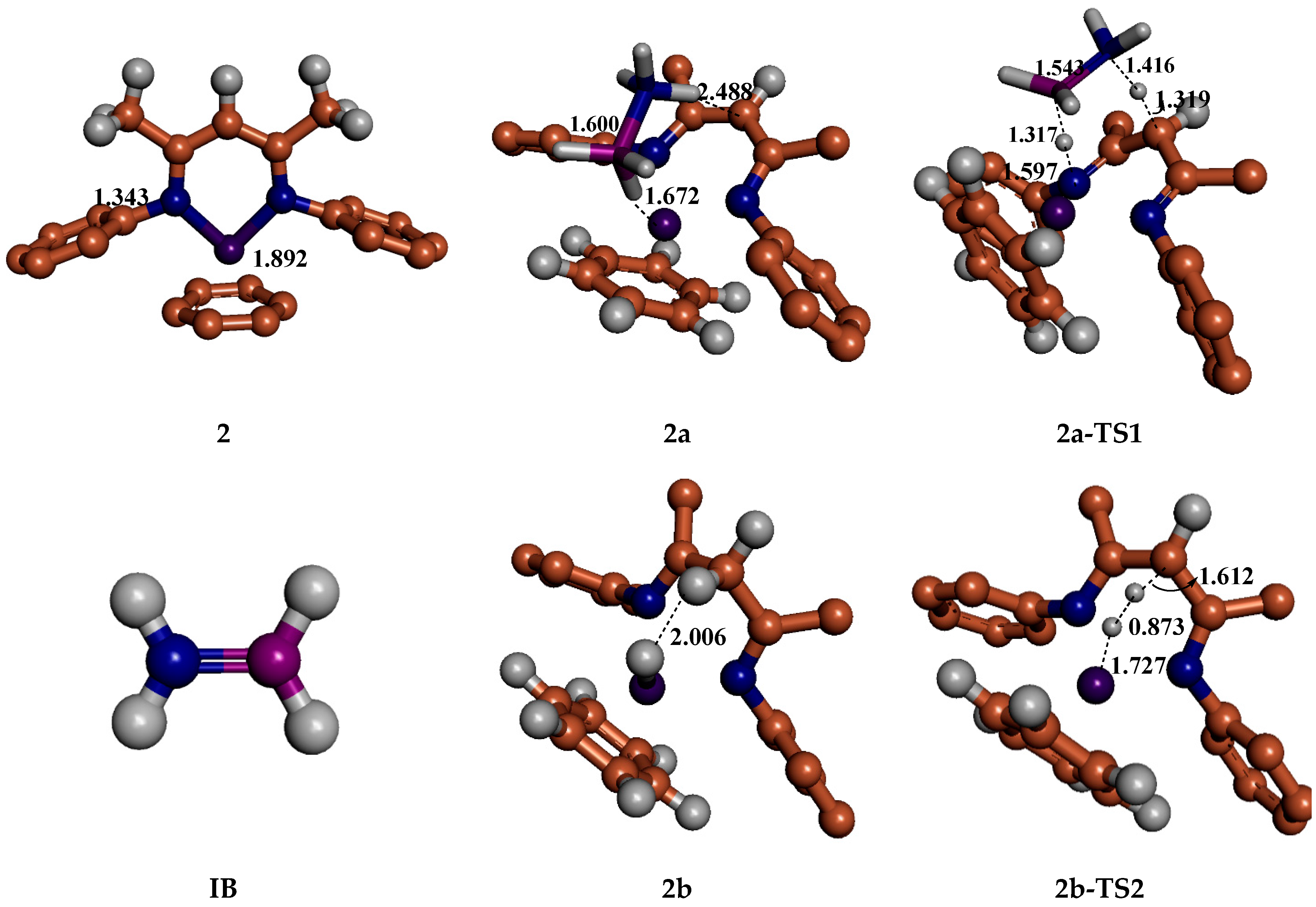
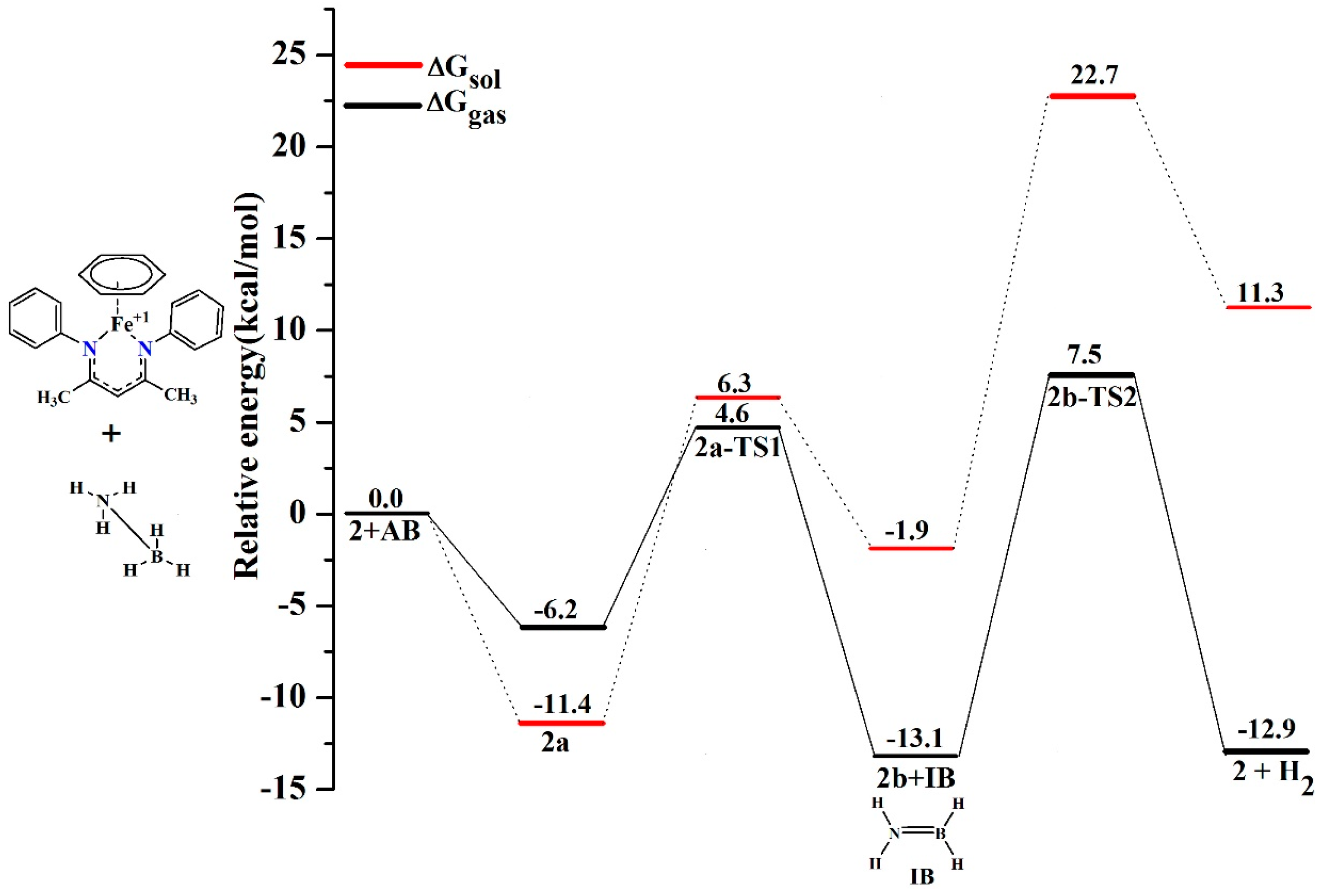
5. Mechanisms Involving Metal Catalyst “2” Addition to Ammonia Borane
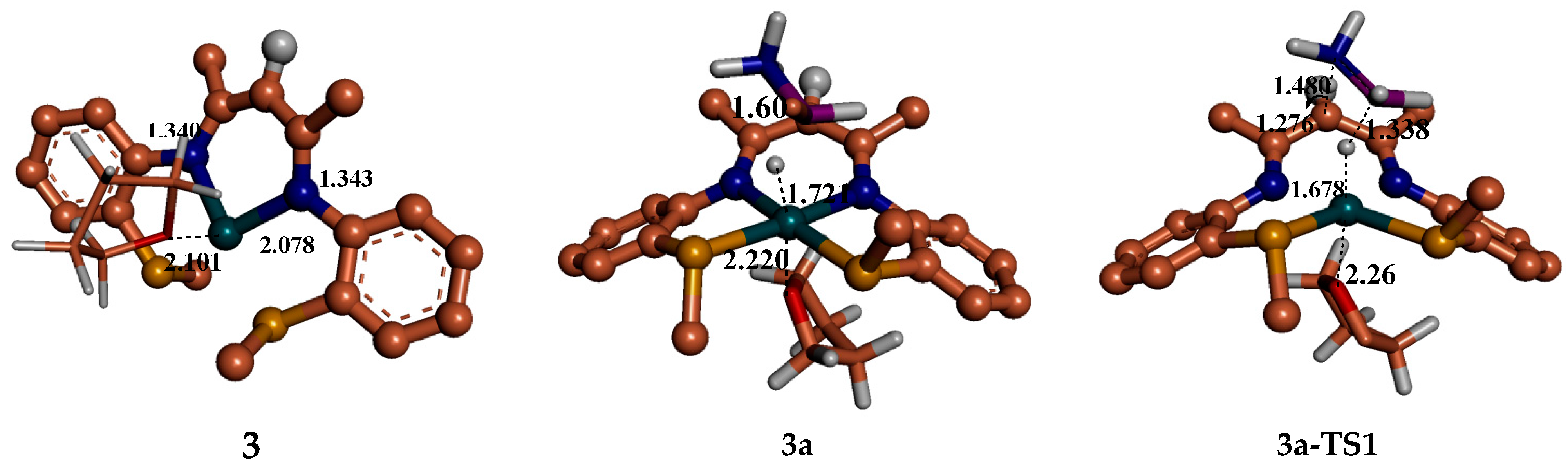
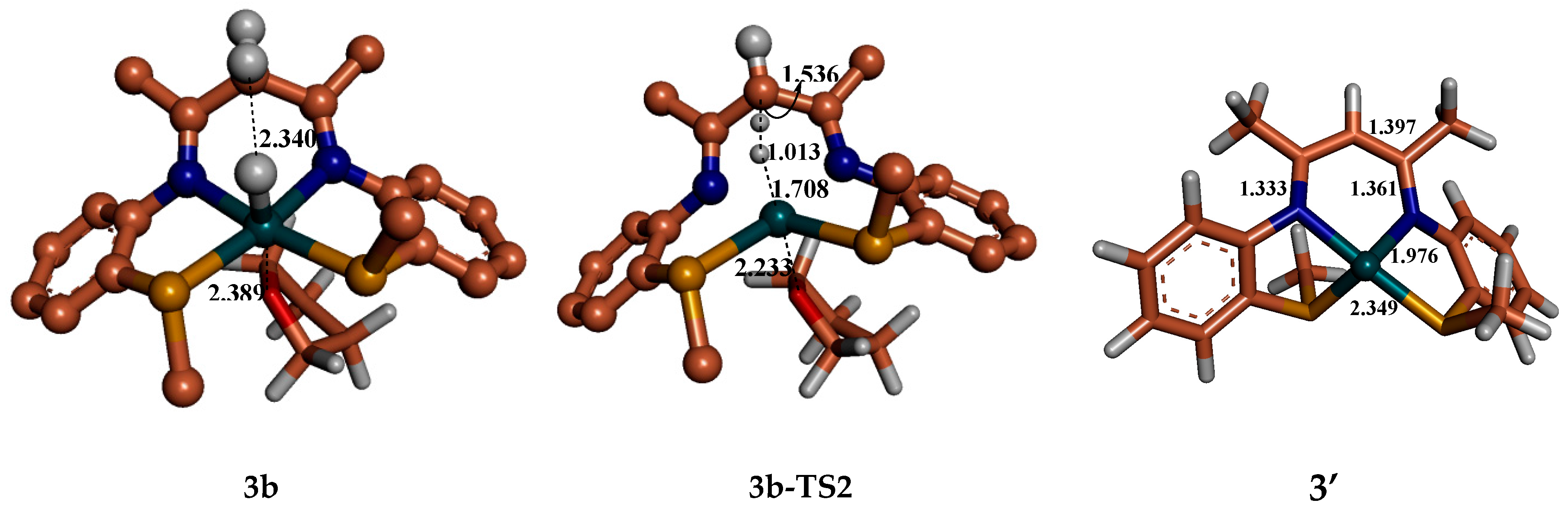
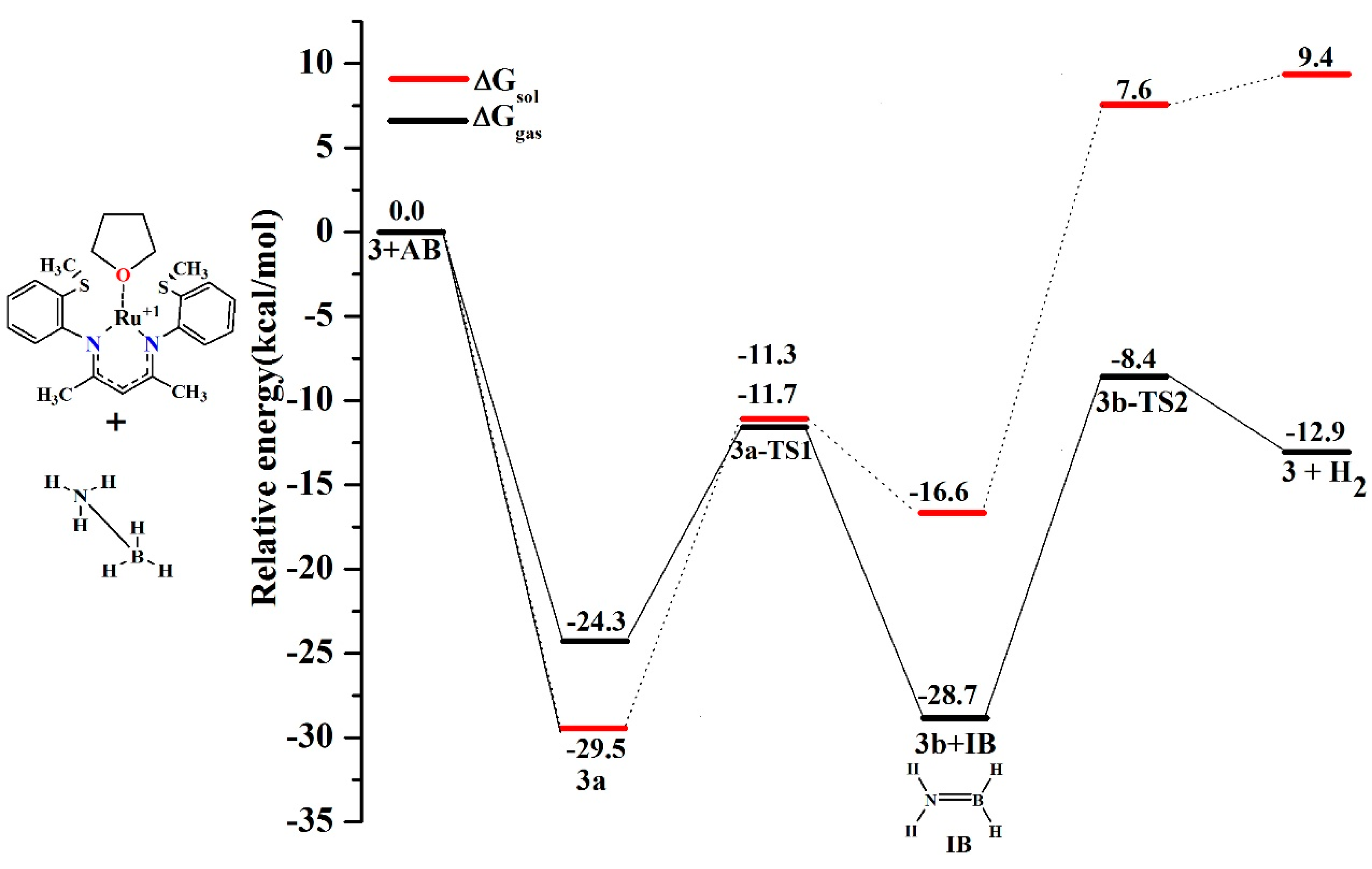
6. Mechanism Involving Metal Catalyst “3” and “4” Addition to Ammonia Borane
7. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coontz, R.; Hanson, B. Not So Simple. Science 2004, 305, 957. [Google Scholar] [CrossRef]
- Crabtree, G.W.; Dresselhaus, M.S.; Buchanan, M.V. The Hydrogen Economy. Phys. Today 2004, 57, 39–44. [Google Scholar] [CrossRef]
- Bandaru, S.; English, N.J.; MacElroy, J.M.D. Implicit and explicit solvent models for modeling a bifunctional arene ruthenium hydrogen-storage catalyst: A classical and ab initio molecular simulation study. J. Comput. Chem. 2014, 35, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.T.; Nguyen, V.S.; Matus, M.H.; Gopakumar, G.; Dixon, D.A. Molecular Mechanism for H2 Release from BH3NH3, Including the Catalytic Role of the Lewis Acid BH3. J. Phys. Chem. A 2007, 111, 679–690. [Google Scholar] [CrossRef] [PubMed]
- Aska, C.A.; Temple, K.; Lough, A.J.; Manners, I. Transition Metal-Catalyzed Formation of Boron−Nitrogen Bonds: Catalytic Dehydrocoupling of Amine-Borane Adducts to Form Aminoboranes and Borazines. J. Am. Chem. Soc. 2003, 125, 9424–9434. [Google Scholar]
- Stephens, F.H.; Baker, R.T.; Matus, M.H.; Grant, D.J.; Dixon, D.A. Acid Initiation of Ammonia–Borane Dehydrogenation for Hydrogen Storage. Angew. Chem. 2007, 119, 649–652. [Google Scholar] [CrossRef]
- Stephens, F.H.; Baker, R.T.; Matus, M.H.; Grant, D.J.; Dixon, D.A. Acid Initiation of Ammonia–Borane Dehydrogenation for Hydrogen Storage. Angew. Chem. Int. Ed. 2007, 46, 746–749. [Google Scholar] [CrossRef] [PubMed]
- Keaton, R.J.; Blacquiere, J.M.; Baker, R.T. Base Metal Catalyzed Dehydrogenation of Ammonia−Borane for Chemical Hydrogen Storage. J. Am. Chem. Soc. 2007, 129, 1844–1845. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fulton, J.L.; Linehan, J.L.; Autrey, T. In Situ XAFS and NMR Study of Rhodium-Catalyzed Dehydrogenation of Dimethylamine Borane. J. Am. Chem. Soc. 2005, 127, 3254–3255. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.J.; Russell, C.A.; Manners, I. Homogeneous, Titanocene-Catalyzed Dehydrocoupling of Amine−Borane Adducts. J. Am. Chem. Soc. 2006, 128, 9582–9583. [Google Scholar] [CrossRef] [PubMed]
- Denney, M.C.; Pons, V.; Hebden, T.J.; Heinekey, D.M.; Goldberg, K.J. Efficient Catalysis of Ammonia Borane Dehydrogenation. J. Am. Chem. Soc. 2006, 128, 12048–12049. [Google Scholar] [CrossRef] [PubMed]
- Bluhm, M.E.; Bradley, M.G.; Butterick, R.; Kusari, U.; Sneddon, L.G. Amineborane-Based Chemical Hydrogen Storage: Enhanced Ammonia Borane Dehydrogenation in Ionic Liquids. J. Am. Chem. Soc. 2006, 128, 7748–7749. [Google Scholar] [CrossRef] [PubMed]
- Balazs, N.; Brahim, K.; Claude, G.; Veszprémi, T. Differences Between Amine- and Phosphine-Boranes: Synthesis, Photoelectron Spectroscopy, and Quantum Chemical Study of the Cyclopropylic Derivatives. Inorg. Chem. 2010, 49, 4854–4864. [Google Scholar]
- Swinnen, S.; Nguyen, V.S.; Nguyen, M.T. Hydrogen release from ammonia borane and derivatives in the presence of a ruthenium complex incorporating cooperative PNP ligands. Chem. Phys. Lett. 2011, 513, 195–200. [Google Scholar] [CrossRef]
- Swinnen, S.; Nguyen, V.S.; Nguyen, M.T. Theoretical study of the hydrogen release mechanism from a lithium derivative of ammonia borane, LiNH2BH3–NH3BH3. Chem. Phys. Lett. 2011, 517, 22–28. [Google Scholar] [CrossRef]
- Schreiber, D.F.; O’Connor, C.; Grave, C.; Ortin, Y.; Müller-Bunz, H.; Phillips, A.D. Application of β-Diketiminato Arene-Substituted Ru(II) Complexes in Highly Efficient H2 Dehydrocoupling of Amine Boranes. ACS Catal. 2012, 2, 2505–2511. [Google Scholar] [CrossRef]
- Bandaru, S.; English, N.J.; Phillips, A.D.; MacElroy, J.M.D. Towards the design of novel boron- and nitrogen-substituted ammonia-borane and bifunctional arene ruthenium catalysts for hydrogen storage. J. Comput. Chem. 2014, 35, 891–903. [Google Scholar] [CrossRef] [PubMed]
- Boddien, A.; Mellmann, D.; Gärtner, F.; Jackstell, R.; Junge, H.; Dyson, P.J.; Laurenczy, G.; Ludwig, R.; Beller, M. Efficient Dehydrogenation of Formic Acid Using an Iron Catalyst. Science 2011, 333, 1733–1736. [Google Scholar] [CrossRef] [PubMed]
- Boddien, A.; Grtner, F.; Jackstell, R.; Junge, H.; Spannenberg, A.; Baumann, W.; Ludwig, R.; Beller, M. ortho-Metalation of Iron(0) Tribenzylphosphine Complexes: Homogeneous Catalysts for the Generation of Hydrogen from Formic Acid. Angew. Chem. Int. Ed. 2010, 49, 8993–8996. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.M.; Zhang, X.B.; Han, S.; Shioyama, H.; Xu, Q. Iron-Nanoparticle-Catalyzed Hydrolytic Dehydrogenation of Ammonia Borane for Chemical Hydrogen Storage. Angew. Chem. Int. Ed. 2008, 47, 2287–2289. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.T.; Gordon, J.C.; Hamilton, C.W.; Henson, N.J.; Lin, P.H.; Maguire, S.; Murugesu, M.; Scott, B.L.; Smythe, N.C. Iron Complex-Catalyzed Ammonia–Borane Dehydrogenation. A Potential Route toward B–N-Containing Polymer Motifs Using Earth-Abundant Metal Catalysts. J. Am. Chem. Soc. 2012, 134, 5598–5609. [Google Scholar] [CrossRef] [PubMed]
- Douglas, T.M.; Chaplin, A.B.; Weller, A.S.; Yang, X.; Hall, M.B. Monomeric and Oligomeric Amine−Borane σ-Complexes of Rhodium. Intermediates in the Catalytic Dehydrogenation of Amine−Boranes. J. Am. Chem. Soc. 2009, 131, 15440–15456. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Priest, I.K.; Hooper, T.N.; Weller, A.S. Variable coordination modes and catalytic dehydrogenation of B-phenyl amine–boranes. Dalton Trans. 2016, 45, 6183–6195. [Google Scholar] [CrossRef] [PubMed]
- Douglas, T.M.; Chaplin, A.B.; Weller, A.S. Amine-Borane σ-Complexes of Rhodium. Relevance to the Catalytic Dehydrogenation of Amine-Boranes. J. Am. Chem. Soc. 2008, 130, 14432–14433. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Ishibashi, J.S.A.; Hooper, T.N.; Mikulas, T.C.; Dixon, D.A.; Liu, S.-Y.; Weller, A.S. The Synthesis, Characterization and Dehydrogenation of Sigma-Complexes of BN-Cyclohexanes. Chem. Eur. J. 2016, 22, 310–322. [Google Scholar] [CrossRef] [PubMed]
- Butera, V.; Russo, N.; Sicilia, E. The Role of Chelating Phosphine Rhodium Complexes in Dehydrocoupling Reactions of Amine-Boranes: A Theoretical Investigation Attempting To Rationalize the Observed Behaviors. ACS Catal. 2014, 4, 1104–1113. [Google Scholar] [CrossRef]
- Butera, V.; Russo, N.; Sicilia, E.A. Hydrogen Release from Dialkylamine–Boranes Promoted by Mg and Ca Complexes: A DFT Analysis of the Reaction Mechanism. Chem. Eur. J. 2014, 20, 5967–5976. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hall, M.B. Role of the Chemically Non-Innocent Ligand in the Catalytic Formation of Hydrogen and Carbon Dioxide from Methanol and Water with the Metal as the Spectator. J. Am. Chem. Soc. 2015, 137, 12330–12342. [Google Scholar] [CrossRef] [PubMed]
- Alberico, E.; Lennox, A.J.J.; Vogt, L.K.; Jiao, H.; Baumann, W.; Drexler, H.-J.; Nielsen, M.; Spannenberg, A.; Checinski, M.P.; Junge, H. Unravelling the Mechanism of Basic Aqueous Methanol Dehydrogenation Catalyzed by Ru–PNP Pincer Complexes. J. Am. Chem. Soc. 2016, 138, 14890–14904. [Google Scholar] [CrossRef] [PubMed]
- Jinga, Y.; Chena, X.; Yang, X. Theoretical study of the mechanism of ruthenium catalyzed dehydrogenation of methanol-water mixture to H2 and CO2. J. Org. Organomet. Chem. 2016, 820, 55–61. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Chai, J.D.; Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Yang, W.T. Empirical correction to density functional theory for van der Waals interactions. J. Chem. Phys. 2002, 116, 515–524. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Nicklass, A.; Dolg, M.; Stoll, H.; Preuss, H. Ab initio energy-adjusted pseudopotentials for the noble gases Ne through Xe: Calculation of atomic dipole and quadrupole polarizabilities. J. Chem. Phys. 1995, 102, 8942–8952. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 2257–2261. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Carpenter, J.E.; Weinhold, F. Analysis of the geometry of the hydroxymethyl radical by the “different hybrids for different spins” natural bond orbital procedure. J. Mol. Struct. (THEOCHEM) 1988, 169, 41–62. [Google Scholar] [CrossRef]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Cammi, R.; Tomasi, J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comput. Chem. 1995, 16, 1449–1458. [Google Scholar] [CrossRef]
- English, N.J.; MacElroy, J.M.D. Atomistic simulations of liquid water using Lekner electrostatics. Molec. Phys. 2002, 100, 3753–3769. [Google Scholar] [CrossRef]
- English, N.J. Effect of electrostatics techniques on the estimation of thermal conductivity via equilibrium molecular dynamics simulation: application to methane hydrate. Mol. Phys. 2008, 106, 1887–1898. [Google Scholar] [CrossRef]
- Phillips, A.D.; Laurenczy, G.; Scopelliti, R.; Dyson, P.J. Facile, Thermoreversible Cycloaddition of Small Molecules to a Ruthenium(II) Arene β-Diketiminate. Organometallics 2007, 26, 1120–1134. [Google Scholar] [CrossRef]
- Ledger, A.E.W.; Ellul, C.E.; Mahon, M.F.; Williams, J.M.J.; Whittlesey, M.K. Ruthenium Bidentate Phosphine Complexes for the Coordination and Catalytic Dehydrogenation of Amine– and Phosphine–Boranes. Chem. Eur. J. 2011, 17, 8704–8713. [Google Scholar] [CrossRef] [PubMed]
- Phillips, A.D.; Grave, C.; Singh, G.; O’Connor, C.; Khlebnikov, C. Catalyst and Process for the Production of Hydrogen from Ammonia Boranes. International Patent WO2014174465A3, 23 April 2014. [Google Scholar]
| Structure | Theory | Ru-N | Ru-Ccent | N-Ru-N | Ccent-Ru-Ncent | Ru-Ncent-C14 |
|---|---|---|---|---|---|---|
 | X-ray | 2.021 | 1.730 | 88.5 | 178.0 | 174.5 |
| M06L | 2.044 | 1.692 | 88.4 | 177.7 | 179.0 | |
| M05-2X | 2.032 | 1.763 | 88.6 | 177.0 | 178.5 | |
| B3LYP | 1.991 | 1.764 | 89.4 | 177.3 | 178.8 | |
| B97D | 2.019 | 1.724 | 89.6 | 177.5 | 179.1 | |
| wB97XD | 2.032 | 1.748 | 88.6 | 178.8 | 178.6 |
| Structure | B | H(B) | N | H(N) | C(β) | M(Ru) | ωi |
|---|---|---|---|---|---|---|---|
| 1 | - | - | - | - | 0.234 | 0.167 | - |
| 1a | −0.030 | −0.027 | −0.978 | 0.465 | −0.247 | 0.054 | - |
| 1a-TS1 | 0.170 | −0.007 | −1.126 | 0.417 | −0.483 | −0.053 | (−839.2i) |
| C(β) | M(Ru) | H(Cβ) | H(Ru) | ωi | - | - | |
| 1b | −0.413 | −0.279 | 0.335 | 0.092 | - | - | - |
| 1b-TS2 | −0.351 | −0.099 | 0.228 | 0.024 | (−1002.2i) | - | - |
| B | H(B) | N | H(N) | C(β) | M(Fe) | ωi | |
| 2 | - | - | - | - | −0.352 | 0.297 | - |
| 2a | 0.020 | −0.086 | −0.979 | 0.467 | −0.481 | 0.371 | - |
| 2a-TS1 | 0.068 | −0.044 | −1.104 | 0.398 | −0.653 | 0.307 | (−1196.3i) |
| C(β) | M(Fe) | H(Cβ) | H(Fe) | ωi | - | - | |
| 2b | −0.573 | −0.203 | 0.318 | 0.094 | - | - | - |
| 2b-TS2 | −0.541 | 0.069 | 0.226 | 0.020 | −648.9i | - | - |
| Structure | B | H(B) | N | H(N) | C(β) | M(Ru) | THF(O) | ωi |
|---|---|---|---|---|---|---|---|---|
| 3 | - | - | - | - | −0.395 | 0.110 | −0.525 | - |
| 3a | −0.011 | −0.007 | −0.963 | 0.463 | 0.304 | −0.240 | −0.546 | - |
| 3a-TS1 | 0.096 | −0.020 | −1.113 | 0.396 | −0.646 | −0.285 | −0.555 | −880.6i |
| C(β) | M(Ru) | H(Cβ) | H(M) | THF(O) | ωi | - | - | |
| 3b | −0.565 | −0.588 | 0.320 | 0.054 | −0.574 | - | - | - |
| 3b-TS2 | −0.576 | −0.403 | 0.259 | 0.052 | −0.555 | −1281.9i | - | - |
| B | H(B) | N | H(N) | C(β) | M(Fe) | THF(O) | ωi | |
| 4 | - | - | - | −0.430 | 0.382 | −0.588 | −0.430 | - |
| 4a | −0.024 | −0.076 | −0.974 | 0.459 | −0.468 | 0.151 | −0.597 | - |
| 4a-TS1 | 0.060 | −0.097 | −1.121 | 0.391 | −0.648 | 0.079 | −0.597 | −627.3i |
| C(β) | M(Ru) | H(Cβ) | H(M) | THF(O) | ωi | - | - | |
| 4b | −0.573 | −0.365 | 0.328 | −0.043 | −0.587 | - | - | - |
| 4b-TS2 | −0.592 | −0.132 | 0.274 | −0.443 | −0.580 | −1278.6i | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bandaru, S.; English, N.J.; Phillips, A.D.; MacElroy, J.M.D. Exploring Promising Catalysts for Chemical Hydrogen Storage in Ammonia Borane: A Density Functional Theory Study. Catalysts 2017, 7, 140. https://doi.org/10.3390/catal7050140
Bandaru S, English NJ, Phillips AD, MacElroy JMD. Exploring Promising Catalysts for Chemical Hydrogen Storage in Ammonia Borane: A Density Functional Theory Study. Catalysts. 2017; 7(5):140. https://doi.org/10.3390/catal7050140
Chicago/Turabian StyleBandaru, Sateesh, Niall J. English, Andrew D. Phillips, and J. M. Don MacElroy. 2017. "Exploring Promising Catalysts for Chemical Hydrogen Storage in Ammonia Borane: A Density Functional Theory Study" Catalysts 7, no. 5: 140. https://doi.org/10.3390/catal7050140
APA StyleBandaru, S., English, N. J., Phillips, A. D., & MacElroy, J. M. D. (2017). Exploring Promising Catalysts for Chemical Hydrogen Storage in Ammonia Borane: A Density Functional Theory Study. Catalysts, 7(5), 140. https://doi.org/10.3390/catal7050140






