Time- and Temperature-Varying Activation Energies: Isobutane Selective Oxidation to Methacrolein over Phosphomolybdic Acid and Copper(II) Phosphomolybdates
Abstract
:1. Introduction
2. Results
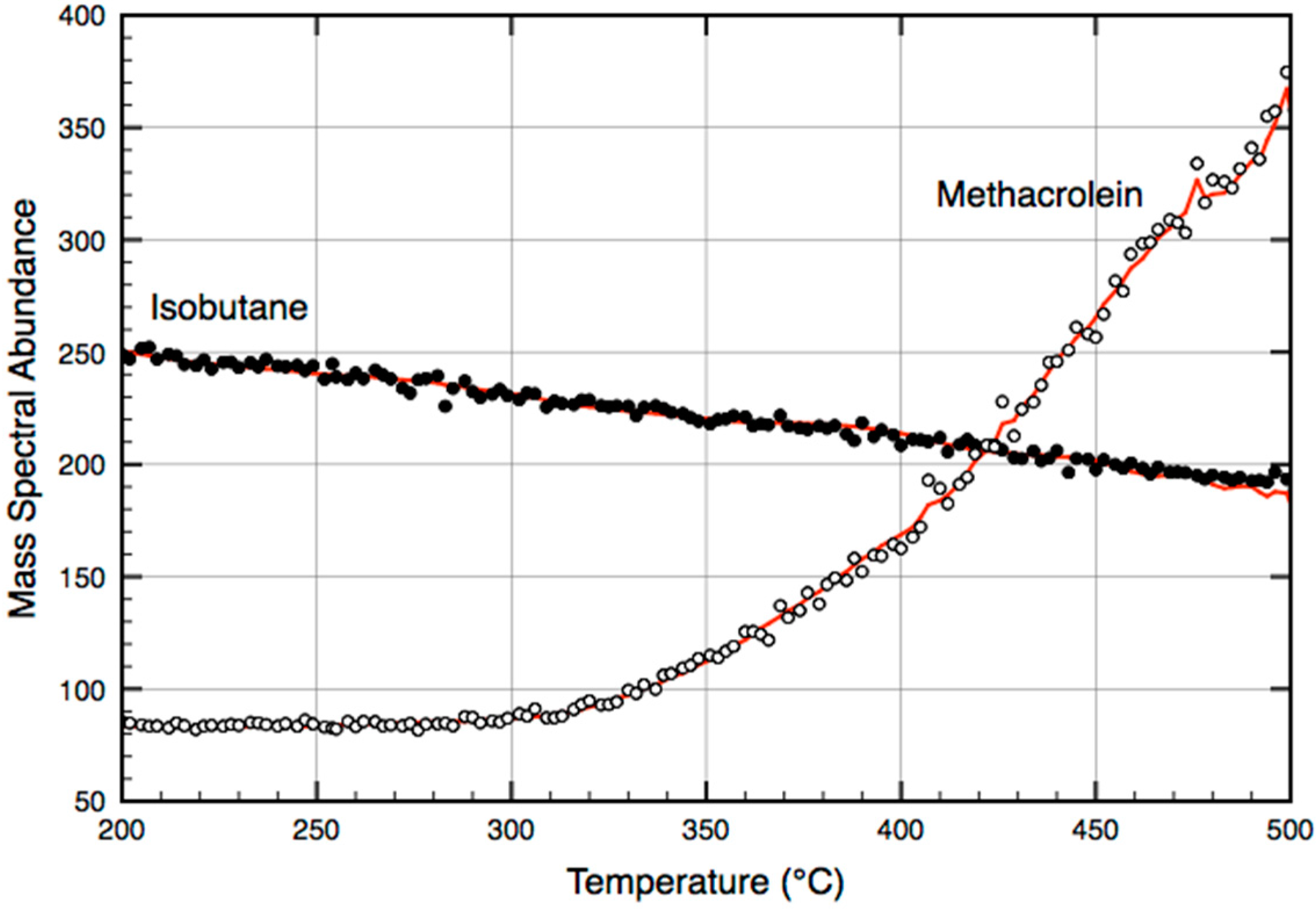
2.1. Temperature-Programmed, Low-Pressure, Pseudo Steady-State Methacrolein Formation
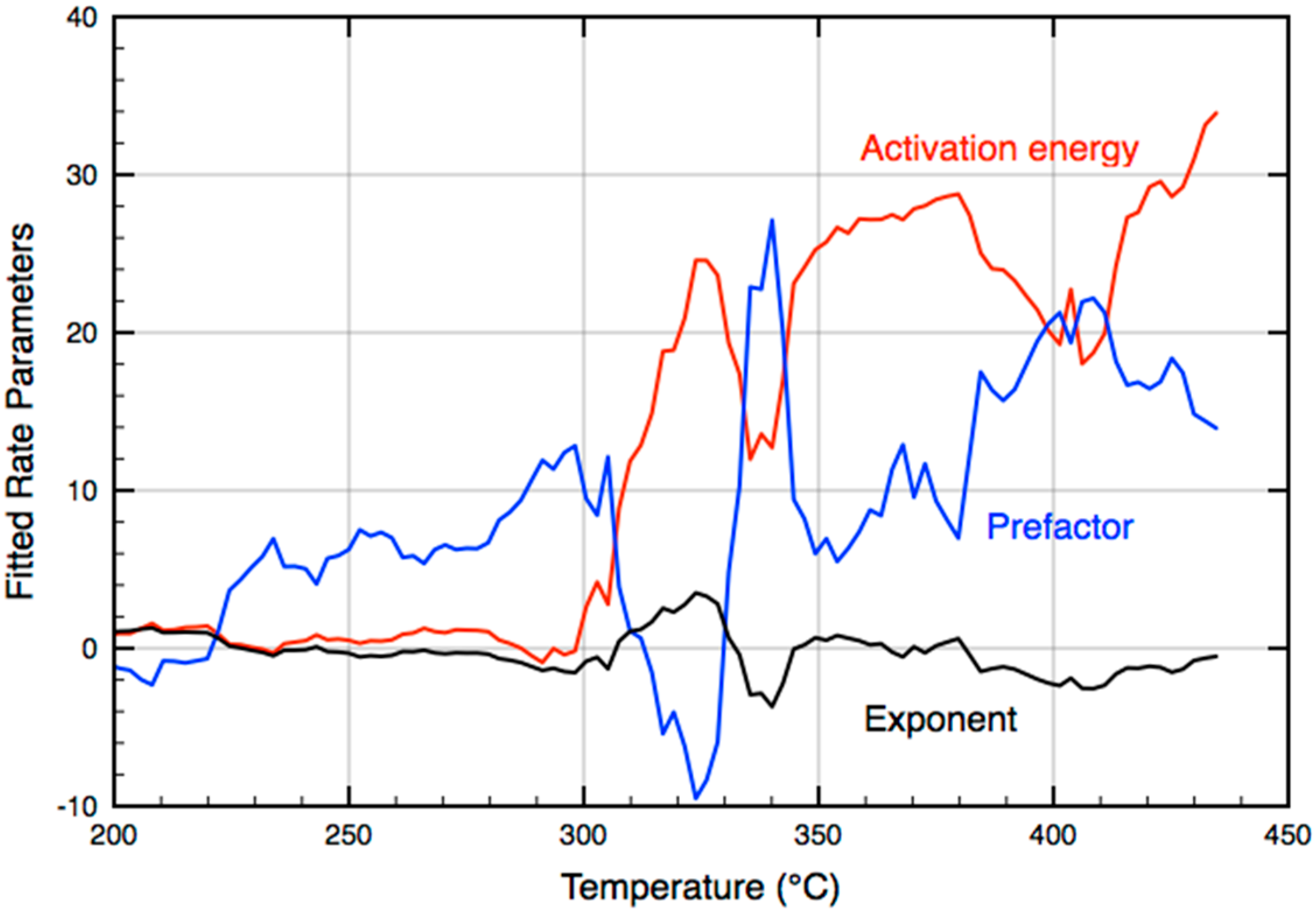
2.2. Rate Parameters from Temperature-Programmed, Low-Pressure Experiments
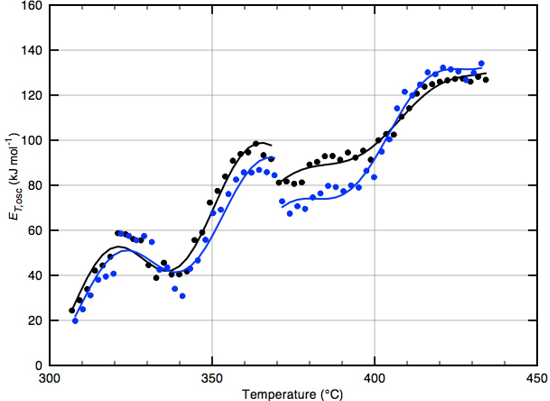
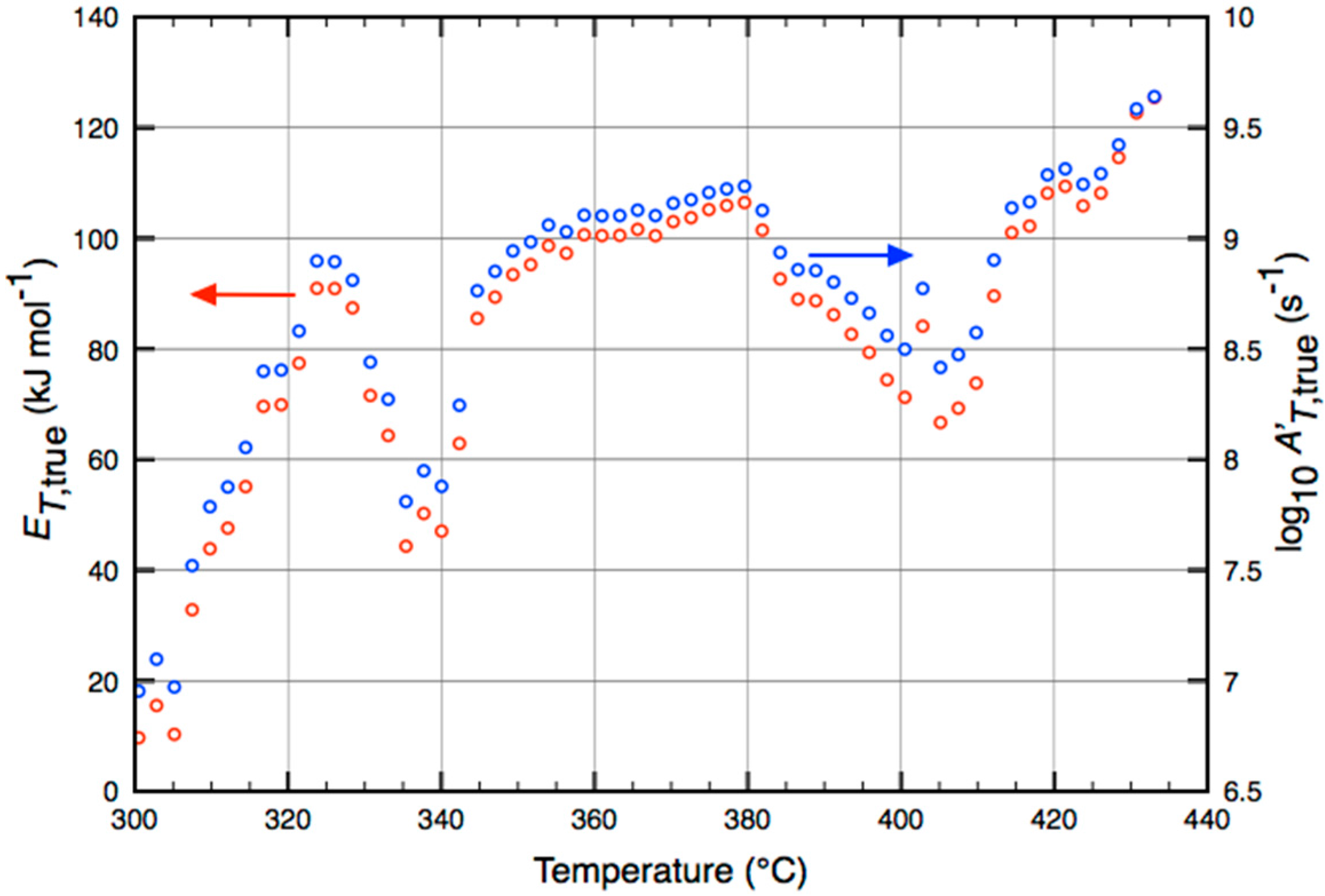
2.3. Calculating Time- and Temperature-Varying Activation Energies
3. Discussion
3.1. High-Temperature, Average Rate-Parameters for Methacrolein Formation
3.2. Detailed Rate-Parameter Distributions for Methacrolein Formation
3.3. Oscillations in High-Temperature Activation Energies
4. Materials and Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, M.; Zhang, J.; Putaj, P.; Caps, V.; Lefebvre, F.; Pelletier, J.; Basset, J.-M. Catalytic Oxidation of Light Alkanes (C1–C4) by Heteropoly Compounds. Chem. Rev. 2014, 114, 981–1019. [Google Scholar] [CrossRef] [PubMed]
- Kendell, S.M.; Nguyen, N.H.; Brown, T.C. Electronic Activity Relationship for Methacrolein Formation Over 4th Period Transition Metal Phosphomolybdates. Catal. Lett. 2013, 143, 61–70. [Google Scholar] [CrossRef]
- Huynh, Q.; Shuurman, Y.; Delichere, P.; Loridant, S.; Millet, J.M.M. Study of Te and V as counter-cations in Keggin type phosphomolybdic polyoxometalate catalysts for isobutane oxidation. J. Catal. 2009, 261, 166–176. [Google Scholar] [CrossRef]
- Jing, F.; Katryniok, B.; Dumeignil, F.; Bordes-Richard, E.; Paul, S. Catalytic selective oxidation of isobutane to methacrylic acid on supported (NH4)3HPMo11VO40 catalysts. J. Catal. 2014, 309, 121–135. [Google Scholar] [CrossRef]
- Jing, F.; Katryniok, B.; Dumeignil, F.; Bordes-Richard, E.; Paul, S. Catalytic selective oxidation of isobutane over Csx(NH4)3−xHPMo11VO40 mixed salts. Cat. Sci. Technol. 2014, 4, 2938–2945. [Google Scholar] [CrossRef]
- Grasselli, R.K. Fundamental principles of selective heterogeneous catalysis. Top. Catal. 2002, 21, 79–88. [Google Scholar] [CrossRef]
- Mizuno, N.; Tateishi, M.; Iwamoto, M. Direct oxidation of isobutane into methacrylic acid and methacrolein over Cs2.5Ni0.08-substituted H3PMo12O40. J. Chem. Soc. Chem. Commun. 1994, 1411–1412. [Google Scholar] [CrossRef]
- Sun, Y.; Brown, T.C. Catalytic cracking, dehydrogenation, and aromatization of isobutane over Ga/HZSM-5 and Zn/HZSM-5 at low pressures. Int. J. Chem. Kinet. 2002, 87, 467–480. [Google Scholar] [CrossRef]
- Le Minh, C.; Brown, T.C. Rate parameters from low-pressure steady-state protolytic cracking and dehydrogenation of isobutane over zeolite catalysts. Appl. Catal. 2006, 310, 145–154. [Google Scholar] [CrossRef]
- Kendell, S.M.; Brown, T.C.; Burns, R.C. Accurate low-pressure kinetics for isobutane oxidation over phosphomolybdic acid and copper(II) phosphomolybdates. Catal. Today 2008, 131, 526–532. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-State Kinetic Models: Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef] [PubMed]
- Tan, G.; Wang, Q.; Zheng, H.; Zhao, W.; Zhang, S.; Liu, Z. Concept of Variable Activation Energy and Its Validity in Nonisothermal Kinetics. J. Phys. Chem. A 2011, 115, 5517–5524. [Google Scholar] [CrossRef] [PubMed]
- Khawam, A.; Flanagan, D.R. Basics and applications of solid-state kinetics: A pharmaceutical perspective. J. Pharm. Sci. 2006, 95, 472–498. [Google Scholar] [CrossRef] [PubMed]
- Arshad, M.A.; Maaroufi, A-K. An innovative reaction model determination methodology in solid state kinetics based on variable activation energy. Thermochim. Acta 2014, 360, 25–35. [Google Scholar] [CrossRef]
- Imbihil, R.; Ertl, G. Oscillatory Kinetics in Heterogeneous Catalysis. Chem. Rev. 1995, 95, 697–733. [Google Scholar] [CrossRef]
- Rosenthal, D. Functional surfaces in heterogeneous catalysis: A short review. Phys. Status Solidi 2011, 208, 1217–1222. [Google Scholar] [CrossRef]
- Kaichev, V.V.; Gladjy, A.Y.; Prosvirin, I.P.; Saraev, A.A.; Hävecker, M.; Knop-Gericke, A.; Schlögl, R.; Bukhtiyarov, V.I. In situ XPS study of self-sustained oscillations in catalytic oxidation of propane over nickel. Surf. Sci. 2013, 609, 113–118. [Google Scholar] [CrossRef]
- Kokkofitis, C.; Stoukides, M. Rate and oxygen activity oscillations during propane oxidation on Pt/YSZ. J. Catal. 2006, 243, 428–437. [Google Scholar] [CrossRef]
- Kalaba, R.; Tesfatsion, L.C. Time-varying linear regression via flexible least squares. Comput. Math. Appl. 1989, 17, 1215–1245. [Google Scholar] [CrossRef]
- Le Minh, C.; Alanazi, A.K.; Miron, D.J.; Brown, T.C. Carbon–Carbon Bond Cleavage and Dehydrogenation of Isobutane Over HZSM-5 at Low Pressures and Temperatures. Catal. Lett. 2012, 142, 1470–1473. [Google Scholar] [CrossRef]
- Brown, T.C.; Miron, D.J.; Alanazi, A.K.; Le Minh, C. Rate Parameter Distributions for Isobutane Dehydrogenation and Isobutene Dimerization and Desorption over HZSM-5. Catalysts 2013, 3, 922–941. [Google Scholar] [CrossRef]
- Miron, D.J.; Kendell, S.M.; Munshi, A.M.; Alanazi, A.K.; Brown, T.C. Time-Varying Flexible Least Squares for Thermal Desorption of Gases. Int. J. Chem. Kinet. 2013, 45, 374–386. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
- Nason, G. Wavethresh: Wavelet Statistics and Transforms, version 4.6.2. Available online: http://cran.rproject.org/web/packages/wavethersh/index.html (accessed on 2 April 2013).
- Golden, D.M.; Spokes, G.N.; Benson, S.W. Very low-pressure pyrolysis (VLPP). A versatile kinetic tool. Angew. Chem. Int. Ed. 1973, 12, 534–546. [Google Scholar] [CrossRef]
- Budrugeac, P. Some methodological problems concerning nonisothermal kinetic analysis of heterogeneous solid-gas reactions. J. Therm. Anal. Calorim. 2007, 89, 143–151. [Google Scholar] [CrossRef]
- Kendell, S.M.; Brown, T.C. Comprehensive Study of Isobutane Selective Oxidation Over Group I and II Phosphomolybdates: Structural and Kinetic Factors. Catal. Lett. 2011, 141, 1767–1785. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Kendell, S.M.; Le Minh, C.; Brown, T.C. Mechanistic Investigation into the Rearrangement of Lactone into Methacrylic Acid over Phosphomolybdic Acid Catalyst. Catal. Lett. 2010, 136, 28–34. [Google Scholar] [CrossRef]
- Deshlahra, P.; Iglesia, E. Methanol Oxidative Dehydrogenation on Oxide Catalysts: Molecular and Dissociative Routes and Hydrogen Addition Energies as Descriptors of Reactivity. J. Phys. Chem. C 2014, 118, 26115–26129. [Google Scholar] [CrossRef]
- Kemmer, G.; Keller, S. Nonlinear least-squares data fitting in Excel spreadsheets. Nat. Protoc. 2010, 5, 267–281. [Google Scholar] [CrossRef] [PubMed]
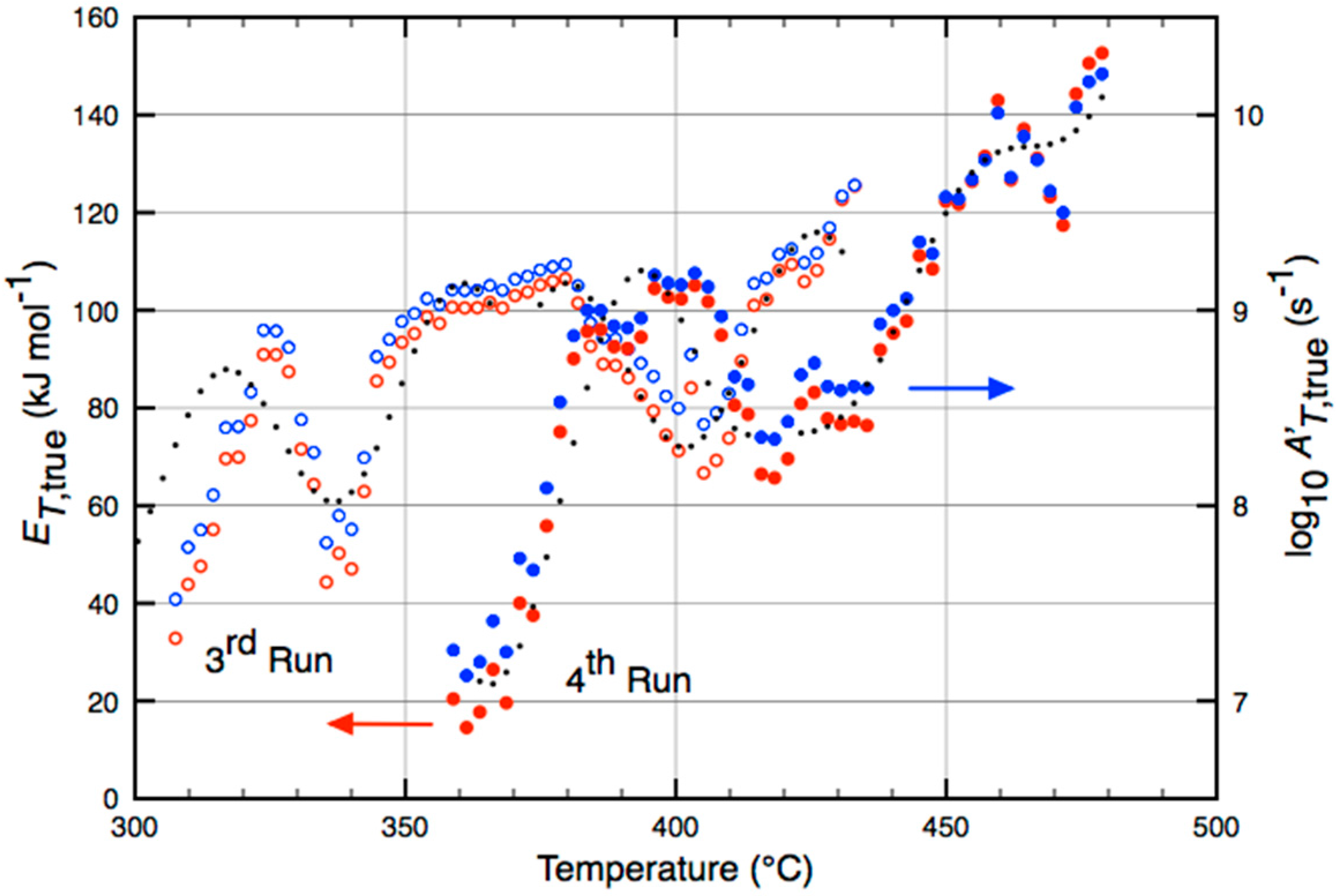
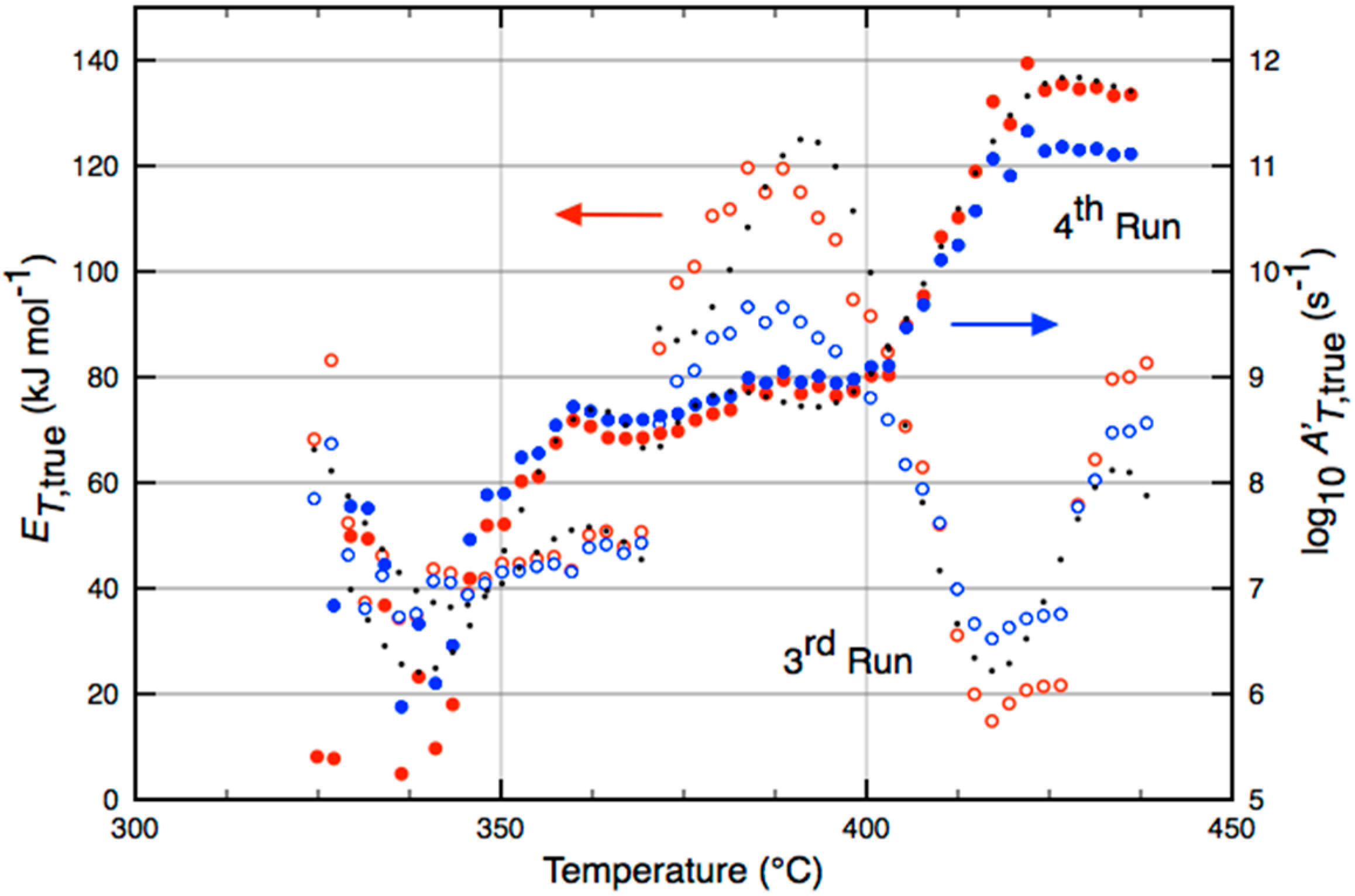
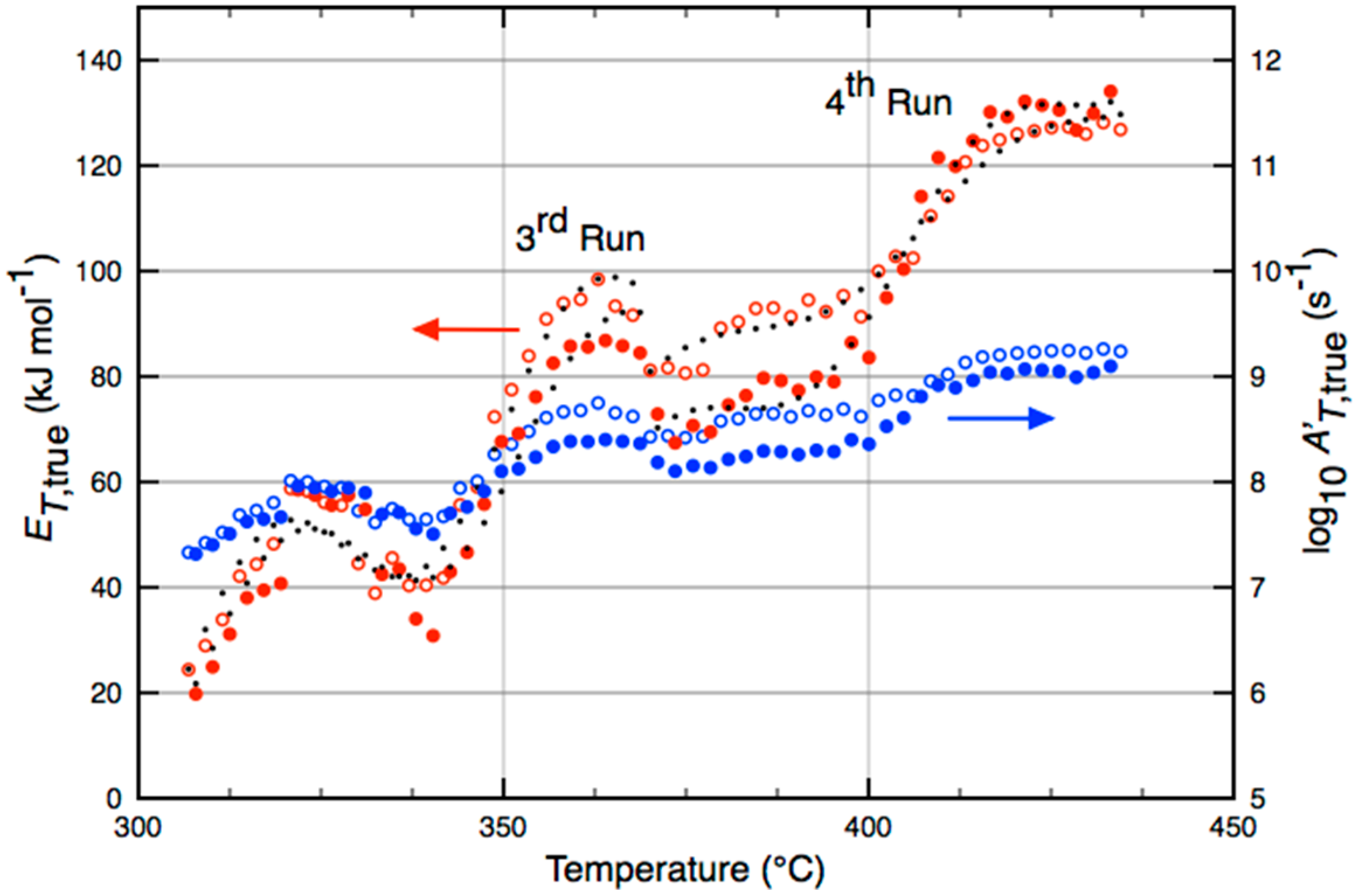
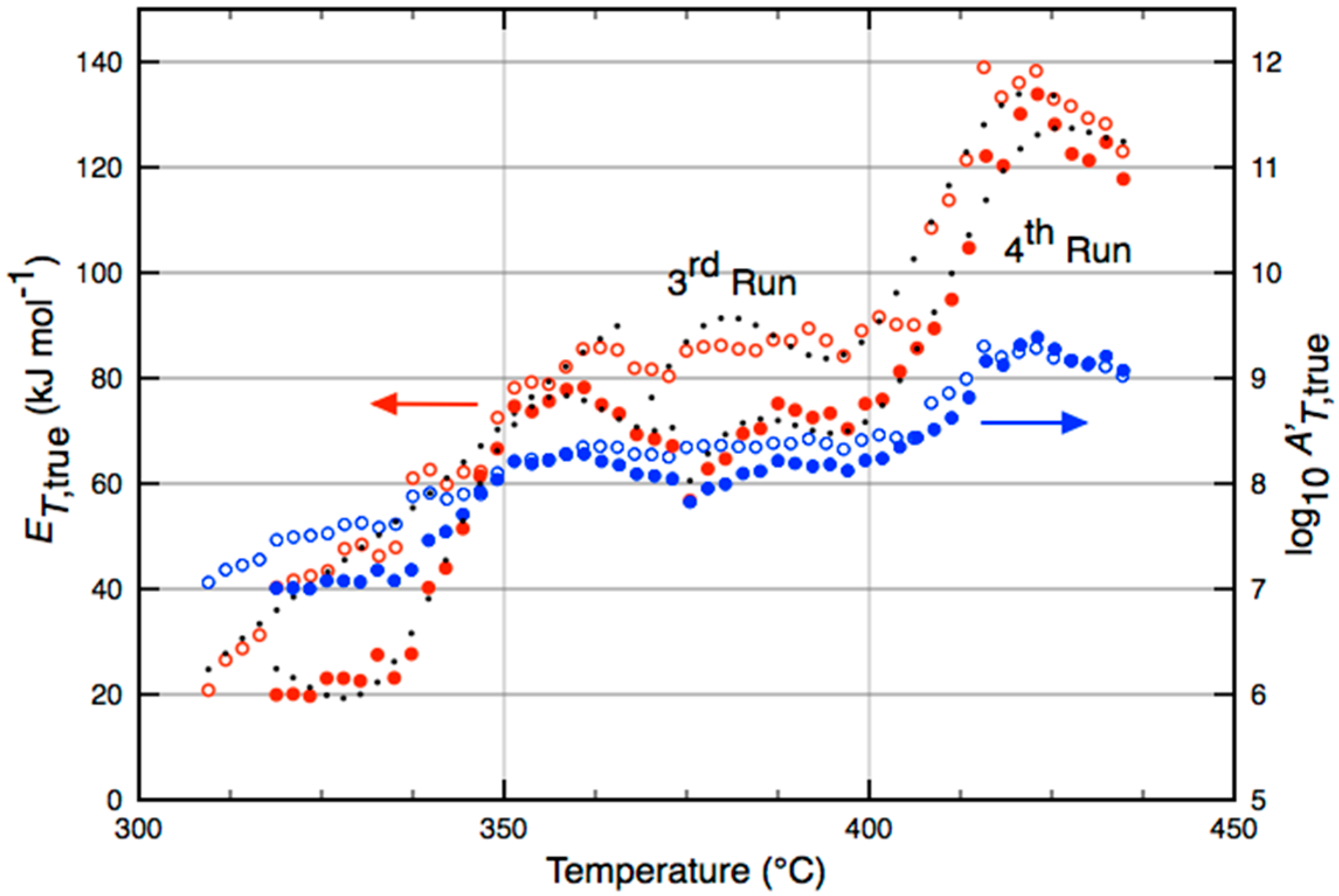
| Catalyst | Temperature (°C) | (kJ·mol−1) |
|---|---|---|
| H3PMo12O40 | 246–451 | 99.3 ± 1.1 |
| Cu0.5H2PMo12O40 | 353–502 | 61.3 ± 1.8 |
| CuHPMo12O40 | 325–501 | 58.4 ± 0.9 |
| Cu1.25H0.5PMo12O40 | 329–501 | 52 ± 4 |
| Cu1.5PMo12O40 | 342–500 | 75.4 ± 1.2 |
| Catalyst | Temperature (°C) | (s−1) | (kJ·mol−1) | |
|---|---|---|---|---|
| Min–Max | Average | |||
| 3rd Run | ||||
| H3PMo12O40 | 300–433 | 8.7 ± 0.6 | 10–125 | 82 ± 27 |
| CuHPMo12O40 | 310–435 | 8.3 ± 0.6 | 21–139 | 82 ± 31 |
| Cu1.25H0.5PMo12O40 | 307–435 | 8.4 ± 0.6 | 24–128 | 83 ± 30 |
| Cu1.5PMo12O40 | 311–438 | 7.8 ± 1.0 | 23–120 | 63 ± 30 |
| 4th Run | ||||
| H3PMo12O40 | 359–479 | 8.9 ± 0.8 | 15–153 | 91 ± 35 |
| Cu0.5H2PMo12O40 | 320–435 | 8.1 ± 0.7 | 20–134 | 72 ± 33 |
| Cu1.25H0.5PMo12O40 | 308–433 | 8.3 ± 0.5 | 22–134 | 78 ± 32 |
| Cu1.5PMo12O40 | 316–436 | 8.8 ± 1.4 | 22–139 | 76 ± 35 |
| Catalyst | Temperature (°C) | (s−1) | (kJ·mol−1) | Reaction Type |
|---|---|---|---|---|
| 3rd Run | ||||
| H3PMo12O40 | 345–384 | 10 9.1 ± 0.1 | 99 ± 9 | III |
| 387–412 | 10 8.7 ± 0.2 | 80 ± 8 | II | |
| 414–433 | 10 9.3 ± 0.2 | 111 ± 9 | IV | |
| CuHPMo12O40 | 351–406 | 10 8.34 ± 0.07 | 85 ± 4 | III |
| 413–435 | 10 9.04 ± 0.04 | 131 ± 6 | I | |
| Cu1.25H0.5PMo12O40 | 353–399 | 10 8.6 ± 0.1 | 90 ± 5 | III |
| 413–435 | 10 9.2 ± 0.03 | 126 ± 2 | I | |
| Cu1.5PMo12O40 | 331–369 | 10 7.1 ± 0.2 | 44 ± 5 | V |
| 379–393 | 10 9.5 ± 0.1 | 115 ± 4 | IV | |
| 414–427 | 10 6.7 ± 0.1 | 19 ± 3 | V | |
| 429–438 | 10 8.3 ± 0.3 | 73 ± 12 | II | |
| 4th Run | ||||
| H3PMo12O40 | 381–408 | 10 9.0 ± 0.1 | 98 ± 5 | III |
| 413–435 | 10 8.6 ± 0.1 | 76 ± 6 | II | |
| 450–479 | 10 9.8 ± 0.2 | 131 ± 10 | I | |
| Cu0.5H2PMo12O40 | 351–402 | 10 8.1 ± 0.1 | 72 ± 5 | II |
| 416–435 | 10 9.2 ± 0.1 | 125 ± 5 | I | |
| Cu1.25H0.5PMo12O40 | 352–400 | 10 8.3 ± 0.1 | 79 ± 6 | II |
| 414–433 | 10 9.04 ± 0.04 | 130 ± 3 | I | |
| Cu1.5PMo12O40 | 357–403 | 10 8.8 ± 0.2 | 74 ± 4 | II |
| 417–436 | 10 11.1 ± 0.1 | 134 ± 3 | I | |
| Catalyst | Temperature (°C) | (kJ·mol−1) | (K) | (kJ·mol−1·K−1) | (kJ·mol−1) |
|---|---|---|---|---|---|
| 3rd Run | |||||
| H3PMo12O40 | 307–368 | 18 | 44 | 0.40 | −58 |
| 370–435 | 19 | 46 | 0.23 | 0.074 | |
| CuHPMo12O40 | 310–366 | 1.2 | 44 | 1.2 | −334 |
| 368–425 | 13 | 43 | 1.1 | −320 | |
| Cu1.25H0.5PMo12O40 | 307–368 | 15 | 44 | 1.1 | −298 |
| 370–435 | 5.0 | 45 | 0.88 | −249 | |
| Cu1.5PMo12O40 | 313–369 | 12 | 44 | −0.45 | 202 |
| 372–438 | 33 | 43 | −1.5 | 669 | |
| 4th Run | |||||
| H3PMo12O40 | 359–421 | 28 | 47 | 1.1 | −340 |
| 423–479 | 9.0 | 44 | 1.3 | −484 | |
| Cu0.5H2PMo12O40 | 319–373 | 14 | 43 | 1.2 | −358 |
| 375–435 | 12 | 41 | 1.3 | −454 | |
| Cu1.25H0.5PMo12O40 | 308–371 | 14 | 44 | 0.93 | −263 |
| 374–433 | 9.6 | 45 | 1.3 | −415 | |
| Cu1.5PMo12O40 | 316–369 | 20 | 44 | 0.40 | −93 |
| 372–436 | 13 | 46 | 1.3 | −430 | |
| Catalyst | Reaction | ||||
|---|---|---|---|---|---|
| (kJ·mol−1·K −1) | (kJ·mol−1) | (kJ·mol−1) | (K) | ||
| H3PMo12O40 | Type I | 1.3 | −484 | 130 ± 3 | 745 ± 7 |
| Type II | 1.3 | −484 | 76 ± 3 | 704 ± 7 | |
| Type III | 1.1 | −340 | 93 ± 7 | 667 ± 25 | |
| Cu0.5H2PMo12O40 | Type I Type II | 1.3 1.3 | −433 −433 | 130 ± 3 76 ± 3 | 706 ± 9 665 ± 9 |
| Cu1.25H0.5PMo12O40 | |||||
| Cu1.5PMo12O40 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, T.C.; Miron, D.J.; Brown, S.L.; Kendell, S.M. Time- and Temperature-Varying Activation Energies: Isobutane Selective Oxidation to Methacrolein over Phosphomolybdic Acid and Copper(II) Phosphomolybdates. Catalysts 2016, 6, 137. https://doi.org/10.3390/catal6090137
Brown TC, Miron DJ, Brown SL, Kendell SM. Time- and Temperature-Varying Activation Energies: Isobutane Selective Oxidation to Methacrolein over Phosphomolybdic Acid and Copper(II) Phosphomolybdates. Catalysts. 2016; 6(9):137. https://doi.org/10.3390/catal6090137
Chicago/Turabian StyleBrown, Trevor C., David J. Miron, Susannah L. Brown, and Shane M. Kendell. 2016. "Time- and Temperature-Varying Activation Energies: Isobutane Selective Oxidation to Methacrolein over Phosphomolybdic Acid and Copper(II) Phosphomolybdates" Catalysts 6, no. 9: 137. https://doi.org/10.3390/catal6090137
APA StyleBrown, T. C., Miron, D. J., Brown, S. L., & Kendell, S. M. (2016). Time- and Temperature-Varying Activation Energies: Isobutane Selective Oxidation to Methacrolein over Phosphomolybdic Acid and Copper(II) Phosphomolybdates. Catalysts, 6(9), 137. https://doi.org/10.3390/catal6090137