Abstract
Covalent organic frameworks (COFs) have emerged as unique catalysts for photocatalysis; however, the relationship between their building block units and optoelectronic properties remains elusive. Herein, we explored the influence of building blocks on the optoelectronic properties of benzotrithiophene-based COFs (BTT-COFs) using density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations. The calculation results suggested that three critical factors—the conjugated structure, planarity, and the introduction of nitrogen heteroatoms—significantly influenced charge separation and transfer within BTT-COFs. Structure–property relationships were established through several critical quantitative parameters, such as Sr, t, and CT. Among seven BTT-COFs, BTT-Tpa (Tpa: 4,4′,4″-triaminotriphenylamine) exhibited the most efficient charge separation and the highest charge transfer capability due to the electronegativity of triphenylamine, the delocalization of its lone pair electrons, and its unique star-shaped configuration. These theoretical results will provide an essential foundation for selecting donor–acceptor units in the design of novel COF materials for photocatalytic reaction applications.
1. Introduction
In recent years, covalent organic frameworks (COFs) have attracted much attention in the field of photocatalysis mainly due to their unique optoelectronic properties and structural adjustability [1,2,3,4]. COFs serve as a class of crystalline porous materials. By integrating diverse building blocks, it is feasible to attain high porosity, a large surface area, good structural connectivity, and functionalized active sites within the frameworks of COFs [5,6,7]. Owing to their structural diversity and designability, COFs have been employed in various photocatalytic platforms, including the photosynthesis of hydrogen peroxide [8], the photocatalysis of hydrogen evolution [9], carbon dioxide reduction reactions [10], nitroreductions [11], and photodynamic therapy [12]. In addition, the periodic and well-defined building block units of COFs facilitate charge transfer, carrier transport, and a reduction in exciton recombination [13,14]. Using donor–acceptor structures as the building blocks for the preparation of COFs is considered a highly effective strategy. This approach markedly enhances the light absorption and charge generation capabilities of COFs, significantly improving their photocatalytic activity [15].
Benzotrithiophene (BTT) is a stable π-aromatic ring compound, exhibiting high hole mobility and favorable optical absorption [16]. The incorporation of BTT and counter aromatic building blocks within COF frameworks facilitates the formation of donor–acceptor structures, rendering COFs highly suitable for photocatalytic applications [8,17]. Recently, a series of BTT-COFs (as illustrated in Scheme 1) have been successfully synthesized and have demonstrated remarkable photocatalytic activity for hydrogen evolution under visible light irradiation [18,19,20,21,22,23,24,25,26]. For example, through a reversible Schiff-base condensation reaction, Kwak and Baek et al. synthesized five novel BTT-COFs by using BTT and various aromatic diamines, including phenyl-1,4-diamine (PDA), naphthalene-2,6-diamine (NDA), anthracene-2,6-diamine (AnthDA), and [1,1′-biphenyl]-4,4′-diamine (BPhDA), as the building blocks [26]. These BTT-COFs demonstrated excellent performance in photocatalytic hydrogen production. The remarkable photocatalytic activity of BTT-COFs can be attributed to the high electron affinity and charge trapping capability of the donor–acceptor structure units, which facilitate rapid charge separation and transfer. Furthermore, Zhan and Wang, along with their co-workers, successfully synthesized three types of imine-linked COFs by combining BTT units with 4,4′,4″-triaminotriphenylamine (Tpa), 1,3,5-tris(4-aminophenyl)-benzene (Tapb), and 2,4,6-tris(4-aminophenyl)-1,3,5-triazine (Tapt) [8]. Owing to the differences in charge density and energy levels between the BTT and aromatic building units, donor–acceptor structures were formed within these imine-linked COFs. These unique structures make them highly selective for H2O2 photogeneration. However, most experimental studies on BTT-COFs primarily focus on constructing novel COF frameworks or enhancing the efficiency of photocatalytic processes while overlooking in-depth theoretical investigations into the optoelectronic properties and structure–function relationships of BTT-COFs. Moreover, a comprehensive understanding of the structure–activity relationship between the building block units of COFs is crucial for the design of efficient photocatalysts.
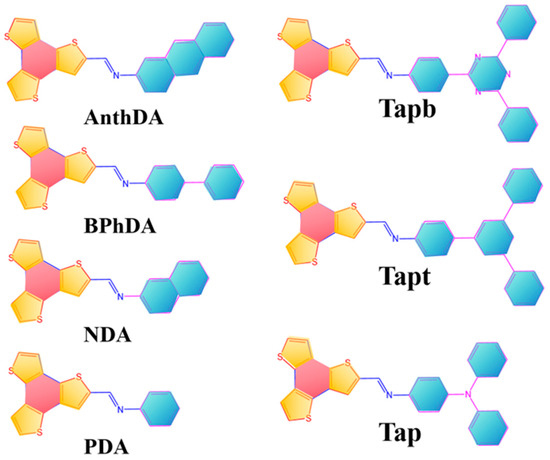
Scheme 1.
BTT-COFs assembled from BTT and various aromatic units.
Rapid advances in computer technology and theoretical knowledge have made quantum chemical calculations an essential tool for explaining and predicting experimental results. Density functional theory (DFT) calculations have been successfully employed to investigate porous materials, including zeolites [27,28,29], metal–organic frameworks (MOFs) [30,31], and covalent organic frameworks (COFs) [32,33]. It offers microscopic insights into the applications of porous materials in catalysis [34,35], adsorption [36,37], separation [38], fluorescence, and the information industry [39]. In addition, time-dependent density functional theory (TD-DFT) can be employed to simulate UV–vis spectroscopy, characterize charge transfer, optimize the electronic structure, and calculate the energy levels of organic molecules in their excited states [40]. For example, Bredas et al. employed DFT calculations to investigate the impact of imine bonds on the charge-transport properties of 2D imine COFs [41]. Berend Smit et al. conducted research on ionization potential (IP) and electron affinity (EA) energies to evaluate the thermodynamic feasibility of photoredox reactions in COFs [42]. Jiang et al. demonstrated that the intrinsic electronic properties of enaminone-linked COFs can be attributed to π-delocalization over the carbon-rich framework, as evidenced by the analysis of the HOMO and LUMO of the building blocks [43]. Sun et al. preformed hole–electron analysis to characterize the number of charge transfers in the donor–acceptor (D-A) structure of organic emitters [44]. The structural, electronic, and optical properties of a series of benzotrithiophene (BTT) derivatives were explored by using DFT calculations [45,46,47,48]. Although these theoretical works have contributed to the understanding of charge transfer issues within donor–acceptor (D-A) structures, there has been no theoretical study evaluating charge transfer and separation for various building units in conjunction with BTT units within COFs. Indeed, it is crucial to establish quantitative parameters that can assist researchers in more comprehensively understanding and accurately describing the relationship between the building block units and the optoelectronic properties of BTT-COFs.
In this work, we combine DFT and TD-DFT calculations to investigate the impact of conjugated and heteroatomic building blocks on the optoelectronic properties of BTT-COFs. Seven types of BTT-COFs, as shown in Scheme 1, were examined as examples to illustrate their D-π-A structures, analyze the charge transfer mechanism, and calculate frontier molecular orbitals and energy levels in excited states. A benchmark test was conducted to evaluate and compare the effects of various DFT functionals on the simulation of absorption spectra for BTT-COFs. The planarity of the BTT-COFs was characterized through the calculation of the dipole moment and the dihedral angle between the building block units. Furthermore, the ionization potential (IP), electron affinity (EA), and reorganization energies were evaluated to assess the hole and electron injection properties of BTT-COFs. Through hole–electron analysis, a set of critical parameters was obtained, providing insight into charge transfer and separation between the building block units. The charge difference density (CDD) and centroid region of charge transfer (CRCT) were employed to quantitatively visualize the degree and distribution of charge transfer at a molecular level. This study aims to provide an in-depth analysis of the optoelectronic behavior and offer valuable guidance for the design and development of COF catalysts, specifically for applications in photocatalytic hydrogen evolution.
2. Results and Discussion
2.1. Benchmarking
By taking BTT-Tapt as an example, which has been reported to exhibit the best photocatalytic performance in experiments [8], we conducted simulations of its UV–vis absorption spectra using the B3LYP, M06-2X, M06L, and PBE functionals to evaluate their impact on the UV–vis absorption spectra, as illustrated in Figure 1a. The λmax of BTT-Tapt exhibits a redshift in the following order: M06-2X (348.64 nm) < B3LYP (408.43 nm) < M06L (461.7 nm) < PBE (502.16 nm). The functional test demonstrated that the M06L functional is in agreement with the experimental value of 450 nm. In conclusion, the M06L functional can be identified as the most suitable method for studying COF systems in their excited states.
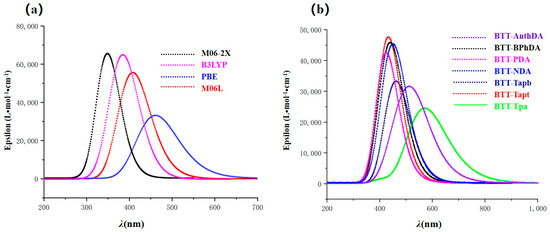
Figure 1.
Simulated maximum wavelength of UV–vis absorption spectra (λmax): (a) for BTT-Tapt based on various TD-DFT functionals; (b) for BTT-COFs.
2.2. Optimized Geometries of BTT-COFs
In general, the optoelectronic properties of BTT-COFs are primarily determined by their ability to utilize ultraviolet light and efficiently separate charges, which is closely associated with the building block units within the COF framework. In this work, the stable configurations of BTT-COFs in the excited state are shown in Figure 2. The important geometrical parameters of BTT-COFs, including the dihedral angle Φ1 (pink symbol) between BTT units and various aromatic diamine units, as well as the dihedral angle Φ2 (red symbol) observed in biphenyls, terphenyls, and tertiary amine units, along with the dipole moments in the ground state (S0) and excited states (S1 or S2), are listed in Table 1. The dihedral angle Φ1 between the D and A units in COFs exhibits excellent coplanarity within the range of 175.1° to 178.4°, regardless of whether it is in the S0 or S1 state. Good coplanarity will enhance the efficiency of charge transfer between the donor and acceptor [49]. It is worth mentioning that the sulfur-rich BTT unit has a highly planar conjugated system with C3h symmetry. In the presence of conjugated naphthalene, anthracene, and triazine units, the coplanarity of BTT-COFs is remarkably enhanced by these conjugated units as well as the BTT unit. The dihedral angle Φ2 observed in biphenyls, terphenyls, and tertiary amine units exhibits a slight torsion within the range of 29.0° to 40.9°, implying the presence of steric hindrance between the D and A units in BTT-BPhDA, BTT-Tapb, and BTT-Tapt. We compared the DFT optimized geometric structure with the experimentally simulated crystal structure of BTT-COFs. The discrepancy between the theoretically calculated and experimentally observed geometric structures of BTT-COFs arises from the intrinsic characteristics of the research methods. Experimental data reflect the equilibrium structure of periodic crystals regulated by intermolecular forces, such as the symmetry constraints, where the observed planarity (180° dihedral angles as shown in Figure S1 of the Supporting Information) represents the statistically averaged atomic configuration within the lattice. In contrast, the isolated cluster model employed in DFT calculations reveals the inherent conformational preferences of the molecules, the optimized C-C single bond torsion (typically in 10–30°) accurately reflecting the energy-minimized state of the flexible structure in the absence of environmental constraints. Furthermore, upon comparing the dipole moments in the S0 and S1/S2 states, it is evident that the majority of COFs demonstrate a reduction in the dipole moment in the excited state. However, BTT-Tapt exhibits negligible change in its dipole moment, whereas BTT-NDA shows a significant increase in its dipole moment at the S1 excited state. Among these BTT-COFs, BTT-Tpa possesses the largest dipole moment (3.6 Debye) in the excited state, indicating the greatest charge separation.
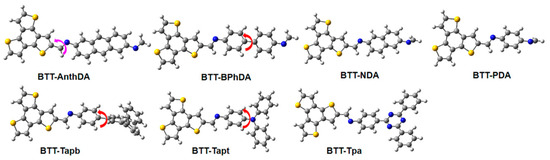
Figure 2.
Optimized geometry of photo-excited BTT-COFs in water.

Table 1.
Dihedral angles (∠Φ1 and ∠Φ2 in degree) and dipole moments (μ in Debye) of BTT-COFs in water at s in S0 and S1 states, respectively.
2.3. Frontier Molecular Orbitals
It is well known that the behavior of intramolecular charge transfer (ICT) from the donor to the acceptor units is commonly characterized by frontier molecular orbitals (FMOs) [50]. In Figure 3, the FMOs and their corresponding orbital energies as well as the energy gaps for BTT-COFs in water in the excited state are presented. It can be seen that the transition of electrons from HOMOs to LUMOs in BTT-COFs in the S1 state exhibits π-π* characteristics. The HOMOs of BTT-Tpa and BTT-AnthDA are predominantly localized in the triphenylamine and anthracene units, as depicted in Figure 3. Conversely, the HOMOs of BTT-Tapt exhibit a distinct distribution in the BTT unit. Following intramolecular charge transfer, the LUMOs can be found across the BTT, imine, and aromatic units. Therefore, for BTT-tapt, the donor (D) is associated with the BTT unit, while the internal acceptor (A) corresponds to the triazine unit. For BTT-Tpa and BTT-AnthDA, the donors are triphenylamine and anthracene, respectively, while the acceptors remain within the BTT units. These results also indicate efficient electron separation between the HOMOs and LUMOs in BTT-AnthDA, BTT-Tpa, and BTT-Tapt, which facilitates intramolecular charge transfer transitions. In contrast, for the other BTT-COFs, the HOMOs in the BTT and aromatic amine units are involved, whereas the LUMOs are also distributed across the BTT and imine units. It is worth mentioning that the imine groups serve as π bridges connecting the BTT and aromatic amine units, facilitating charge transfer between the donor and the acceptor. Consequently, all BTT-COFs are assigned to the D-π-A system. Additionally, the small energy gap indicates that electrons can be easily excited, allowing a wider range of light wavelengths to be utilized by the photocatalyst. As shown in Figure 3, BTT-Tpa has the smallest value of Eg (192.9 kJ/mol). The Eg values of various BTT-COFs have decreased in the following order: BTT-Tapb (250.8 kJ/mol) ≈ BTT-PDA ≈ BTT-BPhDA > BTT-Tapt (241.0 kJ/mol) ≈ BTT-NDA > BTT-AnthDA (202.5 kJ/mol) > BTT-Tpa (192.9 kJ/mol). These suitable energy levels and gaps in the BTT-COFs are conducive to photocatalytic hydrogen evolution in the presence of hole scavengers. The energies of the HOMOs, the LUMOs, and the energy gap for BTT-Tapt, as reported from experiments [23], were −552.6, −307.5, and 243.1 kJ/mol, respectively. This result demonstrates the consistency between our calculations and the experimental findings. Furthermore, we discovered that highly conjugated groups like anthracene effectively raised the HOMO energy (−472.5 kJ/mol), while nitrogenous heterocyclic groups, such as triazine, led to a decrease in the LUMO energy (−279.7 kJ/mol).
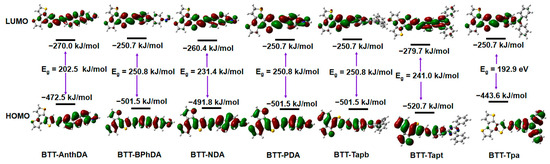
Figure 3.
FMOs, orbital energy, and the energy gap of BTT-COFs in the excited state.
2.4. Optical Properties of BTT-COFs
BTT-COFs possessing a broad absorption band can effectively capture sunlight photons, resulting in enhanced photocatalytic activity for hydrogen evolution. The UV–vis absorption spectra of BTT-COFs with various building block units were determined using the TD-DFT/M06/6-31+G(d) level in an aqueous solution, as shown in Figure 1b. The oscillator strength (ƒ), excitation energy (Eex in eV), maximum wavelength of UV–vis absorption spectra (λ max), and major orbital contribution, as well as the apparent charge transfer percentage (CT %) and local excitation percentage (LE %), are listed in Table 2. The UV–vis absorption spectra of these BTT-COFs display a single peak in the UV and visible regions. The absorption bands of BTT-COFs in the range of 350 ~ 650 nm are assigned to the typical π-π* and charge transfer transitions [51].

Table 2.
TD-DFT calculated the state, oscillator strength (ƒ), excitation energy (Eex in eV), maximum wavelength of UV–vis absorption spectra (λmax in nm), major orbital contribution, apparent charge transfer percentage (CT %), and local excitation percentage (LE %) for BTT-COFs.
As listed in Table 2, the λmax in most BTT-COFs, except for BTT-Tapt (S0→S2), can primarily be attributed to the S0→S1 electronic transition, which corresponds to the major electronic transition between the HOMOs and LUMOs. The λmax of the BTT-COFs increases with the conjugation length of the building block units in the order of BTT-PDA (428.6 nm) < BTT-BPhDA (446.1 nm) < BTT-NDA (454.9 nm) < BTT-AnthDA (524.2 nm). Furthermore, the coplanarity of the aromatic units and the electronegativity of the heteroatom-containing units in the BTT-COFs significantly influence the λmax. An increased number of nitrogen heteroatoms and the enhanced coplanarity lead to a more pronounced redshift of λ max, as demonstrated by the following order: BTT-Tapb (431.5 nm) < BTT-Tapt (461.7 nm) < BTT-Tpa (571.4 nm). Notably, the photocatalytic hydrogen evolution activity of the BTT-COFs was observed to increase as its λmax exhibited a redshift, as observed in experiments [20]. Meanwhile, the presence of rotatable bonds in biphenyl and terphenyl leads to a blueshift in λmax. A comprehensive comparison was made between our computational results and the reference theoretical/experimental values. Our calculated Eex and λmax for BTT-COFs show consistent trends with those reported in the literature [8], with values obtained based on the CAM-B3LYP/def2-SVP level. Specifically, BTT-Tpa exhibits the lowest Eex (2.2 eV in this work as compared to 3.28 eV in the literature) and the longest λmax (571.4 nm in this work as compared to 378 nm in the literature). Although experimental UV–vis diffuse reflectance spectroscopy (DRS) shows systematic redshifts for BTT-COFs due to the inherent limitations of theoretical models and computational methods, our approach demonstrates a superior agreement with the experimental data when compared to the literature calculations. As listed in Table 2, the values of CT % revealed that BTT-Tpa (78.2%), BTT-Tapt (54.8%), and BTT-AnthDA (46.9%) exhibit a significant charge transfer between building block units and possess good photon-harvesting capabilities from sunlight. In addition, we found that Eex decreases with a smaller energy gap, increased conjugation, and the introduction of nitrogen heteroatoms.
2.5. IP, EA, and Reorganization Energies
The ionization potential (IP) [52] represents the minimum energy required for injecting a hole into the HOMO when an electron is removed from a molecule. On the other hand, electron affinity (EA) refers to the energy released by a molecule upon injection of an electron. A higher EA value indicates that the organic material is more likely to acquire electrons. Importantly, organic materials may undergo conformational reorganization, resulting in an energy cost during photoexcitation. This energy change is referred to as the reorganization energy (λ) of the organic material [53]. It is known that the electron transfer rate (KET) is related to the λ, which should have a smaller value to achieve higher electron injection efficiency [54,55]. As shown in Equation (5), λdiff is the difference between the hole reorganization energy (λhole) and the electron reorganization energy (λelectron). The DFT-calculated values of IP, EA, λhole, λelectron, and λdiff for seven BTT-COFs are shown in Figure 4 and listed in Table 3. All of the BTT-COFs exhibited higher IP values as compared to their EA values. The EA values (2.72~3.10 eV) of the BTT-COFs are remarkably similar, suggesting that these structures maintain high stability when electrons are injected. BTT-Tpa has the lowest IP value (4.71 eV), which is consistent with it having the smallest Eg (2.0 eV) and Eex (2.2 eV). The λhole values for BTT-Tapt and BTT-Tpa are found to be as low as 0.11 eV, while the λdiff values are relatively high at 0.18 eV. This result indicates that these two BTT-COFs exhibit superior hole transport capabilities compared to the others. Combining the analysis of the values of EA and IP, we concluded that the small value of λhole enhances charge transfer and facilitates exciton formation. Meanwhile, a low value of IP suggests a favorable condition for electron generation. Furthermore, the reduction in λhole can be attributed to the introduction of nitrogen heteroatoms and the enhanced coplanarity of the building block units in BTT-COFs.
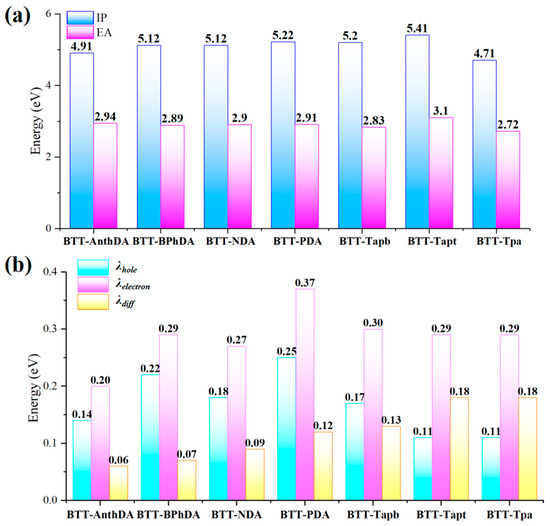
Figure 4.
DFT-calculated values (eV) of (a) IP, EA; (b) λhole, λelectron, and λdiff for seven BTT-COFs.

Table 3.
IP, EA, and reorganization energy (eV) of BTT-COFs.
2.6. Hole–Electron Quantitative Analysis
We employed quantitative analysis to characterize the hole–electron behavior of BTT-COFs. As shown in Figure 5, the charge density difference (CDD) and centroid region of charge transfer (CRCT) were used to visualize the regions of charge transfer and separation between the building block units. The blue and purple orbitals in the CDD correspond to a decrease and increase in charge density relative to the BTT and aromatic diamine units, respectively. The green and blue ellipsoids of CRCT represent the regions where charge transfer occurs in the excited state, corresponding to the holes and electrons of BTT-COFs, respectively. The path and direction of charge transfer in the BTT-COFs are effectively visualized at the molecular level through the CDD and CRCT plots.
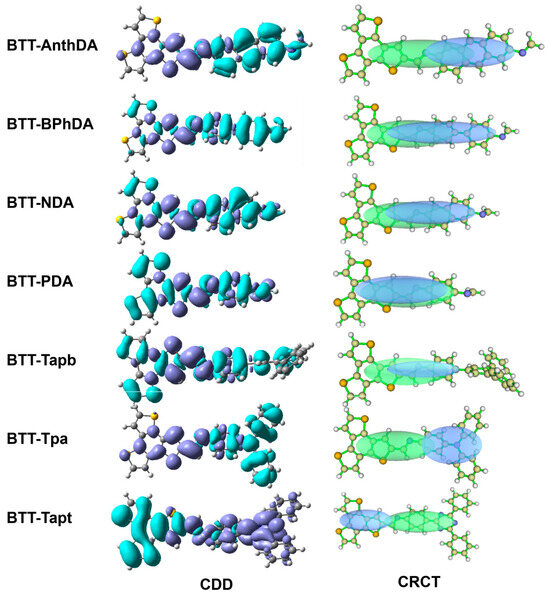
Figure 5.
Charge density difference (CDD) and centroid region of charge transfer (CRCT) plots of BTT-COFs.
By comparing the CDD and CRCT plots, it is evident that the shape of the blue–green ellipsoidal region, the degree of electron overlap between the hole and the electron, and the charge transfer pathway in the various BTT-COFs exhibit significant differences. The CDD plot reveals that there is a remarkable charge transfer from the blue (negative) region to the purple (positive) region between the building block units in most BTT-COFs. The BTT unit acts as the electron acceptor, and charge transfer occurs from the aromatic units to the BTT unit. Significantly, the direction of charge transfer was altered in BTT-Tapt, with electrons transferring from the BTT unit to the triazine unit. As shown in the CRCT plot, BTT-PDA exhibits the presence of holes and electrons in both the BTT and benzene units, leading to inconspicuous charge separation, as illustrated in the CDD and the HOMO/LUMO plot (Figure 2).
We also utilized a set of parameters (Table 4) to establish a quantitative correlation between the building block units and the charge separation and charge transfer within the different BTT-COFs. The Sr index quantifies the degree of overlap between electron and hole distributions; a lower Sr value indicates better charge separation in COFs. As listed in Table 4, it is evident that conjugated aromatic units result in larger Sr values (0.74 in BTT-AnthDA), thereby reducing charge separation (as shown in the CRCT plot in Figure 5). In addition, the introduction of nitrogen heteroatoms (such as triazine and triphenylamine) and a non-coplanar structure (such as triphenylbenzene) into the BTT-COFs can reduce Sr values and enhance charge separation efficiency. The t-index is another parameter that characterizes the degree of charge separation between the donor and acceptor units. A negative t value signifies that the hole and electron overlap, with greater absolute values indicating a larger overlap region. Conversely, a positive t value suggests that the donor and acceptor units are separated. BTT-AnthDA, BTT-Tapt, and BTT-Tpa exhibit positive t values (0.43, 3.66, and 3.57 Å in Table 4) and good charge separation between the holes and electrons, as shown in Figure 5. D is a parameter used to quantify the centroid distance between the electron and hole. BTT-PDA exhibits difficulty in separating holes and electrons, resulting in a shortened charge transfer distance with the minimum D value (0.7 Å). This finding is also consistent with its smallest t value (−3.01 Å). The CT index parameter quantitatively calculates the amount of charge (e) transferred between D-A units. By increasing the conjugation length of the aromatic units, the crucial parameters D, t, and CT decrease in the following order: BTT-AnthDA (5.33 Å, 0.43 Å, 0.46 e) < BTT-BPhDA (3.85 Å, −0.66 Å, 0.38 e) < BTT-NDA (2.67 Å, −1.62 Å, 0.42 e) < BTT-PDA (0.74 Å, −3.01 Å, 0.14 e). In contrast, BTT-Tapt demonstrates the highest degree of charge separation, with a t value of 3.66 Å, and the longest distance D value (7.75 Å) for charge transfer. Interestingly, the largest CT value (0.78 e) appears in BTT-Tpa, which may be attributed to the electronegativity of triphenylamine, the delocalization of its lone pair electrons, and the star-shaped configuration. These characteristics render it an optimal material for charge separation and charge transfer. The HDI and EDI indices signify the extent of hole and electron delocalization. These two parameters are closely associated with the geometric configuration of building block units in BTT-COFs.

Table 4.
Quantitative parameter of hole and electron for BTT-COFs.
By quantitatively analyzing the parameters and the CDD and CRCT plots that characterize the behavior of holes and electrons in BTT-COFs, we identified three critical factors—the conjugated structure, planarity, and the introduction of nitrogen heteroatoms—which significantly influence charge separation and transfer. The relationship between the building block units and the optoelectronic properties of BTT-COFs can be established by considering these parameters. It is noteworthy that the incorporation of triphenylamine as a building block unit in BTT-COFs significantly enhances charge separation and transfer as well as the charge-transport properties. A longer charge transfer distance between building block units leads to enhanced charge transfer and reduced excitation energy. This crucial observation serves as a fundamental basis for the selection of aromatic units in the design of innovative BTT-COFs for applications in photocatalytic reactions.
3. Computational Details
All of the calculations were performed in Gaussian 16 software [56]. We utilized a fragment to develop theoretical models, which comprised one BTT unit and seven conjugated and heteroatomic building units to represent BTT-COFs. The structures of BTT-COFs were optimized by using the DFT method at the M06L/6-31+G(d) level [57] to obtain their stable ground-state geometries in an aqueous environment. The M06L functional can provide an accurate depiction of charge transfer and long-range interactions [58]. We conducted frequency calculations to identify the local energy minima for each theoretical model at the M06L/6-31+G(d) level. We confirmed that the stable geometry for each BTT-COF corresponds to the local minima in energy, and they have no imaginary vibrational frequencies. The TD-DFT calculations were performed taking into account a total of ten excited states [59]. A solvent model (SMD) was employed in both the DFT and TD-DFT calculations [60]. Photocatalytic hydrogen generation catalyzed by BTT-COFs occurs in an aqueous solution, with water as the solvent. Consequently, water was the only solvent considered in the SMD model. Analysis of the frontier molecular orbitals (FMOs) and the geometries of BTT-COFs in an excited state was performed using single-point calculations at the M06L/6-31+G(d) level of theory. Based on the stable geometries of BTT-COFs, we calculated the ionization energy (IP), electron affinity (EA), hole recombination energy (λhole), electron recombination energy (λelectron), and the difference between hole and electron recombination energies (λdiff), as illustrated in Equations (1)–(5) [61,62].
IP = E+ (M+) − E0 (M0)
EA = E0 (M0) − E− (M−)
λhole = E0 (M+) − E0 (M0)
λelectron = E0 (M−) − E0 (M0)
λdiff = ∣λhole − λelectron∣
Here, E0 (M0), E+ (M+), and E− (M−) represent the energies of the neutral, anionic, and cationic species. E0 (M−) and E0 (M+) represent the energies of the neutral species with the geometries of the anionic and cationic species, respectively.
The electron cloud functions of the BTT-COFs were employed to quantitatively determine the parameters associated with the characteristics of holes and electrons in their excited states. Multiwfn 3.8 software [63] was used to analyze the characteristics of the holes and electrons of the BTT-COFs in excited states. The UV–vis absorption spectra of the BTT-COFs were simulated and plotted. Additionally, the charge difference density (CDD) [64] and centroid region of charge transfer (CRCT) [65] were visualized to elucidate the charge transfer regions of the BTT-COFs in the excited state. The quantitative parameters [66], including Sr, t, HDI, EDI, D, and CT, were utilized to characterize hole–electron properties and to establish the relationship between the D-π-A structures of BTT-COFs and their charge separation and charge transfer capabilities. The detailed presentation of the calculated quantitative parameters is provided as follows:
t = D − HCT
D represents the centroid distance between the hole and the electron, while x, y, and z represent the cartesian coordinates of the centroid hole and the electron; r represents the density of either holes or electrons; Sr (range [0, 1]) denotes the function that measures the degree of overlap between their distributions, with its value signifying how much they overlap; t represents the degree of separation between the holes and electrons; HCT measures the average dispersion of the holes and electrons in the direction of charge transfer; HDI represents the extent of hole delocalization; and EDI represents the extent of electron delocalization.
4. Conclusions
In this study, we explored the influence of building blocks on the optoelectronic properties of BTT-COFs by integrating DFT and TD-DFT calculations. The calculation results indicated that the BTT unit and various aromatic units within BTT-COFs formed D-π-A structures. Three critical factors—the conjugated structure, planarity, and the introduction of nitrogen heteroatoms—significantly influenced charge separation and transfer within BTT-COFs. The highly conjugated anthracene unit raised the HOMO energy, while the triazine unit lowered the LUMO energy. Quantifying the dihedral angle between the building block units enabled a precise assessment of planarity within BTT-COFs. Furthermore, the coplanarity of BTT-COFs was efficiently enhanced through the integration of conjugated units into the BTT unit. The introduction of nitrogen heteroatoms and the enhancement of coplanarity in BTT-COFs led to a notable redshift in the UV–vis absorption spectrum. The charge difference density (CDD) and centroid region of charge transfer (CRCT) were employed to quantitatively visualize the degree and distribution of charge transfer at a molecular level. The relationship between the “building block and optoelectronic properties” of BTT-COFs was established through several critical quantitative parameters, including Sr, t, and CT. By calculating the CT index, the amount of charge (e) transferred between the building block units of COFs could be quantitatively determined, which was utilized to predict the efficiency of light utilization. At the molecular level, the smaller Sr and more positive t values of COFs also suggested superior charge separation between building block units. The two parameters, along with CT, played a crucial role in predicting the photocatalytic performance of COFs. Among the seven BTT-COFs, BTT-Tap exhibited the most efficient charge separation and the highest charge transfer capability. This superior performance can likely be attributed to the electronegativity of triphenylamine, the delocalization of its lone pair electrons, and its unique star-shaped configuration. The molecular-level insights gained from this theoretical study help elucidate the relationship between building blocks and the optoelectronic properties in BTT-COFs. These observations provide the essential foundation for selecting D-A units in the design of novel BTT-COFs for photocatalytic reaction applications.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal15070647/s1, Figure S1: Crystal structure and its planarity from experimental simulation data. The atomic coordination structure of the optimized BTT-COFs.
Author Contributions
X.L.: Reviewing, editing, and supervision. Y.N., K.M., X.H.: Writing—original draft preparation. Q.W. Resources, conceptualization, and supervision. Z.L.: Software, reviewing, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number [21905053], the Open Project of the State Key Laboratory of Inorganic Synthesis and Preparation of Jilin University grant number [2022-14], the Hainan Normal University Student Innovation and Entrepreneurship Open Fund grant number [X11658024, X11658014], Teaching Reform Project of Hainan Normal University grant number [hsjg2025-12] and Less Developed Regions of the National Natural Science Foundation of China grant number [62463003].
Data Availability Statement
Data is contained within the supplementary material.
Acknowledgments
The authors acknowledge the support provided by the “Innovation Center of Academician Sun Shigang’s Team in Hainan Province” for supplying all computing resources.
Conflicts of Interest
The authors declare no competing financial interests.
References
- Diercks, C.S.; Yaghi, O.M. The atom, the molecule, and the covalent organic framework. Science 2017, 355, eaal1585. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Wang, L.; Xu, H.; Wu, X.; Yang, J. A simple molecular design strategy for two-dimensional covalent organic framework capable of visible-light-driven water splitting. J. Am. Chem. Soc. 2020, 142, 4508–4516. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, Y.; Jiang, L.; Li, J.; Li, J.; Jia, J.; Yavuz, C.T.; Cui, F.; Jing, X.; Zhu, G. Ultrahigh Single Au Atoms Loaded Porous Aromatic Frameworks for Enhanced Photocatalytic Hydrogen Evolution. Adv. Mater. 2024, 36, 2404791. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, D. Covalent Organic Frameworks for Heterogeneous Catalysis: Principle, Current Status, and Challenges. ACS Cent. Sci. 2020, 6, 869–879. [Google Scholar] [CrossRef]
- Li, W.; Huang, X.; Zeng, T.; Liu, Y.A.; Hu, W.; Yang, H.; Zhang, Y.B.; Wen, K. Thiazolo [5, 4-d] thiazole-based donor–acceptor covalent organic framework for sunlight-driven hydrogen evolution. Angew. Chem. Int. Ed. 2021, 60, 1869–1874. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, L.; He, H.; Sun, L.; Wang, H.; Fang, X.; Zhao, Y.; Zheng, D.; Qi, Y.; Li, Z. In situ photodeposition of platinum clusters on a covalent organic framework for photocatalytic hydrogen production. Nat. Commun. 2022, 13, 1355. [Google Scholar] [CrossRef]
- Stegbauer, L.; Zech, S.; Savasci, G.; Banerjee, T.; Podjaski, F.; Schwinghammer, K.; Ochsenfeld, C.; Lotsch, B.V. Tailor-Made Photoconductive Pyrene-Based Covalent Organic Frameworks for Visible-Light Driven Hydrogen Generation. Adv. Energy Mater. 2018, 8, 1703278. [Google Scholar] [CrossRef]
- Qin, C.; Wu, X.; Tang, L.; Chen, X.; Li, M.; Mou, Y.; Su, B.; Wang, S.; Feng, C.; Liu, J. Dual donor-acceptor covalent organic frameworks for hydrogen peroxide photosynthesis. Nat. Commun. 2023, 14, 5238. [Google Scholar] [CrossRef]
- Yang, Q.; Luo, M.; Liu, K.; Cao, H.; Yan, H. Covalent organic frameworks for photocatalytic applications. Appl. Catal. B Environ. 2020, 276, 119174. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Z.; Zhang, L.; Zhang, Q. Covalent Organic Frameworks for Photocatalytic Reduction of Carbon Dioxide: A Review. ACS Nano 2024, 18, 21804–21835. [Google Scholar] [CrossRef]
- Wang, L.; Liu, L.; Li, Y.; Xu, Y.; Nie, W.; Cheng, Z.; Zhou, Q.; Wang, L.; Fan, Z. Molecular-Level Regulation Strategies Toward Efficient Charge Separation in Donor− Acceptor Type Conjugated Polymers for Boosted Energy-Related Photocatalysis. Adv. Energy Mater. 2024, 14, 2303346. [Google Scholar] [CrossRef]
- Gao, P.; Wang, M.; Chen, Y.; Pan, W.; Zhou, P.; Wan, X.; Li, N.; Tang, B. A COF-based nanoplatform for highly efficient cancer diagnosis, photodynamic therapy and prognosis. Chem. Sci. 2020, 11, 6882–6888. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Wang, Z.; Tang, L.; Zeng, G.; Xu, P.; Chen, M.; Xiong, T.; Zhou, C.; Li, X. Covalent organic framework photocatalysts: Structures and applications. Chem. Soc. Rev. 2020, 49, 4135–4165. [Google Scholar] [CrossRef]
- Wang, G.-B.; Li, S.; Yan, C.-X.; Zhu, F.-C.; Lin, Q.-Q.; Xie, K.-H.; Geng, Y.; Dong, Y.-B. Covalent organic frameworks: Emerging high-performance platforms for efficient photocatalytic applications. J. Mater. Chem. A 2020, 8, 6957–6983. [Google Scholar] [CrossRef]
- Sun, R.; Yang, X.; Hu, X.; Guo, Y.; Zhang, Y.; Shu, C.; Yang, X.; Gao, H.; Wang, X.; Hussain, I. Unprecedented photocatalytic hydrogen peroxide production via covalent triazine frameworks constructed from fused building blocks. Angew. Chem. Int. Ed. 2025, 137, e202416350. [Google Scholar] [CrossRef]
- Nicolas, Y.; Blanchard, P.; Levillain, E.; Allain, M.; Mercier, N.; Roncali, J. Planarized star-shaped oligothiophenes with enhanced π-electron delocalization. Org. Lett. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Wei, H.; Ning, J.; Cao, X.; Li, X.; Hao, L. Benzotrithiophene-Based Covalent Organic Frameworks: Construction and Structure Transformation under Ionothermal Condition. J. Am. Chem. Soc. 2018, 140, 11618–11622. [Google Scholar] [CrossRef]
- Liu, X.; Yang, X.; Ding, X.; Wang, H.; Cao, W.; Jin, Y.; Yu, B.; Jiang, J. Covalent organic frameworks with imine proton acceptors for efficient photocatalytic H2 production. Chin. Chem. Lett. 2023, 34, 108148. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Nie, R.; Li, C.; Sun, Q.; Shi, W.; Chu, W.; Long, Y.; Li, H.; Liu, X. Construction of stable donor–acceptor type covalent organic frameworks as functional platform for effective perovskite solar cell enhancement. Adv. Funct. Mater. 2022, 32, 2112553. [Google Scholar] [CrossRef]
- Liu, H.; Zheng, X.; Xu, J.; Jia, X.; Chao, M.; Wang, D.; Zhao, Y. Structural regulation of thiophene-based two-dimensional covalent organic frameworks toward highly efficient photocatalytic hydrogen generation. ACS Appl. Mater. Inter. 2023, 15, 16794. [Google Scholar] [CrossRef]
- Kou, J.; Wang, G.; Guo, H.; Li, L.; Fang, J.; Ma, J.; Dong, Z. Photocatalytic benzylamine coupling dominated by modulation of linkers in donor-acceptor covalent organic frameworks. Appl. Catal. B Environ. 2024, 352, 124020. [Google Scholar] [CrossRef]
- Liu, M.; He, P.; Gong, H.; Zhao, Z.; Li, Y.; Zhou, K.; Lin, Y.; Li, J.; Bao, Z.; Yang, Q. Benzotrithiophene-based covalent organic frameworks as efficient catalysts for artificial photosynthesis of H2O2 in pure water. Chem. Eng. J. 2024, 482, 148922. [Google Scholar] [CrossRef]
- Che, Q.; Li, C.; Chen, Z.; Yang, S.; Zhang, W.; Yu, G. High Performance Memristors Based on Imine-Linked Covalent Organic Frameworks Obtained Using a Protonation Modification Strategy. Angew. Chem. Int. Ed. 2024, 136, e202409926. [Google Scholar] [CrossRef]
- Luo, B.; Zhang, Y.; Chen, Y.; Huo, J. Photocatalytic conversion of arylboronic acids to phenols by a new 2D donor–acceptor covalent organic framework. Mater. Adv. 2022, 3, 4699–4706. [Google Scholar] [CrossRef]
- Cui, W.-R.; Li, Y.-J.; Jiang, Q.-Q.; Wu, Q.; Liang, R.-P.; Luo, Q.-X.; Zhang, L.; Liu, J.; Qiu, J.-D. Tunable covalent organic framework electrochemiluminescence from non-electroluminescent monomers. Cell Rep. Phys. Sci. 2022, 3, 100630. [Google Scholar] [CrossRef]
- Jeon, J.P.; Kim, Y.J.; Joo, S.H.; Noh, H.J.; Kwak, S.K.; Baek, J.B. Benzotrithiophene-based Covalent Organic Framework Photocatalysts with Controlled Conjugation of Building Blocks for Charge Stabilization. Angew. Chem. Int. Ed. 2023, 135, e202217416. [Google Scholar] [CrossRef]
- Feng, G.; Cheng, P.; Yan, W.; Boronat, M.; Li, X.; Su, J.-H.; Wang, J.; Li, Y.; Corma, A.; Xu, R. Accelerated crystallization of zeolites via hydroxyl free radicals. Science 2016, 351, 1188. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Liu, J.; Duan, F.; Yu, J. In silico prediction and screening of modular crystal structures via a high-throughput genomic approach. Nat. Commun. 2015, 6, 8328. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J. Methanol-to-olefin conversion in ABC-6 zeolite cavities: Unravelling the role of cavity shape and size from density functional theory calculations. Phys. Chem. Chem. Phys. 2018, 20, 14322. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J. Molecular design of chiral zirconium metal–organic frameworks for asymmetric transfer hydrogenation of imines. Catal. Sci. Technol. 2019, 9, 4888. [Google Scholar] [CrossRef]
- Xu Li, A.K.C. Jianwen Jiang, CO2 cycloaddition with propylene oxide to form propylene carbonate on a copper metal-organic framework: A density functional theory study. Mol. Catal. 2019, 463, 37. [Google Scholar]
- Dong, J.; Li, X.; Peh, S.B.; Yuan, Y.D.; Wang, Y.; Ji, D.; Peng, S.; Liu, G.; Ying, S.; Yuan, D.; et al. Restriction of Molecular Rotors in Ultrathin Two-Dimensional Covalent Organic Framework Nanosheets for Sensing Signal Amplification. Chem. Mater. 2018, 31, 146. [Google Scholar] [CrossRef]
- Jiao, J.; Li, Z.; Qiao, Z.; Li, X.; Liu, Y.; Dong, J.; Jiang, J.; Cui, Y. Design and self-assembly of hexahedral coordination cages for cascade reactions. Nat. Commun. 2018, 9, 4423. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lu, J.; Li, Y.; Yu, J. Roles of Hydroxyl Groups During Side-Chain Alkylation of Toluene with Methanol over Zeolite Na-Y: A Density Functional Theory Study. Chin. J. Chem. 2017, 35, 716–722. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, H.; Li, X.; Hou, B.; Gong, W.; Wu, X.; Han, X.; Zheng, F.; Liu, Y.; Jiang, J. Chiral phosphoric acids in metal–organic frameworks with enhanced acidity and tunable catalytic selectivity. Angew. Chem. Int. Ed. 2019, 131, 14890. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Krishna, R.; Liu, Y.; Cui, Y.; Du, J.; Liang, Z.; Song, X.; Yu, J. Enhancing CO2 adsorption and separation properties of aluminophosphate zeolites by isomorphous heteroatom substitutions. ACS Appl. Mater. Interfaces 2018, 10, 43570. [Google Scholar] [CrossRef]
- Sun, X.; Li, X.; Yao, S.; Krishna, R.; Gu, J.; Li, G.; Liu, Y. A multifunctional double walled zirconium metal–organic framework: High performance for CO2 adsorption and separation and detecting explosives in the aqueous phase. J. Mater. Chem. A 2020, 8, 17106. [Google Scholar] [CrossRef]
- Liu, K.; Li, B.; Li, Y.; Li, X.; Yang, F.; Zeng, G.; Peng, Y.; Zhang, Z.; Li, G.; Shi, Z. An N-rich metal–organic framework with an rht topology: High CO2 and C2 hydrocarbons uptake and selective capture from CH4. Chem. Commun. 2014, 50, 5031. [Google Scholar] [CrossRef]
- Tang, H.; Duan, L.; Jiang, J. Leveraging Machine Learning for Metal–Organic Frameworks: A Perspective. Langmuir 2023, 39, 15849. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Li, L.; Shi, T. Effect of methyl trifluoride substitution on colorless transparency of polyimide: A DFT/TD-DFT study. J. Mol. Liq. 2024, 411, 125691. [Google Scholar] [CrossRef]
- Xun, S.; Li, H.; Sini, G.; Bredas, J.-L. Impact of Imine Bond Orientations on the Geometric and Electronic Structures of Imine-based Covalent Organic Frameworks. Chem. Asian J. 2021, 16, 3781. [Google Scholar] [CrossRef] [PubMed]
- Mourino, B.; Jablonka, K.M.; Ortega-Guerrero, A.; Smit, B. In Search of Covalent Organic Framework Photocatalysts: A DFT-Based Screening Approach. Adv. Funct. Mater. 2023, 33, 2301594. [Google Scholar] [CrossRef]
- Guan, X.; Qian, Y.; Zhang, X.; Jiang, H.L. Enaminone-Linked Covalent Organic Frameworks for Boosting Photocatalytic Hydrogen Production. Angew. Chem. 2023, 135, e202306135. [Google Scholar] [CrossRef]
- Shi, Y.; Ma, H.; Sun, Z.; Zhao, W.; Sun, G.; Peng, Q. Optimal dihedral angle in twisted donor–acceptor organic emitters for maximized thermally activated delayed fluorescence. Angew. Chem. Int. Ed. 2022, 134, e202213463. [Google Scholar] [CrossRef]
- Calbo, J.; Viruela, R.; Aragó, J.; Ortí, E. Theoretical insights into the structural, electronic and optical properties of benzotrithiophene-based hole-transporting materials. Theor. Chem. Acc. 2017, 136, 73. [Google Scholar] [CrossRef]
- Dhiman, A.; Ramachandran, C.N. Stacking interaction and opto-electronic properties of star-shaped benzotrithiophene and its extended derivatives. Chem. Phys. Let. 2024, 852, 141503. [Google Scholar] [CrossRef]
- Tripathi, A.; Chetti, P. Optoelectronic properties of benzotrithiophene isomers: A density functional theory study. J. Chin. Chem. Soc. 2019, 66, 891. [Google Scholar] [CrossRef]
- Tripathi, A.; Kozaderov, O.; Shikhaliev, K.; Prabhakar, C. A DFT study on optical, electronic, and charge transport properties of star-shaped benzo [1, 2-b: 3, 4-b′: 5, 6-b′trithiophene oligomers. J. Phys. Org. Chem. 2020, 33, e4037. [Google Scholar] [CrossRef]
- Zhu, C.; Wei, T.; Wei, Y.; Wang, L.; Lu, M.; Yuan, Y.; Yin, L.; Huang, L. Unravelling intramolecular charge transfer in donor–acceptor structured g-C3N4 for superior photocatalytic hydrogen evolution. J. Phys. Chem. A 2021, 9, 1207. [Google Scholar] [CrossRef]
- Song, X.-F.; Jiang, C.; Li, N.; Miao, J.; Li, K.; Yang, C. Simultaneously enhancing the planarity and electron-donating capability of donors for through-space charge transfer TADF towards deep-red emission. Chem. Sci. 2023, 14, 12246. [Google Scholar] [CrossRef]
- Shao, S.; Hu, J.; Wang, X.; Wang, L.; Jing, X.; Wang, F. Blue Thermally Activated Delayed Fluorescence Polymers with Nonconjugated Backbone and Through-Space Charge Transfer Effect. J. Am. Chem. Soc. 2017, 139, 17739. [Google Scholar] [CrossRef] [PubMed]
- Zhan, C.-G.; Nichols, J.A.; Dixon, D.A. Ionization Potential, Electron Affinity, Electronegativity, Hardness, and Electron Excitation Energy: Molecular Properties from Density Functional Theory Orbital Energies. J. Phys. Chem. A 2003, 107, 4184. [Google Scholar] [CrossRef]
- Brunschwig, B.S.; Sutin, N. Energy surfaces, reorganization energies, and coupling elements in electron transfer. Coord. Chem. Rev. 1999, 187, 233. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of electron-transfer reactions. VI. Unified treatment for homogeneous and electrode reactions. J. Chem. Phys. 1965, 43, 679. [Google Scholar] [CrossRef]
- Tant, J.; Geerts, Y.H.; Lehmann, M.; De Cupere, V.; Zucchi, G.; Laursen, B.W.; Bjørnholm, T.; Lemaur, V.; Marcq, V.; Burquel, A. Liquid crystalline metal-free phthalocyanines designed for charge and exciton transport. J. Phys. Chem. B 2005, 109, 20315. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.B.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16; Gaussian. Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157. [Google Scholar] [CrossRef]
- Walker, M.; Harvey, A.J.; Sen, A.; Dessent, C.E. Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions. J. Phys. Chem. A. 2013, 117, 12590. [Google Scholar] [CrossRef] [PubMed]
- Laurent, A.D.; Jacquemin, D. TD-DFT benchmarks: A review. Nt. J. Quantum Chem. 2013, 113, 2019. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378. [Google Scholar] [CrossRef]
- Tripathi, A.; Prabhakar, C. Optoelectronic and charge-transport properties of truxene, isotruxene, and its heteroatomic (N, O, Si, and S) analogs: A DFT study. J. Phys. Org. Chem. 2019, 32, 9. [Google Scholar] [CrossRef]
- Ren, X.F.; Ren, A.M.; Feng, J.K.; Sun, C.C. A density functional theory study on photophysical properties of red light-emitting materials: Meso-substituted porphyrins. J. Photoch. Photobio. A 2009, 203, 92. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.; Srivastava, A.; Kumar, P.; Tandon, P.; Maurya, R.; Singh, R. Vibrational spectroscopic, NBO, AIM, and multiwfn study of tectorigenin: A DFT approach. J. Mol. Struct. 2020, 1217, 128443. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, Y.; Li, Z.; Tang, Z.; Tian, J.; Fei, X. Investigating the influence of electronic effects of functional groups on the fluorescence mechanism of probes in water samples. J. Phys. Chem. A 2021, 125, 2866. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Chen, Q. An sp-hybridized all-carboatomic ring, cyclo [18] carbon: Electronic structure, electronic spectrum, and optical nonlinearity. Carbon 2021, 165, 461. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).