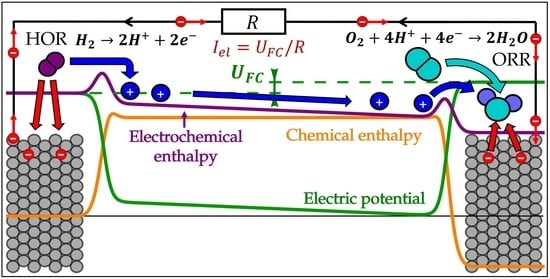
Educational Scale-Bridging Approach towards Modelling of Electric Potential, Electrochemical Reactions, and Species Transport in PEM Fuel Cell
Abstract
1. Introduction
- Why do two different reactants fed to two electrodes produce a finite voltage or potential difference?
- Why and how does the choice of reactants affect the fuel cell voltage?
- Why do hydrogen molecules at the anode of the fuel cell preferentially decompose into two protons and two electrons, even though the products have much higher chemical energy?
- What is overpotential or, an even more intriguing version of this question: is overpotential a cause or a consequence of the electrochemical process in the fuel cell?
- Why does the voltage of a fuel cell decrease with increasing current density?
- What forces the protons to travel through the membrane from the anode to the cathode side of the fuel cell?
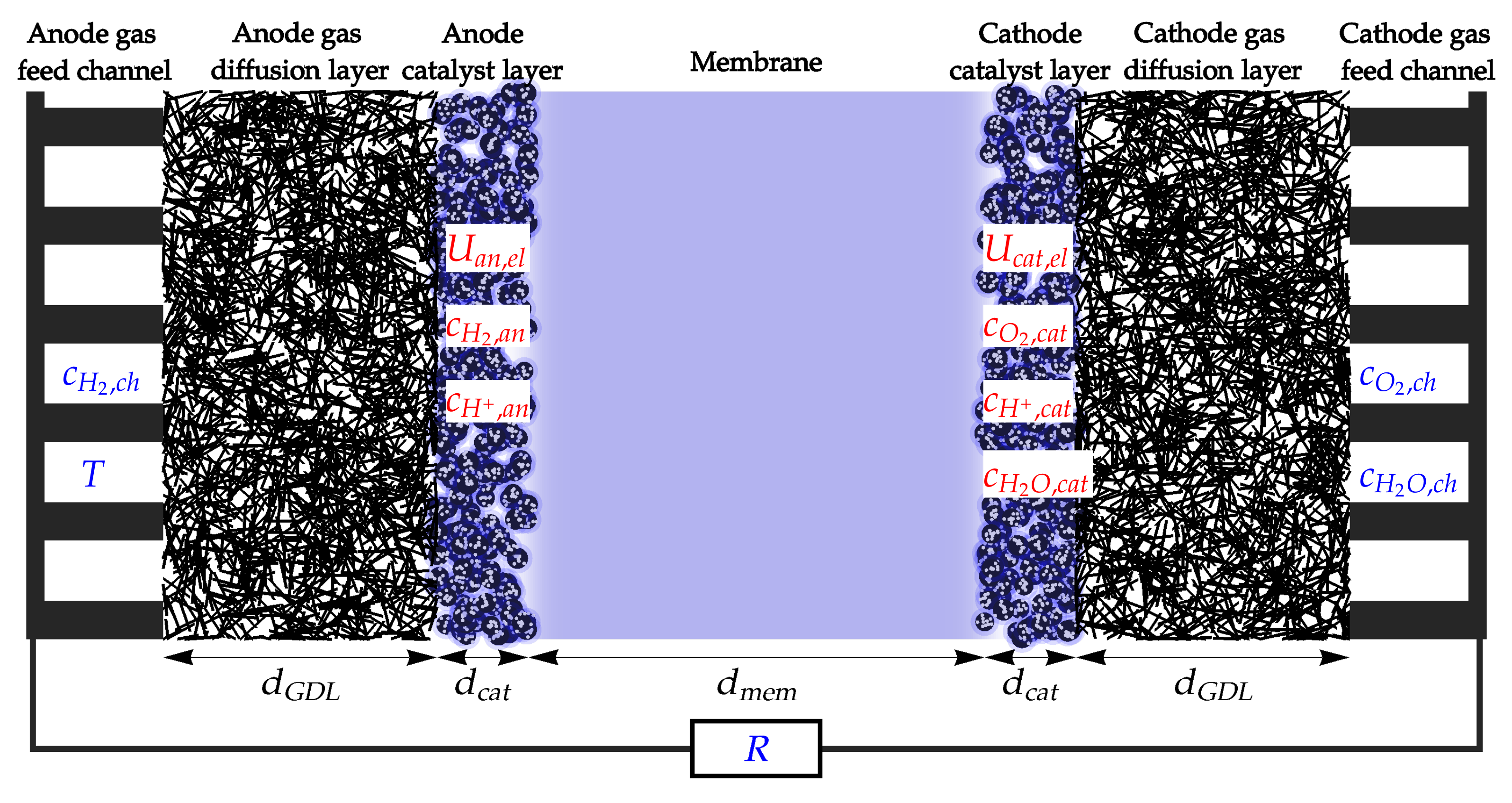
2. Model Description
- – hydrogen concentration in the anode catalyst layer;
- – oxygen concentration in the cathode catalyst layer;
- – water concentration in the cathode catalyst layer;
- – proton concentration in the anode catalyst layer;
- – proton concentration in the cathode catalyst layer;
- – anode catalyst electric potential;
- – cathode catalyst electric potential.
- – hydrogen concentration in the anode gas feed channel;
- – oxygen concentration in the cathode gas feed channel;
- – water concentration in the cathode gas feed channel;
- – fuel cell temperature;
- – electric resistivity of the external load.
- Electrochemical (EC) processes in the anode and cathode catalyst layer;
- Diffusion (dif) of gaseous reactants and products through the GDL;
- Proton transport through the membrane (mem);
- Electron (el) transport through the external electric load.
3. Electrochemical Processes on Hydrogen Electrode
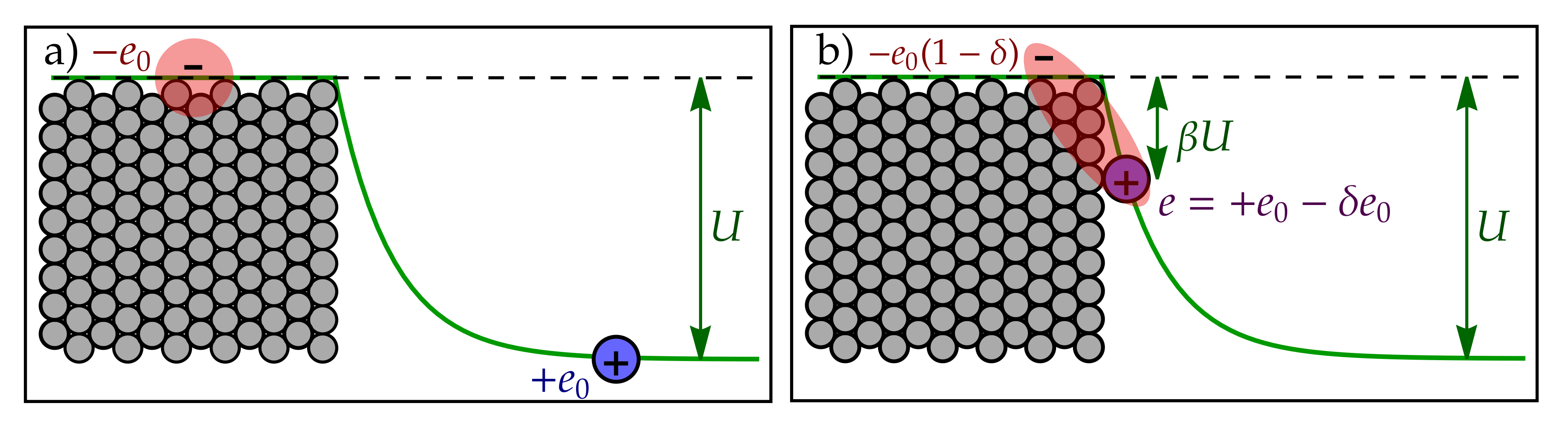
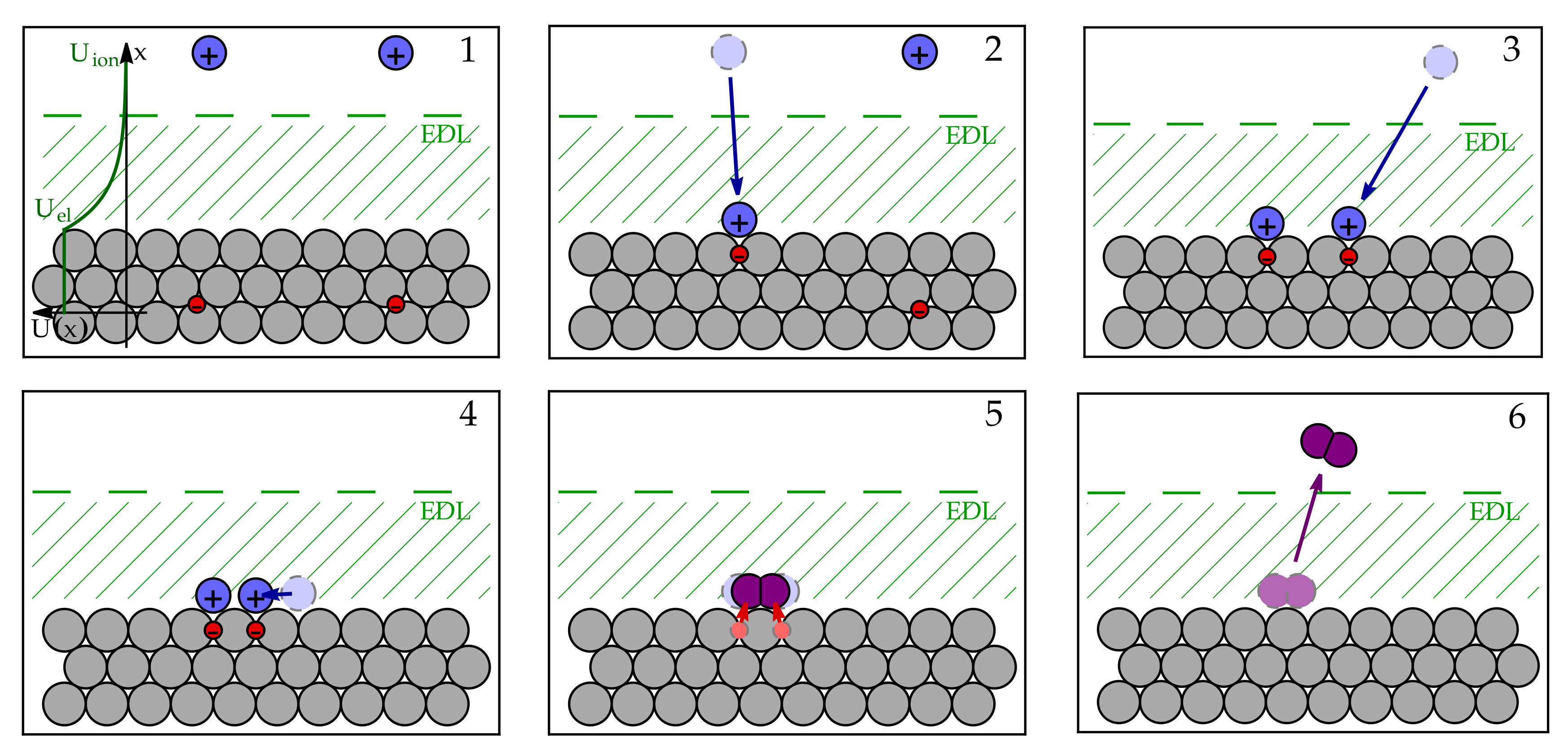
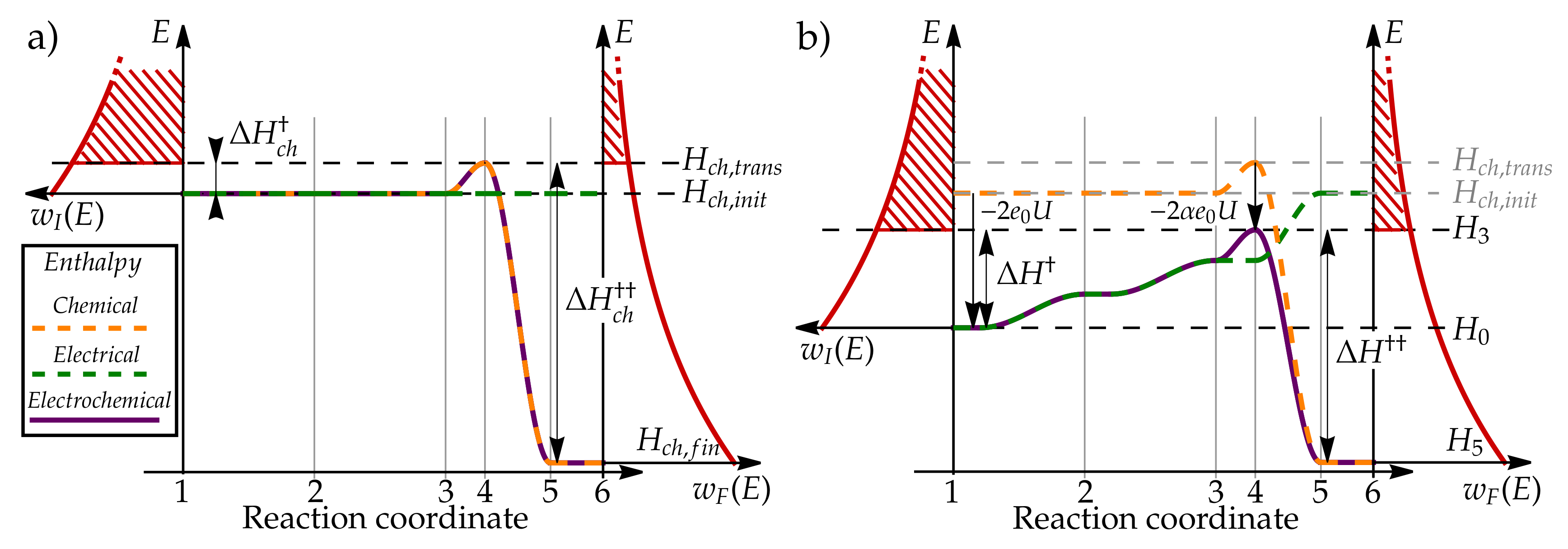
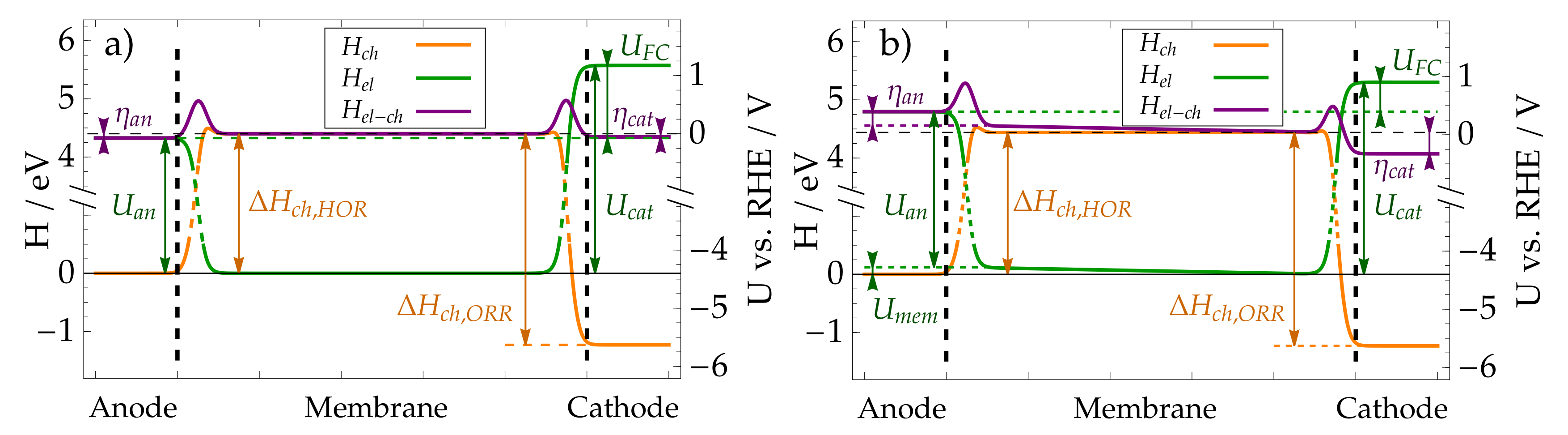
3.1. Microscopic Picture of an Electrochemical Reaction
3.2. Simple Kinetic Model of Electrochemical Reaction Rates
3.3. Equilibrium Electric Potential
3.4. Nernst Equation
3.5. Butler–Volmer Equation
3.6. Electrochemical Processes in the Fuel Cell Anode Catalyst Layer
4. Cathode Electrochemical Processes
4.1. Kinetic Model of Cathode Reaction Rates
4.2. Butler–Volmer Equation
4.3. Electrochemical Processes in Fuel Cell Cathode Catalyst Layer
5. Gaseous Species Transport
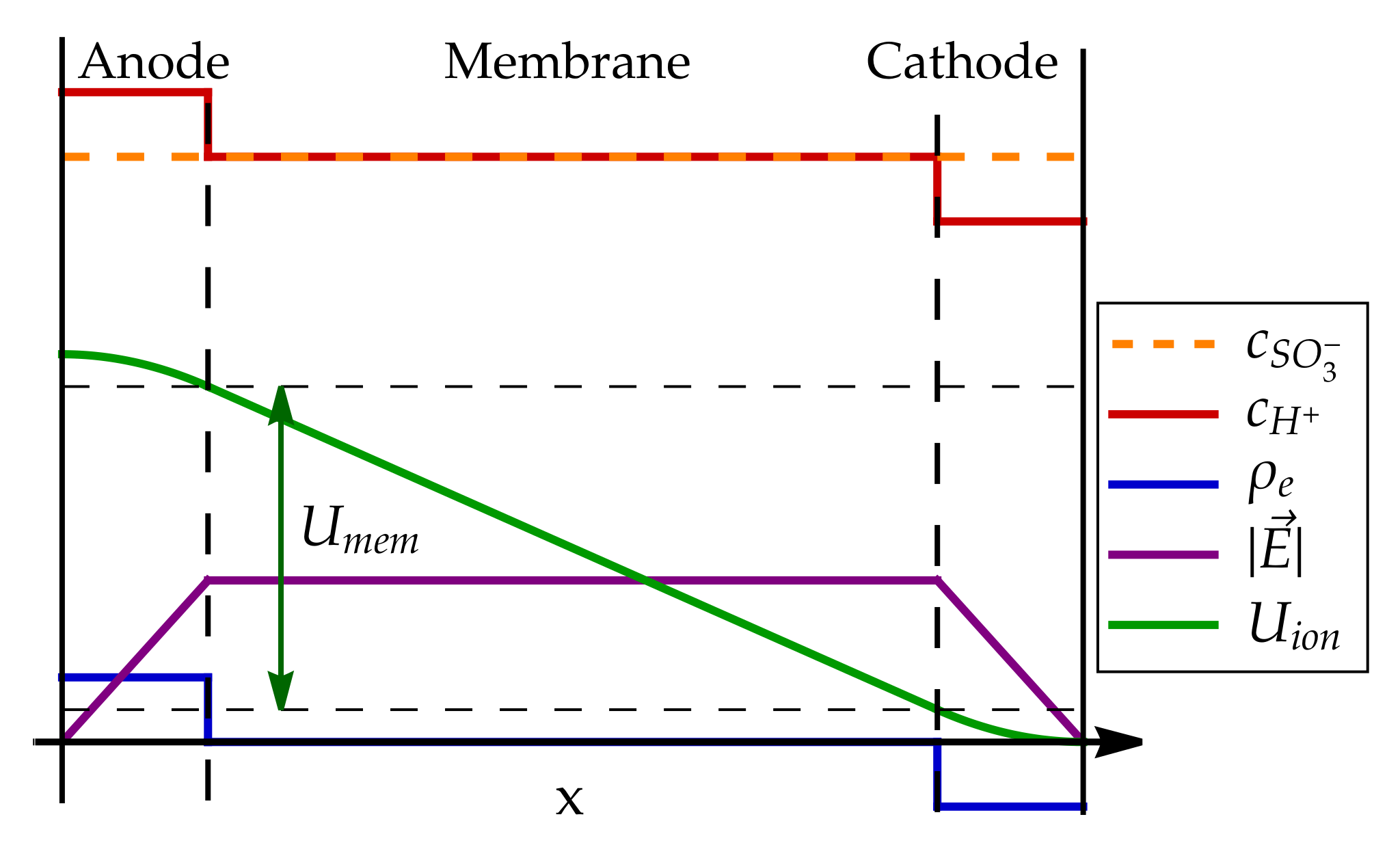
6. Proton Transport in the Fuel Cell Membrane
7. Electron Transport
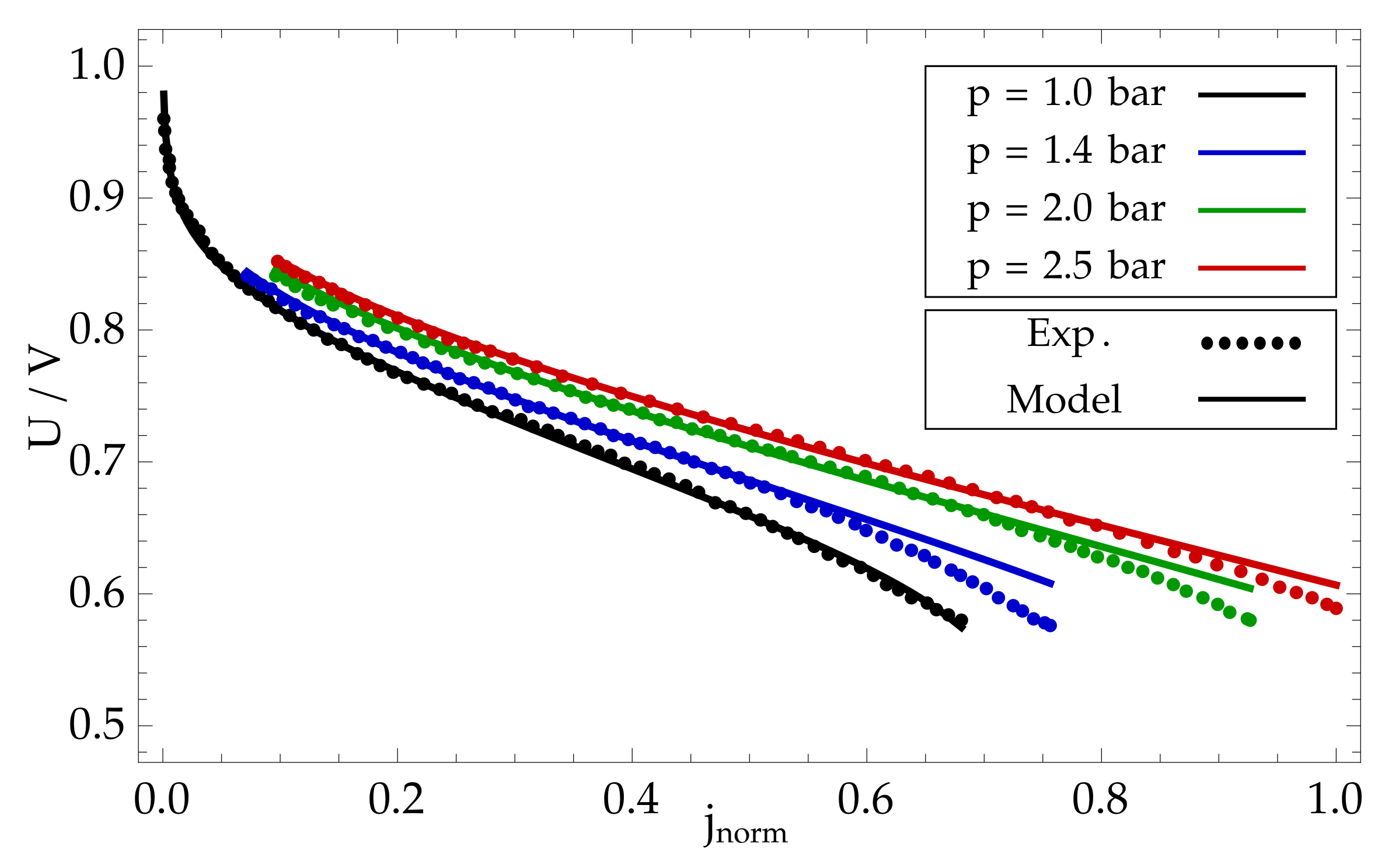
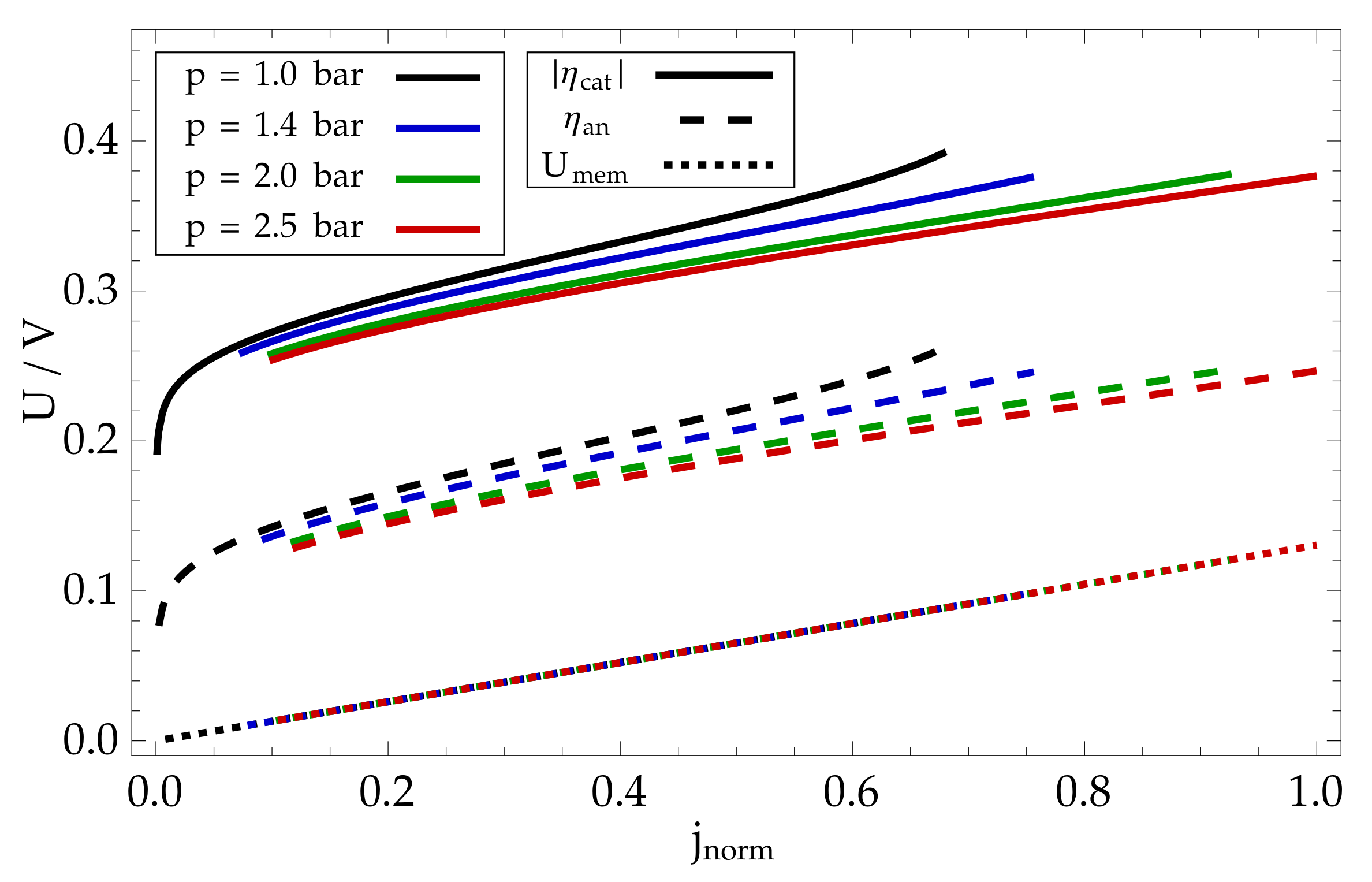
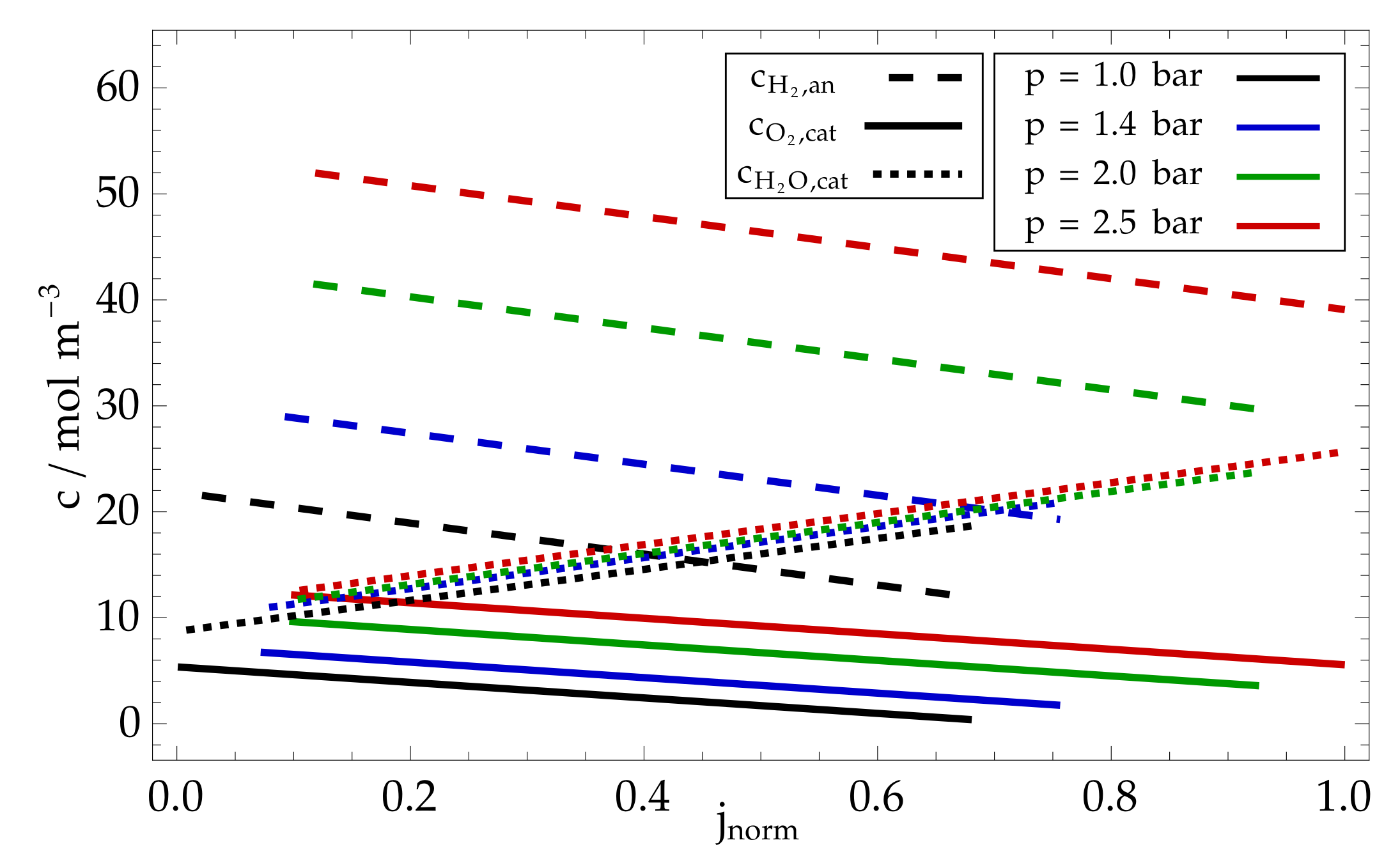
8. Modelling Results and Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Electrostatic Energy of Transition States
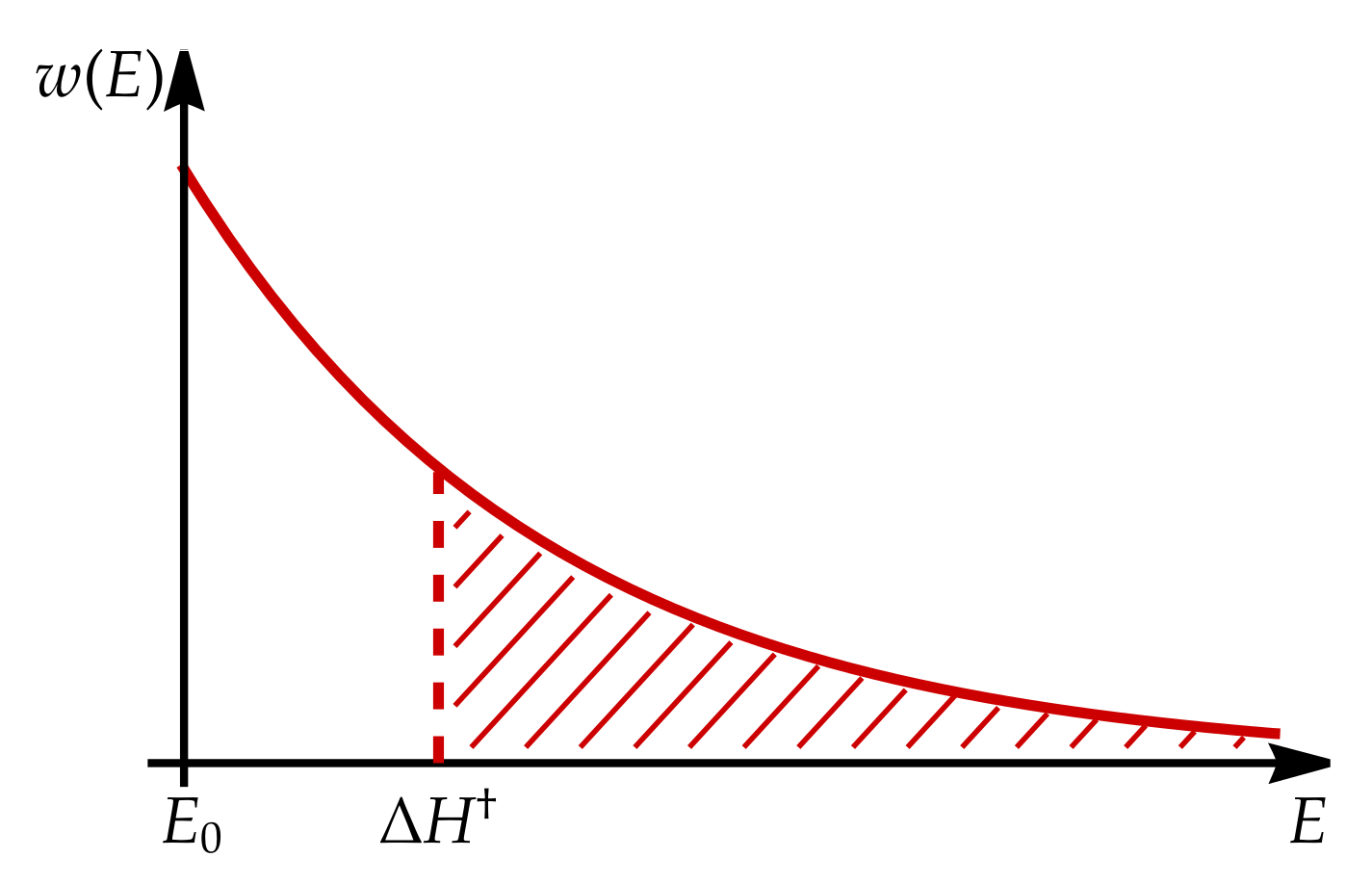
Appendix B. Boltzmann Distribution
Appendix C. Model Calibration
| Fixed Parameter | Value | Source | Fitted Parameter | Value | Source |
|---|---|---|---|---|---|
| 25 cm | assumed | mol/m s | fitted | ||
| 1 m | assumed | mol/m s | fitted | ||
| 5 m | assumed | 0.65 | fitted | ||
| 30 m | assumed | 0.74 | fitted | ||
| 30% | Ref. [45] | 0.29 | fitted | ||
| 50% | Ref. [45] | m/s | fitted | ||
| 60 m/g | assumed | S/m | fitted | ||
| 3 g/m | assumed | ||||
| 20 | Ref. [42] | ||||
| 0.122 nm | Calc. from [46] |
References
- Atkins, P.; de Paula, J. Physical Chemistry, 8th ed.; W. H. Freeman and Company: New York, NY, USA, 2006. [Google Scholar]
- Zaidi, S.M.J.; Rauf, M.A. Fuel Cell Fundamentals. In Polymer Membranes for Fuel Cells; Springer: Boston, MA, USA, 2008; pp. 1–6. [Google Scholar] [CrossRef]
- O’Hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Lee, T.W.; Tseng, A.A.; Bae, K.S.; Do, Y.H. Simulation of the Proton-Exchange Membrane (PEM) Fuel Cell Life-Cycle Performance with Data-Driven Parameter Estimation. Energy Fuels 2010, 24, 1882–1888. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zerhouni, N.; Hissel, D. Prognostics of Proton Exchange Membrane Fuel Cells stack using an ensemble of constraints based connectionist networks. J. Power Sources 2016, 324, 745–757. [Google Scholar] [CrossRef]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.; Briois, P.; Gao, F. Data-driven proton exchange membrane fuel cell degradation predication through deep learning method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Silva, R.; Gouriveau, R.; Jemeï, S.; Hissel, D.; Boulon, L.; Agbossou, K.; Yousfi Steiner, N. Proton exchange membrane fuel cell degradation prediction based on Adaptive Neuro-Fuzzy Inference Systems. Int. J. Hydrogen Energy 2014, 39, 11128–11144. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Zhu, C.; Su, H.; Hou, M. Prognostics of Proton Exchange Membrane Fuel Cells Using A Model-based Method. IFAC-PapersOnLine 2017, 50, 4757–4762. [Google Scholar] [CrossRef]
- Pisani, L.; Murgia, G.; Valentini, M.; D’Aguanno, B. A new semi-empirical approach to performance curves of polymer electrolyte fuel cells. J. Power Sources 2002, 108, 192–203. [Google Scholar] [CrossRef]
- Haji, S. Analytical modeling of PEM fuel cell i–V curve. Renew. Energy 2011, 36, 451–458. [Google Scholar] [CrossRef]
- Hao, D.; Shen, J.; Hou, Y.; Zhou, Y.; Wang, H. An Improved Empirical Fuel Cell Polarization Curve Model Based on Review Analysis. Int. J. Chem. Eng. 2016, 2016, 4109204. [Google Scholar] [CrossRef]
- Youssef, M.; Al-Nadi, K.E.; Khalil, M.H. Lumped model for proton exchange membrane fuel cell (PEMFC). Int. J. Electrochem. Sci. 2010, 5, 267–277. [Google Scholar] [CrossRef]
- Larminie, J. Fuel Cell Systems Explained; Larminie, J., Dicks, A., Eds.; J. Wiley: Chichester, UK, 2003. [Google Scholar]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harris, T.J. Performance Modeling of the Ballard Mark IV Solid Polymer Electrolyte Fuel Cell: II. Empirical Model Development. J. Electrochem. Soc. 1995, 142, 9–15. [Google Scholar] [CrossRef]
- Mann, R.F.; Amphlett, J.C.; Hooper, M.A.; Jensen, H.M.; Peppley, B.A.; Roberge, P.R. Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. J. Power Sources 2000, 86, 173–180. [Google Scholar] [CrossRef]
- Correa, J.M.; Farret, F.A.; Canha, L.N.; Simoes, M.G. An electrochemical-based fuel-cell model suitable for electrical engineering automation approach. IEEE Trans. Ind. Electron. 2004, 51, 1103–1112. [Google Scholar] [CrossRef]
- Robin, C.; Gerard, M.; Franco, A.A.; Schott, P. Multi-scale coupling between two dynamical models for PEMFC aging prediction. Int. J. Hydrogen Energy 2013, 38, 4675–4688. [Google Scholar] [CrossRef]
- Chandesris, M.; Vincent, R.; Guetaz, L.; Roch, J.S.; Thoby, D.; Quinaud, M. Membrane degradation in PEM fuel cells: From experimental results to semi-empirical degradation laws. Int. J. Hydrogen Energy 2017, 42, 8139–8149. [Google Scholar] [CrossRef]
- Weydahl, H.; Thomassen, M.S.; Børresen, B.T.; Møller-Holst, S. Response of a proton exchange membrane fuel cell to a sinusoidal current load. J. Appl. Electrochem. 2010, 40, 809–819. [Google Scholar] [CrossRef]
- Gu, W.; Baker, D.R.; Liu, Y.; Gasteiger, H.A. Proton exchange membrane fuel cell (PEMFC) down-the-channel performance model. In Handbook of Fuel Cells; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Chan, S.; Khor, K.; Xia, Z. Complete polarization model of a solid oxide fuel cell and its sensitivity to the change of cell component thickness. J. Power Sources 2001, 93, 130–140. [Google Scholar] [CrossRef]
- Laoun, B. Simulation of PEMFC performance. Rev. Energies Renouvelables 2011, 14, 441–448. [Google Scholar]
- Kulikovsky, A.A. A Physically–Based Analytical Polarization Curve of a PEM Fuel Cell. J. Electrochem. Soc. 2014, 161, F263–F270. [Google Scholar] [CrossRef]
- Kulikovsky, A. Analytical Modelling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Tavčar, G.; Hametner, C.; Jakubek, S.; Katrašnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Kravos, A.; Kregar, A.; Penga, Ž.; Barbir, F.; Katrašnik, T. Real-time capable transient model of liquid water dynamics in proton exchange membrane Fuel Cells. J. Power Sources 2022, 541, 231598. [Google Scholar] [CrossRef]
- Eberle, D.; Horstmann, B. Oxygen Reduction on Pt(111) in Aqueous Electrolyte: Elementary Kinetic Modeling. Electrochim. Acta 2014, 137, 714–720. [Google Scholar] [CrossRef]
- Wang, J.X.; Zhang, J.; Adzic, R.R. Double-trap kinetic equation for the oxygen reduction reaction on pt(111) in acidic media. J. Phys. Chem. A 2007, 111, 12702–12710. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Zhang, J. Electrocatalytic Oxygen Reduction Reaction. In PEM Fuel Cell Electrocatalysts and Catalyst Layers: Fundamentals and Applications; Springer: London, UK, 2008; pp. 89–134. [Google Scholar] [CrossRef]
- Stamenkovic, V.; Mun, B.S.; Mayrhofer, K.J.; Ross, P.N.; Markovic, N.M.; Rossmeisl, J.; Greeley, J.; Nørskov, J.K. Changing the Activity of Electrocatalysts for Oxygen Reduction by Tuning the Surface Electronic Structure. Angew. Chem. Int. Ed. 2006, 45, 2897–2901. [Google Scholar] [CrossRef] [PubMed]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Choi, P.; Jalani, N.H.; Datta, R. Thermodynamics and proton transport in Nafion II. Proton diffusion mechanisms and conductivity. J. Electrochem. Soc. 2005, 152, E123–E130. [Google Scholar] [CrossRef]
- Stoicheff, B. On the dissociation energy of molecular hydrogen. Can. J. Phys. 2001, 79, 165–172. [Google Scholar] [CrossRef]
- Boltzmann, L. Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten. Wien. Berichte 1868, 58, 517–560. [Google Scholar] [CrossRef]
- Skúlason, E.; Karlberg, G.S.; Rossmeisl, J.; Bligaard, T.; Greeley, J.; Jónsson, H.; Nørskov, J.K. Density functional theory calculations for the hydrogen evolution reaction in an electrochemical double layer on the Pt(111) electrode. Phys. Chem. Chem. Phys. 2007, 9, 3241–3250. [Google Scholar] [CrossRef]
- Trasatti, S. The absolute electrode potential: An explanatory note (Recommendations 1986). Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar] [CrossRef]
- Ferreira, P.J.; la O’, G.J.; Shao-Horn, Y.; Morgan, D.; Makharia, R.; Kocha, S.; Gasteiger, H.A. Instability of Pt/C Electrocatalysts in Proton Exchange Membrane Fuel Cells. J. Electrochem. Soc. 2005, 152, A2256. [Google Scholar] [CrossRef]
- Anderson, A.B.; Albu, T.V. Catalytic Effect of Platinum on Oxygen Reduction An Ab Initio Model Including Electrode Potential Dependence. J. Electrochem. Soc. 2000, 147, 4229. [Google Scholar] [CrossRef]
- Athanasaki, G.; Jayakumar, A.; Kannan, A. Gas diffusion layers for PEM fuel cells: Materials, properties and manufacturing—A review. Int. J. Hydrogen Energy 2023, 48, 2294–2313. [Google Scholar] [CrossRef]
- Cussler, E. Diffusion: Mass Transfer in Fluid Systems; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Frühwirt, P.; Kregar, A.; Törring, J.T.; Katrašnik, T.; Gescheidt, G. Holistic approach to chemical degradation of Nafion membranes in fuel cells: Modelling and predictions. Phys. Chem. Chem. Phys. 2020, 22, 5647–5666. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Polizos, G.; Macdonald, D.D.; Manias, E. State of Water in Perfluorosulfonic Ionomer (Nafion 117) Proton Exchange Membranes. J. Electrochem. Soc. 2008, 155, B163. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Antoine, M.C. Nouvelle relation entre les tensions et les temperatures. C. R. Held Seanc. Acad. Sci. Paris 1888, 107, 681–684. [Google Scholar]
- Passalacqua, E.; Lufrano, F.; Squadrito, G.; Patti, A.; Giorgi, L. Nafion content in the catalyst layer of polymer electrolyte fuel cells: Effects on structure and performance. Electrochim. Acta 2001, 46, 799–805. [Google Scholar] [CrossRef]
- Smith, A.M.; Lee, A.A.; Perkin, S. The Electrostatic Screening Length in Concentrated Electrolytes Increases with Concentration. J. Phys. Chem. Lett. 2016, 7, 2157–2163. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kregar, A.; Zelič, K.; Kravos, A.; Katrašnik, T. Educational Scale-Bridging Approach towards Modelling of Electric Potential, Electrochemical Reactions, and Species Transport in PEM Fuel Cell. Catalysts 2023, 13, 1131. https://doi.org/10.3390/catal13071131
Kregar A, Zelič K, Kravos A, Katrašnik T. Educational Scale-Bridging Approach towards Modelling of Electric Potential, Electrochemical Reactions, and Species Transport in PEM Fuel Cell. Catalysts. 2023; 13(7):1131. https://doi.org/10.3390/catal13071131
Chicago/Turabian StyleKregar, Ambrož, Klemen Zelič, Andraž Kravos, and Tomaž Katrašnik. 2023. "Educational Scale-Bridging Approach towards Modelling of Electric Potential, Electrochemical Reactions, and Species Transport in PEM Fuel Cell" Catalysts 13, no. 7: 1131. https://doi.org/10.3390/catal13071131
APA StyleKregar, A., Zelič, K., Kravos, A., & Katrašnik, T. (2023). Educational Scale-Bridging Approach towards Modelling of Electric Potential, Electrochemical Reactions, and Species Transport in PEM Fuel Cell. Catalysts, 13(7), 1131. https://doi.org/10.3390/catal13071131