Role of Chiral Skeleton in Chiral Phosphoric Acids Catalyzed Asymmetric Transfer Hydrogenation: A DFT Study
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
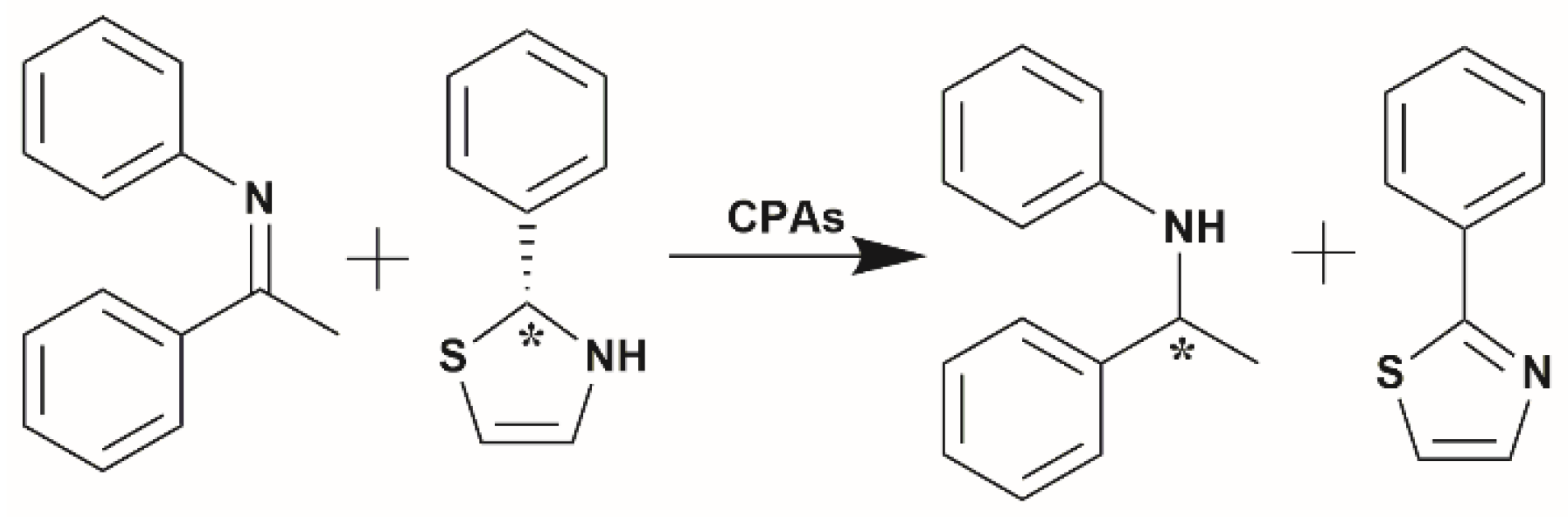
3.1. Mechanism and Reactivity
3.2. Acidity of CPAs
3.3. Origin of Enantioselectivity on CPAs
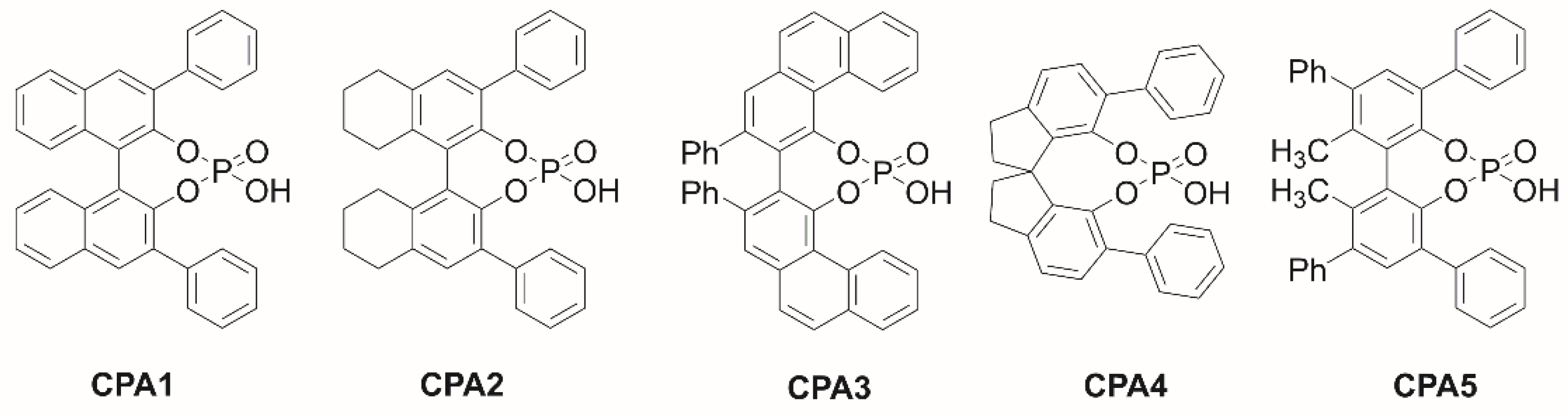
3.4. Chiral Skeletons of CPAs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akiyama, T.; Itoh, J.; Yokota, K.; Fuchibe, K. Enantioselective Mannich-type reaction catalyzed by a chiral Brønsted acid. Angew. Chem. 2004, 116, 1592–1594. [Google Scholar] [CrossRef]
- Uraguchi, D.; Terada, M. Chiral Brønsted Acid-Catalyzed Direct Mannich Reactions via Electrophilic Activation. J. Am. Chem. Soc. 2004, 126, 5356–5357. [Google Scholar] [CrossRef] [PubMed]
- Monaco, M.R.; Fazzi, D.; Tsuji, N.; Leutzsch, M.; Liao, S.; Thiel, W.; List, B. The Activation of Carboxylic Acids via Self-Assembly Asymmetric Organocatalysis: A Combined Experimental and Computational Investigation. J. Am. Chem. Soc. 2016, 138, 14740–14749. [Google Scholar] [CrossRef] [PubMed]
- Changotra, A.; Das, S.; Sunoj, R.B. Reversing enantioselectivity using noncovalent interactions in asymmetric dearomatization of β-naphthols: The power of 3, 3′ substituents in chiral phosphoric acid catalysts. Org. Lett. 2017, 19, 2354–2357. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, M.; Hoshino, M.; Katoh, T.; Mori, K.; Akiyama, T. Kinetic Resolution in Chiral Phosphoric Acid Catalyzed Aldol Reactions: Enantioselective Robinson-Type Annulation Reactions. Chem. Eur. J. 2012, 2012, 4508–4514. [Google Scholar] [CrossRef]
- Reid, J.P.; Simón, L.; Goodman, J.M. A practical guide for predicting the stereochemistry of bifunctional phosphoric acid catalyzed reactions of imines. Acc. Chem. Res. 2016, 49, 1029–1041. [Google Scholar] [CrossRef]
- Kim, K.-H.; Lee, C.-Y.; Cheon, C.-H. Enantioselective Synthesis of β-Arylamines via Chiral Phosphoric Acid-Catalyzed Asymmetric Reductive Amination. J. Org. Chem. 2015, 80, 6367–6374. [Google Scholar] [CrossRef]
- Maji, R.; Mallojjala, S.C.; Wheeler, S.E. Chiral phosphoric acid catalysis: From numbers to insights. Chem. Soc. Rev. 2018, 47, 1142–1158. [Google Scholar] [CrossRef]
- Meng, S.-S.; Yu, P.; Yu, Y.-Z.; Liang, Y.; Houk, K.; Zheng, W.-H. Computational Design of Enhanced Enantioselectivity in Chiral Phosphoric Acid-Catalyzed Oxidative Desymmetrization of 1, 3-Diol Acetals. J. Am. Chem. Soc. 2020, 142, 8506–8513. [Google Scholar] [CrossRef]
- Shibata, Y.; Yamanaka, M. DFT Study of the Mechanism and Origin of Enantioselectivity in Chiral BINOL-Phosphoric Acid Catalyzed Transfer Hydrogenation of Ketimine and α-Imino Ester Using Benzothiazoline. J. Org. Chem. 2013, 78, 3731–3736. [Google Scholar] [CrossRef]
- Kikuchi, J.; Aramaki, H.; Okamoto, H.; Terada, M. F10BINOL-derived chiral phosphoric acid-catalyzed enantioselective carbonyl-ene reaction: Theoretical elucidation of stereochemical outcomes. Chem. Sci. 2019, 10, 1426–1433. [Google Scholar] [CrossRef] [PubMed]
- Falcone, B.N.; Grayson, M.N. Understanding the mechanism of the chiral phosphoric acid-catalyzed aza-Cope rearrangement. Org. Biomol. Chem. 2021, 19, 3656–3664. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zheng, S.; Rajkumar, S.; Xie, J.; Yu, N.; Peng, Q.; Yang, X. Chiral phosphoric acid-catalyzed stereodivergent synthesis of trisubstituted allenes and computational mechanistic studies. Nat. Commun. 2020, 11, 5527. [Google Scholar] [CrossRef] [PubMed]
- Champagne, P.A. Identifying the true origins of selectivity in chiral phosphoric acid catalyzed N-acyl-azetidine desymmetrizations. Chem. Sci. 2021, 12, 15662–15672. [Google Scholar] [CrossRef]
- Li, Y.-P.; Li, Z.-Q.; Zhou, B.; Li, M.-L.; Xue, X.-S.; Zhu, S.-F.; Zhou, Q.-L. Chiral Spiro Phosphoric Acid-Catalyzed Friedel–Crafts Conjugate Addition/Enantioselective Protonation Reactions. ACS Catal. 2019, 9, 6522–6529. [Google Scholar] [CrossRef]
- Wang, Y.-B.; Yu, P.; Zhou, Z.-P.; Zhang, J.; Wang, J.J.; Luo, S.-H.; Gu, Q.-S.; Houk, K.; Tan, B. Rational design, enantioselective synthesis and catalytic applications of axially chiral EBINOLs. Nat. Catal. 2019, 2, 504–513. [Google Scholar] [CrossRef]
- See, J.Y.; Yang, H.; Zhao, Y.; Wong, M.W.; Ke, Z.; Yeung, Y.-Y. Desymmetrizing enantio-and diastereoselective selenoetherification through supramolecular catalysis. ACS Catal. 2018, 8, 850–858. [Google Scholar] [CrossRef]
- Tribedi, S.; Sunoj, R.B. Molecular insights into chirality transfer from double axially chiral phosphoric acid in a synergistic enantioselective intramolecular amination. Chem. Sci. 2022, 13, 1323–1334. [Google Scholar] [CrossRef]
- Qiu, Y.; Yuan, H.; Zhang, X.; Zhang, J. Insights into the Chiral Phosphoric Acid-Catalyzed Dynamic Kinetic Asymmetric Hydroamination of Racemic Allenes: An Allyl Carbocation/Phosphate Pair Mechanism. J. Org. Chem. 2021, 86, 4121–4130. [Google Scholar] [CrossRef]
- Hoffmann, S.; Seayad, A.M.; List, B. A powerful Brønsted acid catalyst for the organocatalytic asymmetric transfer hydrogenation of imines. Angew. Chem. 2005, 117, 7590–7593. [Google Scholar] [CrossRef]
- Zhu, L.; Mohamed, H.; Yuan, H.; Zhang, J. The control effects of different scaffolds in chiral phosphoric acids: A case study of enantioselective asymmetric arylation. Catal. Sci. Technol. 2019, 9, 6482–6491. [Google Scholar] [CrossRef]
- Zhang, L.; Xiang, S.-H.; Wang, J.J.; Xiao, J.; Wang, J.-Q.; Tan, B. Phosphoric acid-catalyzed atroposelective construction of axially chiral arylpyrroles. Nat. Commun. 2019, 10, 566. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.; Lin, X. Development and application of chiral spirocyclic phosphoric acids in asymmetric catalysis. Org. Biomol. Chem. 2018, 16, 4753–4777. [Google Scholar] [CrossRef]
- Gutierrez, E.G.; Moorhead, E.J.; Smith, E.H.; Lin, V.; Ackerman, L.K.; Knezevic, C.E.; Sun, V.; Grant, S.; Wenzel, A.G. Electron-Withdrawing, Biphenyl-2, 2′-diol-Based Compounds for Asymmetric Catalysis. Eur. J. Org. Chem. 2010, 2010, 3027–3031. [Google Scholar] [CrossRef]
- Accelrys Software Inc. Materials Studio V5.5; Accelrys Software Inc.: San Diego, CA, USA, 2005. [Google Scholar]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.; Goddard III, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Fukui, K. The path of chemical reactions-the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Shermo: A general code for calculating molecular thermochemistry properties. Comput. Theor. Chem. 2021, 1200, 113249. [Google Scholar] [CrossRef]
- Laidler, K.J.; King, M.C. The development of transition-state theory. J. Phys. Chem 1983, 87, 2657–2664. [Google Scholar] [CrossRef]
- Schneebeli, S.T.; Hall, M.L.; Breslow, R.; Friesner, R. Quantitative DFT modeling of the enantiomeric excess for dioxirane-catalyzed epoxidations. J. Am. Chem. Soc. 2009, 131, 3965–3973. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M. Understanding reactivity with Kohn–Sham molecular orbital theory: E2–SN2 mechanistic spectrum and other concepts. J. Comput. Chem. 1999, 20, 114–128. [Google Scholar] [CrossRef]
- van Zeist, W.-J.; Bickelhaupt, F.M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef]
- Ess, D.H.; Houk, K. Distortion/interaction energy control of 1,3-dipolar cycloaddition reactivity. J. Am. Chem. Soc. 2007, 129, 10646–10647. [Google Scholar] [CrossRef]
- Ess, D.H.; Houk, K. Theory of 1,3-dipolar cycloadditions: Distortion/interaction and frontier molecular orbital models. J. Am. Chem. Soc. 2008, 130, 10187–10198. [Google Scholar] [CrossRef]
- Wang, J.; Chen, M.-W.; Ji, Y.; Hu, S.-B.; Zhou, Y.-G. Kinetic Resolution of Axially Chiral 5- or 8-Substituted Quinolines via Asymmetric Transfer Hydrogenation. J. Am. Chem. Soc. 2016, 138, 10413–10416. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, H. Li, X.; Hou, B.; Gong, W.; Wu, X.; Han, X.; Zheng, F.; Liu, Y.; Jiang, J.; et al. Chiral phosphoric acids in metal–organic frameworks with enhanced acidity and tunable catalytic selectivity. Angew. Chem. 2019, 131, 14890–14899. [Google Scholar] [CrossRef]
- Yang, C.; Xue, X.-S.; Jin, J.-L.; Li, X.; Cheng, J.-P. Theoretical Study on the Acidities of Chiral Phosphoric Acids in Dimethyl Sulfoxide: Hints for Organocatalysis. J. Org. Chem. 2013, 78, 7076–7085. [Google Scholar] [CrossRef]
- He, L.; Chen, X.-H.; Wang, D.-N.; Luo, S.-W.; Zhang, W.-Q.; Yu, J.; Ren, L.; Gong, L.-Z. Binaphthol-Derived Bisphosphoric Acids Serve as Efficient Organocatalysts for Highly Enantioselective 1,3-Dipolar Cycloaddition of Azomethine Ylides to Electron-Deficient Olefins. J. Am. Chem. Soc. 2011, 133, 13504–13518. [Google Scholar] [CrossRef] [PubMed]
- Deshlahra, P.; Iglesia, E. Reactivity descriptors in acid catalysis: Acid strength, proton affinity and host–guest interactions. Commun. Chem. 2020, 56, 7371–7398. [Google Scholar] [CrossRef]
- Li, X.; Sun, Q.; Li, Y.; Wang, N.; Lu, J.; Yu, J. Confinement effect of zeolite cavities on methanol-to-olefin conversion: A density functional theory study. J. Phys. Chem. C. 2014, 118, 24935–24940. [Google Scholar] [CrossRef]
- Lessa, M.D.; Fajardo, J.R.D.; Delarmelina, M.; Carneiro, J.W.d.M. A DFT study on the mechanism for polymerization of δ-valerolactone initiated by N-heterocyclic carbene (NHC) catalysts. Mol. Catal. 2021, 515, 111896. [Google Scholar] [CrossRef]
- Rothermel, K.; Melikian, M.; Hioe, J.; Greindl, J.; Gramüller, J.; Žabka, M.; Sorgenfrei, N.; Hausler, T.; Morana, F.; Gschwind, R.M. Internal acidity scale and reactivity evaluation of chiral phosphoric acids with different 3, 3′-substituents in Brønsted acid catalysis. Chem. Sci. 2019, 10, 10025–10034. [Google Scholar] [CrossRef]
- Champagne, P.A.; Houk, K. Origins of selectivity and general model for chiral phosphoric acid-catalyzed oxetane desymmetrizations. J. Am. Chem. Soc. 2016, 138, 12356–12359. [Google Scholar] [CrossRef]
- Seguin, T.J.; Wheeler, S.E. Electrostatic Basis for Enantioselective Brønsted-Acid-Catalyzed Asymmetric Ring Openings of meso-Epoxides. ACS Catal. 2016, 6, 2681–2688. [Google Scholar] [CrossRef]
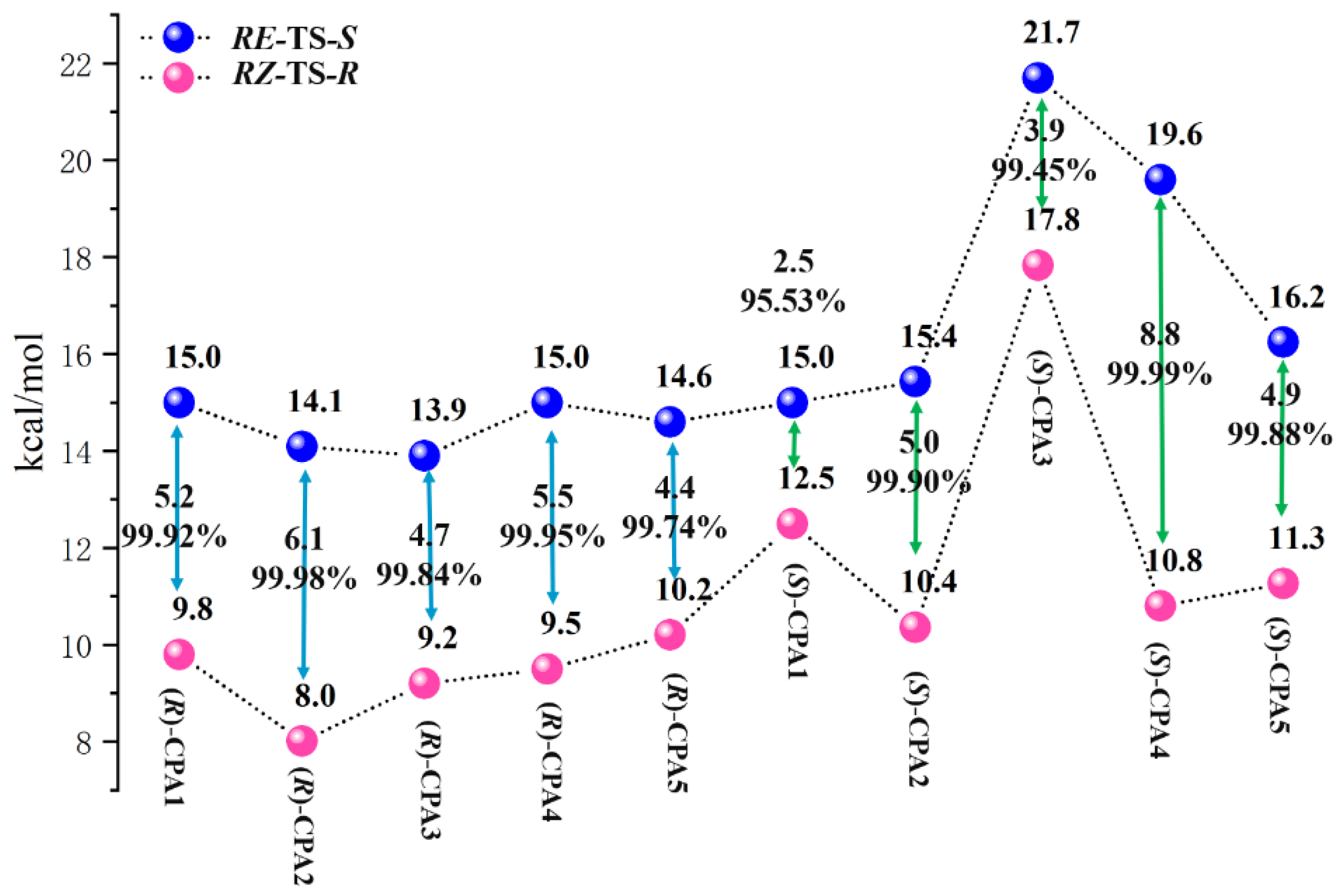



| CPAs | Boltzmann-Weight | ΔG‡barrier | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RE-TS-S | RZ-TS-R | SE-TS-S | SZ-TS-R | RE-TS-S | RZ-TS-R | SE-TS-S | SZ-TS-R | ||
| (R)-CPA1 | 4.88 | 94.26 | 0.85 | 0.02 | 15.0 | 9.8 | 15.9 | 17.8 | |
| (R)-CPA2 | 1.44 | 98.01 | 0.54 | 0.01 | 14.1 | 8.0 | 15.2 | 16.9 | |
| (R)-CPA3 | 2.74 | 97.25 | 0.00 | 0.00 | 13.9 | 9.2 | 18.3 | 18.2 | |
| (R)-CPA4 | 0.03 | 99.24 | 0.07 | 0.66 | 15.0 | 9.5 | 15.8 | 13.3 | |
| (R)-CPA5 | 8.65 | 91.35 | 0.00 | 0.01 | 14.6 | 10.2 | 23.6 | 16.5 | |
| (S)-CPA1 | 3.96 | 88.65 | 7.33 | 0.06 | 15.0 | 12.5 | 13.1 | 17.6 | |
| (S)-CPA2 | 31.35 | 67.73 | 0.80 | 0.12 | 15.4 | 10.4 | 16.4 | 15.0 | |
| (S)-CPA3 | 4.55 | 3.61 | 90.74 | 1.10 | 21.7 | 17.8 | 15.2 | 18.8 | |
| (S)-CPA4 | 0.00 | 82.83 | 16.31 | 0.86 | 19.6 | 10.8 | 11.2 | 15.6 | |
| (S)-CPA5 | 10.98 | 84.81 | 4.17 | 0.04 | 16.2 | 11.3 | 13.0 | 17.1 | |
| CPAs | CPA1 | CPA2 | CPA3 | CPA4 | CPA5 |
|---|---|---|---|---|---|
| 293.5 | 297.3 | 292.0 | 296.8 | 295.2 |
| CPAs | ΔΔE | ΔΔEdist | ΔΔEint | ΔΔEdist-cata | ΔΔEdist-sub |
|---|---|---|---|---|---|
| (R)-CPA1 | 3.7 | 2.8 | 0.9 | 0.0 | 2.8 |
| (R)-CPA2 | 6.2 | 3.2 | 3.0 | 0.4 | 2.8 |
| (R)-CPA3 | 4.7 | 3.3 | 1.4 | 0.1 | 3.2 |
| (R)-CPA4 | 5.4 | 4.7 | 0.7 | 3.5 | 1.2 |
| (R)-CPA5 | 5.3 | 2.9 | 2.4 | 0.0 | 2.9 |
| (S)-CPA1 | 2.7 | 5.2 | −2.5 | 2.1 | 3.1 |
| (S)-CPA2 | 4.5 | 8.6 | −4.1 | 4.3 | 4.3 |
| (S)-CPA3 | 2.3 | 1.3 | 1.0 | 0.4 | 0.9 |
| (S)-CPA4 | 8.6 | 6.9 | 1.7 | 4.2 | 2.7 |
| (S)-CPA5 | 3.6 | 4.8 | −1.2 | 2.5 | 2.3 |
| CPAs | Parameter | Initial | (R)-CPAs | (S)-CPAs | ||
|---|---|---|---|---|---|---|
| RE-TS-S | RZ-TS-R | RE-TS-S | RZ-TS-R | |||
| CPA1 | CA | 56.4 | 1.4 | −1.4 | 2.5 | −1.6 |
| PD | 12.0 | 1.3 | −0.3 | 1.0 | 0.4 | |
| CPA2 | CA | 56.6 | 3.7 | 3.4 | 3.5 | 2.1 |
| PD | 11.9 | 1.4 | −0.1 | 1.0 | 1.2 | |
| CPA3 | CA | 73.8 | −15.3 | −18.5 | 19.5 | 18.7 |
| PD | 13.3 | 0.1 | −0.4 | 0.8 | 0.6 | |
| CPA4 | CA | 28.8 | 2.7 | 0.1 | −4.8 | −0.4 |
| PD | 10.2 | 1.4 | 1.4 | 3.0 | 1.6 | |
| CPA5 | CA | 57.3 | 0.3 | −0.8 | −3.1 | −1.7 |
| PD | 11.9 | 1.3 | −0.1 | −1.3 | −0.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Dong, S.; Fan, T.; Wang, Q.; Shi, T. Role of Chiral Skeleton in Chiral Phosphoric Acids Catalyzed Asymmetric Transfer Hydrogenation: A DFT Study. Catalysts 2023, 13, 98. https://doi.org/10.3390/catal13010098
Li X, Dong S, Fan T, Wang Q, Shi T. Role of Chiral Skeleton in Chiral Phosphoric Acids Catalyzed Asymmetric Transfer Hydrogenation: A DFT Study. Catalysts. 2023; 13(1):98. https://doi.org/10.3390/catal13010098
Chicago/Turabian StyleLi, Xu, Shanshan Dong, Ting Fan, Qingji Wang, and Tongfei Shi. 2023. "Role of Chiral Skeleton in Chiral Phosphoric Acids Catalyzed Asymmetric Transfer Hydrogenation: A DFT Study" Catalysts 13, no. 1: 98. https://doi.org/10.3390/catal13010098
APA StyleLi, X., Dong, S., Fan, T., Wang, Q., & Shi, T. (2023). Role of Chiral Skeleton in Chiral Phosphoric Acids Catalyzed Asymmetric Transfer Hydrogenation: A DFT Study. Catalysts, 13(1), 98. https://doi.org/10.3390/catal13010098








