Kinetic Modeling of Dihydroxyacetone Production from Glycerol by Gluconobacter oxydans ATCC 621 Resting Cells: Effect of Fluid Dynamics Conditions
Abstract
1. Introduction
2. Results
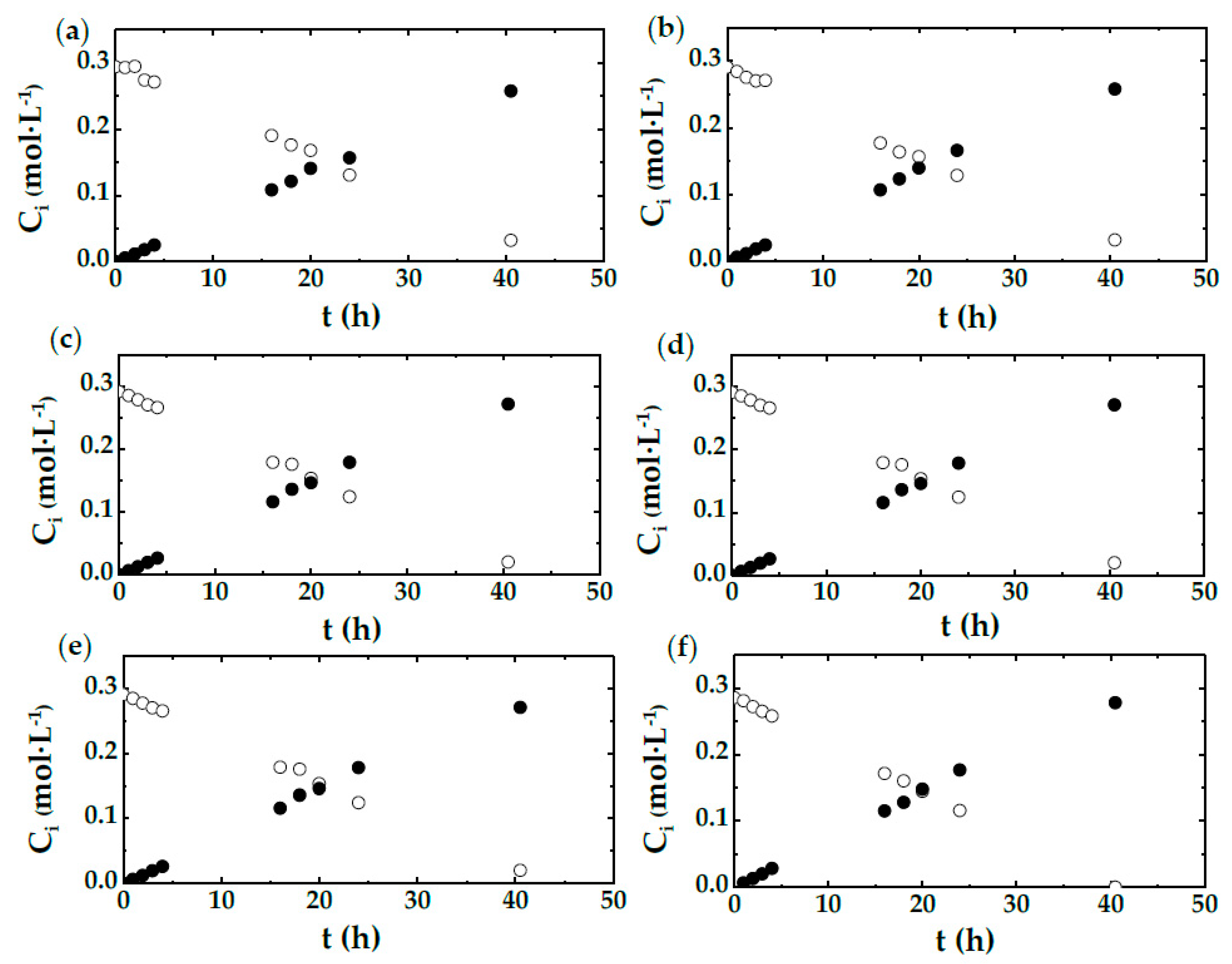
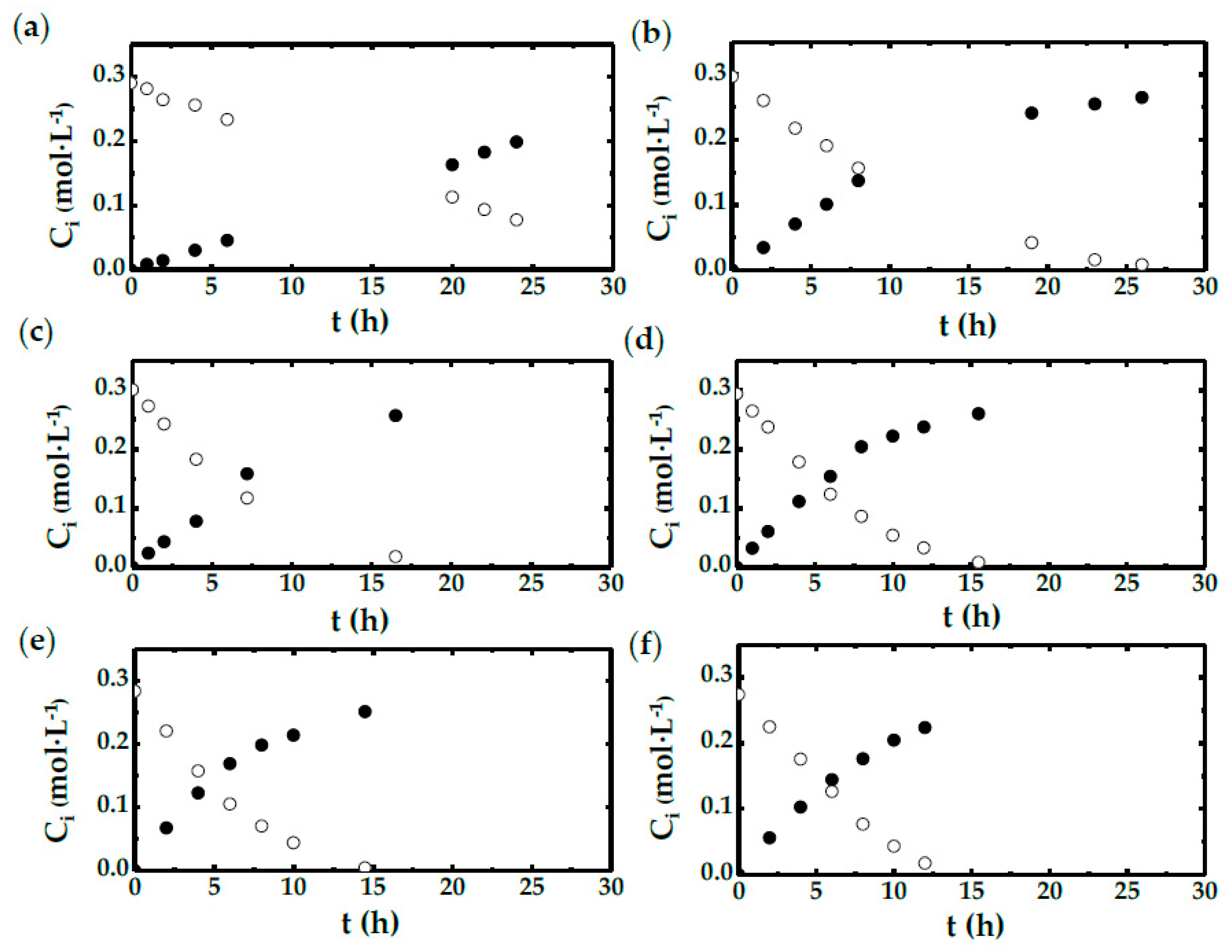
2.1. Shake Flask Experiments
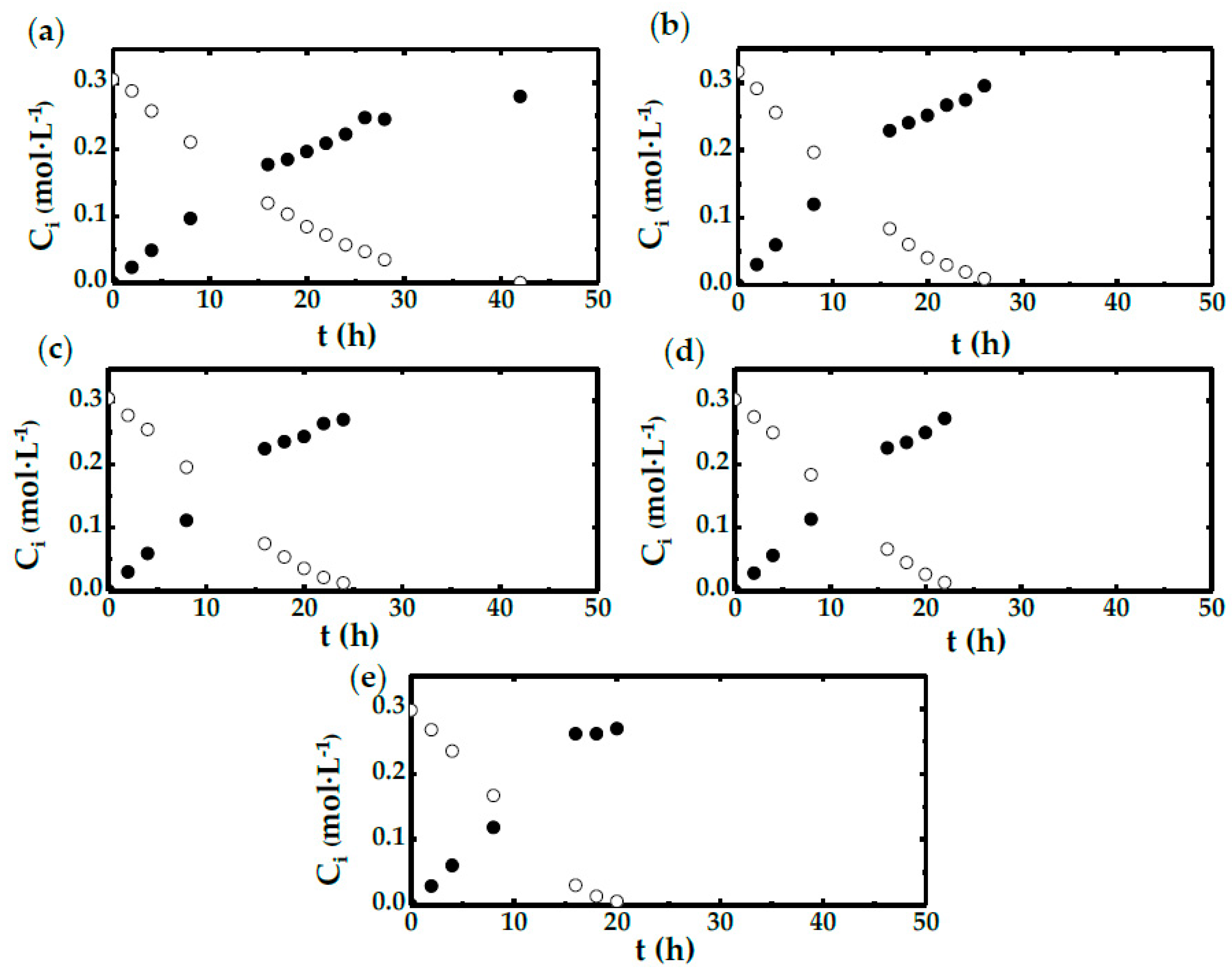
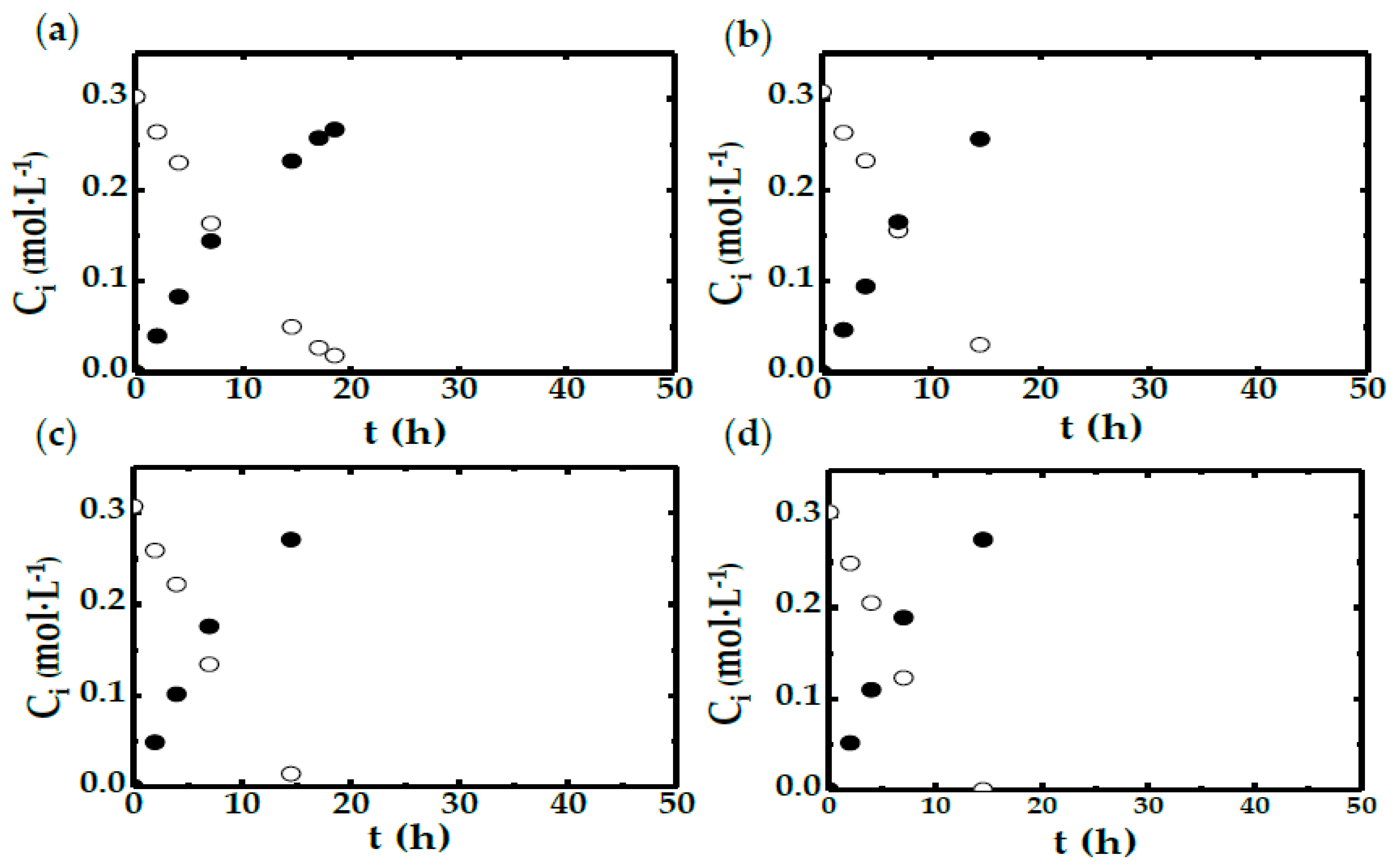
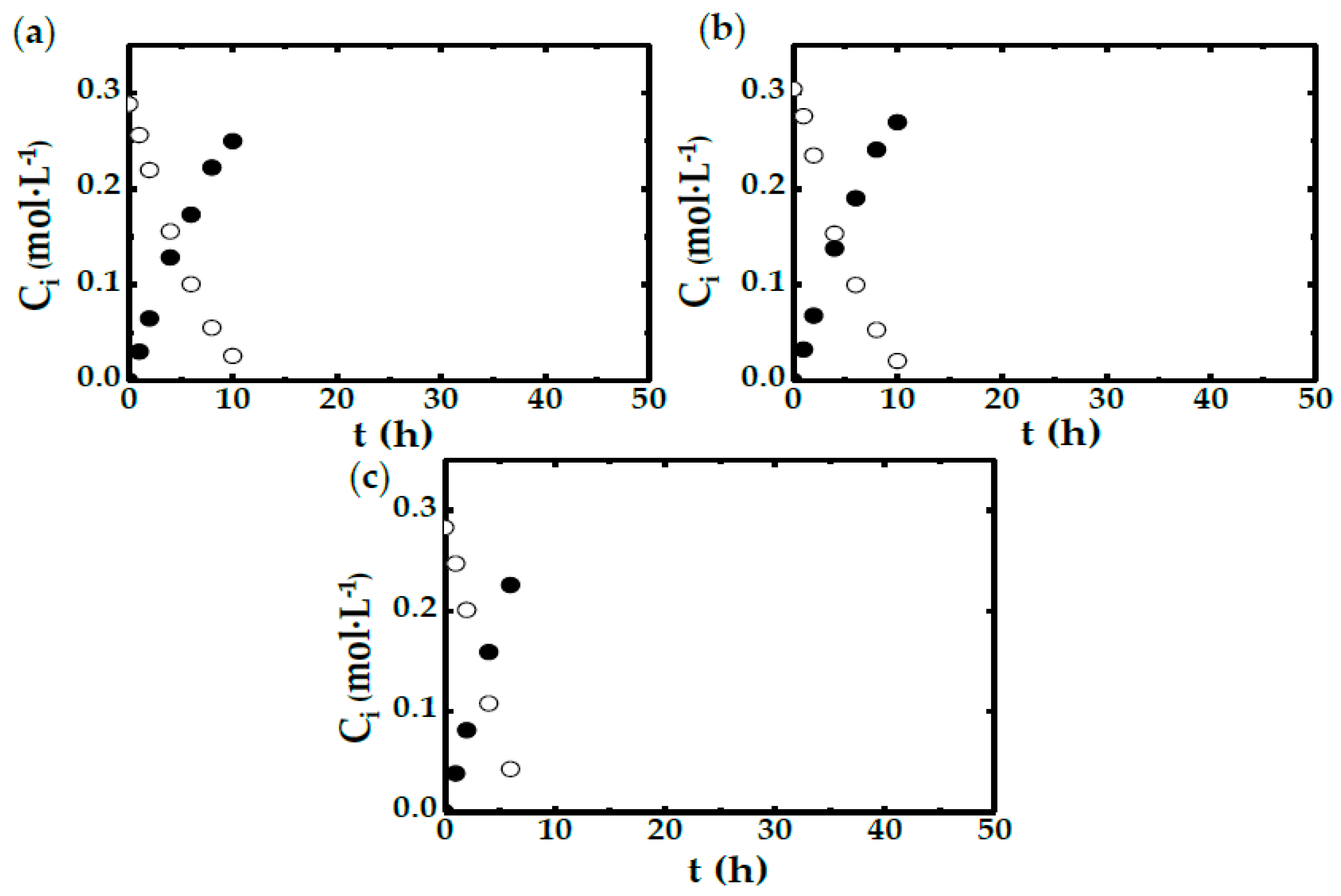
2.2. STBR Experiments
3. Discussion
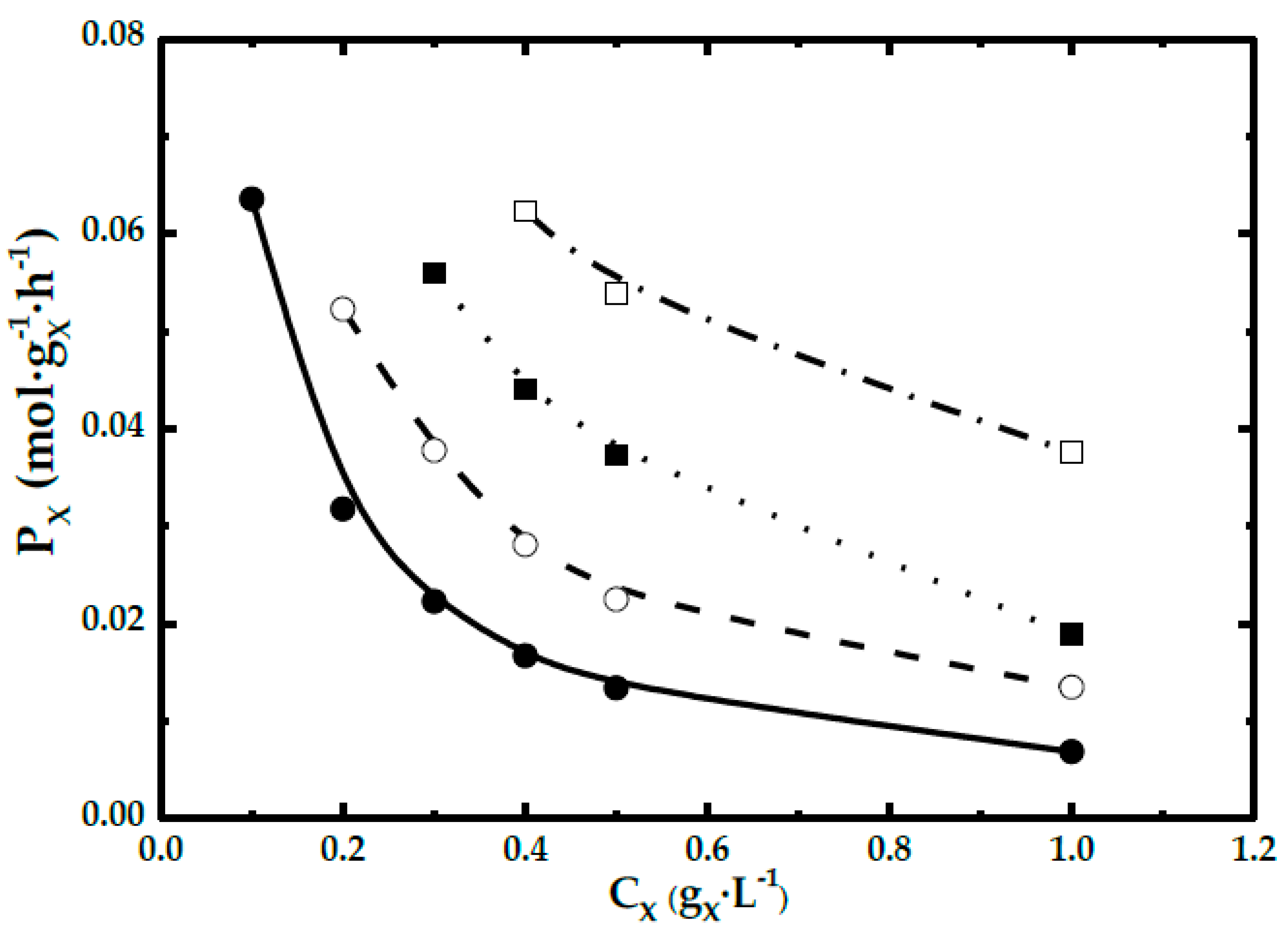
- There are three different observed patterns, which depend on the stirring speed employed. This is valid for both shake flasks and STBR.
- For low agitation, DHA production is strongly related to the stirring speed and, therefore, to the mass transfer rate.
- For high stirring speeds, biomass concentration exerts a strong influence on DHA evolution. When the amount of biocatalyst is maintained, DHA evolution is not affected by agitation speed. Thus, the production rate of DHA depends on the chemical reaction rate.
- There is a mixed behavior when the agitation takes a medium value; in this case, the process rate seems to depend on the oxygen availability, or the OTR from gas to the culture media, which is directly related to the stirring speed.
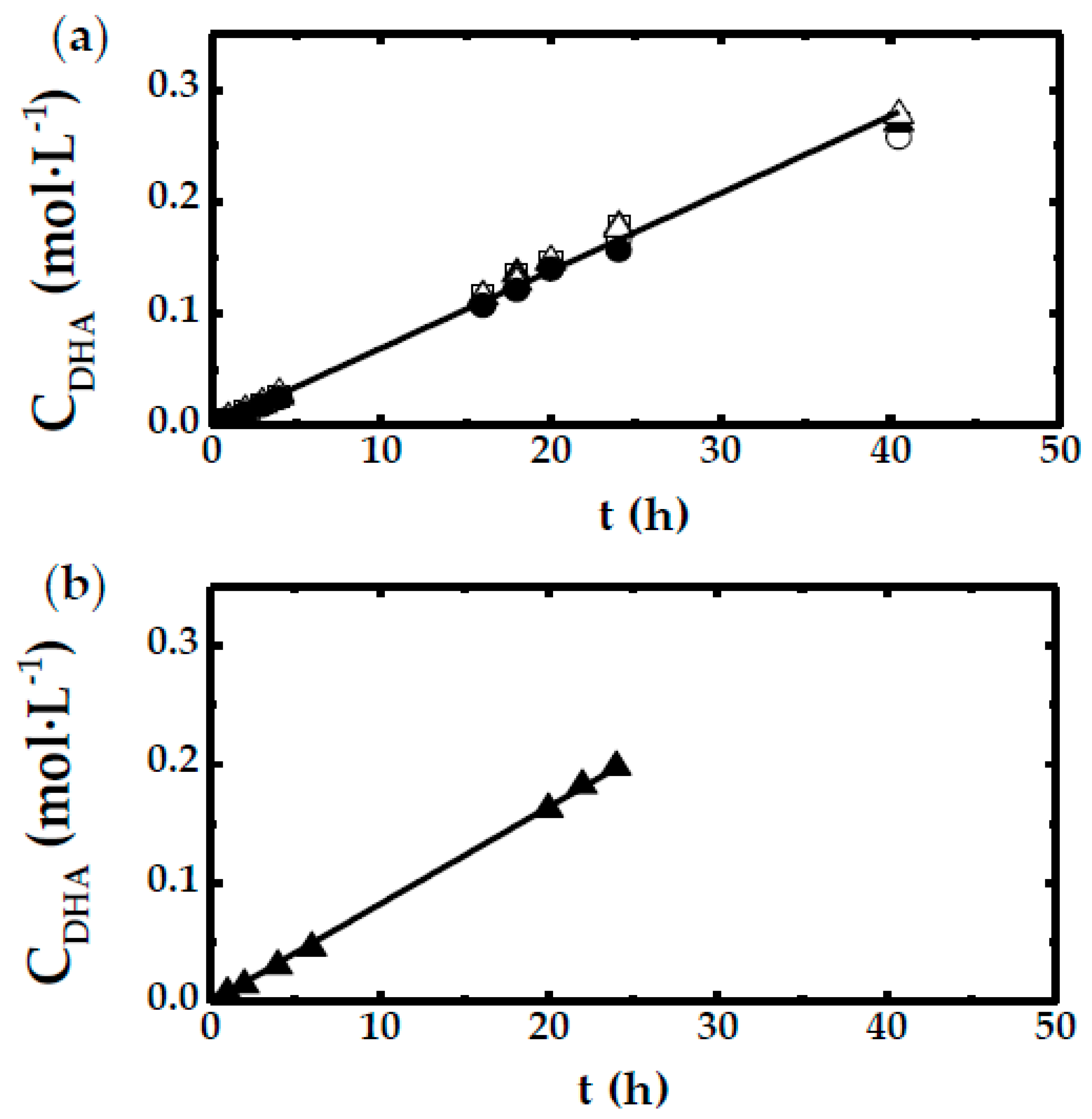
3.1. Kinetic Model for Low Agitation: Mass Transfer Rate Evaluation
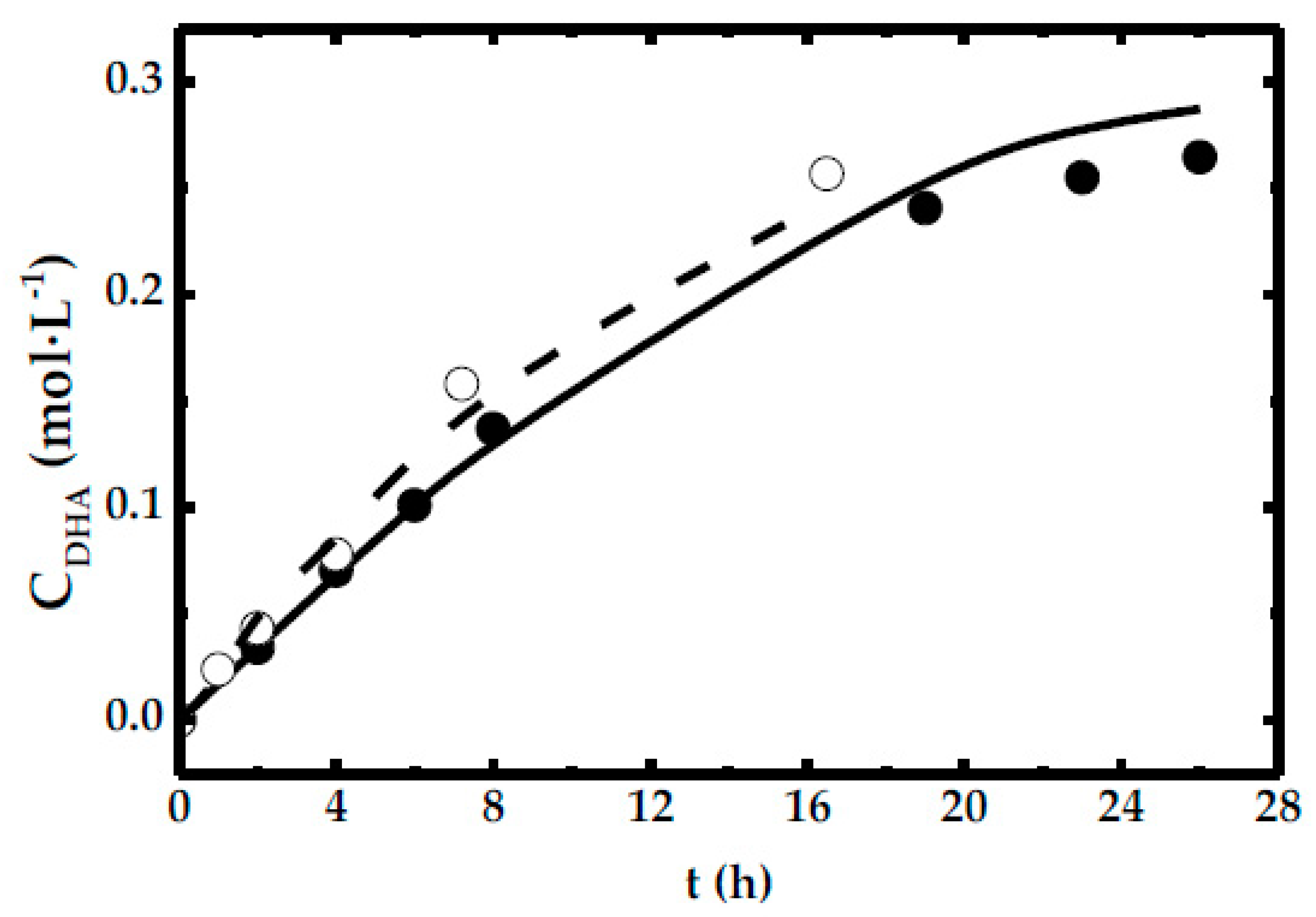
- For low agitation rate, the linear trend of DHA concentration with time adjusts to the tendency shown in Equation (3).
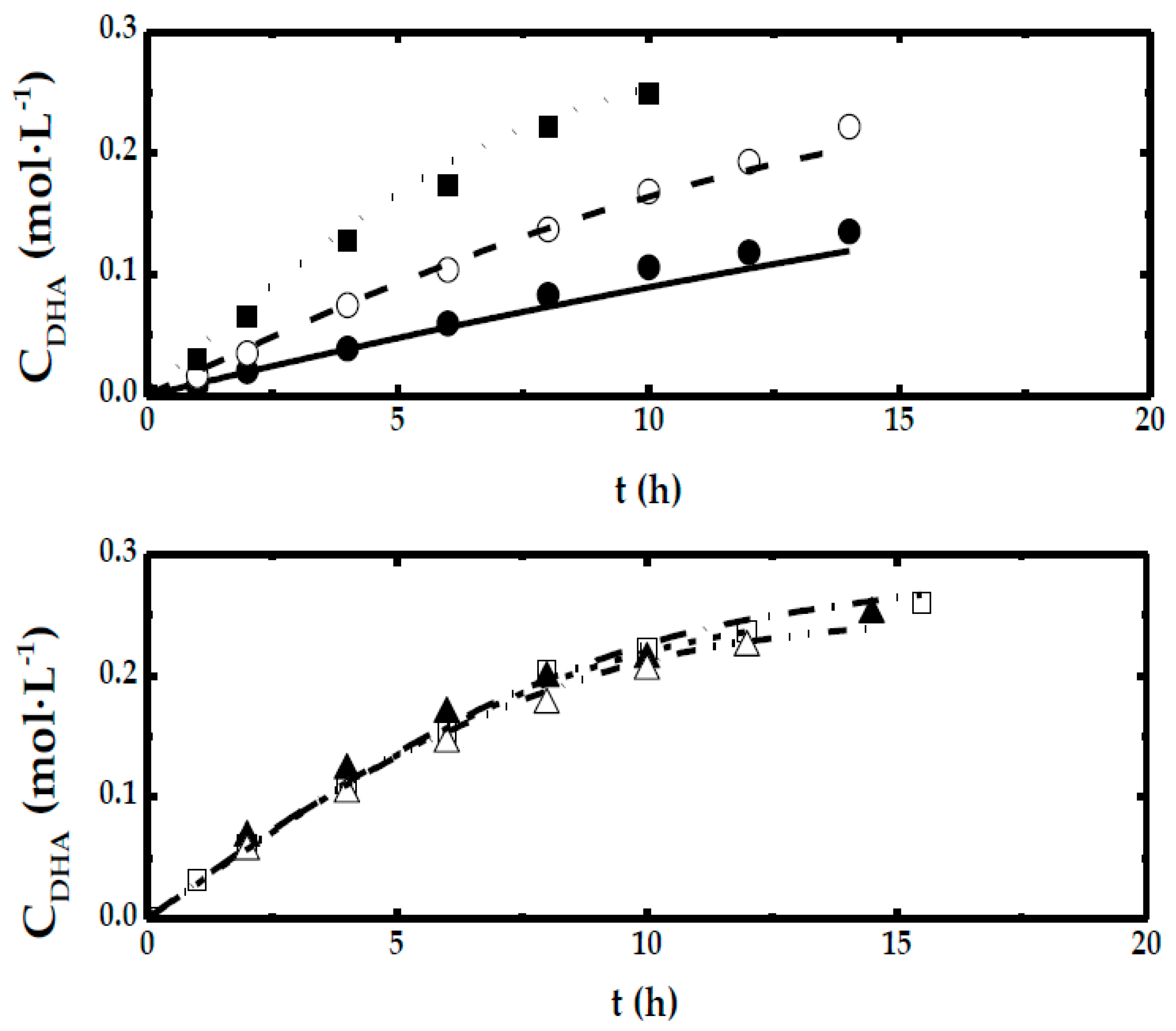
- For the rest of experiments, only the first stage, at short times, DHA concentration evolves following a linear relationship with time.
3.2. Kinetic Model for High Agitation: Chemical Reaction Rate Calculation
3.3. Kinetic Model for Intermediate Cases: Oxygen Concentration Effect
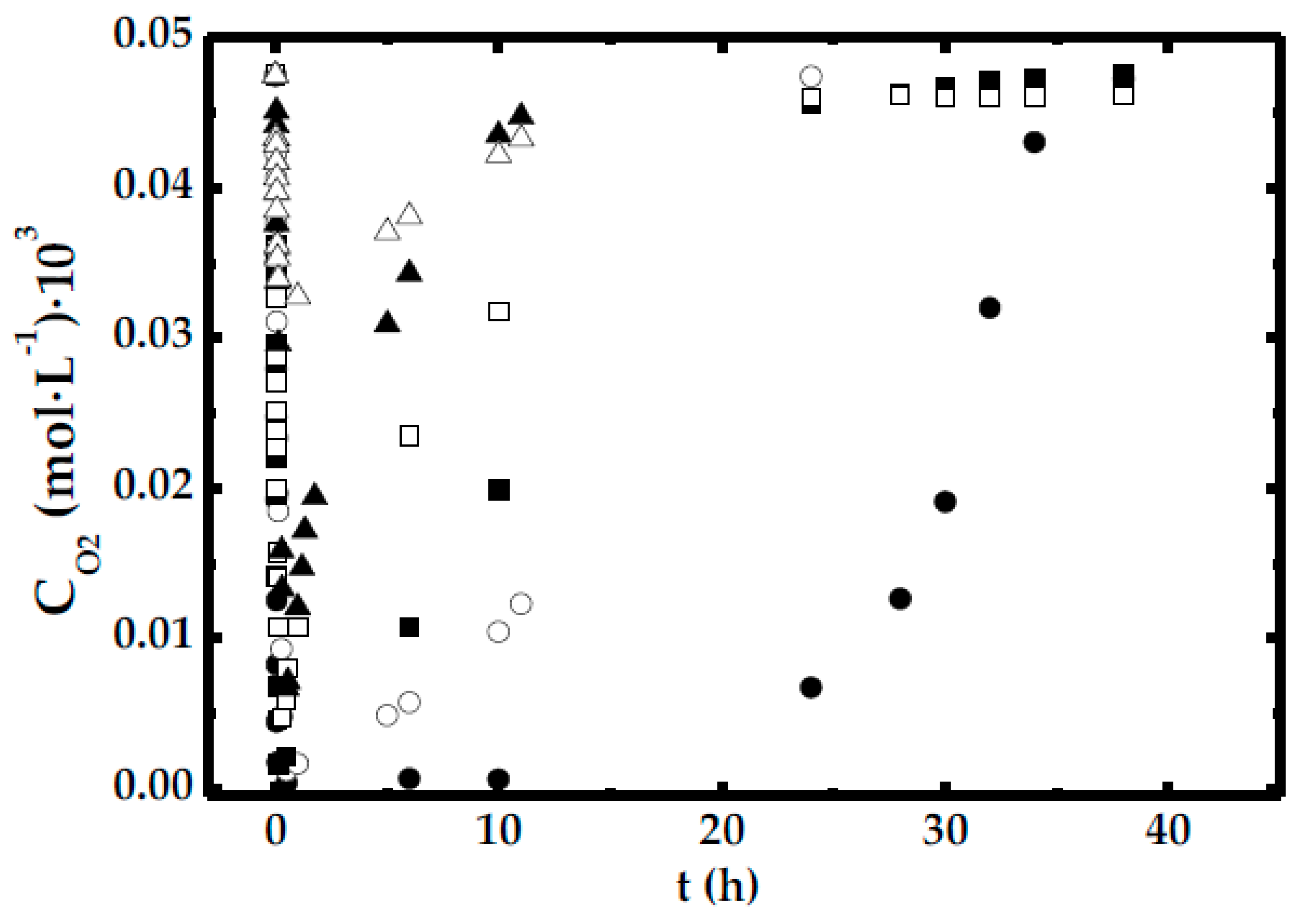
- In the run with less agitation (300 rpm), DO concentration reduces to 0 shortly after the start of the experiments. This reinforces the idea that in this case, there is a shortage in oxygen availability caused by the low mass transfer rate.
- In the experiments performed with more than 560 rpm, it can be seen that the DO concentration never reaches 0. Therefore, it is safe to say that the OTR is far greater than the DHA production rate (chemical reaction).
- There are two runs, corresponding to those carried out at 360 and 420 rpm, in which the DO concentration reaches 0 in the first 3 h. However, in both cases, this oxygen shortage only lasts for a short time period.
- Therefore, it is necessary to take into account the DO concentration in order to explain the DHA production rate. Thus, Equation (7) was formulated with these premises:
4. Materials and Methods
4.1. Microorganism
4.2. Experimental Procedure
4.3. Analytical Methods
4.4. Mathematics and Calculations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Veluturla, S.; Archna, N.; Subba Rao, D.; Hezil, N.; Indraja, I.S.; Spoorthi, S. Catalytic valorization of raw glycerol derived from biodiesel: A review. Biofuels 2018, 9, 305–314. [Google Scholar] [CrossRef]
- Monteiro, M.R.; Kugelmeier, C.L.; Pinheiro, R.S.; Batalha, M.O.; da Silva César, A. Glycerol from biodiesel production: Technological paths for sustainability. Renew. Sustain. Energy Rev. 2018, 88, 109–122. [Google Scholar] [CrossRef]
- Nda-Umar, U.; Ramli, I.; Taufiq-Yap, Y.; Muhamad, E. An overview of recent research in the conversion of glycerol into biofuels, fuel additives and other bio-based chemicals. Catalysts 2019, 9, 15. [Google Scholar] [CrossRef]
- Mitrea, L.; Trif, M.; Cătoi, A.-F.; Vodnar, D.-C. Utilization of biodiesel derived-glycerol for 1,3-PD and citric acid production. Microb. Cell Factories 2017, 16, 190. [Google Scholar] [CrossRef] [PubMed]
- Hekmat, D.; Bauer, R.; Fricke, J. Optimization of the microbial synthesis of dihydroxyacetone from glycerol with Gluconobacter oxydans. Bioprocess Biosyst. Eng. 2003, 26, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Jain, V.K.; Tear, C.J.Y.; Lim, C.Y. Dihydroxyacetone production in an engineered Escherichia coli through expression of Corynebacterium glutamicum dihydroxyacetone phosphate dephosphorylase. Enzym. Microb. Technol. 2016, 86, 39–44. [Google Scholar] [CrossRef]
- Lin, X.; Liu, S.; Xie, G.; Chen, J.; Li, P.; Chen, J. Enhancement of 1,3-dihydroxyacetone production from Gluconobacter oxydans by combined mutagenesis. J. Microbiol. Biotechnol. 2016, 26, 1908–1917. [Google Scholar] [CrossRef]
- Zheng, X.J.; Jin, K.Q.; Zhang, L.; Wang, G.; Liu, Y.P. Effects of oxygen transfer coefficient on dihydroxyacetone production from crude glycerol. Braz. J. Microbiol. 2016, 47, 129–135. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, X.; Xu, Y.; Yu, S. Improving the production yield and productivity of 1,3-dihydroxyacetone from glycerol fermentation using Gluconobacter oxydans NL71 in a compressed oxygen supply-sealed and stirred tank reactor (COS-SSTR). Bioprocess Biosyst. Eng. 2016, 39, 1315–1318. [Google Scholar] [CrossRef]
- Hu, Z.-C.; Tian, S.-Y.; Ruan, L.-J.; Zheng, Y.-G. Repeated biotransformation of glycerol to 1,3-dihydroxyacetone by immobilized cells of Gluconobacter oxydans with glycerol- and urea-feeding strategy in a bubble column bioreactor. Bioresour. Technol. 2017, 233, 144–149. [Google Scholar] [CrossRef]
- Poljungreed, I.; Boonyarattanakalin, S. Dihydroxyacetone production by Gluconobacter frateurii in a minimum medium using fed-batch fermentation. J. Chem. Technol. Biotechnol. 2017, 92, 2635–2641. [Google Scholar] [CrossRef]
- Dikshit, P.K.; Moholkar, V.S. Batch and repeated-batch fermentation for 1,3-Dihydroxyacetone production from waste glycerol using free, immobilized and resting Gluconobacter oxydans cells. Waste Biomass Valorizat. 2018, 10, 2455–2465. [Google Scholar] [CrossRef]
- Stasiak-Różańska, L.; Berthold-Pluta, A.; Dikshit, P.K. Valorization of waste glycerol to dihydroxyacetone with biocatalysts obtained from Gluconobacter oxydans. Appl. Sci. 2018, 8, 2517. [Google Scholar] [CrossRef]
- Sudarshan, B.; Sanjay, K. Optimization of fermentation conditions for production of 1,3-Dihydroxyacetone from glycerol obtained as a byproduct during biodiesel production. Microbiol. Res. J. Int. 2018, 1–9. [Google Scholar] [CrossRef]
- de la Morena, S.; Acedos, M.G.; Santos, V.E.; García-Ochoa, F. Dihydroxyacetone production from glycerol using Gluconobacter oxydans: Study of medium composition and operational conditions in shaken flasks. Biotechnol. Prog. 2019, 35, e2803. [Google Scholar] [CrossRef]
- de la Morena, S.; Santos, V.E.; García-Ochoa, F. Influence of oxygen transfer and uptake rates on dihydroxyacetone production from glycerol by Gluconobacter oxydans in resting cells operation. Biochem. Eng. J. 2019, 147, 20–28. [Google Scholar] [CrossRef]
- Keliang, G.; Dongzhi, W. Asymmetric oxidation by Gluconobacter oxydans. Appl. Microbiol. Biotechnol. 2006, 70, 135–139. [Google Scholar] [CrossRef]
- Deppenmeier, U.; Hoffmeister, M.; Prust, C. Biochemistry and biotechnological applications of Gluconobacter strains. Appl. Microbiol. Biotechnol. 2002, 60, 233–242. [Google Scholar]
- Rocha-Martin, J.; Acosta, A.; Berenguer, J.; Guisan, J.M.; Lopez-Gallego, F. Selective oxidation of glycerol to 1,3-dihydroxyacetone by covalently immobilized glycerol dehydrogenases with higher stability and lower product inhibition. Bioresour. Technol. 2014, 170, 445–453. [Google Scholar] [CrossRef]
- Xu, M.-Q.; Li, F.-L.; Yu, W.-Q.; Li, R.-F.; Zhang, Y.-W. Combined cross-linked enzyme aggregates of glycerol dehydrogenase and NADH oxidase for high efficiency in situ NAD+ regeneration. Int. J. Biol. Macromol. 2019. [Google Scholar] [CrossRef]
- Ma, L.; Lu, W.; Xia, Z.; Wen, J. Enhancement of dihydroxyacetone production by a mutant of Gluconobacter oxydans. Biochem. Eng. J. 2010, 49, 61–67. [Google Scholar] [CrossRef]
- Stasiak-Różańska, L.; Błażejak, S.; Gientka, I.; Bzducha-Wróbel, A.; Lipińska, E. Utilization of a waste glycerol fraction using immobilized cell extract from Gluconobacter oxydans ATCC 621 and its possible re-use. Electron. J. Biotechnol. 2017, 27, 44–48. [Google Scholar] [CrossRef]
- Dikshit, P.K.; Moholkar, V.S. Kinetic analysis of dihydroxyacetone production from crude glycerol by immobilized cells of Gluconobacter oxydans MTCC 904. Bioresour. Technol. 2016, 216, 948–957. [Google Scholar] [CrossRef] [PubMed]
- Dikshit, P.K.; Padhi, S.K.; Moholkar, V.S. Process optimization and analysis of product inhibition kinetics of crude glycerol fermentation for 1,3-Dihydroxyacetone production. Bioresour. Technol. 2017, 244, 362–370. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef]
- Rodriguez, A.; Escobar, S.; Gomez, E.; Santos, V.E.; Garcia-Ochoa, F. Behavior of several Pseudomonas putida strains growth under different agitation and oxygen supply conditions. Biotechnol. Prog. 2018, 34, 900–909. [Google Scholar] [CrossRef]
- Acedos, M.G.; Hermida, A.; Gomez, E.; Santos, V.E.; Garcia-Ochoa, F. Effects of fluid-dynamic conditions in Shimwellia blattae (p424IbPSO) cultures in stirred tank bioreactors: Hydrodynamic stress and change of metabolic routes by oxygen availability. Biochem. Eng. J. 2019, 149, 107238. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E.; Merchuk, J.C. Oxygen uptake rate in microbial processes: An overview. Biochem. Eng. J. 2010, 49, 289–307. [Google Scholar] [CrossRef]
- Jackson, E.; Ripoll, M.; Betancor, L. Efficient glycerol transformation by resting Gluconobacter cells. Microbiol. Open 2019, 8, e926. [Google Scholar] [CrossRef]
- Klöckner, W.; Büchs, J. Advances in shaking technologies. Trends Biotechnol. 2012, 30, 307–314. [Google Scholar] [CrossRef]
- de la Torre Pascual, I.; Acedos, M.G.; Ladero, M.; Santos Mazorra, V. On the use of resting L. delbrueckii spp. delbrueckii cells for D-lactic acid production from orange peel wastes hydrolysates. Biochem. Eng. J. 2019, 145, 162–169. [Google Scholar] [CrossRef]
| Run | CX 1 (g·L−1) | N 2 (rpm) | Experimental Device |
|---|---|---|---|
| 1 | 0.1 | 100 | Shake flasks |
| 2 | 0.2 | ||
| 3 | 0.3 | ||
| 4 | 0.4 | ||
| 5 | 0.5 | ||
| 6 | 1.0 | ||
| 7 | 0.2 | 200 | |
| 8 | 0.3 | ||
| 9 | 0.4 | ||
| 10 | 0.5 | ||
| 11 | 1.0 | ||
| 12 | 0.3 | 300 | |
| 13 | 0.4 | ||
| 14 | 0.5 | ||
| 15 | 1.0 | ||
| 16 | 0.4 | 400 | |
| 17 | 0.5 | ||
| 18 | 1.0 | ||
| 19 | 0.5 | 300 | STBR (Stirred tank bioreactor) |
| 20 | 360 | ||
| 21 | 420 | ||
| 22 | 560 | ||
| 23 | 650 |
| N | PX (mol·gx−1·L−1)·102 |
|---|---|
| 300 | 1.65 |
| 360 | 2.03 |
| 420 | 3.11 |
| 560 | 3.34 |
| 650 | 3.46 |
| 750 | 3.73 |
| Run | CX (g·L−1) | kLa·103·(h−1) | r2 | |
|---|---|---|---|---|
| 1 | 0.1 | 4.75 | 6.92 ± 0.05 | 0.997 |
| 2 | 0.2 | |||
| 3 | 0.3 | |||
| 4 | 0.4 | |||
| 5 | 0.5 | |||
| 6 | 1.0 | |||
| 19 | 0.5 | 4.75 | 8.21 ± 0.05 | 0.9997 |
| Run | kLa·103·(h−1) | N (rpm) | Run | kLa·103·(h−1) | N (rpm) | Run | kLa·103·(h−1) | N (rpm) |
|---|---|---|---|---|---|---|---|---|
| 7 | 8.2 ± 0.4 | 200 | 13 | 14.6 ± 0.7 | 300 | 20 | 10.0 ± 0.7 | 360 |
| 8 | 14 | 21 | 12.5 ± 0.3 | 420 | ||||
| 9 | 15 | 22 | 17.7 ± 0.5 | 560 | ||||
| 10 | 16 | 19.9 ± 0.5 | 400 | 23 | 19.6 ± 0.6 | 650 | ||
| 11 | 17 | 24 | 23.6 ± 0.5 | 750 | ||||
| 12 | 14.6 ± 0.7 | 300 | 18 |
| Device | Parameter | Value |
|---|---|---|
| Shake flasks | kC (L·gx−1·h−1)·10 | 1.67 ± 0.71 |
| KG (mol·L−1)·10 | 1.94 ± 1.60 | |
| SQR 1·103 | 2.07 | |
| SEE 2·103 | 9.50 | |
| RMSE 3·102 | 4.55 | |
| Fcalc/Ftab | 81.6/2.5 | |
| VE 4 (%) | 98.5 | |
| STBR | kC (L·gx−1·h−1)·102 | 9.50 ± 2.49 |
| KG (mol·L−1)·10 | 1.55 ± 0.82 | |
| SQR1·103 | 2.85 | |
| SEE 2·102 | 1.00 | |
| RMSE 3·103 | 9.74 | |
| Fcalc/Ftab | 3990/2.5 | |
| VE 4 (%) | 98.7 |
| Parameter | Value |
|---|---|
| kC (L·gx−1·h−1)·10 | 5.2 ± 1.3 |
| KG (mol·L−1)·10 | 5.6 ± 2.2 |
| n | 0.14 ± 0.02 |
| SQR·103 | 6.26 |
| SEE·102 | 2.40 |
| RMSE·102 | 2.11 |
| Fcalc/Ftab | 187/4.3 |
| VE (%) | 97.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Morena, S.; Wojtusik, M.; Santos, V.E.; Garcia-Ochoa, F. Kinetic Modeling of Dihydroxyacetone Production from Glycerol by Gluconobacter oxydans ATCC 621 Resting Cells: Effect of Fluid Dynamics Conditions. Catalysts 2020, 10, 101. https://doi.org/10.3390/catal10010101
de la Morena S, Wojtusik M, Santos VE, Garcia-Ochoa F. Kinetic Modeling of Dihydroxyacetone Production from Glycerol by Gluconobacter oxydans ATCC 621 Resting Cells: Effect of Fluid Dynamics Conditions. Catalysts. 2020; 10(1):101. https://doi.org/10.3390/catal10010101
Chicago/Turabian Stylede la Morena, Susana, Mateusz Wojtusik, Victoria E. Santos, and Felix Garcia-Ochoa. 2020. "Kinetic Modeling of Dihydroxyacetone Production from Glycerol by Gluconobacter oxydans ATCC 621 Resting Cells: Effect of Fluid Dynamics Conditions" Catalysts 10, no. 1: 101. https://doi.org/10.3390/catal10010101
APA Stylede la Morena, S., Wojtusik, M., Santos, V. E., & Garcia-Ochoa, F. (2020). Kinetic Modeling of Dihydroxyacetone Production from Glycerol by Gluconobacter oxydans ATCC 621 Resting Cells: Effect of Fluid Dynamics Conditions. Catalysts, 10(1), 101. https://doi.org/10.3390/catal10010101







