Abstract
Voters whose yes-or-no decision never makes a difference to the outcome in a simple voting game are known as “null players”. Luxembourg’s role in the Council of Ministers during the first period of the European Economic Community (EEC) is often cited as a real-world case. The paper contrasts the textbook claim that Luxembourg was a null player with a more comprehensive picture of Luxembourg’s role in EEC’s voting system. The assessment of Luxembourg’s voting power is sensitive to the role played by the European Commission in the decision-making procedure and the measurement concepts underlying power evaluations.
JEL Classification:
C71; D70; N44
1. Introduction
On 25 March 1957, Germany, France, Italy and the Benelux countries signed the Treaty of Rome which established the European Economic Community (EEC). Sixty years later, it seems a well-established stylized fact that the founding fathers of what has now become the European Union unwittingly chose an odd voting rule: they rendered Luxembourg a “null player” in the Council of Ministers (CM) from 1958 to 1972.
In fact, the case of Luxembourg is often invoked as a textbook example in the analysis of voting power. It illustrates that a positive number of votes does not necessarily come with a positive share of power. Although it wielded one vote out of a total of 17 votes, there was not a single configuration of votes in which Luxembourg’s decision could theoretically have made a difference. This matches the definition of a null player. Consequently, standard power indices like the Shapley-Shubik index [1,2] and the Penrose-Banzhaf index [3,4] indicate zero voting power for Luxembourg.
The first thing which is forgotten in this context is that Luxembourg was formally a null player only under specific conditions. That is, when the EEC Treaty required the Council to (i) use weighted voting and (ii) act on a proposal of the European Commission. A closer look into the decision rules specified in the EEC Treaty reveals that in all other cases—in particular if Council decisions had to be taken by weighted voting without an initial proposal of the Commission—Luxembourg was not a null player, i.e., had positive voting power.
Secondly, if one recalls the deep bond between the Benelux countries and the important role that Luxembourg has always played (and still plays) in fostering European integration, there were probably other sources of influence for Luxembourg—sources that cannot so straightforwardly be captured by power indices which rest on the assumption of voters acting independently of each other. We provide historical arguments that support this thesis. We also use a composite game with a Benelux Union and invoke a popular power index for games with communication structure in order to get a more refined picture of Luxembourg’s role in the first period of the EEC. Our findings lead us to the conclusion that Luxembourg was no null player during the early days of the EEC.
The remainder of this note is organized as follows: Section 2 will first introduce the different decision rules used by the then Council of Ministers and give a short account of the historical background which motivates later modeling choices. Then we introduce notation, weighted voting games and the two most prominent standard power indices in Section 3. Section 4 recalls the results of traditional power analysis for the early EEC. Section 5 takes account of the Benelux Union by means of a composite game; communication structures within the EEC are captured in Section 6. Section 7 concludes.
2. Historical Background
2.1. The Council’s Internal Decision Rule
The manner in which the Council of Ministers took decisions between 1958 to 1972 was established in Art. 148 of the EEC Treaty. Even though Art. 148(1) allowed for simple majority voting, most of the Council decisions had to be taken by weighted voting and required a so-called prescribed majority as specified in Art. 148(2).1 The corresponding weights were four votes each to Germany, France and Italy, two votes each to the Netherlands and Belgium, and one vote to Luxembourg.
For those decisions that had to be made by weighted voting, two different cases were distinguished. If the EEC Treaty required the Council to act on a proposal of the European Commission, the decision rule was a pure weighted rule that asked for at least 12 out of the 17 total votes in order to adopt a decision. For decisions in policy areas that did not require an initial proposal of the Commission, a double majority rule had to be used: (i) at least 12 votes and (ii) the approval of at least four of the six member states were needed.2
2.2. The Benelux as a Key Driver of European Integration
Economic partnership between Belgium, the Netherlands and Luxembourg dates back at least to 1922 when Belgium and Luxembourg established an economic union, the Union Economique Belgo-Luxembourgeoise.3 In the 1930s, the three Benelux and the Scandinavian states signed the Oslo Convention and Ouchy Convention with the aim to lower tariffs. At the end of the Second World War, the Benelux countries agreed on an even deeper economic relationship among themselves. They signed the Benelux Monetary Agreement in 1943 and the Netherlands-Belgium-Luxembourg Customs Convention in 1944. The former fixed the exchange rates between the Dutch guilder and the Belgian-Luxembourg franc; the latter established a tariff union between the three Benelux countries. They introduced a common external tariff, unified their tax rates and established common institutions like a Council of the Economic Union, a Council for Trade Agreements and an Administrative Council for Customs. In 1945 the Benelux countries and France signed the Economic Agreement on Mutual Consultation, setting up a Tripartite Council for Economic Cooperation. This was not very successful and only lasted until 1948.
In the following years, the Benelux states continued to extend their partnership on different levels. Having signed a military treaty in 1948, they agreed on a common agricultural market in 1955 and unified their labour markets in 1956. Two years later, they signed a treaty that established a new economic union—the well-known Benelux Union—beginning in 1960 and intended to last for 50 years.4 The so-called Benelux Treaty aimed at achieving free movement of capital, goods, people and services. Moreover, the signatories agreed on coordinating economic, financial and social policies. Important common institutions of the Benelux Union are the Committee of the Ministers, consisting of the three foreign ministers, the Benelux Parliament and the Council of the Union.
The Benelux countries were one of the main drivers of European integration. After the European Coal and Steel Community (ECSC) had been established in 1951 by the Treaty of Paris with France, Germany and Italy, the Benelux states insisted on a Council of Ministers to monitor the so-called High Authority of the ECSC and to defend the interests of the smaller member states. The inaugural session of the High Authority and the first session of the Council of Ministers both took place in Luxembourg in 1952.
The most important contribution of the Benelux countries to European integration was then made in 1955. They preferred much deeper integration than that achieved by the ECSC and therefore suggested a comprehensive economic community. The so-called Benelux Memorandum of 1955 resulted in the meeting of Messina, Italy—chaired by Joseph Bech, the Prime Minister of Luxembourg. This was the starting point for the 1957 Treaty of Rome that established the European Economic Community. The Messina Declaration was heavily based on common positions of the Benelux states regarding sectoral integration and a common market.
The deep integration between Belgium, Luxembourg and the Netherlands was explicitly acknowledged in the EEC Treaty. According to Art. 233 “the provisions of this Treaty shall not be an obstacle to the existence or completion of regional unions between Belgium and Luxembourg, and between Belgium, Luxembourg and the Netherlands, in so far as the objectives of these regional unions are not achieved by application of this Treaty.”
In the first crisis of the EEC in 1965, France boycotted every meeting of the Council.5 During this crisis, Luxembourg readily took the role of an arbitrator. In particular, it was Pierre Werner, the Prime Minister of Luxembourg and President of the Council, who used his good personal relations with the other members to keep up communication. During a number of meetings held in Luxembourg in 1966, Werner, who also chaired the meetings, proposed a compromise that entailed that whenever a member state’s vital national interests were affected adversely, negotiations had to continue as long as a mutually acceptable compromise was reached. That gave each member an informal veto right. According to his own account, Werner (as cited in [9]) regarded his presidency “as an opportunity, primarily, for creating an atmosphere and a climate of negotiation which took account of the delicate sensitivities of partners aspiring to reach agreement.”
Pierre Werner’s mediating role during the “empty chair” crisis was not his only important contribution to European integration. Nowadays he is first and foremost known as the “father” of the euro. His so-called “Werner Plan” of 1970 laid the foundations for a European monetary union.
To complete our historical overview, it seems fair to conclude that the Netherlands, Belgium and Luxembourg have not only been the driving force of the European Community, but have also revived the process of European integration over and over again. Acting as one player, they have not only managed to establish a high degree of political cooperation that is unique in Europe but also speak “with one voice and [...] adopt common positions on international issues” [10]. The former particularly applies to Luxembourg. Due to its geostrategic position, Luxembourg has advocated international cooperation ever since the end of World War II. It is often perceived as a privileged partner within institutions. Especially at the European level, its importance is much larger than its land area and population size leads one to assume. In addition to Pierre Werner, prominent Luxembourg politicians that attest to this include Gaston Thorn and Jacques Santer as two former Presidents of the European Commission and Jean-Claude Juncker as former President of the Eurogroup and current President of the European Commission. It is needless to say that their voices matter(ed) for communication and decision-making within the European Community (Union).
3. Preliminaries
3.1. Simple and Weighted Voting Games
A simple game is a special case of a cooperative game in which denotes the non-empty and finite set of players and . A coalition S is referred to as winning if and as losing if . A winning coalition is called minimal winning if every proper subcoalition is losing. It is generally required from that (i) the empty coalition ⌀ is losing (i.e., ), (ii) the grand coalition N is winning (i.e., ) and (iii) v is monotone (i.e., ).
A weighted voting game is a simple game that can be represented by a set of non-negative weights and a positive quota q such that if and only if . We then write interchangeably with , i.e., .6
A few definitions pertaining to players’ roles in a simple game are worth recalling.
Definition 1.
A player in game is called anull playerif for all
A null player contributes nothing to any coalition. If i is a null player, then .
Definition 2.
A player in game is called adummy playerif for all
Intuitively, a dummy player i only contributes his standalone value to any coalition , i.e., his cooperation creates no complementarities and he has no meaningful strategic role in the game. Every null player is also a dummy player. Moreover, if is a simple game, then a dummy player i can either be a null player or a dictator (i.e., ).
To our knowledge, the notion of a null player goes back to von Neumann and Morgenstern [13] (Ch. 10). They dedicated a full chapter’s attention to simple and weighted games and pointed out that it may happen ”that no minimal winning coalition contains a certain player i” (p. 436)—without directly referring to such a player as a null player. Presumably the first to explicitly make use of the term “dummy player” as defined above was Shapley [1]. The subtle difference between null and dummy players got somewhat lost in subsequent years. The literature often speaks of a “dummy player” but is actually referring to a “null player”. The recent book by Maschler et al. [14] is among the few that explicitly distinguishes both types.
3.2. Power Indices
A power index for simple games is a family of functions which map each simple game to a vector of real numbers , where indicates the voting power of player i in game .
The two most prominent indices are the Shapley-Shubik index (SSI) and the Penrose-Banzhaf index (PBI) defined by
where is a probability distribution over the coalitions not including player i. For the PBI
and for the SSI
Here s denotes the cardinality of coalition S and is defined to equal 1. Regarding its probabilistic interpretation, the PBI assumes that all coalitions are equally likely while the SSI assumes all coalition sizes s to be equally likely and any coalition of a given size to be equally likely.7
The bracketed term is usually referred to as player i’s marginal contribution to coalition S. In a simple game if and only if is winning and S is losing. Player i is then also called pivotal or decisive for coalition S. If , i.e., and S are either both winning or both losing, then player i contributes nothing to coalition S.
4. Luxembourg in Traditional Voting Power Analysis
The two versions of the weighted decision rule used by the Council of Ministers from 1958–1972 amount to two different weighted games. The pure weighted rule simply is . The double majority rule, by contrast, is described in the EEC Treaty as the intersection of two weighted games . The first one is and captures the weight dimension. The second is and refers to the majority of countries dimension. A coalition is winning if and only if it is winning in both dimensions, i.e.,
It turns out that the double majority rule can also be translated into a single-dimensional weighted voting game that can be represented by . That is, the intersection of and is equivalent to .
Applying the SSI and PBI to the two decision rules we get the results reported in Table 1. As one can immediately see, Luxembourg was formally powerless under the pure weighted rule. There was not a single configuration in which the vote of Luxembourg did matter, i.e., it was never part of a minimal winning coalition. If, however, in addition to at least 12 votes a majority of the six member countries had to approve the motion, then Luxembourg suddenly played a relevant role. In particular, there existed one coalition that was losing without the support of Luxembourg but turned winning with Luxembourg: the coalition comprising Germany, France and Italy had a total of 12 votes but failed to satisfy the majority of the countries requirement; if Luxembourg joins, the losing coalition turned winning. Thus, claiming that Luxembourg was a null player crucially depends on which of the two decision rules of Art. 148(2) had to be used.

Table 1.
SSI and PBI in 1958–72 CM under pure weighted and double majority rule.
Luxembourg’s role in EEC decision making often serves as a prominent example in the literature on voting power in general and the European Union in particular. See, e.g., Straffin [17] (p. 1131), Felsenthal and Machover [18] (p. 43), Leech [19] (p. 831), Pacelli and Taylor [20] (p. 81) and Le Breton et al. [21] (p. 159).
Unfortunately, it is in most cases simply claimed that Luxembourg was a “dummy player” (more specifically a null player).8 Few authors mention the two different rules in Art. 148(2) and the positive power of Luxembourg under the double majority rule as well as under the simple majority and unanimity provisions of the Treaty. It rather seems like received wisdom that Luxembourg was a null player from 1958–72.
To our knowledge, Affuso and Brams [22,23] and Felsenthal and Machover [5] are the only investigations that explicitly refer to the different decision rules specified in Art. 148. Felsenthal and Machover [5] also claim that Luxembourg was a “dummy player” (although they mean a null player), but they make clear that they are just concerned with the pure weighted rule. Affuso and Brams [22,23] stress the difference between the pure weighted and the double majority rule and highlight that “these slightly more stringent decision rules afforded Luxembourg some nonzero voting power on the 1958 Council [...]” [22] (p. 43).
5. Power in a Composite Game with a Benelux Union
The case distinction between the pure and the double majority weighted voting game notwithstanding, one is tempted to wonder why Luxembourg agreed to being a null player under the pure weighted rule.9 Were they unaware of the fact that there was not a single conceivable configuration of votes in which they could make a difference? Or, and this leads us to the next argument, did they anticipate that their role within the Benelux Union gave them an important say nonetheless?
Given the historical background which we presented in Section 2, it seems natural to assume that the Benelux countries agreed to speak with one voice in the EEC. This section therefore treats Belgium, the Netherlands and Luxembourg as a bloc that acts like a single player. They are presumed to internally agree on the bloc’s position before meeting the other three players.10
The standard framework we have used so far is not able to take such an arrangement directly into account. It is best to employ a composite game to model the situation.11 We can think of the Benelux Union’s decision-making as the first stage in a two-staged process in which all union members are bound to vote according to their within-union decision in the second stage.12
Formally, let be k nonempty and disjoint sets of players such that . In addition, let describe k simple games with respective player sets and a simple game with player set . The so-called -composition of is then denoted by
The characteristic function of this composite game u is given by
for .
The composite game represents a division of player set N into disjoint subsets . The members of have to come to an internal decision via game . Intuitively, one can think of the members of electing a representative who is committed to the internal decision. In the second stage, the k representatives then come together and play game among themselves.
Applied to our context with a Benelux Union and the EEC’s pure weighted rule, player set is partitioned into sets , , and . They face
where is the internal simple game of the Benelux Union and , and are the trivial simple games whose sole voter is Germany, France or Italy.
Regarding decision making within the Benelux Union, two options immediately emerge as natural candidates for . One could (i) use simple majority voting with the weights being those assigned by the EEC Treaty or (ii) simply require the support of at least two of the three countries. The former can be represented by and the latter by . From an analytical perspective it does not matter which of the two is used: they are just different representations of the same game. Namely, every two-player coalition is minimal winning in .
Finally, with is the four-player simple game played between the Benelux Union, Germany, France and Italy and assuming that Belgium, the Netherlands and Luxembourg are bound to their within union decision and cast a joint voting weight of five. This can be represented by .
There are two types of minimal winning coalitions in . One consists of the three large countries Germany, France and Italy. The other involves just two large countries plus the Benelux Union. Overall, a coalition of the three large countries and every coalition that involves two large countries and two Benelux countries is minimal winning in the composite game .
Let and denote the SSI and PBI calculated for above composite game with a Benelux Union.13 We obtain
and
To see why Luxembourg no longer is a null player in , consider the minimal winning coalition . Obviously, since and since . The crucial point is that coalition S loses the five votes of the Benelux Union in one go if Luxembourg decides to leave S.
6. Power in a Game with Communication Structure
Another modeling option which reflects the probable real importance of Luxembourg in early EEC decision-making is by means of games with communication structure. The basic assumption underlying such games is that coalitions can only form between players that are connected in a communication graph, i.e., that can “communicate” with each other. This connection can, e.g., be interpreted as reflecting ideological or spatial proximity.
Formally, a simple game with communication structure is a simple game augmented by an undirected and unweighted graph on N where means that players i and j can communicate, i.e., they are linked to each other. If the underlying simple game allows for a weighted representation, we call a weighted voting game with communication structure.
Players i and j in a coalition S are said to be connected by g if either or there is a path within S from i to j, i.e., we can find players with , and . Coalition S is called connected by g if all players are connected.
A power index for games with communication structure is a family of functions which assign a vector of real numbers to each game , where is interpreted as the power of player i in game .
One of several prominent power indices for games with communication structure is the position value (PV) [29].14 It evaluates the power associated with players’ links. It can be obtained by first calculating the SSI of the so-called link game in which links in g are treated as the “players” and then assigning each player half of the SSI of each link he participates in.15
In what follows, we will only focus on the full graph, i.e., cases where . In our specific political context it seems natural to assume that every player is connected to all the other players. That is, for all players the link is a member of .16 Then,
where denotes the simple game played by links in the full graph and is the characteristic function such that a coalition Q of links is winning if and only if it connects a winning coalition of the original simple game .
Intuitively, one can think of the position value as reflecting scenarios in which links are established randomly one after another until all links have been activated and the coalition in question is connected. The key feature of the PV is that the worth of a new link is shared equally between the two players i and j that are connected by it.
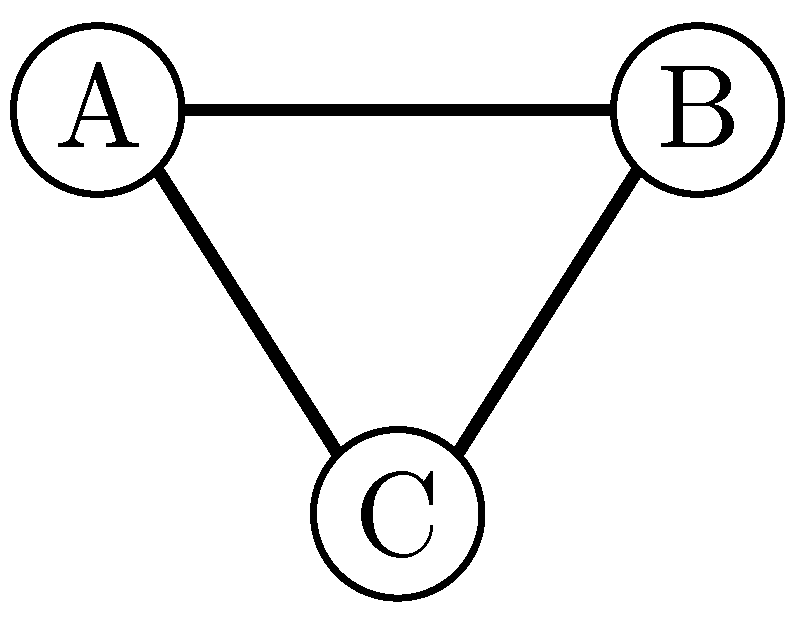
To illustrate the idea behind the PV before looking at the EEC’s pure weighted rule consider the game with and . The corresponding full graph is depicted in Figure 1.
Figure 1.
Full graph with .
In a first step, one has to calculate the SSI of the three links , and in the link game. The minimal winning coalitions are {} and {}. It is easy to see that link is never pivotal and links and are each pivotal in half of the orderings. Thus, . The position value of a player is the sum of half of the SSI of all links in which a given player is involved, i.e., .
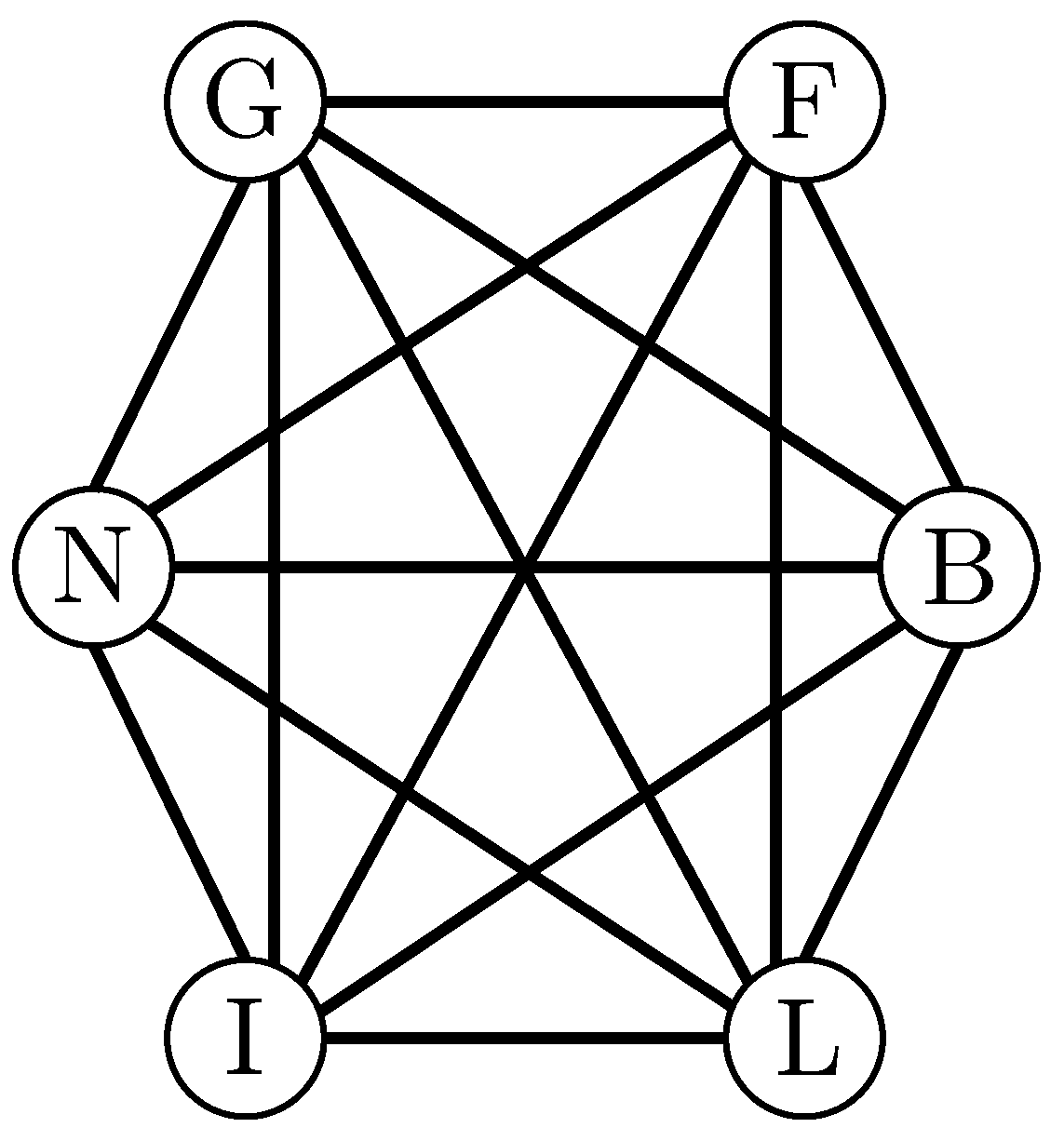
When applying the PV to the early EEC under the assumption that all six players are connected to each other and with , we get
The corresponding full graph is depicted in Figure 2.

Figure 2.
Full graph with .
The fact that Luxembourg does have power in is no surprise. A null player i in a full graph connects the grand coalition and is thus involved in some links that have a positive marginal contribution in the link game, which implies if is non-dictatorial. For illustration, conceive of a sequence of bilateral talks before the actual voting takes place. Assume, e.g., that first France talks to Germany and they agree to support the proposal in question. Then France also manages to get the support of Belgium. This coalition of links and already captures 10 votes. If we next assume that after some talking to each other, the Netherlands and Luxembourg are also in favor of the proposal, the coalition of links is minimal winning. That is, the link between the Netherlands and Luxembourg is pivotal and Luxembourg gets half of its worth.
Note that our finding of Luxembourg having a positive position value does not hinge on using the full graph . It is sufficient to have one maximal losing coalition T that is connected and Luxembourg being linked to one country outside T.
We further remark that there are also non-cooperative ways to model the communication that is necessary to reach the required majority in a decision-making body like the EEC Council. See, e.g., Banks and Duggan [35], Montero [36] and Drouvelis et al. [37] when division of a given surplus is concerned. These models consider legislative bargaining in the tradition of Baron and Ferejohn [38]: some voter is randomly selected to propose a division of a fixed surplus. The proposal is voted upon immediately. If a winning coalition of the corresponding simple game is in favor of the proposal, it is implemented and the game ends; otherwise the game proceeds to the next period in which a new proposer is randomly selected. A voter’s power can then be measured by its expected equilibrium payoff. In the absence of veto players (i.e., players that belong to all minimal winning coalitions) and for sufficiently low discounting, null players turn out to have positive voting power if their recognition probability of being the proposer is positive. The intuition behind this is straightforward: if a null player ends up as the proposer, the other players at least have to discuss the proposal and may even accept it in the face of bargaining frictions. Without any doubt, Luxembourg had such a positive recognition probability in the early days of the EEC. Although it may not have been pivotal by its voting weight itself, it was a sought-after partner and proposer of compromises in the EEC. When Luxembourg raised its voice, the others listened.
7. Concluding Remarks
The case of Luxembourg is the textbook example for illustrating the concept of a null player (which is often confused with that of a dummy player). As shown above, this is somewhat misleading: whether Luxembourg was a null player from 1958–1972 depends on the institutional context, i.e., the two different decision rules embodied in Art. 148(2) of the EEC Treaty. Moreover, even if one is aware of the exact rule being utilized, standard power indices like the SSI and PBI may not be able to pay proper attention to the importance of Luxembourg for European decision-making. If we take factors like the Benelux Union or a potentially sequential bilateral structure of decision-making behind the “veil of ignorance” in a priori analysis of power, we see that unqualified claims that Luxembourg was a null player fall short of the truth.
Although the paper is a specific case study, our observations have broader implications for the evaluation of small voters in institutions. Especially games with communication structure seem to be a natural framework to model decision-making within legislatures. Moreover, “communication” can also be considered in the light of agenda-setting. As an extreme case, consider today’s European Commission and its role in the EU’s codecision procedure (also known as ordinary legislative procedure). The Commission formally only has agenda power but no gate-keeping power since both the Council and the Parliament can—under Art. 225 and Art. 241 of the Treaty on the Functioning of the European Union—prompt the Commission to submit a proposal. The Commission has therefore been regarded as a null player in several theoretical studies on the distribution of influence on EU legislation, including Crombez [39], Napel and Widgrén [40] and Maaser and Mayer [41]. A model of EU codecision which incorporates frictions, analogous to considering in non-cooperative models of legislative bargaining, would arguably be more accurate (but also quite tedious to analyze). It will, however, indicate positive voting power for the Commission despite its null player role in the “codecision simple game”.
Some may argue that this makes use of information that goes beyond a pure a priori perspective. To some extent, we agree. Power indices for composite games or games with communication structure hold a middle ground between fully a priori and a posteriori analysis. However, the respective analysis does neither presume any specific issues that are voted on. Nor does it take historical preferences or individual personalities into account. It analyzes the role of Luxembourg from a constitutional perspective that considers important legal and structural elements of the EEC’s wider institutional framework, notably the Benelux Union which is explicitly referred to in the EEC Treaty.
To give a conclusive answer for the question raised in the title of this paper, one needs to answer a more general question: which properties that go with different indices fit a specific application best? Aumann [42] (p. 535) remarked:
“Which solution concept is ‘right’? None of them; they are indicators, not predictions. Different solution concepts are like different indicators of an economy; different methods for calculating a price index; different maps […]; different stock indices […]; different batting statistics […]; different kinds of information about rock climbs […]; accounts of the same event by different people or different media; different projections of the same three-dimensional object […]. They depict or illuminate the situation from different angles; each one stresses certain aspects at the expense of others.”
For the specific application considered in this paper, both the concepts of games with a priori unions and games with communication structure in our view provide a better perspective than standard simple games. They give a more fitting description of the institutional environment during the first period of the EEC than the models underlying traditional power indices like the PBI and SSI. Be it Luxembourg’s role within the Benelux Union or its importance for maintaining intra-European communication (recall the “empty chair” crisis), Luxembourg clearly influenced decision-making in the EEC. Taking all relevant aspects into the model, Luxembourg was no null player in the early days of the EEC.
Acknowledgments
I gratefully acknowledge financial support from the Knowledge Unlatched initiative for covering the costs to publish in open access. I am indebted to Stefan Napel for constructive comments on earlier drafts. The paper additionally benefited from helpful suggestions by four anonymous reviewers.
Conflicts of Interest
The author declares no conflict of interest.
References
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume II, pp. 307–317. [Google Scholar]
- Shapley, L.S.; Shubik, M. A method for evaluating the distribution of power in a committee system. Am. Political Sci. Rev. 1954, 48, 787–792. [Google Scholar] [CrossRef]
- Penrose, L.S. The elementary statistics of majority voting. J. R. Stat. Soc. 1946, 109, 53–57. [Google Scholar] [CrossRef]
- Banzhaf, J.F. Weighted voting doesn’t work: A mathematical analysis. Rutgers Law Rev. 1965, 19, 317–343. [Google Scholar]
- Felsenthal, D.S.; Machover, M. The Measurement of Voting Power; Edward Elgar: Cheltenham, UK, 1998. [Google Scholar]
- Urwin, D.W. The Community of Europe: A History of European Integration since 1945, 2nd ed.; Routledge: Abingdon, UK, 1995. [Google Scholar]
- Dedman, M.J. The Origins and Development of the European Union 1945–1995: A History of European Integration; Routledge: London, UK, 1996. [Google Scholar]
- Gilbert, M. European Integration: A Concise History; Rowman & Littlefield: Lanham, MD, USA, 2012. [Google Scholar]
- The Luxembourg Compromise (January 1966). Available online: https://www.cvce.eu/en/education/unit-content/-/unit/d1cfaf4d-8b5c-4334-ac1d-0438f4a0d617/a9aaa0cd-4401-45ba-867f-50e4e04cf272 (accessed on 22 April 2018).
- Benelux. Available online: https://www.cvce.eu/en/recherche/unit-content/-/unit/02bb76df-d066-4c08-a58a-d4686a3e68ff/02d476c7-815d-4d85-8f88-9a2f0e559bb4 (accessed on 22 April 2018).
- Taylor, A.D.; Zwicker, W.S. Simple Games; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Freixas, J.; Freixas, M.; Kurz, S. On the characterization of weighted simple games. Theory Decis. 2017, 83, 469–498. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior, 3rd ed.; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Maschler, M.; Solan, E.; Zamir, S. Game Theory; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Napel, S. Voting power. In Oxford Handbook of Public Choice; Congleton, R., Grofman, B., Voigt, S., Eds.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Isbell, J.R. A class of majority games. Q. J. Math. 1956, 7, 183–187. [Google Scholar] [CrossRef]
- Straffin, P.D., Jr. Power and stability in politics. In Handbook of Game Theory; Aumann, R., Hart, S., Eds.; North-Holland: Amsterdam, The Netherlands, 1994; Volume 2, pp. 1127–1151. [Google Scholar]
- Felsenthal, D.S.; Machover, M. The weighted voting rule in the EU’s Council of Ministers, 1958–95: Intentions and outcomes. Elect. Stud. 1997, 16, 33–47. [Google Scholar] [CrossRef]
- Leech, D. Computing power indices for large voting games. Manag. Sci. 2003, 49, 831–837. [Google Scholar] [CrossRef]
- Pacelli, A.M.; Taylor, A.D. Mathematics and Politics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Le Breton, M.; Montero, M.; Zaporozhets, V. Voting power in the EU Council of Ministers and fair decision making in distributive politics. Math. Soc. Sci. 2012, 63, 159–173. [Google Scholar] [CrossRef]
- Affuso, P.J.; Brams, S.J. Power and size: A new paradox. Theory Decis. 1976, 7, 29–56. [Google Scholar]
- Affuso, P.J.; Brams, S.J. New paradoxes of voting power on the EC Council of Ministers. Elect. Stud. 1985, 4, 135–139. [Google Scholar]
- Widgrén, M. Voting power in the EC decision making and the consequences of two different enlargements. Eur. Econ. Rev. 1994, 38, 1153–1170. [Google Scholar] [CrossRef]
- Hosli, M.O. Coalitions and power: Effects of qualified majority voting in the Council of the European Union. J. Common Market Stud. 1996, 34, 255–273. [Google Scholar] [CrossRef]
- Felsenthal, D.S.; Machover, M. Annexations and alliances: When are blocs advantageous a priori? Soc. Choice Welf. 2002, 19, 295–312. [Google Scholar] [CrossRef]
- Felsenthal, D.S.; Machover, M. Further reflections on the expediency and stability of alliances. In Power, Freedom, and Voting; Braham, M., Steffen, F., Eds.; Springer: Berlin, Germany, 2008; pp. 39–55. [Google Scholar]
- Owen, G. Game Theory, 3rd ed.; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Borm, P.; Owen, G.; Tijs, S. On the position value for communication situations. SIAM J. Discret. Math. 1992, 5, 305–320. [Google Scholar] [CrossRef]
- Myerson, R.B. Graphs and cooperation in games. Math. Oper. Res. 1977, 2, 225–229. [Google Scholar] [CrossRef]
- Owen, G. Values of graph-restricted games. SIAM J. Algebraic Discret. Methods 1986, 7, 210–220. [Google Scholar] [CrossRef]
- Herings, P.J.-J.; van der Laan, G.; Talman, G. The average tree solution for cycle-free graph games. Games Econ. Behav. 2008, 62, 77–92. [Google Scholar] [CrossRef]
- Herings, P.J.-J.; van der Laan, G.; Talman, A.J.J.; Yang, Z. The average tree solution for cooperative games with communication structure. Games Econ. Behav. 2010, 68, 626–633. [Google Scholar] [CrossRef]
- Ghintran, A. Weighted position values. Math. Soc. Sci. 2013, 65, 157–163. [Google Scholar] [CrossRef]
- Banks, J.S.; Duggan, J. A bargaining model of collective choice. Am. Political Sci. Rev. 2000, 94, 73–88. [Google Scholar] [CrossRef]
- Montero, M. Noncooperative foundations of the nucleolus in majority games. Games Econ. Behav. 2006, 54, 380–397. [Google Scholar] [CrossRef]
- Drouvelis, M.; Montero, M.; Sefton, M. Gaining power through enlargement: Strategic foundations and experimental evidence. Games Econ. Behav. 2010, 69, 274–292. [Google Scholar] [CrossRef]
- Baron, D.P.; Ferejohn, J.A. Bargaining in legislatures. Am. Political Sci. Rev. 1989, 83, 1181–1206. [Google Scholar] [CrossRef]
- Crombez, C. Institutional reforms and co-decision in the European Union. Const. Political Econ. 2000, 11, 41–57. [Google Scholar] [CrossRef]
- Napel, S.; Widgrén, M. The inter-institutional distribution of power in EU codecision. Soc. Choice Welf. 2006, 27, 129–154. [Google Scholar] [CrossRef]
- Maaser, N.; Mayer, A. Codecision in context: Implications for the balance of power in the EU. Soc. Choice Welf. 2016, 46, 213–237. [Google Scholar] [CrossRef]
- Aumann, R. Game theory. In The New Palgrave Dictionary of Economics, 2nd ed.; Durlauf, S.N., Blume, L.E., Eds.; Macmillan: London, UK, 2008; Volume 3, pp. 529–558. [Google Scholar]
| 1 | The original version of the EEC Treaty used the term “prescribed majority”. It was changed to “qualified majority” later. Constitutional measures and derogation from the Treaty always required unanimity. For further information on weighted voting in the Council of Ministers during the first period of the EEC, see Felsenthal and Machover [5] (Ch. 5.2). |
| 2 | There was moreover a transition period of eight years (until 31 December 1965) during which every country had a veto right. Unanimity was also required if the Council wanted to amend a Commission proposal (Art. 149). |
| 3 | If not mentioned otherwise, the material in this section is mainly based on Urwin [6], Dedman [7] and Gilbert [8]. |
| 4 | Two years before expiration, an unlimited extension was agreed. |
| 5 | Among the reasons for France’s so-called “policy of the empty chair” were discrepancies regarding the admission of Britain, farm prices and increased budgetary power of the European Parliament. The remainder of this paragraph is based on [9]. |
| 6 | Not every simple game has such a weighted representation. Examples include the qualified majority rule of the Council of the EU as specified in the Treaty of Lisbon, or the Canadian Constitution. See Taylor and Zwicker [11]. Ongoing progress on the problem of verifying if a given simple game is weighted is, e.g., reported by Freixas et al. [12]. |
| 7 | See Napel [15] for an overview on different approaches to the measurement of voting power. PBI and SSI often give similar values, but not always. They induce the same ordinal ranking of players if the players can be ordered by Isbell’s desirability relation [16]. |
| 8 | This is not wrong since a null player is always a dummy player. Still, the concepts are not equivalent. |
| 9 | For the rest of this paper, we will only deal with the pure weighted rule. Under the double majority rule, Luxembourg has positive voting power anyway. |
| 10 | Other contributions dealing with coalition formation within the European Union are by Widgrén [24], Hosli [25] and Felsenthal and Machover [26,27]. |
| 11 | For a thorough treatment of composite games, see Owen [28] (Ch. 11–12) and Felsenthal and Machover [5] (Ch. 2). |
| 12 | At least for the PBI, this has already been pointed out by Felsenthal and Machover [27]. |
| 13 | The calculation of the PBI is particularly easy: for the large countries it is just the PBI in the second stage game ; for a member of the Benelux Union it is the product of its PBI in the first-stage game and the Union’s PBI in the second stage game . Unfortunately, the SSI does not have such a product property; we calculate it directly from its definition. |
| 14 | The main other ones are the Myerson value [30], the restricted Banzhaf index [31] and the average tree solution [32,33]. |
| 15 | Extensions of the position value also allow for an unequal division of a link’s SSI [34]. |
| 16 | For a general definition of the PV, also applying to cases , one needs to introduce the concept of a restricted game. This would, however, just complicate the exposition without adding useful insights for our setting. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).