1. Introduction
In 1952, Markowitz proposed a paradigm for dealing with risk issues concerning choices which involve many possible financial instruments [
1]. Formally, it deals with only two discrete time periods (e.g., “now” and “3 months from now”), or equivalently, one accounting period (e.g., “3 months”). In this scheme, the goal of an Investor is to select the portfolio of securities that will provide the best distribution of future consumption, given their investment budget. Two measures of the prospects provided by such a portfolio are assumed to be sufficient for evaluating its desirability: the expected value at the end of the accounting period and the standard deviation or its square, the variance, of that value. If the initial investment budget is positive, there will be a one-to-one relationship between these end-of-period measures and comparable measures relating to the percentage change in value, or return over the period. Thus, Markowitz’ approach is often framed in terms of the expected return of a portfolio and its standard deviation of return, with the latter serving as a measure of risk. A typical example of risk in the current market is the evolution of the prices [
2,
3] of the cryptocurrencies (bitcoin, litecoin, ethereum, dash, etc). The Markowitz paradigm (also termed as mean-variance paradigm) is often characterized as dealing with portfolio risk and (expected) return [
4,
5]. We address this problem when several entities are involved. Game problems in which the state dynamics is given by a linear stochastic system with a Brownian motion and a cost functional that is quadratic in the state and the control are often called linear–quadratic–Gaussian (LQG) games. For the continuous time LQG game problem with positive coefficients, the optimal strategy is a linear state-feedback strategy which is identical to an optimal control for the corresponding deterministic linear–quadratic game problem, where the Brownian motion is replaced by the zero process. Moreover, the equilibrium cost only differs from the deterministic game problem’s equilibrium cost by the integral of a function of time. For LQG control and LQG zero-sum games, it can be shown that a simple square completion method provides an explicit solution to the problem. It was successfully developed and applied by Duncan et al. [
6,
7,
8,
9,
10,
11] in the mean-field-free case. Interestingly, the method can be used beyond the class of LQG framework. Moreover, Duncan et al. extended the direct method to more general noises, including fractional Brownian noises and some non-quadratic cost functionals on spheres, torus, and more general spaces.
The main goal of this work is to investigate whether these techniques can be used to solve mean-field-type game problems which are non-standard problems [
12]. To do so, we modify the state dynamics to include mean-field terms which are (i) the expected value of the state, (ii) the expected value of the control-actions, in the drift function. We also modify the instant cost and terminal cost function to include (iii) the square of the expected values of the state and (iv) the square of the expected values of the control action. When the state dynamics and/or the cost functional involve a mean-field term (such as the expected value of the state and/or expected values of the control actions), the game is said to be an LQG game of mean-field type, or MFT-LQG. We aim to study the behavior of such MFT-LQG game problems when mean-field terms are involved. If in addition the state dynamics is driven by a jump-diffusion process, then the problem is termed as an MFT-LQJD game problem.
For such game problems, various solution methods such as the stochastic maximum principle (SMP) ([
12]) and the dynamic programming principle (DPP) with Hamilton–Jacobi–Bellman–Isaacs equation and Fokker–Planck–Kolmogorov equation have been proposed [
12,
13,
14]. Most studies illustrated these solution methods in the linear–quadratic game with an infinite number of decision-makers [
15,
16,
17,
18,
19,
20,
21]. These works assume indistinguishability within classes, and the cost functions were assumed to be identical or invariant per permutation of decision-makers indexes. Note that the indistinguishability assumption is not fulfilled for many interesting problems, such as variance reduction or and risk quantification problems, in which decision-makers have different sensitivity towards the risk. One typical and practical example is to consider an energy-efficient multi-level building in which every resident has its own comfort zone temperature and aims to use the Heating, ventilation, and air conditioning (HVAC) system to be closer to its comfort temperature and to maintain it within its own comfort zone. This problem clearly does not satisfy the indistinguishability assumption used in the previous works on mean-field games. Therefore, it is reasonable to look at the problem beyond the indistinguishability assumption. Here we drop these assumptions and solve the problem directly with an arbitrary finite number of decision-makers. In the LQ-mean-field-type game problems, the state process can be modeled by a set of linear stochastic differential equations of McKean–Vlasov, and the preferences are formalized by quadratic cost functions with mean-field terms. These game problems are of practical interest, and a detailed exposition of this theory can be found in [
7,
12,
22,
23,
24,
25]. The popularity of these game problems is due to practical considerations in signal processing, pattern recognition, filtering, prediction, economics, and management science [
26,
27,
28,
29].
To some extent, most of the risk-neutral versions of these optimal controls are analytically and numerically solvable [
6,
7,
9,
11,
24]. On the other hand, the linear quadratic robust setting naturally appears if the decision makers’ objective is to minimize the effect of a small perturbation and related variance of the optimally controlled nonlinear process. By solving a linear–quadratic game problem of mean-field type, and using the implied optimal control actions, decision-makers can significantly reduce the variance (and the cost) incurred by this perturbation. The variance reduction and minimax problems have very interesting applications in risk quantification problems under adversarial attacks and in security issues in interdependent infrastructures and networks [
27,
30,
31,
32,
33].
Table 1 summarizes some recent developments in MF-LQ-related games.
In this work, we propose a simple argument that gives the best-response strategy and the Nash equilibrium cost for a class of MFT-LQJD games without the use of the well-known solution methods (SMP and DPP). We apply the square completion method in the risk-neutral mean-field-type game problems. It is shown that this method is well-suited to MF-LQJD games, as well as to variance reduction performance functionals. Applying the solution methodology related to the DPP or the SMP requires an involved (stochastic) analysis and convexity arguments to generate necessary and sufficient optimality criteria. We avoid all of this with this method.
1.1. Contribution of This Article
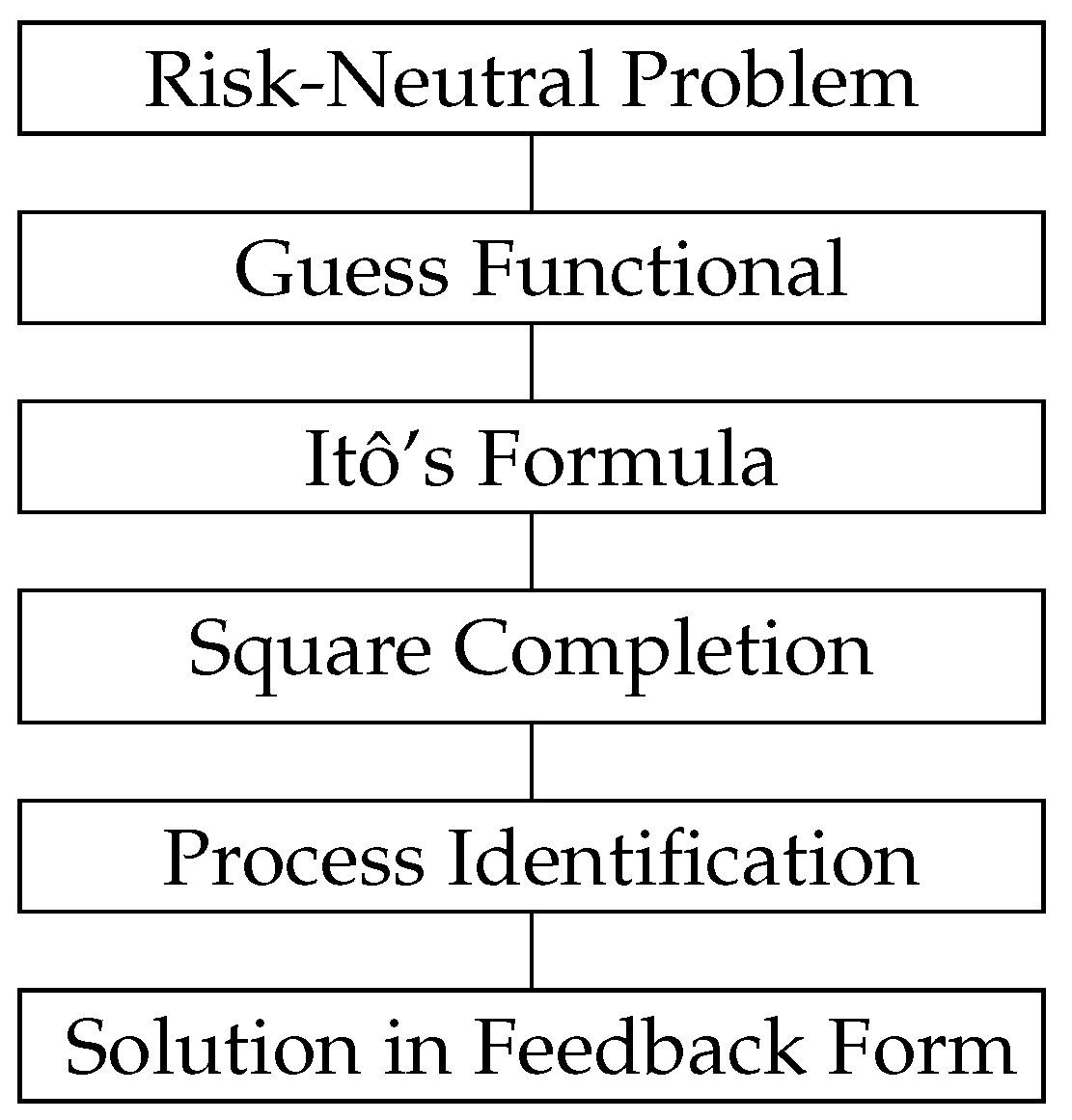
Our contribution can be summarized as follows. We formulate and solve a mean-field-type game described by a linear jump-diffusion dynamics and a mean-field-dependent quadratic or robust-quadratic cost functional for each generic decision-maker. The optimal strategies for the decision-makers are given semi-explicitly using a simple and direct method based on square completion, suggested by Duncan et al. (e.g., [
7,
8,
9]) for the mean-field-free case. This approach does not use the well-known solution methods such as the stochastic maximum principle and the dynamic programming principle with Hamilton–Jacobi–Bellman–Isaacs equation and Fokker–Planck–Kolmogorov equation. It does not require extended backward–forward integro-partial differential equations (IPDEs) to solve the problem. In the risk-neutral linear–quadratic mean-field-type game, we show that there is generally a best response strategy to the mean of the state, and provide a sufficient condition of existence of mean-field Nash equilibrium. We also provide a global optimum solution to the problem in the case of full cooperation between the decision-makers. This approach gives a basic insight into the solution by providing a simple explanation for the additional term in the robust Riccati equation, compared to the risk-neutral Riccati equation. Sufficient conditions for the existence and uniqueness of mean-field equilibria are obtained when the horizon lengths are small enough and the Riccati coefficient parameters are positive. The method (see
Figure 1) is then extended to the linear–quadratic robust mean-field-type games under disturbance, formulated as a minimax mean-field-type game.
Only a very limited amount of prior work seems to have been done on the MF-LQJD mean-field-type game problems. As indicated in
Table 1, the jump term brings a new feature to the existing literature, and to the best of our knowledge, it is the first work that introduces and provides a bargaining solution [
34] in mean-field-type games using a direct method.
The last section of this article is devoted to the validation of the novel equations derived in this article using other approaches. We confirm the validity of the optimal feedback strategies. In the
Appendix we provide a basic example illustrating the sub-optimality of the mean-field game approach (which consists of freezing the mean-field term) compared with the mean-field-type game approach (in which an individual decision-maker can significantly influence the mean-field term).
1.2. Structure
A brief outline of the article follows. The next section introduces the non-cooperative mean-field-type game problem and provides its solution. Then, the fully-cooperative game and the bargaining problems and their solutions are presented. The last part of the article is devoted to adversarial problems of mean-field type.
Notation and Preliminaries
Let be a fixed time horizon and be a given filtered probability space on which a one-dimensional standard Brownian motion is given, is a centered jump process with Lévy measure defined over The filtration is the natural filtration generated by the union augmented by null sets of The processes B and N are mutually independent. In practice, B is used to capture smaller disturbance and N is used for larger jumps of the system.
We introduce the following notation:
Let be the set of functions such that .
is the set of -adapted -valued processes such that .
denotes the expected value of the random variable
An admissible control strategy
of decision-maker
i is an
-adapted and square-integrable process with values in a non-empty subset
of
. We denote the set of all admissible controls by
:
2. Non-Cooperative Problem
Consider n risk-neutral decision-makers () and let be the objective functional of decision-maker given by
Then, the best-response of decision-maker
i to the process
solves the following risk-neutral linear–quadratic mean-field-type control problem
where
, and
are real-valued functions, and where
is the expected value of the state created by all decision-makers under the control action profile
The method below can handle time-varying coefficients. For simplicity, we impose an integrability condition on these coefficient functions over
:
Under condition (
3), the state dynamics of (
2) has a solution for each
Note that we do not impose boundedness or Lipschitz conditions (because quadratic functionals are not necessarily Lipschitz).
Definition 1 (BR
i: Best Response of decision-maker
i)
. Any strategy satisfying the infimum in (2) is called a risk-neutral best-response strategy of decision-maker i to the other decision-makers strategy The set of best-response strategies of i is denoted by where denotes the set of subsets of Note that if , there are multiple optimizers of the best-response problem.
Definition 2 (Mean-Field Nash Equilibrium)
. Any strategy profile such that for every i and is called a Nash equilibrium of the LQ-MFJD game above.
The risk-neutral mean-field-type Nash equilibrium problem we are concerned with is to find and characterize the processes
such that for every decision-maker
is an optimizer of the best response problem (
2) and the expected value of the resulting common state
created by all the decision-makers coincides with
This means that an equilibrium is a fixed-point of the best response correspondence
, where
is the best-response correspondence of decision-maker
We rewrite the expected objective functional and the state coefficients in terms of
and
Note that the expected value of the first term in the integral in can be seen as a weighted variance of the state, since Taking the expectation of the state dynamics, one arrives at the deterministic linear dynamics
The direct method consists of writing a generic structure of the cost functional, with unknown deterministic functions to be identified. Inspired from the structure of the terminal cost function, we try a generic solution in a quadratic form. Let where are deterministic functions of time, such that
At the final time one can identify
Recall that Itô’s formula for the jump-diffusion process is
where
D is the drift term
. We compute the derivative terms:
Using (
7) in (
6) and taking the expectation yields
where we have used the following equalities:
We compute the gap between and as
2.1. Best Response to Open-Loop Strategies
In this subsection, we compute the best-response of decision-maker
i to open-loop strategies
The information structure for the others players is limited to time and initial point; i.e., the mappings
are measurable functions of time (and do not depend on
x) and initial point
where
The best response of decision-maker i to the open-loop strategies is , and its expected value is , where are deterministic functions of time Clearly, the best response to open-loop strategies is in state-and-mean-field feedback form. Here the mean-field feedback terms are the expected value of the state and the expected value of the control action
Therefore, we examine optimal strategies in state-and-mean-field feedback form in the next section.
2.2. Feedback Strategies
The information structure for feedback solution is as follows. The model and the objective functions are assumed to be common knowledge. We assume that the state is of perfect observation. We will show below that the mean-field term is computable (via the initial mean state and the model). If the other decision-makers play their optimal state-and-mean-field feedback strategies, then the functions
are identically zero at any given time. We compute again
and complete the squares using the elements of
where we have used the following square completions:
It follows that
provides a mean-field Nash equilibrium in feedback strategies.
These Riccati equations are different from those of open-loop control strategies. The coefficient of the coupling terms
are different, reflecting the coupling through the state and the mean state. Notice that the optimal strategy is in state-and-mean-field feedback form, which is different from the standard LQG game solution. As
vanish in (
15), one gets the Nash equilibrium of the corresponding stochastic differential game in closed-loop strategies with
and
becomes mean-field-free. When the diffusion coefficient
and the jump rate
vanish, one obtains the noiseless deterministic game problem, and the optimal strategy solution will be given by the equation in
because
in the deterministic case.
How to feedback the mean-field term
? Here the mean-field term can be explicitly computed if the initial mean state
is given and the model known:
4. LQ Robust Mean-Field-Type Games
We now consider a robust mean-field-type game with two decision-makers. Decision-maker 1 minimizes with respect to
and Decision-maker 2 maximizes with respect to
The minimax problem of mean-field type is given by
where the objective functional is
The risk-neutral robust mean-field-type equilibrium problem we are concerned with is to characterize the processes
such that for every decision-maker,
is the minimizer and
is the maximum of the best response problem (
24), and the expected value of the resulting common state created by all the decision-makers is
Below, we solve Problem (
24) for
where we have used the following square completions:
It follows that the equilibrium solution is
When and the functions are explicitly given by
Notice that under the conditions , the minimax solution is also a maximin solution: there is a saddle point, and the saddle point is It solves
The value of the game is
5. Checking Our Results
In this section, we verify the validity of our results above using a Bellman system. Due to the non-Markovian nature of
one needs to build an augmented state. A candidate augmented state is the measure
m, since one can write the objective functionals in terms of the measure
This leads to a dynamic programming principle in infinite dimensions. Below, we use functional derivatives with respect to
The Bellman equilibrium system (in infinite dimension) is
where the terminal equilibrium payoff functional at time
T is
and the integrand Hamiltonian is
It is important to notice that the last term in the integrand Hamiltonian
is coming from the jump process involved in the state dynamics. From this Hamiltonian. we deduce that, generically, the optimal strategy is state-and-mean-field feedback form, as the RHS of (
35) is. We now solve explicitly McKean–Vlasov integro-partial differential equation above. Inspired by the structure of the final payoff
, we choose a guess functional in the following form:
The reader may ask why the term is missing in the guess functional. This is because we are looking for the expected value optimization (risk-neutral case), and its expected value is zero. The term does not appear because there is no constant shift in the drift and no cross-terms in the loss function.
We now utilize the functional directional derivative. Consider another measure
and compute
Differentiating the latter term with respect to yields
We deduce the following equalities:
where we have used the following orthogonal decomposition:
Noting that the expected value of the following term
is zero, the optimization yields the optimization of
Thus, the equilibrium strategy of decision-maker
i is
which are exactly the expressions of the optimal strategies obtained in (
15). Based on the latter expressions, we refine our statement. The optimal strategy is state-and-(mean of) mean-field feedback form.
We now solve explicitly the McKean–Vlasov integro-partial differential equation above.
Using the time derivative of
and identifying the coefficients, we arrive at
We retrieve the expressions in (
15), confirming the validity of our approach.