1. Introduction
Project management emerged in the 1950s and expanded its applications in an increasing number of industries. According to the guide to the Project Management Body of Knowledge (PMBOK Guide 5th edition) [
1], a project is a “temporary endeavour undertaken to create a unique product, service, or result”. The delivery of a project usually involves a wide range of stakeholders, among which the project owner and contractor (also known as the supplier) are arguably the most important players.
There are two well-known challenges in the owner-contractor management [
2]:
The divergence of interests may induce conflict, which in return can lead to greater risk and lengthened project duration.
The participants’ behaviour is often tacit, requiring clarifications which may be obtained through rigorous modelling.
These challenges underlie possible conflicts and disputes, which may not only cause damage to the project owner and the contractor, but also may directly impair the outcome of projects. Having a relatively low-cost negotiation is the most popular resolution to settle disputes in comparison with other alternatives, such as partnering, arbitration, and dispute review boards [
3]. Therefore, modelling negotiation as a way to settle conflicts between the project owner and the contractor has attracted research interest. While earlier studies concentrate on developing a framework or tactic for the negotiating parties, the more contemporary research incorporates game theory to obtain the optimal outcome. Game theory may offer solutions to the problem by providing quantitative models of conflict and co-operation between intelligent, rational decision-makers [
4]. It also suggests insights on how one’s decision will influence that of another and thus can be used to resolve conflicts and optimise risk handling between stakeholders in project management. By using game theory, project managers could reduce the chances of conflicts and gain better control in managing the owner-contractor liaison [
5]. A number of studies have employed game theory in specific project settings in recent years, by focusing on the negotiation between the government and the private funding parties in Public-Private Partnership projects [
6,
7,
8], and/or over some particular types of contracts, such as the BOT (Build-Operate-Transfer) contracts [
9,
10]. However, project management is known to be a broad discipline and the practitioners are keen to obtain a holistic and pluralistic understanding of stakeholder engagement [
2]. It is therefore of interest to establish game theory as a means to provide a generalised negotiation model that can fit into different project environments.
This paper investigates the feasibility of utilising the evolutionary game theory in project management by setting up a representative model of a conflict between the owner and the contractor. The game is set in the context of the classical Hawk-Dove game, and the stability of Nash equilibria is studied through both analytical derivations and computational simulations. In doing so, the well-known Hawk-Dove evolutionary game is generalised by introducing cost sharing ratios for both players. Follow-up analysis is conducted by analysing the adaptation of optimal strategies and stability of the resultant equilibria under noisy and latent conditions which are typical in practical scenarios.
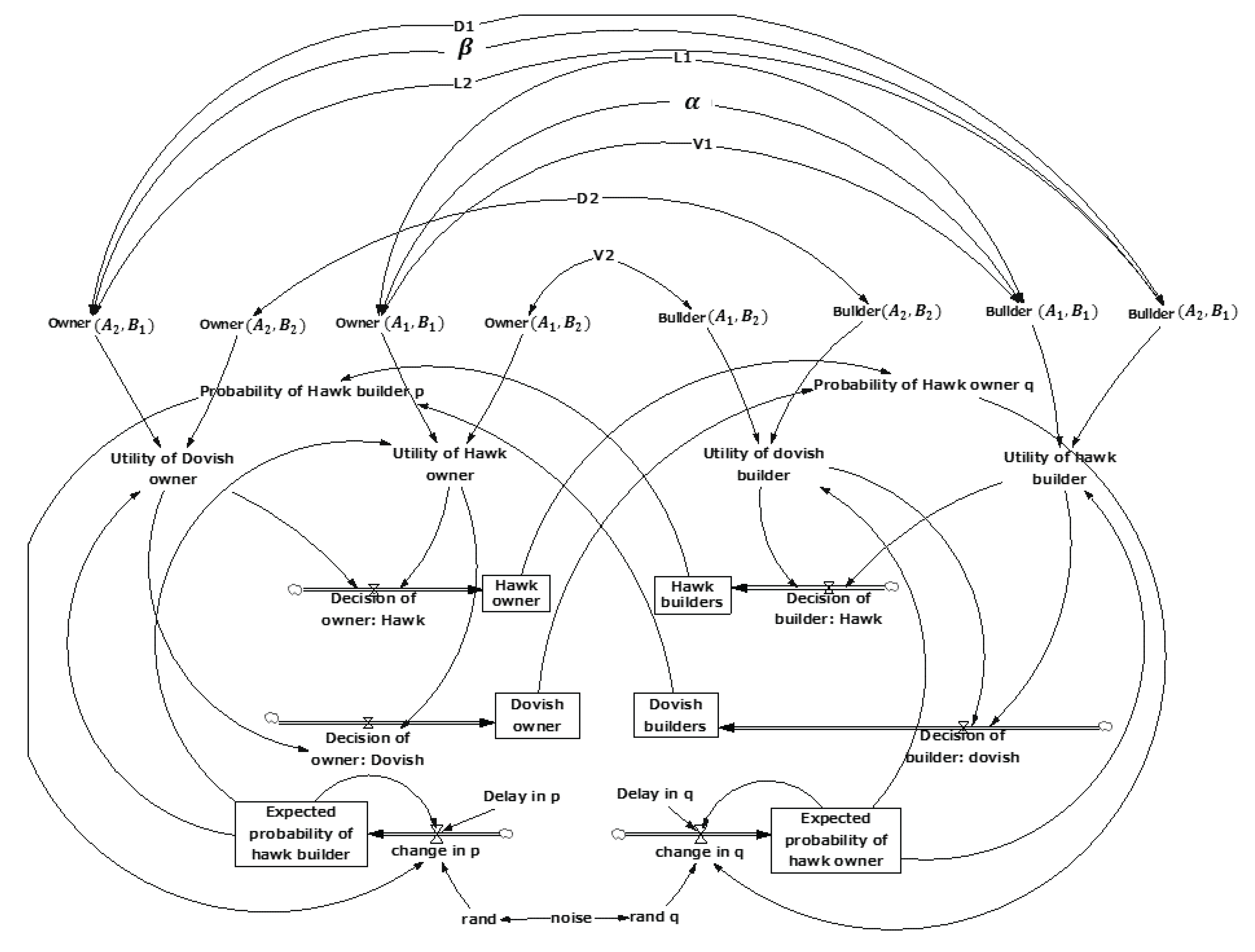
2. Evolutionary Game Theory: Generalised Hawk-Dove Model
The Hawk-Dove game originally developed by Maynard Smith [
11] is one of the well-recognised standard paradigms of evolutionary game theory. It draws inspiration from the biology and models two players, hawk and dove, engaging in a single symmetric contest over a resource [
12]. The payoff matrix for the Hawk-Dove game includes the value of the contested resource
v, and the cost of an escalated fight
c (
Table 1). It is almost always assumed that the value of the resource is less than the cost of a fight, i.e.,
[
11]. The cost of fight only incurs if a hawk confronts another hawk, producing the resultant payoff for each player as
. When a dove meets another dove, however, no fight will engage and they share the resource equally, each with payoff
. The payoffs for a hawk encountering a dove reflect the discrepancy of the fighting ability for the two species so that the hawk receives the resource
v in full while the dove has nothing.
An evolutionarily stable strategy (ESS) is a strategy such that if all members of a population adopt the ESS then no other strategy can replace it. The concept of ESS is the refinement of a Nash equilibrium, a stable strategy where a player gains no benefit from changing to a different strategy. In the classical two-player Hawk-Dove model, there are typically three Nash equilibria: two appear as a pure strategy and one as a mixed strategy [
13]. The classical Hawk-Dove game is a symmetric contest where the cost of confrontation is equally shared; and the resultant ESS is a mixed strategy in the sense that “the population will be genetically polymorphic or individuals will be behaviourally variable” [
14]. Later studies extended the consideration of contests to a two-stage game where the contest repeats twice [
15], and more importantly, to an asymmetric form in terms of the role dominance, unequal payoffs [
14] and payoff relevance where differences in the value of winning were introduced for different players [
16]. The ESS in asymmetric contests usually appears to avoid an escalation of the confrontation [
14]. This conclusion also holds if the players are allowed to communicate prior to the game, e.g., if they are allowed to threaten each other before choosing their moves [
17]. The modern applications of the Hawk-Dove game include the bargaining and negotiation processes. If the Hawk-Dove game is multi-stage while the two players play the game in order (i.e., the second player moves after knowing the first player’s strategy), the equilibrium covers a fully cooperative case when both players act as doves in both symmetric and asymmetric settings, together with multiple asymmetric equilibria [
18]. The interaction has also been extended to allow the players to confirm the proposed strategy before committing to a Hawk-Dove agreement [
19]. These applications in the negotiation process, however, assume that no pre-established positions are held before bargaining. This assumption, unfortunately, does not hold in the scenario of project conflicts because the inherent role of the project participants is to decide their positions in the negotiation process, and so they are not likely to cooperate willingly acting as doves. Informally, the optimal results for the players’ individual interests emerge when two parties deliberately choose the opposite (“confrontational”) strategies [
20].
The interaction between two players in a contract-based project management setting involving the owner and the contractor are often modelled using the single-stage Hawk-Dove model with modified asymmetric payoff matrix [
21,
22]. This selection of player roles is representative of resource-sharing in project management, and this context can be easily modified to represent other stakeholders given that the decision-making involves negotiation over some resource. Two strategies are, therefore, available in this model for the project participants, representing the hawk (aggressive) and the dove (acquiescent), as summarised in
Table 2, mapping to the classical form. By pairing the strategies, four scenarios are available:
,
,
and
. The matrix elements are modified to reflect two traits in the negotiation of the tendering process:
The project owner makes an offer at a price for some work to be carried out, represented with a negative sign of the corresponding payoff; the project contractor, on the other hand, accepts the quote, making gains shown with a positive sign. The project owner naturally has higher governance over the project and therefore is not penalised for taking a strong stance opting for strategy , whereas the project contractor would incur some additional cost when he/she decides to initiate negotiation by choosing strategy . The cost of negotiation, however, is most definitely not shared equally, as is the case considered in the classical Hawk-Dove game; instead, the fraction that each player needs to bear varies in accordance to his/her attitude towards risks.
Noting the above mentioned two traits, the payoff matrix of the Hawk-Dove model constructed for the project management setting is refined by:
A hawk owner does not incur an additional cost but a hawk contractor would. The cost of negotiation varies with the attitude of the two parties.
Owner’s payoff is represented as a (negative) “loss” (constituting the payment amount), while the contractor payoff, conversely, is positive and includes the received payment amount.
In a realistic project conflict scenario, however, it should be expected that even when facing a hawk contractor, a dove owner should pay an agreed amount subject to some additional costs. This can be modelled, in our generalisation of the Hawk-Dove payoff matrix, by introducing a distinction between agreed payment amounts V (owner as a hawk) and D (owner as a dove), while also including different (cost sharing) penalty components and .
Formally, four parameters,
,
,
,
, are used to represent initial contracted payments in four scenarios
,
,
, and
respectively, as shown in
Table 3, extending the study of [
21]. In cases of
and
, when the contractor acts as a hawk (
), the additional costs may be incurred, for instance, from communication and contract negotiation. These costs are represented by
if the project owner also acts as a hawk, and
if the owner steps down as a dove. The introduction of sharing ratios,
and
that range from 0 to 1, decides how the penalties are distributed between the two parties. In
, the owner’s portion of
is
and the contractor’s one is
; similarly, in
, the owner’s share of
is
and the contractor’s one is
, resulting in the payoff matrix shown in
Table 3.
An assumption holds that the payment amount (i.e., resource) varies with both players’ attitude. The project owner, by nature, is more dominant in shaping the contract terms; therefore, if the owner “steps down” by acting dovish, the contractor who compromises (i.e., acting dovish too) receives a higher contract amount than those who stay rigid and aggressive. In cases where the owner is acting as a hawk, a more demanding hawk contractor would get paid more. The confrontation between the hawk owner and the hawk contractor surely requires a longer time to resolve the dispute, translating to the higher incurred additional cost. These conditions are expressed in constraints (
1).
To ensure that in the generalised Hawk-Dove game the best outcome for the owner and for the contractor still occur in scenarios
and
, further constraints are needed:
These constraints set the conditions capturing the scenarios in which the opposing strategies,
and
, are the optimal cases for the project owner and the project contractor respectively. This is consistent with the canonical Hawk-Dove game where the Hawk-Dove pair is always the most advantageous for the hawk player. By applying the conditions, when the project owner is using strategy
acting as a hawk, the project contractor has a tendency to move from
being a hawk to
being a dove, and vice versa. It is a common practice in the negotiation process known as the “strategic and pragmatic approach” where both parties accept the adjustment to the original plan and is believed to be the preferred method for producing cost effective outcomes [
23]. Mathematically, Equation (
2) set an upper boundary
for
and a lower bound
for
so that when the contractor acts as a hawk (
), there is a maximum cap
for the project owner to absorb
if he/she plays strategy
; if the project owner decides on strategy
, the compromise is reflected by sharing at least
.
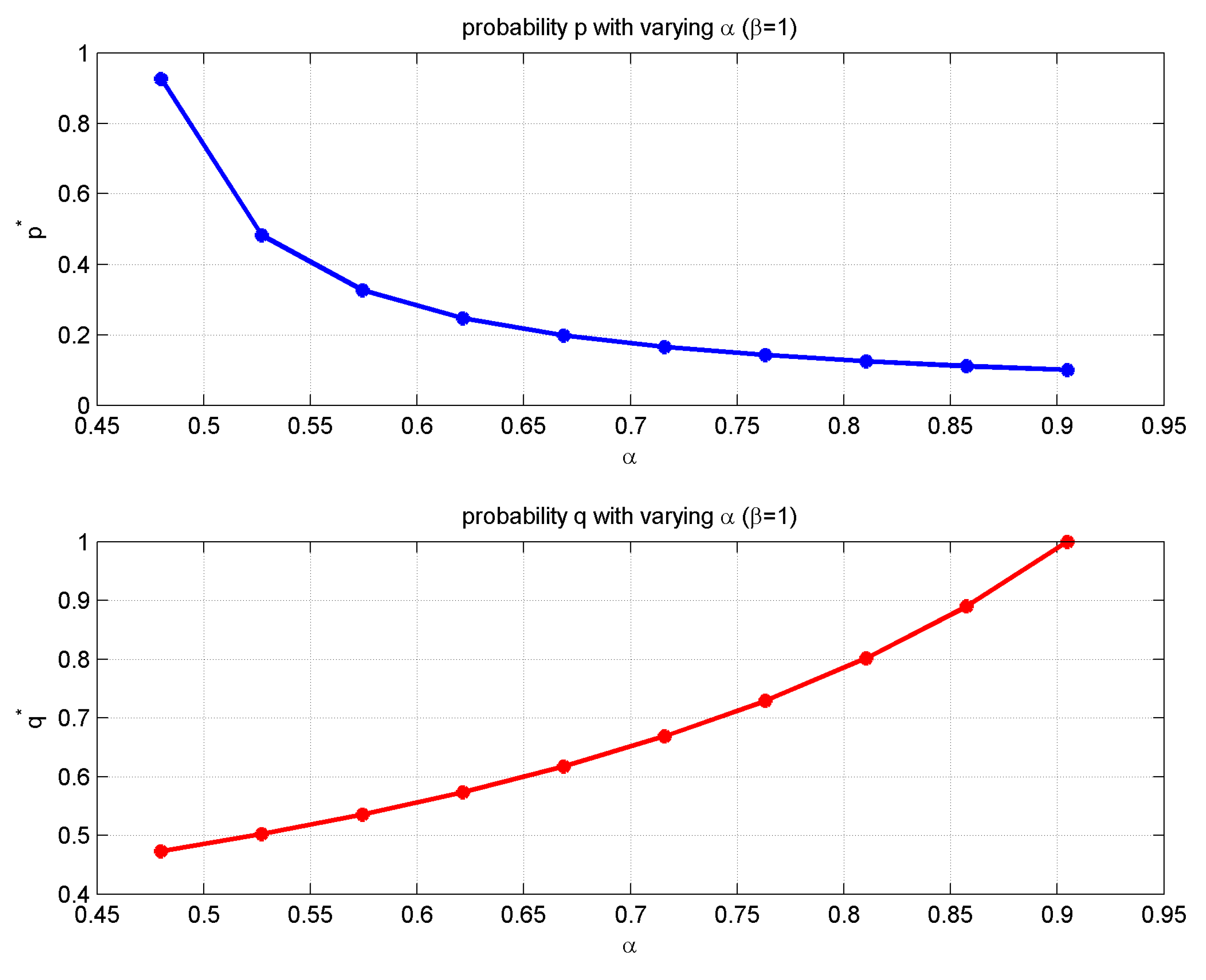
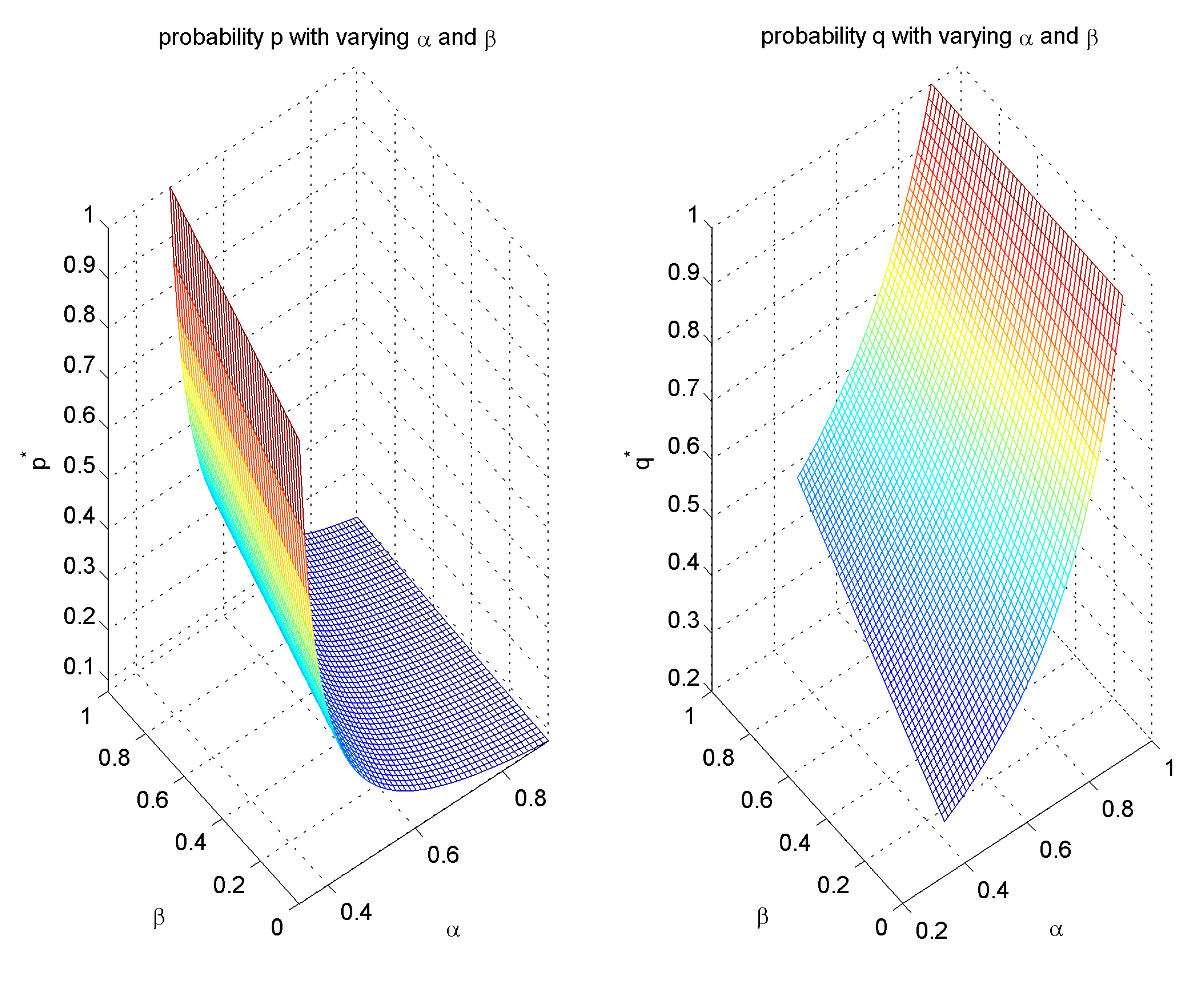
In , when equals to 1, the owner absorbs all additional costs with the contractor being damage-free. This case evidently resembles the original Hawk-Dove model as the payoff clearly favours the hawk contractor: having no loss from the confrontation. Conversely, when slides to 0, the payoff favours the dove owner while the hawk contractor pays the heavy toll for their aggression by absorbing all the additional cost and the game is no longer a Hawk-Dove game.
3. Analytical Solutions
Let us set the expected probability of owner taking strategy
as
q, and the expected probability of owner taking strategy
holds as
. Similarly, the expected probabilities of the contractor adapting strategy
and
are
p and
respectively. The partial expected revenue,
and
for owner, and
and
, for contractor, correspond to the revenue generated from carrying out strategy as hawk or dove, given the mixed strategy of the opponent, expressed as follows:
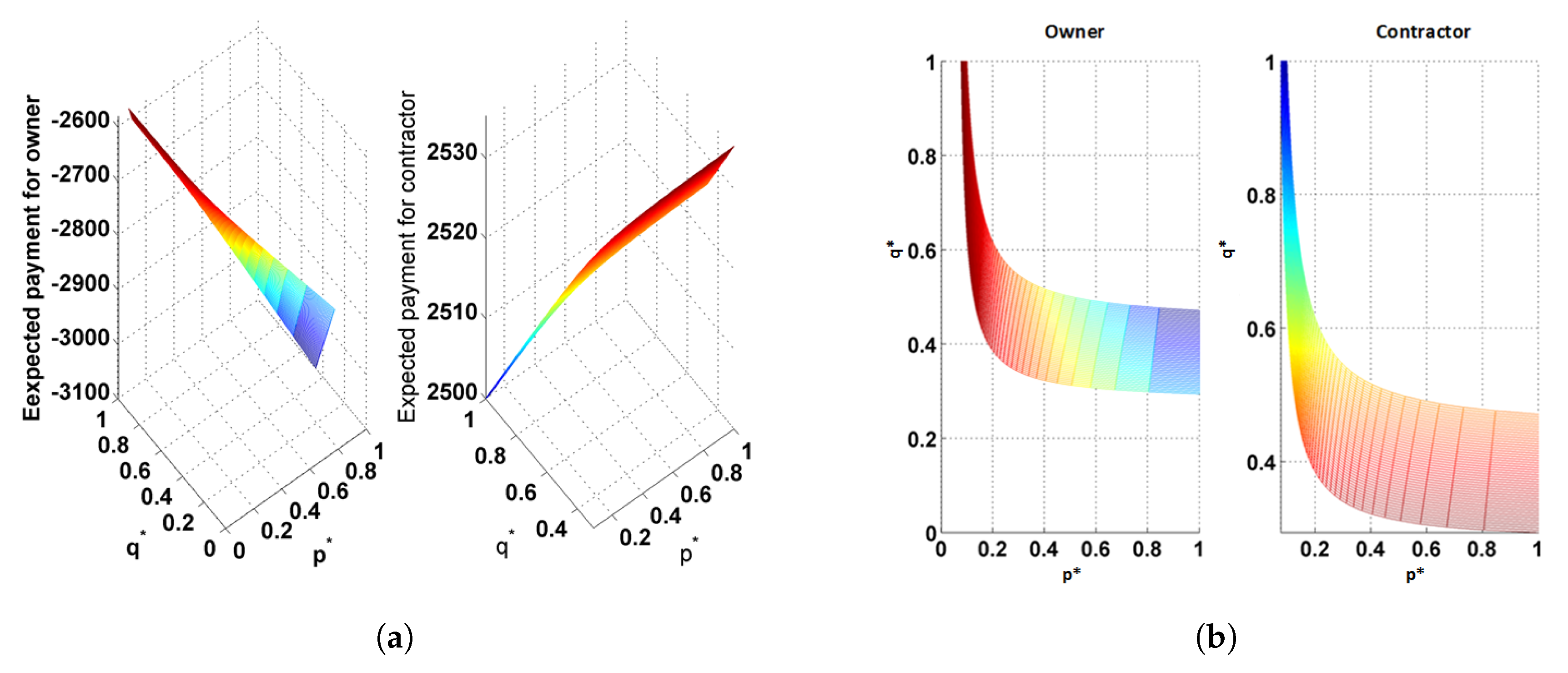
The total expected revenue for the owner,
, is thus derived as:
Expected partial revenue for the contractor follows the same mechanism and can be written as:
Therefore, the total expected revenue for the contractor,
, is obtained as:
As pointed out by [
21,
24], the replicator equation shows the growth rate of a strategy, which describes the selection process where the more successful strategy spreads until it becomes dynamically stable. In other words, the strategy keeps adapting if the strategy’s payoff results in a higher payoff. Hence, the replicator equation (i.e., growth rate) of the contractor acting as a hawk is:
Analogously, the growth rate of the owner acting hawk is:
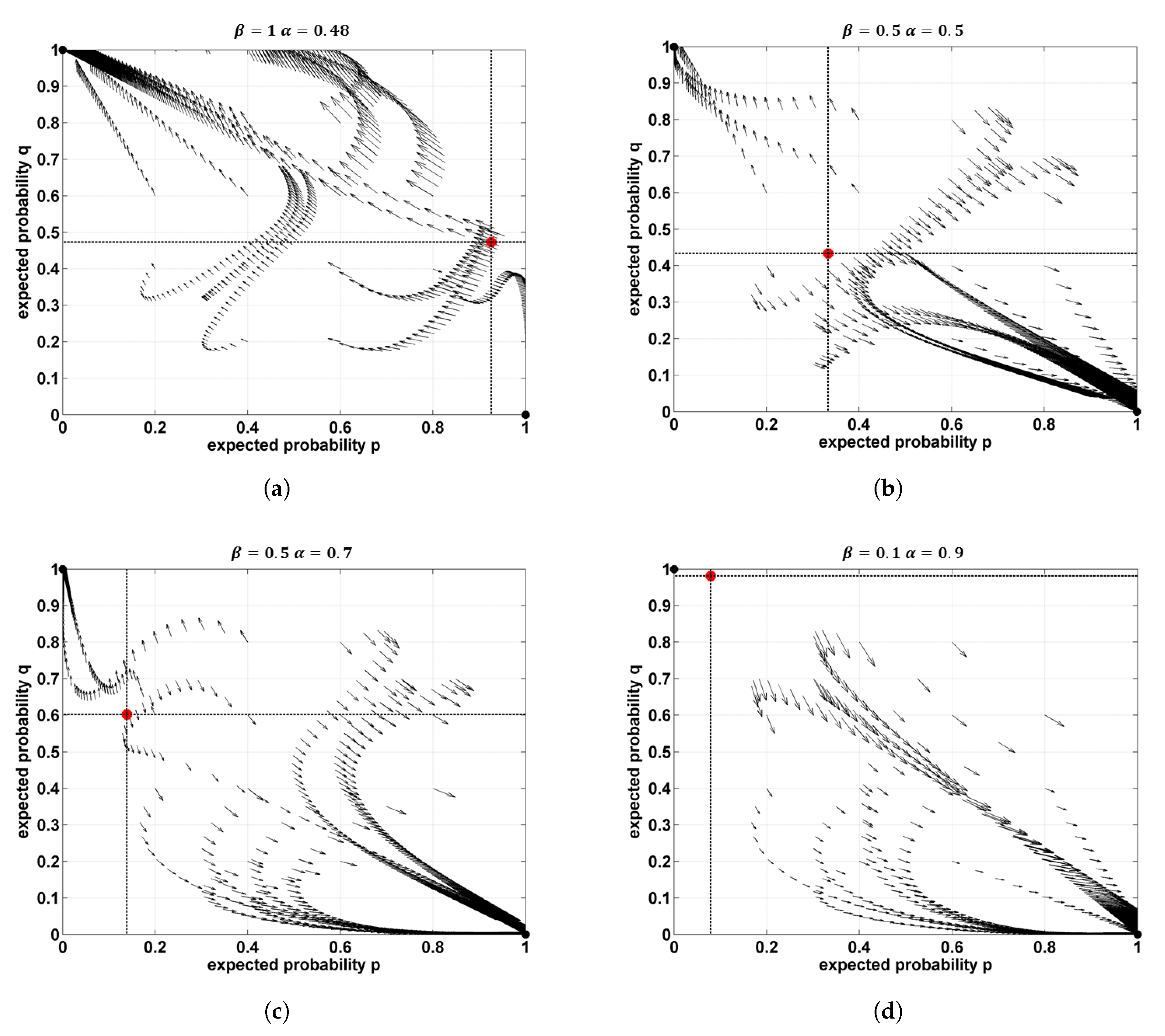
By solving the differential equations, the equilibrium points are obtained as:
where
From Equation (
7),
p and
q can be obtained as constant roots
,
,
,
, as well as a parameter-dependent root pair
p* and
q*, yielding:
The solutions
p* and
q* can be written in terms of the payment variables and cost sharing ratios:
When
p and
q take constant roots
,
,
,
, their combinations form the equilibrium points (0,0), (0,1), (1,0) and (1,1), each of which corresponds to scenario
,
,
and
. Pure and stable Nash equilibria are found at combinations (0,1), (1,0) [
25]. When
p* and
q* are taken, the equilibrium shifts to the unstable mixed strategy where the choice of strategy is dependent on
and
.
6. Conclusions
Game theory can be described as the “conflict and co-operation analysis” [
4], providing much needed answers to conflict and negotiation management. It has been widely applied in natural and social sciences, but its application in project management has not gained much prevalence [
30].
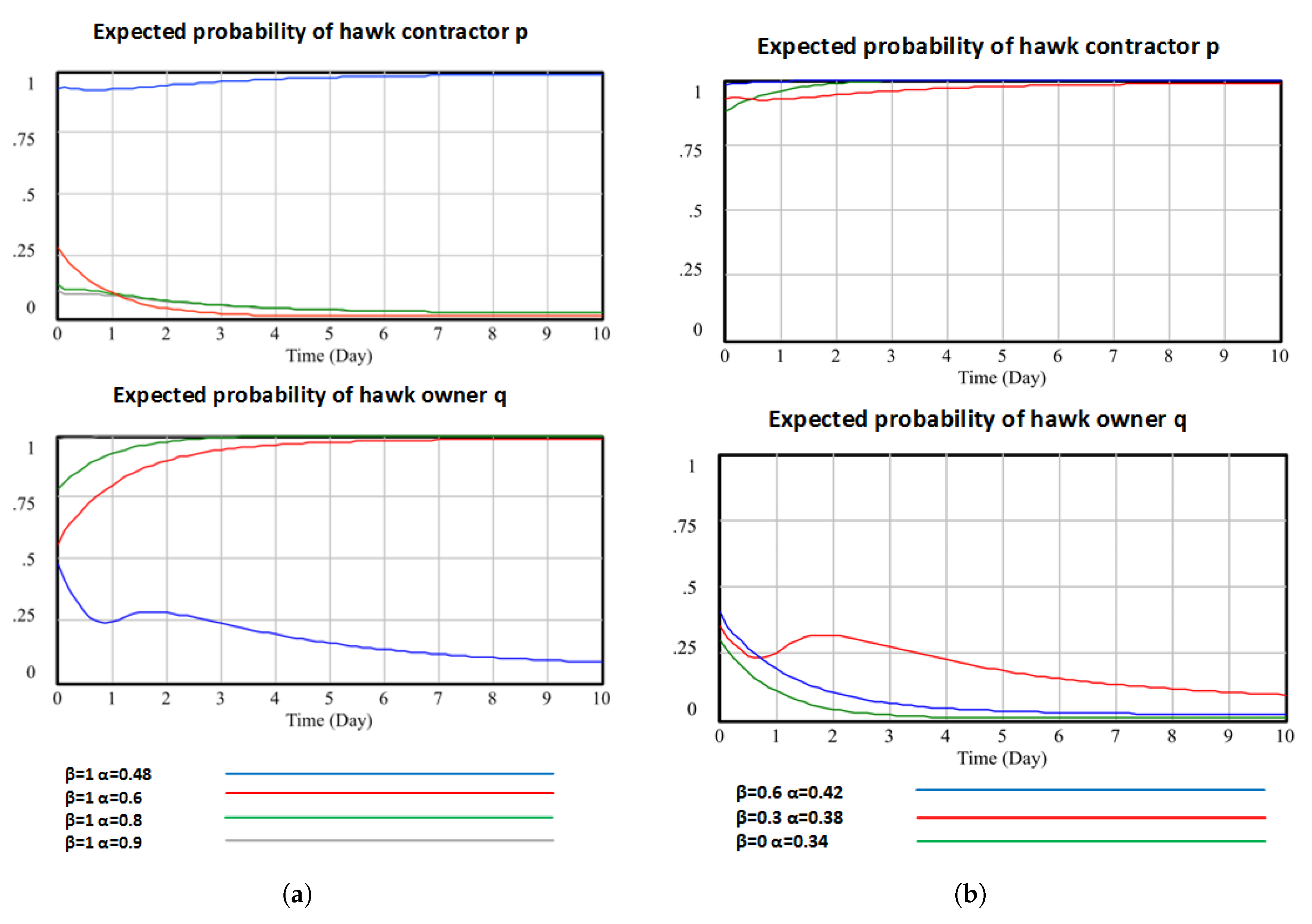
In this paper, a generalised Hawk-Dove model is introduced to simulate the dynamics of strategy adaptation between two parties: the owner and the contractor. The model includes cost sharing ratios, studying their role and impact on strategy adaptation.
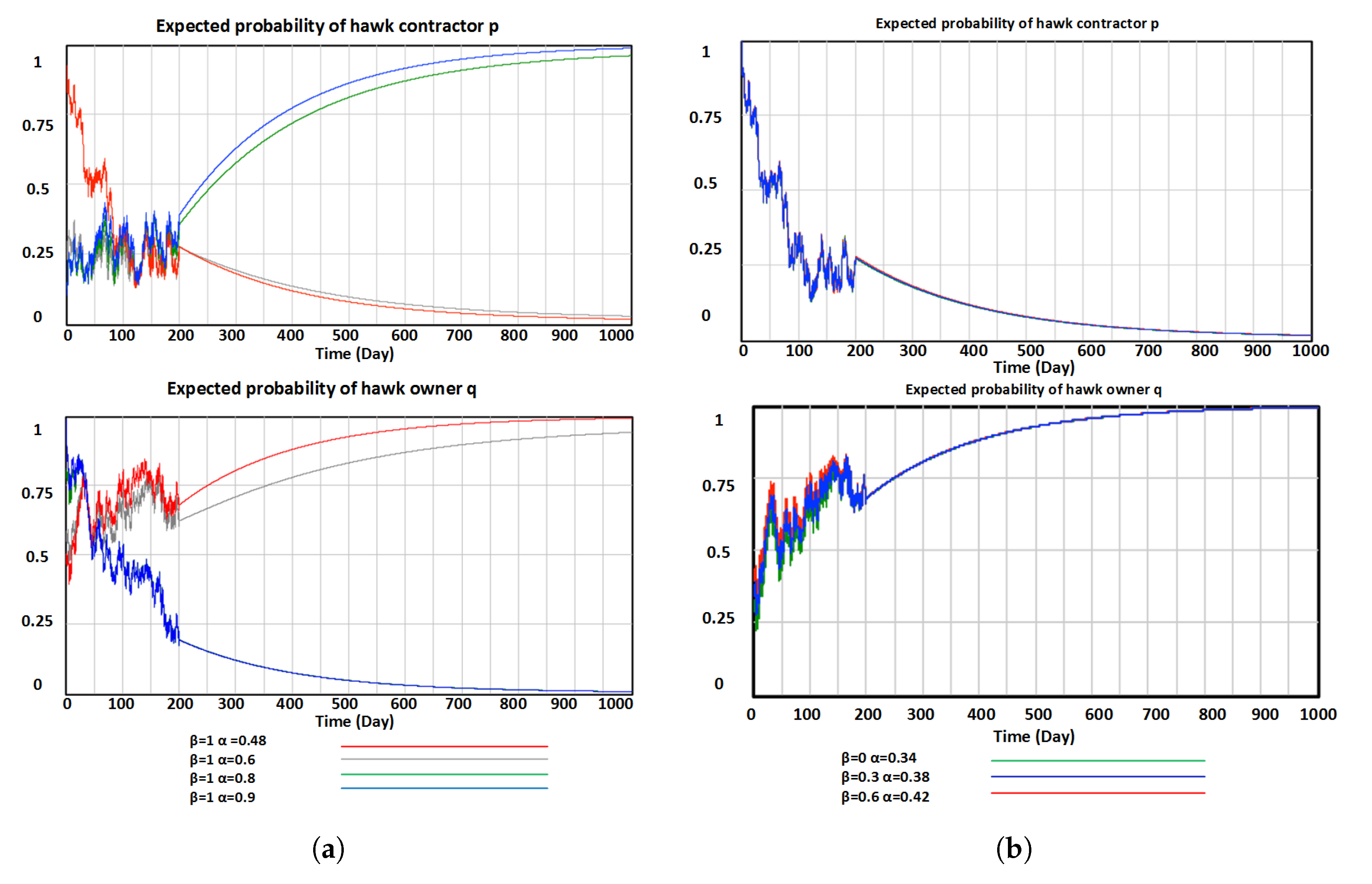
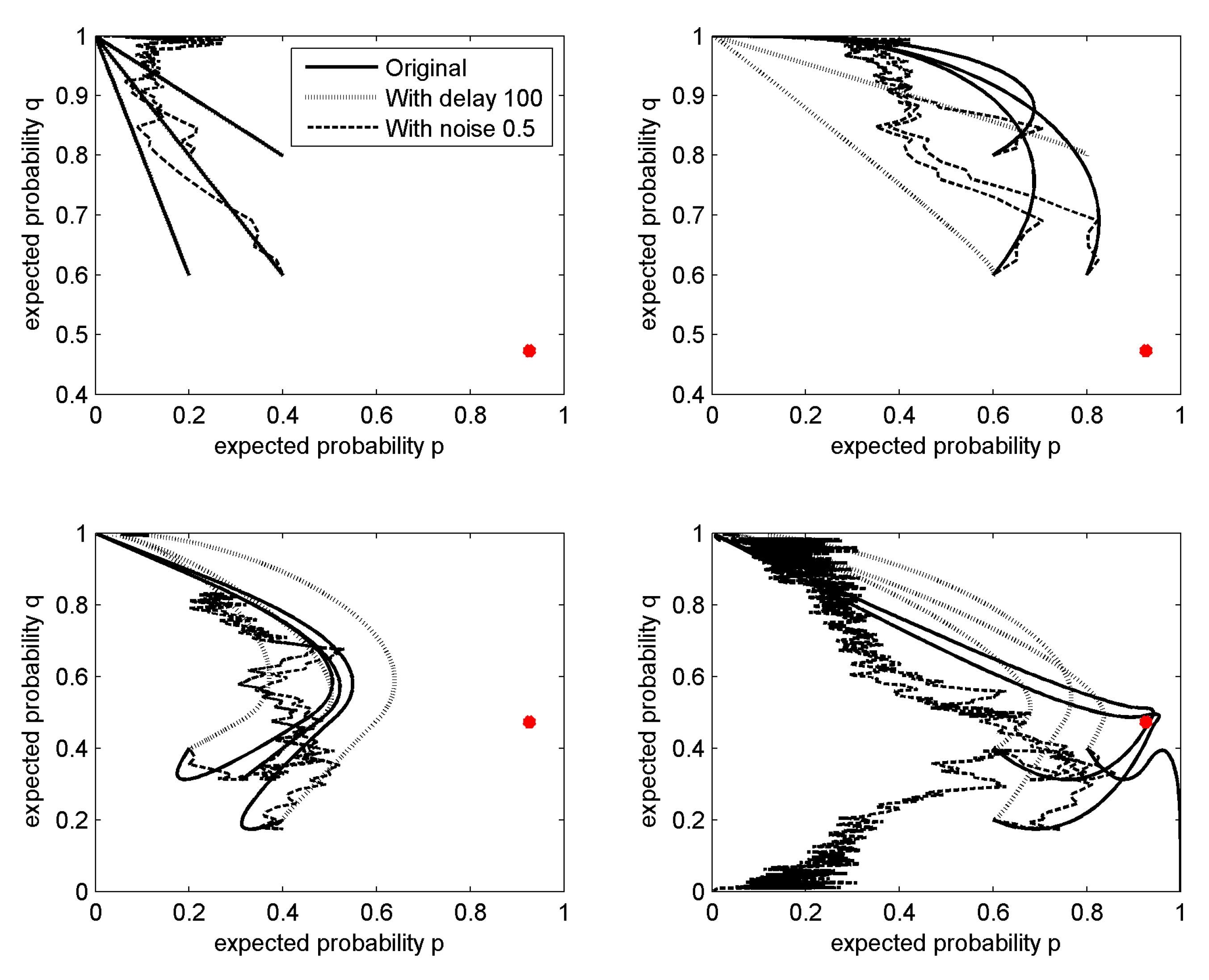
The results are verified in three stages: analytical solutions are derived for the generalised model, followed by simulation of stationary and dynamic behaviour. It is found that pure Nash equilibria are stable, as expected, while the mixed strategy is a saddle point with unstable dynamics.
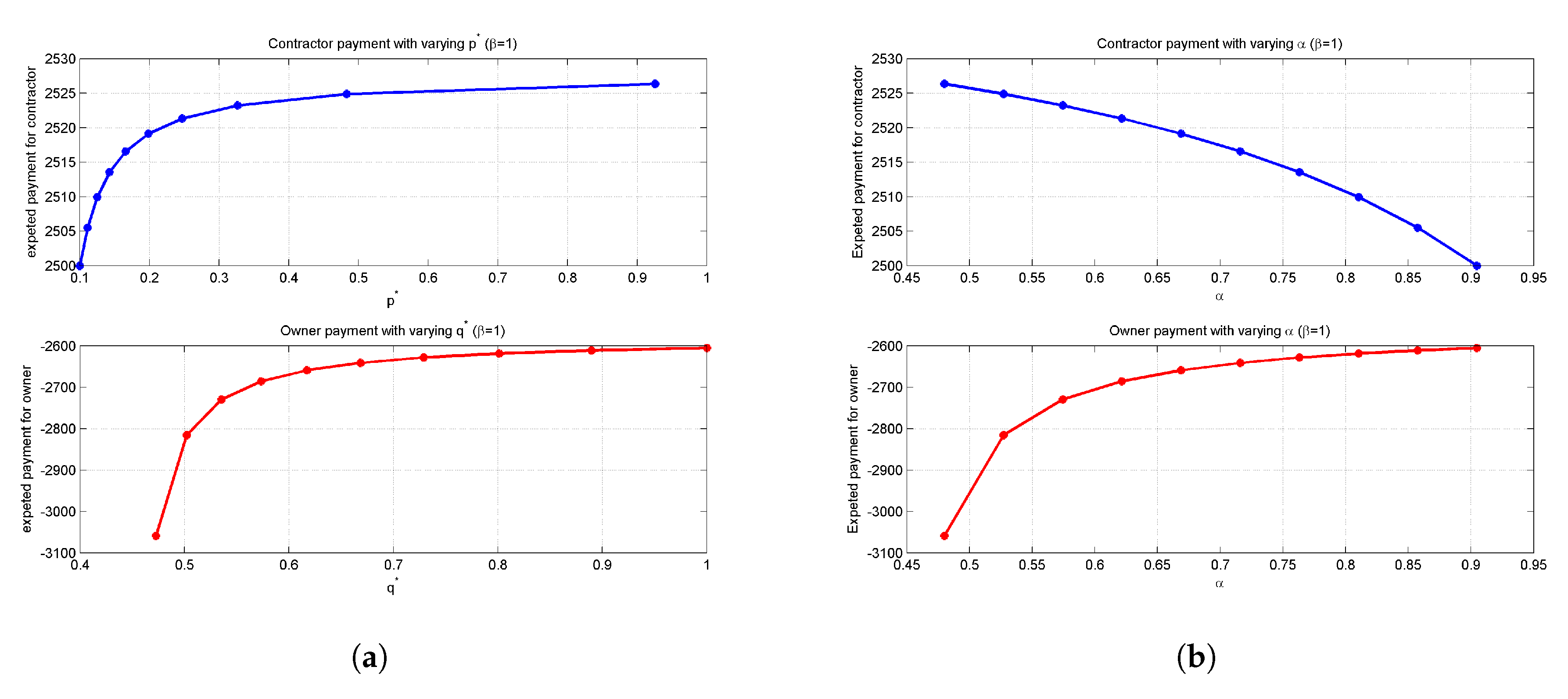
Confrontational practice between the project owner and the contractors is also noted, as the optimal case occurs when one acts as a hawk and the other plays as a dove, and vice versa. The prediction of a specific confrontational strategy is not easily achievable, and so cost sharing ratios are considered to simplify decision-making. When the project contractor steps up acting as a hawk, taking the strategy , the additional efforts in the communication and negotiation process produce financial costs to be shared between the two parties, shown as when the project owner acts as a hawk () and when the project owner acts as a dove (). A hawk project owner would share the penalty with the hawk contractor via cost sharing ratio while a dovish owner’s share of cost in is manipulated by . It is found that although the introduction of and does not challenge the general convergence to a pure Nash equilibrium, their combination drives the destination of the pure Nash equilibrium, in which case either the owner favours large with any in the allowed range, or the contractor leans towards small and .
This study may also apply to other roles of project participants engaged in a conflict of interest. The generic feature of the constructed model fits into an array of projects and the scope can be further expanded by including more than two players, unveiling the possibility of incorporating more sharing ratios, and leading to different Nash equilibria. Though the case with multiple players is not explored in this paper, future research in this direction may prove fruitful, expanding the significance of game theory applications in project management.