The Impact of Previous Action on Bargaining—An Experiment on the Emergence of Preferences for Fairness Norms
Abstract
1. Introduction
2. Material and Methods
2.1. Treatment Design
- (1)
- Agreement: If , only the available tokens are distributed. Each participant receives the number of tokens they wanted to keep.
- (2)
- No agreement: If , the participants distributed more tokens than available. Hence, both participants receive a disagreement payoff of tokens.
2.2. Experimental Procedure
3. Results
3.1. Comparison of Payoffs and Tokens
3.2. Frequency of Experimental Benchmarks
3.3. Influencing Factors
4. Discussion
Supplementary Materials
Author Contributions
Conflicts of Interest
Appendix A. Experimental Data
| Group | Dictator Treatment | Baseline Treatment | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dictator | Bargaining Game | Bargaining Game | ||||||||||
| Game | Offer | Agreement | Offer | Agreement | ||||||||
| P. 1 | P. 2 | P. 1 | P. 2 | P. 1 | P. 2 | |||||||
| 1 | 65 | 35 | 40 | (40) | 60 | (60) | Exact | 20 | (20) | 80 | (80) | Exact |
| 2 | 90 | 10 | 30 | (30) | 70 | (70) | Exact | 22 | (22) | 78 | (78) | Exact |
| 3 | 50 | 50 | 16 | (16) | 84 | (84) | Exact | 20 | (20) | 80 | (80) | Exact |
| 4 | 90 | 10 | 50 | (50) | 50 | (50) | Exact | 50 | (50) | 50 | (50) | Exact |
| 5 | 100 | 0 | 50 | (50) | 50 | (50) | Exact | 17 | (17) | 83 | (83) | Exact |
| 6 | 90 | 10 | 60 | (60) | 60 | (40) | No | 100 | (-) | 100 | (-) | No |
| 7 | 70 | 30 | 30 | (30) | 70 | (70) | Exact | 40 | (40) | 60 | (60) | Exact |
| 8 | 90 | 10 | 80 | (20) | 80 | (80) | No | 100 | (100) | 0 | (0) | Exact |
| 9 | 80 | 20 | 80 | (-) | 60 | (-) | No | 20 | (20) | 80 | (80) | Exact |
| 10 | 100 | 0 | 50 | (50) | 50 | (50) | Exact | 20 | (20) | 80 | (80) | Exact |
| 11 | 100 | 0 | 20 | (20) | 80 | (80) | Exact | 45 | (45) | 55 | (55) | Exact |
| 12 | 50 | 50 | 20 | (20) | 20 | (80) | Underbid. | 17 | (17) | 83 | (83) | Exact |
| 13 | 6 | 94 | 18 | (18) | 82 | (82) | Exact | 16 | (16) | 20 | (80) | Underbid. |
| 14 | 100 | 0 | 50 | (50) | 50 | (50) | Exact | 100 | (100) | 0 | (0) | Exact |
| 15 | 100 | 0 | 30 | (30) | 70 | (70) | Exact | 30 | (30) | 70 | (70) | Exact |
| 16 | 80 | 20 | 30 | (30) | 70 | (70) | Exact | 20 | (20) | 80 | (80) | Exact |
| 17 | 8 | 92 | 17 | (17) | 83 | (30) | Exact | 20 | (20) | 80 | (80) | Exact |
| 18 | 50 | 50 | 20 | (20) | 80 | (80) | Exact | 83 | (17) | 83 | (83) | No |
| 19 | 100 | 0 | 80 | (20) | 80 | (80) | Exact | 100 | (100) | 0 | (0) | Exact |
| 20 | 90 | 10 | 30 | (30) | 70 | (70) | Exact | |||||
References
- Tsiropoulou, E.; Kapoukakis, A.; Papavassiliou, S. Energy-efficient subcarrier allocation in SC-FDMA wireless networks based on multilateral model of bargaining. In Proceedings of the IFIP Networking Conference, Brooklyn, NY, USA, 22–24 May 2013. [Google Scholar]
- Tsiropoulou, E.; Ziras, I.; Papavassiliou, S. A Non-Cooperative Approach to the Joint Subcarrier and Power Allocation Problem in Multi-Service SCFDMA Networks. EAI Endorsed Trans. Mob. Commun. Appl. 2016, 16, 1–10. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U.; Gächter, S. Strong Reciprocity, Human Cooperation and the Enforcement of Social Norms. Hum. Nat. 2002, 13, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Seinen, I.; Schram, A. Social Status and Group Norms: Indirect Reciprocity in a Helping Experiment. Eur. Econ. Rev. 2006, 50, 581–602. [Google Scholar] [CrossRef]
- Lauer, T.; Rockenbach, B.; Walgenbach, P. Not just hot air: Normative codes of conduct induce cooperative behavior. Rev. Manag. Sci. 2008, 2, 183–197. [Google Scholar] [CrossRef]
- Fehr, E.; Kirchler, E.; Weichbold, A.; Gächter, S. When social norms overpower competition: Gift exchange in experimental labor markets. J. Labor Econ. 1998, 16, 324–351. [Google Scholar] [CrossRef]
- Fehr, E.; Fischbacher, U. Social norms and human cooperation. Trends Cogn. Sci. 2004, 8, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Krupka, E.L.; Weber, R.A. Identifying Social Norms Using Coordination Games: Why Does Dictator Game Sharing Vary? J. Eur. Econ. Assoc. 2013, 11, 495–524. [Google Scholar] [CrossRef]
- Nash, J. The bargaining problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Güth, W. On ultimatum bargaining experiments—A personal review. J. Econ. Behav. Organ. 1995, 27, 329–344. [Google Scholar] [CrossRef]
- Anbarci, N.; Feltovich, N. How sensitive are bargaining outcomes to changes in disagreement payoffs? Exp. Econ. 2013, 16, 560–596. [Google Scholar] [CrossRef]
- Rubinstein, A. Perfect Equilibrium in a Bargaining Model. Econometrica 1982, 50, 97–109. [Google Scholar] [CrossRef]
- Burrows, P.; Loomes, G. The impact of fairness on bargaining behavior. Empir. Econ. 1994, 19, 21–41. [Google Scholar] [CrossRef]
- Kroll, E.; Morgenstern, R.; Neumann, T.; Schosser, S.; Vogt, B. Bargaining power does not matter when sharing losses—Experimental evidence of equal split in the Nash bargaining game. J. Econ. Behav. Organ. 2014, 108, 261–272. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A Theory of Equity, Reciprocity, and Competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A Theory of Fairness, Competition, and Cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Engelmann, D.; Strobel, M. Inequality Aversion, Efficiency, and Maximin Preferences in Simple Distribution Experiments. Am. Econ. Rev. 2004, 94, 857–869. [Google Scholar] [CrossRef]
- Bock, O.; Nicklisch, A.; Baetge, I. Hroot: Hamburg registration and organization online tool; WiSo-HH Working Paper Series No. 1. Eur. Econ. Rev. 2012, 71, 117–120. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Berg, J.; Dickhaut, J.; McCabe, K. Trust, reciprocity, and social history. Games Econ. Behav. 1995, 10, 122–142. [Google Scholar] [CrossRef]
- Ostrom, E. Collective Action and the Evolution of Social Norms. J. Econ. Perspect. 2000, 4, 137–158. [Google Scholar] [CrossRef]
| 1 | To clearly distinguish between Pareto efficiency and efficiency in terms of payoff sums, we will call the latter simply “efficiency” and the former “Pareto efficiency” throughout the paper. |
| 2 | Using a pie of tokens give participants the opportunity to consider a different kind of equal split, namely, an equal token split. |
| 3 | When reporting our results, we focus on the share of the strong player as in both games, dictator game and Nash bargaining game, the shares add up to 100, the share of the weak player can easily be derived by subtracting the share of the strong player from 100. Participants also come to an agreement, if they distribute less than the 100 available tokens. In our experiment this happened once in each treatment (see “Underbid.” in column ”Agreement” of Appendix A). However, given the chat protocols in both cases player 2 most likely entered the share of player 1 instead of his share. |
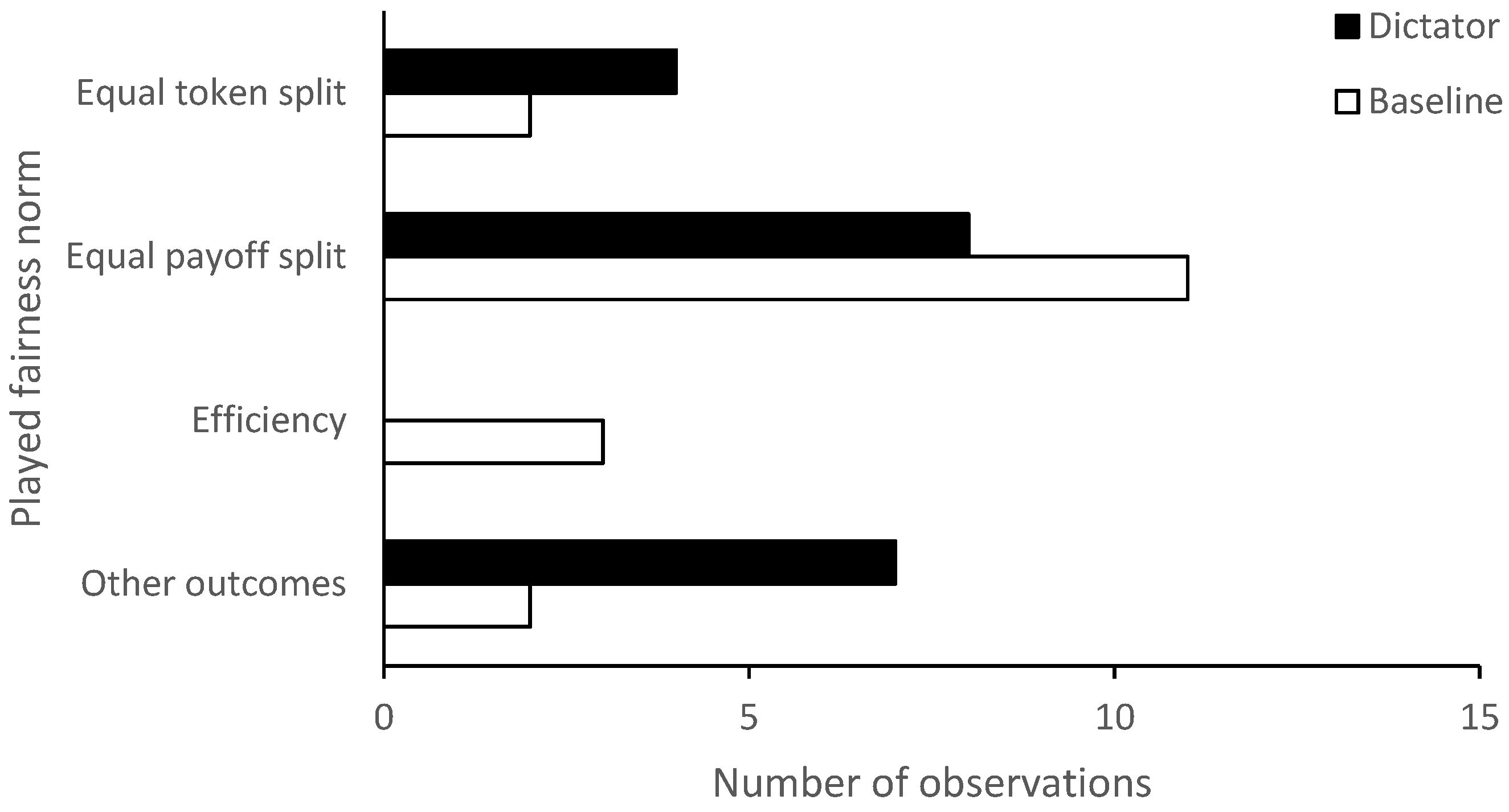
| Role | Factors () | Equal Token Split | Equal Payoff Split | Efficiency |
|---|---|---|---|---|
| Strong player | 6.0 | 50 | 17 | 100 |
| Weak player | 1.2 | 50 | 83 | 0 |
| Treatment | Bargaining (Result) | Bargaining (Chat) | ||
|---|---|---|---|---|
| Avg. | SD | Avg. | SD | |
| Dictator | 41% | 32% | 37% | 30% |
| Baseline | 38% | 20% | 32% | 14% |
| Treatment | # Messages | |
|---|---|---|
| Avg. | SD | |
| Dictator | 9.11 | 6.34 |
| Baseline | 21.94 | 15.07 |
| All Data | Dictator Treatment | |||||
|---|---|---|---|---|---|---|
| # Messages | # Messages | Dictator Game | ||||
| # Messages | 0.571 | (0.288) * | −0.737 | (0.507) | −0.486 | (0.467) |
| Dictator game | 0.226 | (0.099) ** | ||||
| Intercept | 25.696 | (5.756) *** | 38.340 | (5.579) *** | 19.048 | (9.796) * |
| R2 | 0.076 | 0.058 | 0.246 | |||
| N | 37 | 19 | 19 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neumann, T.; Schosser, S.; Vogt, B. The Impact of Previous Action on Bargaining—An Experiment on the Emergence of Preferences for Fairness Norms. Games 2017, 8, 34. https://doi.org/10.3390/g8030034
Neumann T, Schosser S, Vogt B. The Impact of Previous Action on Bargaining—An Experiment on the Emergence of Preferences for Fairness Norms. Games. 2017; 8(3):34. https://doi.org/10.3390/g8030034
Chicago/Turabian StyleNeumann, Thomas, Stephan Schosser, and Bodo Vogt. 2017. "The Impact of Previous Action on Bargaining—An Experiment on the Emergence of Preferences for Fairness Norms" Games 8, no. 3: 34. https://doi.org/10.3390/g8030034
APA StyleNeumann, T., Schosser, S., & Vogt, B. (2017). The Impact of Previous Action on Bargaining—An Experiment on the Emergence of Preferences for Fairness Norms. Games, 8(3), 34. https://doi.org/10.3390/g8030034





