A Note on Disbelief in Others regarding Backward Induction

Abstract

We present experimental results on the role of beliefs in the cognitive ability of others in a problem involving backward induction. Using a modified version of the so-called race game, our design allows the effects of a player’s own inability to perform backward induction to be separated from the effects of her disbelief in the ability of others to do so. We find that behavior is responsive to the dependence on others who might fail in backward induction as well as information regarding their backward induction skills.

1. Introduction

By now, extensive experimental research has driven home the point that the behavior of inexperienced players in novel strategic situations is in stark contrast to game-theoretical predictions [1,2,3,4,5,6,7,8,9,10,11]. Several factors can be identified as potential causes for out-of-equilibrium behavior in “initial responses” [12]. These include unobservable other-regarding preferences as well as a general inability to understand the rules of the game [13,14]. Special attention has been directed at studying two factors of out-of-equilibrium behavior; i.e., bounded rationality and disbelief in the cognitive abilities of co-players. Aumann, for instance, has drawn upon arguments from epistemic game theory to show that typical observations regarding the centipede game can be partially explained by a “slight” amount of irrationality and a relaxation of common knowledge of rationality [15,16]. The underlying intuition is clear: Playing according to equilibrium predictions might be unwise when paired with irrational players or players who believe in the irrationality of their co-players, or mutual knowledge of rationality of higher order is violated.

A considerable amount of research has been conducted to assess the relative importance of disbelief in the cognitive abilities of co-players (for brevity: disbelief in others) in explaining out-of-equilibrium behavior. Unfortunately, the resulting experimental evidence is mixed. That is, some studies find evidence for disbelief in others in the centipede game [9] or the guessing game [11], other studies find no effects [17,18]. Against this background, this paper sheds light on the question of whether and to what extent subjects take the cognitive skills of their co-players into account when dealing with problems involving backward induction. We use an extended version of the so-called race game [19,20,21] (i.e., a two-person zero-sum game in which one player can enforce a win by playing a weakly dominant strategy, which can be identified by applying backward induction). The basic race game is extended by a stage in which the players choose among two payoff options, which allows measurement of their confidence in winning the respective race game. Treatments differ regarding whether subjects play solo or are matched in teams of two when playing against an algorithm which was programmed to mimic a perfectly rational co-player with the sole motivation of winning the game. Treatments also differ with respect to the available information regarding the skills in backward induction of the respective team member. We find clear evidence for disbelief in others: that is, subjects condition their behavior on the information they have regarding the skills in backward induction of their team member. We also observe that subjects generally overestimate the strategic skills of their team member; i.e., subjects having no information regarding their co-player behave identically to subjects who know that they are teamed up with a (relatively) skilled team member.

2. Experimental Procedure and Design

The experiment was conducted in German at the experimental laboratory of the Leipzig University, Germany, in spring 2015.1 A total of 188 subjects participated in 15 sessions, which lasted for about 60 min. The sample consisted of students and seven former students, who had graduated only recently. The mean age was 24, and females were slightly overrepresented (66%). On average, subjects earned 9.74 Euro.

Subjects played a so-called extended race games (hereafter: ERG). The basic race game is an extensive two-person game in which one player can enforce a win by playing a weakly dominant strategy that can be identified by applying backward induction [19,20,21]. At the beginning of a race game, a certain number of balls are laid out. The first player then has to choose a number of balls that will be removed. Right afterward, the second player gets to choose a number of balls to be removed. The two players alternate in this manner until a player removes the last ball and by doing so wins the game. A specific basic race game is characterized by a triple $\left(m,\ell ,u\right)$, in which m denotes the number of initial balls and $0<\ell <u$ describe the lower and upper bounds of balls that can be removed on each turn.

Similar to the literature [21], in each game subjects knowingly play against an algorithmic co-player (AI) which was programmed to mimic a perfectly rational co-player with the sole motivation of winning the game. In each game, subjects start in a position in which a win was enforceable by playing a backward-induction strategy.2

The extension of the basic race game comprises two dimensions. First, we measure subjects’ confidence to win each specific game. To achieve this, subjects are informed about the game parameters before the game starts and have to choose among two payoff options which differ with respect to the chances of obtaining a fixed monetary price of 80 cents in the case of a win or a loss. The payoff options are presented to the subjects as option A and B, respectively. Option A results in a 100% chance of obtaining the fixed price if the current game is won, but results in a 0% chance of obtaining the price if the game is lost. Option B on the other hand, offers a 70% chance in case of a win and a 30% chance in case of a loss. Clearly, option A is more attractive if the subject believes that winning is more likely than losing, whereas option B is more attractive in case the subject believes that losing is more likely than winning. Note that subjects had two minutes for choosing a payoff option and winning the game, otherwise they lost automatically and got no monetary reward for this game.

Second, we assess the impact of disbelief in others on subjects’ behavior by varying the winning condition. Specifically, subjects play two series of seven distinct ERGs (The games implemented can be seen in

Table 1. The two extended race game (ERG) series implemented.

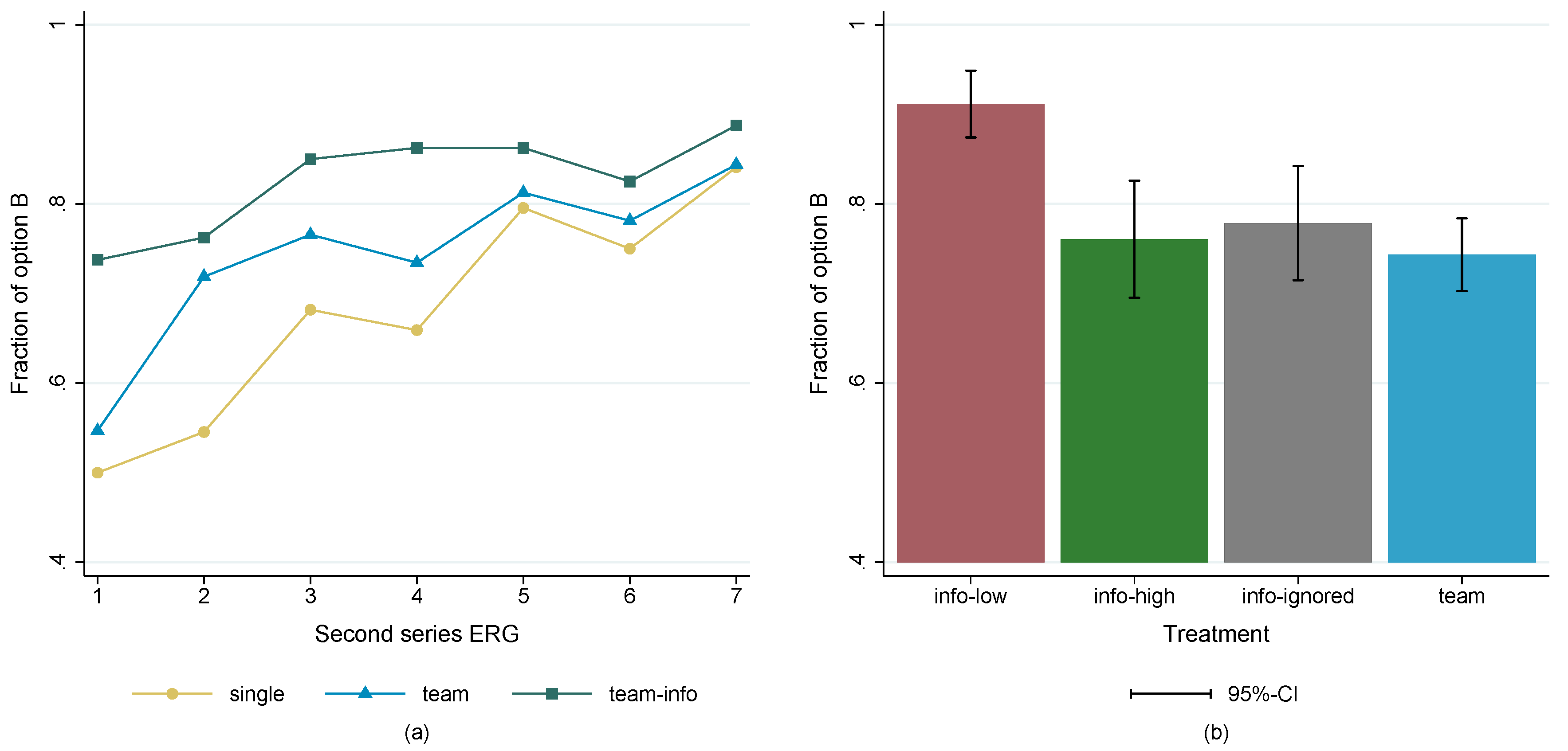
Series	Parameter	Game Number
		0 *	1	2	3	4	5	6	7
FirstERG1	ℓ	1	2	1	2	1	2	1	2
	u	$\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{-}$3$\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{-}$
	m	6	6	11	11	13	13	18	18
SecondERG2	ℓ	1	2	1	2	1	2	1	2
	u	$\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{-}$4$\stackrel{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}{-}$
	m	7	10	12	13	14	16	17	19

Notes: * practice round (not included in the analysis).

).3 In the first series (ERG1), subjects win a game if they take the last ball in the play against the AI. The idea behind this series is simply to measure subjects’ skills in backward induction. We will henceforth refer to the number of games won in this series as the subject’s BI-score. In the second series (ERG2), subjects are randomly allocated into one of three treatments (see

Table 2. Experimental design and number of subjects (number of observations in parentheses).

Treatment		First Series		Second Series		Subjects
Single		ERG1 (308)		ERG2 single (308)		$N=44$
Team		ERG1 (448)		ERG2 team (448)		$N=64$
Team-info		ERG1 (560)		ERG2 team-info (560)		$N=80$

). In the single treatment, which serves as the control treatment, the winning condition is identical to the first series. In the team treatment, subjects are matched in teams of two; this matching was done randomly and anew for each game in the second series. Neither team member directly interacts with the other. However, in this treatment, each subject wins if and only if both the subject and her team member beat the AI in their respective game. Subjects were made aware that both team members play the same game against the AI. Importantly, in this treatment, the beliefs of the subjects regarding the cognitive skills of their team members are vital for their choice between the payoff options. Note also that only the first-order belief in the rationality of the team member is under scrutiny; i.e., it does not matter for ego’s choice of payoff options whether the team member believes in ego’s rationality or not (nor does any higher-order belief matter). The team-info treatment is similar to the team treatment, but differs with respect to the available information regarding the skills in backward induction of the team members; i.e., in the team treatment, subjects are only informed that they are matched in teams, whereas in the team-info treatment, subjects can obtain information concerning the skills of their team member in backward induction (precisely, the team member’s BI-score). In order to observe whether subjects in the team-info treatment care about this information, the info is initially hidden until subjects manually reveal it. To suppress learning, subjects in the team treatment as well as in the team-info treatment did not receive any feedback regarding the performance of their team members (except their respective BI-score) until the second series was finished.4

The gist of this design is as follows: if subjects are influenced by disbelief in others, we should observe the choice of option B more frequently in the team and team-info treatment than in the single treatment. Further, subjects in the team-info treatment should choose option A more often, the higher the BI-score of their team member.

3. Results

Concerning subjects’ abilities in backward induction, we observe that in both series, less than 20% of the subjects won more than half of the games. Additionally, the number of games won in the first series (i.e., the BI-Score) is on average 2.43, backing the finding that applying backward induction is troublesome in initial response [20].

To answer the question of whether disbelief in others affects decisions in backward induction problems, we look at treatment effects regarding the choice of payoff options in the second series. Figure 1a shows the proportion of choices of option B (henceforth: B-choices) in each game of the second series, separated by treatment. We observe the following strict monotonic order: in each particular game, option B was chosen most frequently in the team-info treatment, followed by the team treatment, and least frequently in the single treatment. In addition, we observe that the differences between the treatments get smaller in later (and, by design, more complex) games. This makes sense, since the more complex the game, the less confident subjects should be in their capacity to win their own game against the AI, and hence the less important are their doubts in the abilities of their team member. When pooled, these differences are highly significant between the team-info treatment and the team as well as the single treatment (both: $p<0.002$; ${\chi }^2$-test), and weakly significant between the team and the single treatment ($p<0.065$; ${\chi }^2$-test). Hence, we conclude that disbelief in others influences the subjects.

Regarding the effect of information on the co-player’s backward induction skill, panel (b) of Figure 1 depicts the proportion of B-choices in the team treatment as well as in the team-info treatment. With respect to the team-info treatment, the figure differentiates between three kinds of subjects: those subjects who decide to ignore the information about the BI-score of their team member (info-ignored), as well as two groups of subjects who examine this information and whose team member belongs either to the 50% of top performers (info-high) or 50% of low performers (info-low). Among those subjects who have a look at the BI-score of their team member, those who are paired with a relatively low-skilled co-player chose option B significantly more often than those paired with a high-skilled co-player ($p<0.001$; ${\chi }^2$-test). Further, we observe that subjects receiving the information of a relatively high BI-score do not show behavior that differs significantly from that of subjects who did not have any information either by treatment condition or by simply ignoring the information (info-high vs. team: $p<0.664$, info-high vs. info-ignored: $p<0.698$; ${\chi }^2$-test). This finding suggests that subjects tend to overestimate their team members’ abilities, which explains why disbelief in others shows more of an impact in the team-info than in the team treatment.

Finally, we estimate three random effects logit regressions. In each model, the dependent variable is a dummy indicating whether option B is chosen. The first model (see

Table 3. Random effects logit regressions of B-choices in both race series.

Choosing Option B?		Model
		(1)		(2)		(3)
	Team condition? (no = 0, yes = 1)	0	579 (0.253) **	0	580 (0.253) **	0	596 (0.274) **
	Info condition? (no = 0, yes = 1)	0	768 (0.241) ***	0	468 (0.332)	0	393 (0.345)
	Second series? (no = 0, yes = 1)	0	917 (0.193) ***	0	918 (0.193) ***	0	953 (0.206) ***
	Info. examined? (no = 0, yes = 1)			2	564 (0.583) ***	2	681 (0.607) ***
	If info. examined: Team member’s BI-score			−0	812 (0.174) ***	−0	828 (0.181) ***
	Male (no = 0, yes = 1)					−0	449 (0.296)
	Age (in years)					−0	058 (0.044)
	Father’s education (1 [low]−6 [high])					0	105 (0.073)
	Constant	0	007 (0.135)	0	006 (0.136)	1	126 (1.116)
	Observations	2632		2632		2352

Notes: Logit coefficients, standard errors in parentheses. * $p<0.1$, ** $p<0.05$, *** $p<0.01$.

) includes basic treatment conditions as well as a dummy indicating whether the game at hand stems from the first or from the second series. We observe that playing in teams, as well as the availability of information regarding the team member’s performance, significantly increase the probability of choosing option B. In addition, we observe that subjects tend to choose option B more frequently in the second series than in the first series. This is quite reasonable, since games of the second series are cognitively more demanding.

In the second model, we add two variables which give a more nuanced picture of the influence of the information regarding the team member’s performance. The first one is a dummy which captures whether subjects actually examine the information of their team members’ BI-scores (regardless of whether subjects ignore the information or are simply not in an information condition). The second variable is an interaction term that is the product of the aforementioned dummy and the team member’s BI-score. This results in a variable ranging from 0 to 5. Most importantly, we observe that subjects who examine the information are more likely to choose option B; however, this effect is mediated by the actual information observed (i.e., the higher the observed BI-score of the team member, the less likely it is that a subject will opt for option B). We find that the odds of choosing option B for subjects who could not or did not look at the information are roughly the same as for subjects who examine the information and observe that their team member has a BI-score of 3. While the effect of the team condition is almost identical in model 1 and 2, the effect of the information condition vanishes to insignificance. This indicates that the behavioral changes between the team and team-info treatments are caused solely by the information.

The third model validates that our findings are robust when controlling for essential demographic characteristics.5

4. Conclusions

In this paper, we present experimental evidence on backward induction and shed light on the question of whether and to what extent disbelief in others influences behavior in such a setting. We find clear evidence that disbelief in others affects behavior in problems involving backward induction. In addition, this paper documents that subjects condition their choice on their information regarding the co-player. Interestingly, subjects who have no information about their co-players tend to overestimate their cognitive skills, resulting in a behavior that is similar to subjects who know that they are playing with a relatively highly-skilled co-player.