1. From Rationality Assumptions to Empirical Research
The history of game theory has been characterized by repeated shifts of attention from one aspect of interactive decision making to another. Among the first problems to be recognized were anomalies of coalition formation that are nowadays studied in cooperative game theory, as exemplified by the following two striking examples. In the first century AD, the Roman lawyer and senator Pliny the Younger wrote about a consul who had been found slain, raising doubts about whether he had died by his own hand or been killed by his freedmen [
1]. When the matter came before the Senate, Pliny argued that the freedmen should be acquitted; another senator that they should be banished to an island; and a third that they should be condemned to death. Pliny worked out that if every senator voted sincerely for his first preference, then the accused men would be condemned to death, because those in favor of condemning them to death formed the largest voting bloc, whereas if he and the others in favor of acquittal voted to banish the accused men, then banishment would win a majority. In what may be the first recorded example of strategic voting, Pliny and the other senators who favored acquittal therefore voted for banishment, an option they obviously preferred to condemning the accused men to death. The other early report of an anomaly of coalition formation is found in the Babylonian Talmud, written between the third and fifth centuries AD, where the problem is discussed of the right way to divide the estate of a person who dies with more debts than assets. The solution prescribed in the Talmud is not simple-minded proportional division, as one might have expected, but allocation that turns out to correspond exactly to a far more sophisticated game-theoretic solution that was not formalized until centuries later, namely the nucleolus of the corresponding coalition game [
2].
During the 18th century, attention focused on problems of understanding risky decisions in games against nature. Daniel Bernoulli [
3] presented the St Petersburg Academy with a problem that is nowadays called the
St Petersburg paradox. Suppose you are invited to play the following game. A fair coin will be tossed; if it falls heads, then you will be paid one dollar and the game will end. If it falls tails, then it will be tossed again, and if it falls heads you will be paid two dollars and the game will end. This process will continue for as long as necessary, with the payoff doubling each time, until heads comes up and you win something, whereupon the game will end. Assuming that the house has unlimited funds, how much should you be willing to pay for the privilege of playing this game? You win one dollar with probability 1/2, two dollars with probability 1/4, four dollars with probability 1/8, and so on, and the infinite sum of this series is infinitely large, because each term is equal to exactly half a dollar. If your sole concern is to maximize your expected value, then you should be willing to stake your entire fortune, however large it may be, on playing this game. However, this is self-evidently absurd, because there is a high probability that you would lose almost everything; in fact, there is a 50% chance of reducing your entire fortune to one dollar after the very first toss, if the coin falls heads. According to the
expected value principle, this is more than counterbalanced by the very small probability of winning a vastly larger sum after a long series of tails. But it is obvious that human decision makers do not normally have such preferences: we may consider two dollars to be twice as desirable as one dollar, but we do not normally consider $200 million dollars to be twice as desirable as $100 million. In the second edition of their landmark book,
Theory of Games and Economic Behavior, von Neumann and Morgenstern [
4] introduced an axiomatic
expected utility theory, according to which decision makers do not seek to maximize expected value but rather expected utility, defined by their actual preferences between outcomes that can include risky gambles.
The classical game theory that grew out of this work was based on the assumption that players are instrumentally rational, in the sense of always choosing options that maximize their individual expected utility, given their knowledge and beliefs at the time of choosing, on the assumption that their co-players are similarly rational. Game theorists came to believe that players who are rational in this sense would invariably choose a
strongly dominant strategy when it is available, a strongly dominant strategy being one that yields a better payoff than any other available strategy irrespective of the strategies chosen by the co-players in the game, and that a rational solution to any game must be a
Nash equilibrium, that is, a combination of strategies in which every player chooses a utility-maximizing
best reply to the strategies of the others. After Lewis [
5] introduced the idea of
common knowledge into game theory, the additional assumption was made that the specification of the game being played and the players’ rationality is common knowledge, in the sense that all the players know these facts, know that they all know them, know that they all know that they all know them, and so on, and this concept was later formalized by Aumann [
6]. Before the late 1960s, it was generally believed that rational decisions could never be specified rigorously in games in which players have incomplete information about their co-players’ payoffs, but then Harsanyi [
7,
8,
9] provided a method, using Bayesian analysis, of applying the standard assumptions to games of incomplete information.
An influential article by Maynard Smith and Price [
10] introduced game theory into the theory of evolution, generating a highly fruitful branch of research that continues to flourish. In
evolutionary game theory, strategies are not options chosen by rational agents but behavioral genotypes inherited from parents and passed on to offspring, and there is no assumption of rationality. Payoffs do not represent expected utility but are measured in units of Darwinian fitness—expected number of offspring or lifetime reproductive success. Before the advent of the evolutionary approach, game theory had relied on the fundamental assumption of rational (expected utility-maximizing) decision makers, but evolutionary game theory replaces the rationality assumption with the mechanism of natural selection that, as is well known, can mimic rational choice.
Not long after the radical innovation of evolutionary game theory, the rationality assumption began to be weakened in other branches of game theory as well. From the beginning of the 1990s, researchers began to acknowledge the fact that human decision makers are limited by
bounded rationality and seldom have full common knowledge, especially of one another’s rationality. The
prospect theory of Kahneman and Tversky [
11] and their
heuristics and biases research program [
12] forced neoclassical economists to question their assumption of perfect human rationality. In 1986, an influential conference at the University of Chicago attracted many influential psychologists, economists, and other social scientists, and very soon after that the research field of
behavioral economics was born.
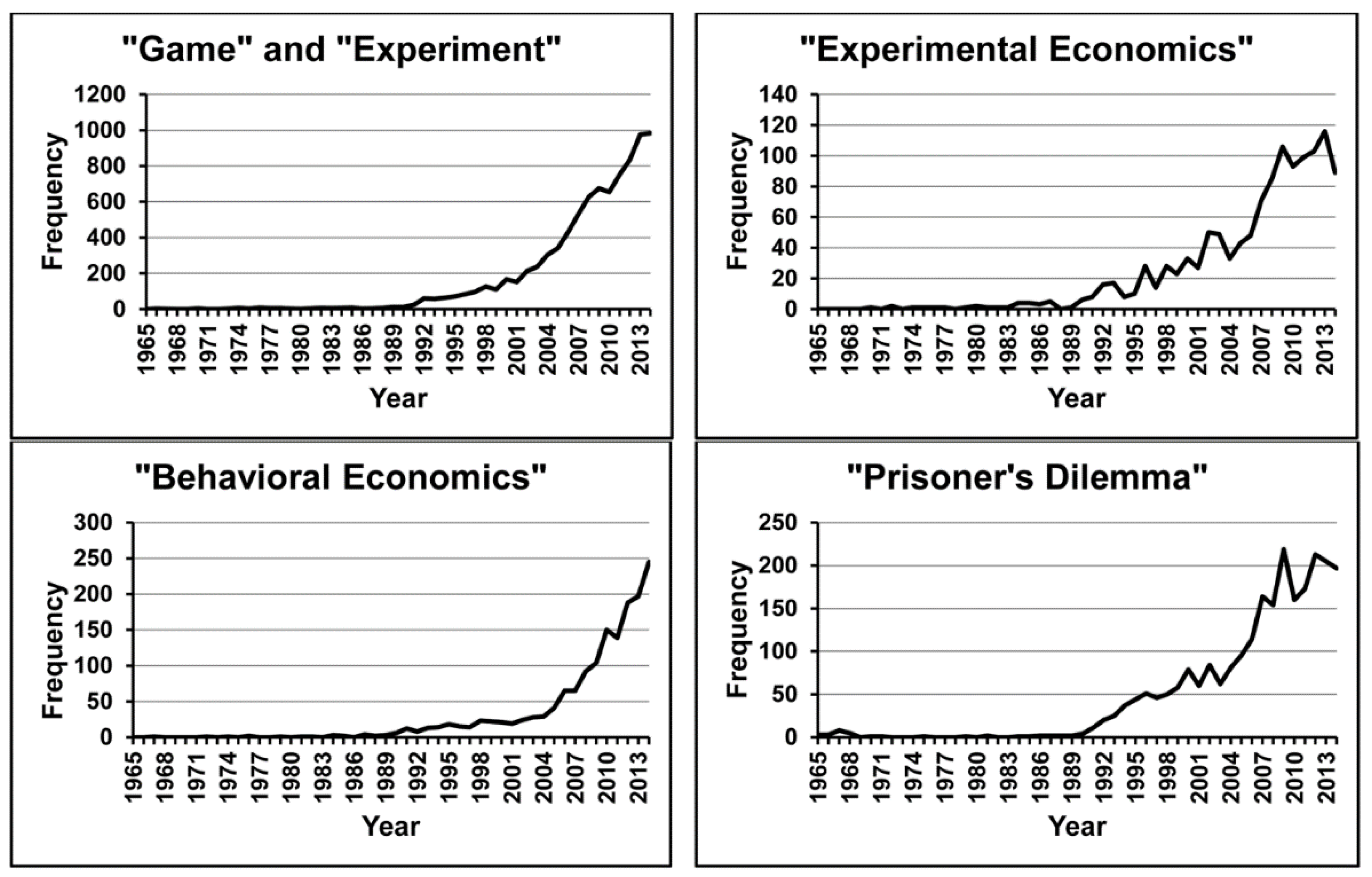
The current focus of attention in game theory is on theoretical and empirical investigations of how decision makers with bounded rationality choose strategies. The accelerating growth of this new approach is depicted in
Figure 1, where the per annum frequencies of keywords in the topic fields of publications in the Web of Science databases from 1965 to 2014 are graphed. The terms
game and
experiment co-occurred rarely between 1965 and 1989, mostly in psychological publications reporting experimental games, but from 1990 onwards an apparently exponential increase is evident, reaching almost 1000 co-occurrences per annum by 2014. The growth curves of the terms
experimental economics,
behavioral economics, and
Prisoner’s Dilemma have similar forms. These curves are worrying or even alarming for researchers in experimental games and behavioral economics, because the accelerating increase in publications is not being met by a proportional expansion in journal space devoted to these matters. It is increasingly difficult to publish research on experimental games in the journals that have traditionally taken them, acceptance rates have plummeted, and some researchers have been tempted to stop trying. We are reminded of the remark of the US baseball player Yogi Berra about a restaurant that used to be his favorite: “Nobody goes there anymore. It’s too crowded” [
13]. Leading journals of cognitive psychology are generally reluctant to publish research on experimental games, and an insidious tendency has arisen to call them “economic games” as if to emphasize their detachment from psychology. Fortunately, at least a few new journals devoted to these topics have begun publishing in recent years, including
Games, the journal in which this Special Issue appears.
Figure 1.
Per annum frequency of keywords game and experiment (co-occurring), experimental economics, behavioral economics, and Prisoner’s Dilemma in the Web of Science databases, 1965 through 2014.
Figure 1.
Per annum frequency of keywords game and experiment (co-occurring), experimental economics, behavioral economics, and Prisoner’s Dilemma in the Web of Science databases, 1965 through 2014.
2. Contributions to this Special Issue
The contributions to this Special Issue include articles in behavioral economics, experimental games, and evolutionary game theory using mathematical, experimental, and agent-based modeling techniques. This is a diverse collection of research articles, but what knits them together is a common purpose of enlarging our understanding of psychological aspects of strategy choices in games.
The first contribution (Krockow, Pulford, and Colman, this issue) is an experimental investigation of strategy choices in Centipede games. The two-player Centipede game, in all its forms, is arguably the most puzzling and paradoxical of all experimental games, even more so than the familiar Prisoner’s Dilemma game. The uniquely rational way of playing it, according to a standard
backward induction argument that is widely accepted in the game theory literature, results in both players earning very meager payoffs, whereas more cooperative play yields much larger payoffs to both players. In view of the fact that rationality is defined in terms of expected payoff maximization, the game-theoretic solution is almost intolerably paradoxical, and we have, in fact, subjected it to critical scrutiny elsewhere [
14]. Previous experimental research with Centipede games has established that a combination of large payoff inequality between the players and zero payoffs after the last decision node tend to inhibit cooperation in the game. The problem addressed in the contribution to this Special Issue is disentangling the joint and separate effects of these two factors, and the results are rather unexpected.
The second contribution (Riefer and Love, this issue) is devoted to an experimental investigation of strategy choices in dynamic environments, when the payoff structure is changing in ways that may not be fully known by the players. Riefer and Love investigate whether players can effectively identify relevant information to explore in locally changing environments when they are distracted by irrelevant global trends. This is potentially relevant to everyday situations in which people are usually exposed to both relevant local and irrelevant global information when they make exploratory decisions in their lives. The results reveal that global trends do not appear to affect players’ exploration frequency nor the timing of their exploratory choices, as might have been expected.
A theoretical and experimental contribution (Leland and Schneider, this issue) formulates and tests experimentally a new model of strategy choices by players with bounded rationality. The model assumes that players base their choices primarily on the perceived salience of their own payoffs or, in cases in which their own payoff salience is uninformative, on the perceived salience of their co-players’ payoffs. It turns out that this simple model makes determinate predictions in all 2 × 2 games as to when Nash equilibria will or will not be selected by the players. The experimental data support the model predictions, at least for most of the games included in the investigation: the model correctly predicts the modal outcome in 19 of the 20 experimental 2 × 2 games, and in the remaining game, the model predicts random play not very different from what is observed. At the level of individual players, the model correctly predicts more than 90% of strategy choices for about half the experimental subjects.
The Special Issue includes a contribution (Merrick, this issue) that is partly in the area of evolutionary game theory. It uses the computational methodology of agent-based modeling to investigate the effects of agents being motivated by different implicit incentives, namely power, achievement, or affiliation, on learning from experience in social interactions with the strategic structure of the Prisoner’s Dilemma game and the Snowdrift game. A second model is used to simulate the evolution of a society of motivated individuals in multiplayer versions of the same games, namely a common pool resource game and a multiplayer Hawk–Dove game, respectively. The evolutionary model incorporates a possibility of misperception that can cause agents to play differently, and the results show that misperception, when it occurs among motivated agents, can increase the payoff to the population as a whole. Agent-based modeling, used in both the learning and evolutionary phases of the research reported in this article, is neither purely analytical in the mathematical sense nor purely experimental in the usual sense of manipulating independent variables and observing the behavior of human subjects or participants as dependent variables.
The last contribution to the Special Issue (al-Nowaihi and Dhami, this issue) is not empirical, although it is motivated by published empirical evidence; it provides a formal mathematical model of
evidential reasoning, a type of reasoning in games that departs from the standard rationality assumptions. It is worth commenting here, partly because the authors do not spell this out in their article, that evidential reasoning was first suggested as an explanation for the powerful intuition that many people have for a particular choice in
Newcomb’s problem, generally recognized by logicians as one of the most intractable of all decision problems [
15]. The problem itself can be described quite simply. On the table is a transparent box containing $1000 and an opaque box containing either $1 million or nothing. A decision maker has the choice of taking either the opaque box only or taking both boxes. The decision maker is told, and believes, that a predictor of human behavior, such as a sophisticated computer programmed with psychological information, has already put $1 million in the opaque box if and only if it has predicted that the decision maker will take only that box, and not the transparent box as well, and the decision maker knows that the predictor is correct in most cases (95 percent of cases, say, although the exact figure is not critical). Both strategies can be justified by simple and apparently irrefutable arguments. If we assume that utility is equivalent to cash value, then expected utility theory supports the strategy of taking the opaque box only, because then:
EU(one box) = 0.95 × $1,000,000 = $950,000,
EU(both boxes) = 0.05 × $1,000,000 + $1,000 = $50,000 + $1000 = $51,000.
In spite of this, the strategy of taking both boxes is a strongly dominant strategy, because it yields a higher payoff whether the predictor is right or wrong—$1000 rather than nothing if the prediction is right and $1,001,000 rather than $1000 if the prediction is wrong. Although both arguments seem convincing, for many decision theorists and game theorists the dominance argument is decisive. Nevertheless, other authorities believe that it is rational to take one box rather than both, and it is generally agreed that this arises from a form of evidential reasoning, because it is based on the assumption that one’s own behavior provides evidence about what is likely to be in the opaque box. In their contribution, al-Nowaihi and Dhami provide a formal game-theoretical framework for defining and understanding evidential reasoning, and they show how it can explain cooperation in the Prisoner’s Dilemma game.
3. Putting It All in Context
Although behavioral economics began in earnest only at the beginning of the 1990s (see
Figure 1), and the term
behavioral economics entered the lexicon of social science in its modern sense only during that period, scattered experimental games had been performed and published in the preceding decades. In particular, social psychologists reported many experiments using the Prisoner’s Dilemma game in the 1960s and early 1970s, followed by experiments on multi-player social dilemmas from the mid-1970s onwards: for a detailed review, see [
16]. The term
experimental economics appears to have been introduced by Castro and Weingarten [
17], who began their article: “Our purpose in this paper is to explain the manner in which experimental techniques may be systematically applied to the analysis of basic economic behavior” (p. 598). However, by that time a number of experimental studies had already been published in economics. Among the earliest were Rousseas and Hart’s [
18] experimental study of indifference curves; market experiments of Chamberlin [
19], Smith [
20], and Friedman [
21]; and studies using experimental games by Kalisch, Milnor, Nash, and Nering [
22], Sidowski, Wyckoff, and Tabory, [
23],Vinacke and Arkoff [
24], Atkinson and Suppes [
25], Deutsch [
26], Flood [
27], Scodel, Minas, Ratoosh, and Lipetz [
28], and Thibaut and Kelley [
29].
The emergence of behavioral economics in the 1990s was accompanied by significant improvements in the methodology of experimental games. By then, computer technology was bringing computer-controlled experiments within the scope of ordinary researchers, and that greatly facilitated control of extraneous variables. Experiments involving deception of the participants or subjects, which had been commonplace in earlier decades, became strictly taboo to the point of rendering manuscripts involving deception unpublishable in leading journals. Above all, a general consensus rapidly developed that experimental participants or subjects need to be incentivized with significant monetary payments. Smith [
20] reported the first experimental data comparing the behavior of experimental participants rewarded with points or valueless tokens with the behavior of those rewarded with significant cash payments. These and later experiments suggested that, without suitable incentives, participants’ behavior is likely to be “weak, erratic, and ... readily satiated” [
30]. Later research has corroborated those early findings, and it is generally acknowledged that incentives reduce the variance in participants’ behavior and generally improve decision making, often bringing decisions closer to predictions based on rational choice and game theory [
31,
32], especially in tasks of intermediate difficulty [
33], such as typical experimental games.
If we are to understand how human decision makers behave in interactive decisions, then empirical research is indispensable, because classical game theory relies on assumptions of perfect rationality and full common knowledge that are far removed from the cognitive capacities of human players and of limited use in explaining human strategic behavior. On the other hand, blind experimentation is also unhelpful, because the proper use of experiments is to test hypotheses, and without good hypotheses, no useful progress can be made; therefore, theoretical development is as necessary today as it ever was. Furthermore, the range of methodologies now available for studying interactive decision making and for discovering and understanding the reasons behind strategy choices now includes important techniques such as agent-based modeling that do not fit neatly into either experimentation or theoretical development. All of these approaches are represented in the articles in this Special Issue.