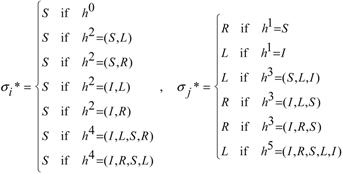Bargaining over Strategies of Non-Cooperative Games

Abstract

We propose a bargaining process supergame over the strategies to play in a non-cooperative game. The agreement reached by players at the end of the bargaining process is the strategy profile that they will play in the original non-cooperative game. We analyze the subgame perfect equilibria of this supergame, and its implications on the original game. We discuss existence, uniqueness, and efficiency of the agreement reachable through this bargaining process. We illustrate the consequences of applying such a process to several common two-player non-cooperative games: the Prisoner’s Dilemma, the Hawk-Dove Game, the Trust Game, and the Ultimatum Game. In each of them, the proposed bargaining process gives rise to Pareto-efficient agreements that are typically different from the Nash equilibrium of the original games.

1. Introduction

In several two-player non-cooperative games, like the Prisoner’s Dilemma or the Trust Game, Nash equilibrium is not Pareto-efficient. However, laboratory experiments have shown that in these games human subjects often choose strategies that are Pareto-efficient. This is even more obvious in real world situations, in which Pareto superior outcomes are sustained, despite their deviation from equilibrium. In fact, while this type of behavior cannot be considered to be rational in the game-theoretic sense, a lot has been written on the ways in which societies and individuals implement socially desirable deviations from the non-cooperative equilibrium outcome.

In real-life situations, individuals often bargain on how to behave in a strategic context. For example, while firms cooperate to form a cartel or a joint venture, an individually profitable deviation that would lead the agreement to collapse, can be avoided by explicit commitments to the cooperative profile. In fact, the evidence shows that cartels are more likely to be abandoned by individual defectors than joint ventures because the former, being illegal, are restricted to depend on tacit agreements, whereas the latter can normally be formed on the basis of a fully specified agreement regulating individual actions. Therefore, rather than a theoretical curiosity, the protocol outlined below corresponds to usual practices in contract negotiation, where the proposer contributes a commitment rule, developed also by the second party, fully describing the actions to be followed by both.

It is therefore interesting to analyze how bargaining procedures over game strategies can be modeled and which are the consequences on efficiency in the context of the original strategic situation. While the efficiency of outcomes has been a central issue in non-cooperative game theory,1 the role of bargaining as a determinant of individual actions in non-cooperative games has not been systematically explored both from a theoretical and from an experimental point of view.

In this paper, we illustrate the consequences of using alternating proposal protocols as the means of letting players reach an agreement about how to behave in a non-cooperative two-player game G of complete information.

The two players must play the original game G, and we assume that they know which will be the equilibrium outcome(s) of G. Before playing G, they may bargain over which strategy they will play in G, according to a specific bargaining mechanism, which we call Confirmed Proposal process (CP(G) henceforth). Through this process they can reach an agreement over the strategy profiles to be played in G. We call “confirmed agreement” the outcome of CP(G), i.e., the agreed strategy profile of G.

The two players have the possibility, but not the duty, to bargain through CP(G). Moreover, after CP(G), they have the possibility, but not the duty, to play G according to the confirmed agreement in CP(G). They commit to play G according to the confirmed agreement in CP(G) only if this is profitable for both players.

Therefore, a confirmed agreement in CP(G) does not imply the commitment to play it in G: if the confirmed agreement yields each player a payoff at least equal to the one obtained in the Nash equilibrium of G, then both players commit—through third-party implementation—to play G according to the agreed strategy profile; otherwise they play G directly, i.e., without any agreement over strategies.

The bargaining process CP(G) over the strategy profile can be illustrated by the following dialogue between the two players i and j:

Player (i):

“If I play strategy $s_i^1$, which strategy would you play?”.

Player (j):

“If you play $s_i^1$, I would play $s_j^2$”.

Player (i):

Either “Ok, I confirm that I’ll play strategy $s_i^1$, and so let us play ($s_i^1$,$s_j^2$)”, or “No, if you play $s_j^2$, I would play $s_i^3$”.

In the former case, the bargaining process ends. In the latter case,

Player (j):

Either “Ok, I confirm that I’ll play strategy $s_j^2$, and so let us play ($s_i^3$,$s_j^2$)”, or “No, if you play $s_i^3$, I would play $s_j^4$.

If player j confirms, the bargaining process ends. Otherwise the bargaining process continues with player i either accepting the proposed strategy profile or proposing another strategy. And so on and so forth.

Therefore, there is an original game G whose playing leads to the two players’ final payoffs, and a supergame CP(G) whose playing may lead—in case an agreement is reached—to the two players’ chosen strategies in the original game G. Indeed, CP(G) is an interactive strategic situation where a player, in order to give official acceptance of a contract, must confirm her proposed strategy combined with the strategy counterproposed by her opponent after having heard the former player’s proposal. We call equilibrium confirmed agreement the corresponding equilibrium contract between players in the bargaining supergame CP(G), leading to a strategy profile to be played in the original game G if it yields both players a payoff that is not smaller than the one obtained by playing G directly.

Notice that our confirmed proposal process is a simple bargaining process that does not make a player intrude upon her opponent’s strategic choice. In fact, each player only indicates her strategy in G, with the other one indicating her own strategy after having heard this proposal. This makes our work different from [4], where Rubinstein’s [5] model is extended introducing bargaining without commitment: in [4], Rubinstein’s [5] idea of letting the first player proposing the whole strategy profile—thereby intruding upon her opponent’s strategic choice—is maintained.

A similar remark can be made about the “Proposer Commitment Procedure” in [6]: the randomly selected proposer suggests an agreement for the whole set of active players. Similarly to our process, the agreement concerns players’ strategies. Differently from ours, the proposer also suggests the strategy of other players. For this reason, the procedure in [6] cannot be seen as a generalization of our process. In fact, we will show in the following that in our case a subgame perfect equilibrium may not exist, while in their case it always exists.

Finally, our approach is similar to Brams’ [7] “theory of moves” in the fact that he imposes a dynamic process over players’ pairs of strategies whose final state determines players’ payoffs. However, [7] conceives a sequence of players’ actual strategies so as to reach a pair of strategies that would not be further modified, while in our approach there is a sequence of proposals of possible strategies to be performed once confirmed.

The concept of “confirmed proposals” has been first examined in the game-theoretical literature by [8], focusing on the Prisoner’s Dilemma as the original game G. They let the two players bargain over the strategies to play in the Prisoner’s Dilemma: the bargaining supergame CP(G) ends when one of the two players confirms her proposal given the proposal of her opponent. At that point, the original Prisoner’s Dilemma is played according to the proposed and confirmed strategy profile. It is shown that when players alternate in exerting the power to end the bargaining supergame CP(G) played over the strategies of a Prisoner’s Dilemma, the unique equilibrium confirmed agreement is the cooperative (Pareto-efficient) outcome. The authors test their theory in the lab: the experimental results provide support for the prediction of cooperation in social dilemma games with confirmed proposals.

In this paper, we provide a general analysis of the confirmed proposal process over a complete-information game G with two players and finite strategy spaces. We discuss existence, uniqueness, and efficiency of an equilibrium agreement in CP(G). Furthermore, we illustrate the consequences, in terms of equilibrium behavior, of applying such bargaining process to some non-cooperative games very common in the experimental literature: the Prisoner’s Dilemma, the Hawk-Dove Game, the Trust Game, and the Ultimatum Game.

The remaining part of the paper is structured as follows. In Section 2, we describe the bargaining process with confirmed proposals introduced in the paper. In Section 3, we discuss existence, uniqueness, and efficiency of the equilibrium agreement obtained through this process. In Section 4 we apply the confirmed proposal process to some two-player non-cooperative games extensively used in the experimental research. Section 5 concludes.

2. The Bargaining Supergame

Throughout the paper, we consider only non-cooperative games G with complete information and we restrict the analysis to the two-player case. We assume that players are rational (i.e., they have complete and transitive preferences over the set of payoffs), G has at least one equilibrium in pure or mixed strategies, and players know the equilibrium/a.

Before playing G, they can bargain over which strategy to play in G, eventually not the equilibrium one. However, the bargaining process CP(G) starts only if both players go along with entering this procedure and which one of them will be the first mover in the supergame CP(G). Therefore, while the standard description of G assumes that any communication between players is forbidden, our bargaining process CP(G) implicitly leads players to “tacitly communicate” and bargain before playing G, eventually implementing binding agreements on how to play G.

CP(G) is an infinite-horizon dynamic game in which the two players alternate proposals. Any proposal by a player is one of the possible strategies that she can adopt in G. The supergame CP(G) ends when a player confirms the proposal she made the previous period in which she was active: at this point, if it is worth it for both of them (compared to the Nash equilibrium of G), the two players can commit to play G according to the confirmed strategies in CP(G). In the case of no confirmation, the player indicates a different strategy, which becomes the counter-proposal to the last strategy proposed by the opponent. Then, the opponent may confirm or not the latter strategy.2

Except for the selection of the first mover at the beginning of the supergame,3 the rules of the game are symmetric.

Let us denote by S_k the finite strategy space for player k (with $k=i,j$) in the original non-cooperative game G. Player k’s set of possible proposals in the supergame with confirmed proposals CP(G) coincides with S_k. As a consequence, the set of possible agreements in CP(G) coincides with the set of strategies of G, i.e., the product set $S_i\times S_j$ contains all the possible agreements of CP(G).

Denote by $s_k^t$ the strategy proposed by player k in period t. Suppose that player i starts the supergame CP(G). The sequence of alternating proposals is as follows:

Period 1.

Player i proposes a strategy $s_i^1\in S_i$ to player j. Player i would actually play $s_i^1$ if (and only if) she would confirm this strategy after the counter-proposal of player j.

Period 2.

Player j proposes a strategy $s_j^2\in S_j$ to player i. This strategy would actually be played if (and only if) either i will confirm her previous strategy $s_i^1$ or j will confirm her proposal $s_j^2$ after the counter-proposal of player i.

Period 3.

Player i chooses whether or not to confirm her previous strategy $s_i^1$. If she confirms $s_i^1$, i.e., $s_i^3$ = $s_i^1$, then the bargaining process ends, through the sequence ($s_i^1$,$s_j^2$,$s_i^1$), with the confirmed agreement ($s_i^1$,$s_j^2$), and the two players receive the payoffs corresponding to the strategy profile ($s_i^1$,$s_j^2$) in the original game G. If she does not confirm, i.e., she proposes a new strategy $s_i^3\ne s_i^1$, the bargaining process continues with $s_j^2$ as player j’s proposal and $s_i^3$ as player i’s counter-proposal to j’s proposal.

Period 4.

Player j chooses whether or not to confirm her previous strategy $s_j^2$. If she confirms $s_j^2$, i.e., $s_j^4=s_j^2$, then the bargaining process ends, through the sequence ($s_j^2$,$s_i^3$,$s_j^2$), with the confirmed agreement ($s_j^2$,$s_i^3$), and the two players receive the payoffs corresponding to the strategy profile ($s_i^3$,$s_j^2$) in the original game G. If she does not confirm, i.e., she proposes a new strategy $s_j^4\ne s_j^2$, the bargaining process continues with $s_i^3$ as player i’s proposal and $s_j^4$ as player j’s counter-proposal to i’s proposal. And so on and so forth.

Therefore, CP(G) is characterized by sequences of proposals ${(s_k^t)}_{t=1}^T$, one for each period t and for the active player k at period t, with $k=i$ in odd periods and $k=j$ in even periods, and $T=3,4,\dots ,+\infty .$ A sequence ${(s_k^t)}_{t=1}^T$ is a feasible history h of CP(G) if $s_i^1,s_i^3,\dots \in S_i$ and $s_j^2,s_j^4,\dots \in S_j$, where the set of possible proposals in each period t of CP(G) is the finite strategy space S_k for player k (with $k=i,j$) in the original non-cooperative game G.4 Let $\overline{H}$ be the set of all feasible histories h, where $h^0$ indicates the initial, empty history of CP(G), i.e., before period 1, and $h^t$ for $t=1,2,\dots$ indicates a feasible history before period $t+1$.

A history $z={(s_k^t)}_{t=1}^T\in \overline{H}$ of CP(G) is terminal if $s_k^T=s_k^{T-2}$, i.e., player k active at period T confirms her previous proposal, made two periods before. Denote with Z the set of terminal histories of CP(G) and let $H:=\overline{H}\backslash Z$ denote the complementary set of non-terminal (or partial) histories. For instance, $h^0$, $h^1$ and $h^2$ always indicate non-terminal histories by construction, since no confirmation is possible before period 3, while $h^T$ for $T=3,4,\dots$ can indicate either a non-terminal or (in the case of confirmation in period $T$) a terminal history.

A strategy for player k in CP(G) is a function ${\text{σ}}_k:H\to S_k$ such that $s_i^1,s_i^3,\dots \in S_i$ and $s_j^2,s_j^4,\dots \in S_j$ for all $h\in H.$ Notice that, since in each period the only active player k can always choose among all of her possible strategies $s_k\in S_k$ of G, the set of possible proposals $s_k^t(h^{t-1})$ at each history $h^{t-1}$ does not depend on the specific history $h^{t-1}$, but only on the player’s identity (i or j): it is S_i if the active player $k=i$, and S_j otherwise.

If no strategy profile of G is ever confirmed by either player in any t = 3, 4,… in CP(G), then no agreement is reached through bargaining, i.e., CP(G) has no equilibrium, and G is played directly (i.e., without any agreement over strategies). The original game G is played directly also if there is a confirmed agreement in CP(G), but it does not lead each player a payoff at least equal to the one she would get in equilibrium by playing G directly. In this case, a commitment to play G according the agreed strategy profile in CP(G) is not possible.

Let us now introduce assumptions about players’ preferences over agreements in CP(G).

Denote with $f(s_k^{t-2},s_{-k}^{t-1})$ the outcome of G in the case the agreement $(s_k^{t-2},s_{-k}^{t-1})$ over the strategy profile to be played in G would be confirmed in the supergame CP(G) in period t, with t = 3, 4,… We assume that each player k’s preference relation $\succsim$_k satisfies stationarity, i.e., the preference between two agreements does not depend on time: if $s_k^{t-2}=s_k^{t\prime -2}$, $s_k^{t-1}=s_k^{t\prime -1}$, ${\tilde{s}}_k^{t-2}={\tilde{s}}_k^{t^{\prime }-2}$ and ${\tilde{s}}_k^{t-1}={\tilde{s}}_k^{t^{\prime }-1}$, then $f(s_k^{t-2},s_{-k}^{t-1})$ $\succsim$_k $f({\tilde{s}}_k^{t-2},{\tilde{s}}_{-k}^{t-1})$ if and only if $f(s_k^{t\prime -2},s_{-k}^{t\prime -1})$ $\succsim$_k $f({\tilde{s}}_k^{t\prime -2},{\tilde{s}}_{-k}^{t\prime -1})$ for all t ≠ t′, with $t,t\prime =3,4,\dots$ The assumption of stationarity of preferences means that a player’s preferences do not depend on period t of an agreement in CP(G), but only on the outcome of G due to this agreement.

A player k is impatient if the time of the agreement is relevant and she prefers to reach the same agreement in an earlier than later period, i.e., if $s_k^{t-2}=s_k^{t\prime -2}$ and $s_k^{t-1}=s_k^{t\prime -1}$, then $f(s_k^{t-2},s_{-k}^{t-1}){\succ }_{k}f(s_k^{t\prime -2},s_{-k}^{t\prime -1})$ for all t < t′, with $t,t\prime =3,4,\dots$; she is patient if the time of the agreement is irrelevant, i.e., if $s_k^{t-2}=s_k^{t\prime -2}$ and $s_k^{t-1}=s_k^{t\prime -1}$, then relation $f(s_k^{t-2},s_{-k}^{t-1})$ $~$_k $f(s_k^{t\prime -2},s_{-k}^{t\prime -1})$ for all t < t′, with $t,t\prime =3,4,\dots$

The assumption of impatience helps in selecting, among several payoff-equivalent strategy profiles of CP(G), those leading to the earliest confirmed agreement. In the following analysis, we will show that the number of stationary equilibria of CP(G), which generate the same equilibrium in G, shrinks if players are impatient.

3. General Results about the Equilibrium of the Bargaining Supergame

In this section we discuss existence, uniqueness and efficiency of the equilibrium confirmed agreement of CP(G) through several examples of original games G.

A Subgame Perfect Nash Equilibrium of CP(G) is a pair of strategies $({\sigma }_k*,{\sigma }_{-k}*)$ in the supergame such that one of the two players k at period t makes a proposal $s_k^t$ that is the same as in period t–2, i.e., $s_k^t=s_k^{t-2}$. This leads to the equilibrium confirmed agreement $(s_k^{t-2},s_{-k}^{t-1})$, which leads to the agreed strategy profile $(s_k*,s_{-k}*)$ to be played in G.

We look for equilibria of CP(G) by applying the following reasoning. Notice that CP(G) is a dynamic (super)game, which we represent below through a game tree. In every decision node after period 2, the active player can confirm her previous proposal. We apply the following weak-dominance argument: we assume that the active player confirms at period t her previous proposal at period t–2 if confirmation gives her an outcome that is not worse than the best outcome she can get in the subgame of CP(G) that she enters in the case of no confirmation at period t. Then, in those subgames that are “finite” because of confirmation, we apply backward induction.

Example 1 shows an original game G with several subgame perfect equilibria of CP(G), all leading to the same equilibrium confirmed agreement.

The existence of a subgame perfect equilibrium of CP(G), and therefore of an equilibrium confirmed agreement, is not guaranteed. This is shown in Example 2. There is no equilibrium if, in each period t of CP(G), no player has an incentive to confirm the proposal she made in period $t-2.$ A player does not confirm her proposal because she believes she can obtain either a better agreement in the continuation game of CP(G), or a better equilibrium outcome by playing G directly.

Furthermore, it can happen that, although there exists a subgame perfect equilibrium of CP(G), for one player the corresponding equilibrium confirmed agreement is worse off than the equilibrium outcome obtainable by playing G directly. In this case players are not able to commit on playing G according to the equilibrium confirmed agreement of CP(G), hence G is played directly. Example 3 shows such a situation.

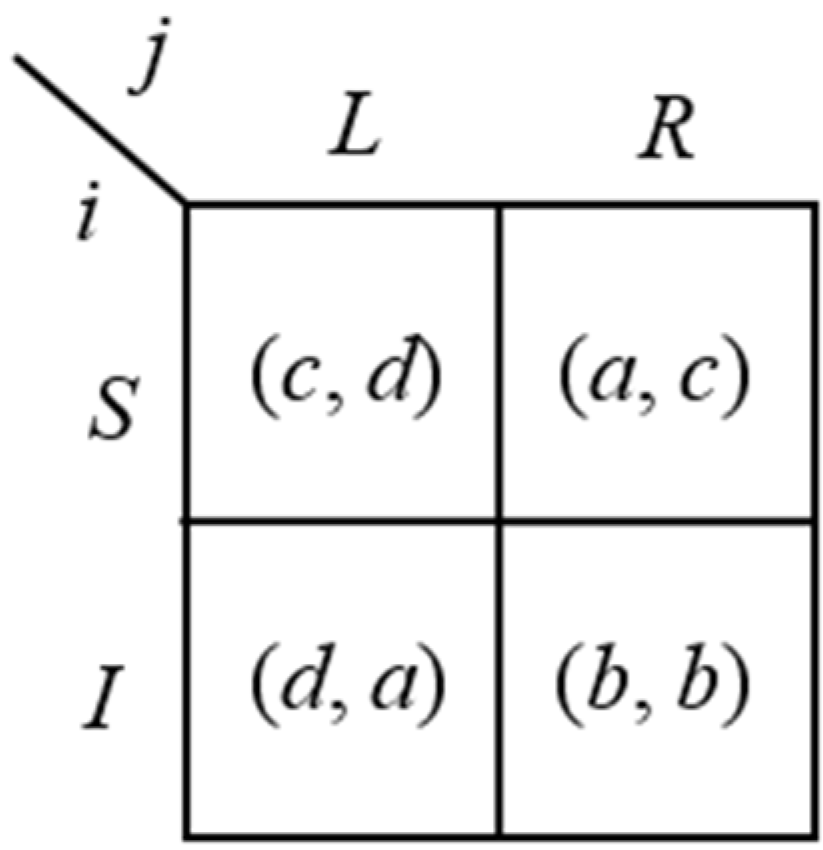
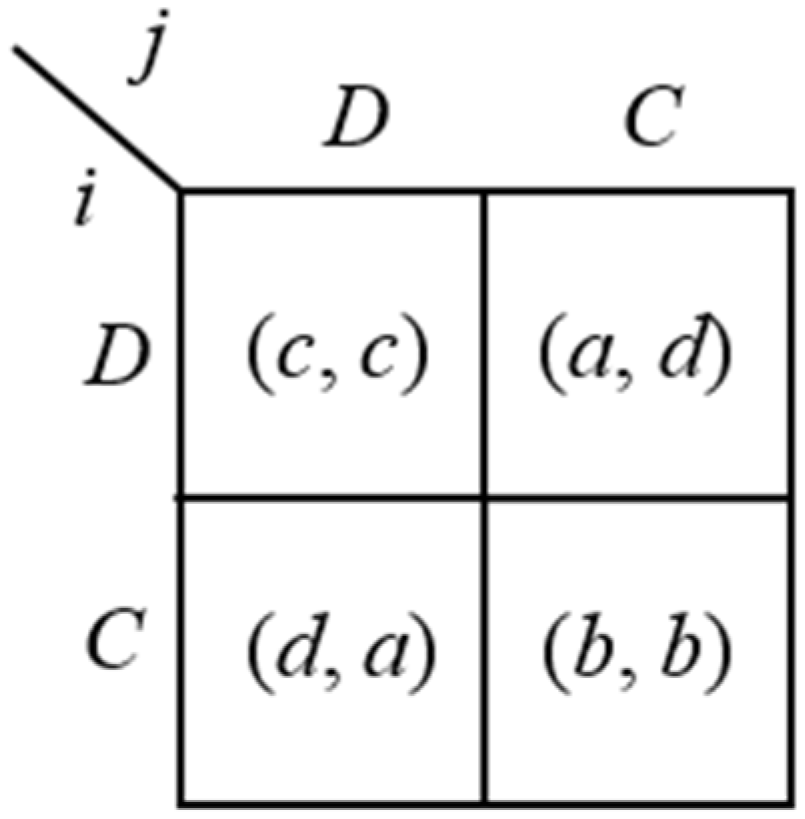
Example 1: One equilibrium confirmed agreement. Consider the two-player simultaneous game G in Figure 1. The set of strategies for player i and player j is, respectively, S_i = {Superior, Inferior}, henceforth S_i = {S, I}, and S_j = {Left, Right}, henceforth S_j = {L, R}. Figure 1, with a > b > c > d, shows, besides the simultaneous-move original game G, also all the possible agreements of CP(G), the bargaining supergame with confirmed proposals built on it.

Figure 1. Original game G with one equilibrium confirmed agreement.

Figure 1. Original game G with one equilibrium confirmed agreement.

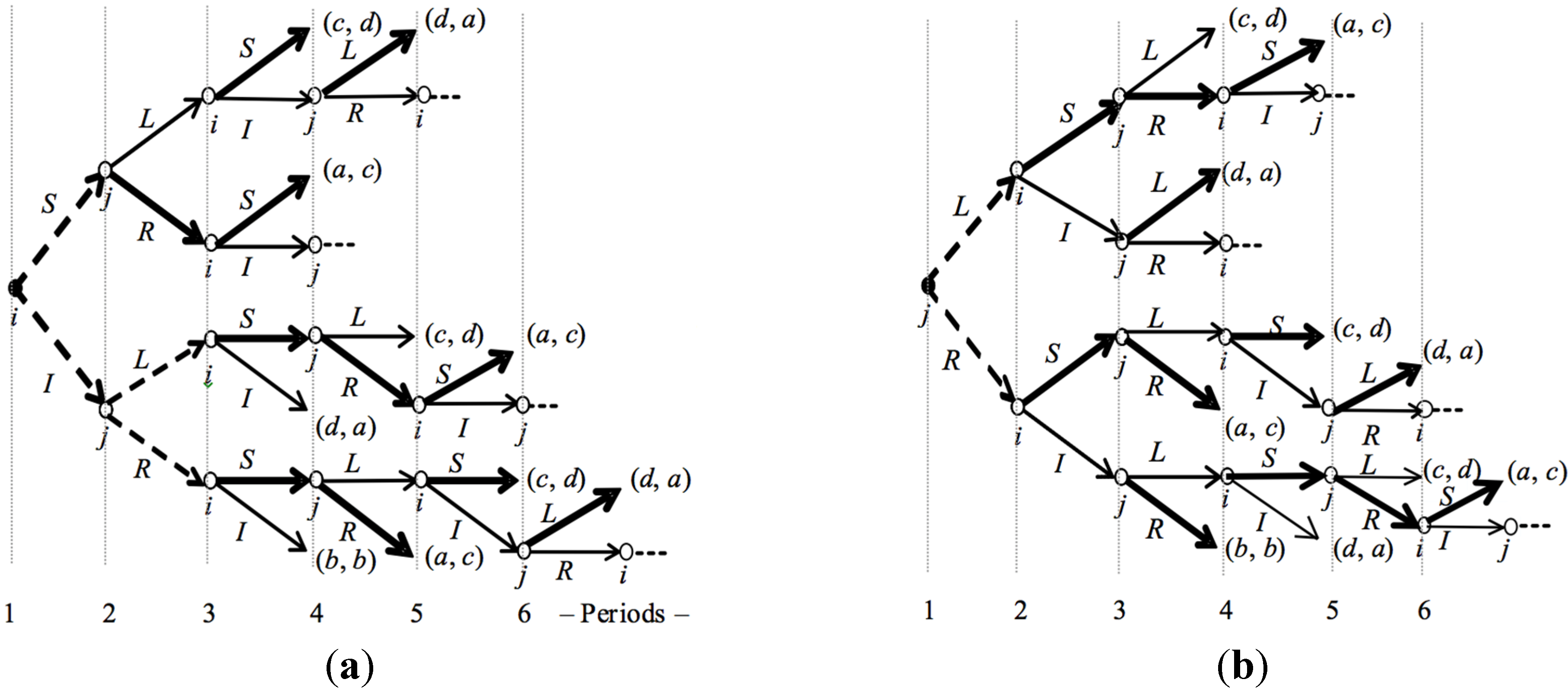
The original game G has the profile (S, R) as Nash equilibrium. Let us now calculate the subgame perfect equilibrium outcome of the bargaining supergame CP(G). Observe Figure 2. The set of feasible payoffs of CP(G) is the same as the original game G in Figure 1. The first of the two payoffs always refers to player i, as in G. In Figure 2a (left-hand side) it is assumed that the first mover in CP(G) is player i. In Figure 2b (right-hand side) it is assumed that the first mover in CP(G) is player j.

Figure 2. CP(G), G being the original game in Figure 1, with i (a) or j (b) as first mover.

Figure 2. CP(G), G being the original game in Figure 1, with i (a) or j (b) as first mover.

The above mentioned weak-dominance argument applies to each of the two CP(G) in Figure 2 as follows: In every decision node ξ in period t, the active player weakly prefers the proposal which leads, in the subgame with root ξ, to an outcome which is better or indifferent for her than the best outcome that is obtained by choosing another proposal at ξ. We call this proposal weakly dominant, and we mark the corresponding branch from period t to t+1 with a bold line. Whenever there are two or more weakly-dominant proposals at a given node in t, the corresponding branches from t to t+1 are marked with dotted bold lines.

For instance, in Figure 2a, player j, after the history (S, L, I), proposes L and so she confirms the agreement (I, L), because in this way she obtains the highest possible payoff a. Using backward induction, we find that player i, after history (S, L), proposes S and so she confirms the agreement (S, L), because in this way she obtains the payoff c rather than the payoff she would obtain by indicating I (her payoff in this case would be d). Going backward, player j, after i’s initial proposal S, counter-proposes R, since this leads to obtain the payoff c rather than the payoff d, which she would obtain by counter-proposing L. Using the same reasoning throughout CP(G), we find that there are three subgame perfect equilibria $({\sigma }_i*,{\sigma }_j*)$ in pure (supergame) strategies of CP(G), the corresponding histories being (S, R, S) for the first equilibrium, and (I, L, S, R, S) and (I, R, S, R) for the other two. In each of them, the equilibrium confirmed agreement is (S, R). This is true if patience is assumed. If, instead, both players are impatient, then the unique subgame perfect equilibrium leads to the history (S, R, S), where the agreement (S, R) is confirmed by player i in period 3, the earliest possible period of confirmation.5

The same equilibrium confirmed agreement is obtained if the first mover in CP(G) is player j (see Figure 2b). Also in this case, we find that (S, R) is confirmed in two subgame perfect equilibria if patience is assumed—the corresponding histories being (L, S, R, S) and (R, S, R), and in only one equilibrium—leading to history (R, S, R)—if players are impatient.

Therefore, independently of players’ level of (im)patience, and of whoever is the first mover in CP(G), after the end of CP(G), the two players commit to play (S, R) in G. In this specific example, this is also the Nash equilibrium of G: in the following, we will show that a necessary (but not sufficient) condition for a Nash equilibrium of G to be an equilibrium confirmed agreement of CP(G) is weak Pareto efficiency (see Proposition 2).

Example 2: No equilibrium confirmed agreement. Our solution procedure does not always allow for an equilibrium of CP(G). Consider Figure 3. The original game G has only one Nash equilibrium in mixed strategies, with player one choosing strategy S with probability $p(S)=0.25$ and player two choosing strategy L with probability $q(L)=\mathrm{0.5.}$ This leads to expected payoffs V_i = V_j = 1.5. Both expected payoffs are larger than 1, the second-lowest possible payoff of G.

Figure 3. Original game G with no equilibrium confirmed agreement.

Figure 3. Original game G with no equilibrium confirmed agreement.

In Figure 4 we show the bargaining supergame CP(G) with player i as first mover. Assuming patience, the weak-dominance argument implies that none of the two players k makes a proposal which leads to obtain the payoff of either 0 or 1, since she can obtain a higher expected payoff V_k in the mixed-strategy Nash equilibrium of G by not bargaining through CP(G).

Figure 4. CP(G), G being the original game in Figure 3, with i as first mover.

Figure 4. CP(G), G being the original game in Figure 3, with i as first mover.

This implies that no player k is able to confirm in CP(G) an agreement where she gets a payoff higher than V_k. In fact, if player i’s first proposal in period 1 is S, the history that results by taking into account weak dominance and backward induction is the initial history (S, R, I, L) repeated infinite times.6 If, instead, player i’s first proposal in period 1 is I, the history that results by taking into account weak dominance and backward induction is the initial history (I, L, S, R) repeated infinite times.

Thus, no equilibrium confirmed agreement is obtained in CP(G). This is the case also when the first mover would be player j. Since the reasoning is analogous, we omit the graphical representation of this supergame in Figure 4.

Given that there is no equilibrium confirmed agreement in CP(G), players have to directly play the original game G, thereby getting the expected payoffs V_i = V_j = 1.5.

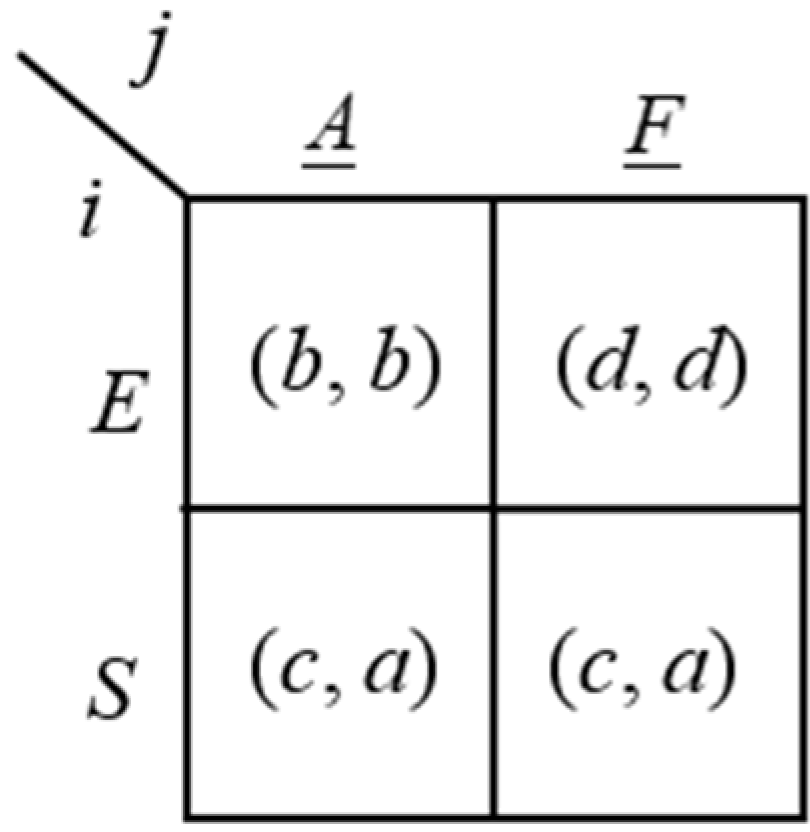
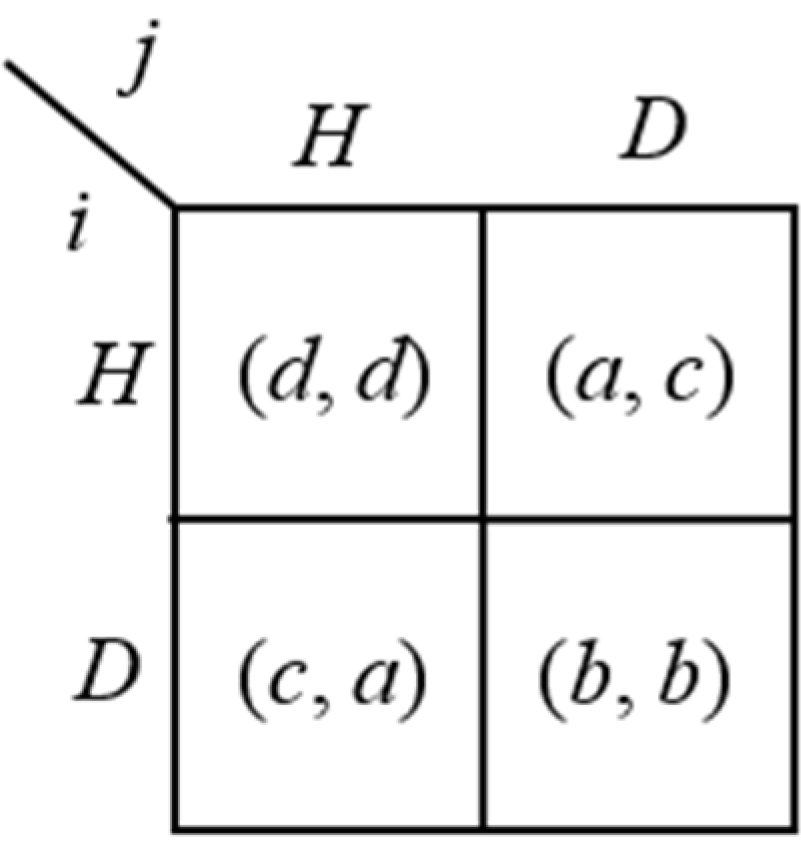
Example 3: One equilibrium confirmed agreement that is not played. It can be the case that, although CP(G) has an equilibrium confirmed agreement, no commitment to play G according to the equilibrium confirmed agreement of CP(G) is possible, since one of the two players would get a higher payoff by directly playing G, i.e., in the Nash equilibrium of G. This happens, for example, when the original game G is the Entry Game. In this two-stage game, player i (the potential entrant) chooses whether to Enter (E) or to Stay Out (S) of the market, with j (the incumbent) deciding whether to Accommodate (A) or to Fight(F) if the entrant decides to enter. The strategic form of the game in Figure 5, where x:= “x if E”, with $x=A,F$, and a > b > c > d, represents all the possible agreements of CP(G). Notice that the highest possible payoff for player i is b.

Figure 5. Original game G with one equilibrium confirmed agreement that is not played.

Figure 5. Original game G with one equilibrium confirmed agreement that is not played.

In the unique (subgame perfect) Nash equilibrium of G, i’s entry takes place, with j accommodating it. Hence, both players get a payoff equal to b.

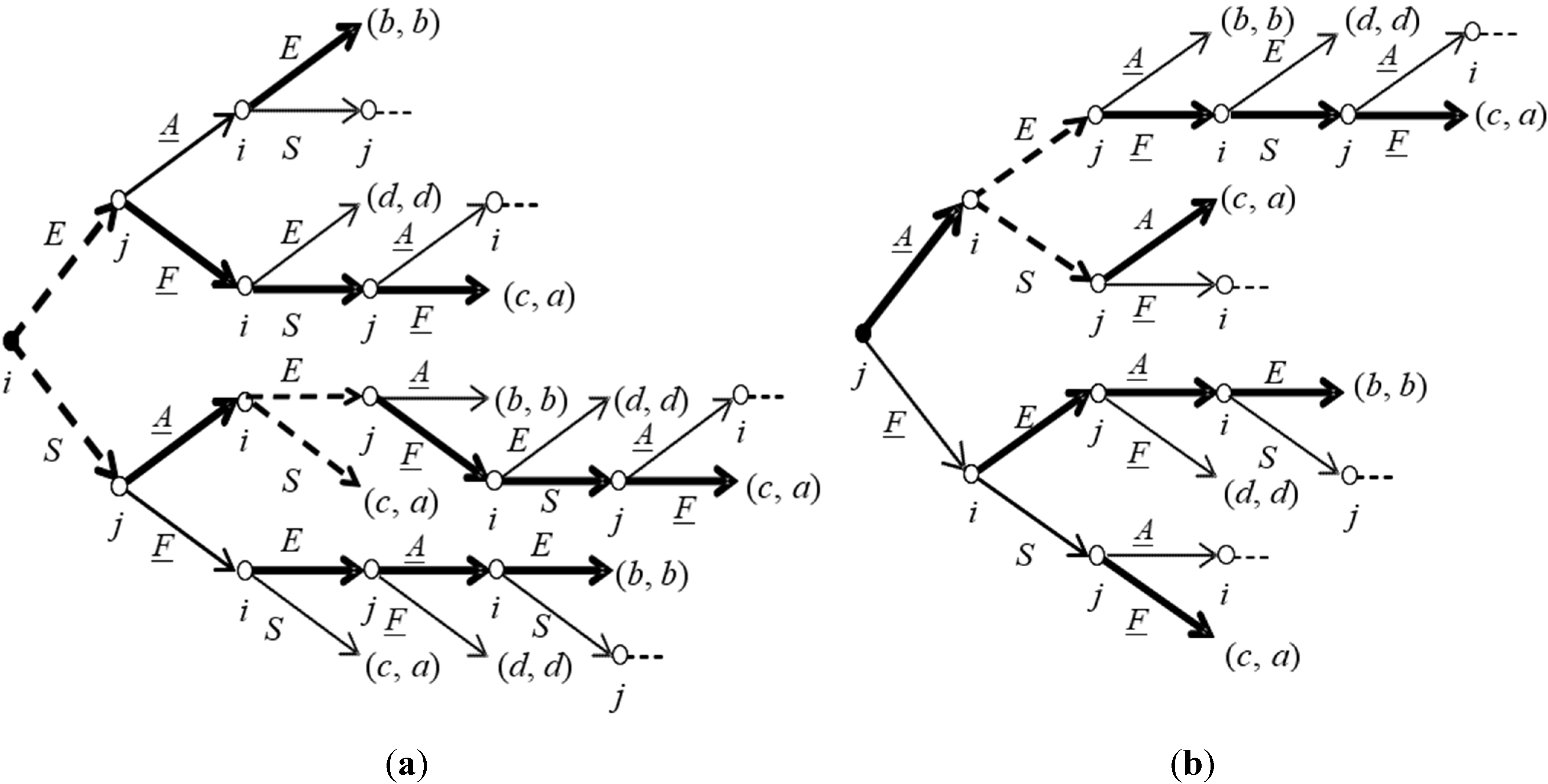
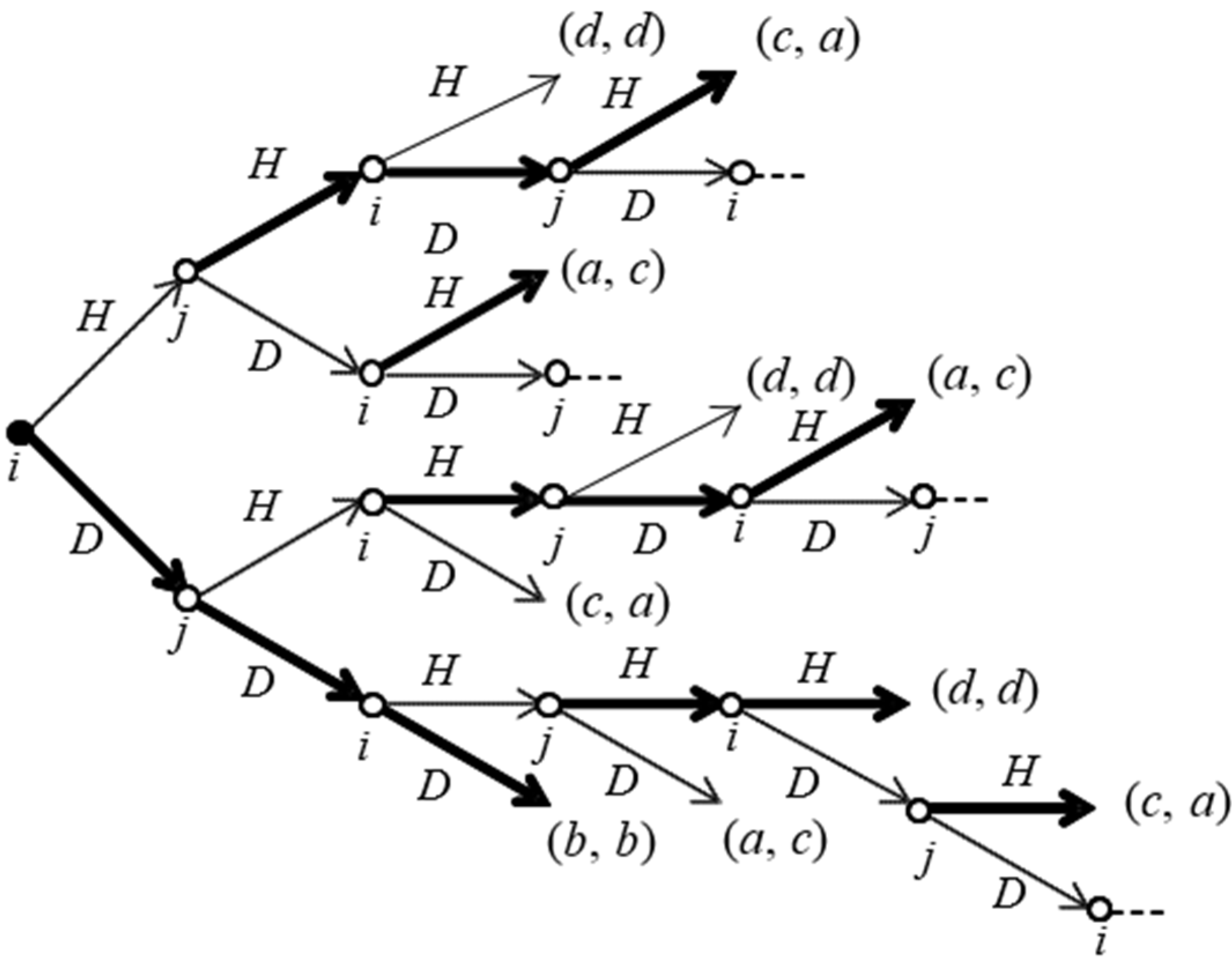
Conversely, in all subgame perfect equilibria of CP(G), the entrant stays out. The two possible versions of CP(G) when G is the Entry Game are in Figure 6. The first version, in Figure 6a, represents the case in which player i, the potential entrant in the original game, moves first in CP(G). In the second version, Figure 6b, player j, the incumbent in the original game, is the first mover.

For both CP(G) in Figure 6, there are two payoff-equivalent equilibrium confirmed agreements, which involve the entrant to stay out. When the first mover is player i (Figure 6a), there are three equilibrium terminal histories: (E,F,S,F), (S,A,E,F,S,F), and (S,A,S). When the first mover is player j (Figure 6b), there are two equilibrium terminal histories: (A,E,F,S,F) and (A,S,A).

Figure 6. CP(G), G being the original game in Figure 5, with i (a) or j (b) as first mover.

Figure 6. CP(G), G being the original game in Figure 5, with i (a) or j (b) as first mover.

In the two equilibrium confirmed agreements, (S,A) and (S,F), player i gets a payoff equal to c. Conversely, by playing directly G, she obtains a payoff of b. Consequently, she will not commit to play G according to the strategy profile agreed in CP(G), and the players must play G directly. This result also holds in the case both players would be impatient. In fact, the unique equilibrium confirmed agreement in both CP(G) in Figure 6a and CP(G) in Figure 6b would be (S,A), confirmed in period 3: player i would get c by bargaining through CP(G) and b by playing directly G.

Uniqueness of the equilibrium confirmed agreement. If an equilibrium exists, we can introduce Proposition 1, concerning the uniqueness of the equilibrium confirmed agreement.

Proposition 1. If the equilibrium for CP(G) exists for a given first mover, and G is generic, then the equilibrium confirmed agreement is unique, hence players agree on a unique behavior in G. If G is not generic, then multiple confirmed agreements are possible, although being payoff-equivalent for at least one player.

The intuition behind Proposition 1 is as follows.

Consider an original game G. It is generic if each player is not indifferent between two outcomes stemming from two different strategy profiles of G, i.e., it cannot be $f(s_i,s_j)$ $~$_k $f(s_i\prime ,s_j\prime )$ if $s_i\ne s_i\prime$ and/or $s_j\ne s_j\prime$ for $k=i,j$.

Suppose that CP(G) has two equilibrium confirmed agreements, $(s_i*,s_j*)$ and $(s_i\prime *,s_j\prime *)$. An equilibrium confirmed agreement in CP(G) is associated to one or more terminal histories. A terminal history is a branch of the game tree of CP(G) that starts at period 1 and ends with a confirmation.

Let us now reason by contradiction.

If G is generic, then one of the two equilibrium confirmed agreements should be better than the other for player i, and player j could have the same preference or the opposite preference. Supposing that player i is the first mover in CP(G) and that $f(s_i*,s_j*){\succ }_{i}f(s_i\prime *,s_j\prime *)$, one could have either $f(s_i*,s_j*){\succ }_{j}f(s_i\prime *,s_j\prime *)$ or $f(s_i*,s_j*){\prec }_{j}f(s_i\prime *,s_j\prime *)$.

In the former case, it is $f(s_i*,s_j*){\succ }_{k}f(s_i\prime *,s_j\prime *)$ for $k=i,j$. The supergame CP(G) is with complete information, hence players know the game tree of the bargaining process. The equilibrium confirmed agreements are associated to two different terminal histories. There are, in general, several terminal histories associated to the same equilibrium confirmed agreement: let us consider all pairs of terminal histories where each history leads to a different equilibrium confirmed agreement. For any pair, there is a period $\overline{t}$ of CP(G) where the two terminal histories diverge, thereby including each one after $\overline{t}$ a different sub-branch of the game. This sub-branch, and hence the consequent equilibrium confirmed agreement, is chosen by the player active at $\overline{t}$: she chooses the sub-branch that will lead to the equilibrium confirmed agreement that is better for her. Since both players have the same preferences over the two supposed equilibrium confirmed agreements, no equilibrium terminal history will lead to $(s_i\prime *,s_j\prime *)$. Thus, $(s_i\prime *,s_j\prime *)$ cannot be an equilibrium confirmed agreement.

For instance, in Figure 2b, the agreement (S, L) cannot be confirmed in equilibrium (the same is true in Figure 2a). In fact, both players prefer the agreement (S, R) to (S, L). The terminal histories leading to (S, L) are: (L, S, L), (R, S, L, S), and (R, I, L, S, L). The terminal histories leading to (S, R) are: (L, S, R, S), (R, S, R), and (R, I, L, S, R, S). Compare pairwise terminal histories leading to (S, L) with terminal histories leading to (S, R): the player active at the period where the two terminal histories diverge chooses the sub-branch leading to (S, R). For instance, considering the pair (L, S, L) and (L, S, R, S), the two histories diverge at period 3, where player j is active: she prefers proposing R instead of L.

In the latter case, it is $f(s_i*,s_j*){\succ }_{i}f(s_i\prime *,s_j\prime *)$ and $f(s_i*,s_j*){\prec }_{j}f(s_i\prime *,s_j\prime *)$. Consider all terminal histories leading to either $(s_i*,s_j*)$ or $(s_i\prime *,s_j\prime *)$. Take a pair of terminal histories where one leads to $(s_i*,s_j*)$ and the other one leads to $(s_i\prime *,s_j\prime *)$. For this pair, there is a period $\overline{t}$ of CP(G) where the two terminal histories diverge, thereby including each one after $\overline{t}$ a different sub-branch of the game. This sub-branch, and hence the equilibrium confirmed agreement, is chosen by the player active at $\overline{t}$: she chooses the sub-branch that will lead to the equilibrium confirmed agreement that is better for her. If the active player making this choice is i, then in the pair of histories the one leading to $(s_i\prime *,s_j\prime *)$ is eliminated; if this active player is j, the terminal history leading to $(s_i*,s_j*)$ is eliminated. Then, the number of terminal histories leading to either $(s_i*,s_j*)$ or $(s_i\prime *,s_j\prime *)$ reduces by 1. Iterating this procedure, only terminal histories leading to the same equilibrium confirmed agreement would survive: only one equilibrium confirmed agreement exists.

For instance, in Figure 2b, the agreement (I, R) cannot be confirmed in equilibrium (the same is true in Figure 2a). In fact, consider the two agreements (I, R) and (S, R): player j prefers (I, R), while player i prefers (S, R). The only terminal history leading to (I, R) is (R, I, R). The terminal histories leading to (S, R) are: (L, S, R, S), (R, S, R) and (R, I, L, S, R, S). First, compare (R, I, R) with (L, S, R, S). The two histories diverge at period 1, where player j is active: she prefers proposing R instead of L, thereby eliminating (L, S, R, S). Then, compare (R, I, R) with (R, I, L, S, R, S): the two histories diverge at period 3, where player j is active; she prefers proposing R instead of L, thereby eliminating (R, I, L, S, R, S). Finally, compare (R, I, R) with (R, S, R): the two histories diverge at period 2, where player i is active; she prefers proposing S instead of I, thereby eliminating (R, I, R). Consequently, the only equilibrium confirmed agreement is (S, R), which can be obtained also through the other two terminal histories (L, S, R, S) and (R, I, L, S, R, S). In fact, although they have been eliminated in the comparison with (R, I, R), they are still equilibrium terminal histories of CP(G) in Figure 2b.

Finally, notice that for different first movers in CP(G), a different equilibrium confirmed agreement may emerge.7

If G is not generic, it can be $f(s_i,s_j)$ $~$_k $f({s^{\prime }}_i,{s^{\prime }}_j)$ if $s_i\ne {s^{\prime }}_i$ and/or $s_j\ne {s^{\prime }}_j$ for $k=i,j$. Suppose that $f(s_i*,s_j*){\succ }_{i}f(s_i\prime *,s_j\prime *)$ and $f(s_i*,s_j*)$ $~$_j $f(s_i\prime *,s_j\prime *)$. If the player confirming the agreement is player j, then either $(s_i*,s_j*)$ or $(s_i\prime *,s_j\prime *)$ can be confirmed. Hence, both agreements can be confirmed in equilibrium, with player j being indifferent between the two. If the player confirming the agreement is player i, if she is given the possibility to confirm $(s_i*,s_j*)$, she certainly does it. If she is given the possibility to confirm $(s_i\prime *,s_j\prime *)$, she does it if, by not confirming, player j would confirm an agreement yielding player i a lower payoff than in $(s_i\prime *,s_j\prime *)$. All this is shown in next example.

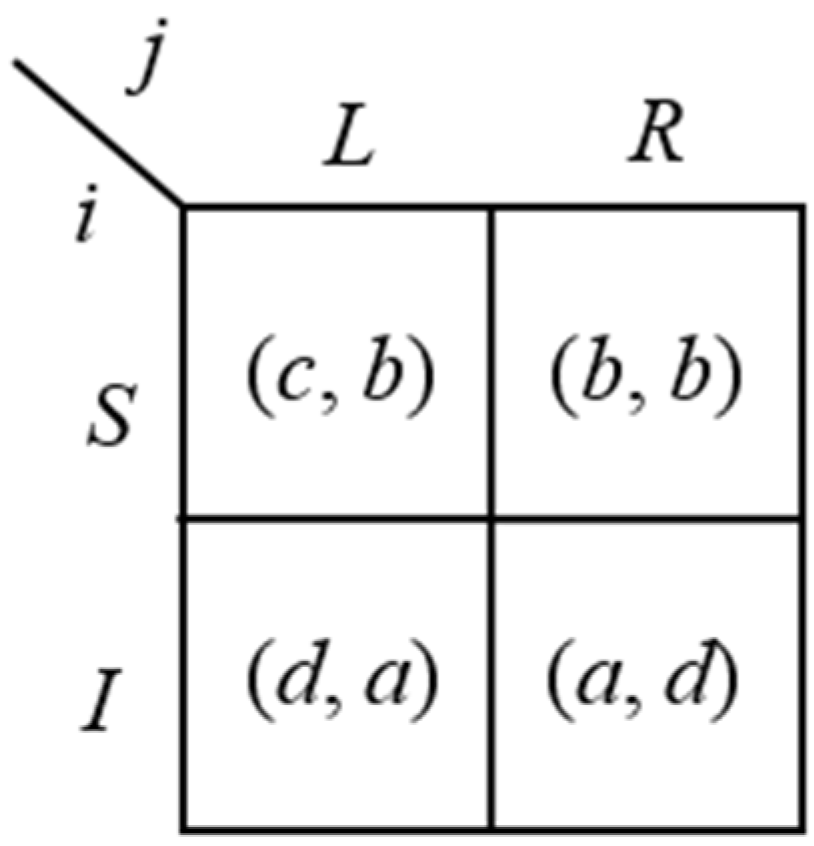
Example 4: Multiple equilibrium confirmed agreements. As stated in Proposition 1, a non-generic game may have multiple equilibrium confirmed agreements. Figure 7, with a > b > c > d, provides an example of a non-generic original game G with two equilibrium confirmed agreements in CP(G). G is non-generic since player j gets the same payoff for L and R if player i plays S.

Figure 7. Original game G with multiple confirmed agreements.

Figure 7. Original game G with multiple confirmed agreements.

Figure 8 shows CP(G) with player i (Figure 8a) and player j (Figure 8b) as first mover.

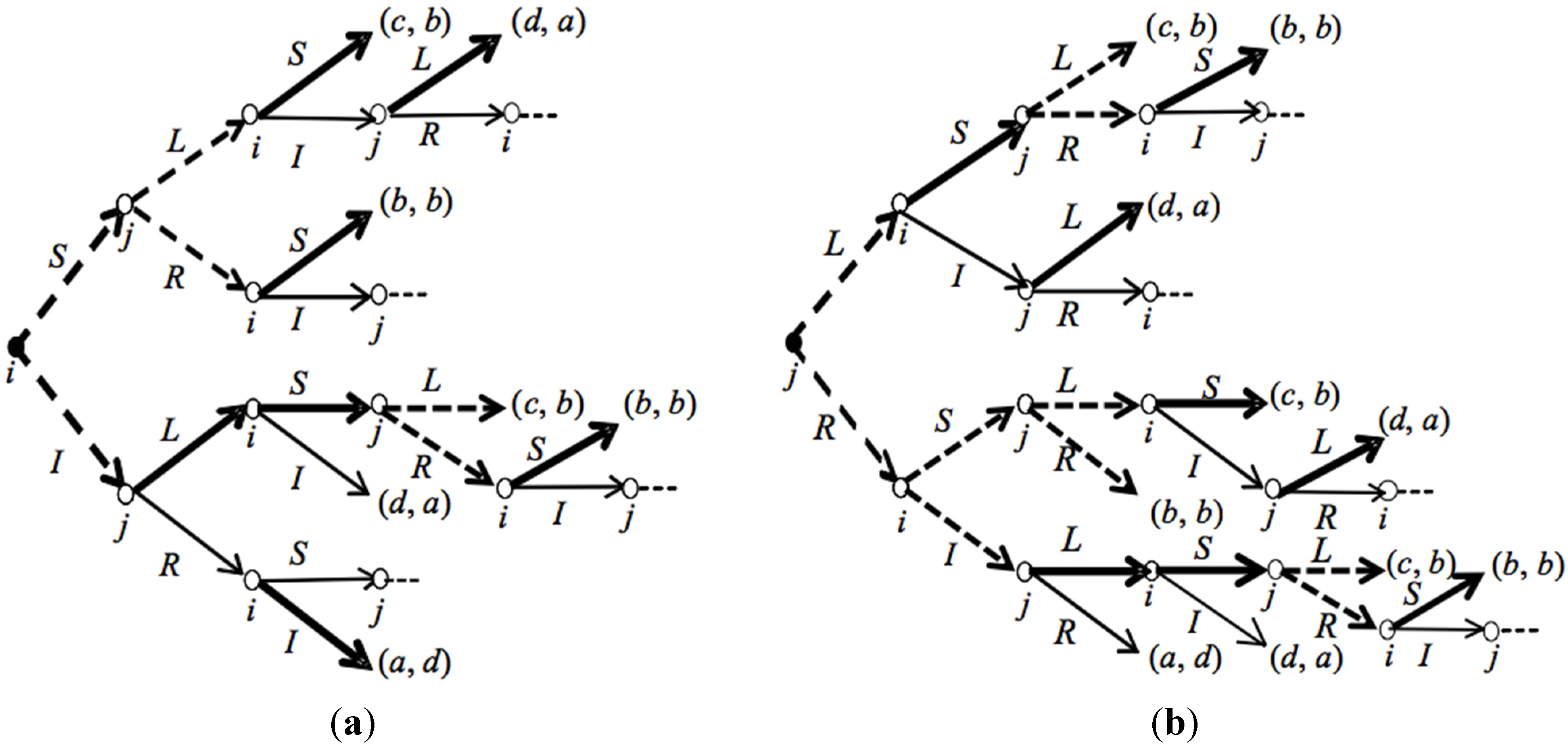
In both CP(G) in Figure 8, the two equilibrium agreements are (S, L) and (S, R). In fact, neither of the two players is able to confirm an agreement allowing one player to get the highest possible payoff a. If such an agreement would be confirmed, one of the two players would get a, and the other one would receive d (the lowest possible payoff). Hence, the player getting d would never confirm this contract. Further, this player would not counter-propose a strategy of G that would allow the other player to confirm such a contract. This means that, in any period of CP(G), player i does not reply with proposal I to j’s proposal L, and player j does not reply with proposal R to i’s proposal I.

Thus, for each player the highest reachable payoff in a confirmed agreement is b. Thus, when a player has the possibility to get b by confirmation, she confirms the previous proposal. Given that G is non-generic, when it is player j confirming an agreement in equilibrium, player i gets either b—agreement (S, R)—or c—agreement (S, L). However, player i can confirm an agreement that gives her c when, by not confirming at t, she would allow j to confirm at t + 1 an agreement giving i a payoff equal to d.

Figure 8. CP(G), G being the original game in Figure 7, with i (a) or j (b) as first mover.

Figure 8. CP(G), G being the original game in Figure 7, with i (a) or j (b) as first mover.

Multiplicity of confirmed agreements holds also if both players are impatient. As expected, impatience reduces the number of subgame perfect equilibria of CP(G): if j is the first mover, the two equilibrium histories are (L, S, L) and (R, S, R); if i is the first mover, the two equilibrium histories are (S, L, S) and (S, R, S). In particular, terminal history (S, L, S)—with i confirming an agreement yielding her a payoff equal to c—emerges in equilibrium because if player i would not confirm (S, L) in period 3, player j would confirm (I, L) in period 4.

Pareto efficiency of the equilibrium confirmed agreement. If an equilibrium exists, we can introduce Proposition 2, concerning the Pareto efficiency of the equilibrium confirmed agreement.

Proposition 2. Every equilibrium confirmed agreement in CP(G) is weakly Pareto-efficient.

The intuition behind Proposition 2 is the following.

Proposition 2 states that a terminal history leads to an equilibrium confirmed agreement of CP(G) only if no other terminal history leads to an agreement which strongly Pareto dominates the equilibrium one. Consequently, the equilibrium confirmed agreement is weakly Pareto-efficient, since the set of agreements that can be confirmed in CP(G) coincides with the set of strategy profiles of G.

Let us now reason by contradiction. Suppose that there exists a strategy profile of G and thus a terminal history of CP(G) that leads to an agreement which strongly Pareto dominates the equilibrium confirmed agreement (with regard to the case where there is only one equilibrium confirmed agreement). Then, there is a period $\overline{t}$ of CP(G) where this terminal history diverges from the equilibrium one, thereby including, after $\overline{t}$, a different sub-branch of the game. The player active at $\overline{t}$ chooses the sub-branch leading to the Pareto dominating agreement. Consequently, the candidate inefficient equilibrium agreement is not reached: an inefficient equilibrium cannot exist.

Let us now consider the case where there is more than one equilibrium confirmed agreement. By Proposition 1, all these agreements are payoff-equivalent for at least one player. Then, none of them is strongly Pareto superior to the other one: both are weakly Pareto-efficient (see Example 4 in the previous paragraph, Figure 7 and Figure 8).

4. Confirmed Agreements in Standard Two-Player Games

In this section we apply our bargaining process CP(G) to some well-known G extensively analyzed in the experimental literature. In particular, we focus on those games where subjects in the lab often choose strategies leading to Pareto-efficient outcomes that do not coincide with the Nash equilibria of the game. We will show that in all these games G our bargaining process CP(G) gives rise to Pareto-efficient agreements that differ from the Nash equilibrium of the original games G.

First, we analyze two examples in which the original game G is a 2 × 2 simultaneous game. Then, by maintaining the assumption of two players only, we concentrate on two examples where the original game G is a two-stage dynamic game with perfect information. Notice that the fact that G is dynamic does not matter for the scope of bargaining. Indeed, in CP(G) players bargain over strategies of G. Hence, we directly represent these dynamic games through their strategic form. This shows how our bargaining process can be applied to every two-player dynamic game with finite strategy spaces.

Prisoner’s Dilemma. The original game G is a standard simultaneous-move Prisoner’s Dilemma. The sets of players’ feasible proposals CP(G) coincide with their sets of actions in the original game: S_i = S_j = {Defect, Cooperate}, henceforth {D, C}. Figure 9, with a > b > c > d, shows the simultaneous-move original game and all the possible agreements of CP(G).8

Figure 9. Prisoner’s Dilemma as original game G.

Figure 9. Prisoner’s Dilemma as original game G.

The original game G has the profile (D,D) as equilibrium in dominant actions.

Let us now find the subgame perfect equilibrium outcome of CP(G). Observe Figure 10, where CP(G) is represented with player i as first mover. Given that the original game is symmetric, CP(G) with player j as first mover is totally analogous to the one in Figure 10.

The theoretical prediction for CP(G) where G is the Prisoner’s Dilemma is the following:

Proposition 3. The subgame perfect equilibrium of CP(G) where G is the Prisoner’s Dilemma is unique, and leads, in period 3, to an equilibrium confirmed agreement where both players cooperate (C, C).

The intuition behind Proposition 3 is as follows.

Figure 10. CP(G), G being the Prisoner’s Dilemma, with player i as first mover.

Figure 10. CP(G), G being the Prisoner’s Dilemma, with player i as first mover.

Consider Figure 10 (player i is the first mover in CP(G)). After history (D, D, C), player j can confirm D in period 4, thereby getting the highest payoff a. Thus, history (D, D, C, C) is weakly dominated, and so we eliminate the subgame starting with C after (D, D, C). By backward induction, player i confirms D after history (D, D). Reasoning in the same way, player i confirms D after history (D, C), thereby getting the highest payoff a. Thus, history (D, C, C) is weakly dominated, and so we eliminate the subgame starting with C after (D, C). By backward induction, player j counter-proposes D to i’s initial proposal D. Analogously, player i confirms D after history (C, D, D, C), and player j confirms D after history (C, C, D, D, C). By backward induction, the equilibrium terminal history (C, C, C) emerges.

The same subgame perfect equilibrium is found when player j is the first mover.

Thus, in the unique subgame perfect equilibrium of CP(G) in Figure 10, player i (j) starts by proposing strategy C to player j (i), who counter-proposes strategy C. Then, player i (j) confirms her strategy C, such that the strategy profile (C,C) is the (unique) equilibrium confirmed agreement. This is reached already in period t = 3, after the first interaction among players takes place.

The equilibrium confirmed agreement of CP(G), (C,C), (D,D)Pareto-dominates , the Nash equilibrium of G. Therefore, both players commits to play G according to the agreement confirmed through CP(G).

Hawk-Dove Game. The original game G is the Hawk-Dove simultaneous-move game (see [9]). The set of players’ feasible proposals, which coincides with the set of players’ strategies in the original game G, is S_i = S_j = {Hawk, Dove}, henceforth {H, D}. Figure 11 shows the simultaneous-move original game and, also, all the possible agreements in CP(G). Parameters are such that a > b > c > d.

Figure 11. Hawk-Dove Game as original game G.

Figure 11. Hawk-Dove Game as original game G.

The original game G has two Nash equilibria in pure strategies: (H,D) and (D,H).

CP(G) is represented in Figure 12, with player i as first mover. Given that the original game G is symmetric, CP(G) with player j as first mover is totally analogous to the one in Figure 12.

Figure 12. CP(G), G being the Hawk-Dove Game, with player i as first mover.

Figure 12. CP(G), G being the Hawk-Dove Game, with player i as first mover.

The theoretical prediction for CP(G) where G is the Hawk-Dove game is the following:

Proposition 4. The subgame perfect equilibrium of CP(G) where G is the Hawk-Dove Game is unique, and leads, in period 3, to an equilibrium confirmed agreement where both players cooperate (D, D).

The statement in Proposition 4 can be obtained following the same intuitive reasoning as the one we have provided for Proposition 3 (in each subgame from period 3 onward, each active player confirms the agreement giving her the highest possible payoff, and by backward induction the equilibrium terminal history emerges). The equilibrium is the same if either player i or player j is the first mover in CP(G).

Thus, in the unique subgame perfect equilibrium of CP(G) in Figure 12, player i (j) starts by proposing strategy D to player j (i), who counter-proposes strategy D. Then, player i (j) confirms her strategy D, such that the strategy profile (D, D) is the (unique) equilibrium confirmed agreement, reached already in period t = 3, after the first interaction among players takes place.

Notice that the equilibrium confirmed agreement of CP(G) does not Pareto-dominate any of the two Nash equilibria of G. If the Nash equilibrium is (D, H), then player j prefers to play directly G rather than participating in CP(G). If the Nash equilibrium is (H, D), then player i prefers to play directly G rather than participating in CP(G). In these two cases, a commitment over playing G according to (D, D) is not possible. If instead players do not know which of the two Nash equilibria will be played, they could commit over playing G according the strategies agreed through CP(G). For instance, this happens if they attribute a probability of 50% to each of the two Nash equilibria of G, and b > 0.5(a + c).

Trust Game. The original game G is the Trust Minigame, a two-stage game with both the trustor and the trustee having only two possible actions (see [10]). Player i (the trustor) decides whether to Trust (T) or to Not trust (N) player j (the trustee). In case i trusts j, total profits are higher. In that case, j would decide whether to Grab (G) or to Share (S) the higher profits. The strategic form of the Trust Minigame is depicted in Figure 13, where x :=“x if T”, with $x=G,S$, and b_i > c_i > d, a > b_j > c_j, a + d = b_i + b_j. This figure also represents all the possible agreements of CP(G).

Figure 13. Trust Minigame as original game G.

Figure 13. Trust Minigame as original game G.

In the unique subgame perfect equilibrium of the original game G, i does not trust j, while the latter would choose to grab if i had trusted her in the first place, i.e., (N,G).

Figure 14 represents the two possible versions of CP(G): In Figure 14a the trustor (i) in the original game G is the first mover in CP(G), while in Figure 14b the trustee (j) in the original game G is the first mover in CP(G). In the latter case, j’s initial proposal in CP(G) is her intention to grab or to share the higher total profits in the case i would trust her.

Figure 14. CP(G), G being the Trust Minigame, with i (a) or j (b) as first mover.

Figure 14. CP(G), G being the Trust Minigame, with i (a) or j (b) as first mover.

Notice that, since G is a dynamic game, players bargain in CP(G) over strategies that eventually induce the same terminal history in G. However, in order for j to confirm an agreement in CP(G), a player has to re-propose the same strategy of G in two subsequent periods of CP(G) where she is active. According to this rule, (S,N,G) is not a terminal history of CP(G) in Figure 14b, even though both strategy profiles (N,S) and (N,G) induce the same terminal history in the original game G.

The theoretical prediction for CP(G) where G is the Trust Minigame is the following:

Proposition 5. The equilibrium confirmed agreement of CP(G) where G is the Trust Minigame is unique, and leads player i to trust player j and player j to share the higher profits (T,S).

The intuition behind Proposition 5 is as follows.

Independently from the identity of the first mover in CP(G), the agreement (T,G) allowing j to get the highest possible payoff a would never be confirmed in equilibrium. If such an agreement would be confirmed, j would get a, and i would receive d (the lowest possible payoff). Hence, player i would never confirm this contract. Further, this player would not counter-propose strategy T, when this strategy would allow j to confirm such a contract: in any period of CP(G) where she is active, player i does not reply with proposal T to j’s proposal $\underset{\_}{G}$. Thus, the highest reachable payoff in an agreement is b_j for player j: when player j has the possibility to get b_j by confirmation, she does it.

Therefore, in Figure 14a, where the first mover is player i, player j would confirm $\underset{\_}{S}$ both after history (N,S,T) and after history (T,G,N,S,T). In both cases, she would get b_j. Moreover, player i would confirm T after history (T,S). Consequently, the equilibrium terminal histories are (N,S,T,S), (T,G,N,S,T,S) and (T,S,T). All lead to the same equilibrium confirmed agreement (T,S).

In Figure 14b, where the first mover is player j, player j would confirm S both after the history (G,N,S,T) and after history (S,T), and she would get b_j. Consequently, the equilibrium terminal histories are (G,N,S,T,S) and (S,T,S). All lead to the same equilibrium confirmed agreement (T,S).

If both players are impatient, there is just one subgame perfect equilibrium and therefore one equilibrium terminal history in both CP(G) in Figure 14. When the first mover is player i, this history is (T,S,T); when the first mover is player j, this history is (S,T,S). Therefore, in both cases, the agreement (T,S) is confirmed in period 3.

The equilibrium confirmed agreement of CP(G) Pareto-dominates the Nash equilibrium of G. Therefore, players commit to play G according to the agreement confirmed through CP(G).

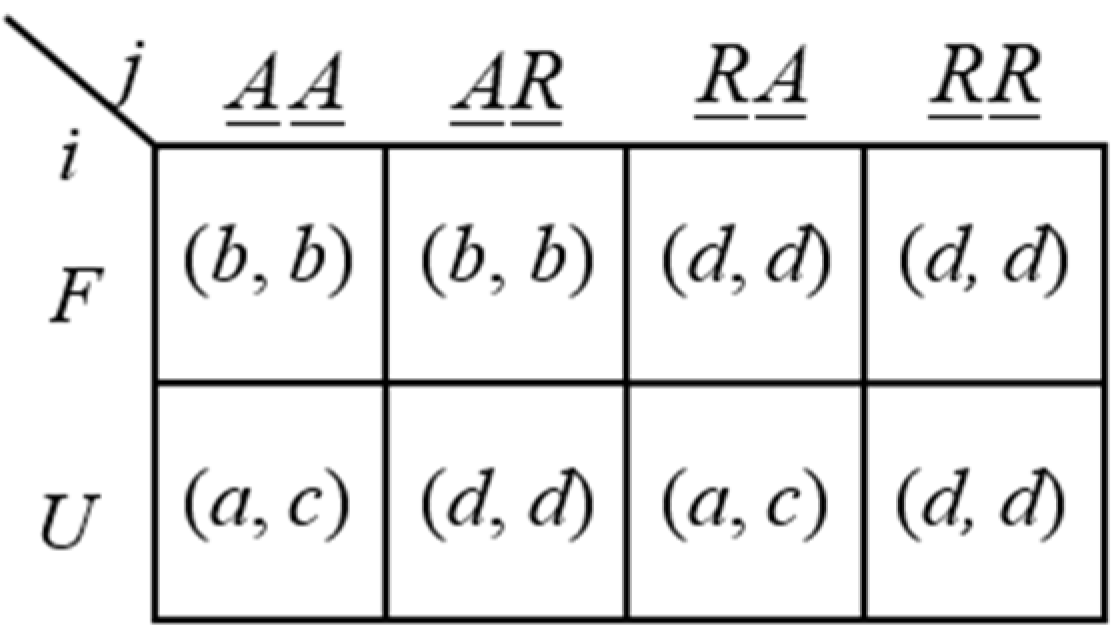
Ultimatum Game. The original game G is the Ultimatum Minigame, a two-stage game with both the proposer and the respondent having only two possible actions (see [11]). In the original game G, i (proposer) can offer a fair (F) or unfair (U) division to j (respondent); the latter, after having received i’s offer, may either accept (A) or reject (R). The set of i’s possible strategies coincides with the set of her possible actions, while the set of j’s possible strategies is S_j = {AA,AR,RA,RR}, with xy := “x if F and y if U”, with $x=A,R$ and $y=A,R$. The strategic form of the Ultimatum Minigame in Figure 15 (with a > b > c > d) also represents all the possible agreements of CP(G).9

Figure 15. Ultimatum Minigame as original game G.

Figure 15. Ultimatum Minigame as original game G.

In the unique subgame perfect equilibrium of the original game G, unfair division takes place, with j accepting both i’s offers, i.e., (U,AA).

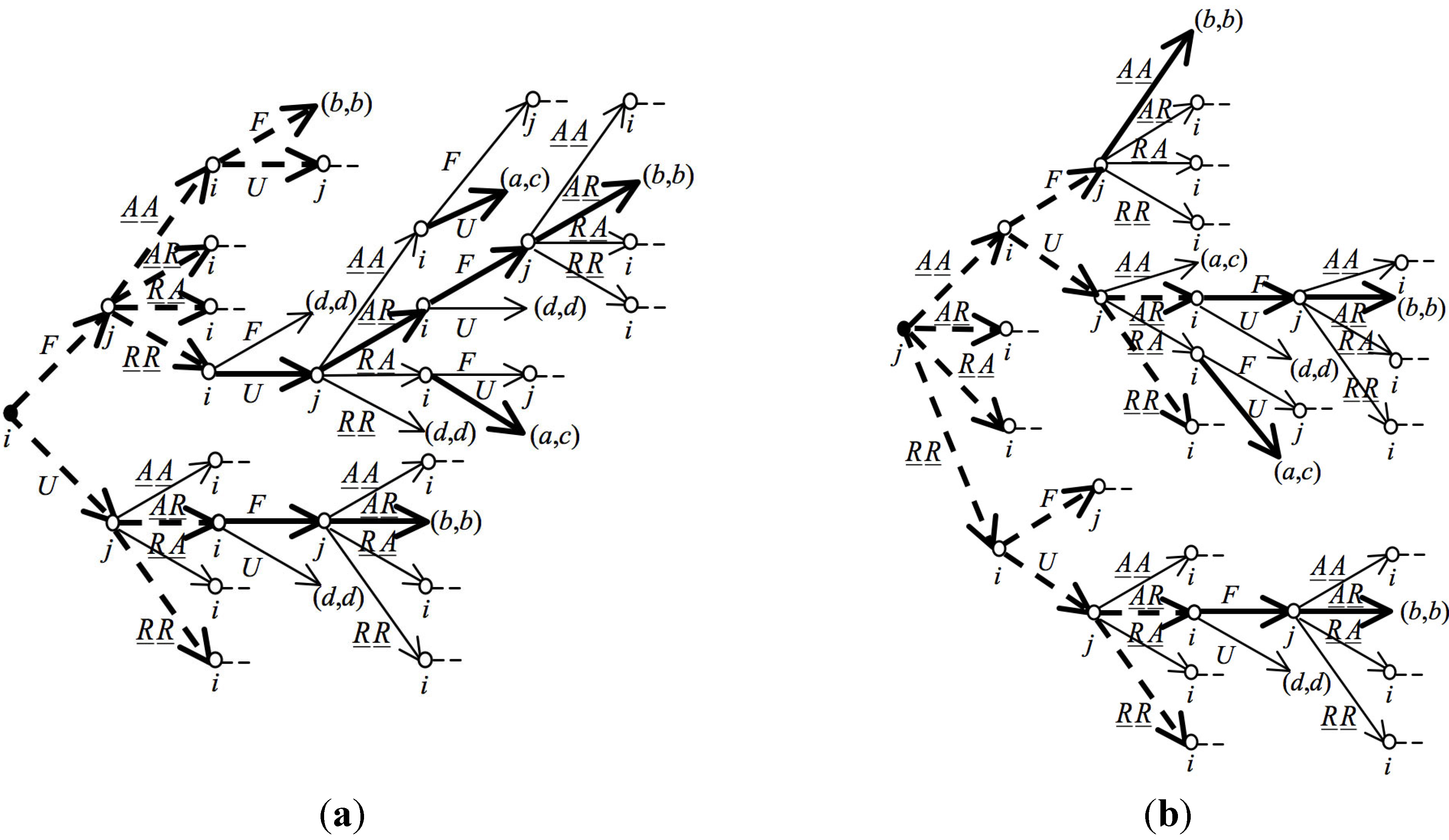
Figure 16 represents the two possible versions of CP(G): in Figure 16a the proposer (i) in the original game G is the first mover in CP(G), while in Figure 16b the respondent (j) in the original game G is the first mover in CP(G). In this latter case, j’s initial proposal in CP(G) is her intention to accept or to reject for each of the two possible strategies (fair or unfair) of player i.

Figure 16. CP(G), G being the Ultimatum Minigame, with i (a) or j (b) as first mover.

Figure 16. CP(G), G being the Ultimatum Minigame, with i (a) or j (b) as first mover.

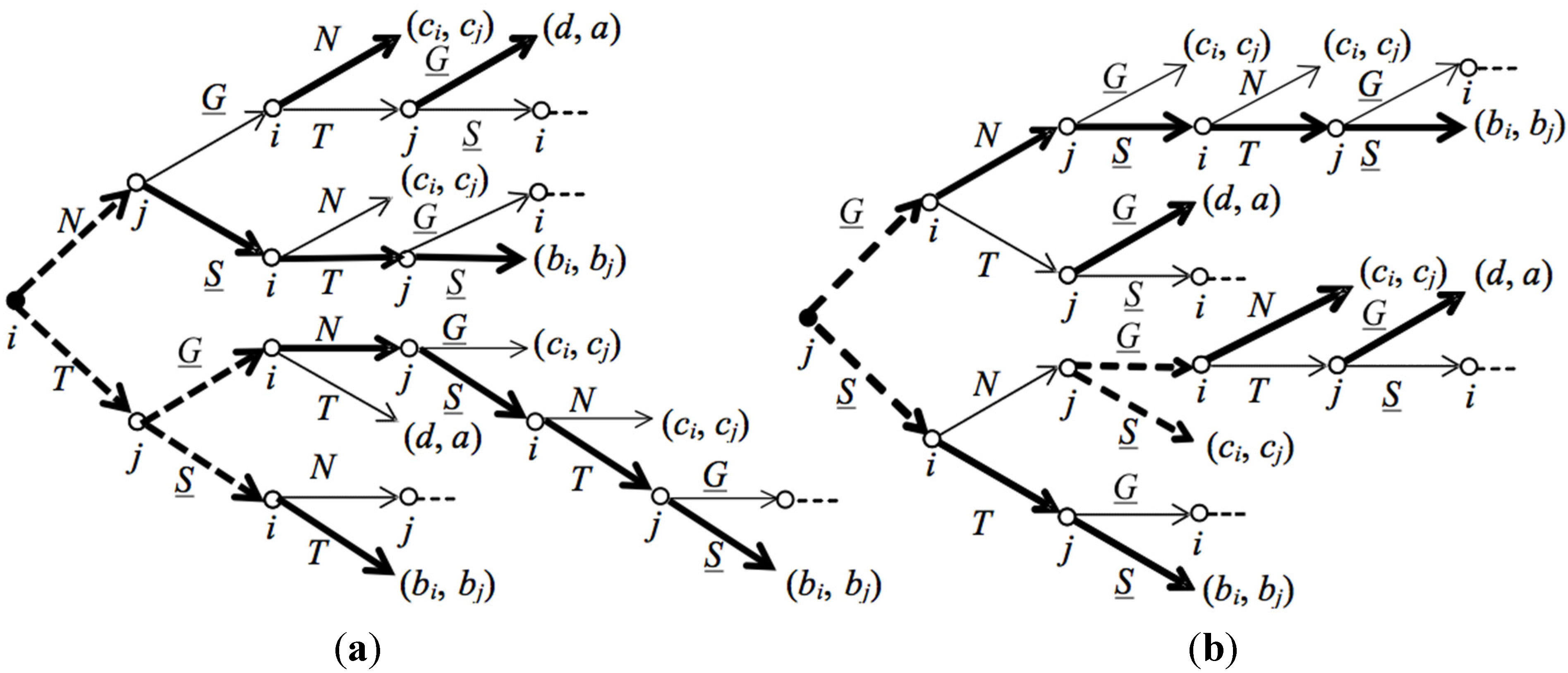
The theoretical prediction for CP(G) where G is the Ultimatum Minigame is the following:

Proposition 6. There are two payoff-equivalent equilibrium confirmed agreements of CP(G) where G is the Ultimatum Minigame, both leading to the egalitarian outcome in G.

The intuition behind Proposition 6 is as follows.

If player i is the first mover (Figure 16a), player j can obtain her highest possible payoff (which is b) by behaving as follows. If player i starts by proposing F, player j counter-proposes RR. Then, after history (F,RR,U,AR,F), she can confirm AR. By backward induction, (F,RR,U,AR,F,AR) is an equilibrium terminal history. If player i starts by proposing U, player j counter-proposes AR. Then, after history (U,AR,F), she can confirm AR. By backward induction, (U,AR,F,AR) is an equilibrium terminal history. Therefore, in any possible subgame perfect equilibrium of CP(G) in Figure 16a, player j obtains b. If both players are impatient, the equilibrium confirmed agreement is reached in period 3. This will be either (F,AR) or (F,AA).

If player j is the first mover (Figure 16b), she can obtain b by proposing AA in period 1. Then, if player i counter-proposes F, player j will confirm AA, thereby obtaining b: the equilibrium confirmed agreement is (F,AA). If player i counter-proposes U, player j will propose AR, which leads i to propose F and j to confirm AR: the equilibrium confirmed agreement is (F,AR). Therefore, in any possible equilibrium of CP(G) in Figure 16b player j obtains b. If both players are impatient, the equilibrium confirmed agreement is reached in period 3.

The two payoff-equivalent equilibrium confirmed agreements in Figure 16, (F,AR) and (F,AA), yield b to player i. However, by playing G directly, she obtains payoff a in the unique subgame perfect equilibrium of G, (U,AA). Consequently, she will not accept a commitment over playing G according to one of the two confirmed agreements in CP(G). Therefore, the two players must play G directly.

5. Relevance of Two-Player and Possible Extensions to n-Player Original Game

Like in all processes involving offer-acceptance sequences, including Rubinstein’s [5] alternating proposals and Güth et al.’s [12] ultimatum bargaining, our protocol is rather specific to two-person negotiating contexts. This corresponds to several real-world cases of offer-acceptance/rejection-counter offer bargaining sequences involving two parties.

Even when the agreement affects more than two decision-makers, the bargaining process usually takes place and is signed by two parties. In fact, it is more often the case than an exception that the terms of a bilateral agreement do not have effects on third parties. Then, it is often the case that signed formal contracts have only bilateral effects and other parallel contracts have to be signed by pairs among the remaining players. Also, in the recent Eurogroup meetings among the EU countries on the Greek crisis, sequential bargaining took place between Greece and the remaining countries in the form of pairwise sequential offers and counteroffers. In fact, following the strategic importance attributed to whether Greece should negotiate with each institution alone or with all of them as a Troika, an interesting extension of our framework to the n-player case would be to determine the coalition of players which will act as one of the two negotiating parties. This is in line with Hart and Mas-Collell’s [6] Proposer Commitment Procedure, where in each bargaining period there is a coalition of inactive players, essentially not participating in the proposal-counterproposal process in that period.

The extension of our confirmed proposal process to the case of $n>2$ players is not straightforward.

First of all, one has to admit that even attempts to extend the model of [5] to the case of more than two players have not been so particularly successful in preserving either the implementability or the theoretical properties of the model. Furthermore, recall that our process, due to the finite number of feasible agreements, suffers from multiplicity of equilibria that does not occur in the standard Rubinstein’s [5] cake division model (see [13]).

In the remainder of this section, we discuss whether and how the most well-known n-player extensions of [5] would apply to our confirmed proposal process, by producing n-player processes that are easy to implement and that eventually lead to the existence and uniqueness of an n-player equilibrium confirmed agreement.

Consider the simplest possible n-player extension of [5]: player 1 proposes an agreement. In the second period, all other n–1 players simultaneously decide whether to accept or reject player one’s proposal. If all other n–1 players accept, the game ends. If any player rejects 1’s proposal, play moves to the third period in which player two proposes an agreement, and so on. With these rules, any player can veto a proposal and only unanimous agreements can be executed. However, as pointed out by Shaked (reported by [14] and [15]), this game has many subgame perfect equilibria. Indeed, if players are sufficiently patient, any feasible agreement can be achieved in a perfect equilibrium.10 A similar extension of our confirmed proposal game CP(G) would be the following: in period 1, player one proposes her strategy of G; in period 2, all other players simultaneously counter-propose their own strategies of G; in period 3, the supergame ends if and only if player one proposes again the same strategy proposed in period 1, otherwise in period 4 player two proposes a strategy and in period 5 all other n–1 players counter-propose their own strategy. The game ends in period 5 if: player two has re-proposed in period 4 the same strategy proposed in period 2, player one re-proposes in period 5 the same strategy proposed in period 3, and all other n–2 players re-propose in period 5 the same strategy proposed in period 2. And so on and so forth. However, this process does not fully respect the logic of “proposals confirmed by all players”: unanimity is not always required to confirm an agreement. For instance, in case player one confirms in period 3, the supergame ends and an agreement—confirmed by player one only—emerges. When, in period 3, the n–1 players active in period 2 know the proposals simultaneously made by the other n–2 players in the same period, at least one of them could prefer not to confirm the proposal she made in this period. However, this possibility is not allowed.

Other interesting n-player extensions of [5] have been independently suggested by [17] and by [18] and [19]. All these procedures ask players to engage in a series of bilateral negotiations; any player that reaches a satisfactory agreement “exits” the game. A player exiting the game after a bilateral negotiation receives a contingent share of the pie by the other player: this is the price paid to represent the exiting player in future negotiations. The remaining player selects one of the other n–2 for the next bilateral negotiation. This procedure leads to a unique subgame perfect equilibrium in the n-player bargaining of [5]. A similar extension of our confirmed proposal game CP(G) would be the following: player 1 selects one of the other n–1 players so as to bargain through the supergame CP(G) over the strategy pair to eventually play in G. If an agreement, contingent on the strategies of the other n–2 players, is confirmed in this two-player CP(G), then the selected player gives the right to player one to propose specific strategy pairs as best replies in the next two-player CP(G). Player one will play this supergame with the next selected player among the n–2 remaining players. And so on and so forth. Given that after each successful bilateral negotiation the remaining player constrains herself to propose a specific meta-strategy (the one agreed in the previous bilateral negotiation), this n-player procedure could lead to a unique subgame perfect equilibrium outcome, if such an equilibrium would exist. However, the equilibrium confirmed agreement would crucially depend on which player is randomly selected to be the first mover.11

To the best of our knowledge, the n-player extension of [5] that better fits to our confirmed proposal process is the one proposed by [21]. As in the first (simplest) extension introduced above, player one proposes an agreement and the game ends if all other n–1 players accept. However, the other n–1 players decide sequentially (from 2 to n) whether to accept or reject player one’s proposal. If one of the n–1 players decides to reject, then player two becomes the proposer, with players 3, 4, …, n and 1 deciding in sequence whether to accept or reject player two’s proposal. This extension easily applies to our confirmed proposal process CP(G). Suppose that n = 3. In period 1 player one proposes $s_1^1$; in period 2 player two counter-proposes $s_2^2$ to $s_1^1$; in period 3 player 3 counter-proposes $s_3^3$ to $(s_1^1,s_2^2)$ in period 4 player one counter-proposes $s_1^4$ to $(s_2^2,s_3^3)$; in period 5 player two counter-proposes $s_2^5$ to $(s_3^3,s_1^4)$. If $s_1^4=s_1^1$ an $s_2^5=s_2^2$, then CP(G) ends with the confirmed agreement $(s_1^1,s_2^2,s_3^3)$. If $s_1^4\ne s_1^1$, it means that player one has rejected the previous path $(s_1^1,s_2^2,s_3^3)$, and decides to start a new path with $s_1^4$. The same holds if $s_1^4=s_1^1$ and $s_2^5\ne s_2^2$: player two has rejected the previous path $(s_2^2,s_3^3,s_1^1)$ and decides to start a new path with $s_2^5$.

Furthermore, notice that our weak-dominance and backward-induction solution procedure is in line with the theory of social situations of [22], which is assumed in the supergame proposed by [21]: A player can reject a suggested path by departing from the path at one of her decision nodes and suggesting a new path to be followed by later players. She rejects the suggested path if this is profitable, i.e., she gains more than $\text{ε}>0$. A path is acceptable if and only if no player can profitably reject it by suggesting another acceptable path. Asheim [21] shows that only the stationary division in [5] is acceptable for any $\text{ε}>0$. This is the unique subgame perfect equilibrium of his n-player extension of [5]. We leave the equilibrium analysis of the parallel n-player extension of CP(G) for further research.

6. Conclusions

Throughout the paper, we have defined a bargaining process over the strategies of a two-player non-cooperative original game. We have called this process “confirmed proposal process”, the outcome of the process being a confirmed agreement (a strategy profile of the original game) that commit players to play the original game accordingly.

The confirmed proposal process is a dynamic supergame that may or may not have a subgame perfect equilibrium. If the equilibrium exists, we have shown that the outcome of the bargaining process is always weakly Pareto-efficient and may not coincide with the Nash equilibrium of the original game. Furthermore, if the original game is generic, the equilibrium confirmed agreement is unique, even if the original game presents more than one Nash equilibrium.

Since players are not obliged to participate in the bargaining process, they could prefer playing the original game directly rather than bargain over its strategies. This happens when for one of the two players the payoff obtained through the bargaining process is lower than the one received in the Nash equilibrium of the original game.

In Section 4 of the paper, we have theoretically analyzed the consequences of introducing such bargaining process before playing several common two-player non-cooperative games: the Prisoner’s Dilemma, the Hawk-Dove Game, the Trust Game, and the Ultimatum Game. In each of these original games, the proposed bargaining process gives rise to Pareto-efficient agreements that are different from the Nash equilibrium of the original games.

However, only in the Prisoner’s Dilemma and in the Trust Game the two players would certainly participate in the bargaining process, thereby committing to play the original game according to the agreement confirmed in the bargaining process.

In the Hawk-Dove Game, the equilibrium confirmed agreement allows to each player an intermediate payoff between the payoffs of two Nash equilibria of the original game. Thus, players may or may not decide to bargain.

In the Ultimatum Game, the confirmed proposal process leads players agreeing on the egalitarian payoff. Therefore, the proposer in the original game should refuse entering the bargaining process: she would get a higher payoff by playing the original game directly.

In Section 5 we have stressed the relevance of the two-player confirmed proposal process in real-world contexts, and discussed possible theoretical extensions of this process to the case of n > 2 players.

We think that our study is relevant for behavioural and experimental economists. The fact that the predictions of efficient outcomes in the games analyzed here reflect what it is often detected when these games are played one-shot in the laboratory12 could be seen as a rationalist explanation of the mental process subjects rely on when facing such social dilemmas in experiments.