If
then a member maximizes his own monetary payoff by contributing zero to the public good. This familiar logic motivates the simple prediction that every member of the group will contribute zero to the public good if
.
2 A positive contribution does, however, generate a positive externality for other group members. Specifically, if
then it is socially efficient for a group member to contribute his entire endowment
E. This can motivate an alternative prediction, namely that every player contributes
E to the public good if
and contributes zero otherwise.
According to these most basic of predictions, the size of the MPCR should only influence choice around the and critical values. Whether the game is a leader-follower or follower-average game should make no difference. Neither should it matter whether the member is a leader or follower. In the remainder of this section we motivate some basic hypotheses as to why the size of MPCR and type of game may make a more substantial difference. We consider in turn the role of followers and leaders.
In order to motivate our hypotheses we shall draw on two of the leading models of social preferences. Specifically, in an
Appendix to this paper we work through in detail the consequences of inequality aversion using the model of Fehr and Schmidt [
13]. This will be complemented by discussing a result due to Falk and Fischbacher [
12] that details the consequences of sequential reciprocity. Clearly, there are other models of social preferences we could consider. Both of these models, however, are frequently used as explanations for conditional cooperation and our primary objective in this section is to demonstrate that the MPCR and game timing could reasonably be expected to influence behavior in a systematic way.
3.1. Conditional Cooperation
The existing evidence suggests that a large proportion of followers will behave in a conditionally cooperative way. Conditional cooperation comes, however, in different guises and so we introduce some terminology. We shall say that member
is a strong conditional cooperator in game
if
for all
. In other words, member
is a strong conditional cooperator if he exactly matches the average leader contribution. We say that member
is a weak conditional cooperator in game
if
but
for some
. Therefore, member
’s contribution is increasing in the average leader contribution but potentially less than the leader contribution (Fischbacher and Gächter [
6]). Finally, we say that member
is a free- rider if
for all
.
It is useful for us to capture the distinction between strong and weak cooperation and free-riding. Thus, we introduce cooperation factor, as a measure of the extent of conditional cooperation of member . If member is a strong conditional cooperator then and if she is a free-rider . More generally, the higher is then the higher the extent of conditional cooperation. It is important to clarify that we characterize members as strong or weak cooperators or free-riders taking a particular game as given. To capture this we will, where appropriate, write to acknowledge that the cooperation factor is game specific.
Let us focus first on the follower-average game and the Falk and Fischbacher [
12] theory of sequential reciprocity. Proposition 11 of Falk and Fischbacher (see their online
Appendix) shows that if the follower believes the
leaders each contributed
then she will contribute
3
where
measures member
n’s level of reciprocity. The basic intuition behind this result is that a positive leader contribution is intentional kindness and so the follower will want to reciprocate with a positive contribution of her own. Equation (2) gives some clear predictions on the extent of conditional cooperation. For instance, only weak (not strong) conditional cooperation is predicted. In evaluating the role of the MPCR we highlight that the value of
should not be game specific. If, therefore,
we get
for any game
.
4 Conversely, if
we get
for any game
. This leads to our first hypothesis.
Hypothesis 1: (a) The proportion of conditional cooperators is independent of the MPCR. (b) The cooperation factor of conditional cooperators is increasing in the MPCR.
Hypothesis 1 suggests that changes in the MPCR influence the extent of weak cooperation but do not switch a member between cooperation and free-riding. This hypothesis will now be contrasted with a prediction derived from the Fehr and Schmidt [
13] model of inequality aversion. In the
Appendix, we demonstrate that if the follower believes the
leaders each contributed
then she will contribute
if
and contribute 0 otherwise, where
measures member
n’s aversion to earning more than others. Therefore, the follower is either a strong conditional cooperator or a free-rider. Moreover, there is predicted to be some critical value of the MPCR
above which she will be a conditional cooperator. Because
can take any value between zero and one the critical value of the MPCR can also take any value between zero and one. Different members are likely to have a different critical value. This leads to our second hypothesis.
Hypothesis 2: (a) The proportion of conditional cooperators is increasing in the MPCR. (b) The cooperation factor of conditional cooperators does not depend on the MPCR.
In comparing hypotheses 1 and 2 we see quite distinct ways in which the MPCR can influence conditional cooperation. We will not be pushing this as a way to distinguish between competing models of social preferences. Hypothesis 1 could, for example, be derived from a non-linear model of inequality aversion (e.g., [
22]). The point is more to show that changes in the MPCR can plausibly have very different effects on behavior. An increase in the MPCR could increase the extent of conditional cooperation of existing cooperators and/or switch members from free-riders to conditional cooperators. Hypotheses 1 and 2 also suggest the previously distinguished critical values of
and
lose their importance. Indeed, a follower who is strongly averse to inequality,
, or has desire for reciprocation,
, is predicted to be a conditional cooperator even if the MPCR is below the level at which it is socially efficient to contribute to the public good. We shall discuss this possibility more fully in
Section 5.
Let us now briefly turn our attention to a leader-follower game. This game is distinguished from the follower-average game by less information. Specifically, in a follower-average game the follower knows the total contribution of all other group members. In a leader-follower game a follower only knows the contribution of one other group member. This means that beliefs about the contributions of others become important, and there are various assumptions one could make (see the
Appendix). For plausible assumptions it is simple to obtain direct analogs of hypotheses 1 and 2. More relevant is that a clear difference between the leader-follower and follower-average game shows up. This difference is captured in our next hypothesis.
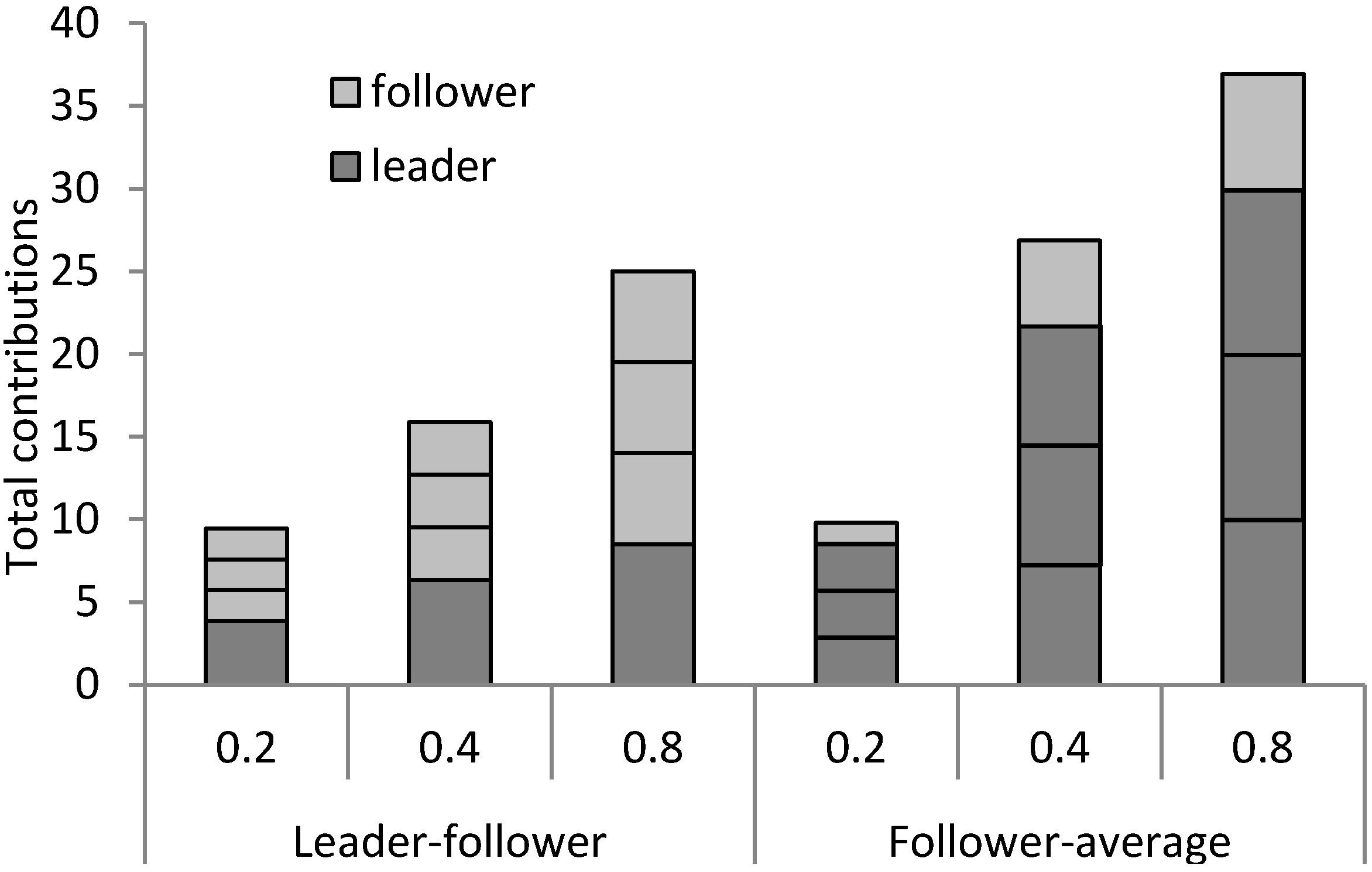
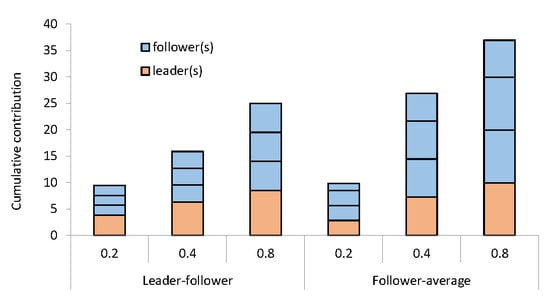
Hypothesis 3: The average cooperation factor is, ceteris paribus, lower in a leader-follower game than follower-average game.
The intuition behind Hypothesis 3 follows directly from the lack of information in a leader-follower game. In particular, in a leader-follower game, a follower knows only that the leader has been kind or that the leader will earn a relatively low payoff. The kindness and relative payoff of others is unknown. This uncertainty means a follower is less willing to contribute.
5 For instance, with the Fehr and Schmidt [
13] model we see that a follower may want to only contribute a fraction of the leader contribution,
for all
L where
. This can be compared with the strong cooperation predicted in the follower-average game.
3.2. Leader Contribution
We turn next to the contribution of a leader. Crucial here are the beliefs of a leader and, in particular, whether a leader expects conditional cooperation. In the model of Falk and Fischbacher [
12] it is assumed that the reciprocity parameters,
to
, are common knowledge. This means that a leader must be aware that followers may reciprocate. Fehr and Schmidt [
13] make the weaker assumption that each person has some prior beliefs about the inequality aversion of others. The clear suggestion, however, is again that a leader should expect the possible presence of conditional cooperators.
To see the implications of this consider, first of all, a purely ‘selfish’ leader in the leader-follower game. Suppose, the leader expects that each follower is, independently, a strong conditional cooperator with probability
and a free-rider with probability
Then the expected payoff of the leader if she chooses
can be written
Thus, the leader maximizes her payoff by contributing the full endowment
if
She has an incentive to contribute because she recognizes her contribution can have a positive effect on the contributions of others.
This picture is highly stylized in that we have ignored the possibility that weak conditional cooperation or that the leader is not selfish. The general picture, however, is clear enough and summarized in our next hypothesis.
Hypothesis 4: There exists a critical value of the MPCR above which the leader has an incentive to contribute the full endowment towards the public good.
This critical value will depend on beliefs about others, and on the type of game. We shall come back to this point shortly. Before doing that we want to highlight the critical value of need not be too extreme. For instance, in a ‘standard’ setting where and
we get an estimated critical value of .
Let us now contrast the leader-follower game with follower-average game. In a leader-follower game the leader has the chance to influence
followers while in a follower-average game she can only influence one follower. This makes a big difference to incentives. To illustrate this point we note that in a follower-average game the difference in expected payoff for a selfish player from contributing
E rather than 0 can be written
Thus, the leader gains by contributing
if
A critical value for
m still exists but at a much higher level.
Hypothesis 5: The critical value above which a leader has an incentive to contribute is higher in a follower-average game than leader-follower game.
And note that the critical value of does now take relatively extreme values. For instance, in the ‘standard’ setting where and we get an estimated critical value of .
The final issue we address is that of a ‘non-selfish’ leader. Under quite mild conditions one obtains the following prediction from either the Fehr and Schmidt [
13] or Falk and Fischbacher [
12] models.
Hypothesis 6: The critical value above which a leader has an incentive to contribute is higher for a conditional cooperator than free-rider.
In other words, conditional cooperators are ‘less willing’ to contribute as leaders. This prediction may be surprising. The intuition, however, is straightforward. To explain consider a leader-follower game. If the leader contributes 0 then all the followers will contribute 0 meaning no inequality and (in the terminology of Falk and Fischbacher [
12]) no unkindness. If the leader makes a positive contribution then inequality and intentional unkindness are almost inevitable.
6 A non-selfish leader has to, therefore, trade off gains from the public good with a lower social payoff. A selfish player focuses only on the returns from the public good.
Hypothesis 6 suggests a potential ‘mismatch’ between conditional and unconditional contribution. For example, someone who is not inequality averse may make a positive contribution as a leader but not as follower. Conversely, someone who is highly inequality averse may make a positive contribution as follower but not as leader.