Abstract
Using the political-economic history of the development of telephony during the 1870s as a backdrop, this paper studies a two-player Tullock contest that includes both research effort (R&D) and legal effort (i.e., rent-seeking effort). The two types of efforts complement each other and positively influence the payoff of the contest. We assume that legal effort affects the prize value, increasing the winner’s prospective rents, and research effort impacts the probability of winning the contest. The results of the model break new ground in showing that research effort is a function of legal effort, wherein research effort increases with rent-seeking effort. The model also shows the existence of a strategic equivalence between rent seeking and patent races.
JEL codes:
C70; D72; L12; L96
1. Introduction
This paper provides a two-player game-theoretic model of a Tullock [1] contest that includes both research effort (R&D) and legal effort (i.e., rent-seeking effort). The two dimensions of effort discussed here not only complement each other, they also influence the winning payoff of the contest. We assume that legal effort affects the prize value because it produces legal arguments in favor of extending the period and/or region where the monopoly rights are valid, therefore increasing the winner’s prospective rents. We follow the literature by assuming that the research effort impacts positively the probability of winning the contest. The results of the model break new ground in showing that research effort is a function of legal or rent-seeking effort, wherein research effort increases with rent-seeking effort. The model also indicates that strategic equivalence exists between patent races and rent seeking.
There are a number of articles in the literature examining the influence of two or more types of effort on the prize value. One of these is Epstein, Nitzan and Schwarz [2], which considers two-sided contests that involve two types of efforts. The rent and the rent-seeking efforts induced in two-sided contests are both contested. There are two types of players, the contestants and those who determine the contest’s outcome—politicians or bureaucrats—who are the leaders in the sequential setting. Contestants expend resources to win the prize, while politicians or bureaucrats, who are the potential recipients of the rent-seeking efforts, expend resources in order to increase their shares in those efforts. Next, Clark and Konrad [3] analyze contests with multi-tasking. They consider the case in which the number of prizes that can be awarded is smaller than the number of dimensions along which contestants compete with each other. Agents compete along several dimensions, providing several types of effort that generate many types of output. The principal, the contest (tournament) designer, chooses the number of tournament dimensions in which an agent needs to prevail in order to win the prize. Relatedly, Pelosse [4] investigates a noisy-ranking contest in which players also compete in several dimensions. In his model the contest designer randomly samples a number of dimensions and awards a prize to the most productive agent. If the contest is optimally designed there is a structural equivalence between noisy-ranking contests and Tullock contests. Most recently, Arbatskaya and Mialon [5] develop a dynamic multi-activity contest, in which a contestant’s long-run and short-run efforts complement each other. These authors show that rent dissipation is lower in the two-stage multi-activity contest than in the one-stage contest.
With regard to the literature on the influence of effort on the value of the prize, it is helpful to recall that firms in the Tullock [1] rent-seeking game compete for a fixed prize (or rent). Hillman and Riley [6] and Leininger [7] are among the first to study models where the value of the prize varies among contestants. Chung [8] extends Tullock’s rent-seeking model by introducing a positive externality into the contest, and by making the rent increase with the aggregate efforts of the players. Alexeev and Leitzel [9] examine a rent shrinking situation, characterized by the fact that the size of a prize to the winner falls as the expenditures of competing firms increase. Our approach is closer to Chowdhury and Sheremata [10]. They analyze a model wherein the payoff to a player is a linear function of prizes, own effort, and the effort of the rival.
As per the existence of the strategic equivalence between patent races and rent seeking, this result is reached given that the unique Nash equilibrium of the rent-seeking contest (game) is also the unique Nash equilibrium of the patent-race game developed herein. Thus, this study supports and builds upon prior work by Baye and Hoppe [11].
The political-economic history of the development of telephony during the 1870s provides a nice example for displaying the two-dimensionality of effort that is the centerpiece of our model. Thus, a brief recounting of the history of telephony appears in the next section. It is followed in Section 3 by the presentation and discussion of our game-theoretic model. Lastly, Section 4 offers concluding comments.
2. A Brief History of Telephony
As Lemley [12] explains, “simultaneous invention” occurs when two or more individuals (or teams), each working independently of the other(s), achieve the same or similar innovation at roughly the same point in time. The political-economic history of the development of telephony followed a similar path. Although the history of the telephone began in 1558, it was in 1865 that it becomes most intriguing. It was then that Amos Dolbear conceived of the idea of a telegraph that used permanent magnets instead of batteries [13]. In 1867, the competition to produce a working telephone was joined by famous inventor Elisha Gray, who conceived the idea of a harmonic telegraph, while in 1870 Alexander Graham Bell entered the contest with his idea of creating a telegraph to communicate messages simultaneously over a single circuit [13,14]. During the period 1865–1870, a “patent race” had developed, wherein inventors were making large gains in the development of the telephone, and patent applications were being filed every time some progress was made in the race [12].
In 1874, Gray filed his first patent application for a series of transmitters that tuned to different pitches, and he demonstrated his instruments to the Western Union Telegraph Company [13]. That same year Bell explained his idea of a harmonic-multiple telegraph to Gardiner Greene Hubbard, a lawyer, and Thomas Sandars, both of whom formed an agreement to fund Bell’s research, with the three dividing equally any profits from Bell’s inventions [13,15]. (Funding from Hubbard and Sandars provided to Bell assistance from a student, the now-famous Thomas Watson, who contributed electrical knowledge, as well as a small workshop [13]). In late 1874, Bell filed a patent for his harmonic-multiple telegraph, but he was informed by the patent office that Gray had filed an interfering patent, so Bell returned to his work [13]. In early 1865, Bell obtained a patent for a harmonic-multiple telegraph that used an electro-magnet, rather than the permanent magnet employed in Dolbear’s experiments [13,15]. This patent application failed to mention anything regarding the transmission of electrical speech, and his invention had theretofore failed to capture articulate words [13].
It was not until early 1876 that Bell filed a patent on a telephone. Although Bell’s lawyers asked patent office officials for special, expeditious treatment of Bell’s application, those same officials mandated a competition between Bell and Gray, who had filed a caveat with the patent office for an electric speaking telephone [13]. Both Bell and Gray were informed in February of that year that there would be a 90-day period during which Bell’s patent would be suspended and Gray would have an opportunity to file another application. However, Bell’s attorneys argued in response that Bell’s patent had been filed earlier on the same day (in 1876) that Gray had filed the caveat, an argument that persuaded patent officials to immediately lift the suspension on Bell’s patent [13].
It was at this point that Bell’s lawyers took the liberty of informing Gray of the patent office’s reversal. Gray, however, did not understand the circumstances as they were explained to him by Bell’s attorneys, and he remained under the impression that he still had 90 days to file his own patent [13]. To Gray’s surprise, Bell was awarded a patent in March of 1876 that was nearly identical to Gray’s caveat filing earlier that same year, leading to rampant speculation about how Bell’s attorneys had manipulated the patent-filing process. Support for such speculation came in May of 1876, when Bell’s invention could produce only inaudible sounds [13].
Meanwhile, Dolbear was working to improve his permanent magnet telephone, which, in the fall of 1876, was fit for a patent application. Before applying for a patent, Dolbear took his device to a machine shop to have the rods re-magnetized [13]. Unfortunately for Dolbear, this was the same shop that was set up for Bell’s experiments, and Bell’s attorneys, upon learning of Dolbear’s intentions, informed Dolbear’s benefactor that Bell had already patented a permanent magnet telephone. Receiving this news, Dolbear abandoned the effort to patent his invention [13,16]. Bell would, in January of 1877, for the first time file a patent application for a permanent magnetic telephone. This application giving Bell a legal monopoly in telephony was approved in only four days, fueling further speculation about rent seeking activity with regard to Bell’s access to officials in the patent office [13].
3. The Game-Theoretic Model
In the following model we analyze the role of two different effort levels, research effort and legal effort, in two equivalent games, a rent-seeking contest and a patent-race game. Bell’s efforts to win the patent race in telephony and curb current and future competition through litigation can be rationalized by our model. In order to keep the model relatively simple, it is assumed that Bell and his company, Bell Telephone Company, have just one competitor at a time, let us say, Western Union Telegraph Company. (Given the brief political-economic history of telephony presented in the previous section of this study, these were the two companies that were vying for the eventual legal monopoly in telephony). Let xB, xW denote the research effort levels of Bell Telephone and Western Union, respectively; let v(LB, LW) represent the value of the contested prize, where LB, LW are the legal efforts of Bell Telephone and Western Union, respectively. Legal effort in the current context includes all judicial and rent-seeking efforts necessary in order to register a patent and, thus, to guarantee a legal monopoly and its concomitant rents. (The judicial and rent-seeking efforts mentioned here include litigation and court corruption (e.g., judges’ participation in future profits of the company)).
The probability of player i winning the contest (game) is given by pi (xB, xW). Player i’s expected payoff in the rent-seeking contest (game) is,
where P is the unitary cost of legal effort. Notice that (1) is a generalization of the rent-seeking contest (game) because it stipulates that the value of the contested prize is given by v, a function of a second set of variables separate from the research effort. Dixit [17] corresponds to the special case where v is constant and pi is a symmetric function of players’ efforts. Baye, Kovenock and De Vries [18] is the case where v is constant and pi is discontinuous). In the original Tullock [1] model, two players bid for a political favor given by v, and xi denotes the bids of agents. In the present model, the agents’ bids are captured by the players’ legal effort, Li and they affect the actual size of the political favor v.
πi (xB, xW, LB, LW) = v(LB, LW) pi (xB, xW) − xi − PLi, i = B,W
As shown above, spillovers come from litigation (i.e., the legal effort of both sides), and they affect positively the value of the prize, given that we assume they have an effect on trial outcomes. (This is in line with Chowdhury and Sheremata [10], wherein the payoff of a player is a linear function of prizes, own effort, and the effort of the rival. Baye, Kovenock and De Vries [19] examine a non-cooperative game where parties in the dispute rationally choose whether to settle out of court or litigate. In the absence of a pre-trial settlement, the parties purchase legal services in order to influence the observable merit of their respective sides of (and, thus, their probabilities of winning) the litigation). The legal efforts increase the size of the prize because they produce successful legal arguments in favor of extending the period and/or area of the monopoly rights, therefore increasing the winner’s prospective rents.
We assume a concave prize function v, such as that given by,
where,
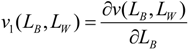
v1(LB, LW) > 0, v2(LB, LW) > 0; v11(LB, LW) < 0, v22(LB, LW) < 0, v12(LB, LW) ≥ 0
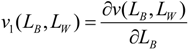
We adopt the Tullock [1] probability function of winning the contest (see also [20]), which is given by,
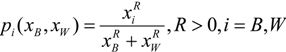 where the power R can assume any positive value; if 0 < R< 1 we have decreasing returns, while R > 1 represents increasing returns to aggressive bidding [21,22,23]. Farmer and Pecorino [24] use as the probability function of winning the contest Katz’s [25] specification of the probability the plaintiff prevails at trial, such that in their model the probability of victory is a function of the legal expenditures by the plaintiff and defendant. It is important to stress that in our model legal effort and R&D effort complement each other in the winning payoff function v(LB, LW) pi (xB, xW).
where the power R can assume any positive value; if 0 < R< 1 we have decreasing returns, while R > 1 represents increasing returns to aggressive bidding [21,22,23]. Farmer and Pecorino [24] use as the probability function of winning the contest Katz’s [25] specification of the probability the plaintiff prevails at trial, such that in their model the probability of victory is a function of the legal expenditures by the plaintiff and defendant. It is important to stress that in our model legal effort and R&D effort complement each other in the winning payoff function v(LB, LW) pi (xB, xW).
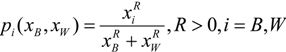
Introducing the Tullock [1] game’s probability function (3) into our rent-seeking contest (game) yields,
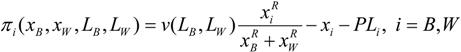 Solving the model for the Bell Telephone Company, we have as first order conditions,
Solving the model for the Bell Telephone Company, we have as first order conditions,
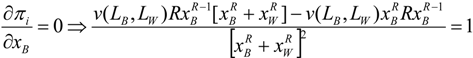 and,
and,
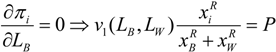 Given that function v is concave, the second order conditions are fulfilled assuming R < 1 (see Appendix 1). (See [26] for a complete characterization of the pure strategy equilibria).
Given that function v is concave, the second order conditions are fulfilled assuming R < 1 (see Appendix 1). (See [26] for a complete characterization of the pure strategy equilibria).
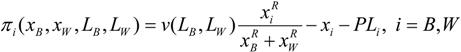
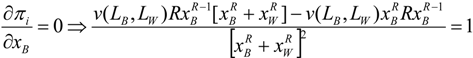
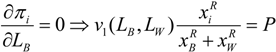
In order to obtain crisp and explicit solutions to illustrate the workings of the model, we assume that function v is given by,
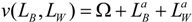 where 0 < a< 1, and where Ω is the constant part of the winning prize, which can be considered equal to zero without loss of generality. In addition, we assume a symmetric equilibrium, where xB = xW = x*; LB = LW = L*.
where 0 < a< 1, and where Ω is the constant part of the winning prize, which can be considered equal to zero without loss of generality. In addition, we assume a symmetric equilibrium, where xB = xW = x*; LB = LW = L*.
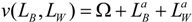
The unique symmetric Nash equilibrium of the above rent-seeking contest (game) is given by,
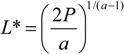 and,
and,
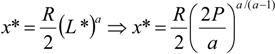
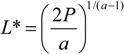
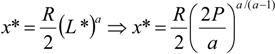
The main results of the model are given by the comparative statics of this unique, symmetric Nash equilibrium. First, note that research effort grows with legal effort, (dx*/dL*) > 0. This is an appealing result given that it states that Bell Telephone Company and its competitor, Western Union, undertake more research the more legal effort they put into winning the patent race. The model, therefore, suggests that legal effort ultimately drives research effort.
Also, from the comparative statics analysis of the Nash equilibrium it is easy to show that an increase in judicial costs P reduce legal and research efforts, (dL*/dP) < 0, and (dx*/dP) < 0. An increase in the power R does not change the equilibrium legal effort, yet it positively affects research effort, (dL*/dR) = 0, and (dx*/dR) > 0. Lastly, but importantly, the legal effort elasticity of the prize value, given by parameter a, has a negative effect on research and legal efforts, (dL*/da) < 0, and (dx*/da) < 0 (i.e., if a percentage increase in legal effort leads to a percentage increase in the value of the contested prize, then equilibrium research and legal efforts will decrease). Parameter a gives an approximation of the prize elasticity of patent (or research) effort if,
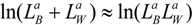
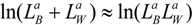
One may inquire whether these appealing qualitative results come from the arbitrary choice of Equation (7) and whether they would persist if other specifications were chosen. Note that the function v in Equation (7) is a concave function that is separable in its arguments, LB, LW. Appendix 2 shows that these qualitative results also hold true for a concave function v that is a non-separable function in its arguments, LB, LW.
In what follows we use the seminal results obtained by Baye and Hoppe [11] regarding strategic equivalence of rent-seeking, innovation, and patent-race games to show that the above unique Nash equilibrium is also the result of a patent-race game. In a patent-race game (e.g., [27]) firm i’s payoff is given by,
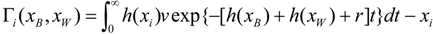 where r is the interest rate, v is the value of the patent and h(xi) is the hazard rate [28] of firm i, which captures the conditional probability of firm i making a discovery between time t and time t + dt, given that no innovation has occurred at or before time t. Assuming a hazard rate
where r is the interest rate, v is the value of the patent and h(xi) is the hazard rate [28] of firm i, which captures the conditional probability of firm i making a discovery between time t and time t + dt, given that no innovation has occurred at or before time t. Assuming a hazard rate 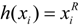 , with 0 < R< 1, and (1) that the value of the patent v is affected by legal efforts v(LB, LW), and (2) that firms pay their respective legal costs, the patent race in (11) can be expressed as,
, with 0 < R< 1, and (1) that the value of the patent v is affected by legal efforts v(LB, LW), and (2) that firms pay their respective legal costs, the patent race in (11) can be expressed as,
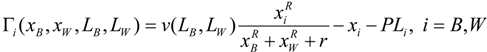
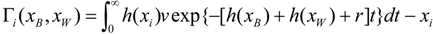
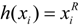 , with 0 < R< 1, and (1) that the value of the patent v is affected by legal efforts v(LB, LW), and (2) that firms pay their respective legal costs, the patent race in (11) can be expressed as,
, with 0 < R< 1, and (1) that the value of the patent v is affected by legal efforts v(LB, LW), and (2) that firms pay their respective legal costs, the patent race in (11) can be expressed as,
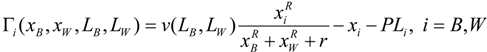
Appendix 3 shows that solving this model introducing (7) into (12) yields that r must be equal to zero in the symmetric equilibrium, r = 0. When r = 0 the solution of the patent-race game is the same as the solution of the rent-seeking contest. This result is robust to any specification of the value of the prize depending on the legal efforts (i.e., the function v can be either separable or non-separable in its arguments, LB, LW, as long as it is concave).
Note that in the limit when the interest rate goes to zero we have,
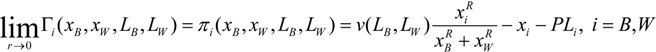
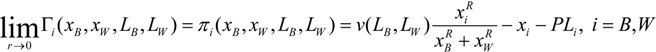
In Equation (13) there is a strategic equivalence with our rent-seeking contest and the patent-race game. It is important to stress that this result holds true only in the case of a zero interest rate—that is, when firms have no time preference in the patent-race game. The consequence of the strategic equivalence is that the unique Nash equilibrium of the rent-seeking contest given by Equations (8) and (9) is also the unique Nash equilibrium of the patent-race game.
4. Concluding Remarks
This paper studies a Tullock [1] contest game with two players and two types of effort, research effort (R&D) and legal effort (i.e., rent-seeking effort). The two types of efforts complement each other and positively influence the payoff of the contest, which in our study relates to the historical development of telephony. We assume that legal effort increases the winner’s prospective rents given that they produce successful legal arguments in favor or extending the period and/or area where the monopoly rights are to be enforced. Research effort impacts positively the probability of winning the contest. The main result of the model is that optimal research effort is a function of optimal legal effort, wherein research effort increases with rent-seeking effort. Lastly, we also show the strategic equivalence between patent races and rent seeking.
Appendix 1: The Second Order Conditions
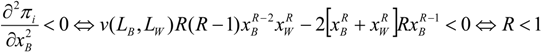
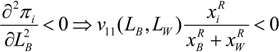
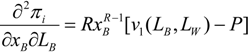
Assuming a symmetric equilibrium, where xB = xW = x*; LB = LW = L*, from Equation (6) in the text we have, v1(LB, LW) = v2(LB, LW) = 2P then 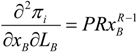 , therefore the condition
, therefore the condition 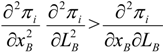 is always satisfied if:
is always satisfied if:
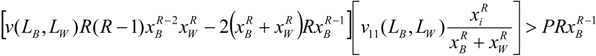
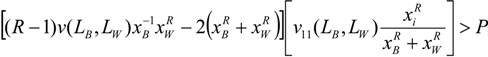
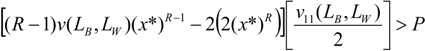
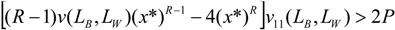
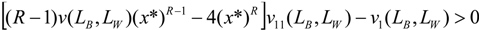
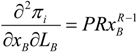 , therefore the condition
, therefore the condition 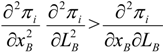 is always satisfied if:
is always satisfied if:
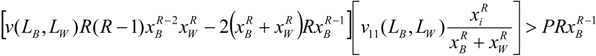
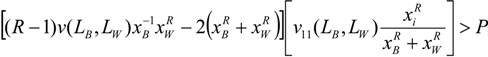
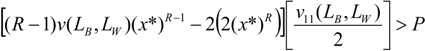
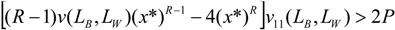
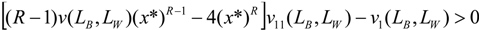
Appendix 2: Equilibrium with a Non-Separable Function v
Assume a non-separable function v as:
v(LB, LW) = (LBLW)a, where 0 < a< 1/2
In the symmetric equilibrium, where xB = xW = x*; LB = LW = L*, the unique symmetric Nash equilibrium is given by,
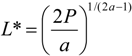 and,
and,
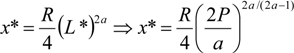
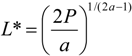
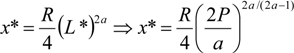
It is easy to see that for 0 < a < 1/2, the qualitative results hold true: (dL*/dP) < 0, and (dx*/dP) < 0; (dL*/dR) = 0, and (dx*/dR) > 0; (dL*/da) < 0, and (dx*/da) < 0.
The second order conditions are fulfilled, as long as:
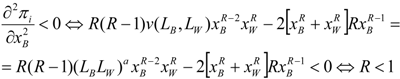
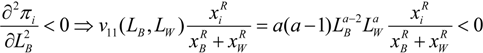
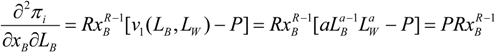
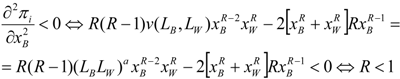
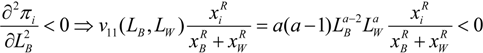
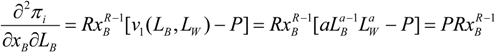
And, the condition 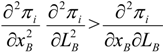 becomes
becomes
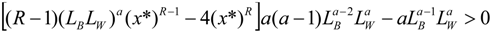
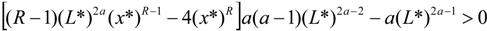
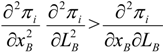 becomes
becomes
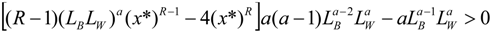
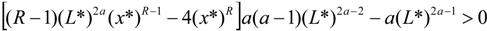
Appendix 3: The Solution to the Patent-Race Game
Assuming a symmetric equilibrium: xB = xW = x*; LB = LW = L*:
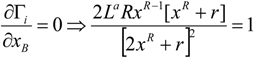 and,
and,
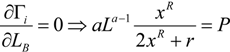
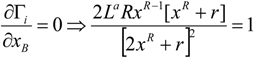
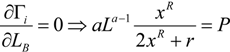
As in Appendix 1, v1(LB, LW) = 2P, which implies aLa−1 = 2P. Introducing this into (A18) yields that r must be equal to zero in the symmetric equilibrium, r = 0. When r = 0 the solution of the patent-race game is the same as the solution of the rent-seeking contest. Note that this result is robust for other specification forms, given that it holds true for the non-separable function v, as in (A9) in Appendix 2. Additionally, r must also be equal to zero in the symmetric equilibrium, r = 0. When r = 0 the solution of the patent-race game is the same as the solution of the rent-seeking contest.
References
- Tullock, G. Efficient Rent-Seeking. In Toward a Theory of the Rent-Seeking Society; Buchanan, J.M., Tollison, R.D., Tullock, G., Eds.; Texas A&M University Press: College Station, TX, USA, 1980; pp. 97–112. [Google Scholar]
- Epstein, G.S.; Nitzan, S.; Schwarz, M.E. Efforts in two-sided contests. Public Choice 2008, 136, 283–291. [Google Scholar] [CrossRef]
- Clark, D.J.; Konrad, K.A. Contests with multi-tasking. Scand. J. Economics 2007, 109, 303–319. [Google Scholar] [CrossRef]
- Pelosse, Y. Equivalence of optimal noisy-ranking contests and Tullock contests. J. Math. Econ. 2011, 47, 740–748. [Google Scholar] [CrossRef]
- Arbatskaya, M.; Mialon, H.M. Dynamic multi-activity contests. Scand. J. Econ. 2012, 114, 520–538. [Google Scholar] [CrossRef]
- Hillman, A.L.; Riley, J.G. Politically contestable rents and transfers. Economics Politics 1989, 1, 17–39. [Google Scholar] [CrossRef]
- Leininger, W. More efficient rent-seeking—A Münchhausen solution. Public Choice 1993, 75, 43–62. [Google Scholar] [CrossRef]
- Chung, T.Y. Rent-seeking contest when the prize increases with aggregate efforts. Public Choice 1996, 87, 55–66. [Google Scholar] [CrossRef]
- Alexeev, M.; Leitzel, J. Rent-shrinking. South. Econ. J. 1996, 62, 620–626. [Google Scholar] [CrossRef]
- Choudhury, S.M.; Sheremeta, R.M. “A generalized Tullock contest”. Public Choice 2011, 147, 413–420. [Google Scholar] [CrossRef]
- Baye, M.R.; Hoppe, H.C. The strategic equivalence of rent-seeking, innovation, and patent-race games. Games Econ. Behav. 2003, 44, 217–226. [Google Scholar] [CrossRef]
- Lemley, M.A. The myth of the sole inventor. Mich. Law Rev. 2012, 110, 709–760. [Google Scholar]
- Dolbear, I.S. Amos Emerson Dolbear: A Biography; Dolbear: New York, NY, USA, 1963. [Google Scholar]
- Gray, E. Experimental Researches in Electro-Harmonic Telegraphy and Telephony; Appleton: Appleton, MN, USA, 1878; pp. 1867–1878. [Google Scholar]
- Watson, T.A. How Bell invented the telephone. Proc. Am. Inst. Electr. Eng. 1915, 34, 1503–1511. [Google Scholar] [CrossRef]
- Warner, W.E. Telephone etiquette. Ohio Wesley. Mag. 1994, 72, 8–12. [Google Scholar]
- Dixit, A. Strategic behavior in contests. Am. Econ. Rev. 1987, 77, 891–898. [Google Scholar]
- Baye, M.R.; Kovenock, D.; De Vries, C.G. The all-pay auction with complete information. Econ. Theory 1996, 8, 291–305. [Google Scholar] [CrossRef]
- Baye, M.R.; Kovenock, D.; De Vries, C.G. Comparative analysis of litigation systems: An auction-theoretic approach. Econ. J. 2005, 115, 583–601. [Google Scholar] [CrossRef]
- Skaperdas, S. Contest success functions. Economic Theory 1996, 7, 283–290. [Google Scholar] [CrossRef]
- Applebaum, E.; Katz, E. Transfer seeing and avoidance: On the full social costs of rent-seeking. Public Choice 1986, 48, 175–181. [Google Scholar]
- Millner, E.L.; Pratt, M.D. Risk aversion and rent-seeking: An extension and some experimental evidence. Public Choice 1989, 69, 81–92. [Google Scholar] [CrossRef]
- Baye, M.R.; Kovenock, D.; De Vries, C.G. The solution to the Tullock rent-seeking game when R>2: Mixed-strategy equilibria and mean dissipation rates. Public Choice 1994, 81, 363–380. [Google Scholar] [CrossRef]
- Farmer, A.; Pecorino, P. Legal expenditure as a rent-seeking game. Public Choice 1999, 100, 271–288. [Google Scholar] [CrossRef]
- Katz, A. Judicial decision making and litigation expenditure. Int. Rev. Law Economics 1998, 8, 127–143. [Google Scholar]
- Perez-Castrillo, J.D.; Verdier, T. A General analysis of rent-seeking games. Public Choice 1992, 73, 335–350. [Google Scholar]
- Loury, G.C. Market structure and innovation. Q. J. Economics 1979, 93, 395–410. [Google Scholar]
- Kiefer, N.M. Economic duration data and hazard functions. J. Econ. Lit. 1988, 26, 646–679. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
