Examining Monotonicity and Saliency Using Level-k Reasoning in a Voting Game

Abstract

This paper presents an experiment that evaluates the effect of financial incentives and complexity in political science voting experiments. To evaluate the effect of complexity we adopt a level-k reasoning model concept. This model by Nagel [1] postulates that players might be of different types, each corresponding to the level of reasoning in which they engage. Furthermore, to postulate the effect of financial incentives on subjects’ choice, we used the Quantal Response Equilibrium (QRE) concept. In a QRE, players’ decisions are noisy, with the probability of playing a given strategy increasing in its expected payoff. Hence, the choice probability is a function of the magnitude of the financial incentives. Our results show that low complexity promotes the highest degree of level-k strategic reasoning in every payment treatment. Standard financial incentives are enough to induce equilibrium behavior, and the marginal effect of extra incentives on equilibrium behavior seems to be negligible. High complexity, instead, decreases the rate of convergence to equilibrium play. With a sufficiently high complexity, increasing payoff amounts does promote more strategic behavior in a significant manner. Our results show with complex voting games, higher financial incentives are required for the subjects to exert the effort needed to complete the task.

1. Introduction

Financial incentives are used in political science election and committee voting experiments to control or induce individual preferences posited by the theory that is being tested. Controlling preferences in models and experiments is a hallmark in the advancement of political science methodology since it allows researchers to focus on the key aspect of politics; institutions. Financial incentives allow us to examine how changes in institutional features impact individual decision making and subsequent institutional outcomes by assuming subjects, like the decision makers assumed in the model being tested, maximize expected utility. This assumption allow researchers to test the validity of their theoretical model by populating it with “real” decision makers to determine if the observed behavior confirms to the behavior predicted by the model or the equilibrium outcome of the model. The argument that financial incentives can effectively induce subjects to behave maximally for theory evaluation and validity is referred to as the labor theory of cognition or Induced Value Theory (IVT) [2,3,4].

In political science voting experiments financial incentives let us posit that subjects care about or “maximize alternatives they are voting on such that their payment in the experiment is a function of the choices made in the experiment. If subject preferences are controlled for then it is possible to vary how choices translate into payments and measure how their behavior responds to these changes. For example, a researcher may have a theory about how different legislative rules affect how members vote and the policies chosen. To evaluate the theory, the researcher would like to be able to compare how subjects, acting like legislators, choose under the different rules. By keeping the relationship between voting outcomes and payments constant across different institutions, the researcher can then compare the institutions. These types of causal inferences are difficult using non-experimental data because of the difficulties in making cross-country and cross-time comparisons given the co-variation in other relevant variables. Controlling preferences within an institutional framework allow researchers to disentangle specific causal effects.

Financial incentives are also used because they can provide the results with greater external validity. As noted in [5], external validity has to do with whether empirical results hold over variations in persons, settings, treatment variables, and measurement variables.1 The important concern is if results from one dataset (either experimental or observational) generalize to another (either experimental or observational). To the extent that financial incentives make the choices facing the subjects as salient as they are in other settings, particularly observational ones, then financial incentives increase external validity. Subjects in experiments may, because of the environment in which the choices take place, have different motivations that can complicate the ability to generalize to other settings. Financial incentives can reduce those conflicting motivations, focusing subjects on the cognitive tasks as an individual might be focused in settings outside of the experiment as in legislatures or other political contexts.

Although it is generally agreed that financial incentives implemented properly in an experiment can control preferences and increase validity, there is no general agreement on how financial incentives impact subjects’ task performance or the cognitive task subjects engage in.2 The issue is whether increasing financial incentives increase the cognitive ability such that subject behavior is more likely to converge toward expected equilibrium outcomes, i.e., does increasing financial incentives make for better subjects since they will be more focused on task performance, or do financial incentives have a diminutive effect such that increasing incentives only trivially affects performance? This issue is important because there is general consensus that financial incentives are needed but what is not known is how much is enough to induce behavior dictated by IVT. This theory assumes that if an experimenter follows its precepts then financial incentives motivate subjects to devote all of their cognitive attention to task performance; however experiments have shown that subjects often deviate from the experimental task, and the concern is whether these deviations are a result of failure of the experimenter to fulfil the conditions of IVT [8]. In this article we examine the tenants of IVT by reporting on experiments that measure the interaction of financial incentives and cognitive ability by varying simple and complex cognitive tasks.

Simple voting experiments allow us to vary complexity by varying the information subjects have about alternatives and determining whether subjects maximize utility which can be observed by documenting either sincere (naive) or strategic behavior. The difference between the two is that strategic behavior entails more (complex) cognitive ability since to maximize utility subjects must vote against their sincere (and higher) preference to prevent getting a lower utility. This computation proves to be difficult for subjects in experiments that examine three alternatives (or candidates) where little strategic behavior is found due to the seemingly complex nature of the task [9]. To reduce some of the computational aspects associated with being strategic and to separate complex from simple cognitive tasks we examine strategic behavior using only two alternatives [10,11]. This simplicity allows us to use the level-k reasoning model which enables the separation of different subject types based on different levels of complexity or the level of reasoning in which they engage [1]. Moreover, to examine the effects of financial incentives we use the Quantal Response Equilibrium (QRE) concept [12,13]. A QRE allows us to isolate the effects of financial incentives since it assumes that the probability of playing a given strategy is increasing in its expected payoff making the choice probability a function of the magnitude of the financial incentives. Our results provide evidence that under certain conditions when confronted with complexity increasing financial incentives evoked more strategic behavior resulting in increased convergence to the equilibrium outcome.

2. Induced Value Theory

Induced Value Theory presumes that incentives that are salient will cause subjects to devote cognitive labor and effort in making choices in the experiment in the same way they would outside of the experiment. How subjects make these choices may not necessarily be rational as defined by satisfying a game theoretic prediction in which the actors selfishly maximize their payoffs. Subjects may choose to be altruistic, display motives that illustrate fairness or reciprocity, make systematic cognitive errors, or be influenced by racial, ethnic, or gender stereotypes in how the experiment is framed or in response to priming. When subjects make these types of choices in the face of salient financial consequences, then the proof that these other motivations are significant for the subjects is more robust than when subjects face no financial consequences to their decisions. Similarly, if subjects are more likely to choose according to the game theoretic prediction as saliency or financial incentives increase, then how much subjects receive in the form of financial incentives is an important factor to consider in evaluating the results of the research.

The four conditions of Induced Value Theory (IVT):

• The reward medium should be monotonic such that subjects prefer more to less.
• The reward medium should be salient such that subjects care about getting more.
• The reward payoff to individual subjects should be private.
• The subject's behavior should be “dominant” such that only the reward medium matters.

Condition I establishes that a subject will make choices that maximize her monetary reward and she will always prefers more of the reward medium. Hence, if the reward medium is money then subjects will always prefer more money to less. Condition II establishes that the rewards are a by produce of a subject’s labor or the choices that are made during the experiment. This is usually referred to as performance-based incentives since subjects earn rewards in the experiment based on the decision that they make. For example, if a subject is participating in an experiment that has ten rounds, then the subjects will be paid an amount ten times based on the ten decisions that a subject makes in the ten rounds. The subjects total earnings will be the accumulated amount earned over the experiment’s ten rounds. This method of payment is as opposed to a flat sum incentive structure where subjects are paid a lump sum amount to participate in the experiment.

2.1. Conditions III and IV Not a Concern

Condition III establishes that the choices made in the experiment are based solely on the reward medium and not some other factors such as the rewards earned by other subjects, i.e., a subject is not concerned about the utilities of other subjects. Condition IV establishes that interpersonal utility considerations will be minimized. That is, subjects are unaware of what other subjects are being awarded which in effect guarantees dominance. Conditions III and IV together imply that if a subject is unaware of what other subjects are earning in the experiment then they will only be focused on their performance. Why are these two conditions not a concern? Because the committee and election experiments we are concerned with protect anonymity of actions and identities by conducting experiments over computer terminals referred to as laboratory experiments. These experiments use computers so they it is possible to control the information that subjects have access to and since computer screens are displayed such that subjects cannot see each other screens subjects do not know what actions other subjects have selected.

In the typical voting experiments with repeated elections subjects often know the distribution of payments since election payoffs are announced after each round of play. Consequently, subjects do know that some subjects are earning more, less or the same payoffs as themselves. However, conditions III and IV can be satisfied if subject identities in the experiment are anonymous and if this anonymity is protected while they are being paid. Under these conditions subjects’ identities remain anonymous during the experiment since they do not know which subject is associated with which action and they do not know how much a particular subject earned since they are paid individually and in private. Conditions III and IV are fulfilled because an individual subject will know his or her payoff but only know the distribution of the payoff of the other subjects. Most experiments pass this basic requirement so conditions III and IV are usually met. Other experiments where interaction among the subjects are a concern, such as in bargaining experiments, then controls such as this nature need to be explicitly addressed and endogenized in the experimental design.

2.2. Monotonicity

Monotonicity assumes that an agent values an item (such as money or lottery tickets) and that he/she prefers to have more of this item than less. This assumption concerns how much money to pay subjects so that if the subjects are playing for pennies then monotonicity probably will not be satisfied since subjects will not value the difference between $0.10 and $0.30. However, the subjects probably will value the difference between $10.00 and $30.00. Given varying rates that an experimenter can pay subjects another related questions is will low payments hamper the performance of subjects and will high payment increase the performance of subjects? Currently the conventional wisdom is that an experimenter should pay enough money so that it matters to subjects, which is usually 50 to 100 percent above the minimum wage per hour ([14], p.50). But this is only a rule of thumb and does not answer the question of what are the upper and lower limits which will ensure that subject motivations have been controlled for in the laboratory. Also please understand that nonfinancial incentives such as playing for lottery tickets to win a prize has this same monotonic effect, the more a subject gets the greater his or her chances of winning a prize and thus they value more of them.

2.3. Saliency and the Crowding-Out Effects

Some believe that financial incentives should be used only such that they support the subjects’ intrinsic goals so that they can be more easily measured. Furthermore, financial incentives can crowd out a subject’s intrinsic motivations for completing experimental tasks and lead to lower task performance yielding false conclusions about subjects’ behavior in voting games. The crowding out effect could mean that the use of financial incentives does not accomplish the goals of the experimenters. In terms of theory evaluation, if subjects are intrinsically motivated without financial incentives to devote cognitive activity to the choices before them and the cognitive activity is reduced when financial incentives are introduced, then financial incentives could have a perverse effect and hinder the ability to use the experiments for theory testing. In terms of external validity, if it is true that the intrinsic motivations of subjects are closer to the motivations that subjects have in non-experimental settings, then crowding out could be a problem for the generalizability of the results. For example, in voting experiments it may be the case that subjects have an intrinsic motivation to express their preferences in a naïve manner and to not engage in strategic behavior. If these motivations are suppressed by financial incentives, then the incentives can be problematic for external validity.

However, subjects in experiments may have intrinsic motivations that are experiment specific. They may simply want to finish the experiment as quickly as possible and make choices that allow them to do so, devoting little cognitive activity to the task, so that they can do other things more salient to them. Or they may overvalue minor aspects of the experiment (candidate names, colors used, etc.) that would be irrelevant to them in a comparable choice environment outside of the experiment.Or subjects may think that the experimenter has a particular research outcome in mind and make choices that either support or oppose that research outcome based on their own personal views of the research. If financial incentives crowd out these types of intrinsic motivations, then crowding out is desirable. The conjecture behind the labor theory of cognition and the use of financial incentives is that intrinsic motivations of subjects are of this sort.

Saliency requires performance-based rewards where the payment of money is tied to the actions or choices that a subject makes within the controlled environment of the experimental laboratory. For example, in a voting experiment a subject votes for a candidate in one election period and is paid an amount based on the position of the winning candidate. In the next election period the subject votes again, and again she wins a payoff higher or lower depending on whom she voted for and which candidate wins the elections. Hence, in each election period the voter’s individual decisions decide how much money she will eventually accumulate. Performance-based rewards ensure that a subject’s decisions are motivated by the reward medium of the experiment. Even if the saliency condition is implemented correctly in the laboratory some argue that rewards schemes based on performance-based incentives might actually cause subjects to perform poorly in the experiment. Psychologists differentiate between intrinsic and extrinsic motivations. Ryan and Deci ([15], p.55) note that “the basic distinction is between intrinsic motivation, which refers to doing something because it is inherently interesting or enjoyable, and extrinsic motivation, which refers to doing something because it leads to separable outcomes.” The authors go on to note that extrinsically motivated actions can be performed with “resentment, resistance, and disinterest.” Some psychologists argue that when money is contingent on the actions of subjects within an experiment then the intrinsic motivation is replaced by extrinsic motivation and the performance of subjects will be negatively affected. Deci ([16], p.108) comments:

If a person is engaged in some activity for reasons of intrinsic motivation, and if he begins to receive the external reward, money, for performing the activity, the degree to which he is intrinsically motivated to perform activity decreases.

The important question is whether money decreases the performance of subjects in the experiment. To answer this question we must understand what controls and financial incentive are used for—to reduce performance variability in the data. That is, to reduce randomness in the data cause by subjects making choices outside of the realm of the theory. Davis and Holt ([17], p.25) remark that “in the absence of financial incentives, it is more common to observe nonsystematic deviations in behavior from the norm.”

2.4. What if the Conditions of IVT are Not Perfectly Met?

According to IVT if these four conditions are implemented in the laboratory then an experimenter can say that he/she has controlled motivations within the controlled experimental environment. Hence, the experimenter can make accurate inferences from the laboratory to the theory that is being posited. It is important to note that Smith did not specify that these four conditions were necessary conditions to control subject behavior but rather only sufficient conditions [3]. Guala ([18], p.233) points out that IVT is not really a theory but rather broad guidelines.

First, the conditions identified by the precepts [of Induced Value theory] were not intended to be necessary ones; that is, according to the original formulation, a perfectly valid experiment may in principal be built that nevertheless violates some or all of the precepts. Second, the precepts should be read a hypothetical conditions (“if you want to achieve control, you should do this and that”) and should emphatically not be taken as axioms to be taken for granted... Consider also that the precepts provide broad general guidelines concerning the control of individual preferences, which may be implemented in various ways and may require ad hoc adjustments depending on the context and particular experimental design one is using.

If this is true then it is unclear how much experimenters should adhere to these precepts in order to be able to claim that monotonicity and saliency are satisfied.

2.5. Behavior that Deviates from the Theory when Conditions I and II are Satisfied

Since the above argument means that nothing will be controlled for perfectly then financial incentives do produce the desired behavior but with admitted noise. That is, subjects like financial incentives but apparently they like other things not specified in the theory being tested. Even when financial incentive are high and controlled for there is evidence of behavior that is considered to be deviations from the theory. Moreover it is unclear if these deviations are a result of altering financial schemes. Kagel and Roth ([19], p.80) note:

The same issues arise with experimental designs intended to control subject’s preferences, starting with the simplest design in which subjects are paid in money and the predictions of the theories being tested are formulated as if the subjects were interested only in maximizing their own income. As I have discussed in the context of both public goods and bargaining, there is abundant experimental evidence that these designs may sometimes fail to control subject’s preferences, because subjects may in fact also be concerned with the payoff of other subjects.

In fact experiments which have built in the “proper” controls of induced value theory have seen behavior outside of the realm of expected utility such as altruism or fairness

The basic idea is illustrated by an example. Consider an experimenter gives a subject two $5 bills and tells the subject she can keep both $5 bills and leave the experimental room, or she can give one or both of her $5.00 to a person sitting in another room, and then leave the experimental room. The game theoretical prediction is for the person to leave the room with both $5, but what about cases where this person gives up one or both of her bills? In this instance, was her behavior dictated by the fact that $5.00 was a trivial sum with no financial attachment, or was it the case that the subject felt some type of altruistic feelings and gave her money away as a result of that, or was it the case that the model being tested was wrong? It is unclear because we do not fully understand the connection between financial incentives and behavior that is induced by it in the laboratory.

The problem that this example illustrates is that we have no comparative results so we do not know if this behavior would persist if the subject was given two $500 bills instead of just two $5 bills. We do not even understand what would happen if the experiment revolved around two quarters. In terms of voting experiments which entails selecting among alternatives we do not know if subjects do maximize in a choice between one set of alternative, say $1.00 and $2.00, and another set of alternative with a higher magnitude in payoffs say $90.00 and $100.00. We also do not know if voters care about the magnitude of the payoffs rather than the difference such as in the payoffs $5.10 and $5.00

3. Research on Financial Incentives in Experiments

The existing research on the effects of financial incentives does not lead to a clear conclusion. Economists suggest that performance-based incentives lead to reductions in framing effects, the time it takes for subjects to reach equilibrium in market experiments, and mistakes in predictions and probability calculations.3 Furthermore, a growing number of field and marketing experiments show that choices made by subjects in hypothetical situations are significantly different from the choices made by subjects in comparable real situations in which financial incentives are involved, suggesting that using hypothetical situations in place of financial incentives leads to biased and inefficient predictions about behavior.4

In a political science experiment, Prior and Lupia [38] found that giving subjects financial incentives to give correct answers in a survey experiment on political knowledge induced subjects to take more time and to give more accurate responses. In another voting experiment Hoelzl and Rustichini [39] consider the effects of financial incentives where subjects voted over a reward scheme for performance on individualized tasks.5 One scheme gave a prize to 50% of the subjects independent of their performance on the task, while the alternative rewarded with a prize only those subjects who scored at the median or better on the task. Although it is common to find that the majority of survey respondents believe they are better than the median on tasks, the voting responses demonstrated less overconfidence, and even under-confidence, as financial incentives were increased.

In contrast, a large number of studies by psychologists have found evidence that financial incentives lower task performance by crowding out intrinsic motivations.6 Most of this research focuses on individualized decision making rather than choices within the context of a group or game situation as in political economy experiments. Heyman and Ariely [40] study showed the consequences of varying payment levels on the performance of subjects engaged in individualized tasks which ranged from boring, repetitive ones to solving puzzle problems which progressed in difficulty during the experiment. They studied the effects of a small payment, a sizeable one, and whether the payment was monetary or candy. They also ran the experiment without paying subjects for performance.

Heyman and Ariely found that when subjects were not given incentive payments (either money or candy) the number of completed tasks was higher than with small incentive payments. Further, when the incentive payment was not explicitly monetary, that is, candy, the performance was higher than in the small monetary payment condition. Increasing incentive payments of both types increased performance, although not always reaching the levels of task performance in the control condition with no payment. These results support the contention that financial incentives crowd out intrinsic motivations and lead to less task performance.7 Cameron and Pierce [41,42] conducted a meta study of experiments in social psychology and education and found:

…[financial] rewards can be used effectively to enhance or maintain intrinsic interest in activities. The only negative effect of reward occurs under a highly specific set of conditions that be easily avoided.

([41], p.49)

The negative effect is “when subjects are offered a tangible reward (expected) that is delivered regardless of level of performance, they spend less time on a task that control subjects once the reward is removed.” ([42], p.395). That is, as predicted by induced value theory flat payment schemes hinder subjects’ performance.

3.1. Why Financial Incentives Could Be Bad

A number of possible explanations for why explicit financial incentives might worsen task performance in experiments have been proposed. One is that the cognitive effort induced by the incentives may be counter-productive, causing subjects to overthink a problem and miss simple solutions as subjects try more complex cognitive strategies in order to maximize payoffs. Financial incentives may cause subjects to think they should exert more effort than necessary when simpler decision processes such as heuristics are sufficient.8 According to this explanation we would expect that financial incentives are most harmful for simple, easy tasks or ones where cognitive shortcuts can be effective even in a situation that is complicated.

A second proposed cause is suggested by Meloy, Russo, and Miller [45] who find that financial incentives in experiments can elevate a subject’s mood and this contributes to worsened task performance. They note that the effect they and others find might be mitigated if the subjects receive feedback and experience. This suggests that financial incentives interact with feedback and experience and failure to provide those additional features leads to inaccurate estimates of their effects.9 Endogeneity of social norm preferences has been projected as a third reason. In this view we think of the experimental subjects as workers and the experimenter as their employer. Some theorists have contended that firms who pay well regardless of performance can motivate workers by inducing them to internalize the goals and objectives of the firm, change their preferences to care about the firm. If workers are paid on an incentive basis such that lower performance lowers wages, they are less likely to internalize these goals and there is less voluntary cooperation in job performance [47,48]. Miller and Whitford [49] make a similar argument about the use of incentives in general in principal agent relationships in politics.

Somewhat related is an explanation suggested by [40] based on their experimental analysis discussed above. That is, they contend that when tasks are tied to monetary incentives, individuals see the exchange as part of a monetary market and respond to the incentives monotonically but if the tasks are tied to incentives that do not have clear monetary value, individuals see the exchange as part of a social market and their response is governed by the internalization of social norms outside of the experiment10.

Finally, a fourth explanation of crowding out is informational. Benabou and Tirole [53] show that when information about the nature of a job is asymmetric, incentive based payments may signal to workers that the task is onerous and although increasing compensation increases the probability the agent will supply effort, it also signals to the agent that the job is distasteful and affects their intrinsic motivations to complete the task.

These last two explanations (the social norm perspective and the informational theory) suggest a nonmonotonic relationship between financial incentives and task performance. That is, when financial incentives are introduced, but are small, subjects task performance is worsened as compared to the no payment condition (either because they now think of the exchange with the experimenter as a market one instead of a social one or because they see the task as more onerous than before), but as financial incentives are increased, task performance increases if the financial incentives are sizable enough. We now turn to our experimental design and how we study these questions.

3.2. Varying Financial Incentives

Gneezy and Rustichini [54] considered how varying the reward medium in an experiment affected subject performance. They conducted an experiment in which subjects answered questions on an IQ test. Subjects were randomly assigned to one of four treatments that varied the reward medium. In all the treatments subjects were given a flat sum payment and treatments varied over an additional amount that the subjects could earn depending on whether they answered questions correctly. In the first treatment subjects were not given an additional opportunity to earn more, in the second treatment subjects were given a small amount for each questions they got correct, and in the third treatment subjects were a substantial amount for each question they received correctly, and in the fourth treatments subjects were given three times the amount given in the third treatment. The authors found that essentially Treatment 1 and 2 were the same and the performance on the IQ tests in those treatments were significantly worse than in Treatments 3 and 4. The interesting finding is that there was no difference between the high payoff conditions in Treatments 3 and 4. Hence, what mattered in the experiment was that subjects who received substantive rewards performed better than subjects with minimum rewards, but there was no difference between the two types of substantive rewards. This finding suggests that financial incentives in the laboratory are not strictly monotonic in the sense that increasing the reward medium will increase the performance of subjects. Rather the subject only has to perceive that the reward medium is sufficient. So the conclusion that we can reach is as the authors titled their paper—“[p]ay enough or don’t pay at all.”

In this experiment subjects were requested to fill out a survey and there were no controls over what subjects saw in terms of the other subjects. Hence, in this experiment dominance was questionable as well as privacy so that conditions II and IV were not adhered to. In the experiments reported here we carefully control for dominance and privacy so we can isolate the effect of saliency and monotonicity.

Bassi, Morton, Williams [55] conducted a series of voting experiments in which they varied financial incentives controlling for condition III and IV and the level of information a subjects possesses. In this design information about different alternatives represents different levels of complexity, where full information treatments represent low complexity and partial information represents complexity. They also found that high levels of financial incentives are important in inducing equilibrium behavior and that increasing financial incentive is related to the complexity of the decision. They note:

In the incomplete information case we also find evidence that financial incentives have an effect on voter behavior but we also find evidence that financial incentives have an effect on voter behavior but we also find evidence that increasing financial incentives strongly affects behavior as well, which is different from what we found when information was complete. Increasing financial incentives, hence, is more consequential in affecting behavior when the voting game is more complex.

([55], p.368)

They concluded that their results showed that financial incentive were related to the “cognitive attention” to the problem. In this paper we analyze this cognitive component by varying the degree of complexity with the level of financial rewards using level-k reasoning to examine cognition attention. Our analysis should provide greater insight into the way in which complexity and financial incentives (in terms of monotonicity and saliency) affect equilibrium behavior.

3. Experimental Design

We conducted 15 sessions of computerized experiments using undergraduate students at a large public university who participated in only one session each. A total of seventy five participants were recruited (five in each session). Each session involved between eight and 24 rounds (eight rounds for each profile treatment), allowing for a total of 1,320 observations. The experiments employed a 3 × 2 fractional factorial design, with three “payment treatments” and two “complexity treatments”. We employed a fractional factorial design that allowed us to analyze both the direct effect of the “payment” and “complexity” treatments and the interaction effect. We utilized both within and between-subjects designs across treatments. That is, in some sessions subjects participated sequentially in more than one payment or complexity treatment and in others they participated in only one of the payment and/or complexity treatments. The order of the payment treatments has been randomized to eliminate any order effect.

Subjects were divided into groups of five voters. Subjects were asked to choose to vote for one of two alternatives labeled “green” or “red” which we denote as G and R, respectively (abstention was not allowed). In each round, a matching algorithm assigned subjects to one of two types: “g” for green or “r” for red. Subjects were re-matched to a new type at any subsequent round to avoid possible repeated game effects. Subjects were told that each subject’s type was a random, independent draw. However, draws were not purely random as the matching algorithm draws were designed to ensure that in each period at least one subject was of each type (that is, the possible combinations were either 4 green and 1 red, 3 green and 2 red 2 green and 3 red, or 1 green and 4 red).11

Table 1. Payoff schedule.

Subject’s Type	“g” Type		“r” Type
Election outcome	G wins	R wins	G wins	R wins
Vote for "G"	1.5x	0.5x	x	0
Vote for "R"	0	x	0.5x	1.5x

Table 1. Payoff schedule.

Subject’s Type	“g” Type		“r” Type
Election outcome	G wins	R wins	G wins	R wins
Vote for "G"	1.5x	0.5x	x	0
Vote for "R"	0	x	0.5x	1.5x

Preferences were induced in the experiment by a vector of payoffs, which was function of which alternative received the most votes and the player’s type. Table 1 summarizes the payment schedule used throughout the experimental sessions. Payment treatments differed in the amount of the scalar x.

Table 1 shows how subjects’ payoffs depend not only on which alternative won but also on how they voted independent of the effect of their vote on the outcome of the election. When G wins, a “g-type” subject receives her highest payoff, 1.5x, if she votes for G, and her lowest payoff, 0, if she votes for R. Instead, when R wins she receives x if she votes for R, and only 0.5x if she votes for G. As a consequence, subjects have an incentive to vote for the alternative that is most likely to win but also had a preference over which alternative won the election. Hence, subjects are better off if their first preference won and they voted for that alternative than if the other alternative won and they voted for that alternative, but both of these situations were preferable to voting for a losing alternative.

We used three different payment treatments: (1) a “no payment” treatment (x = 0), where subjects were paid no financial incentives based on behavior but a flat fee for participation equivalent to the average payment in most political economy experiments; (2) a “low payment” treatment (x = 1), where subjects were given financial incentives that are typical of those used in most political economy experiments; and (3) “high payment” treatment (x = 2), where subjects were given financial incentives that were double those used in most political economy experiments.

In the “no payment” treatment subjects were told to make choices as if the alternatives yielded the same payoffs reported in Table 1 even though subjects were told they would have been paid a flat fee only. Thus, in this treatment, although voters were encouraged to think of the payoffs attached with each strategy and contingency, they were given no financial incentive that was function of their behavior. If subjects only participated in the no payment treatment, they received a fixed payment of $22.00 for their participation in the experiment as well as the show-up fee received by all subjects across payment treatments. Subjects who participated in the low payment or the high payment treatment only, received on average $22.00 and $44.00, respectively.

We varied the complexity of the task by varying the information available to the subjects. We used two “information treatments.” (1) In the “full information” treatment, each subject was told his/her own type and the type of the four other subjects in their group; (2) in the “partial information” treatment, each subject was told his/her own type as well as the type of two other subjects in his/her group, but not the type of the remaining two subjects in the group. Subjects were told that every voter in the group was informed about the type of other two members of the group and that the information that each member in a group received was an independent random draw. Thus, subjects in a same group might have different information. Hence, in this treatment, subjects must not only consider how others will vote but also consider the information that others may or may not have when voting.

In the partial information treatment, subjects might receive three different types of information: 2a, two subjects in the group are of the same type as themselves; 2b, two subjects in the group have a different type than themselves; 2c, one subject is of the same type and one subject is of different type. The three types of partial information also yield different levels of complexity since the decision to vote correctly is easier in 2a where subjects know that there is a majority of voters of their own type than in 2b and 2c where, depending on the type of the two remaining members, either type can be the majority type. We discuss how the different types of information affect the complexity of the game in greater detail in our discussion of the theoretical predictions.

Table 2 presents a summary of how payment and information treatments were distributed across experimental sessions. In order to analyze the direct effect of different “payment treatments”, we ran six sessions where the complexity was kept fixed while varying only the payment treatments (sessions 1–4 and 11–12). By the same token, we analyze the direct effect of complexity by keeping the payment treatments fixed and allow information to vary (sessions 8–10). Note that we have no session where the partial information treatments followed full information ones because in such cases subjects might suspect, given their experience under full information, that the types of other subjects were not purely random (in the partial information treatments subjects were never revealed the ex post distributions of types in a particular period, only the winner of the election in that period, so such updating was not possible).

Conditions III and IV were controlled for since all experiments reported here were conducted in a computer laboratory with 32 wired connected computer terminals. There were partitions between each computer screen to prevent subjects from viewing each other’s screens. Subjects were also prohibited from any verbal communication other than directed at the experimenter. At the end of the experiment each subject was escorted into a separate room and paid their earnings in cash away from the view of other subjects.

Table 2. Fractional factorial design.

	Round 1-8		Round 9-16		Round 17-24
Treatments	Information	Payment	Information	Payment	Information	Payment
Session 1	Full	No	Full	Low	Full	High
Session 2	Partial	No	Partial	Low	Partial	High
Session 3	Full	High	Full	Low	Full	No
Session 4	Partial	High	Partial	Low	Partial	No
Session 5	Full	No	--	--	--	--
Session 6	Full	Low	--	--	--	--
Session 7	Full	High	--	--	--	--
Session 8	Partial	No	Full	No	--	--
Session 9	Partial	Low	Full	Low	--	--
Session 10	Partial	High	Full	High	--	--
Session 11	Partial	Low	Partial	No	Partial	High
Session 12	Partial	High	Partial	No	Partial	Low
Session 13	Partial	No	Partial	No	--	--
Session 14	Partial	Low	Partial	Low	--	--
Session 15	Partial	High	Partial	High	--	--

Table 2. Fractional factorial design.

	Round 1-8		Round 9-16		Round 17-24
Treatments	Information	Payment	Information	Payment	Information	Payment
Session 1	Full	No	Full	Low	Full	High
Session 2	Partial	No	Partial	Low	Partial	High
Session 3	Full	High	Full	Low	Full	No
Session 4	Partial	High	Partial	Low	Partial	No
Session 5	Full	No	--	--	--	--
Session 6	Full	Low	--	--	--	--
Session 7	Full	High	--	--	--	--
Session 8	Partial	No	Full	No	--	--
Session 9	Partial	Low	Full	Low	--	--
Session 10	Partial	High	Full	High	--	--
Session 11	Partial	Low	Partial	No	Partial	High
Session 12	Partial	High	Partial	No	Partial	Low
Session 13	Partial	No	Partial	No	--	--
Session 14	Partial	Low	Partial	Low	--	--
Session 15	Partial	High	Partial	High	--	--

4. Theoretical Predictions and Conjectures

As often happens with n-players games, in both the full and partial information treatments there are multiple Nash equilibria and Bayesian Nash equilibria of the game. In order to pin down the set of possible equilibrium outcomes, we might either adopt equilibrium refinements or to look for behavioral concepts that might suggest what equilibrium is “focal” for the players.

Equilibrium refinements such as the Strong Nash Equilibrium [56] or the Coalition–Proof Equilibrium [57] have been used in voting games to select “stable” equilibria [58,59]. While the Nash equilibrium concept defines stability only in terms of individual deviations, both the Strong Nash and the Coalition–Proof equilibrium allows for deviations by coalitions of players. 12 In our voting games, these refinements would pin down the set of Nash equilibria to a unique equilibrium, the one in which every subject votes for the alternative that gives the majority of voters in the group the highest payoff, i.e., the alternative preferred by the majority of the voters. 13

These refinements yield “focal strategies”: natural and expected mechanisms for voters—or bloc of voters who share the same preferences—to communicate prior to play and try to coordinate their actions in a mutually beneficial way. However, in environments without communication, like in our experimental treatments, it is substantially harder for players to coordinate their actions. Furthermore, when the games present a significant complexity for the subjects, the cognitive requirements for converging to Strong or Coalition-proof equilibria are sufficiently high to prevent agents to realistically calculate their optimal strategy. Recent experiments suggest that in complex strategic settings, a structural non-equilibrium model based on level-k thinking—also referred to as cognitive hierarchy model by Camerer, Ho, and Chong [60], can often out-predict equilibrium behavior. Although the predictive power of level-k models varies considerably as function of the characteristics of the game, level-k models are found to be especially successful in predicting subject behavior in settings with symmetric information and strong coordination motives [61]. In fact, when agents have an incentive to coordinate their strategies with other players to achieve a better outcome, the behavior of others becomes more and more important; consequently, subjects are more likely to try to predict it. Since our voting games present a strong coordination incentive for voters of the same type, the level-k model seems to be the proper fit to predict subjects’ behavior. Hence, we adopt the level-k behavioral model to analyze the effect of complexity on voting behavior.

The level-k model of strategic reasoning takes into consideration players' beliefs about how the other players will play. This model assumes that people do not reason all the way to equilibrium because doing so simply requires too much effort and/or ability [62]. The level-k model proposed by Nagel [1] postulates that players might be of different types, each corresponding to the level of reasoning ahead in a game in which they engage in (all other players are believed to be exactly one level of reasoning below oneself). Some players (call them level-0 players) play the game naїvely (or in a voting setting, sincerely). Level-1 agents play the optimal strategy while assuming that all the other players play naїvely. Level-2 players assume that all the other players are level-1 players, and so on.

This level-k thinking model also provides a step-by-step understanding of the reasoning process in complex voting games ([63] analyzes strategic voting in games with multiple alternatives and a multitude of Nash equilibria). For example, let us consider the full information scenario where there are three type “g” voters and two type “r” voters. In level-0, all the type “g” would vote naїvely for alternative G, while all the type “r” would vote for alternative R. The election would result in G winning. However, voters might engage in strategic reasoning, anticipating other players’ strategies: if type “g” voters assumed that the other voters were going to play naїvely (level-0), they would vote for G, since it is the best response to the level-0 behavior of the other players’ vote. However, the same reasoning process would lead type “r” voters to vote for G rather than R. In higher levels of reasoning, voters would anticipate other players to vote strategically (level-1). Hence, both type “g” and “r” voters would keep voting for G. This suggest that with full information, players who engage in at least one level of strategic reasoning, would not deviate any further, because their strategies are best responses to the other players’ strategies. Hence, the level-k model of reasoning predicts that the only “stable’’ strategy is for every player to vote for the alternative preferred by the majority of the subjects.

Table 3. Level-k cognitive reasoning process for g type.

Full Information Treatment
	Level 0	Level 1	Level 2
g is majority type	G	G
r is majority type	G	R
Partial Information Treatment
Info Type	Level 0	Level 1	Level 2
2 "g" type voters	G	G	G
1 "g" type + 1 "r" type	G	G	G
2 "r" type voters	G	G, R	R

Table 3. Level-k cognitive reasoning process for g type.

Full Information Treatment
	Level 0	Level 1	Level 2
g is majority type	G	G
r is majority type	G	R
Partial Information Treatment
Info Type	Level 0	Level 1	Level 2
2 "g" type voters	G	G	G
1 "g" type + 1 "r" type	G	G	G
2 "r" type voters	G	G, R	R

Table 3 reports the level-k reasoning process for a type “g” voter. The level-k cognitive reasoning for a type “r” voter mirrors Table 3. The top panel of Table 3 displays that in the full information treatment subjects need to engage in one level of cognitive reasoning before converging to a stable strategy both in case the group is populated by a majority of type “g” and by a majority of type “r” voters. The bottom panel of Table 3 reports the level-k reasoning process for a type “g” voter in incomplete information treatment. The table displays the level-0, level-1, and level-2 strategy in case the voter knows that the type of two other voters is “g”, that one voter is type “g” and one is type “r”, or that the type of two other voters is “r”. As displayed by the table, with incomplete/partial information, the subjects need to engage in one extra level of reasoning before converging to a stable strategy. For instance, consider the incomplete information case where a type “g” voter knows that two other voters in the group are of type “r”. In level-0, he/she would vote naїvely for alternative G. In level-1, however, the voter would anticipate other players to vote naїvely. In this case, he would assume the two “r” type voters would vote R. Since the voter does not know the type of the remaining two voters in the group, he/she would need to contemplate three different scenario: a) both of them are type “g” voters (with probability 1/4), b) both of them are type “r” voters (again with probability 1/4), or c) one is a type “g” voter and the other a type “r” voter (with probability ½). Given these three possible cases, the expected utility of voting for G would be exactly equal to the expected utility of voting for R.

U_g(G) = 1/4 × 1.5 + 1/4 × 0.5 + 1/2 × 0.5 = 3/4
U_g(R) = 1/4 × 0 + 1/4 × 1 + 1/2 × 1 = 3/4

(1)

In level-2, the complexity of the required reasoning is dramatically higher. Now, a voter not only needs to consider all the possible draws of types for the two unknown voters, but also the possible types of information that the other voters might receive. For instance, consider scenario (a): the two known type “r” voters might receive two types of information with equal probability, either that two other member are “g” type or that one is “g” and that the other one is “r”. In the first case, the voter would assume the two red voters to be indifferent between G and R, and therefore to vote with equal probability G and R. In the second case, the two “r” type voters are expected to vote for R (see Table 3 for the level-1 strategy of a voter who observes one voter of the same type and one of different type). As for the two “g” unobserved voters, they might receive three types of information: that two other voters are “g” type (with probability 1/6); that one is “g” and that the other one is “r” (with probability 4/6); or that both of them are “r” type (with probability 1/6). In the first and second case, the two “g” voters are assumed to vote for G, while in the third case, they are assumed to be indifferent between G and R, and therefore to vote with equal probability G and R. A voter needs to consider all possible contingencies of type draws and information draws to calculate the expected utility of his feasible strategies.

The cognitive reasoning process varies substantially across information treatments. On the one hand, allowing subjects to know only two voters’ type rather than four voters’ type significantly hardens the cognitive process. First, subjects need to figure out all the possible draws of types of the two unknown voters; then, they need to form their beliefs about their actions, given all the possible partial information the other voters might receive; and last, they need to calculate their best reply given the likelihood of all contingencies. On the other hand, the partial information voting games yield different complexities as a function of the kind of information a player receives. If players know that at least one other player is of the same type as themselves, players need to engage in only one level of reasoning levels before converging to the a stable strategy. However, if players observe two other players of a type different than themselves, they need to go through two levels of reasoning rather than one.

In order to evaluate the effect of financial incentives on the reasoning process we model a type of noisy behavior, which includes the Nash equilibrium predictions as a limiting case, by analyzing the Quantal Response Equilibria of the game [64]. An identical and independently distributed stochastic parameter µ, accounting for the noise in the best replies, is added to the expected payoff of each strategy. In the absence of noise (µ = 0), the Quantal Response Equilibrium (QRE) approaches the Nash Equilibrium. In order to provide parametric estimates, we analyze a logit specification of the QRE, where the quantal response functions are logit curves, and λ (λ = 1/µ) is the response parameter.

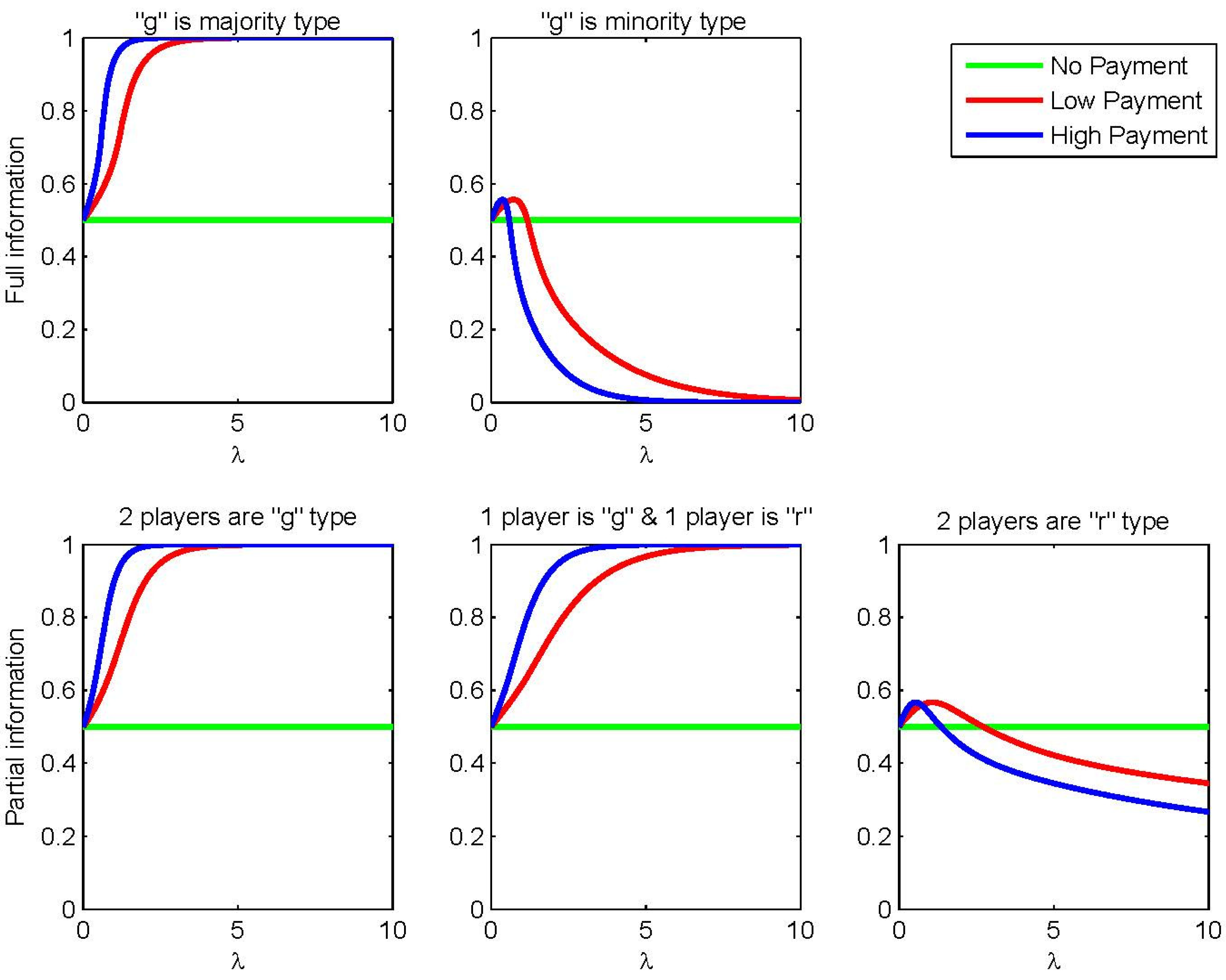
Figure 1 displays the Quantal Response Equilibrium functions for a type “g” voter. The top panel of Figure 1 shows the probability of voting for the “G” alternative in the full information treatment. The left and right subplots show the probability of voting for “G” when type “g” voters are the majority and the minority type, respectively. The bottom panel of Figure 1 presents the probability of voting for the “G” alternative in the partial information treatment. The left, middle, and right subplots show the case in which the player knows that two other voters are type “g”, one voter is type “g” and one is type “r”, and two other voters are type “r”, respectively.

In each subplot, the green line shows the QRE function in the “no payment” treatment; the red line represents the QRE function in the “low payment” treatment; and the blue line refers to the QRE function in the “high payment” treatment. The QRE function in the “no payment” treatment is always equal to 0.5, because voting for either alternative yield a payoff equal to zero. With payoffs greater than zero, instead, the quantal response function converges to the level-k stable strategy in both information treatments. Notice that when the payoffs increase, the QRE function approaches the level-k model prediction faster. Hence, we expect that higher payments elicit a higher probability of strategic/equilibrium behavior.

Figure 1. Probability that a “g” type player votes for “G”.

Figure 1. Probability that a “g” type player votes for “G”.

Consistent with the discussion of the level-k cognitive reasoning in the partial information treatment, subjects converge more slowly when they observe two voters of a different type from themselves (2c). In the quantal response analysis this translates in a higher number of errors, or higher noise.

4.1. Conjectures

The expectations about the experimental results can be described by the following hypotheses:

• Strategic (equilibrium) behavior is more likely when the amounts at stake are higher. Financial rewards have been proved to affect the cognitive process (in terms of effort exerted by the subjects) in a way that subjects make fewer errors as financial rewards increase. As the Quantal Response Equilibrium model predicts, subjects’ behavior is less likely to be affected by noise when the amounts at stake increases. Hence, we expect subjects to play the equilibrium strategy more often when the payoffs are higher.
• Strategic (equilibrium) behavior is more likely with complete information than with partial information. The level-k reasoning analysis shows that full information eases the cognitive reasoning process of the subjects as the number of levels that the subjects need to engage in before converging to the level-k stable strategy is lower than in case of partial information. Hence, we expect the partial information treatment to elicit a lower level of strategic/equilibrium behavior than the full information treatment does.
• Strategic (equilibrium) behavior is less likely when complexity increases. Both the level-k reasoning analysis and the Quantal Response functions in the partial information treatment show that when subjects know that two other players are of a different type from themselves, they need to engage in more reasoning levels before they converge to the QRE/stable strategy than in case they know that at least one other player is of the same type as themselves. Hence, we expect the greater complexity yielded by this type of partial information to elicit a lower level of equilibrium/stable level reasoning than the other types of partial information.

5. Results

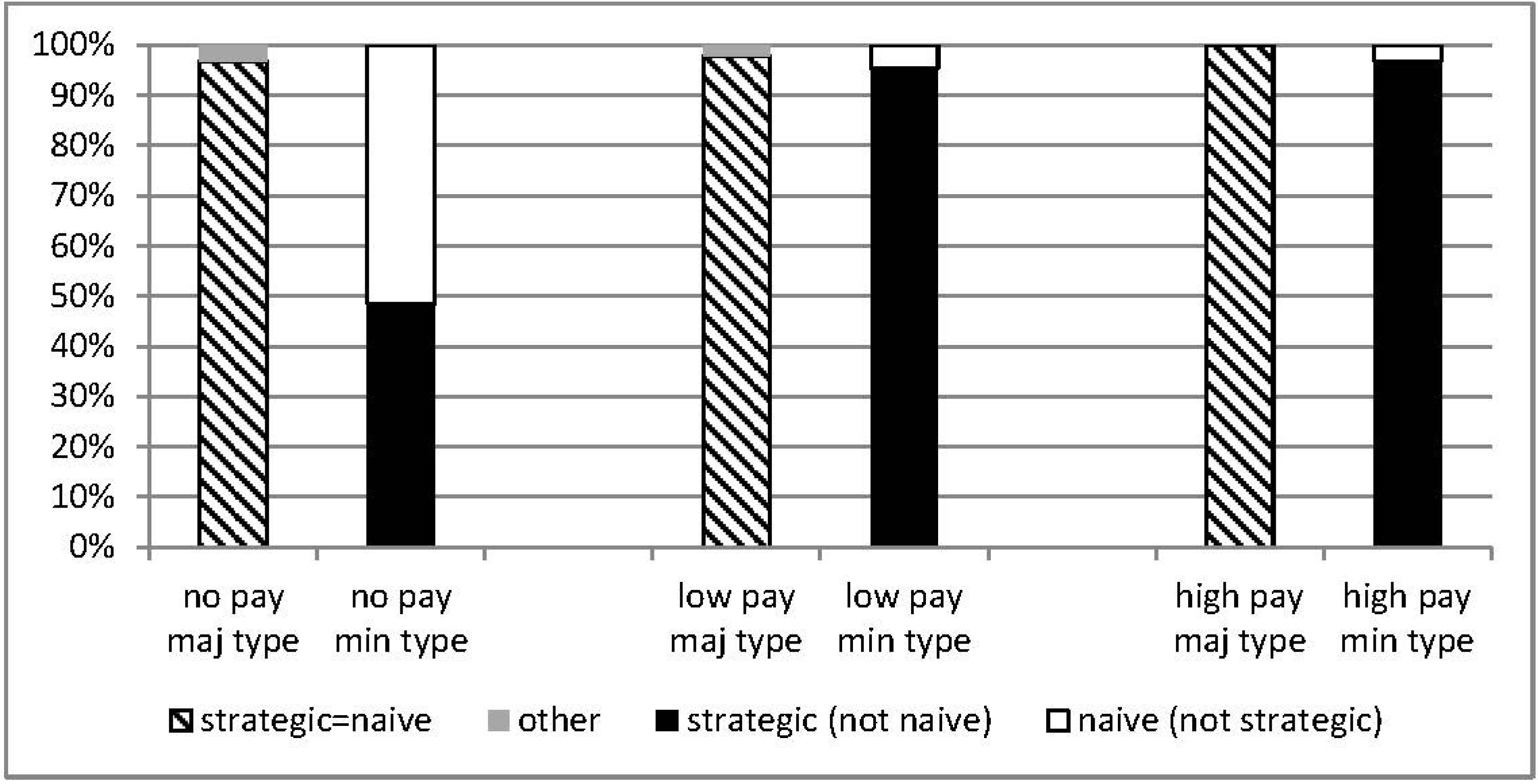
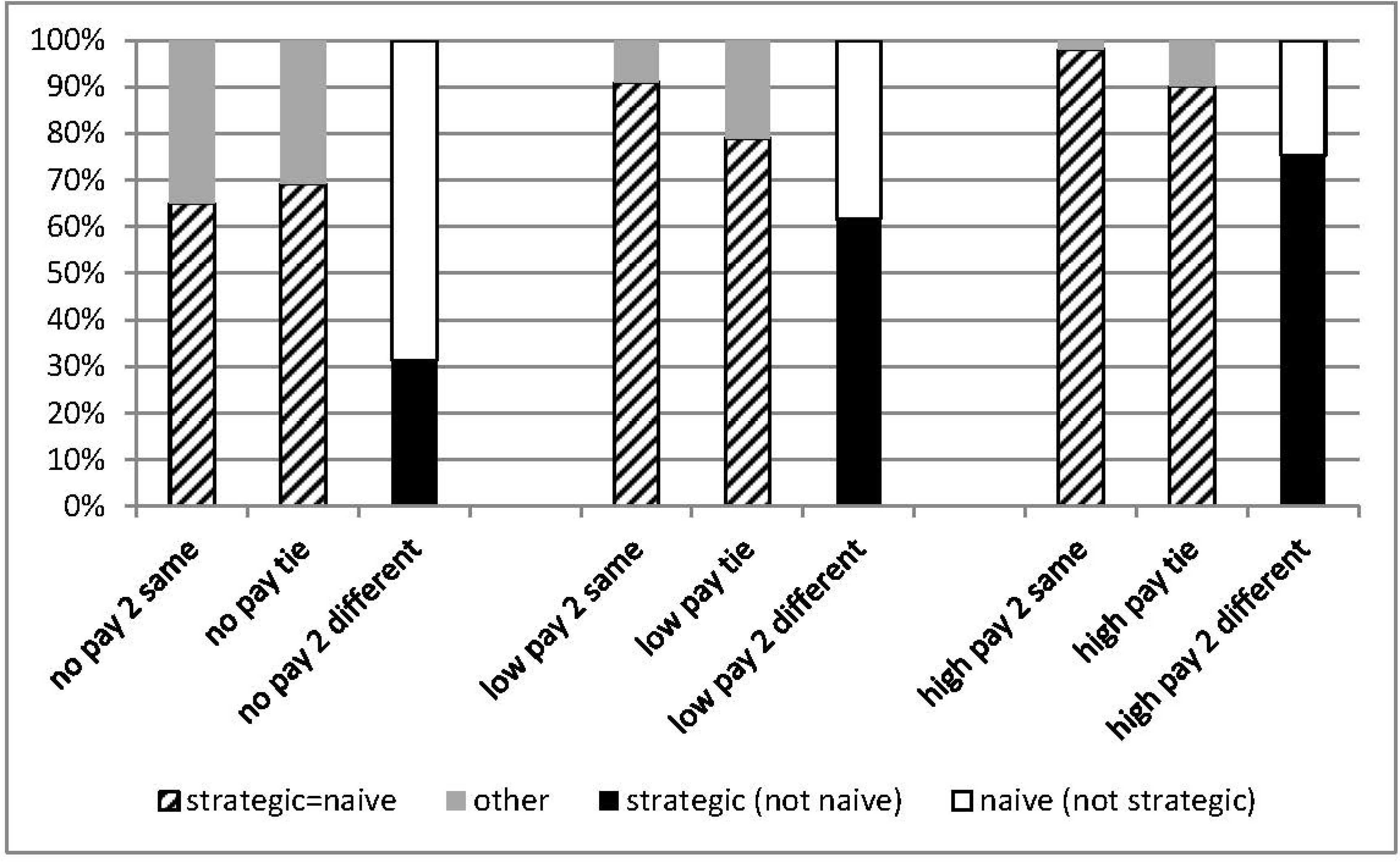
Figure 2 and Figure 3 summarize the frequency with which the subjects chose the naïve strategy (in white), the QRE/level-k stable strategy (in black), and other dominated strategies (in gray) in the full and partial information treatments, respectively. A striped pattern depicts when the equilibrium strategy coincides with the naïve strategy.

Both Figure 2 and Figure 3 show that subjects play the QRE/level-k stable strategy (both when it coincides with a naïve strategy and when it is different) more frequently when the payment increases, consistent with Hypothesis 1. This is particularly apparent when the equilibrium strategy is different from the naïve strategy.

Comparing Figure 2 and 3, it appears that full information elicits a higher level of strategic behavior than partial information, consistent with Hypothesis 2. Furthermore, in the partial information treatment, players play the QRE/level-k stable strategy less often when they observe two players of a different type than when they observe at least one player of the same type as themselves, consistent with Hypothesis 3.

Figure 2. Individual behavior under Full Information Treatment.

Figure 2. Individual behavior under Full Information Treatment.

The descriptive analysis shows that a clear distinction exists between the ability to play the QRE/level-k stable strategy under the three payment treatments and the two complexity treatments. An environment with complete information seems to induce the agents to play the QRE/level-k stable strategy the most. Furthermore, the higher the amounts at stake, the higher the likelihood of the players to play their level-k stable strategy.

Figure 3. Individual behavior under Partial Information Treatment.

Figure 3. Individual behavior under Partial Information Treatment.

5.1. Statistical Analysis

Are the differences in voting choice documented in Figure 1 and Figure 2 statistically significant? To assess the validity of our hypothesis, we calculate the average frequencies of QRE/level-k stable votes for each subject across all elections for each information treatment and payoff treatment. Next we test whether the differences in the average frequencies of strategic behavior are statistically significant across payment treatments (Hypothesis 1) and information treatments (Hypothesis 2) according to a paired t-test or a Welch test, which are both refinements of the Student’s t-test for use with two repeated samples or two samples having possibly unequal size and variance, respectively.

In order to test Hypothesis 1, the paired t-test tests the null hypothesis that the average frequency of equilibrium strategies in high (low) payment treatment exceeds the average frequency of equilibrium strategies in the low (no) payment treatment.

Table 4. Average frequencies of strategic votes and effect of payment.

Complete Information Treatment
	No Payment	Low Payment	High Payment
Average	77.5	96.875	98.75
No Payment	–	p-value = 0.00	p-value = 0.00
Low Payment	–	¬	p-value = 0.33
Partial Information Treatment
	No Payment	Low Payment	High Payment
Average	61.25	76.25	86.875
No Payment	–	p-value = 0.00	p-value = 0.00
Low Payment	–	¬	p-value = 0.00

Table 4. Average frequencies of strategic votes and effect of payment.

Complete Information Treatment
	No Payment	Low Payment	High Payment
Average	77.5	96.875	98.75
No Payment	–	p-value = 0.00	p-value = 0.00
Low Payment	–	¬	p-value = 0.33
Partial Information Treatment
	No Payment	Low Payment	High Payment
Average	61.25	76.25	86.875
No Payment	–	p-value = 0.00	p-value = 0.00
Low Payment	–	¬	p-value = 0.00

Table 4 reports the mean across all subjects’ average frequency of QRE/level-k stable strategies for both information treatments under the three payment treatments. All the differences are statistically significant at a 1% level. The only exception is the difference between low and high payment in the full information treatment. Hence, an increasing payoff does not always elicit a higher level of equilibrium behavior, as predicted by Hypothesis 1. The high payoff treatment promotes strategic behavior only when the amount of complexity is high enough. Otherwise, a moderate (low) payment is enough to induce subjects to engage in strategic reasoning and play optimally.

Table 5. Average frequencies of strategic votes and effect of information.

No Payment Treatment
	Complete Information	Partial Information
Average	77.5	61.25
p-value	0.00
Low Payment Treatment
	Complete Information	Partial Information
Average	99.875	76.25
p-value	0.00
High Payment Treatment
	Complete Information	Partial Information
Average	98.75	86.875
p-value	0.00

Table 5. Average frequencies of strategic votes and effect of information.

No Payment Treatment
	Complete Information	Partial Information
Average	77.5	61.25
p-value	0.00
Low Payment Treatment
	Complete Information	Partial Information
Average	99.875	76.25
p-value	0.00
High Payment Treatment
	Complete Information	Partial Information
Average	98.75	86.875
p-value	0.00

In order to test Hypothesis 2, the Welch statistics test the null hypothesis that the average frequency of QRE/level-k stable strategies in the full information treatment exceeds the average frequency of QRE/level-k stable strategies in the partial information treatment. The equilibrium behavior displayed by the subjects is reported in Table 5. The results are in sound support of our theoretical expectations: full information promotes the highest degree of level-k strategic reasoning in every payment treatment.

Finally, when we compare the QRE/level-k stable behavior induced by the three types of partial information across payment treatments (Hypothesis 3), we find that the strategic behavior is significantly affected by the complexity of the voting game. Table 3 shows that observing two players of different types yields a higher number of reasoning levels before converging to the QRE/level-k stable strategy. Table 6 shows that this greater complexity significantly affects the frequency with which the subjects play the QRE/level-k stable strategy.

Table 6. Average frequencies of strategic votes and effect of complexity.

Partial Information Treatment
	Two different types	Tie	Two identical types
Average	57.67	79.8	87.14
Two different types	–	p-value = 0.00	p-value = 0.00
Tie	–	¬	p-value = 0.12

Table 6. Average frequencies of strategic votes and effect of complexity.

Partial Information Treatment
	Two different types	Tie	Two identical types
Average	57.67	79.8	87.14
Two different types	–	p-value = 0.00	p-value = 0.00
Tie	–	¬	p-value = 0.12

6. Conclusions

Our results confirmed most of our theoretical expectations. We found that the full information condition promotes the highest degree of equilibrium behavior or level-k stable reasoning in every payment treatment. As expected when subjects know the identity of the other types then they play the QRE/level-k stable strategy more so, as opposed to partial information. This treatment revealed that when subjects are paid at least the low payment then equilibrium play is transparent when subjects know the parameters of the game. However, when subjects are not paid then choices become more random. We conjecture that perhaps these random choices are the subjects’ way of trying to be “super” strategic since there is nothing at stake they gain excitement by trying to change the expected voting outcome. That is subjects resort to the “outsmart the experimenter” game where they attempt to alter expected experimental outcomes.

In the partial information treatment we found that increasing the complexity of a subject’s task does decrease the rate of convergence to QRE/level-k stable play and increasing payoff amounts does not always elicit a higher level of equilibrium behavior. Complexity and the high payoff treatment promoted more strategic behavior than complexity and moderate (low) payment, but both payment schemes were sufficient to induce subjects to engage in optimal play using strategic reasoning.

Again our results showed that increasing complexity does decrease the rate at which subjects play equilibrium/stable strategies. However, similar to Lupia and Prior [65], we found that if the experimental task is more complex but subjects are paid more for it, then they generally try harder and equilibrium behavior is observed more when payments are higher.

To postulate the payoff-sensitivity of the subjects’ choice, we used the Quantal Response Equilibrium concept proposed by McKelvey and Palfrey [64]. In a QRE players’ decisions are noisy, with the probability density of each decision increasing in its expected payoff. As the distributions’ precision increases (the noise/error decreases), QRE approaches the stable level-k reasoning prediction. Otherwise, the QRE choice probabilities are a monotonic function of the payoffs: the higher the expected payoffs, the higher the equilibrium choice probabilities.

Like Gneezy [54] and Bassi, Morton, Williams [55] we found that paying subjects a sufficient amount whether low or high is necessary to achieve equilibrium play when complex tasks are involved. The question of how much to pay subject is answered by the current standard of twice minimum wage rate. This amount seems to be a valid amount for voting games.

As compared to [55] our analysis of complexity provides greater insight in the cognition processes subjects use in these types of experiments. The level-k model of strategic reasoning seems to fit the data well. According to the level-k reasoning model, players might be of different types (corresponding to their levels of reasoning). Players are rational, but do not necessarily hold consistent beliefs about other players. Players are assumed to think that they are “a little smarter” than their opponents, who are believed to be exactly one level of reasoning below themselves.

Despite the complexity of the voting games, the level-k model is successful in predicting subject behavior not only with full information (as in the classical applications of this model), but also with incomplete information. However, the introduction of private information into the model weakens level-k behavior since the task of predicting the beliefs and actions of opponents becomes considerably more complex.

One lesson our results showed is that we should be cautious in terms of validity of experiments that have subjects engage in a simple task and do not pay them for their performance in the experiment. For whatever reason under these conditions subjects do not value their task and do not pay much attention to their performance. Importantly, when tasks are involved and tied to payments then subjects become more serious about their performance and equilibrium behavior is displayed more consistently. It is important to give subjects something to do in an experiment, especially in voting experiments. These types of experiments can be repetitive involving multiple rounds, so subjects should be randomized each round so that a new task is presented or a task introduced that interests subjects between voting.