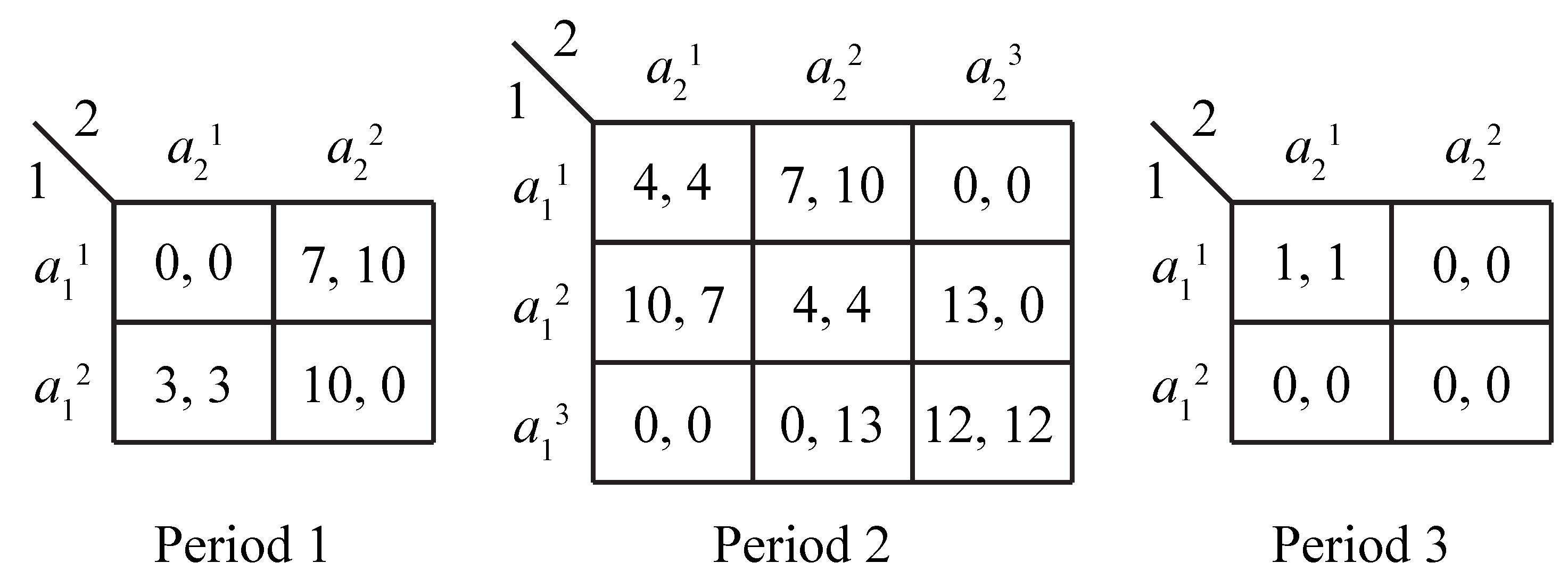
A. Bargaining Protocol Example: Ultimatum Offer
This appendix contains details of the analysis of the ultimatum-offer protocol, which is sketched (in the context of the BoS contracting problem from
Section 2.1) in
Section 3.3.
To calculate the set of equilibrium negotiation values, some additional notation is useful. For any set , let denote the projection on dimension i (player i’s value). Also, for any number , define to equal
if the bracketed set is nonempty and ∞ otherwise. The following lemma characterizes the equilibrium negotiation values for the ultimatum-offer protocol.
Lemma 2: For the ultimatum-offer bargaining protocol, the set of equilibrium negotiation values is
This result is easily proved by calculating, for feasible continuation values, the offers that player 2 can rationally accept or reject.
To calculate the set of equilibrium negotiation values under the Agreement Condition of
Section 3.2, define
to equal
if the bracketed set is nonempty and otherwise.
Lemma 3: For the ultimatum-offer bargaining protocol, the set of equilibrium negotiation values under the Agreement Condition is
Next, I calculate the set of equilibrium negotiation values under the Agreement and Disagreement Conditions. In this case, for a given value , the model of negotiation is equivalent to one in which both the tangible action x and the value y are externally enforced. Define .
Lemma 4: For the ultimatum-offer bargaining protocol, the set of equilibrium negotiation values under the Agreement and Disagreement Conditions is
With the addition of the Random-Proposer Disagreement Condition, the characterization is refined further.
B. Classes of Contractual Relationships and Existence
In this appendix, I delineate three classes of contractual relationships and provide existence results for them. The following subsections define the three classes, in increasing order of complexity.
B.1. Finite Actions
In this class, and are finite sets, which means that Z can also be taken to be finite.
B.2. Finite Except for Spot Transfers
In this class, each joint action can be written as , where is a monetary transfer in the current period. For each , the feasible joint actions satisfy for some set . The default action specifies a transfer of zero. Let . The sets and are assumed to be finite and there is a correspondence such that, for each and , we have .
Furthermore, there exist functions and , such that, for each , , and , the payoff vector in the current period satisfies and the transition function satisfies . Thus, the action spaces and state transition do not depend on transfers made previously, and the transfers affect payoffs additively. The assumptions imply that Z can be taken to be finite.
B.3. Relationships that are Finite Except for Contingent Transfers
I shall first describe the particular structure of this setting and then show how it maps into the general model. In a nutshell, there is an externally enforced productive action p and an externally enforced transfer m in each period, in addition to the individual action a. This public action takes place at the end of the period and is conditioned on the history as specified by the externally enforced component of the players’ contract. Assume , , and , for some sets and , and assume that . Payoffs and feasible actions are assumed to be functions of the productive actions and p taken in each period.
Let H denote the set of histories of productive actions (the a’s and p’s); a representative t-period history is . The initial, null history is defined as . There is a set of terminal histories . Let denote the non-terminal histories. For , the set of feasible individual actions is , where does not depend on the history (this is without loss of generality) and we have . Given h and , the set of feasible public actions is . From history h, if a and p are the individual and public actions selected in the current period, then the history at the start of the next period is , where is the history formed by appending a and p to h.
The players’ externally enforced contract is a vector of functions , with the mappings defined as , , and , with the property that . Given history h to the start of the current period, is the probability distribution for Nature’s action that the contract specifies. For history h and individual action profile a in the current period, the contract specifies (and the external enforcer compels) the productive action and the monetary transfer . Note that the contract can effectively randomize over productive actions by using the random draw . Thus, the function ρ can be viewed as a mapping from to . To represent limited verifiability, we can suppose that ρ and μ are measurable with respect to some partition of .
There is an initial contract in place at the start of the first period. At the beginning of each period, the players can renegotiate the contract. Assume, however, that when renegotiating from any history h, the players are restricted to contracts that are consistent with h occurring—that is, the players are renegotiating on the contractual terms for only the current and future periods. To make this formal, consider some -period history . Contract x is consistent with h if for , where is the t-period truncation (the first t elements) of h. Let denote the set of contracts that are consistent with history h and that satisfy the measurability requirement relative to , with the understanding that all contracts are consistent with .
Payoffs are linear in money and are defined by a function . Specifically, in a period that began with history h and saw productive actions a and p and transfer m (that is, and ), the payoff vector is given by , where . Assume that the function depends neither on the current-period random draw nor on the history of random draws.
I make the following extra technical assumptions. First, I assume that and are finite sets, implying that H is finite. Second, I assume that M is compact and contains the zero transfer . Third, I assume that there is a positive integer τ such that all feasible histories are no more than τ periods in length; this implies Assumption 2.
Here is how the setting of Finite Except for Contingent Transfers maps into the general model. A state is given by , where h is the history of productive actions to the current period and is the contract in effect at the beginning of this period. The set of states is . In the negotiation phase in state , players renegotiate their externally enforced contract by taking a joint action , where is the set of all contracts of the form as described above. The set of feasible joint actions is and the default joint action is . In the individual-action phase, feasible actions are given by . The payoff function is given by , where ρ and μ are components of x. Finally, for any state z, joint action , and individual action profile a, the state transition is given by .
Note that , as a probability distribution over the finite set , is a point in the -dimensional simplex. Also, ρ is a function with a finite domain and codomain, and μ has finite domain and compact codomain. Thus, and are compact subsets of a Euclidean space. That H is finite further implies that Z is compact.
The MW example described in
Section 5.1 (and less formally in the Introduction) is finite except for contingent transfers. The MW example is especially simple in that there is no public productive action
p and no random draw
. Also fitting into this class is the finite-period contracting model of Watson (2005) [
2].
11 B.4. Existence Results
I next provide existence results for the three classes of games just described. To state the first existence result, I use the following definition.
Definition 9: A bargaining solution S is said to be regular if it is non-empty and compact-valued on the set of contracting problems that satisfy Assumption 1.
The three benchmark solutions described in
Section 3.6 and the solution describes in
Section 5.2 are all regular.
Theorem 3: Take as given a contractual relationship and a regular bargaining solution S. If the contractual relationship satisfies Assumption 2 and either has finite actions or is finite except for spot transfers, then contractual equilibrium exists.
The second existence result focuses on settings with externally enforced transfers and some verifiability of actions. Additional assumptions on the bargaining solution are required for this case. In the following definitions, it is understood that , , , and .
Definition 10: A bargaining solution S is said to be continuous in the disagreement set if the following holds for any given X, , , , and sequence , such that and converges to in the Hausdorff metric. We have that converges to in the Hausdorff metric.
The three benchmark solutions described in
Section 3.6 and
defined in
Section 5.2 are all continuous in the disagreement set.
Theorem 4: Take as given a contractual relationship and a regular bargaining solution S. Assume that the contractual relationship satisfies Assumption 2 and is finite except for contingent transfers. If S is continuous and monotone in the disagreement set, then contractual equilibrium exists.
Proofs of the two existence results follow.
B.5. Proof of Theorem 3
Take any . Presume that V is well-defined on and that, for each state in this set, is nonempty and compact (as is true on ). I will show that these properties extend to the domain of . Take any .
Referring to Step 1 of the inductive procedure described in the proof of Theorem 1, I first show that is nonempty for each . An arbitrary function v defined on implies an induced simultaneous-move game in the individual-action phase (in state z following a joint action x). This game has action spaces and and it has payoffs given by . This is a finite game under the assumption that the contractual relationship is essentially finite; thus, the game has a Nash equilibrium, which implies that .
It is further true that is compact. To see this, note that the graph of the Nash equilibrium correspondence, as a function of the payoff parameters, is closed (see Fudenberg and Tirole 1991, Section 1.3.2 for example). Also recall that the set of feasible v functions is closed and bounded by the presumption that V is compact-valued on . These properties together imply that is closed; the boundedness of the set of v functions implies that is bounded.
I next show that the contracting problem at state satisfies Assumption 1. The preceding paragraphs establish the requirements for . To check the properties of , I examine separately the two settings covered by the theorem. In the setting of finite actions, is compact by virtue of each being compact and being finite; hence, Assumption 1 is satisfied.
In a relationship that is finite except for spot transfers,
is not compact, but the arbitrary spot transfers add only
to a compact set. To see this, note that the spot transfer in the current period affects neither incentives in this period nor feasible continuation values from the start of the next period (recall Equation (
1) and the payoff specification). Thus, for each
and
,
holds.
12 This implies that
where
The maximum exists because
is finite. The set
is therefore closed and separated by a line of negative slope, so it satisfies Assumption 1.
Moving to Step 2 of the inductive procedure, and using the assumption that S is regular, we have that exists and is compact. Thus, V extended to is nonempty and compact-valued. By induction, contractual equilibrium exists.
B.6. Proof of Theorem 4
This proof parallels that of Theorem 3. Note that, in the setting of the theorem, the set H can be partitioned into sets such that, for any and , we have if and only if and . Define and, as in the text, .
Take any . Presume that V is well-defined on and that, for each state in this set, is nonempty and compact (as is true on ). Also presume that, on this domain, V is upper hemi-continuous as a function of x on the feasible set ; that is, for a fixed , presume that is upper hemi-continuous. I will show that these properties extend to the domain of .
Take any . The argument used in the proof of Theorem 3 establishes that is nonempty and compact, for each . In addition, we have the following fact.
Lemma 5: Assume the presumptions of Theorem 4. Given , take any sequence such that for all k, (i) ; (ii) maps to and satisfies for all ; (iii) , and (iv) is an uncorrelated distribution over with being the distribution over Nature’s actions that is specified by the contract . Further suppose thatholds and the Nash equilibrium Condition (1) is satisfied (using , , , and in place of y, v, x, and ) for every k. Then there is a subsequence such that converges to some contract and converges to a point .
Proof of Lemma 5: Because is finite and is compact, we can assume (by taking a subsequence) that converges to some distribution and that converges to some contract . The structure of feasible actions implies that . Because and are finite, we can use the same argument to justify assuming that, for every , converges (to a real number). Define function by
for every , and is an arbitrary selection from for every and .
We have
for every
k, so upper hemi-continuity of
V on the domain
implies that
. Thus, we have
for every
. By the convergence of
and finiteness of
, we know that, for a fixed
a there is a history
such that
for all large
k. By construction of
, we thus have that
converges to
. Also, noting that
u is continuous, we know that
converges to
. Thus, we obtain
Another implication of the convergence is that the Nash equilibrium Condition (
1) is satisfied for
,
,
, and
in place of
y,
v,
x, and
. To see this, first note that
is independent of
x, meaning that available individual actions do not depend on the current contract. In addition, if the best-response inequality did not hold for some player
i and some action
, it would imply failure of the same best-response condition for strategy profile
in the context of contract
and continuation-value function
for large enough
k, which is a contradiction. We can thus conclude that
, proving the lemma.
Q.E.D.Returning to the proof of Theorem 4, continue to consider any . Refer to Step 1 of the inductive procedure described in the proof of Theorem 1. The argument used in the proof of Theorem 3 establishes that is nonempty for every . Lemma 5 implies that is compact and that is compact for every . For any particular x, the latter conclusion follows from looking at a sequence with and and getting . Thus, for , the contracting problem satisfies Assumption 1.
Moving to Step 2 of the inductive procedure, and using the assumption that S is regular, we have that exists and is compact. Thus, V extended to is nonempty and compact-valued.
Finally, I must establish that is upper hemi-continuous for all . To this end, fix . Note that and , for all . The second equality holds because the externally enforced contract in force at the beginning of the period ( or ) does not directly affect the attainable continuation payoffs; only the newly chosen contract x affects incentives and payoffs in the continuation. Thus, since h is fixed for the remainder of this proof, I will suppress the state argument and simply write X, , and Y. Also note that, for the fixed h, Lemma 5 implies that is upper hemi-continuous in x. This follows by limiting attention to sequences such that converges.
Next, take any specific sequence
that converges to some
. I will compare various contracting problems that are associated with the sequence. To formulate them, let
be the limit superior of
as
:
For each k, we have the contracting problem , where . Consider also the artificial contracting problem , where we define by for all . In addition, consider the contracting problem and another artificial problem , where is identical to except for joint action for which we define .
By upper hemi-continuity of , we have . Thus, and . That is, the sets of feasible continuation payoffs (over all x) in the artificial contracting problems and are the same as that in the contracting problems and . All of these contracting problems differ only in the disagreement sets. Furthermore, one can easily verify that, by construction of and because Y is compact, converges to in the Hausdorff metric.
Using the fact that
and that
S is monotone in the disagreement set, we have
Because
converges to
and
S is continuous in the disagreement set, we obtain
Finally, using the monotone property of
S again and that
, we have
Along with the sequence
, take a convergent sequence
such that
for each
k. Relations 4-6 above establish that the limit of
is contained in
, which proves upper hemi-continuity of
.
C. Other Proofs
Lemma 1, Theorem 1, and Theorem 2 are restated and proved here.
Lemma 1: If Y is convex then .
Proof: For
, let
. Further, for any fixed
, define
Consider these functions defined on strong Pareto boundary of the set
Y, where (because
Y is convex)
and
are continuous and inverses. These functions characterize the equilibrium of the
K-round bargaining protocol under the Agreement and Disagreement Conditions on
Section 3.2. Suppose, for example, that player 2 would have the offer in round
, where his equilibrium continuation value is
. Then player 1’s equilibrium offer in round
k is a vector that makes player 2 indifferent between accepting and rejecting; this offer gives player 1 the amount
, which is player 1’s equilibrium value from round
k.
Function relates player i’s equilibrium continuation values across two rounds where player i makes the offer. Convexity of Y implies that and are convex functions, which further implies that is a contraction. To see this, consider the differentiable case, where we have . Here and are numbers satisfying . Recalling that and are inverses, this implies that . Thus, .
That
is a contraction implies that player
i’s equilibrium payoff in the finite-round protocol converges to the fixed point of
, which is
i’s equilibrium payoff in the infinite-round protocol. From here, one can use the asymmetric version of Binmore, Rubinstein, and Wolinsky’s (1986) [
27] Proposition 5 to complete the proof.
Q.E.D.Theorem 1: Take as given a contractual relationship and a bargaining solution S. If Assumption 2 is satisfied and contractual equilibrium exists, then there is a unique value correspondence that represents contractual equilibrium.
Proof: A value correspondence V can be identified by backward induction, using the partition of Z that was described earlier in this section. We start with and have, for each z in this set, . Then, for any , presume that we have defined V on . We can extend V to as follows.
Step 1: For every
and every
, define
by Equation (
2). In doing so, note that
v need only be defined on
, because no other states can be reached from
z. If every
is nonempty, then this yields a well-defined contracting problem
at state
z, for every
.
Step 2: Define , for every .
If, during this procedure, we find that for some z and x in Step 1, then the correspondence V is not well-defined and contractual equilibrium does not exist. Likewise, if is empty for some z in Step 2, then contractual equilibrium does not exist. Otherwise, contractual equilibrium exists and the induction procedure identifies a unique value correspondence by construction. Q.E.D.
Theorem 2: Consider a contractual relationship given be a sequence of stage games with spot transfers. Let S and be bargaining solutions that are shift-monotone and invariant to additive constants, and suppose that represents more active contracting than does S. Assume that contractual equilibrium exists for both S and . Let be the contractual equilibrium values for , and let be the contractual equilibrium values for S. Then for each , there exists a vector such that .
Proof: I use an induction argument. Define , which trivially satisfies for . Next suppose that, for some , there is a vector such that . I will show that this implies the existence of a vector such that .
Consider the set of feasible continuation values from period
t. These are the sum of stage-game payoffs in period
t and continuation payoffs from period
, where the action profile in period
t must satisfy the equilibrium incentive condition given by Equation (
1) in
Section 4.2. Recalling Equation (
2), clearly the set of supported action profiles, and thus the set of feasible continuation values, expands with the set of continuation values from period
; furthermore, the continuation values merely shift with an additive constant. This implies that
and
. Because
represents more active contracting than does
S, we obtain:
Because
S is shift-monotone, there is a vector
such that
Finally, because
S is invariant to additive constants, we have
Defining
, which is in
, and combining Equations (
7)–(
9), we obtain
Noting that
and
completes the inductive step.
Q.E.D.

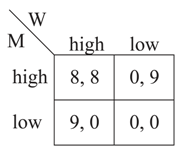
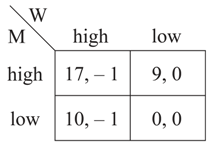
Note that, for this matrix, , , and are the Nash equilibria, and these are ex post inefficient.2 The players agree that, in the event that they fail to renegotiate in the second period, the equilibrium on which they coordinate will be conditioned on the worker’s investment choice. Specifically, if the worker chose then they coordinate on equilibrium , whereas if then they coordinate on equilibrium . That is, the disagreement point for second-period negotiation depends on the worker’s action in the first period.
Assume that the players do renegotiate in the second period so that the efficient profile is achieved. The joint surplus of renegotiation is . Suppose that player 1 has all of the bargaining power and thus negotiates a transfer that gives him the entire surplus. The worker therefore gets 9 if is the disagreement point, whereas he gets 0 if is the disagreement point. Clearly, with this contractual arrangement, the worker optimally selects in the first period.
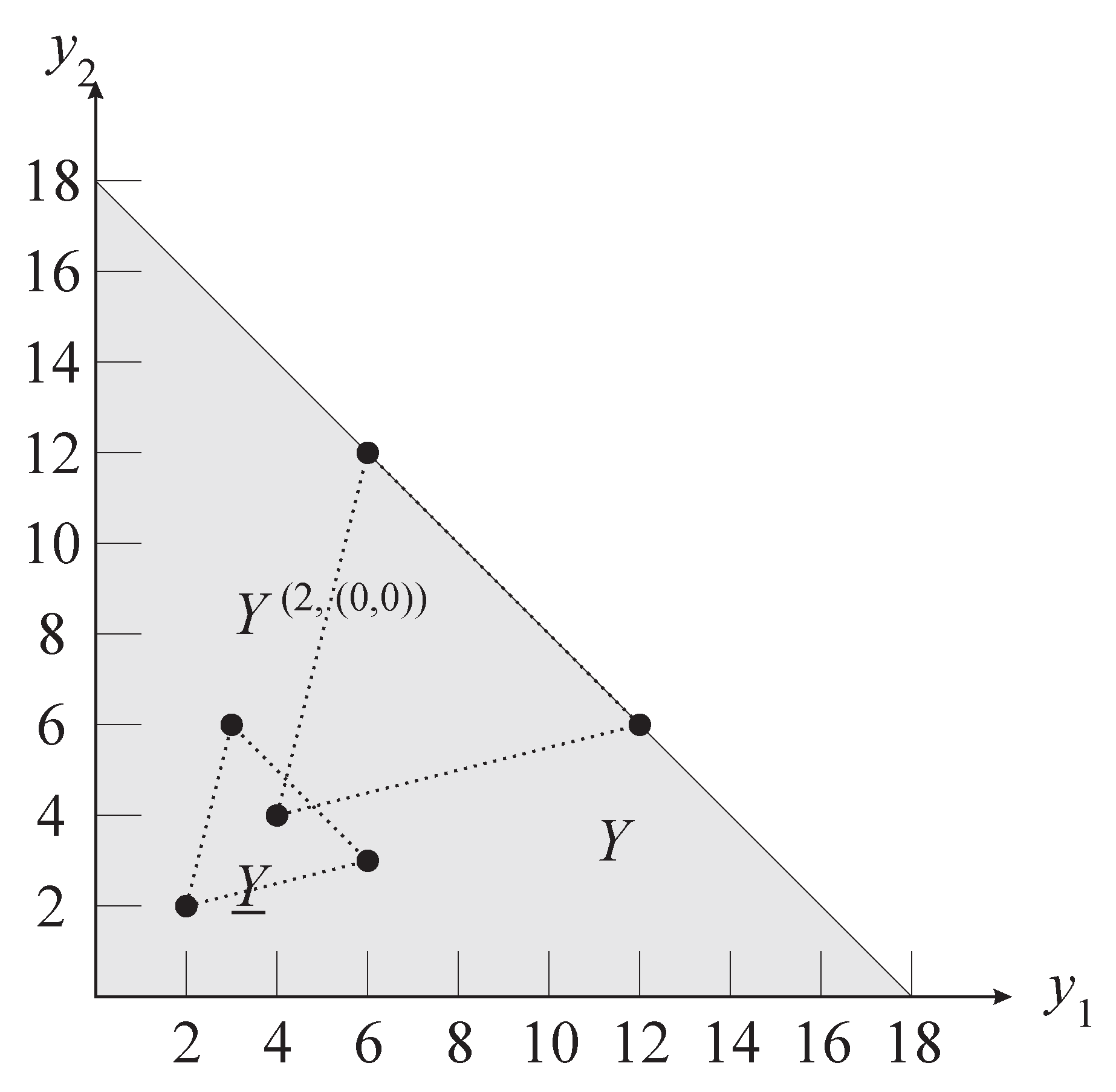

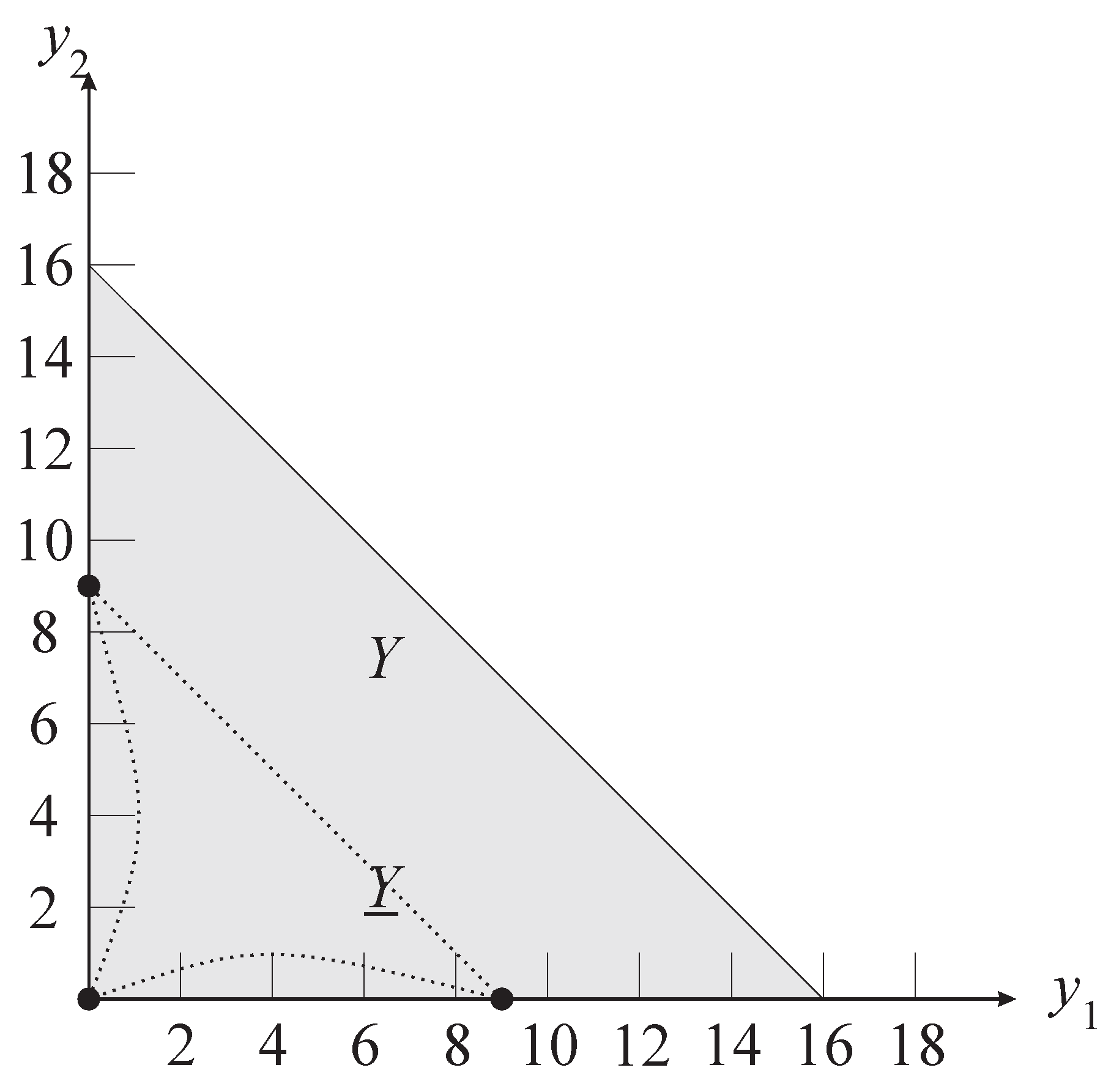


 that is relevant for action profile a.
that is relevant for action profile a.