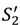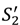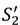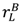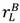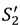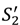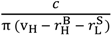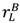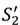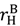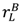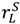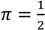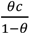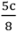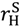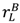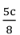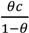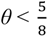Noncontractible Investments and Reference Points
Winner of the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2016
Abstract
:1. Introduction
2. The Model
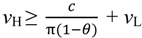
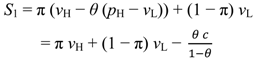
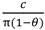 + vL, pL = vL, the “efficient trade” contract, since λ = 1 in both states.
+ vL, pL = vL, the “efficient trade” contract, since λ = 1 in both states.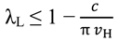
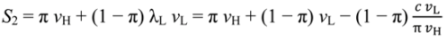
 , pH =
, pH = 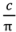 + λLvL, pL = λLvL, the “no aggrievement” contract.
+ λLvL, pL = λLvL, the “no aggrievement” contract.- (1)
- If max (vL, S1 − c, S2 − c) = vL the optimal contract is specific performance. Net surplus is vL.
- (2)
- If max (vL, S1 − c, S2 − c) > vL then there is an optimal contract of the following form: the seller chooses between (λH, pH) and (λL, pL) at date 1 and the buyer can reject without penalty (leading to no trade), where
- (2a)
- If max (vL, S1 − c, S2 – c) = S1 − c, λH = λL = 1, pH =
+ vL, pL = vL (the “efficient trade” contract). Net surplus is S1 − c.
- (2b)
- If max (vL, S1 − c, S2 − c) = S2 − c, λH = 1, λL = 1 –
, pH =
+ λL vL, pL = λLvL (the “no aggrievement” contract). Net surplus is S2 − c.
3. Asset Ownership and Outside Options
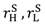 in the high value and low value state, respectively, without trading with the buyer; and the buyer to achieve
in the high value and low value state, respectively, without trading with the buyer; and the buyer to achieve 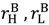 in the high value and low value state without trading with the seller. Note that the buyer’s outside option may vary with the seller’s investment to the extent that the seller’s noncontractible investment in quality can be appropriated by the buyer, e.g., it is embodied in a physical asset rather than in the seller’s human capital or represents an idea that the buyer can “steal”.
in the high value and low value state without trading with the seller. Note that the buyer’s outside option may vary with the seller’s investment to the extent that the seller’s noncontractible investment in quality can be appropriated by the buyer, e.g., it is embodied in a physical asset rather than in the seller’s human capital or represents an idea that the buyer can “steal”.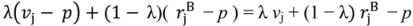
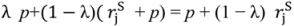
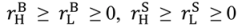
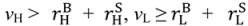
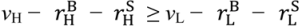
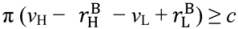
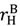 =
= 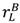 , and (17) is implied by (2). (16) and (17) both limit how much
, and (17) is implied by (2). (16) and (17) both limit how much 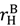 can exceed
can exceed 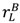 10.
10.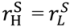
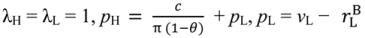
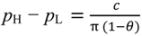 in the good state since the seller earns above her outside option when receiving pL ((15) and (18) imply that
in the good state since the seller earns above her outside option when receiving pL ((15) and (18) imply that 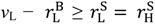 ); hence, the buyer feels entitled to pay pL. The seller is indifferent between investing and not (see (3) with vL replaced by pL). The condition that the buyer does not quit in the good state is
); hence, the buyer feels entitled to pay pL. The seller is indifferent between investing and not (see (3) with vL replaced by pL). The condition that the buyer does not quit in the good state is
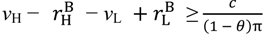
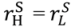
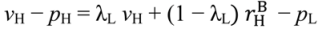
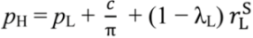
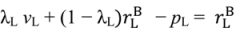
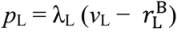
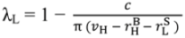
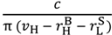 , pH =
, pH = 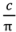 +
+ 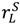 + λL
+ λL 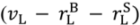 , pL = λL(vL −
, pL = λL(vL − 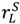 ). Surplus under the “no aggrievement” contract is
). Surplus under the “no aggrievement” contract is
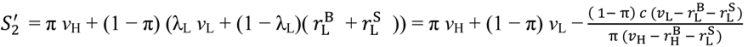
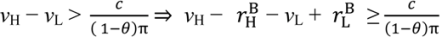
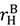 is close to
is close to 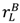 (and certainly if
(and certainly if 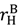 =
= 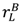 ).
).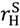 =
= 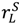 and (27). Then:
and (27). Then:
- (1)
- If max (vL, S1 − c,
− c) = vL the optimal contract is specific performance. Net surplus is vL.
- (2)
- If max (vL, S1 − c,
− c) > vL, then there is an optimal contract of the following form: the seller chooses between (λH, pH) and (λL, pL) at date 1 and the buyer can reject without penalty (leading to no trade), where
- (2a)
- If max (vL, S1 − c,
− c) = S1 − c, λH = λL = 1, pH =
+ vL −
, pL = vL −
(the “efficient trade” contract). Net surplus is S1 − c.
- (2b)
- If max (vL, S1 − c,
− c) =
− c, λH = 1, λL = 1 −
, pH =
+
+ λL(vL −
−
), pL = λL (vL −
)( the “no aggrievement” contract). Net surplus is
− c.
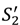 we see that the presence of an outside option for the seller strictly increases surplus in the “no aggrievement” contract:
we see that the presence of an outside option for the seller strictly increases surplus in the “no aggrievement” contract: 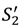 = S2 when
= S2 when 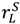 =
= 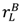 =
= 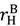 = 0 and
= 0 and 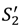 is strictly increasing in
is strictly increasing in 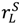 . However, the effect of an outside option for the buyer is ambiguous.
. However, the effect of an outside option for the buyer is ambiguous. 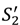 strictly increases if
strictly increases if 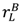 goes up, or if
goes up, or if 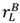 ,
, 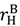 go up equally, but it strictly decreases if
go up equally, but it strictly decreases if 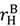 goes up. The intuition behind these results is as follows. An increase in
goes up. The intuition behind these results is as follows. An increase in 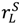 has two effects. It decreases the seller’s incentive to invest and hence λL in (25) must fall to compensate for this; but it also decreases the effects of inefficient trade since value outside the relationship is higher. The second effect dominates. An increase in
has two effects. It decreases the seller’s incentive to invest and hence λL in (25) must fall to compensate for this; but it also decreases the effects of inefficient trade since value outside the relationship is higher. The second effect dominates. An increase in 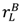 has only the second effect and so increases surplus. An increase in
has only the second effect and so increases surplus. An increase in 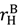 unambiguously decreases surplus because it reduces the amount the seller can be paid in the good state and hence λL in (25) must fall to restore the seller’s investment incentives; and the increase in
unambiguously decreases surplus because it reduces the amount the seller can be paid in the good state and hence λL in (25) must fall to restore the seller’s investment incentives; and the increase in 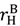 has no beneficial effect on ex post efficiency since λH = 1, i.e.,
has no beneficial effect on ex post efficiency since λH = 1, i.e., 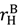 is never earned.
is never earned.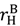 =
= 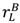
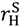 >
> 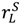 . This case is in many ways more interesting since the property rights literature suggests that a higher outside option in the good state will encourage the seller to invest. Unfortunately, the case is also more complex, the results of Section 4 do not apply, and I have been unable to solve for an optimal contract. Thus, we will simply characterize some leading contracts.
. This case is in many ways more interesting since the property rights literature suggests that a higher outside option in the good state will encourage the seller to invest. Unfortunately, the case is also more complex, the results of Section 4 do not apply, and I have been unable to solve for an optimal contract. Thus, we will simply characterize some leading contracts.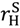 in the good state and so if
in the good state and so if 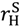 > vL −
> vL − 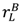 , his aggrievement and shading in the good state will be lower than before (previously the buyer felt entitled to pay vL –
, his aggrievement and shading in the good state will be lower than before (previously the buyer felt entitled to pay vL – 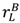 ). In fact, if π (
). In fact, if π ( 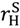 +
+ 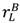 – vL) ≥ c, we can achieve the first-best: set pL = vL −
– vL) ≥ c, we can achieve the first-best: set pL = vL − 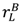 , pH =
, pH = 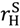 . The buyer is not aggrieved in the good state because he does not feel entitled to an outcome where the seller would quit; and the buyer does not quit himself since, by (15), vH −
. The buyer is not aggrieved in the good state because he does not feel entitled to an outcome where the seller would quit; and the buyer does not quit himself since, by (15), vH − 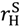 >
> 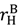 . The buyer is not aggrieved in the bad state since he pays the lowest price. The seller is not aggrieved in the good state since she receives the highest price, and she is not aggrieved in the bad state since the buyer’s participation constraint is binding. Finally, the seller has an incentive to invest since π (
. The buyer is not aggrieved in the bad state since he pays the lowest price. The seller is not aggrieved in the good state since she receives the highest price, and she is not aggrieved in the bad state since the buyer’s participation constraint is binding. Finally, the seller has an incentive to invest since π ( 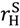 +
+ 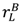 – vL) ≥ c.
– vL) ≥ c.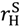 > vL −
> vL − 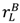 but that π (
but that π ( 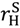 +
+ 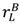 − vL) < c.Now the first-best cannot be achieved. The constraint that the seller is just willing to invest becomes
− vL) < c.Now the first-best cannot be achieved. The constraint that the seller is just willing to invest becomes
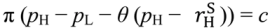
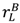 , so that the buyer’s participation constraint is binding in the bad state,
, so that the buyer’s participation constraint is binding in the bad state,
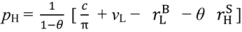
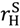 ), social surplus is
), social surplus is

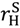 > vL –
> vL – 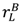 . Here the analysis is as in Section 2. Combining the above three cases, we can write the general formula for the gross social surplus from the “efficient trade” contract as
. Here the analysis is as in Section 2. Combining the above three cases, we can write the general formula for the gross social surplus from the “efficient trade” contract as

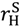 > vL −
> vL − 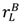 and
and 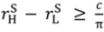 , there is now a second “no aggrievement” contract. To see why, suppose that we set λH = 1 and pH =
, there is now a second “no aggrievement” contract. To see why, suppose that we set λH = 1 and pH = 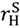 . Then because the buyer does not expect the seller to earn less than her outside option the buyer will not be aggrieved in the good state even if he strictly prefers (λL, pL) to (λH, pH). Now choose (λL, pL) so that the buyer’s participation constraint is binding in the bad state and the seller has an incentive to invest:
. Then because the buyer does not expect the seller to earn less than her outside option the buyer will not be aggrieved in the good state even if he strictly prefers (λL, pL) to (λH, pH). Now choose (λL, pL) so that the buyer’s participation constraint is binding in the bad state and the seller has an incentive to invest:
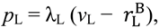
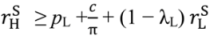
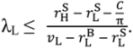
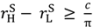 : without this, λL would be negative. For ex post efficiency reasons we want λL to be as large as possible, but λL cannot exceed 1. Thus maximal gross surplus from this second “no aggrievement” contract is
: without this, λL would be negative. For ex post efficiency reasons we want λL to be as large as possible, but λL cannot exceed 1. Thus maximal gross surplus from this second “no aggrievement” contract is
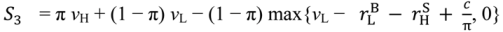
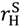 > vL −
> vL − 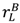 . If this did not hold, the buyer would not prefer (λL, pL) to (λH, pH), the seller would choose (λH, pH) in the bad state, and this would not give her the right incentive to invest. To sum up:
. If this did not hold, the buyer would not prefer (λL, pL) to (λH, pH), the seller would choose (λH, pH) in the bad state, and this would not give her the right incentive to invest. To sum up: 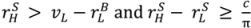 , there is a second “no aggrievement” contract,
λH = 1,
, there is a second “no aggrievement” contract,
λH = 1, 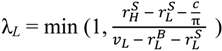 , pH =
, pH = 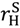 , pL = λL (vL −
, pL = λL (vL − 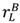 ), yielding gross surplus
), yielding gross surplus 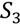 = π vH + (1 − π) vL − (1 − π) max{ vL −
= π vH + (1 − π) vL − (1 − π) max{ vL − 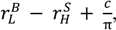 0}.
0}.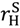 >
> 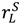 : the efficient trade contract, the “no aggrievement” contract of Proposition 2, and, if
: the efficient trade contract, the “no aggrievement” contract of Proposition 2, and, if 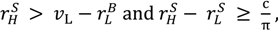 , a new “no aggrievement” contract. In general, when
, a new “no aggrievement” contract. In general, when 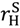 >
> 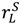 , other contracts may do even better.12 However, the contracts that we have identified provide a lower bound for what can be achieved.
, other contracts may do even better.12 However, the contracts that we have identified provide a lower bound for what can be achieved.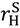 >
> 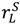 and (27). Then an optimal contract yields surplus at least equal to max (vL,
and (27). Then an optimal contract yields surplus at least equal to max (vL, 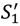 − c,
− c, 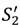 − c, S3 − c).
− c, S3 − c).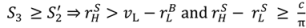 and so we do not need to include these inequalities as extra conditions in Proposition 3 (see (*)).
and so we do not need to include these inequalities as extra conditions in Proposition 3 (see (*)). 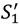 = S1,
= S1, 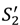 = S2 when all outside options are zero. Also
= S2 when all outside options are zero. Also 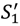 ,
, 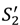 are increasing in the seller’s outside options. We may conclude that as in the case
are increasing in the seller’s outside options. We may conclude that as in the case 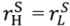 the presence of seller outside options increases surplus. The effect of buyer options on surplus is again ambiguous. However, since
the presence of seller outside options increases surplus. The effect of buyer options on surplus is again ambiguous. However, since 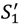 and S3 are increasing in these options, and
and S3 are increasing in these options, and 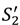 is increasing in them if
is increasing in them if 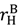 =
= 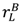 , buyer outside options are unambiguously good for surplus when
, buyer outside options are unambiguously good for surplus when 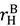 =
= 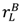
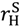 ,
, 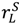 and (
and ( 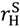 −
− 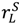 ) rise weakly, and
) rise weakly, and 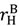 ,
, 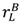 and (
and ( 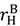 −
− 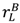 ) fall weakly; and vice versa if ownership shifts from the seller to the buyer.
) fall weakly; and vice versa if ownership shifts from the seller to the buyer.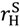 ≡
≡ 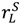 (that is,
(that is, 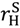 =
= 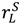 for all asset allocations), and (27) holds. Then Proposition 2 tells us that outside options matter only if the “no aggrievement” contract in (2b) is optimal. In this case it follows from (26) that, keeping
for all asset allocations), and (27) holds. Then Proposition 2 tells us that outside options matter only if the “no aggrievement” contract in (2b) is optimal. In this case it follows from (26) that, keeping 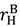 −
− 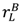 constant, it is optimal to allocate assets to maximize
constant, it is optimal to allocate assets to maximize 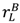 +
+ 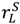 and, keeping
and, keeping 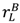 +
+ 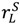 constant, it is optimal to allocate assets to minimize
constant, it is optimal to allocate assets to minimize 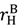 −
− 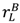 . The first goal improves ex post efficiency whereas the second goal helps with investment incentives. According to (**), the second goal is achieved by allocating ownership to the seller. However, it is possible that the buyer has greater use for the assets than the seller if the relationship breaks down in the bad state, in which case the first goal—maximizing
. The first goal improves ex post efficiency whereas the second goal helps with investment incentives. According to (**), the second goal is achieved by allocating ownership to the seller. However, it is possible that the buyer has greater use for the assets than the seller if the relationship breaks down in the bad state, in which case the first goal—maximizing 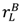 +
+ 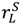 — would be achieved by allocating ownership to the buyer. Thus in general there is a trade-off.
— would be achieved by allocating ownership to the buyer. Thus in general there is a trade-off.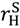 ≡
≡ 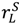 and (27). Then it is optimal for the seller to own any asset that is idiosyncratic to her.
and (27). Then it is optimal for the seller to own any asset that is idiosyncratic to her.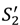 and note that
and note that 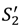 is strictly increasing in
is strictly increasing in 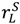 .
.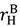 −
− 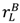 and interfere with the seller’s investment incentives. However, Proposition 4 does extend to the buyer if
and interfere with the seller’s investment incentives. However, Proposition 4 does extend to the buyer if 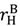 ≡
≡ 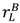 (that is,
(that is, 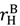 =
= 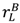 for all asset allocations).
for all asset allocations).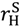 ≡
≡ 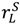 , (27), and
, (27), and 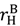 ≡
≡ 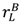 . Then it is optimal for the seller to own any asset that is idiosyncratic to her and for the buyer to own any asset that is idiosyncratic to him.
. Then it is optimal for the seller to own any asset that is idiosyncratic to her and for the buyer to own any asset that is idiosyncratic to him.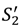 and note that
and note that 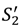 is strictly increasing in
is strictly increasing in 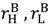 if they are equal.
if they are equal.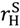 >
> 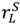 . Here less can be said because we have not characterized an optimal contract. However, we know that seller outside options are good for surplus in this case too. Thus, we can make the following observation. Take the view that, if all the assets are jointly owned, then outside options are zero: we are in the situation of Section 2. Now allocate all the assets to the seller. Given (**) the seller’s outside options rise at least weakly and the buyer’s outside options remain at zero. Apply Proposition 3. This tells us that surplus rises (at least weakly) since
. Here less can be said because we have not characterized an optimal contract. However, we know that seller outside options are good for surplus in this case too. Thus, we can make the following observation. Take the view that, if all the assets are jointly owned, then outside options are zero: we are in the situation of Section 2. Now allocate all the assets to the seller. Given (**) the seller’s outside options rise at least weakly and the buyer’s outside options remain at zero. Apply Proposition 3. This tells us that surplus rises (at least weakly) since 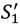 ≥ S1 ,
≥ S1 , 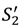 ≥ S2.
≥ S2.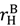 =
= 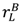 =
= 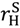 =
= 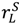 = 0. Then if ownership of each asset is allocated to the seller, surplus rises weakly. Furthermore it rises strictly if
= 0. Then if ownership of each asset is allocated to the seller, surplus rises weakly. Furthermore it rises strictly if 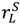 > 0,
> 0, 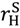 > vL −
> vL − 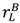 and max {
and max { 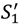 − c,
− c, 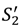 − c, S3 − c} >vL.
− c, S3 − c} >vL.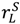 > 0 and
> 0 and 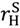 > vL −
> vL − 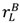 , and
, and 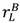 =
= 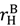 = 0, the right-hand side of (31), (26) exceeds that of (7), (11), respectively.
= 0, the right-hand side of (31), (26) exceeds that of (7), (11), respectively. 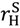 ≡
≡ 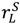 , since we already know that in this case seller outside options increase surplus.
, since we already know that in this case seller outside options increase surplus. 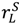 reduces ex post inefficiency if λL < 1, raising
reduces ex post inefficiency if λL < 1, raising 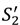 (see (26)); and an increase in
(see (26)); and an increase in 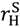 makes it easier to reward the seller in the good state without causing buyer aggrievement:
makes it easier to reward the seller in the good state without causing buyer aggrievement: 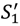 rises (see (32)). The buyer’s outside options do not change since they were zero under joint ownership and are also zero when the seller owns all the assets. Finally, the new outcome yielding S3 may become available (see (35)).
rises (see (32)). The buyer’s outside options do not change since they were zero under joint ownership and are also zero when the seller owns all the assets. Finally, the new outcome yielding S3 may become available (see (35)).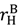 ≡
≡ 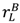 . Suppose that shifting ownership of all the assets to the buyer increases his outside option by an amount k in the low state and at least k in the high state, while shifting ownership to the seller increases her outside option by k in the low state and at least k in the high state. (In a sense, asset ownership has an equally powerful effect on the buyer and seller.) Then, it is easily seen from Propositions 2 and 3 that surplus under seller ownership is at least as high as under buyer ownership. Therefore, seller ownership is better than buyer ownership. The intuition is that asset ownership has an extra kick for the seller since it may improve her investment incentives.
. Suppose that shifting ownership of all the assets to the buyer increases his outside option by an amount k in the low state and at least k in the high state, while shifting ownership to the seller increases her outside option by k in the low state and at least k in the high state. (In a sense, asset ownership has an equally powerful effect on the buyer and seller.) Then, it is easily seen from Propositions 2 and 3 that surplus under seller ownership is at least as high as under buyer ownership. Therefore, seller ownership is better than buyer ownership. The intuition is that asset ownership has an extra kick for the seller since it may improve her investment incentives.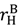 ≡
≡ 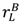 ).
).4. More General Contracts
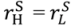 = rS, say—the contracts described in Propositions 1 and 2 are optimal among a class of contracts that includes revelation mechanisms.
= rS, say—the contracts described in Propositions 1 and 2 are optimal among a class of contracts that includes revelation mechanisms.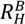 for the buyer’s reservation payoff in the good state and
for the buyer’s reservation payoff in the good state and 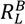 for his reservation payoff in the bad state.
for his reservation payoff in the bad state. 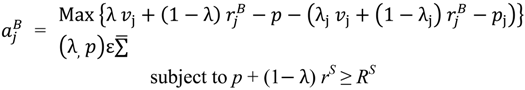

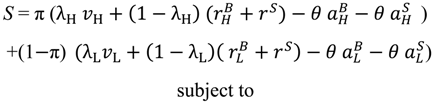
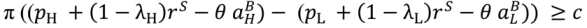
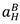 ,
, 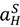 ,
, 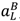 ,
,  are given by (36)–(37) and (λj, pj) is an equilibrium of the mechanism in state j, j = H, L.
are given by (36)–(37) and (λj, pj) is an equilibrium of the mechanism in state j, j = H, L.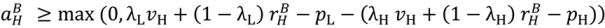
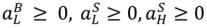
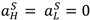 . Also, if λH < 1, S can be raised by increasing λH and pH such that pH − λHrS stays constant, since this increases λH (vH −
. Also, if λH < 1, S can be raised by increasing λH and pH such that pH − λHrS stays constant, since this increases λH (vH − 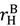 ) − pH and hence reduces the right-hand side of (41), and does not disturb (39). Hence λH = 1. In addition, we always want
) − pH and hence reduces the right-hand side of (41), and does not disturb (39). Hence λH = 1. In addition, we always want 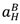 as low as possible. Hence (41) holds with equality. Finally, if (39) holds strictly, we can increase S by lowering pH. Hence (39) holds with equality.
as low as possible. Hence (41) holds with equality. Finally, if (39) holds strictly, we can increase S by lowering pH. Hence (39) holds with equality.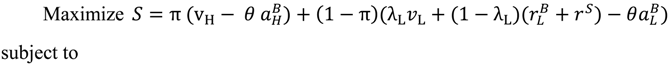
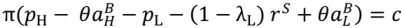
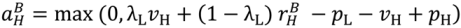

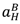 ,
, 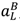 , λL pL, pH.
, λL pL, pH. 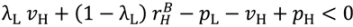 .
.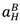 = 0. Furthermore raising λL a little, and adjusting pH to satisfy (44), increases S. Hence at an optimum λL = 1. It follows from the definition of Case 1 that pH < pL, but then (44) can hold only if
= 0. Furthermore raising λL a little, and adjusting pH to satisfy (44), increases S. Hence at an optimum λL = 1. It follows from the definition of Case 1 that pH < pL, but then (44) can hold only if 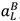 > 0. In this case reducing
> 0. In this case reducing 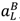 a little and raising pH to keep (44) satisfied increases S. Contradiction.
a little and raising pH to keep (44) satisfied increases S. Contradiction.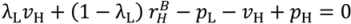 .
.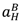 = 0. Combining (44) with the definition of Case 2 yields
= 0. Combining (44) with the definition of Case 2 yields
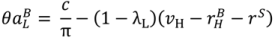
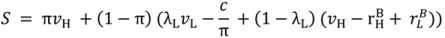
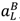 = 0 in (47) or λL = 0. But (15) and (17) imply that
= 0 in (47) or λL = 0. But (15) and (17) imply that 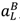 ≤ 0 if λL = 0 .
≤ 0 if λL = 0 .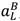 = 0 and we can solve (47) to obtain
= 0 and we can solve (47) to obtain
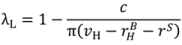
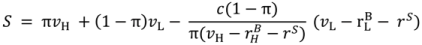
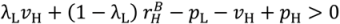 .
.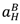 > 0. Using (44) and (45) to solve for
> 0. Using (44) and (45) to solve for 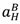 and substituting into (43), we can easily see that S is linear in λL and
and substituting into (43), we can easily see that S is linear in λL and 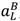 .
.
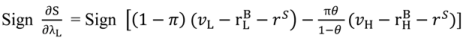
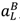 > 0. Then
> 0. Then 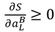 at an optimum and so (51) implies πθ ≥ (1 − π)(1 − θ). But this means, given (52) and (15), that
at an optimum and so (51) implies πθ ≥ (1 − π)(1 − θ). But this means, given (52) and (15), that 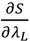 ≤0.
≤0.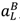 > 0, than in the “no aggrievement” contract identified in Case 2. Hence λH = 1, λL = 0,
> 0, than in the “no aggrievement” contract identified in Case 2. Hence λH = 1, λL = 0, 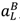 > 0 cannot be optimal.
> 0 cannot be optimal.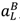 = 0. Since S is linear in λL, either λL = 0 or λL = 1 is optimal (or all 0 ≤ λL ≤ 1). We have already argued that λH = 1, λL = 0 is (weakly) dominated by the “no aggrievement” contract in Case 2. All that remains is λH = λL = 1. But this is the other contract considered in Proposition 2.
= 0. Since S is linear in λL, either λL = 0 or λL = 1 is optimal (or all 0 ≤ λL ≤ 1). We have already argued that λH = 1, λL = 0 is (weakly) dominated by the “no aggrievement” contract in Case 2. All that remains is λH = λL = 1. But this is the other contract considered in Proposition 2.
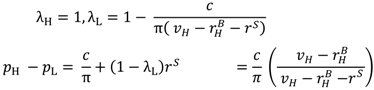
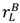 in the first contract and pL = λL(vL −
in the first contract and pL = λL(vL − 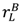 ) in the second. Then it is easy to check that the outcomes in (53) and (54) can both be implemented by allowing the seller to choose between (λH, pH) and (λL, pL) at date 1 with the buyer able to say no, i.e., to quit without penalty. For the argument to work in the case of (53) we need to be sure that (20) holds since otherwise the buyer will quit in the good state. However, as noted in Section 3, if the λL = λH = 1 outcome in (53) is strictly superior to specific performance, then the first inequality in (27) holds. Hence by (27), (20) does indeed hold.
) in the second. Then it is easy to check that the outcomes in (53) and (54) can both be implemented by allowing the seller to choose between (λH, pH) and (λL, pL) at date 1 with the buyer able to say no, i.e., to quit without penalty. For the argument to work in the case of (53) we need to be sure that (20) holds since otherwise the buyer will quit in the good state. However, as noted in Section 3, if the λL = λH = 1 outcome in (53) is strictly superior to specific performance, then the first inequality in (27) holds. Hence by (27), (20) does indeed hold.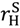 >
> 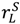 . The reason is that in the good state of the world (λL, pL) may be below the seller’s reservation level and so the buyer may not feel entitled to it. However, following our earlier discussion, if (λH, pH) provides the seller with strictly more than her reservation payoff in the good state, the buyer will feel entitled to a convex combination of (λH, pH) and (λL, pL) such that the seller receives her reservation payoff in expected turns. Convexification destroys the linearity that made the above analysis relatively simple, and I have been unable to characterize an optimum in this case. Among other things it is possible that an optimal contract will now consist of more than two trade-price vectors (This may also be a feature of an optimal contract when (27) fails to hold.).
. The reason is that in the good state of the world (λL, pL) may be below the seller’s reservation level and so the buyer may not feel entitled to it. However, following our earlier discussion, if (λH, pH) provides the seller with strictly more than her reservation payoff in the good state, the buyer will feel entitled to a convex combination of (λH, pH) and (λL, pL) such that the seller receives her reservation payoff in expected turns. Convexification destroys the linearity that made the above analysis relatively simple, and I have been unable to characterize an optimum in this case. Among other things it is possible that an optimal contract will now consist of more than two trade-price vectors (This may also be a feature of an optimal contract when (27) fails to hold.).5. Conclusions
Acknowledgments
Conflict of Interest
References
- Grossman, S.J.; Hart, O. The costs and benefits of ownership: A theory of vertical and lateral integration. J. Polit. Econ. 1986, 94, 691–719. [Google Scholar]
- Hart, O.; Moore, J. Property rights and the nature of the firm. J. Polit. Economy 1990, 98, 1119–1158. [Google Scholar]
- Hart, O. Firms, Contracts, and Financial Structure; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Aghion, P.; Holden, R. Incomplete contracts and the theory of the firm: What have we learned over the past 25 years? J. Econ. Perspect. 2011, 25, 181–197. [Google Scholar] [CrossRef]
- Woodruff, C. Non-Contractible investments and vertical integration in the Mexican footwear industry. Int. J. Ind. Organ. 2002, 20, 1197–1224. [Google Scholar] [CrossRef]
- Baker, G.P.; Hubbard, T. Make v. Buy in trucking: Asset ownership, job design and information. Am. Econ. Rev. 2003, 93, 551–572. [Google Scholar] [CrossRef]
- Baker, G.P.; Hubbard, T. Contractibility and asset ownership: On-Board computers and governance in US Trucking. Q. J. Econ. 2004, 119, 1443–1480. [Google Scholar] [CrossRef]
- Acemoglu, D.; Aghion, P.; Griffith, R.; Zilibotti, F. Vertical integration and technology: Theory and evidence. J. Eur. Econ. Assoc. 2010, 8, 2–45. [Google Scholar]
- Gebhardt, G. Does relationship specific investment depend on asset ownership? Evidence from a natural experiment in the housing market. J. Eur. Econ. Assoc. 2013, 11, 201–227. [Google Scholar] [CrossRef]
- Lafontaine, F.; Slade, M. Vertical integration and firm boundaries: The evidence. J. Econ. Lit. 2007, 45, 629–685. [Google Scholar] [CrossRef]
- Hart, O.; Moore, J. Contracts as reference points. Q. J. Econ. 2008, 123, 1–48. [Google Scholar] [CrossRef]
- Fehr, E.; Hart, O.; Zehnder, C. Contracts as reference points – experimental evidence. Am. Econ. Rev. 2011, 101, 493–525. [Google Scholar] [CrossRef]
- Aghion, P.; Fudenberg, D.; Holden, R.; Kunimoto, T.; Tercieu, O. Subgame-Perfect implementation under value perturbations. Q. J. Econ. 2012, 127, 1843–1881. [Google Scholar] [CrossRef]
- Halonen-Akatwijuka, M.; Hart, O. More is less: Why parties may deliberately write incomplete contract. 2013. NBER working paper #19001(submitted). Available online: http://scholar.harvard.edu/hart/publications/more-less-why-parties-may-deliberately-write-incomplete-contracts (accessed on 12 August 2013).
- Fehr, E.; Schmidt, K. Theories of Fairness and Reciprocity: Evidence and Economic Applications. In Advances in Economics and Econometrics: Theory and Applications, Eighth World Congress; Dewatripont, M., Hansen, L.P., Turnovsky, S.J., Eds.; Cambridge University Press: Cambridge, UK, 2003; Volume 1, pp. 208–257. [Google Scholar]
- Hart, O. Hold-up, asset ownership, and reference points. Q. J. Econ. 2009, 124, 267–300. [Google Scholar] [CrossRef]
- Hart, O.; Holmstrom, B. A theory of firm scope. Q. J. Econ. 2010, 125, 483–513. [Google Scholar] [CrossRef]
- MacLeod, W.B.; Malcomson, J. Investments, holdup, and the form of market contract. Am. Econ. Rev. 1993, 83, 811–837. [Google Scholar]
- Che, Y.K.; Hausch, D.B. Cooperative Investments and the Value of Contracting. Am. Econ. Rev. 1999, 89, 125–147. [Google Scholar] [CrossRef]
- Herweg, F.; Schmidt, K. Loss aversion and ex post inefficient renegotiation. 2012. CESifo Work- ing Paper Series No. 4031(submitted). Available online: http://ideas.repec.org/p/ces/ceswps/_4031.html (accessed on 12 August 2013).
- Fehr, E.; Hart, O.; Zehnder, C. How do informal agreements and renegotiation shape contractual reference points? 2012. Harvard University working paper(submitted). Available online: http://scholar.harvard.edu/hart/publications/how-do-informal-agreements-and-renegotiation-shape-contractual-reference-points (accessed on 12 August 2013).
- Moore, J.; Repullo, R. Subgame perfect implementation. Econometrica 1988, 56, 1191–1220. [Google Scholar] [CrossRef]
- Maskin, E.; Tirole, J. Unforeseen contingencies and incomplete contracts. Rev. Econ. Stud. 1999, 66, 83–114. [Google Scholar]
- 3One does not need to go this far, however. See Halonen-Akatwijuka and Hart [14] for an extension.
- 4Shading is a form of negative reciprocity, as studied in the social preferences literature. See, Fehr and Schmidt [15].
- 5In a recent paper, Herweg and Schmidt [20] develop a model of contracts as reference points based on loss aversion rather than aggrievement and shading. Among other things, they show that parties may prefer not to write specific performance contracts but instead to rely on asset ownership to reduce hold-up problems. Herweg and Schmidt’s focus is different from ours. They analyze a situation where renegotiation is required to achieve ex post efficiency, and they do not study general mechanisms or show that asset ownership has a role even when such mechanisms are allowed.
- 6For a further discussion of shading, including examples of buyer and seller shading, see Hart and Moore [11].
- 7Note that we are assuming that the buyer’s entitlement is defined with respect to prices rather than surplus. A buyer might feel that it is reasonable that he pays a higher price if the value of the good is high. It would be interesting to allow for this possibility in extensions of the model. We conjecture that some version of our results will continue to hold as long as the buyer’s perceived fair price does not increase one to one with the value of the good. Of course, if the increase is one to one, that is, the buyer is willing to accept a constant amount of surplus, independent of the quality of the good, the seller becomes the residual claimant and the first-best can be achieved.
- 8One important assumption that we are making implicitly is that the buyer is not aggrieved about the seller’s investment decision per se. If he were then a specific performance contract might cause some shading as a result of the buyer being disappointed that the seller has not invested. One might even imagine that the seller would invest to forestall the buyer becoming angry and shading. Investigating situations where aggrievement is a result of ex ante as well as ex post actions is an interesting topic for future research. See also footnote 7 for a related point.
- 9In the absence of (17), revelation schemes in combination with third parties and/or lotteries may be required to achieve the first-best even when θ = 0.
- 10Note that we suppose that the parties cannot restrict the impact of outside options on payoffs in (12) - (13) except though the choice of λ, e.g., they cannot write exclusive dealing contracts.
- 11In other words, we convexify things. Section 4 does the same thing for general contracts.
- 12As an example, suppose that vH = 20, vL = 14,
= 0,
= 0,
)= 10,
= 4,
, c < 3. The efficient trade contract yields a loss of
relative to the first-best (see (31)). The first “no aggrievement” contract yields a loss of
relative to the first-best (see (26)). The second “no aggrievement” contract is not feasible since
< vL −
. Now consider the following contract: λH = 1, λL = 1, pH = 10, pL =10 − 2c, where the buyer chooses between the two at date 1 and the seller can quit. There is no longer any buyer aggrievement in the good state since the seller’s participation constraint is binding (and there is no buyer aggrievement in the bad state since the buyer gets the lowest possible price). There is no seller aggrievement in the good state because the seller gets the highest possible price. However, there is seller aggrievement in the bad state: the seller receives 10−2c but feels entitled to 10 since this would still satisfy the buyer’s participation constraint. It is easy to see that the seller invests. Gross social surplus is given by S = π vH + (1 − π) vL - π θ (pH − pL) = π vH + (1 − π) vL − θ c. In other words the loss relative to the first-best is θc, which is less than both
and
as long as
.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hart, O. Noncontractible Investments and Reference Points. Games 2013, 4, 437-456. https://doi.org/10.3390/g4030437
Hart O. Noncontractible Investments and Reference Points. Games. 2013; 4(3):437-456. https://doi.org/10.3390/g4030437
Chicago/Turabian StyleHart, Oliver. 2013. "Noncontractible Investments and Reference Points" Games 4, no. 3: 437-456. https://doi.org/10.3390/g4030437
APA StyleHart, O. (2013). Noncontractible Investments and Reference Points. Games, 4(3), 437-456. https://doi.org/10.3390/g4030437