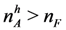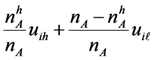Unraveling Results from Comparable Demand and Supply: An Experimental Investigation
Abstract
:1. Introduction
“ The number of positions offered for interns was, from the beginning, greater than the number of graduating medical students applying for such positions, and there was considerable competition among hospitals for interns. One form in which this competition manifested itself was that hospitals attempted to set the date at which they would finalize binding agreements with interns a little earlier than their principal competitors.”
“ Many colleges, experiencing a drop in freshman applications as the population of 18-year-olds declines, are heavily promoting early-acceptance plans in recruiting visits to high schools and in campus tours in hopes of corralling top students sooner.”
“ But why the fervent competition for a handful of young men and women when our law schools spawn hundreds of fine young lawyers every year? Very simply, many judges are not looking just for qualified clerks; they yearn for neophytes who can write like Learned Hand, hold their own in a discussion with great scholars, possess a preternatural maturity in judgment and instinct, are ferrets in research, will consistently outperform their peers in other chambers and who all the while will maintain a respectful, stoic, and cheerful demeanor.... Thus, in any year, out of the 400 clerk applications a judge may receive, a few dozen will become the focus of the competition; these few will be aggressively courted by judges from coast to coast. Early identification of these ” precious few” is sought and received from old-time friends in the law schools - usually before the interview season even begins.”
“ There are more than two thousand four-year colleges in the United States. Only about two hundred reject more students than they accept. The vast majority of American colleges accept eighty per cent or more of those who apply. But among the top fifty there is a constant Darwinian struggle to improve selectivity.”
2. The Model
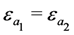 occurs with positive probability. Similarly, the joint distribution of {εf} is such that there is no tie in εf.
occurs with positive probability. Similarly, the joint distribution of {εf} is such that there is no tie in εf.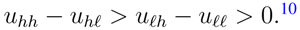
2.1. The Game
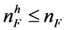 be the number of high quality firms in the market and
be the number of high quality firms in the market and 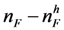 be the number of low quality firms.
be the number of low quality firms.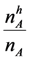 of applicants for some integer
of applicants for some integer 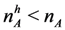 will be of high quality, and the remaining applicants,
will be of high quality, and the remaining applicants, 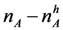 will be of low quality (for example, there might be a special distinction attached to hiring a “ top ten” applicant). To simplify the exposition, and the later experiments, we assume that all applicants have the same ex-ante probability of being of high quality, namely
will be of low quality (for example, there might be a special distinction attached to hiring a “ top ten” applicant). To simplify the exposition, and the later experiments, we assume that all applicants have the same ex-ante probability of being of high quality, namely 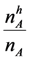 .12 The values of the random variables {ε} are realized at the beginning of the late hiring stage, and become common knowledge. The distribution of {ε} is common knowledge at the beginning of the early hiring stage.
.12 The values of the random variables {ε} are realized at the beginning of the late hiring stage, and become common knowledge. The distribution of {ε} is common knowledge at the beginning of the early hiring stage.2.2. Analysis of Unraveling
 , the number of high quality firms, nA, the total number of applicants, and
, the number of high quality firms, nA, the total number of applicants, and 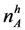 , the total number of high quality applicants:
, the total number of high quality applicants:
- Case 1.
: Every firm can be matched with a high quality applicant, some high quality applicants remain unmatched (if
). There is excess supply.
- Case 2.
: Excess applicants, but shortage of high quality applicants. There is comparable demand and supply.
- Case 3.
- nF ≥ nA: Each applicant can be matched with a firm. There is excess demand. We analyze excess demand in two subcases:
- a.
: Excess firms, but shortage of high quality firms.
- b.
: Every applicant can be matched with a high quality firm, some high quality firms remain unmatched (if
).
nA = 6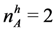 | nA = 12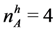 | |
nF = 4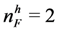 | THIN COMPARABLE MARKET Case 2 (baseline design) SPE Prediction: Low quality firms hire early qualitywise-inefficient outcome | MARKET WITH EXCESS SUPPLY Case 1 SPE Prediction: Late and assortative matching efficient outcome |
nF = 8 | MARKET WITH EXCESS DEMAND Case 3 SPE Prediction: Late and assortative matching efficient outcome | THICK COMPARABLE MARKET Case 2 SPE Prediction: Low quality firms hire early qualitywise-inefficient outcome |
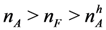 .14
.14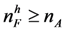 , high firms can hire applicants early under SPE as described by Lemma 3 (in Appendix A), but the outcome will not be qualitywise-inefficient. That is the reason we concentrate on qualitywise-inefficient early hiring (as opposed to all early hiring) in Theorem 1, since only qualitywise-inefficient hiring creates large welfare problems.15 Note also that, while qualitywise-inefficient early matching cannot be a perfect equilibrium outcome except under conditions of comparable demand and supply, whether it is depends on the parameter values in a way that will be detailed in Propositions 3 and 4 in Appendix A (which is also where proofs are).
, high firms can hire applicants early under SPE as described by Lemma 3 (in Appendix A), but the outcome will not be qualitywise-inefficient. That is the reason we concentrate on qualitywise-inefficient early hiring (as opposed to all early hiring) in Theorem 1, since only qualitywise-inefficient hiring creates large welfare problems.15 Note also that, while qualitywise-inefficient early matching cannot be a perfect equilibrium outcome except under conditions of comparable demand and supply, whether it is depends on the parameter values in a way that will be detailed in Propositions 3 and 4 in Appendix A (which is also where proofs are).3. Experimental Design
4. Experimental Results
4.1. The Analysis of Matches and Unraveling

| Actual (SPE) % Firms Hiring Early In the last five markets - Medians | THIN COMPARABLE | EXCESS SUPPLY |
| Low Firms | 100% (100% ) | 25% (0% ) |
| High Firms | 0% (0% ) | 0% (0% ) |
| EXCESS DEMAND | THICK COMPARABLE | |
| Low Firms | 0% (0% ) | 87.5% (100% ) |
| High Firms | 0% (0% ) | 0% (0% ) |
| H0 (For median % high/low firms hiring early) | sample sizes | p-value: High | p-value: Low |
|---|---|---|---|
| Thin Comparable = Thick Comparable | 7,4 | 1 | 0.79 |
| Excess Supply = Excess Demand | 4,7 | 0.67 | 0.76 |
| Thin Comparable = Excess Supply | 7,4 | 0.56 | <0.01** |
| Thin Comparable = Excess Demand | 7,7 | 0.44 | <0.01** |
| Thick Comparable = Excess Supply | 4,4 | 0.43 | 0.03* |
| Thick Comparable = Excess Demand | 4,7 | 0.42 | <0.01** |
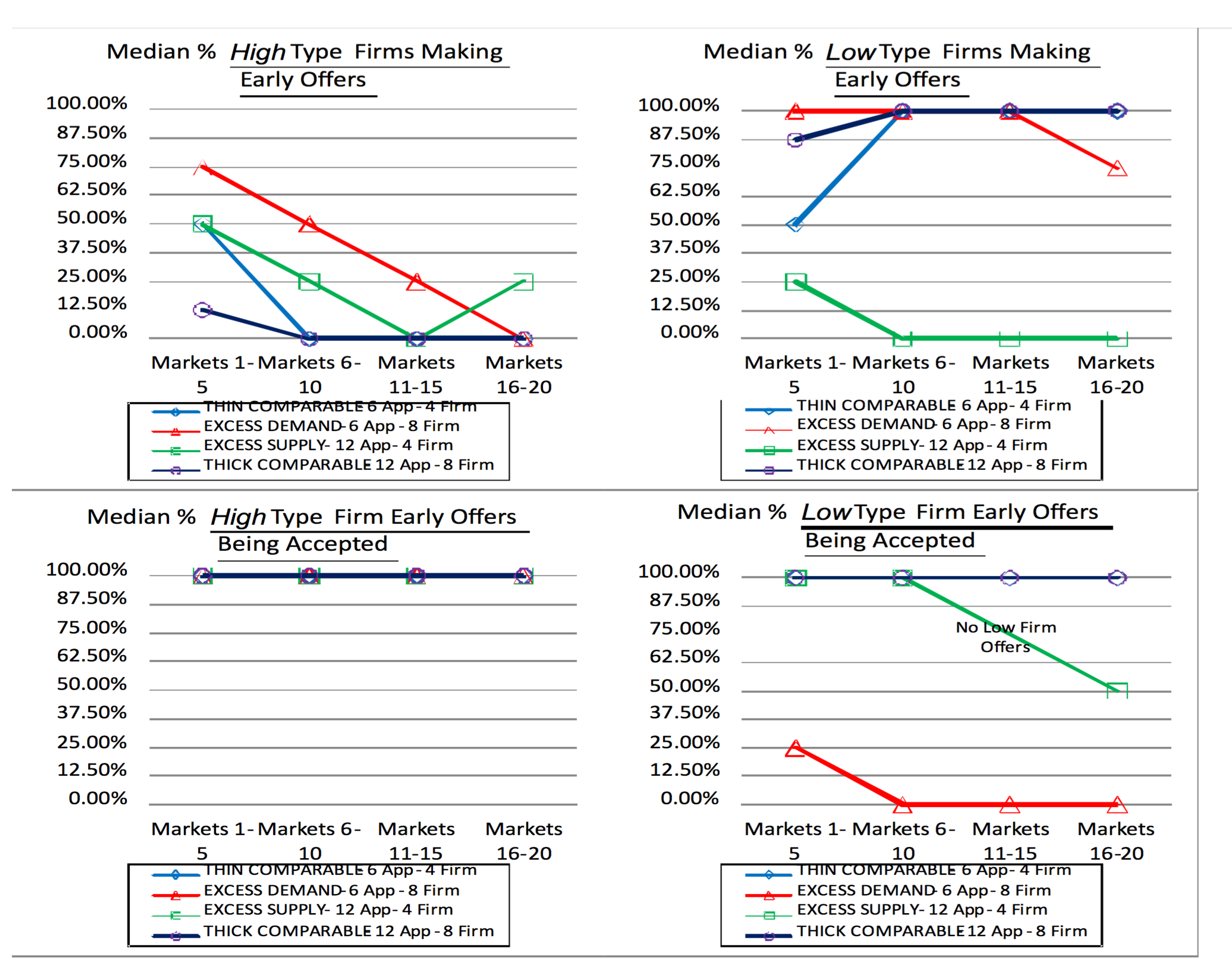
4.2. The Analysis of Early Offer and Acceptance Rates
4.3. The Analysis of Efficiency
| In the last five markets - Medians | THIN COMPARABLE | EXCESS SUPPLY |
| Actual Firm Welfare [Random, Max.] | 108 [102.67, 112] | 124 [102.67, 124] |
Actual (SPE) N.Efficiency= 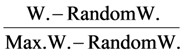 | 57% (57%) | 100% (100%) |
| EXCESS DEMAND | THICK COMPARABLE | |
| Actual Firm Welfare [Random, Max.] | 164 [154, 164] | 220 [205.34, 224] |
Actual (SPE)N. Efficiency= 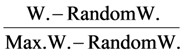 | 100% (100%) | 79% (79) |
| H0 (For median n. efficiency) | sample sizes | p-value |
|---|---|---|
| Thin Comparable = Thick Comparable | 7,4 | 0.12 |
| Excess Supply=Excess Demand | 4,7 | 0.73 |
| Thin Comparable=Excess Supply | 7,4 | 0.33 |
| Thin Comparable=Excess Demand | 7,7 | 0.021* |
| Thick Comparable=Excess Supply | 4,4 | 0.49 |
| Thick Comparable=Excess Demand | 4,7 | 0.048* |
4.4. Further Consequences: Effects of Changing Labor Supply
5. Discussion
Acknowledgements
- 1See [2] for many examples, including markets other than labor markets in which contracts are fulfilled at around the same time but can be finalized substantially earlier, such as the market for college admissions, or for post-season college football bowls.
- 4Titled ”A Cure for Application Fever: Schools Hook More Students with Early Acceptance Offers.” (April 23).
- 6In any model in which offers are made over time, unraveling will occur at equilibrium only if early offers are made and accepted. The theoretical model closest in spirit to the one explored here is that of [24] in which firms and workers unravel to each insure the other against an outcome that leaves their side of the market in excess supply (in an assignment model in which agents on the long side of the market earn zero). [25] looks at a model with a continuum of agents in which unraveling is driven at equilibrium by the fact that it makes later contracting less desirable because of the difficulty of finding a match when everyone else contracts early. Unraveling as insurance is further explored in [26,27,28]. Other theoretical models have unraveling (under conditions of fixed supply and demand) determined by the competition for workers as determined by how correlated firms’ preferences ([29]), or by how well connected firms are to early information about workers’ qualities ([30]), or by the establishment of certain kinds of centralized matching mechanisms ([2,12,31]), or by strategic unraveling and uncertainty imposed by the negative externality caused by an early offer of an agent ([32]). In prior experimental studies, [13,21,33] look at unraveling as a function of what kinds of centralized market clearing mechanism are available at the time when matching may be done efficiently. [9] looks at unraveling as a function of the rules governing exploding offers in a decentralized market. [34] experimentally studies a stylized model of unraveling that can be interpreted as one in which best replies to others’ decisions about when to hire are early, but not too early, compared to the mean time at which competitors are trying to hire.
- 7There is an evolving literature on laboratory experiments regarding different aspects of matching markets. For example, [13,18,21,33], all report experiments on harmful unraveling and how centralized mechanisms can be used successfully or unsuccessfully to stop unraveling in entry-level professional labor markets. These papers report experiments using various mechanisms including stable ones in different environments. [35,36,37,38,39] report experiments on school choice mechanisms, including some stable ones, for public schools enrollment. New York and Boston school districts adopted stable mechanisms to correct market failures due to other reasons than unraveling. Other experiments on two-sided matching markets include [8,40,41,42] that report experiments on different features of decentralized matching markets.
- 8The usual difficulties of measuring supply and demand in the field are compounded when the supply of workers of the highest quality must be evaluated.
- 9The assortative matching is qualitywise-assortative, although the converse doesn’t hold. Note that the ε’s define an absolute standard of efficiency, but we look at qualitywise efficiency and sorting. This is because the "’s play three roles in our treatment: 1. as a technical assumption to give us uniqueness, 2. to reflect the fact that, in future field work, we expect the data might be able to distinguish quality in the large, but not preferences among applicants with similar observables (so that quality would be observable only up to the ε’s); and 3. to make clear in our model that we are not claiming that just because a market isn’t unraveled it is efficient, rather we are only claiming that avoiding unraveling avoids a large source of inefficiency, qualitywise inefficiency.
- 10That is, high quality firms (and applicants) have a strictly higher marginal expected payoff from increasing their partner’s quality than low quality firms (and applicants). I.e., if the production function regarding a firm and worker is the sum of the pay-offs of the firm and the worker, then it is supermodular.
- 11For example, a qualitywise efficient matching may be inefficient when the applicant with the largest " value remains unmatched while an applicant of the same quality is matched. Qualitywise efficiency or its absence is also what can generally be assessed from evaluating field data such as that obtained by using revealed preferences over choices in marriage or dating markets for estimating preferences over observables, i.e., such estimates can determine how important a potential mate’s education is in forming preferences, but cannot observe which among identically educated potential mates will have the best personal chemistry (see e.g., [45,46,47])
- 12For risk-neutral market participants we can equivalently assume that each applicant has a probability
to be of high quality. We instead choose a fixed fraction to reduce variance in the experiment that follows.
- 13There is another asymmetry between cases 2 and 3a, namely that the firms make offers, and applicants accept or reject them. However, this will not be important to determine the SPEs. It may however be important empirically, in the experiment and in the field.
- 14Other results and proofs of this theorem and others regarding the experimental setup are in Appendix A.
- 15In their pioneering theoretical investigation of unraveling, [24] study an assignment market with continuous payoffs in which the supply and demand are assumed to always fall in Case 2. In the early period of their model each worker has a probability of being a productive worker in period 2 (and in period 2 all workers are either productive or unproductive, and only firms matched with a productive worker have positive output). In this context, their assumption that supply and demand fall in Case 2 is that there are more workers than firms, but a positive probability that there will be fewer productive workers than firms. They find, among other things, that inefficient unraveling is more likely “the smaller the total applicant pool relative to the number of positions.” Our framework allows us to see how this conclusion depends on supply and demand remaining in Case 2. When the total applicant pool declines sufficiently, the market enters Case 3a (when the number of workers falls below the number of firms), and inefficient unraveling is no longer predicted. Moreover, we find a characterization of supply and demand conditions necessary for sequentially rational unraveling.
- 16For the graphs and tables, for each session, for each of the markets, we compute the median of the variable in question, in this case the number of firms that hire early. We then compute the median of each market block, for markets 1–5, 6–10, 11–15, 16–20 for each session, and then the median for each market block taking these session medians as data points, to report the final variable.For example, in Session 7 of the thin comparable market treatment, in markets 1 to 5, 100%, 0%, 50%, 0%, and 0% of the high type firms are hiring early, respectively, which results in a 0% median hiring rate. In Sessions 1 to 6, medians are similarly calculated for markets 1–5 as 0%, 50%, 50%, 0%, 50%, and 50%, respectively. The median of these six sessions and Session 7 is 50%, which is marked in the top graph of Figure 1 for markets 1–5.
- 17In Appendix B, we report alternative analyses using means instead of medians. The figures and statistical test results are similar. In general, the mean statistics are noisier than medians due to the fact that the mean takes extreme outcomes into consideration for these samples with relatively small sizes.In the main text, we use medians instead of means for two reasons:First, our statistical test is an ordinal non-parametric median comparison test (i.e., Wilcoxon rank sum test) and not a cardinal parametric mean comparison test. We chose an ordinal test based on the small sample sizes, 7 or 4 for each treatment. Second, many of the empirical distributions are truncated. I.e., even if the efficiency measure is centered around 100%, there will be no observations above 100% while depending on the variance, we will observe lower efficiency levels. Since we use percentages to compare treatments of different size, the appropriate measure of the center of a distribution seems to be a median rather than the mean due to the inevitable skewedness of the empirical distributions.
- 18The mean early firm offer rates in the excess supply treatment are 45.00%, 5.00% 0.00%, and 5.00% within the market groups 1–5, 6–10, 11–15, and 16–20, respectively, and the mean acceptance rates are 100.00% 100.00% and 50.00% in market groups 1–5, 6–10, and 16–20, respectively. For example, 50% acceptance rate means 2.50% of the low firms on average hired early in the last market group on average.
- 19We could also have chosen the welfare of applicants or the sum of applicant and firm payoffs in our efficiency measure. Note that all of these measures will give the same efficiency level, since a firm and a worker who are matched receive exactly the same payoff.
- 20In each treatment, the best full matching is the qualitywise assortative matching, that is, as many high quality firms as possible are matched with high quality applicants, and as many high quality applicants as possible are matched before matching low quality applicants.
- 21The difference in the median of the comparable treatments is due to the small market size of the thin comparable treatment. The mean of both SPE predictions generates 71.38% efficiency. Under a typical matching (i.e., a median SPE matching), in the thick comparable treatment, one low quality firm hires a high quality applicant and the other three low quality firms hire low quality applicants through unraveling, where as in the thin comparable treatment, one low quality firm hires a high quality applicant and the other low quality firm hires a low quality applicant through unraveling.
- 22In our analysis with the averages for the last market block reported in Appendix B, we observe an average of 20–21% of high type firms making early offers which are accepted in the excess demand treatment. SPE predicts that no high quality firms hire early. However, in the excess demand condition, there are only 2 high quality applicants for 4 high quality firms. So, even if 50% of high quality firms were to hire early, efficiency would not be affected given that the other agents follow SPE strategies. And indeed, all seven of our excess demand sessions have close to average 100% efficiency despite of relatively high average of high type firms hiring early.
- 23The firm-optimal stable matching is a stable matching that makes every firm best off among all stable matchings. It always exists in the general Gale-Shapley [43] matching model, and in many of its generalizations (see [48]). In our model, there is a unique stable matching, which is therefore the firm-optimal stable matching.
- 24See [49] for a survey.
- 26This claim is stronger than what we need for the proof of this proposition. However, we will make use of this claim in the proof of Proposition 4.
References
- Fischbacher, U. z-tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Roth, A.E.; Xing, C. Jumping the gun: Imperfections and institutions related to the timing of market transactions. Am. Econ. Rev. 1994, 84, 992–1044. [Google Scholar]
- Niederle, M; Roth, A.E. Unraveling reduces mobility in a labor market: Gastroenterology with and without a centralized match. J. Polit. Econ. 2003, 111, 1342–1352. [Google Scholar]
- Fréchette, G.; Roth, A.E.; Ünver, M.U. Unraveling yields inefficient matchings: Evidence from post-season college football bowls. Rand J. Econ. 2007, 38, 967–982. [Google Scholar] [CrossRef]
- Niederle, M.; Proctor, D.D.; Roth, A.E. What will be needed for the new gi fellowship match to succeed? Gastroenterology 2006, 130, 218–224. [Google Scholar] [CrossRef]
- Niederle, M.; Proctor, D.D.; Roth, A.E. The gastroenterology fellowship match-The first two years. Gastroenterology 2008, 135, 344–346. [Google Scholar]
- Niederle, M.; Roth, A.E. The gastroenterology fellowship match: How it failed, and why it could succeed once again. Gastroenterology 2004, 127, 658–666. [Google Scholar] [CrossRef]
- Niederle, M.; Roth, A.E. The gastroenterology fellowship market: Should there be a match? Am. Econ. Rev., Papers and Proceedings 2005, 95, 372–375. [Google Scholar] [CrossRef]
- Niederle, M.; Roth, A.E. Market culture: How norms governing exploding offers affect market performance. Am. Econ. J-Microecon. 2009, 1, 199–219. [Google Scholar] [CrossRef]
- Roth, A.E.; Peranson, E. The redesign of the matching market for American physicians: Some engineering aspects of economic design. Am. Econ. Rev. 1999, 89, 748–780. [Google Scholar] [CrossRef]
- Roth, A.E. A natural experiment in the organization of entry level labor markets: Regional markets for new physicians and surgeons in the u.k. Am. Econ. Rev. 1991, 81, 415–440. [Google Scholar]
- Ünver, M.U. Backward unraveling over time: The evolution of strategic behavior in the entry-level british medical labor markets. J. Econ. Dyn. Control 2001, 25, 1039–1080. [Google Scholar] [CrossRef]
- Ünver, M.U. On the survival of some unstable two-sided matching mechanisms. Int. J. Game Theory 2005, 33, 239–254. [Google Scholar] [CrossRef]
- Roth, A.E. The evolution of the labor market for medical interns and residents: A case study in game theory. J. Polit. Econ. 1984, 92, 991–1016. [Google Scholar]
- Avery, C.; Fairbanks, A.; Zeckhauser, R. The Early Admissions Game: Joining the Elite; Harvard University Press: Cambridge, MA, USA, 2003. [Google Scholar] [Green Version]
- Santos, C.W.; Sexson, S. Supporting the child and adolescent psychiatry match. J. Am. Acad. Child. Psy. 2002, 41, 1398–1400. [Google Scholar] [CrossRef]
- Gorelick, F.S. Striking up the match. Gastroenterology 1999, 117, 295. [Google Scholar] [CrossRef]
- McKinney, C.N.; Niederle, M.; Roth, A.E. The collapse of a medical labor clearinghouse (and why such failures are rare). Am. Econ. Rev. 2005, 95, 878–889. [Google Scholar] [CrossRef]
- Avery, C.; Jolls, C.; Posner, R.A.; Roth, A.E. The market for federal judicial law clerks. U. Chi. L. Rev. 2001, 68, 793–902. [Google Scholar] [CrossRef]
- Avery, C.; Jolls, C.; Posner, R.A.; Roth, A.E. The new market for federal judicial law clerks. U. Chi. L. Rev. 2007, 74, 447–486. [Google Scholar]
- Haruvy, E.; Roth, A.E.; Ünver, M.U. The dynamics of law clerk matching: An experimental and computational investigation of proposals for reform of the market. J. Econ. Dyn. Control 2006, 30, 457–486. [Google Scholar]
- Wald, P.M. Selecting law clerks. Mich. L. Rev. 1990, 89, 152–163. [Google Scholar] [CrossRef]
- Menand, L. The thin envelope: Why college admissions has become unpredictable. The New Yorker 2003. [Google Scholar] [Green Version]
- Li, H.; Rosen, S. Unraveling in matching markets. Am. Econ. Rev. 1998, 88, 371–387. [Google Scholar]
- Damiano, E.; Li, H.; Suen, W. Unravelling of dynamic sorting. The Rev. Econ. Stud. 2005, 72, 1057–1076. [Google Scholar] [CrossRef]
- Li, H.; Suen, W. Risk sharing, sorting, and early contracting. J. Polit. Econ. 2000, 108, 1058–1091. [Google Scholar] [CrossRef]
- Li, H.; Suen, W. Self-fulfilling early-contracting rush. Int. Econ. Rev. 2004, 45, 301–324. [Google Scholar]
- Suen, W. A competitive theory of equilibrium and disequilibrium unraveling in two-sided matching. RAND J. Econ. 2000, 31, 101–120. [Google Scholar] [CrossRef]
- Halaburda, H. Unravelling in two-sided matching markets and similarity of agents’ preferences. Working paper. 2008. [Google Scholar] [Green Version]
- Fainmesser, I.P. Social networks and unraveling in labor markets. Working paper. 2009. [Google Scholar] [Green Version]
- TSönmez, T. Can pre-arranged matches be avoided in two-sided matching markets? J. Econ. Theory 1999, 86, 148–156. [Google Scholar] [CrossRef]
- Echenique, F; Pereyra, J. Strategic uncertainty and unraveling in matching markets. Working paper. 2013. [Google Scholar] [Green Version]
- Kagel, J.H.; Roth, A.E. The dynamics of reorganization in matching markets: A laboratory experiment motivated by a natural experiment. Q. J. Econ. 2000, 115, 201–235. [Google Scholar] [CrossRef]
- Nagel, R. Unraveling in guessing games: An experimental study. Am. Econ. Rev. 1995, 85, 1313–1326. [Google Scholar]
- Chen, Y.; Sönmez, T. School choice: An experimental study. J. Econ. Theory 2006, 127, 202–231. [Google Scholar] [CrossRef]
- Pais, J.; Pintér, A. School choice and information: An experimental study on matching mechanisms. Game. Econ. Behav. 2008, 64, 303–328. [Google Scholar]
- Calsamiglia, C.; Haeringer, G.; Klijn, F. Constrained school choice: An experimental study. Am. Econ. Rev. 2010, 100, 1860–1874. [Google Scholar] [CrossRef]
- Featherstone, C.; Niederle, M. Ex ante efficiency in school choice mechanisms: An experimental investigation. Working paper. 2008. [Google Scholar] [Green Version]
- Chen, Y.; Kesten, O. School choice: Theory and experiment. Working paper. 2009. [Google Scholar] [Green Version]
- Haruvy, E.; Ünver, M.U. Equilibrium selection and the role of information in repeated matching markets. Econ. Lett. 2007, 94, 284–289. [Google Scholar] [CrossRef]
- Echenique, F.; Katz, G.; Yariv, L. An experimental study of decentralized matching. Working paper. 2009. [Google Scholar] [Green Version]
- Echenique, F.; Wilson, A.; Yariv, L. Clearinghouses for two-sided matching: An experimental study. Working paper. 2009. [Google Scholar] [Green Version]
- Gale, D.; Shapley, L. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Gale, D.; Sotomayor, M. Ms. Machiavelli and the stable matching problem. Am. Math. Mon. 1985, 92, 261–268. [Google Scholar]
- Banerjee, A.; Duflo, E.; Ghatak, M.; Lafortune, J. Marry for what? Caste and mate selection in modern india. working paper. MIT: Cambridge, MA, USA, 2009. [Google Scholar] [Green Version]
- Hitsch, G.J.; Hortacsu, A.; Ariely, D. Matching and sorting in online dating. Am. Econ. Rev. 2010, 100, 130–163. [Google Scholar] [CrossRef]
- Lee, S. Preferences and choice constraints in marital sorting: Evidence from korea. working paper. 2009. [Google Scholar] [Green Version]
- Roth, A.E.; Sotomayor, M. Two-Sided Matching: A Study in Game-Theoretic Modeling and Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar] [Green Version]
- Niederle, M.; Roth, A.E. The effects of a central clearinghouse on job placement, wages, and hiring practices. Autor, D., Ed.; In Labor Market Intermediation; The University of Chicago Press: Chicago, IL, USA, 2009; pp. 199–219. [Google Scholar] [Green Version]
- Roth, A.E.; Ockenfels, A. Last-minute bidding and the rules for ending second-price auctions: Evidence from ebay and amazon auctions on the internet. Am. Econ. Rev. 2002, 92, 1093–1103. [Google Scholar] [CrossRef]
- Ockenfels, A.; Roth, A.E. Late and multiple bidding in second-price internet auctions: Theory and evidence concerning different rules for ending an auction. Game. Econ. Behav. 2006, 55, 297–320. [Google Scholar] [CrossRef]
- Ariely, D.; Ockenfels, A.; Roth, A.E. An experimental analysis of ending rules in internet auctions. Rand J. Econ. 2005, 36, 891–908. [Google Scholar]
A. Appendix: Further Theoretical Results, and Proofs
 (Case 1), and
(Case 1), and 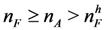 (Case 3a), the unique subgame perfect equilibrium outcome is late, assortative matching.
(Case 3a), the unique subgame perfect equilibrium outcome is late, assortative matching. 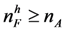 (Case 3b), the outcome of any subgame perfect equilibrium is qualitywise-efficient.
(Case 3b), the outcome of any subgame perfect equilibrium is qualitywise-efficient. 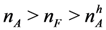 (Case 2), all high quality firms hire in the late stage under any subgame perfect equilibrium. At every subgame perfect equilibrium, at least one low quality firm hires early if and only if
(Case 2), all high quality firms hire in the late stage under any subgame perfect equilibrium. At every subgame perfect equilibrium, at least one low quality firm hires early if and only if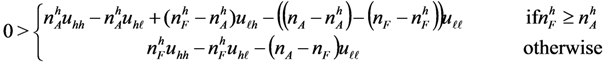
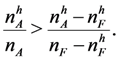
 , then whenever a low quality firm succeeds in hiring early, there is a positive probability that a qualitywise-inefficient matching will result, since the applicant hired by the low quality firm may turn out to be of high quality.
, then whenever a low quality firm succeeds in hiring early, there is a positive probability that a qualitywise-inefficient matching will result, since the applicant hired by the low quality firm may turn out to be of high quality.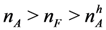 (Case 2), if
(Case 2), if
- We first show that in the last period TL of the late hiring stage, every SPE involves assortative matching among the remaining firms and applicants:
- -
- In every subgame starting with applicants’ information sets in period TL of the late hiring stage, it is a dominant strategy for the applicant to accept the best incoming offer, since otherwise she will either remain unmatched or be matched with a worse firm.
- -
- The best remaining unmatched firm, by making an offer to the best applicant, will be accepted by the applicant, and receive the highest possible payoff. The second best remaining firm, will be rejected if she makes an offer to the best applicant, since the applicant will get an offer from the best firm. The highest applicant who will accept the second best firms’ offer is the second best applicant. Similarly, the kth best remaining unmatched firm maximizes her payoff from making an offer to the kth highest remaining unmatched applicant.
We showed that the outcome of any SPE will involve assortative matching of agents who are available in any last period subgame of the late hiring stage. - Let us assume that we showed for a period t + 1 ≤ TL that SPE strategies for any subgame starting in period t + 1 involve assortative matching among the remaining unmatched firms and applicants. We now show that this implies that for any subgame starting in period t the SPE involve assortative matching among the unmatched applicants in period t Let us relabel the remaining firms and applicants, such that the remaining firms are f1,f2,...,fm and available applicants a1,a2,...,an such that fk is better than fk+1 for any k < m and ak is better than ak+1 for any k < n.
- -
- We show that at any SPE in period t involves applicant a1 not to accept an offer from firm fj for any j > 1 if firm 1 id not make an offer to any applicant. By rejecting firm fj, applicant a1 will be the highest quality remaining applicant in period t+1, and f1 will be the highest quality unmatched firm. That is, by the inductive assumption, a1 can expect to be matched to firm f1 in the SPE.
- -
- We show that at any SPE in period t, firm f1,either makes no offer, or an offer to applicant a1 in period t. This guarantees that f1 is either accepted by applicant a1 in period t, or else both f1 and applicant a1 are unmatched in period t, in which case firm f1 will be matched to applicant a1 before the end of the game by the inductive assumption.
- -
- We show that at any SPE in period tapplicant a2 does not accept an offer from fj, j > 2 if firms f1 and f2 both did not make an offer to an applicant al for any l > 2. As in the case of applicant a1; by rejecting firm fj, a2 can expect to be matched to either f1 or f2 in period t+1, since at least one of the two firms will be unmatched.
- -
- We now show that any SPE in period tinvolves firm f2, not to make an offer to an applicant aj, j > 2. We can follow this line of iterative argument to show that any SPE strategies in any subgame starting in period tinvolve no matches that are not assortative in period t.
(Case 1): We already established by Lemma 1 that once participants are in the late hiring stage, the unique SPE outcome is assortative matching among the remaining firms and applicants. When
, by not hiring any applicant in the early hiring stage each firm guarantees to hire a high quality applicant in the late hiring stage under a SPE. For a firm f of quality i ∈ {h,l}, her expected payoff of hiring an applicant in the early stage is given by
which is strictly smaller than her expected payoff of hiring a high quality applicant in the late stage, uih. Therefore, under any SPE no firm will make any early hiring, and thus, by Lemma 1 the outcome will be assortative.(Case 3a): By Lemma 1, once participants are in the late hiring stage, the unique SPE outcome is assortative matching among the remaining firms and applicants. Since nF ° nA, under a SPE, every applicant will at least be matched with a low quality firm by waiting for the late hiring stage. We will show that no matches will occur in the early hiring stage under a SPE by backward iteration.
First consider the last period (period TE)of the early hiring stage. We will show that no high quality firm is matched under a SPE in this period as long as more applicants than high quality firms are available. We prove this with two claims. Consider an information set Iof applicants located in this period.Claim 1 Under a SPE, no available applicant will accept a low quality firm’s offer in I if there is a high quality firm who did not make an offer in period TE.Proof of Claim 1 Consider a SPE profile and an applicant aavailable in I . Suppose that there is at least one high quality firm that did not make an offer in TE. Then the applicant has a chance to be of high quality and be matched to a high quality firm (of which at least one is available in the late hiring stage), if she is of low quality, she will receive a low quality firm by Lemma 1. Hence her expected payoff from waiting is strictly larger than her expected payoff from accepting a low quality firm offer in period TE. □Consider a subgame starting in the last period (period TE) of the early stage.Claim 2 Under a SPE, no high quality firm makes an offer to an applicant, unless the number of remaining applicants is equal to or smaller than the number of remaining high quality firms (in which case we do not determine the strategies fully).Proof of Claim 2 Suppose there are k*high quality firms left, and k > k* applicants. If a high quality firm fh makes an offer to an applicant, it will hire her and this will be an average quality applicant. If firm fh makes no offer this period, then we have seen that no applicant will accept an offer from a low quality firm. Suppose rH high quality firms are left after the end of the early stage, including the high quality firm fh.This implies that there are rA = k - (k*− rH) > rH applicants unmatched at the end of period TE. Since firm fh has equal chance to be ranked in any place amongst the remaining rH high quality firms, and since by Lemma 1, any SPE matching in the late hiring stage is assortative, firm fh, by not matching early, will match to one of the best rH applicants in the remaining rA, and has an equal chance to match with any of them. The average applicant’s quality amongst the rH (<rA)best applicants of all rA is strictly better than the unconditional average applicant quality. Therefore, fh, by not making an offer, is matched with an applicant with an expected quality higher than the average, receiving higher expected earnings in an SPE than by making an early offer. □We showed that in the last period of the early hiring stage no matches will occur, if the number of high quality firms available is smaller than the number of applicants available under a SPE profile. By iteration, we can similarly prove that in period TE - 1 of the early hiring stage no matches will occur, if the number of high quality firms available is smaller than the number of applicants available under a SPE profile. By backward iteration, we conclude the proof that no matches will occur in the early hiring stage under a SPE. Therefore, all hirings occur in the late hiring stage and these hirings are assortative under any SPE by Lemma 1. ■
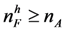 . By Lemma 1, every applicant guarantees to be matched with a high quality applicant by waiting for the late hiring stage under a SPE. Therefore, no applicant will accept an offer from a low quality firm in the path of a SPE. Therefore, all applicants will be matched with high quality firms in every SPE. Every such matching is qualitywise-efficient. ■
. By Lemma 1, every applicant guarantees to be matched with a high quality applicant by waiting for the late hiring stage under a SPE. Therefore, no applicant will accept an offer from a low quality firm in the path of a SPE. Therefore, all applicants will be matched with high quality firms in every SPE. Every such matching is qualitywise-efficient. ■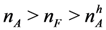 . Let σ be a SPE profile. We will prove the proposition using three claims:
. Let σ be a SPE profile. We will prove the proposition using three claims: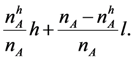 . If the high firm does not match early, and if there are rF high firms left, then there will be rA > rF applicants left (since nA > nF), and the high firm, instead of receiving the average quality of all rA receives the average quality of best rF out of rA applicants, which is strictly better. □
. If the high firm does not match early, and if there are rF high firms left, then there will be rA > rF applicants left (since nA > nF), and the high firm, instead of receiving the average quality of all rA receives the average quality of best rF out of rA applicants, which is strictly better. □

 or
or  , the expected payoff on the left hand side is the expected payoff of accepting a low quality firm offer. In each case, the expected payoff on the right hand side of Inequality 2 can be interpreted as follows: When
, the expected payoff on the left hand side is the expected payoff of accepting a low quality firm offer. In each case, the expected payoff on the right hand side of Inequality 2 can be interpreted as follows: When  , by Lemma 1, the applicant will be matched with a high quality firm, if she is of high quality, or one of the best
, by Lemma 1, the applicant will be matched with a high quality firm, if she is of high quality, or one of the best 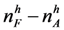 low quality applicants, and she will be matched with a low quality firm, if she is one the next
low quality applicants, and she will be matched with a low quality firm, if she is one the next 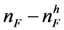 best low quality applicants. When
best low quality applicants. When  , the applicant will be matched with a high quality firm, if she is one the best
, the applicant will be matched with a high quality firm, if she is one the best 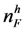 high quality applicants, and she will be matched with a low quality applicant, if she is one of worst
high quality applicants, and she will be matched with a low quality applicant, if she is one of worst 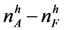 high quality applicants or one of the best
high quality applicants or one of the best  low quality applicants. Inequality 2 can be rewritten as
low quality applicants. Inequality 2 can be rewritten as

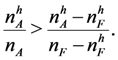
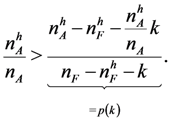

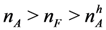 . Let σ be a SPE profile. By Claim 1 of Proposition 3, no high quality firm will hire early under σ. Since
. Let σ be a SPE profile. By Claim 1 of Proposition 3, no high quality firm will hire early under σ. Since  , no low quality firm will go late under σ as long as their offers are accepted early by Claim 3 of Proposition 3.
, no low quality firm will go late under σ as long as their offers are accepted early by Claim 3 of Proposition 3.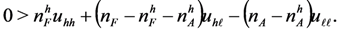
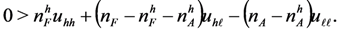
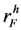 be the number of high quality firms available,
be the number of high quality firms available, 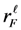 be the number of low quality firms available, and rA be the number of applicants available in the late hiring stage under σ restricted to Γ. By Lemma 1, applicant a will be matched with a high quality firm if she turns out to be one of the best
be the number of low quality firms available, and rA be the number of applicants available in the late hiring stage under σ restricted to Γ. By Lemma 1, applicant a will be matched with a high quality firm if she turns out to be one of the best 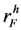 applicants, she will be matched with a low quality firm if she turns out to be one of the
applicants, she will be matched with a low quality firm if she turns out to be one of the  applicants who are not among the best
applicants who are not among the best 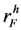 applicants. Under σ restricted to Γ, applicant a’s expected payoff is
applicants. Under σ restricted to Γ, applicant a’s expected payoff is
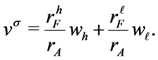
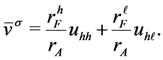
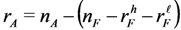 , we have
, we have
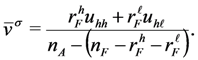
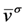 is an increasing function of both
is an increasing function of both 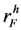 and
and 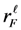 . Therefore,
. Therefore, 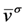 achieves its highest value when
achieves its highest value when 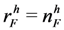 , and
, and  and this value is given by
and this value is given by


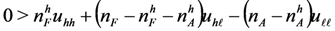 , rearranging the terms and dividing them by nA, we obtain that
, rearranging the terms and dividing them by nA, we obtain that
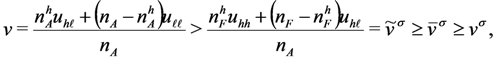
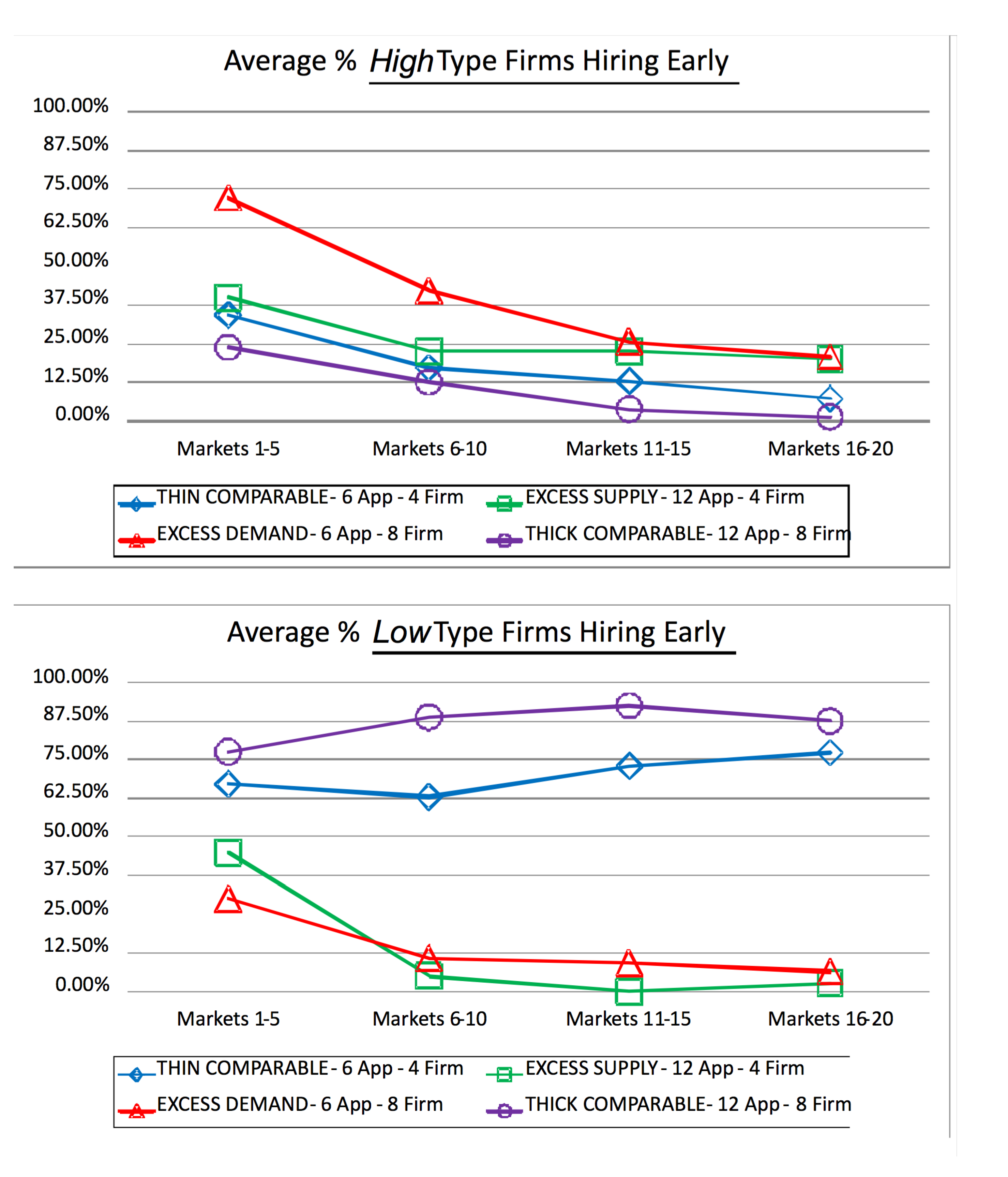
| Actual (SPE) % Firms Hiring Early In the last five markets - Averages | THIN COMPARABLE | EXCESS SUPPLY |
| Low Firms | 77.14% (100%) | 2.5% (0%) |
| High Firms | 7.14% (0%) | 20% (0%) |
| EXCESS DEMAND | THICK COMPARABLE | |
| Low Firms | 6.43% (0%) | 87.5% (100%) |
| High Firms | 20.71% (0%) | 1.25% (0%) |
| H0 (For average % high/low firms hiring early) | sample sizes | p-value: High | p-value: Low |
|---|---|---|---|
| Thin Comparable = Thick Comparable | 7,4 | 1 | 0.33 |
| Excess Supply = Excess Demand | 4,7 | 0.86 | 0.64 |
| Thin Comparable = Excess Supply | 7,4 | 0.56 | <0.01** |
| Thin Comparable = Excess Demand | 7,7 | 0.085 | <0.01** |
| Thick Comparable = Excess Supply | 4,4 | 0.43 | 0.029* |
| Thick Comparable = Excess Demand | 4,7 | 0.15 | <0.01** |
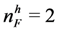 , nA = 4,
, nA = 4, 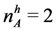 , uhh = 36, uhl = ulh = 26, ull = 20. Since
, uhh = 36, uhl = ulh = 26, ull = 20. Since 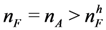 , this market satisfies demand and supply condition Case 1, and therefore by Lemma 2, all SPE outcomes are assortative. So each high quality firm’s expected payoff is uhh. Suppose that the number of applicants increases to
, this market satisfies demand and supply condition Case 1, and therefore by Lemma 2, all SPE outcomes are assortative. So each high quality firm’s expected payoff is uhh. Suppose that the number of applicants increases to 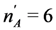 and number of high quality applicants does not change. The new market is the thin comparable market treatment in our experiment,i.e., a market of comparable demand and supply (Case 2). By Proposition 3 since
and number of high quality applicants does not change. The new market is the thin comparable market treatment in our experiment,i.e., a market of comparable demand and supply (Case 2). By Proposition 3 since 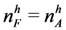 , and
, and  , all low quality firms hire early under a SPE, causing that a high quality firm gets matched with a low quality applicant with positive probability. This expected payoff of a high quality firm is lower than uhh in the new market under any SPE. ■
, all low quality firms hire early under a SPE, causing that a high quality firm gets matched with a low quality applicant with positive probability. This expected payoff of a high quality firm is lower than uhh in the new market under any SPE. ■ B. Appendix: Alternative Analyses with the Means

| In the last five markets - Averages | THIN COMPARABLE | EXCESS SUPPLY |
| Actual Firm Welfare [Random, Max.] | 109.31 [102.67, 112] | 121.2 [102.67, 124] |
Actual (SPE)N. Efficiency = 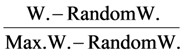 | 71.21% (71.38%) | 86.87% (100%) |
| EXCESS DEMAND | THICK COMPARABLE | |
| Actual Firm Welfare [Random, Max.] | 163.66 [154, 164] | 219.8 [205.34, 224] |
Actual (SPE) N.Efficiency= 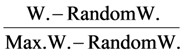 | 96.57% (100%) | 77.49% (71.38%) |
| H0 (For average n. efficiency) | sample sizes | p-value |
|---|---|---|
| Thin Comparable = Thick Comparable | 7,4 | 0.65 |
| Excess Supply=Excess Demand | 4,7 | 0.94 |
| Thin Comparable=Excess Supply | 7,4 | 0.28 |
| Thin Comparable=Excess Demand | 7,7 | 0.014* |
| Thick Comparable=Excess Supply | 4,4 | 0.31 |
| Thick Comparable=Excess Demand | 4,7 | 0.012* |
C. Appendix: Instructions of the Experiment
WELCOME
- When a HIGH quality firm hires a HIGH quality applicant, on average the firm and the applicant each get 36 points.
- When a HIGH quality firm hires a LOW quality applicant, OR a LOW quality firm hires a HIGH quality applicant, on average the firm and the applicant each get 26 points.
- When a LOW quality firm hires a LOW quality applicant, on average the firm and the applicant each get 20 points.
- If you end up unmatched you do not earn any points.
Making and accepting offers
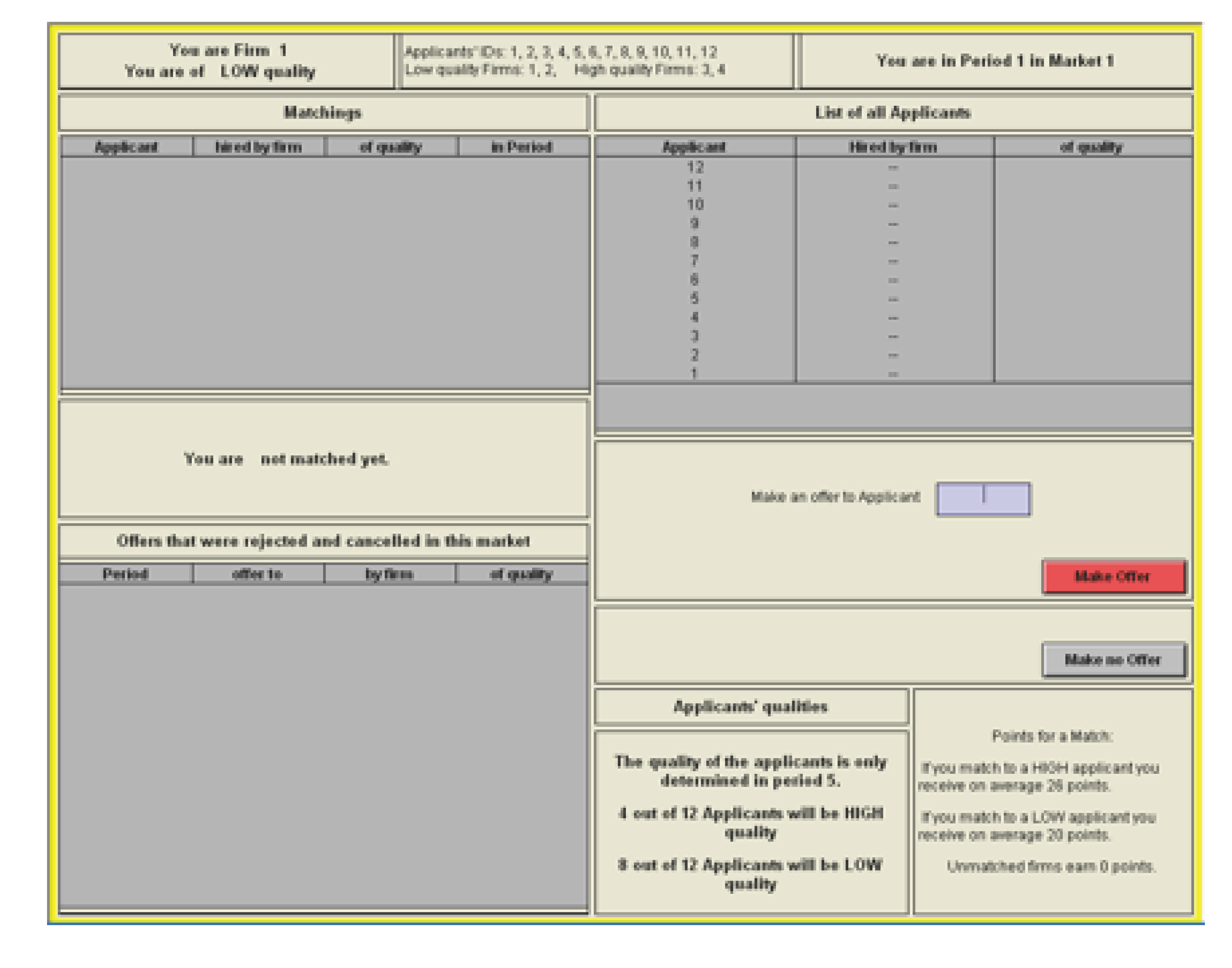
The Information on the Screen of Applicants and Firms:
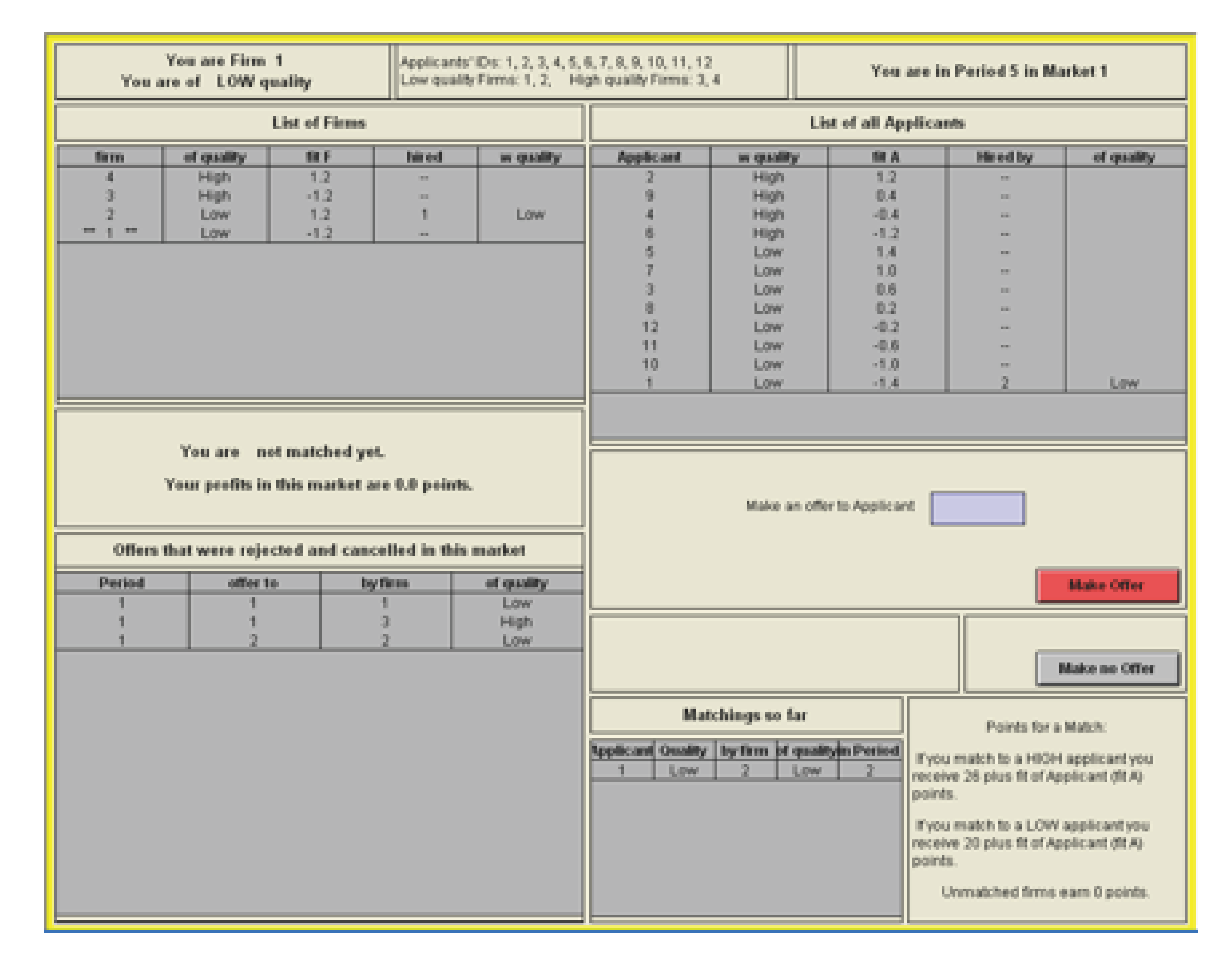
The Information on the Screen of Firms:
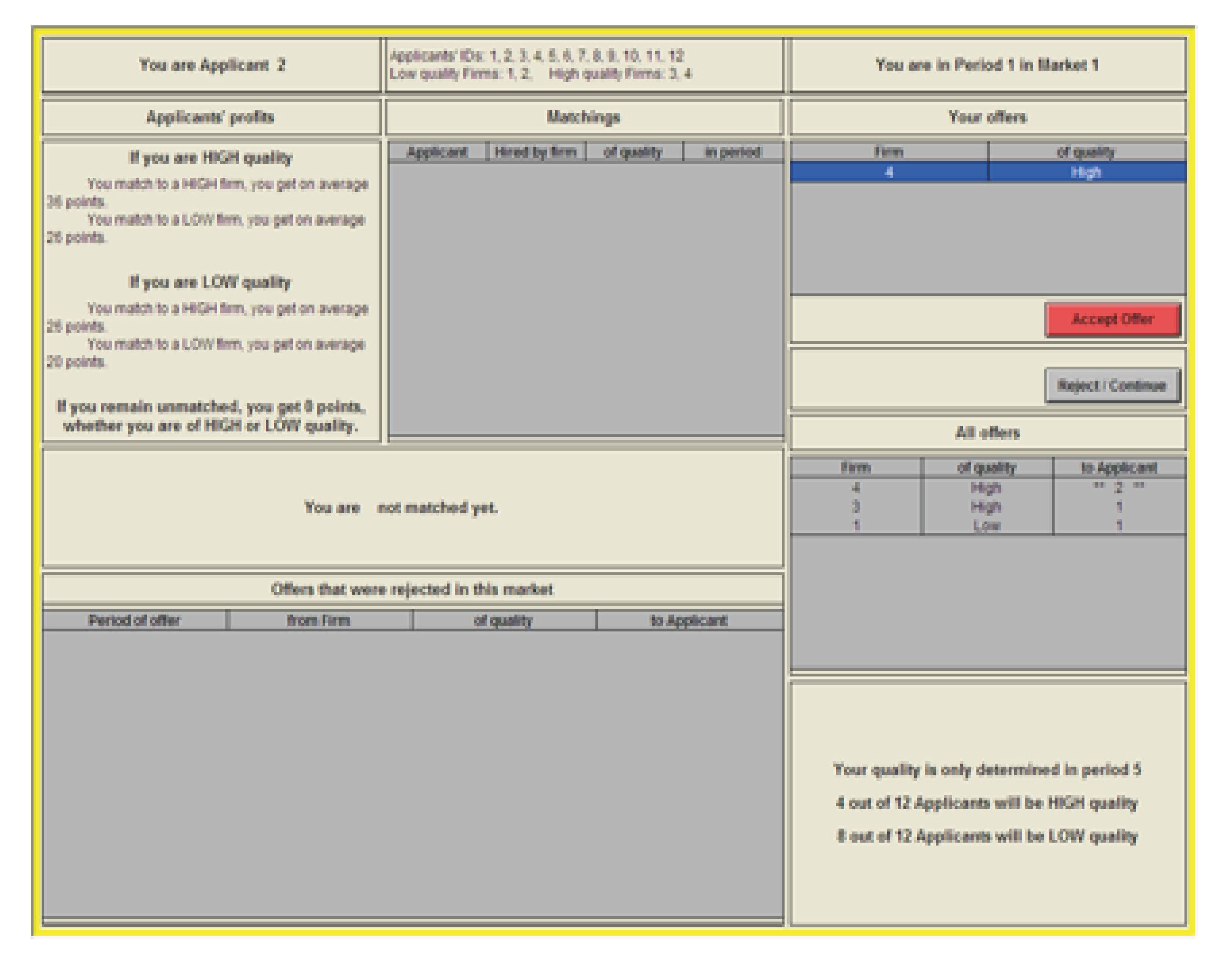
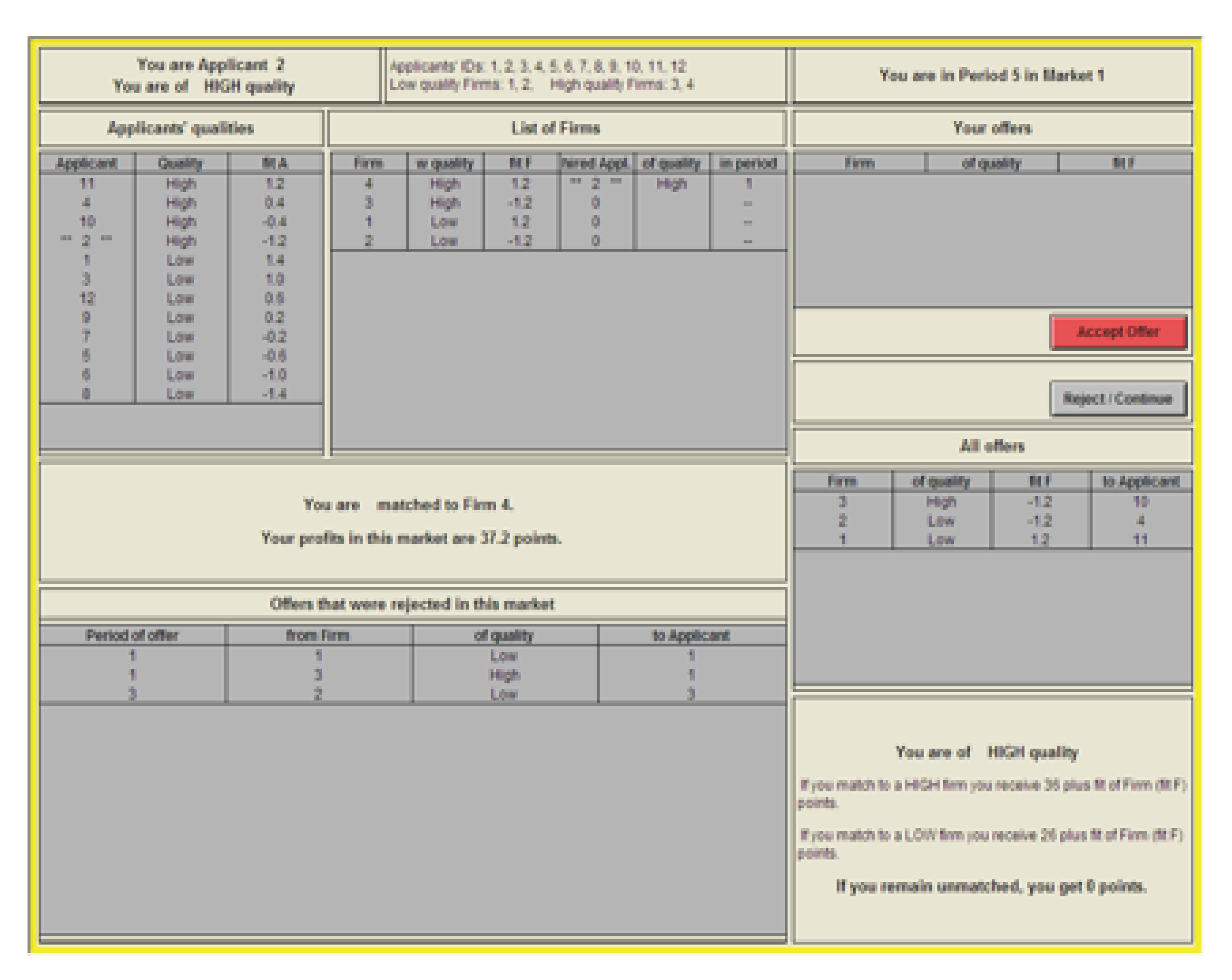
The Information on the Screen of Applicants:
Payment
Summary
- Periods 1–4: Each applicant has equal chance to be a HIGH quality applicant (4 of the 12 that is 1 in 3 applicants will be of HIGH quality) and equal chance to be a LOW quality applicant (8 of the 12 that is 2 in 3 applicants will be of LOW quality).
- Periods 5–8: At the beginning of period 5, four applicants become HIGH quality and the remaining eight applicants become LOW quality applicants.
- Periods 5–8: Firms and applicants are assigned small fit scores. A HIGH quality partner with the lowest fit is still much more desirable than a LOW quality partner with the highest fit. But the higher the fit score, the more desirable that partner is.
- In each period, each firm that has not yet hired an applicant, has to decide whether to make an offer and, if so, to which applicant. Each firm can only make one offer in each period, and only to applicants who have not accepted an offer yet.
- In each period, applicants who receive offers have to decide whether to accept or reject the offer.
- Once an applicant accepted an offer, he cannot accept another offer in the same market, and will no longer receive offers.
- Firms and Applicants that are not matched by the end of period 8 in a market remain unmatched and earn zero points.
- In a HIGH quality-HIGH quality match, firms and applicants each earn 36 points plus the fit scores of their partner.
- In a HIGH quality-LOW quality match, firms and applicants each earn 26 points plus the fit scores of their partner.
- In a LOW quality-LOW quality match, firms and applicants each earn 20 points plus the fit scores of their partner.
- After period 8, a completely new market begins, and everyone is free to try to match once again.
- The experiment has 20 consecutive markets each with 8 periods length.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Niederle, M.; Roth, A.E.; Ünver, M.U. Unraveling Results from Comparable Demand and Supply: An Experimental Investigation. Games 2013, 4, 243-282. https://doi.org/10.3390/g4020243
Niederle M, Roth AE, Ünver MU. Unraveling Results from Comparable Demand and Supply: An Experimental Investigation. Games. 2013; 4(2):243-282. https://doi.org/10.3390/g4020243
Chicago/Turabian StyleNiederle, Muriel, Alvin E. Roth, and M. Utku Ünver. 2013. "Unraveling Results from Comparable Demand and Supply: An Experimental Investigation" Games 4, no. 2: 243-282. https://doi.org/10.3390/g4020243
APA StyleNiederle, M., Roth, A. E., & Ünver, M. U. (2013). Unraveling Results from Comparable Demand and Supply: An Experimental Investigation. Games, 4(2), 243-282. https://doi.org/10.3390/g4020243