Dynamic Properties of Evolutionary Multi-player Games in Finite Populations
Abstract
:1. Introduction

2. Fixation
2.1. Fixation Probability

2.2. Fixation Time

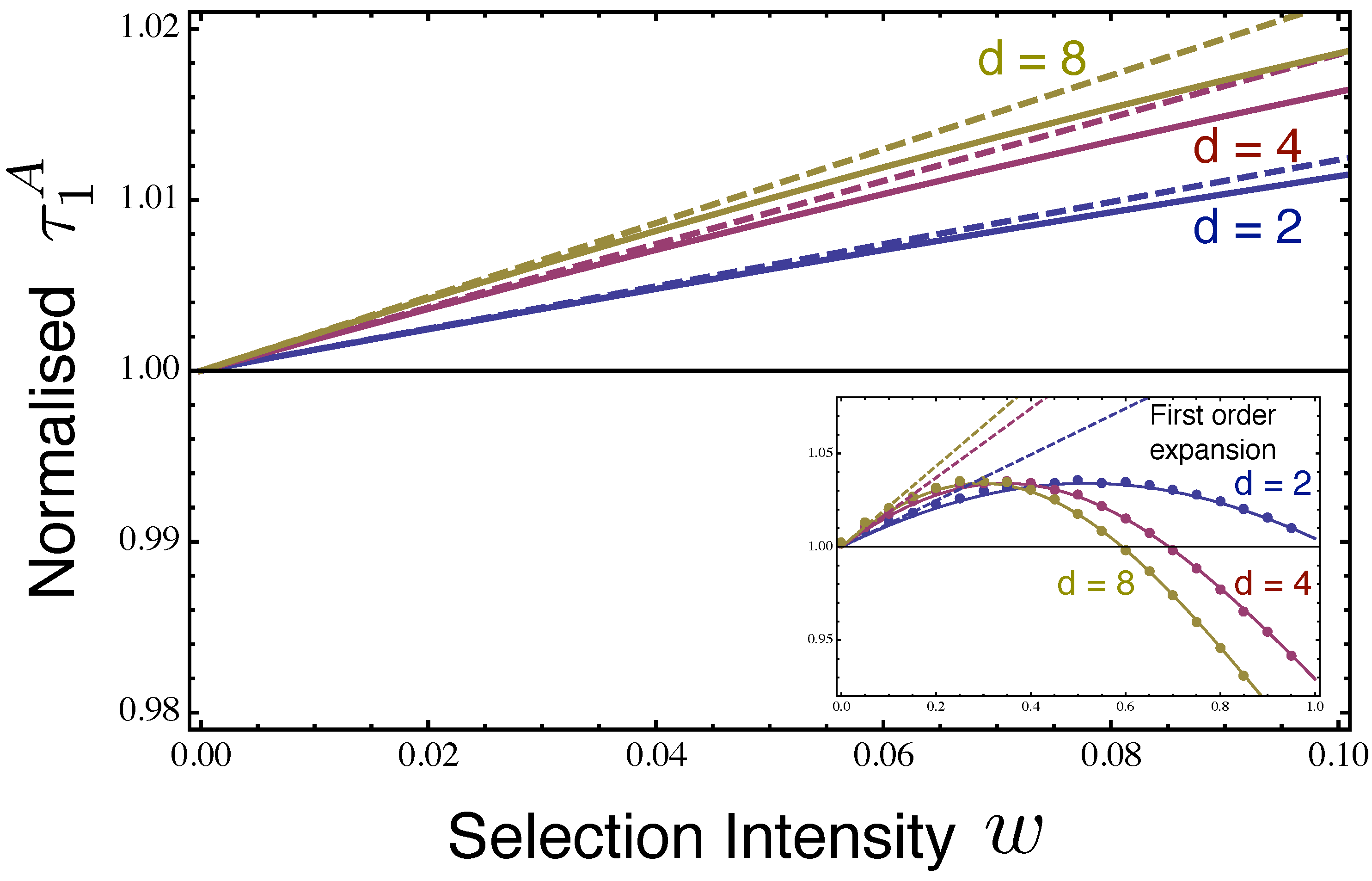
3. Average Abundance
3.1. σ Rule for d-player Games
3.2. Calculating the Structure Parameters : Three Examples
3.2.1. The Moran Process with Mutations in Well Mixed Population
3.2.2. The Death Birth Process on the Cycle
3.2.3. The Aspiration Dynamics in the Well Mixed Population.
4. Summary and Discussion
Acknowledgements
References
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Traulsen, A.; Claussen, J.C.; Hauert, C. Coevolutionary dynamics: From finite to infinite populations. Phys. Rev. Lett. 2005, 95, 238701. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Fudenberg, D.; Nowak, M.A. Evolutionary cycles of cooperation and defection. Proc. Natl. Acad. Sci. USA 2005, 102, 10797–10800. [Google Scholar] [PubMed]
- Fudenberg, D.; Imhof, L.A. Imitation processes with small mutations. J. Econ. Theor. 2006, 131, 251–262. [Google Scholar] [CrossRef]
- Hauert, C.; Traulsen, A.; Brandt, H.; Nowak, M.A.; Sigmund, K. Via freedom to coercion: The emergence of costly punishment. Science 2007, 316, 1905–1907. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Bordalo, P.; Nowak, M.A. The one-third law of evolutionary dynamics. J. Theor. Biol. 2007, 249, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Antal, T.; Scheuring, I. Fixation of strategies for an evolutionary game in finite populations. B. Math. Biol. 2006, 68, 1923–1944. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Nowak, M.A. Stochastic evolutionary dynamics of direct reciprocity. Proc. R. Soc. B 2010, 277, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Qian, H. Fixation, transient landscape, and diffusion dilemma in stochastic evolutionary game dynamics. Phys. Rev. E 2011, 84, 031907. [Google Scholar] [CrossRef]
- Wu, B.; Gokhale, C.S.; Wang, L.; Traulsen, A. How small are small mutation rates? J. Math. Biol. 2012, 64, 803–827. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Gintis, H. Costly signaling and cooperation. J. Theor. Biol. 2001, 213, 103–119. [Google Scholar] [CrossRef] [PubMed]
- Broom, M. The use of multiplayer game theory in the modeling of biological populations. Comments. Theor. Biol. 2003, 8, 103–123. [Google Scholar] [CrossRef]
- Connor, R.C. Cooperation beyond the dyad: On simple models and a complex society. Phil. Trans. R. Soc. B 2010, 365, 2687–2697. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M.; Scheuring, I. Review: Evolution of cooperation in one-shot social dilemmas without assortment. J. Theor. Biol. 2012, 299, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M. The Possibility of Cooperation; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Schelling, T.C. Micromotives and Macrobehavior; W. W. Norton & Company: New York, NY, USA, 2006. [Google Scholar]
- Greig, D.; Travisano, M. The Prisoner’s Dilemma and polymorphism in yeast SUC genes. Biol. Lett. 2004, 271, S25–S26. [Google Scholar] [CrossRef] [PubMed]
- Doebeli, M.; Hauert, C. Models of cooperation based on the Prisoner’s Dilemma and the Snowdrift game. Ecol. Lett. 2005, 8, 748–766. [Google Scholar] [CrossRef]
- Gore, J.; Youk, H.; van Oudenaarden, A. Snowdrift game dynamics and facultative cheating in yeast. Nature 2009, 459, 253–256. [Google Scholar] [CrossRef] [PubMed]
- MacLean, G.; Fuentes-Hernandez, A.; Greig, D.; Hurst, L.D.; Gudelj, I. A mixture of “cheats” and “co-operators” can enable maximal group benefit. PLoS Biology 2010, 8, e1000486. [Google Scholar] [CrossRef] [PubMed]
- Woelfing, B.; Traulsen, A. Stochastic sampling of interaction partners versus deterministic payoff assignment. J. Theor. Biol. 2009, 257, 689–695. [Google Scholar] [CrossRef] [PubMed]
- Broom, M.; Cannings, C.; Vickers, G. Multi-player matrix games. B. Math. Biol. 1997, 59, 931–952. [Google Scholar] [CrossRef]
- Bukowski, M.; Miekisz, J. Evolutionary and asymptotic stability in symmetric multi-player games. Int. J. Game Theory 2004, 33, 41–54. [Google Scholar] [CrossRef]
- Han, T.A.; Traulsen, A.; Gokhale, C.S. On equilibrium properties of evolutionary multi-player games with random payoff matrices. Theor. Popul. Biol. 2012, 81, 264–72. [Google Scholar] [CrossRef] [PubMed]
- Moran, P.A.P. Random processes in genetics. Proc. Cambridge Philos. Soc. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Wu, B.; Altrock, P.M.; Wang, L.; Traulsen, A. Universality of weak selection. Phys. Rev. E 2010, 82, 046106. [Google Scholar] [CrossRef]
- Traulsen, A.; Shoresh, N.; Nowak, M.A. Analytical results for individual and group selection of any intensity. B. Math. Biol. 2008, 70, 1410–1424. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Traulsen, A. Fixation probabilities of random mutants under frequency dependent selection. J. Theor. Biol. 2010, 263, 262–268. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Haubold, B.; Hauert, C.; Traulsen, A. Emergence of stable polymorphism driven by evolutionary games between mutants. Nature Commun. 2012, 3, 919. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Werner, B.; Traulsen, A. The impact of random frequency-dependent mutations on the average population fitness. BMC Evol. Biol. 2012, 12, 160. [Google Scholar] [CrossRef] [PubMed]
- Traulsen, A.; Pacheco, J.M.; Nowak, M.A. Pairwise comparison and selection temperature in evolutionary game dynamics. J. Theor. Biol. 2007, 246, 522–529. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R. The Mathematical Theory of Selection, Recombination, and Mutation; John Wiley and Sons: Chichester, UK, 2000. [Google Scholar]
- Wu, B.; Gokhale, C.S.; Van Veelen, M.; Wang, L.; Traulsen, A. Interpretations arising from Wrightian and Malthusian fitness under strong frequency dependent selection. Ecol. Evol. 2013. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Nowak, M.A. Evolutionary game dynamics in a Wright-Fisher process. J. Math. Biol. 2006, 52, 667–681. [Google Scholar] [CrossRef] [PubMed]
- Traulsen, A.; Pacheco, J.M.; Imhof, L.A. Stochasticity and evolutionary stability. Phys. Rev. E 2006, 74, 021905. [Google Scholar] [CrossRef]
- Lessard, S.; Ladret, V. The probability of fixation of a single mutant in an exchangeable selection model. J. Math. Biol. 2007, 54, 721–744. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S.; Ihara, Y. Emergence of cooperation in public goods games. Proc. R. Soc. B 2009, 276, 1379–1384. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, C.S.; Traulsen, A. Evolutionary games in the multiverse. Proc. Natl. Acad. Sci. USA 2010, 107, 5500–5504. [Google Scholar] [CrossRef] [PubMed]
- Lessard, S. On the robustness of the extension of the one-third law of evolution to the multi-player game. Dynam. Games Appl. 2011, 1, 408–418. [Google Scholar] [CrossRef]
- Altrock, P.M.; Gokhale, C.S.; Traulsen, A. Stochastic slowdown in evolutionary processes. Phys. Rev. E 2010, 82, 011925. [Google Scholar] [CrossRef]
- Altrock, P.M.; Traulsen, A.; Galla, T. The mechanics of stochastic slowdown in evolutionary games. J. Theor. Biol. 2012, 311, 94–106. [Google Scholar] [CrossRef] [PubMed]
- Tarnita, C.E.; Ohtsuki, H.; Antal, T.; Fu, F.; Nowak, M.A. Strategy selection in structured populations. J. Theor. Biol. 2009, 259, 570–581. [Google Scholar] [CrossRef] [PubMed]
- Tarnita, C.E.; Wage, N.; Nowak, M.A. Multiple strategies in structured populations. Proc. Natl. Acad. Sci. USA 2011, 108, 2334–2337. [Google Scholar] [CrossRef] [PubMed]
- Karlin, S.; Taylor, H.M.A. A First Course in Stochastic Processes, 2nd edition ed.; Academic: London, UK, 1975. [Google Scholar]
- Traulsen, A.; Hauert, C. Stochastic evolutionary game dynamics. In Reviews of Nonlinear Dynamics and Complexity; Schuster, H.G., Ed.; Wiley-VCH: Weinheim, Germany, 2009; Vol. II, pp. 25–61. [Google Scholar]
- Kimura, M. On the probability of fixation of mutant genes in a population. Genetics 1962, 47, 713–719. [Google Scholar] [PubMed]
- Kampen, N.G.v. Stochastic Processes in Physics and Chemistry, 2nd ed.; Elsevier: Amsterdam, Netherlands, 1997. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Ewens, W.J. Mathematical Population Genetics. I. Theoretical Introduction; Springer: New York, NY, USA, 2004. [Google Scholar]
- Altrock, P.M.; Traulsen, A. Fixation times in evolutionary games under weak selection. New J. Phys. 2009, 11, 013012. [Google Scholar] [CrossRef]
- Maruyama, T.; Kimura, M. A note on the speed of gene frequency changes in reverse direction in a finite population. Evolution 1974, 28, 161–163. [Google Scholar] [CrossRef]
- Taylor, C.; Iwasa, Y.; Nowak, M.A. A symmetry of fixation times in evolutionary dynamics. J. Theor. Biol. 2006, 243, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Nathanson, C.G.; Tarnita, C.E.; Nowak, M.A. Calculating evolutionary dynamics in structured populations. PLoS Comput. Biol. 2009, 5, e1000615. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Li, X.; Cao, L.; Zhan, J. The σ law of evolutionary dynamics in community-structured population. J. Theor. Biol. 2012, 306, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Antal, T.; Traulsen, A.; Ohtsuki, H.; Tarnita, C.E.; Nowak, M.A. Mutation-selection equilibrium in games with multiple strategies. J. Theor. Biol. 2009, 258, 614–622. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, C.S.; Traulsen, A. Strategy abundance in evolutionary many-player games with multiple strategies. J. Theor. Biol. 2011, 238, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M.; Nowak, M.A. Multi-player games on the cycle. J. Theor. Biol. 2012, 292, 116–128. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Hauert, C. Phase transitions and volunteering in spatial public goods games. Phys. Rev. Lett. 2002, 89, 118101. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Antal, T.; Nowak, M.A.; Traulsen, A. Strategy abundance in 2 × 2 games for arbitrary mutation rates. J. Theor. Biol. 2009, 257, 340–344. [Google Scholar] [CrossRef] [PubMed]
- Allen, B.; Tarnita, C.E. Measures of success in a class of evolutionary models with fixed population size and structure. J. Math. Biol. 2012. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Wu, B.; Wang, L. Evolutionary dynamics of multi-player games driven by aspiration. submitted. 2013. [Google Scholar]
- Eshel, I.; Motro, U. The three brothers’ problem: Kin selection with more than one potential helper. 1. The case of immediate help. Amer. Nat. 1988, 132, 550–566. [Google Scholar] [CrossRef]
- Hauert, C.; Michor, F.; Nowak, M.A.; Doebeli, M. Synergy and discounting of cooperation in social dilemmas. J. Theor. Biol. 2006, 239, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F.; Gordo, I. The tragedy of the commons, the public goods dilemma, and the meaning of rivalry and excludability in evolutionary biology. Evol. Ecol. Res. 2006, 8, 321–332. [Google Scholar]
- Sigmund, K.; De Silva, H.; Traulsen, A.; Hauert, C. Social learning promotes institutions for governing the commons. Nature 2010, 466, 861–863. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, C.S.; Traulsen, A. Mutualism and evolutionary multiplayer games: revisiting the Red King. Proc. R. Soc. B 2012, 279, 4611–4616. [Google Scholar] [CrossRef] [PubMed]
- Claussen, J.C.; Traulsen, A. Non-Gaussian fluctuations arising from finite populations: Exact results for the evolutionary Moran process. Phys. Rev. E 2005, 71, 025101(R). [Google Scholar] [CrossRef]
- Kurokawa, S.S.; Ihara, Y. Evolution of social behavior in finite populations: A payoff transformation in general n-player games and its implications. Theor. Popul. Biol. 2013, 84. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wu, B.; Ho, A.D.; Wang, L. Evolution of cooperation in multilevel public goods games with community structures. Eur. Phys. Lett. 2011, 93, 58001. [Google Scholar] [CrossRef]
- Du, J.; Wu, B.; Wang, L. Evolution of global cooperation driven by risks. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
Appendix
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, B.; Traulsen, A.; Gokhale, C.S. Dynamic Properties of Evolutionary Multi-player Games in Finite Populations. Games 2013, 4, 182-199. https://doi.org/10.3390/g4020182
Wu B, Traulsen A, Gokhale CS. Dynamic Properties of Evolutionary Multi-player Games in Finite Populations. Games. 2013; 4(2):182-199. https://doi.org/10.3390/g4020182
Chicago/Turabian StyleWu, Bin, Arne Traulsen, and Chaitanya S. Gokhale. 2013. "Dynamic Properties of Evolutionary Multi-player Games in Finite Populations" Games 4, no. 2: 182-199. https://doi.org/10.3390/g4020182
APA StyleWu, B., Traulsen, A., & Gokhale, C. S. (2013). Dynamic Properties of Evolutionary Multi-player Games in Finite Populations. Games, 4(2), 182-199. https://doi.org/10.3390/g4020182



