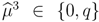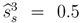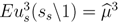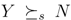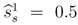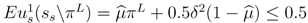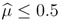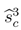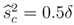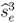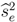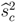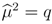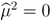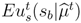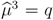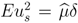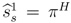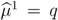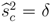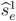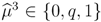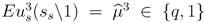Incomplete Information about Social Preferences Explains Equal Division and Delay in Bargaining
Abstract
:1. Introduction
2. Related Literature
3. Model

4. Perfect Bayesian Equilibrium
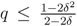 , if 0.5 <
, if 0.5 <  and
and 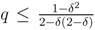 or if q ≤ 0.5, then there is a pooling equilibrium. Its outcome is (0.5,1).
or if q ≤ 0.5, then there is a pooling equilibrium. Its outcome is (0.5,1). 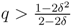 , then there is a separating equilibrium. Its outcome is ((1 − δ(1 − δ),1) if the buyer is self-interested. Its outcome is (δ, 2) if the buyer is envious.
, then there is a separating equilibrium. Its outcome is ((1 − δ(1 − δ),1) if the buyer is self-interested. Its outcome is (δ, 2) if the buyer is envious. and
and  , then there is a separating equilibrium. Its outcome is (1 − δ(1 − δ), 1) if the buyer is self-interested. Its outcome is (0.5, 3) if the buyer is envious.
, then there is a separating equilibrium. Its outcome is (1 − δ(1 − δ), 1) if the buyer is self-interested. Its outcome is (0.5, 3) if the buyer is envious. 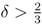 and 0.5 < q < 1, then no PBE in pure strategies exists.
and 0.5 < q < 1, then no PBE in pure strategies exists. or q ≤ 0.5, and if the seller’s belief remains unchanged, i.e ., µt = µt−1, whenever Bayesian updating is not possible.
or q ≤ 0.5, and if the seller’s belief remains unchanged, i.e ., µt = µt−1, whenever Bayesian updating is not possible. 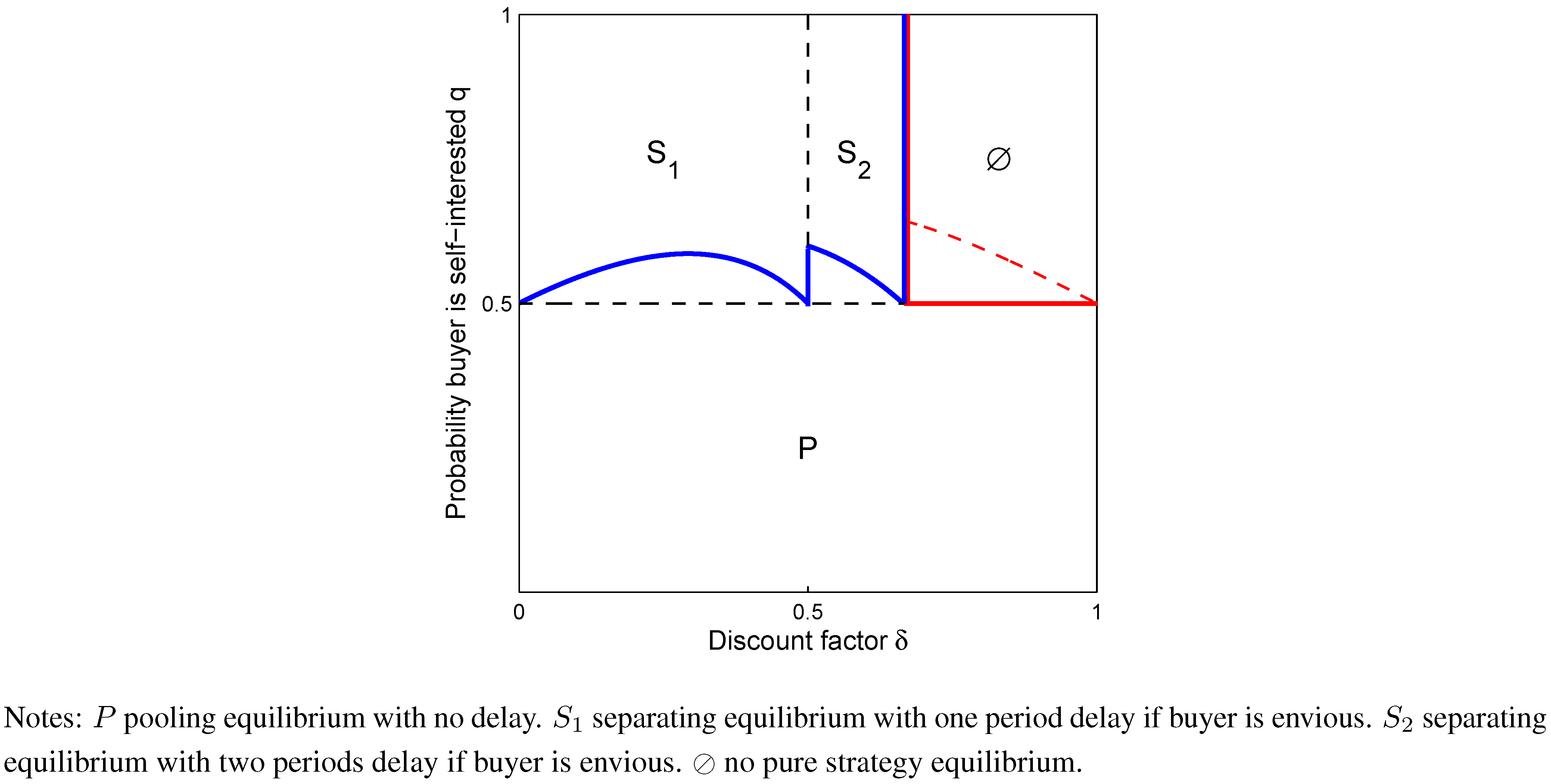
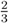 , the upper middle rectangle in Figure 1, in which, depending on the exact parameter values, the equilibrium outcome is either pooling or separating buyer types by risking two periods of delay. The dashed paths in the period 2 continuation games indicate omitted utility values.
, the upper middle rectangle in Figure 1, in which, depending on the exact parameter values, the equilibrium outcome is either pooling or separating buyer types by risking two periods of delay. The dashed paths in the period 2 continuation games indicate omitted utility values. 5. Discussion
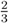 , the seller maximizes his expected utility by offering such that only a self-interested buyer will accept in period 1. In such a separating strategy, delay results from disagreement and continuation of the bargaining with an envious buyer or an imitating self-interested type. If discounting δ ≤ 0.5 is low, imitation of envy is too costly for the self-interested buyer. He accepts the higher price 1 − δ(1 − δ) in the screening period 1. The envious buyer additionally signals his type by rejecting an unequal p1. His period 2 counteroffer δ will be accepted by the seller. Thereby the envious buyer’s counteroffer is less than half of the pie but the seller prefers the low price to the equal division in the final period due to the low patience. If discounting δ ∈ (0.5,
, the seller maximizes his expected utility by offering such that only a self-interested buyer will accept in period 1. In such a separating strategy, delay results from disagreement and continuation of the bargaining with an envious buyer or an imitating self-interested type. If discounting δ ≤ 0.5 is low, imitation of envy is too costly for the self-interested buyer. He accepts the higher price 1 − δ(1 − δ) in the screening period 1. The envious buyer additionally signals his type by rejecting an unequal p1. His period 2 counteroffer δ will be accepted by the seller. Thereby the envious buyer’s counteroffer is less than half of the pie but the seller prefers the low price to the equal division in the final period due to the low patience. If discounting δ ∈ (0.5, 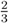 ] is moderate, it costs more time to exclude imitation by a self-interested type and agreement on equal division with an envious buyer follows in period 3 after he signaled his type by rejecting an unequal p1 and offering an unacceptable price p2 in period 2.
] is moderate, it costs more time to exclude imitation by a self-interested type and agreement on equal division with an envious buyer follows in period 3 after he signaled his type by rejecting an unequal p1 and offering an unacceptable price p2 in period 2. 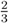 and q > 0.6, then both separating outcome are preferred to the pooling outcome. Whether separating the buyer types in equilibrium requires one or two periods of delay depends merely on the discount factor δ. As the perfectly envious buyer suffers infinitely from accepting any disadvantageous division, he never imitates self-interested behavior. In contrast, a self-interested buyer gains utility through being offered the equal division if he would pass undetected as an envious type. Therefore, the more patient the players become, the more time must pass between the disadvantageous opening price and the equal division that the seller would like to offer to the different buyers in order to separate buyer types.
and q > 0.6, then both separating outcome are preferred to the pooling outcome. Whether separating the buyer types in equilibrium requires one or two periods of delay depends merely on the discount factor δ. As the perfectly envious buyer suffers infinitely from accepting any disadvantageous division, he never imitates self-interested behavior. In contrast, a self-interested buyer gains utility through being offered the equal division if he would pass undetected as an envious type. Therefore, the more patient the players become, the more time must pass between the disadvantageous opening price and the equal division that the seller would like to offer to the different buyers in order to separate buyer types. 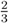 , and the buyer is likely to be self-interested, i.e., q > 0.5, then a delay of two periods before dividing equally is no longer sufficient to deter the self-interested buyer from imitating the envious type. Yet, the seller does not maximize utility by offering the equal division to all buyer types for a sufficiently high chance to bargain with self-interested buyer. In an infinite horizon game, the incentive of a self-interested buyer to imitate envy could be eliminated by the seller and the envious buyer through delaying their agreement on the equal division beyond two periods. In the finite horizon game, the scope for delay is limited through the length of the game. Nevertheless, the players can reduce the incentive of the self-interested buyer to imitate the envious type in addition to a physical delay by playing mixed strategies that exclude, at least sometimes, an agreement between the envious buyer and the seller in period 3. Such equilibria are not considered in the paper, but I established that for sufficiently high q and high δ no pure strategy equilibria exist.
, and the buyer is likely to be self-interested, i.e., q > 0.5, then a delay of two periods before dividing equally is no longer sufficient to deter the self-interested buyer from imitating the envious type. Yet, the seller does not maximize utility by offering the equal division to all buyer types for a sufficiently high chance to bargain with self-interested buyer. In an infinite horizon game, the incentive of a self-interested buyer to imitate envy could be eliminated by the seller and the envious buyer through delaying their agreement on the equal division beyond two periods. In the finite horizon game, the scope for delay is limited through the length of the game. Nevertheless, the players can reduce the incentive of the self-interested buyer to imitate the envious type in addition to a physical delay by playing mixed strategies that exclude, at least sometimes, an agreement between the envious buyer and the seller in period 3. Such equilibria are not considered in the paper, but I established that for sufficiently high q and high δ no pure strategy equilibria exist. 6. Conclusion
Appendix
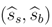 and a set of beliefs of the seller that the buyer is self-interested satisfying the following requirements:
and a set of beliefs of the seller that the buyer is self-interested satisfying the following requirements:- (E1) The seller’s equilibrium strategy
maximizes the seller’s discounted expected utility given the buyer’s equilibrium strategy
.
- (E2) For each buyer type b ∈ {c, e}, the buyer’s equilibrium strategy
maximizes the buyer’s discounted utility given the seller’s equilibrium strategy
.
- (E3) The seller belief
in period t is formed by Bayes’ theorem from the equilibrium strategies at each information set.
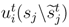 indicates the utility uit of player i in period t if player j adopts his strategy sj = {sj1,sj2,sj3}, in which the t-th element is substituted by
indicates the utility uit of player i in period t if player j adopts his strategy sj = {sj1,sj2,sj3}, in which the t-th element is substituted by 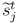 given the other player’s equilibrium strategy
given the other player’s equilibrium strategy  . As ∂ubt/∂pt ≤ 0 and ∂uts/∂pt > 0, it is sufficient to look at the maximal/minimal prices at which behavior of the buyer types/seller changes. πH := 1 − δ(1 − δ) denotes the division that corresponds to the backwards induction outcome of a three period bargaining game with a self-interested buyer. πL := 1 − δ(1 − 0.5δ) denotes the division a self-interested buyer just accepts in period 1 if he could obtain the share of an envious buyer in the continuation game.
. As ∂ubt/∂pt ≤ 0 and ∂uts/∂pt > 0, it is sufficient to look at the maximal/minimal prices at which behavior of the buyer types/seller changes. πH := 1 − δ(1 − δ) denotes the division that corresponds to the backwards induction outcome of a three period bargaining game with a self-interested buyer. πL := 1 − δ(1 − 0.5δ) denotes the division a self-interested buyer just accepts in period 1 if he could obtain the share of an envious buyer in the continuation game.Proof of Proposition 1
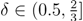 (Figure 2(c)). In each lemma, I show for each player and type that there is no profitable deviation from the equilibrium strategy, emphasized in the figures, given the beliefs at the decision nodes and the equilibrium strategy of the other player. Afterwards, I prove that the assumed beliefs follow from Bayes’ theorem given the equilibrium strategies.
(Figure 2(c)). In each lemma, I show for each player and type that there is no profitable deviation from the equilibrium strategy, emphasized in the figures, given the beliefs at the decision nodes and the equilibrium strategy of the other player. Afterwards, I prove that the assumed beliefs follow from Bayes’ theorem given the equilibrium strategies.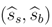 and beliefs
and beliefs  given in Table 1.
given in Table 1.The seller’s equilibrium strategy  and belief and belief  | ||
| t | 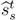 |  |
| 1 | 0.5 | q |
| 2 | Y if p2 ≥ 0.5δ else N | 0 if p1 = πL and p1 = 0.5δ, else q |
| 3 | 0.5 | μ2 |
The buyer’s equilibrium strategy 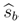 | ||
| t | 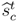 | 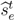 |
| 1 | Y if p1 ≤ πL, else N | Y if p1 ≤ 0.5, else N |
| 2 | 0.5δ | 0.5δ |
| 3 | Y | Y if p3 ≤ 0.5, else N |
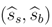 and belief
and belief  satisfy the PBE requirements:
satisfy the PBE requirements: - (E1) In period 3, both buyer types maximize utility by accepting the equal division. Given
and q ≤ 0.5, the seller maximizes expected utility with
because us3(ss\0.5) = 0.5 is weakly larger than
. In period 2, the utility of ss2 ∈{Y, N} is us2 = p2 and us2 = 0.5δ, respectively. Hence,
if p2 ≥ 0.5δ as implied by
. In period 1, the utility of ss1 ∈ {0.5,πL,1} is maximized by
as us1(ss\0.5) = 0.5,
if
and Eus1 (ss\1) = 0.5δ2 ≤ 0.5.
- (E2) In period 3, the self-interested buyer’s best response
is to accept any price as, otherwise, the bargaining ends in disagreement with zero payoff. In period 2, the utility of sc2 ∈{0, 0.5δ} is maximized by
as uc2(sc\0.5δ) = 1 − 0.5δ is larger than uc2(sc\0) = 0.5δ. In period 1, the utility of sc1 ∈ {Y, N} is uc1(sc\Y ) = 1 − p1 and uc1(sc\N) = δ(1 − 0.5δ), respectively. Hence,
if p1 ≤ πL as implied by
. In period 3, the envious buyer’s best response
is to accept any price equal or less than half and to reject otherwise as, afterwards, the bargaining ends with zero payoff to both. In period 2,
equals
because payoffs are larger than half and similar for both buyer types in this subgame. In period 1, the utility of se1 ∈ {Y, N} is ue1(se\Y ) = 1 − p1 if p1 ≤ 0.5, else −∞, and ue1(se\N) = δ(1 − 0.5δ), respectively. Hence,
if p1 ≤ 0.5 as implied by
.
- (E3) In period 1, the seller’s unconditional belief is the frequency of the self-interested buyer in the population. Both buyer types accept an price p1 ≤ 0.5 and reject p1 ∈ (πL, 1]. In period 2, after rejection of p1 ∉ (0.5,πL] both types make counteroffer p2 = 0.5δ and the seller receives no information, i.e.,
. If p1 ∈ (0.5,πL], then only the self-interested buyer accepts and, hence,
. In period 3, the seller moves between information sets and receives no information.
 and δ ≤ 0.5, then there is a pooling equilibrium with outcome (0.5,1). If
and δ ≤ 0.5, then there is a pooling equilibrium with outcome (0.5,1). If 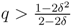 and δ ≤ 0.5, then there is a separating equilibrium. Its outcome is (πH ,1) if bargaining is with a self-interested buyer. Its outcome is (δ,2) if bargaining is with an envious buyer. The equilibrium is supported by the strategy pair
and δ ≤ 0.5, then there is a separating equilibrium. Its outcome is (πH ,1) if bargaining is with a self-interested buyer. Its outcome is (δ,2) if bargaining is with an envious buyer. The equilibrium is supported by the strategy pair 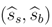 and beliefs
and beliefs  given in Table 2.
given in Table 2.The seller’s equilibrium strategy  and belief and belief  | ||||
| t | 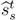 |  | History | |
| 1 | 0.5 if  , else πH , else πH | q | - | |
| 2 | Y if p2 ≥ δ, else N | q | p1 ∉ (0.5,πH] | |
| Y if p2 ≥ δ, else N | 0 if p2 = δ, else q | p1 ∈ (πL,πH] | ||
| Y if p2 ≥ 0.5δ, else N | 0 if p2 = 0.5δ, else q | p1 ∈ (0.5,πL] | ||
| 3 | 1 | μ2 | p1 ∉ (0.5,πH] | |
| 0.5 if p2 = δ, else 1 | μ2 | p1 ∈ (πL,πH] | ||
| 0.5 if p2 = 0.5δ, else 1 | μ2 | p1 ∈ (0.5,πL] | ||
The buyer’s equilibrium strategy 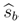 | ||||
| t | 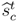 | 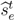 | History | |
| 1 | Y if p1 ≤ πH, else N | Y if p1 ≤ 0.5, else N | - | |
| 2 | δ | δ | p1 ∉ (0.5,πL] | |
| 0.5δ | 0.5δ | p1 ∈ (0.5,πL] | ||
| 3 | Y | Y if p3 ≤ 0.5, else N | Any | |
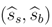 and belief
and belief  satisfy the PBE requirements:
satisfy the PBE requirements: - (E1) In period 3, the action of one or both buyer types changes if ss3 ∈ {0.5, 1}. Given
and q > 0.5, the seller maximizes expected utility
with
because us3(ss\0.5) = 0.5 is smaller than Eus3(ss\1) = q if
, i.e., for histories other than p1 ∈ (0.5,πL] and p2 = 0.5δ or p1 ∈ (πL,πH] and p2 = δ. In period 2, the utility of ss2 ∈ {Y, N} is us2 = p2 and Eus2 =0.5δ or
, respectively. Hence,
if p1 ∈ (0.5,πL] and p2 ≥0.5δ or p1 ∈ (πL,πH] and p2 = δ as implied by
. In period 1, the utility of SS1 ∈ {0.5, πL , πH} is maximized by
if
and by
otherwise as, for
and q > 0.5, the expected utility
is weakly smaller than us1(ss\0.5) = 0.5 and Eus1(ss\πH) = qπH + (1-q)δ2. The comparison of latter implies the threshold.
- (E2) In period 3, the self-interested buyer’s best response
is to accept any price as, otherwise, the bargaining ends in disagreement with zero payoff. In period 2, the utility of Sc2 ∈ {0,0.5δ, δ} is maximized by
if p1 ∈ (0.5,πL] and by
otherwise as, depending on the history, these prices are the discounted period 3 agreements just accepted by the seller who rejects Sc2 = 0 giving the buyer utility uc2(ss\0) = 0. In period 1, the utility of sc1 ∈ {Y, N} is uc1(ss\Y) = 1 - p1 and uc1(ss\N) = δ(1-0.5δ), respectively. Hence,
if p1 ≤ πL as implied by
. In period 3, the envious buyer’s best response
is to accept any price equal or less than half and to reject otherwise as, afterwards, the bargaining ends with zero payoff to both. In period 2,
equals
because payoffs are larger than half and similar for both buyer types in this subgame. In period 1, the utility of se1 ∈ {Y, N} is ue1(se\Y) = 1 - p1 if p1 ≤ 0.5, else −∞, and ue1(se\N) = δ(1-0.5δ), respectively. Hence,
if p1 ≤ 0.5 as implied by
.
- (E3) In period 1, the seller’s unconditional belief is the frequency of the self-interest buyer in the population. Both buyer types accept a price p1 ≤ 0.5 and reject p1 ∈ (πH,1]. In period 2, after rejection of p1 ∉ (0.5,πH] both types make the same counteroffer p2 ∈ {0.5δ,δ}and the seller receives no information, i.e.,
. If p1 ∈ (0.5,πH],then only the self-interested buyer accepts p1 ∈ (0.5,πH]. Hence,
if his acceptance is followed by rational action. In period 3, the seller moves between information sets and receives no information.
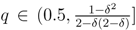 and
and 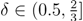 , then there is a pooling equilibrium with outcome (0.5,1). If
, then there is a pooling equilibrium with outcome (0.5,1). If  and
and 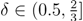 , then there is a separating equilibrium. Its outcome is (πH,1) if bargaining is with a self-interested buyer. Its outcome is (0.5,3) if bargaining is with an envious buyer. The equilibrium is supported by the strategy pair
, then there is a separating equilibrium. Its outcome is (πH,1) if bargaining is with a self-interested buyer. Its outcome is (0.5,3) if bargaining is with an envious buyer. The equilibrium is supported by the strategy pair 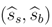 and beliefs
and beliefs  given in Table 3.
given in Table 3. The seller’s equilibrium strategy  and belief and belief  | ||||
| t | 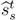 |  | History | |
| 1 | 0.5 if  , else πH , else πH | q | - | |
| 2 | Y if p2 ≥ δ, else N | 0 if p2 = 0, 1 if p2 = δ, else q | p1 ∉ (0.5,πL] | |
| Y if p2 ≥ 0.5δ, else N | 0 if p2 = 0.5δ, else q | p1 ∈ (0.5,πL] | ||
| 3 | 0.5 if p2 = 0, else 1 | μ2 | p1 ∉ (0.5,πL] | |
| 0.5 if p2 = 0.5δ, else 1 | μ2 | p1 ∈ (0.5,πL] | ||
The buyer’s equilibrium strategy 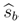 | ||||
| t | 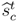 | 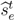 | History | |
| 1 | Y if p1 ≤ πH, else N | Y if p1 ≤ 0.5, else N | - | |
| 2 | δ | 0 | p1 ∉ (0.5,πL] | |
| 0.5δ | 0.5δ | p1 ∈ (0.5,πL] | ||
| 3 | Y | Y if p3 ≤ 0.5, else N | Any | |
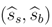 and belief
and belief  satisfy the PBE requirements:
satisfy the PBE requirements: - (E1) In period 3, the action of one or both buyer types changes if ss3 ∈ {0.5, 1}. Given
and q > 0.5, the seller maximizes expected utility with
because us3(ss\0.5) = 0.5 is smaller than
, i.e., for histories other than p1 ∉ (0.5,πL] and p2 = 0 or p1 ∈ (0.5,πL] and p2 =0.5δ. In period 2, the utility of ss2 ∈ {Y, N} is us2 = p2 and Eus2 =0.5δ or
, respectively. Hence,
if p1 ∈ (0.5,πL] and p2 ≥0.5δ or p1 ∉ (0.5,πL] and p2 = δ as implied by
. In period 1, the utility of SS1 ∈ {0.5, πL , πH} is maximized by
if
and by
otherwise as, for
and q > 0.5, the expected utility
is weakly smaller than us1(ss\0.5) = 0.5 and Eus1(ss\πH) = qπH +0.5δ2 (1-q). The comparison of latter implies the threshold.
- (E2) In period 3, the self-interested buyer’s best response
is to accept any price as, otherwise, the bargaining ends in disagreement with zero payoff. In period 2, for
, the utility of Sc2 ∈ {0,0.5δ,δ} is maximized by
if p1 ∈ (0.5,πL] and by
otherwise as, depending on the history, these prices are the discounted period 3 agreements just accepted by the seller who rejects Sc2 = 0 giving the buyer utility uc2(ss\0) = 0.5δ. In period 1, the utility of sc1 ∈ {Y, N} is uc1(ss\Y) = 1-p1 and uc1(ss\N) = δ(1-δ), respectively. Hence,
if p1 ≤ πH as implied by
. In period 3, the envious buyer’s best response
is to accept any price equal or less than half and to reject otherwise as, afterwards, the bargaining ends with zero payoff to both. In period 2, the envious buyer utility of asking an acceptable price p2 may be lower than the utility he gets from a rejection if he can thereby signal his type. The utility of Se2 ∈ {0,0.5δ, δ} is maximized by
if p1 ∈ (0.5,πL] and by
otherwise because, depending on the history, ue2(ss\0.5δ) = 1-0.5δ is larger than ue2(ss\0) = 0 if p1 ∈ (0.5,πL] but ue2(ss\δ) = 1-δ is smaller than ue2(ss\0) = 0.5δ if p1 ∉ (0.5,πL]. In period 1, the utility of se1 ∈ {Y, N}is ue1(se\Y) = 1-p1 if p1 ≤ 0.5, else −∞, and ue1(se\N) = δ(1-0.5δ), respectively. Hence,
if p1 ≤ 0.5 as implied by
.
- (E3) In period 1, the seller’s unconditional belief is the frequency of the self-interest buyer in the population. Both buyer types accept a price p1 ≤ 0.5 and reject p1 ∈ (πH,1]. In period 2, after a p1 ∈ (0.5,πL] both types would make the same counteroffer p2 ∈ 0.5δ but the seller updates his belief on the equilibrium path to
from the self-interested buyer’s acceptance of this price. If p1 ∉ (0.5,πL], each types may make a different counteroffer p2 ∈ {0,δ} and the seller updates his belief to
after p2 = 0,made only by the envious buyer, and to
after p2 = δ, made only by the self-interested buyer. In period 3, the seller moves between information sets and receives no information.
Proof of Proposition 2
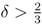 : For
: For 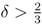 , the self-interested buyer will reject p1 = πH if he can realize either outcome (0.5δ,2) or outcome (0.5,3) in a later period pooling equilibrium. An optimal strategy of the seller
, the self-interested buyer will reject p1 = πH if he can realize either outcome (0.5δ,2) or outcome (0.5,3) in a later period pooling equilibrium. An optimal strategy of the seller  , however, must include a starting price that is at least accepted by the self-interested buyer. Thus, the seller’s best pure strategy candidate either asks p1 = 0.5 in a pooling strategy, or it asks p1 = πL in a separating strategy, or it asks p1 = πH, accepts p2 ≥ δ and demands p3 = 1 in another separating strategy. Comparing the seller utility of the two separating strategies, qπL + 0.5(1-q)δ2 < qπH implies that immediate agreement on πH at the cost of excluding the envious buyer from trade is preferred. Yet, the seller can further gain utility by choosing a mixed separating strategy
, however, must include a starting price that is at least accepted by the self-interested buyer. Thus, the seller’s best pure strategy candidate either asks p1 = 0.5 in a pooling strategy, or it asks p1 = πL in a separating strategy, or it asks p1 = πH, accepts p2 ≥ δ and demands p3 = 1 in another separating strategy. Comparing the seller utility of the two separating strategies, qπL + 0.5(1-q)δ2 < qπH implies that immediate agreement on πH at the cost of excluding the envious buyer from trade is preferred. Yet, the seller can further gain utility by choosing a mixed separating strategy 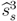 that divides equally in period 3 with probability l such that the envious buyer accepts sometimes but the self-interested buyer continues to weakly prefer immediate acceptance. That is,
that divides equally in period 3 with probability l such that the envious buyer accepts sometimes but the self-interested buyer continues to weakly prefer immediate acceptance. That is, 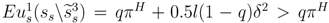 with probability l such that uc1(ss\πH,sc\Y) = πH is just equal to uc1(ss\πH,sc\N) = 0.5lδ2. In period 1, the seller utility is maximized by the equal division if
with probability l such that uc1(ss\πH,sc\Y) = πH is just equal to uc1(ss\πH,sc\N) = 0.5lδ2. In period 1, the seller utility is maximized by the equal division if 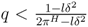 and by the mixed separating strategy
and by the mixed separating strategy  otherwise. The comparison of us1(ss\0.5) = 0.5 and
otherwise. The comparison of us1(ss\0.5) = 0.5 and  implies the threshold. The preference for a pooling strategy is bounded by
implies the threshold. The preference for a pooling strategy is bounded by 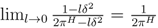 (dashed red curve in Figure 1). As sequential rationality requires the mixed strategy in the separating continuation game even if the pooling outcome is preferred, no PBE exists in pure strategies for
(dashed red curve in Figure 1). As sequential rationality requires the mixed strategy in the separating continuation game even if the pooling outcome is preferred, no PBE exists in pure strategies for 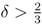 and q > 0.5.
and q > 0.5. Acknowledgments
References
- Ståhl, I. Bargaining Theory; Stockholm School of Economics: Stockholm, Sweden, 1972. [Google Scholar]
- Rubinstein, A. Perfect equilibrium in a bargaining model. Econometrica 1982, 50, 97–109. [Google Scholar] [CrossRef]
- Bolton, G.E. A comparative model of bargaining: Theory and evidence. Am. Econ. Rev. 1991, 81, 1096–1136. [Google Scholar]
- Ochs, J.; Roth, A.E. An experimental study of sequential bargaining. Am. Econ. Rev. 1989, 79, 355–384. [Google Scholar]
- Weg, E.; Rapoport, A.; Felsenthal, D.S. Two-person bargaining behavior in fixed discounting factors games with infinite horizon. Games Econ. Behav. 1990, 2, 76–95. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral Game Theory. Experiments in Strategic Interaction (The Roundtable Series in Behavioral Economics); Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Cooper, D.J.; Kagel, J.H. Other Regarding Preferences: A Selective Survey of Experimental Results. In Handbook of Experimental Economics; Kagel, J.H., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA; Volume 2.
- Smith, R. Envy: Theory and Research; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Chatterjee, K.; Samuelson, L. Bargaining with two-sided incomplete information: An infinite horizon model with alternating offers. Rev. Econ. Stud. 1987, 54, 175–192. [Google Scholar] [CrossRef]
- Chatterjee, K.; Samuelson, L. Bargaining under two-sided incomplete information: The unrestricted offers case. Oper. Res. 1988, 36, 605–618. [Google Scholar] [CrossRef]
- Cramton, P.C. Strategic delay in bargaining with two-sided uncertainty. Rev. Econ. Stud. 1992, 59, 205–225. [Google Scholar] [CrossRef]
- Grossman, S.J.; Perry, M. Sequential bargaining under asymmetric information. J. Econ. Theory 1986, 39, 120–154. [Google Scholar] [CrossRef]
- Gul, F.; Sonnenschein, H. On delay in bargaining with one-sided uncertainty. Econometrica 1988, 56, 601–611. [Google Scholar] [CrossRef]
- Rubinstein, A. A bargaining model with incomplete information about time preferences. Econometrica 1985, 53, 1151–1172. [Google Scholar] [CrossRef]
- Cramton, P.C. Bargaining with incomplete information: An infinite-horizon model with two-sided uncertainty. Rev. Econ. Stud. 1984, 51, 579–593. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K.; Tirole, J. Infinite-Horizon Models of Margaining with One-SidedIncomplete Information. In Game-Theoretic Models of Bargaining; Roth, A.E., Ed.; Cambridge University Press: Cambridge, UK, 1985; pp. 73–98. [Google Scholar]
- Sobel, J.; Takahashi, I. A multistage model of bargaining. Rev. Econ. Stud. 1983, 50, 411–426. [Google Scholar] [CrossRef]
- Ausubel, L.M.; Deneckere, R.J. A direct mechanism characterization of sequential bargaining with one-sided incomplete information. J. Econ. Theory 1989, 48, 18–46. [Google Scholar] [CrossRef]
- Ausubel, L.M.; Cramton, P.; Deneckere, R.J. Bargaining with Incomplete Information. In Handbook of Game Theory with Economic Applications; Aumann, R.J., Hart, S., Eds.; Handbook of Game Theory with Economic Applications, Elsevier: Amsterdam, The Netherlands, 2002; Volume 3, pp. 1897–1945. [Google Scholar]
- Roth, A.E. Bargaining Experiments. In Handbook of Experimental Economics; Kagel, J.H., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; pp. 253–348. [Google Scholar]
- Rasch, A.; Wambach, A.; Wiener, K. Bargaining and inequity aversion: On the efficiency of the double auction. Econ. Lett. 2012, 114, 178–181. [Google Scholar] [CrossRef]
- Srivastava, J. The role of inferences in sequential bargaining with one-sided incomplete information: Some experimental evidence. Org. Behav. Hum. Decis. Process. 2001, 85, 166–187. [Google Scholar] [CrossRef]
- Von Siemens, F.A. Bargaining under incomplete information, fairness, and the hold-up problem. J. Econ. Behav. Org. 2009, 71, 486–494. [Google Scholar] [CrossRef]
- Von Siemens, F.A. Heterogeneous social preferences, screening, and employment contracts. Oxf. Econ. Papers 2010, 63, 499–522. [Google Scholar] [CrossRef]
- De Bruyn, A.; Bolton, G.E. Estimating the influence of fairness on bargaining behavior. Manag. Sci. 2008, 54, 1774–1791. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A. Asymmetric inequality aversion and noisy behavior in alternating-offer bargaining games. Eur. Econ. Rev. 2000, 44, 1079–1089. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Kohler, S. Envy can Promote More Equal Division in Alternating-Offer Bargaining. In MPRA Paper 40761; University Library of Munich: Munich, Germany, 2012. [Google Scholar]
- Kohler, S. Guilt Causes Equal or Unequal Division in Alternating-Offer Bargaining. In MPRA Paper 40760; University Library of Munich: Munich, Germany, 2012. [Google Scholar]
- Driesen, B.; Perea, A.; Peters, H. Alternating offers bargaining with loss aversion. Math. Soc. Sci. 2011, 64, 103–118. [Google Scholar]
- Montero, M. Inequity aversion may increase inequity. Econ. J. 2007, 117, C192–C204. [Google Scholar] [CrossRef]
- Kohler, S. Altruism and fairness in experimental decisions. J. Econ. Behav. Org. 2011, 80, 101–109. [Google Scholar] [CrossRef]
- Tan, J.H.W.; Bolle, F. On the relative strengths of altruism and fairness. Theory Decis. 2006, 60, 35–67. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 1–263. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory: Analysis of Conflict; Harvard University Press: Cambridge, UK, 1991. [Google Scholar]
- Abreu, D.; Gul, F. Bargaining and reputation. Econometrica 2000, 68, 85–117. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kohler, S. Incomplete Information about Social Preferences Explains Equal Division and Delay in Bargaining. Games 2012, 3, 119-137. https://doi.org/10.3390/g3030119
Kohler S. Incomplete Information about Social Preferences Explains Equal Division and Delay in Bargaining. Games. 2012; 3(3):119-137. https://doi.org/10.3390/g3030119
Chicago/Turabian StyleKohler, Stefan. 2012. "Incomplete Information about Social Preferences Explains Equal Division and Delay in Bargaining" Games 3, no. 3: 119-137. https://doi.org/10.3390/g3030119
APA StyleKohler, S. (2012). Incomplete Information about Social Preferences Explains Equal Division and Delay in Bargaining. Games, 3(3), 119-137. https://doi.org/10.3390/g3030119