On SEIR Epidemic Dynamics with Pro- and Anti-Vaccination Strategies: An Evolutionary Game Theory Approach
Abstract
1. Introduction
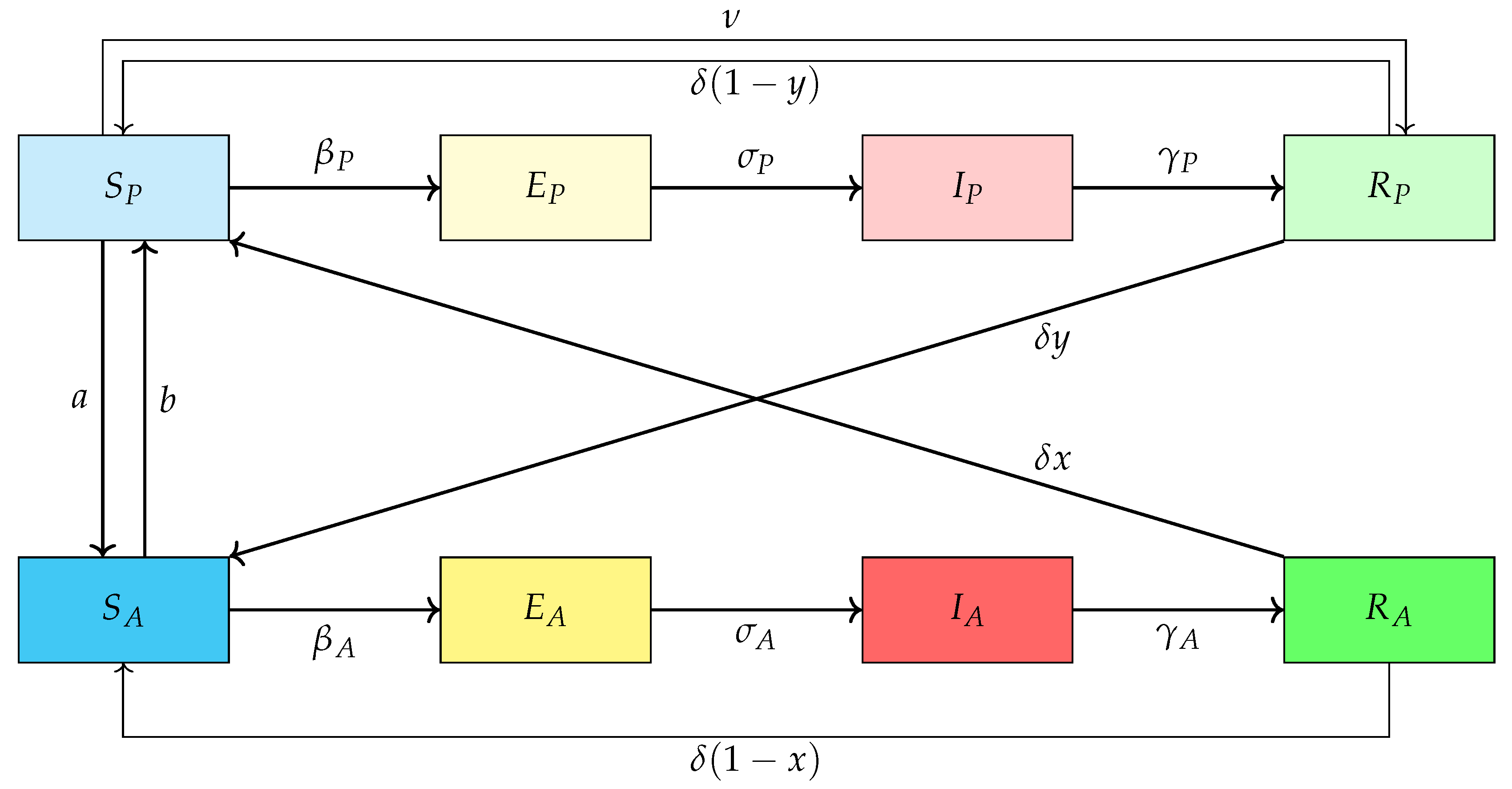
2. Model Presentation, Total Infection and Average Social Payoff
2.1. Model Presentation and Basic Reproduction Number
2.2. Behavior Model
2.3. Total Infection, Average Social Payoff and Social Efficiency Deficit
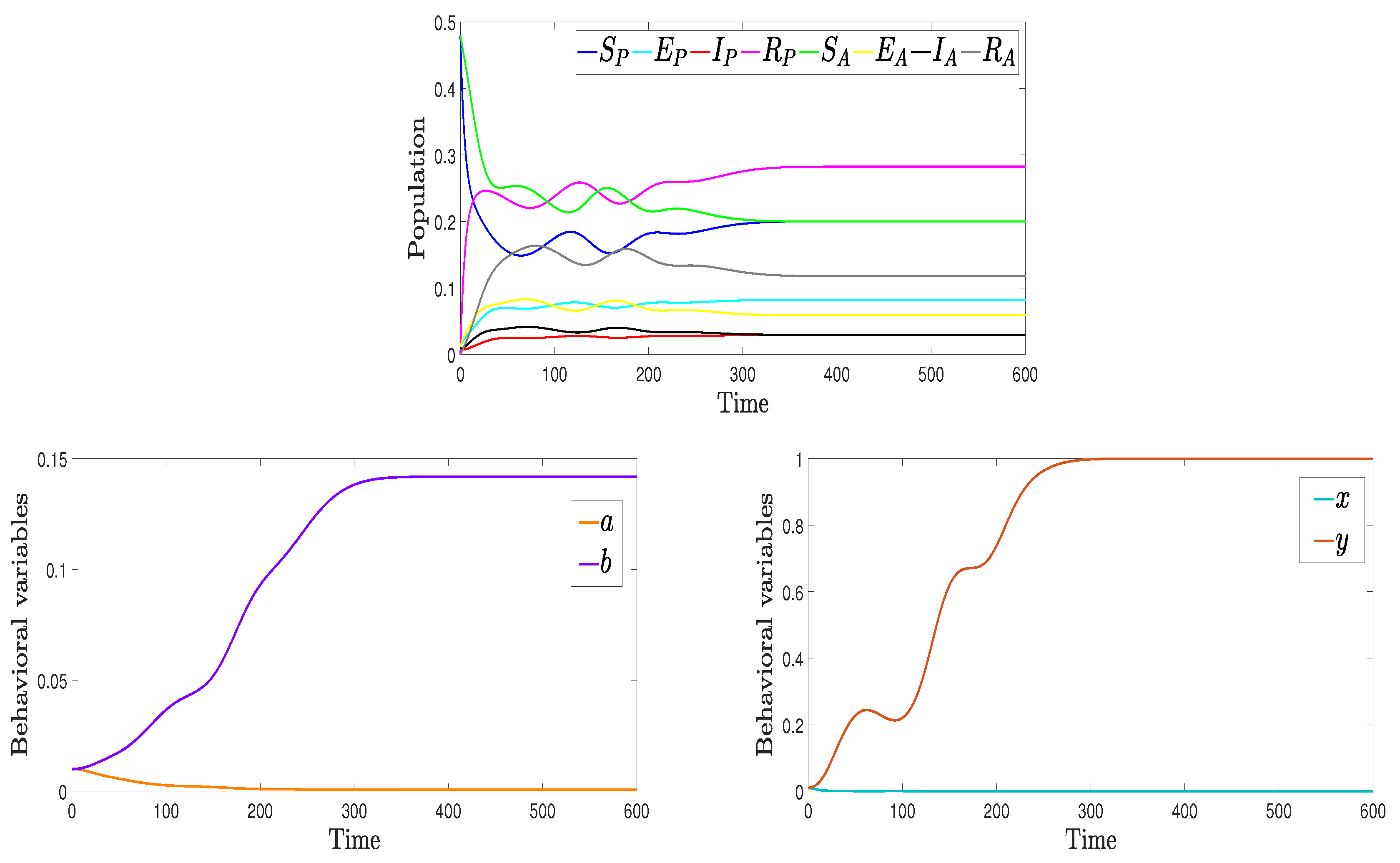
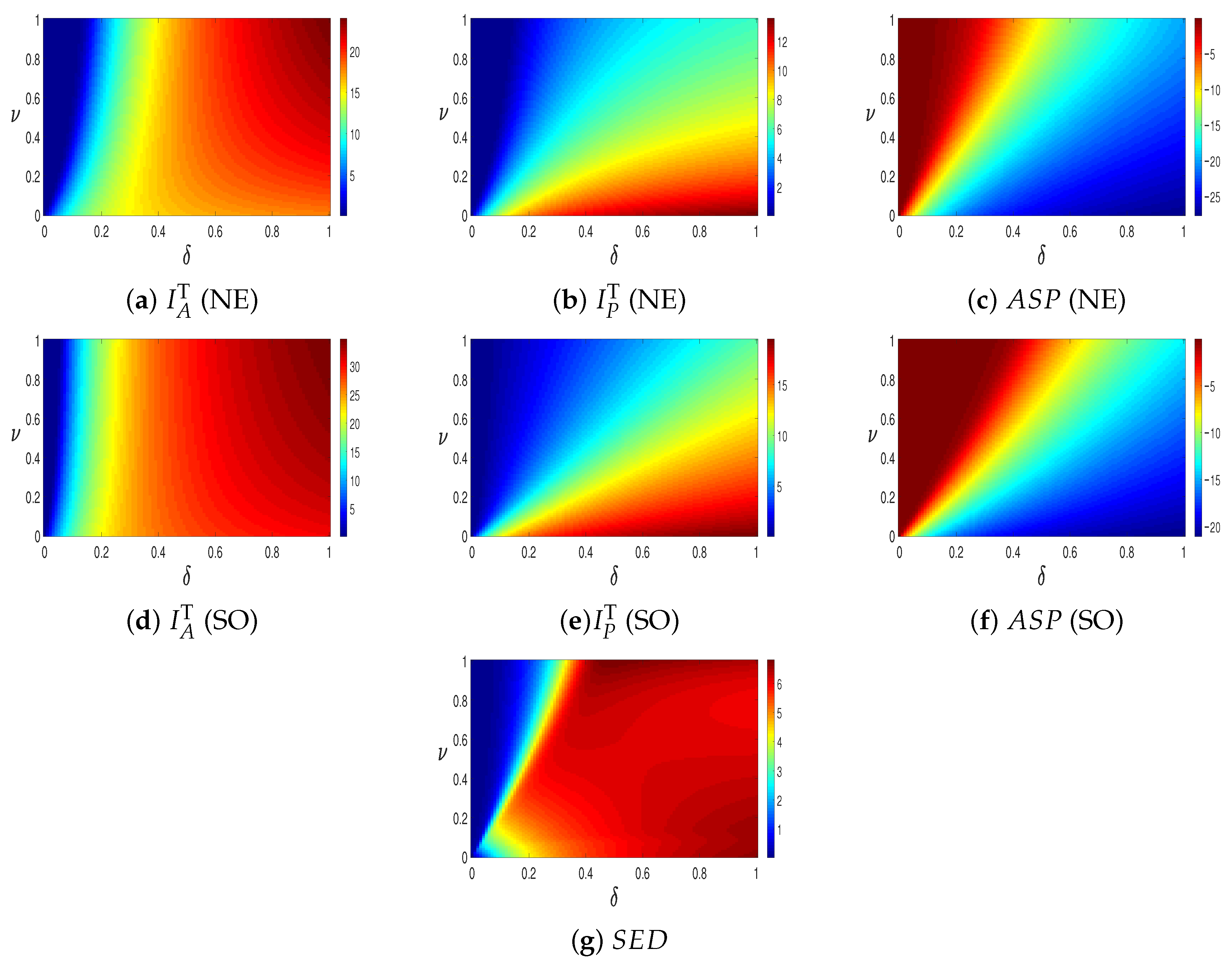
3. Numerical Simulations and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Augsburger, I. B., Galanthay, G. K., Tarosky, J. H., Rychtář, J., & Taylor, D. (2023). Imperfect vaccine can yield multiple Nash equilibria in vaccination games. Mathematical Biosciences, 356, 108967. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R., & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Bauch, C. T. (2005). Imitation dynamics predict vaccinating behaviour. Proceedings of the Royal Society B: Biological Sciences, 272, 1669–1675. [Google Scholar] [CrossRef] [PubMed]
- Bauch, C. T., & Earn, D. J. D. (2004). Vaccination and the theory of games. Proceedings of the National Academy of Sciences, 101, 13391–13394. [Google Scholar] [CrossRef] [PubMed]
- Caasi, J. A. S., Joseph, B. M., Kodiyamplakkal, H. J., Manibusan, J. R. U., Camacho Aquino, L. J., Oh, H., Rychtář, J., & Taylor, D. (2022). A game-theoretic model of voluntary yellow fever vaccination to prevent urban outbreaks. Games, 13(4), 55. [Google Scholar] [CrossRef]
- Darwin, C. (1859). On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray. [Google Scholar]
- Dawes, R. M. (1980). Social dilemmas. Annual Review of Psychology, 31, 169–193. [Google Scholar] [CrossRef]
- Hausken, K., & Ncube, M. (2022). A game theoretic analysis of competition between vaccine and drug companies during disease contraction and recovery. Medical Decision Making, 42(5), 571–586. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J., & Sigmund, K. (1998). Evolutionary games and population dynamics. Cambridge University Press. [Google Scholar]
- Karandikar, R., Mookherjee, D., Ray, D., & Vega-Redondo, F. (1998). Evolving aspirations and cooperation. Journal of Economic Theory, 80, 292–331. [Google Scholar] [CrossRef]
- Kermack, W. O., & McKendrick, A. G. (1927). A contribution to the mathematical theory of Epidemics. Proceedings of the Royal Society A, 115, 700–721. [Google Scholar] [CrossRef]
- Kerr, B., Riley, M. A., Feldman, M. W., & Bohannan, B. J. M. (2002). Local dispersal promotes biodiversity in a real-life game of Rock–Paper–Scissors. Nature, 418, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Khan, M. M. U. R., & Tanimoto, J. (2023). Investigating the social dilemma of an Epidemic model with provaccination and antivaccination groups: An evolutionary approach. Alexandria Engineering Journal, 75, 341–349. [Google Scholar] [CrossRef]
- Marquez, R. M. A., Minas, M. S. C., Santos, J. V. T., Yoon, K., Campo, V. N. S., Oh, H., Rychtář, J., & Taylor, D. (2024). Game-theoretical model of COVID-19 vaccination in the endemic equilibrium. Journal of Biological Systems, 32(02), 349–370. [Google Scholar] [CrossRef]
- Martcheva, M. (2015). An introduction to mathematical epidemiology. Springer. [Google Scholar]
- Martinez, A., Machado, J., Sanchez, E., & Erovenko, I. V. (2025). Optimal vaccination strategies to reduce endemic levels of meningitis in Africa. Games, 16(5), 45. [Google Scholar] [CrossRef]
- Maynard Smith, J. (1982). Evolution and the theory of games. Cambridge University Press. [Google Scholar]
- Nowak, M. A. (2006). Evolutionary dynamics: Exploring the equations of life. Harvard University Press. [Google Scholar]
- Oechssler, J. (2002). Cooperation as a result of learning with aspiration levels. Journal of Economic Behavior & Organization, 49, 405–409. [Google Scholar] [CrossRef]
- Scheckelhoff, K., Ejaz, A., Erovenko, I. V., Rychtář, J., & Taylor, D. (2021). Optimal voluntary vaccination of adults and adolescents can help eradicate hepatitis B in China. Games, 12(4), 82. [Google Scholar] [CrossRef]
- Smith, J. M., & Price, G. R. (1973). The logic of animal conflict. Nature, 246, 15–18. [Google Scholar] [CrossRef]
- Traulsen, A., & Hauert, C. (2009). Stochastic evolutionary game dynamics. In Reviews of nonlinear dynamics and complexity (pp. 25–61). Wiley. [Google Scholar]
- von Neumann, J., & Morgenstern, O. (1944). Theory of games and economic behavior. Princeton University Press. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allali, K. On SEIR Epidemic Dynamics with Pro- and Anti-Vaccination Strategies: An Evolutionary Game Theory Approach. Games 2025, 16, 61. https://doi.org/10.3390/g16060061
Allali K. On SEIR Epidemic Dynamics with Pro- and Anti-Vaccination Strategies: An Evolutionary Game Theory Approach. Games. 2025; 16(6):61. https://doi.org/10.3390/g16060061
Chicago/Turabian StyleAllali, Karam. 2025. "On SEIR Epidemic Dynamics with Pro- and Anti-Vaccination Strategies: An Evolutionary Game Theory Approach" Games 16, no. 6: 61. https://doi.org/10.3390/g16060061
APA StyleAllali, K. (2025). On SEIR Epidemic Dynamics with Pro- and Anti-Vaccination Strategies: An Evolutionary Game Theory Approach. Games, 16(6), 61. https://doi.org/10.3390/g16060061





