Linear Programming for Computing Equilibria Under Truncation Selection and Designing Defensive Strategies Against Malicious Opponents
Abstract
1. Introduction
2. Results
2.1. Games with Malicious Players
2.2. Independent Truncation Selection
3. Discussion
4. Materials and Methods
4.1. Risk Aversion and Partially Malicious Players
4.2. Truncation Selection
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Linear Programming Methods for Computing Maximin Values
Appendix B. Polyhedral Representation Conversion
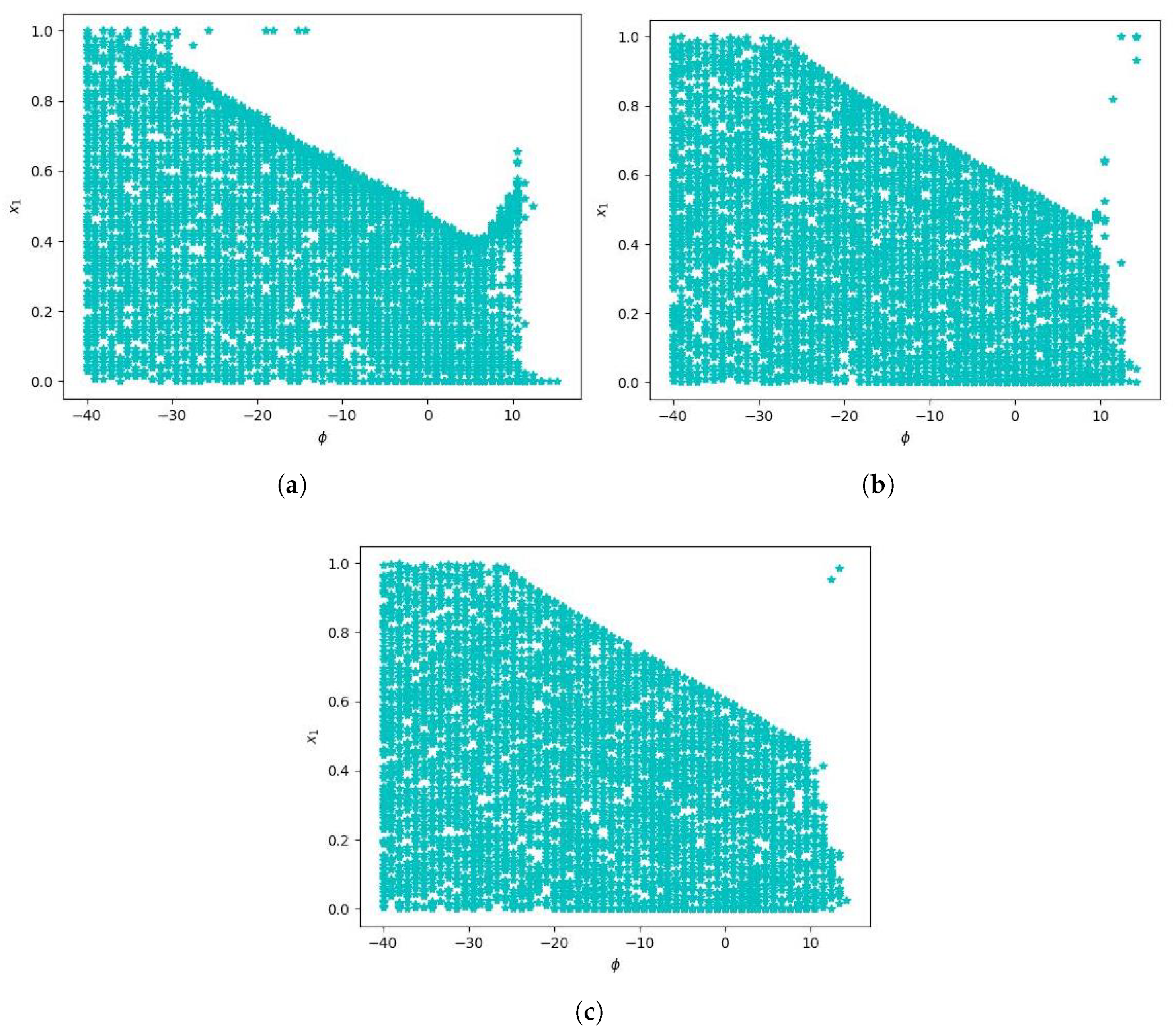
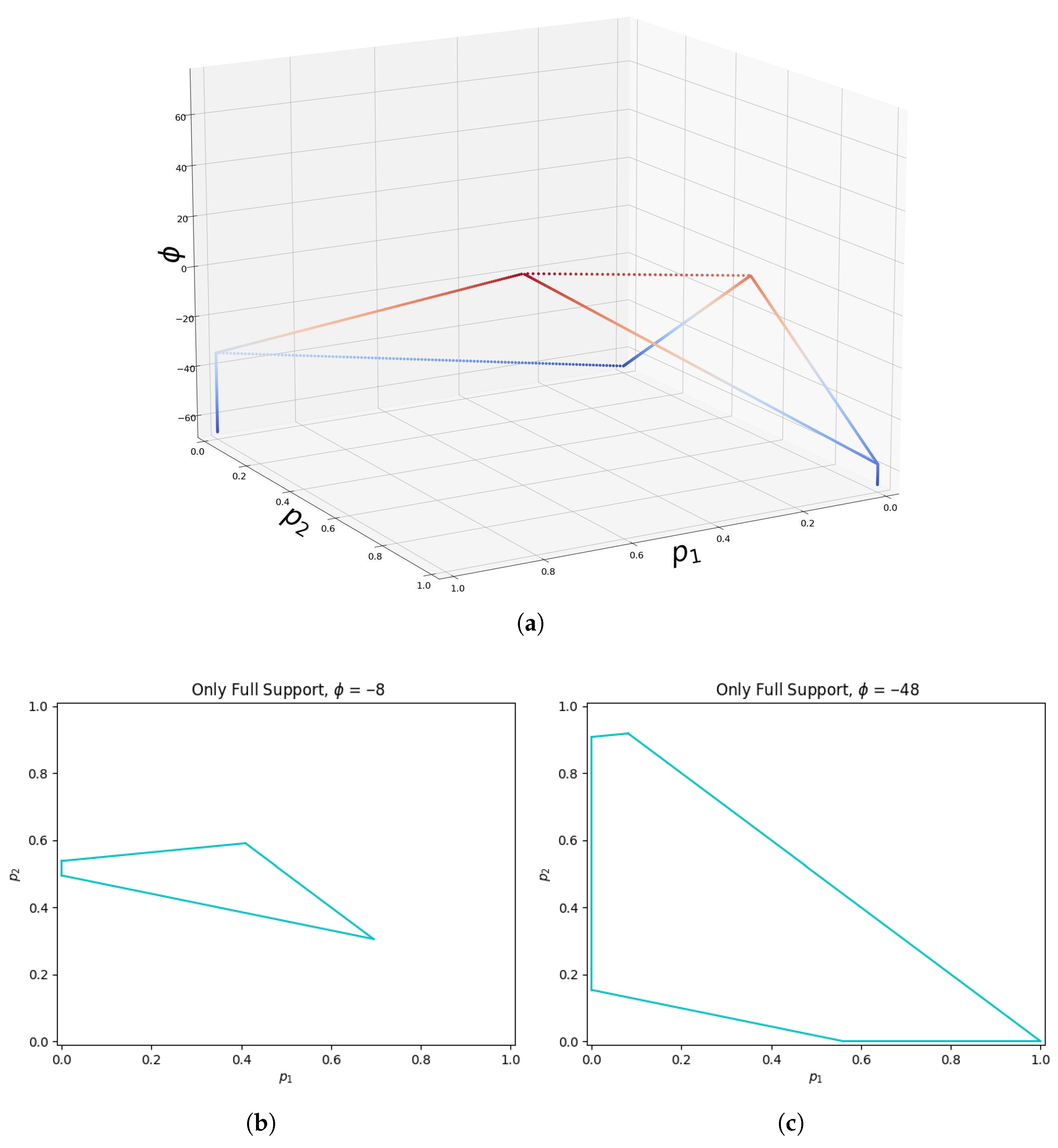
Appendix C. Observing the Vanishing Variance for the Hawk-Dove Game
References
- Avis, D., & Fukuda, K. (1991, June 10–12). A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Seventh Annual Symposium on Computational Geometry (pp. 98–104), North Conway, NH, USA. [Google Scholar]
- Avis, D., Fukuda, K., & Picozzi, S. (2002). On canonical representations of convex polyhedra. In Mathematical software (pp. 350–360). World Scientific. [Google Scholar]
- Binmore, K. (1992). Fun and games. In A text on game theory. D. C. Heath & Co. [Google Scholar]
- Bremner, D., Sikiric, M. D., & Schürmann, A. (2009). Polyhedral representation conversion up to symmetries. In CRM proceedings (Vol. 48, pp. 45–72). Springer. [Google Scholar]
- Bruyere, V., Filiot, E., Randour, M., & Raskin, J.-F. (2014, April 5–6). Expectations or guarantees? I want it all! A crossroad between games and MDPs. 2nd International Workshop on Strategic Reasoning (Vol. 146, pp. 1–8), Grenoble, France. [Google Scholar]
- Burton-Chellew, M. N., El Mouden, C., & West, S. A. (2016). Conditional cooperation and confusion in public-goods experiments. Proceedings of the National Academy of Sciences of the United States of America, 113(5), 1291–1296. [Google Scholar] [CrossRef] [PubMed]
- Cressman, R., & Tao, Y. (2014). The replicator equation and other game dynamics. Proceedings of the National Academy of Sciences of the United States of America, 111(Suppl. 3), 10810–10817. [Google Scholar] [CrossRef]
- Dave, A., & Malikopoulos, A. A. (2024). Approximate information states for worst case control and learning in uncertain systems. IEEE Transactions on Automatic Control, 70(1), 127–142. [Google Scholar] [CrossRef]
- Dickhaut, J., & Kaplan, T. (1993). A program for finding Nash equilibria. In Economic and financial modeling with mathematica® (pp. 148–166). Springer. [Google Scholar] [CrossRef]
- Etessami, K., & Yannakakis, M. (2010). On the complexity of Nash equilibria and other fixed points. SIAM Journal on Computing, 39(6), 2531–2597. [Google Scholar] [CrossRef]
- Ficici, S. G. (2006, July 8–12). A game-theoretic investigation of selection methods in two-population coevolution. 8th Annual Conference on Genetic and Evolutionary Computation (pp. 321–328), Seattle, WA, USA. [Google Scholar] [CrossRef]
- Ficici, S. G., Melnik, O., & Pollack, J. B. (2005). A game-theoretic and dynamical-systems analysis of selection methods in coevolution. IEEE Transactions on Evolutionary Computation, 9(6), 580–602. [Google Scholar] [CrossRef]
- Ficici, S. G., & Pollack, J. B. (2000, July 10–12). Effects of finite populations on evolutionary stable strategies. 2nd Annual Conference on Genetic and Evolutionary Computation (pp. 927–934), Las Vegas, NV, USA. [Google Scholar]
- Ficici, S. G., & Pollack, J. B. (2007). Evolutionary dynamics of finite populations in games with polymorphic fitness equilibria. Journal of Theoretical Biology, 247(3), 426–441. [Google Scholar] [CrossRef]
- Fogel, D. B., Fogel, G. B., & Andrews, P. C. (1997). On the instability of evolutionary stable strategies. BioSystems, 44(2), 135–152. [Google Scholar] [CrossRef]
- Fogel, G. B., Andrews, P. C., & Fogel, D. B. (1998). On the instability of evolutionary stable strategies in small populations. Ecological Modelling, 109(3), 283–294. [Google Scholar] [CrossRef]
- Fogel, G. B., & Fogel, D. B. (2011). Simulating natural selection as a culling mechanism on finite populations with the hawk–dove game. BioSystems, 104(1), 57–62. [Google Scholar] [CrossRef] [PubMed]
- Fudenberg, D., & Liang, A. (2019). Predicting and understanding initial play. American Economic Review, 109(12), 4112–4141. [Google Scholar] [CrossRef]
- Fukuda, K., & Prodon, A. (1995). Double description method revisited. In Franco-Japanese and Franco-Chinese conference on combinatorics and computer science (pp. 91–111). Springer. [Google Scholar]
- Ganzfried, S. (2023, December 13–15). Safe equilibrium. 2023 62nd IEEE Conference on Decision and Control (CDC) (pp. 5230–5236), Singapore. [Google Scholar]
- Garg, J., Jiang, A. X., & Mehta, R. (2011). Bilinear games: Polynomial time algorithms for rank based subclasses. In International workshop on internet and network economics (pp. 399–407). Springer. [Google Scholar]
- Harsanyi, J. C. (1968). Games with incomplete information played by ‘bayesian’ players. Management Science. [Google Scholar]
- Henrich, J., McElreath, R., Barr, A., Ensminger, J., Barrett, C., Bolyanatz, A., Cardenas, J. C., Gurven, M., Gwako, E., & Henrich, N. (2006). Costly punishment across human societies. Science, 312(5781), 1767–1770. [Google Scholar] [CrossRef] [PubMed]
- Holler, M. J. (1990). The unprofitability of mixed-strategy equilibria in two-person games: A second folk-theorem. Economics Letters, 32(4), 319–323. [Google Scholar] [CrossRef]
- Holler, M. J. (1992). Nash equilibrium reconsidered and an option for maximin. Quality and Quantity, 26(3), 323–335. [Google Scholar] [CrossRef]
- Holler, M. J., & Høst, V. (2019). Maximin vs. Nash equilibrium: Theoretical results and empirical evidence. In Optimal decisions in markets and planned economies (pp. 245–255). Routledge. [Google Scholar]
- Htun, Y. (2005). Irrationality in game theory. World Scientific. [Google Scholar]
- Jebari, K., & Madiafi, M. (2013). Selection methods for genetic algorithms. International Journal of Emerging Sciences, 3(4), 333–344. [Google Scholar]
- John von Neumann, O. M. (1944). Theory of games and economic behavior. Princeton University Press. [Google Scholar]
- Li, J., Yang, M., Lewis, F. L., & Zheng, M. (2024). Compensator-based self-learning: Optimal operational control for two-time-scale systems with input constraints. IEEE Transactions on Industrial Informatics, 20(7), 9465–9475. [Google Scholar] [CrossRef]
- Liu, Y., & Zhu, Q. (2023). Event-triggered adaptive neural network control for stochastic nonlinear systems with state constraints and time-varying delays. IEEE Transactions on Neural Networks and Learning Systems, 34(4), 1932–1944. [Google Scholar] [CrossRef]
- Lucchetti, R. (2006). Linear programming and game theory. In Convexity and well-posed problems (pp. 117–137). Springer. [Google Scholar]
- Meyer, D., & Meyer, J. (2006). Measuring risk aversion. Foundations and Trends in Microeconomics, 2, 107–203. [Google Scholar] [CrossRef]
- Morsky, B., & Bauch, C. T. (2016). Truncation selection and payoff distributions applied to the replicator equation. Journal of Theoretical Biology, 404, 383–390. [Google Scholar] [CrossRef]
- Morsky, B., & Bauch, C. T. (2019). The impact of truncation selection and diffusion on cooperation in spatial games. Journal of Theoretical Biology, 466, 64–83. [Google Scholar] [CrossRef]
- Morsky, B., Smolla, M., & Akçay, E. (2020). Evolution of contribution timing in public goods games. Proceedings of the Royal Society B, 287(1927), 20200735. [Google Scholar] [CrossRef]
- Moscibroda, T., Schmid, S., & Wattenhofer, R. (2009). The price of malice: A game-theoretic framework for malicious behavior. Internet Mathematics, 6(2), 125–156. [Google Scholar] [CrossRef]
- Myerson, R. B. (1991). Game theory: Analysis of conflict. Harvard University Press. [Google Scholar]
- Nash, J. F. (1950). Equilibrium points in n-person games. Proceedings of the National Academy of Science of the United States of America, 36(1), 48–49. [Google Scholar] [CrossRef] [PubMed]
- Papadimitriou, C. H. (2007). The complexity of finding Nash equilibria. Algorithmic Game Theory, 2, 30. [Google Scholar]
- Parrilo, P. A. (2006, December 13–15). Polynomial games and sum of squares optimization. 45th IEEE Conference on Decision and Control (pp. 2855–2860), San Diego, CA, USA. [Google Scholar] [CrossRef]
- Porter, R., Nudelman, E., & Shoham, Y. (2008). Simple search methods for finding a Nash equilibrium. Games and Economic Behavior, 63(2), 642–662. [Google Scholar] [CrossRef]
- Pratt, J. W. (1964). Risk aversion in the small and in the large. Econometrica, 32(1/2), 122–136. [Google Scholar] [CrossRef]
- Selten, R., & Bielefeld, R. S. (1988). Examination of the perfectness concept for equilibrium points in extensive games. In Models of strategic rationality (Vol. 2). Theory and Decision Library C. Springer. [Google Scholar]
- Simon, H. A. (1955). A behavioral model of rational choice. The Quarterly Journal of Economics, 69, 99–118. [Google Scholar] [CrossRef]
- Simons, S. (1995). Minimax theorems and their proofs. In Minimax and applications (pp. 1–23). Springer. [Google Scholar]
- Su, R., & Morsky, B. (2024). Relational utility and social norms in games. Mathematical Social Sciences, 127, 54–61. [Google Scholar] [CrossRef]
- Thie, P. R., & Keough, G. E. (2011). An introduction to linear programming and game theory. John Wiley & Sons. [Google Scholar]
- Von Stengel, B. (2021). Game theory basics. Cambridge University Press. [Google Scholar]
- Wright, J., & Leyton-Brown, K. (2014, June 8–12). Level-0 meta-models for predicting human behavior in games. EC 2014—Proceedings of the 15th ACM Conference on Economics and Computation, Palo Alto, CA, USA. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Morsky, B. Linear Programming for Computing Equilibria Under Truncation Selection and Designing Defensive Strategies Against Malicious Opponents. Games 2025, 16, 59. https://doi.org/10.3390/g16060059
Zhang Z, Morsky B. Linear Programming for Computing Equilibria Under Truncation Selection and Designing Defensive Strategies Against Malicious Opponents. Games. 2025; 16(6):59. https://doi.org/10.3390/g16060059
Chicago/Turabian StyleZhang, Zhuoer, and Bryce Morsky. 2025. "Linear Programming for Computing Equilibria Under Truncation Selection and Designing Defensive Strategies Against Malicious Opponents" Games 16, no. 6: 59. https://doi.org/10.3390/g16060059
APA StyleZhang, Z., & Morsky, B. (2025). Linear Programming for Computing Equilibria Under Truncation Selection and Designing Defensive Strategies Against Malicious Opponents. Games, 16(6), 59. https://doi.org/10.3390/g16060059





