Test Me If You Can—Providing Optimal Information for Consumers Through a Novel Certification Mechanism †
Abstract
1. Introduction
2. Related Literature
3. Theory
3.1. Theoretical Framework
3.1.1. Certification Game
Sellers (He/His)
Certifier (It/Its)
Buyers (She/Hers)
3.1.2. Local and Global Dominance, and Dominating Rivals
- if , then ,
- if , then .
- , ,
- , ,
- , ,
- , ,
- , .
3.1.3. Three Versions of the Game
Benchmark CompleteInformation
Any Current Selection Mechanism SellersMayNotApply
New Selection Mechanism SellersMayApply
3.1.4. Two Distribution Assumptions
3.2. Theoretical Results
3.2.1. Benchmark CompleteInformation
3.2.2. Any Current Selection Mechanism SellersMayNotApply
- (i)
- In the first scenario, all product models which would be sold under CompleteInformation are selected for testing. In other words, .
- (ii)
- In the second scenario, all product models which would be sold under CompleteInformation except for the overall cheapest one are selected for testing. In other words, , and . Moreover, the overall cheapest product model is selected by every buyer who would have selected it in under CompleteInformation. In other words, with , the following holds: .
3.2.3. New Selection Mechanism SellersMayApply
3.2.4. Comparing Consumer Surplus Resulting from Any Current and Our New Mechanism
4. Experiment
4.1. Experimental Design and Hypotheses
- SellersMayNotApply-WorstCase
- To model a scenario under any current selection mechanism in which the market functions extremely poorly, we design a worst-case scenario regarding the set of tested product models. In this worst-case scenario, the tested product models are the ones vertically furthest away from the globally non-dominated ones.25
- SellersMayNotApply-Random
- We also design an intermediate scenario under any current mechanism where the set of tested product models is chosen randomly among all available ones. In this random scenario, the share of globally non-dominated, CompleteInformation optimal product models among all tested product models is almost identical to the share of globally non-dominated product models in all markets.26 We include this treatment to investigate whether our new mechanism outperforms chance.
- SellersMayApply-LyingPoss(ible)
- This treatment represents the version of our new mechanism where sellers may apply for testing and may provide a true or a false quality. While the option of providing a false quality does not change the equilibrium predictions (see Proposition 2), it makes the SellersMayApply mechanism more complex. Therefore, we consider it important to investigate this treatment in the lab.
- SellersMayApply-Truth
- This treatment represents another version of our new mechanism where sellers may apply for testing and are not allowed to provide a false quality.
- –
- globally dominated sellers will not apply to be tested.
- –
- with the exception of , globally non-dominated sellers will apply to be tested and will, if applicable, state their true quality.
- –
- no information on globally non-dominated product models under SellersMayNotApply-WorstCase,
- –
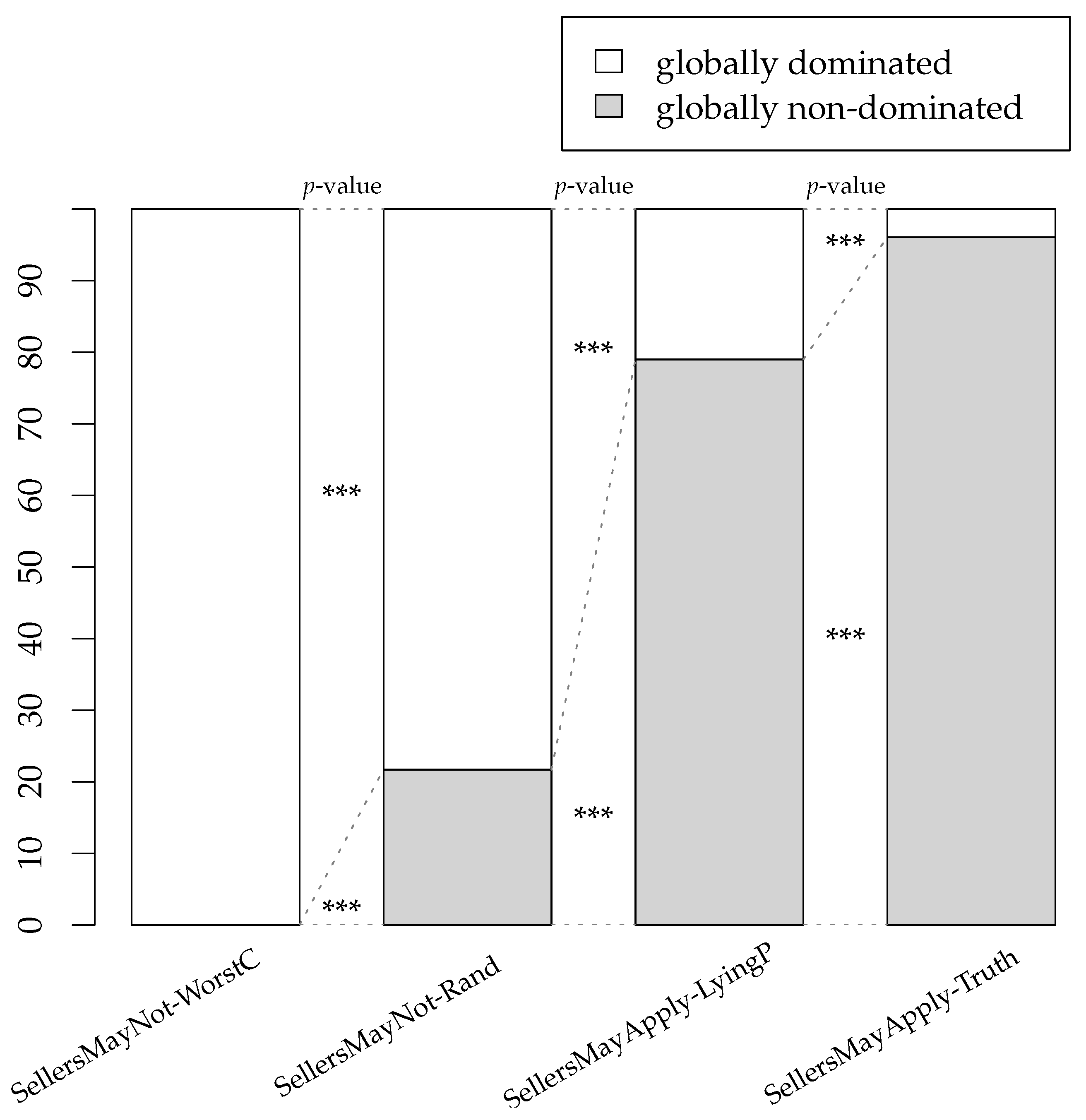
- information on 21.7% of globally non-dominated product models under SellersMayNotApply-Random, and
- –
- information on all globally non-dominated product models under both SellersMayApply-Truth and SellersMayApply-LyingPoss.
- –
- consumer surplus as well as globally non-dominated seller profits are lowest under SellersMayNotApply-WorstCase, higher under SellersMayNotApply-Random, and highest under both SellersMayApply-Truth and SellersMayApply-LyingPoss.
- –
- globally dominated seller profits are highest under SellersMayNotApply-WorstCase, lower under SellersMayNotApply-Random, and lowest under both SellersMayApply-Truth and SellersMayApply-LyingPoss.
4.2. Experimental Results
4.2.1. Seller Behavior
- Result 1
- In line with H1, under SellersMayApply-LyingPoss and SellersMayApply-Truth:
- –
- most globally dominated sellers do not apply to be tested.
- –
- most globally non-dominated sellers do apply to be tested and, if applicable, state their true quality.
However, not in line with H1, there is more out-of-equilibrium behavior under SellersMayApply-LyingPoss than under SellersMayApply-Truth.
4.2.2. Content of the Product Test
- Result 2
- In line with H2, the product test provides the least information on globally non-dominated product models under SellersMayNotApply-WorstCase, more under SellersMayNotApply-Random, and more still under SellersMayApply-LyingPoss. However, not in line with H2, the product test provides even more information on globally non-dominated product models under SellersMayApply-Truth.
4.2.3. Buyer Behavior
- Result 3
- In line with H3, buyers choose the fewest globally non-dominated product models under SellersMayNotApply-WorstCase, more under SellersMayNotApply-Random, and more still under SellersMayApply-LyingPoss. However, not in line with H3, buyers choose an even greater number of globally non-dominated product models under SellersMayApply-Truth.
4.2.4. Surplus and Profits
- Result 4
- In line with H4, per capita
- –
- consumer surplus is lowest under SellersMayNotApply-WorstCase, higher under SellersMayNotApply-Random, and highest under SellersMayApply-LyingPoss and SellersMayApply-Truth.
- –
- globally non-dominated seller profits are lowest under SellersMayNotApply-WorstCase, higher under SellersMayNotApply-Random, and highest under SellersMayApply-Truth and SellersMayApply-LyingPoss.
- –
- globally dominated seller profits are highest under SellersMayNotApply-WorstCase, lower under SellersMayNotApply-Random, and lowest under SellersMayApply-Truth and SellersMayApply-LyingPoss.
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Online Appendix
Appendix A.1. Screenshots of Products with Stiftung Warentest Results



Appendix A.2. Sample of Products
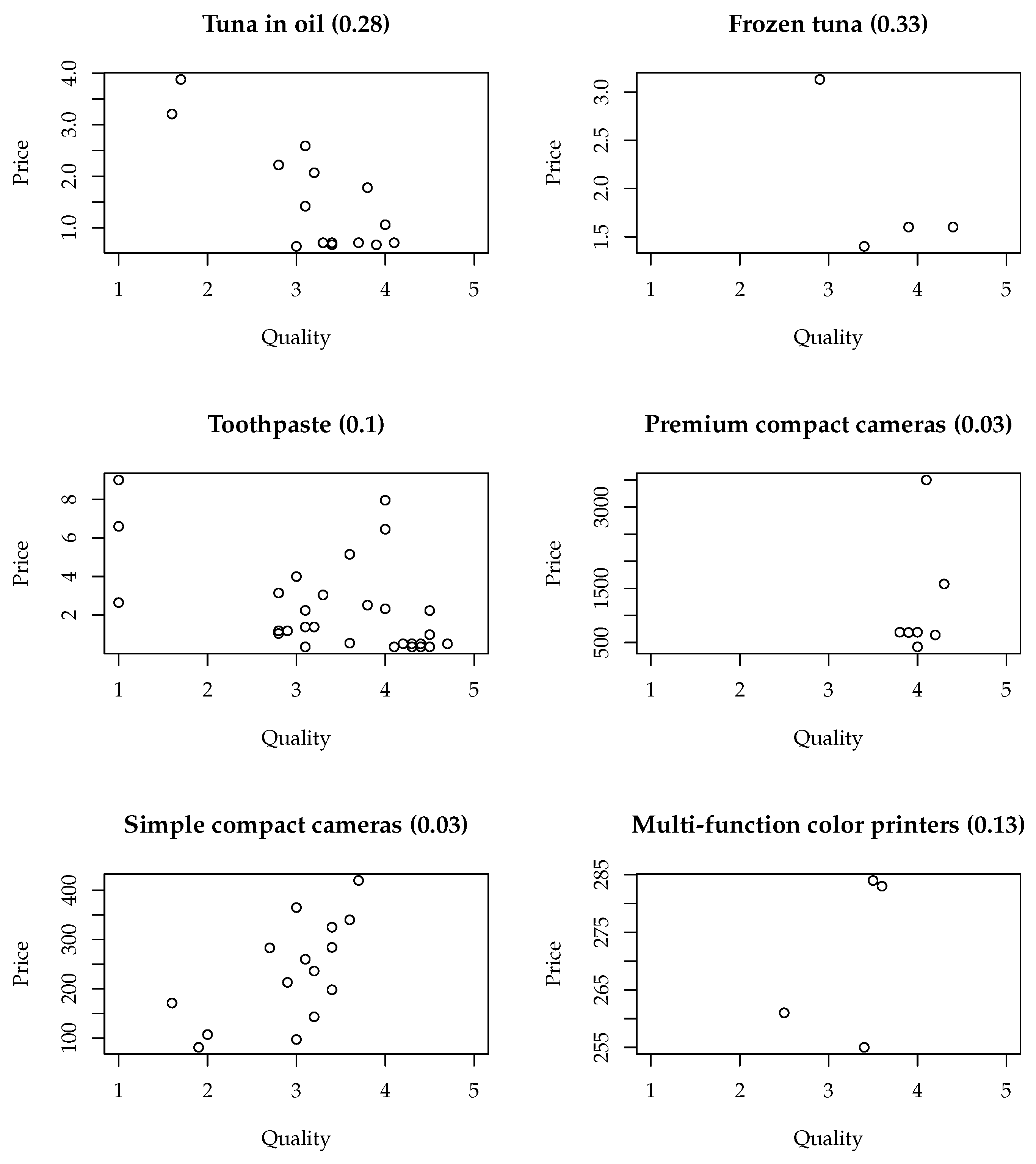
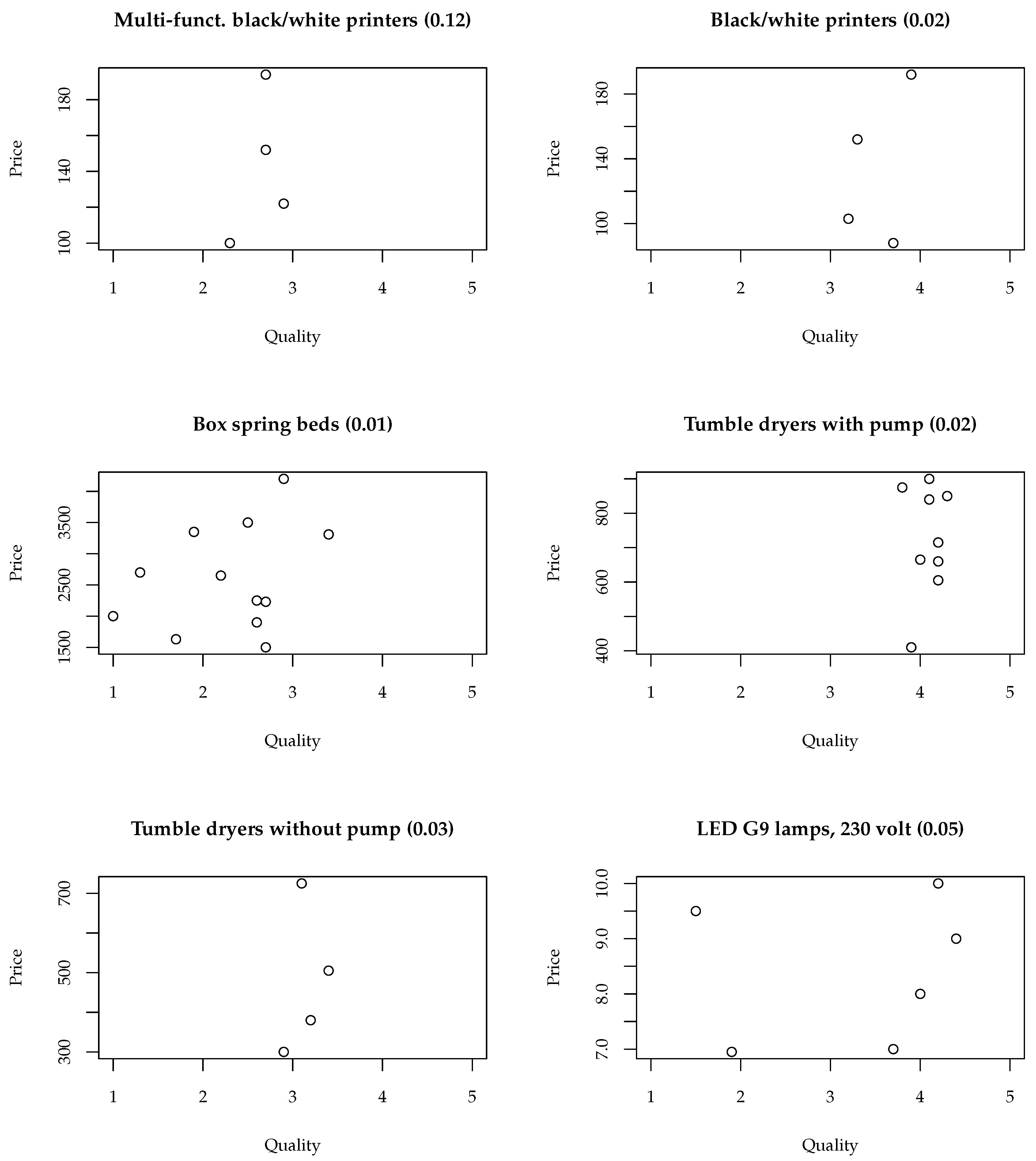
Appendix A.3. Current Product Model Selection Mechanisms
| Product Model Selection Criteria | Product Model Selection Standardized? | |
|---|---|---|
| Stiftung Warentest (Germany) | main criterion: sales numbers/bestsellers; if applicable, organic product models and/or product models with new features will be selected even if they are not among the bestsellers | yes |
| Which? (UK) | popularity, incl. sales numbers brand reliability price if applicable, innovation | no |
| Consumer Reports (US) | spectrum of models: wide availability, incl. sales numbers wide range of prices if applicable, new features | not clear |
Appendix A.4. Out-of-Stock Product Models
Appendix A.5. Visual Comparison of Bagwell and Riordan (1991)’s and Our Setup

Appendix A.6. List of Symbols
| buyer, with , and | |
| B | set of buyers, with , and |
| seller ’s unit costs of production | |
| D | set of globally dominated sellers |
| set of locally dominated sellers within the set Z, with | |
| non-existing seller with and , denoting a buyer’s choice not to purchase a product model | |
| seller offering the overall lowest quality and the overall lowest price | |
| seller, with , and | |
| non-existing seller with | |
| seller who offers the cheapest product model within the set Z, with | |
| seller who maximizes buyer ’s utility within the set Z, with | |
| seller who maximizes buyer ’s expected utility within the set Z, with | |
| F | set of sellers, with , and |
| h | index of buyer and |
| k | certifier’s maximum testing capacity, with |
| K | set of applicant sellers, with |
| set of applicant sellers who state a false product model quality when applying | |
| set of applicant sellers who state their true product model quality when applying | |
| (final) set of tested sellers, with | |
| set of tested sellers in the algorithm iteration | |
| n | number of sellers , with |
| set of globally dominated sellers | |
| set of locally non-dominated sellers within the set Z, with | |
| globally non-dominated sellers who have at least one buyer under complete information | |
| seller ’s price, with | |
| seller ’s quality, with | |
| seller ’s falsely stated quality | |
| overall lowest quality | |
| Q | set of all quality levels |
| set of dominating rivals of seller , with | |
| s | number of buyers , with |
| t | index of seller , quality , and price |
| buyer ’s utility | |
| Z | subset of F |
| buyer ’s valuation of quality, with | |
| seller ’s profit |
Appendix A.7. Additional Formal Descriptions of Section 3
Appendix A.7.1. Formal Algorithm Description of Section 3.1.3
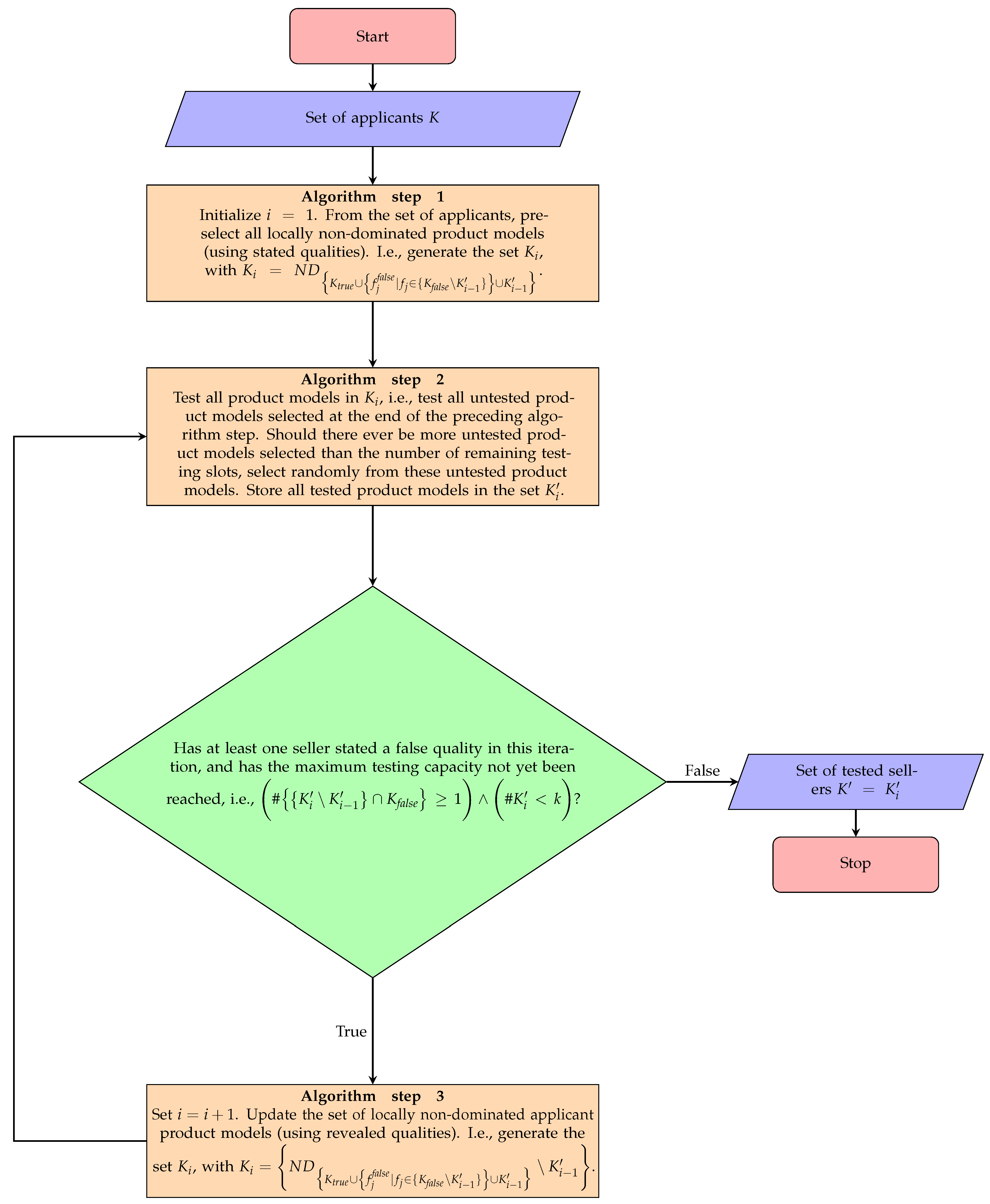
Appendix A.7.2. Illustration of Assumption 2
Appendix A.7.3. Definition of Market Areas of Section 3.2.1 (CompleteInformation)
Appendix A.7.4. Equilibrium Payoffs of Section 3.2.2 (SellersMayNotApply)
Appendix A.7.5. Proofs of Section 3.2
- Lower consumer surplus
- Let . Furthermore, let , with , and with , with , and with . It follows that with
- This inequality holds since, under SellersMayNotApply, selects a product model different from her complete-information-optimal product model since we required that and . Therefore, it follows that ’s utility is strictly lower under SellersMayNotApply compared to a world of CompleteInformation. It follows that the aggregate consumer surplus is also strictly lower.
- Identical consumer surplus
- (i)
- If , then, according to Assumption 2, the following holds: . For each buyer, this leads to the identical optimization problem in both a world of CompleteInformation and under SellersMayNotApply, i.e., . Therefore, ’s utility under SellersMayNotApply is identical to that under CompleteInformation. It follows that the consumer surplus is also identical.
- (ii)
- Let , let , and let . Moreover, with , the following holds: .In this case, it follows that, except with , every buyer selects the same optimal product model as under CompleteInformation by assumption. Therefore, the utility of these buyers under SellersMayNotApply is identical to that in a world of CompleteInformation. Since we assume with , it follows that these buyers also select the same optimal product model as under CompleteInformation. It follows that all buyers select the same optimal product model as under CompleteInformation, and that the consumer surplus is identical.
- and ,
- and ,
- and , or
- and .
- and ,
- and ,
- and , or
- and .
- Step 1:
- In this step, we show that all strategy profiles can be eliminated in which at least one seller applies to be tested stating a false quality.
- Step 1.1:
- In this step, we show that applying to be tested stating a false quality is a strictly dominated strategy for any globally non-dominated seller.If a globally non-dominated seller applies to be tested stating a false quality, this may either result in him being tested, or it may result in him not being tested. If he applies stating a false quality and is tested, his profits would be lower compared to applying stating his true quality and compared to not applying since we assume the is higher than the maximum additional profits any globally non-dominated seller could make when being tested (see Section 3.1.1).If a globally non-dominated seller applies stating a false quality and is not tested, this does not change the set of product models that are tested. Therefore, the globally non-dominated seller could save the by not applying for a test.Combining both results, it follows that applying stating a false quality is a strictly dominated strategy for all globally non-dominated sellers and can thus be eliminated for these sellers.
- Step 1.2:
- In this step, we show that, when analyzing all remaining strategy profiles after step 1.1, a strategy profile in which at least one globally dominated seller applies stating a false quality cannot be a Nash equilibrium.If a globally dominated seller applies to be tested stating a false quality, this may either result in him being tested, or it may result in him not being tested. Analogously to step 1.1, if a globally dominated seller applies stating a false quality and is not tested, this does not change the set of product models that are tested. Therefore, the globally dominated seller could save the by not applying for a test.If a globally dominated seller, e.g., , applies stating a false quality and is tested, we can distinguish two cases: at least one of his dominating rivals is tested, too, or none of his dominating rivals is tested. In the former case, would not receive any demand. Therefore, he would receive the same profit as if he had not applied, and additionally would have to pay the compared to applying stating his true quality.In the latter case—a globally dominated seller applies stating a false quality, and is tested, while none of his dominating rivals is tested—we can furthermore distinguish two subcases: either the globally dominated seller incurs losses (or makes zero profit) after having been tested, or he receives a positive profit after having been tested. In the first subcase, the globally dominated seller could save the compared to not applying.In the second subcase, we can furthermore distinguish two subcases: either receives higher profits than those had he applied stating his true quality, or he receives lower or equal profits. In the latter subcase, could have saved the by applying stating his true quality.As to the former subcase, we will show by a proof by contradiction that any strategy profile resulting in the latter subcase cannot be a Nash equilibrium. In order to show this, we furthermore distinguish two subcases: Either at least one of ’s dominating rivals applies for a test stating his true quality, but is not tested (subcase 1), or none of ’s dominating rivals applies for a test stating his true quality (subcase 2).Subcase 1Recall that the first subcase contains all strategy profiles in which
- seller applies stating a false quality such that he is tested, makes positive profits which are higher than those had he applied stating his true quality
- at least one of ’s dominating rivals applies stating his true quality, but neither he nor any other dominating rival is tested.
In order for this subcase to occur, all of ’s dominating rivals who applied stating their true quality would have to be locally dominated within the set of applicants given stated qualities, i.e., within , since they would have been tested otherwise. (Recall that we assume the following. There is no pair of sellers offering their product model at the same price (see Section 3.1.1). The certifier provides at least as many testing slots as there are quality levels (see Section 3.1.1). Therefore, there is at most one locally non-dominated applicant in per quality level, and the certifier is able to test all locally non-dominated sellers in .)If all of ’s dominating rivals who applied stating their true quality were locally dominated within the set of applicants given stated qualities, at least one seller, e.g., , would need to exist for each of these dominating rivals, for whom the following holds according to Lemma A3: He is locally non-dominated within the set , and he dominates all of ’s dominating rivals who applied stating their true quality, but is not tested. Is there any seller who would do so in equilibrium?According to Lemma A2, seller would also dominate seller within the set . Since we require, in this subcase, that none of ’s dominating rivals is tested, and since would be one of ’s dominating rivals if he applied stating his true quality, it follows that has to be a seller who applied stating a false quality. Moreover, according to step 1.1, cannot be a globally non-dominated seller; i.e., could only be a globally dominated seller.According to Lemma A3, seller has at least one dominating rival since he is globally dominated. Moreover, would only have an incentive to apply stating a false quality if none of his dominating rivals is tested. This implies that either there are none of ’s dominating rivals in , or, if there is at least one of ’s dominating rivals in , all of them are locally dominated within this set.If there were none of ’s dominating rivals in , he could have saved the by applying stating his true quality. Therefore, there would have to be at least one of ’s dominating rivals in , and all of them would have to be locally dominated within this set. Note that these dominating rivals would also have to be dominated in by other sellers, which in turn would also have to be dominated in the same set, etc.It follows that there would have to be a group of globally dominated sellers who apply stating their false quality, are tested, receive positive profits, congest each others’ dominating rivals testing slots, and who would not receive equal or higher profits when applying stating their true quality. However, within any of these groups of globally dominated sellers, there is no seller who would be able to congest the testing slot of the overall cheapest seller within this group since we assume there is no pair of sellers offering their product model at the same price (see Section 3.1.1). Therefore, the overall cheapest seller within any of these groups will not have an incentive to apply stating a false quality. This leads to a chain reaction causing sellers, whose dominating rivals in would be dominated by this seller, not to apply either, etc. This implies that seller would also not have an incentive to apply stating a false quality.Subcase 2If the globally dominated seller were locally non-dominated in when applying stating his true quality, he could have saved the by applying stating his true quality. It follows that he has to be locally dominated in . Since none of ’s dominating rivals is tested as none of them applied, has to be locally dominated in by another globally dominated seller who applied stating a false quality. Since none of this seller’s dominating rivals is tested as none of them applied, and according to Lemma A2, this seller has to be locally dominated in by another globally dominated seller who applied stating a false quality, etc. Note that the overall cheapest seller in this group of sellers cannot be dominated by any other seller in the group in . Therefore, the overall cheapest seller in this group does not have an incentive to apply stating a false quality. This leads to a chain reaction causing sellers who would have been dominated by this seller in to refrain from applying stating their false quality, etc. This contradicts the requirement that applied stating a false quality.It follows that, given all remaining strategy profiles after step 1.1, a strategy profile in which at least one globally non-dominated seller applies stating a false quality cannot be a Nash equilibrium.
Combining steps 1.1 and 1.2, it follows that all strategy profiles can be eliminated in which at least one seller applies to be tested stating a false quality. - Step 2:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which seller or at least one globally dominated seller applies to be tested stating his true quality.
- Step 2.1:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which seller applies to be tested stating his true quality.By definition, seller offers the overall lowest quality. Therefore, his true quality is always smaller than or equal to his expected quality for any possible strategy profile. Thus, his demand would never increase if he applied to be tested stating his true quality (compared to not applying), but he would have to pay the . It follows that, given all remaining strategy profiles after step 1, a strategy profile in which seller applies to be tested stating his true quality cannot be a Nash equilibrium.
- Step 2.2:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which at least one globally dominated seller applies to be tested stating his true quality.By definition, any globally dominated seller has at least one dominating rival. If both and his dominating rival applied to be tested stating their true quality, our selection algorithm would have excluded in algorithm step 1, and would not have been tested. In this case, could have saved the by not applying.Seller would only be tested if none of his dominating rivals applied for testing. The only reason for ’s dominating rivals not to apply for testing could be that they expect the additional profit from applying to be lower than the . This could either be because they do not expect to be tested after having applied, or because they do not expect any additional demand even if they were tested after having applied. If any dominating rival did not expect to be tested after having applied, would also be excluded from testing in algorithm step 1. If a dominating rival did expect to be tested after having applied, but did not expect any additional demand, would also not expect any additional demand if tested, and thus, should not have applied. (By definition, any of ’s dominating rivals is cheaper and potentially also of higher quality compared to . If buyers preferred another seller (or refraining from buying) over ’s dominating rival, they would also prefer this other seller (or refraining from buying) over .)It follows that all strategy profiles can be eliminated in which at least one globally dominated seller applies to be tested stating his true quality.
Combining steps 2.1 and 2.2, it follows that all strategy profiles can be eliminated in which seller or at least one globally dominated seller applies to be tested stating his true quality. - Step 3:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which at least one seller in does not apply to be tested stating his true quality.Let () denote the seller with the highest (second-highest) quality level in . According to Assumption 1, it follows that, for any strategy profile in which applies to be tested (stating his true quality) and in which no globally dominated seller applies for testing, untested is dominated in expectation by tested . For any strategy profile in which neither , nor any globally dominated seller applies for testing, untested is not the cheapest untested seller within his price range. It follows that would not receive any demand if he were untested.If seller applies for testing stating his true quality, he will be tested since
- (i)
- in equilibrium, no seller will apply stating a false quality
- (ii)
- will be locally non-dominated on according to Lemma A1
- (iii)
- there are enough testing slots for all sellers in as
- (a)
- the certifier is assumed to provide at least as many testing slots as there are quality levels (see Section 3.1.1)
- (b)
- there are at most as many sellers in as there are quality levels because we assume there is no pair of sellers offering their product model at the same price (see Section 3.1.1).
Moreover, if seller is tested, he will receive additional profits since any buyer who would have selected him under CompleteInformation will also select him if tested, irrespective of whether any seller in applies for testing or not. (By definition, buyer prefers tested over any tested seller in . According to Assumption 2, buyer also prefers tested over any cheaper untested seller.) Since are assumed to be lower than the profit margin of each seller in (see Section 3.1.3), will make positive, and therefore, higher profits when applying compared to not applying.It follows that all strategy profiles can be eliminated in which the seller with the highest quality level in does not apply for testing. Therefore, the expected quality of all cheaper untested product models decreases.Given all remaining strategy profiles, the seller with the second-highest (third-highest, …, pre-lowest) quality level in , e.g., seller , would not receive any demand if he were untested since any buyer would receive a higher utility when selecting the seller with the third-highest (fourth-highest, …, pre-lowest) quality level in , irrespective of whether any seller in applies for testing or not—according to Assumption 1.Analogously, if the seller with the second-highest (third-highest, …, pre-lowest) quality level in applies for testing, he will be tested since- (i)
- in equilibrium, no seller will apply stating a false quality
- (ii)
- will be locally non-dominated on according to Lemma A1
- (iii)
- there are enough testing slots for all sellers in as
- (a)
- the certifier is assumed to provide at least as many testing slots as there are quality levels (see Section 3.1.1)
- (b)
- there are at most as many sellers in as there are quality levels because we assume there is no pair of sellers offering their product model at the same price (see Section 3.1.1).
Moreover, if seller is tested, he will receive additional profits since any buyer who would have selected him under CompleteInformation will also select him if tested, irrespective of whether any seller in applies for testing or not. (By definition, buyer prefers tested over any tested seller in . According to Assumption 2, buyer also prefers tested over any untested seller in .) Since are assumed to be lower than the profit margin of each seller in (see Section 3.1.3), will make positive, and therefore, higher profits when applying compared to not applying.It follows that all strategy profiles can be eliminated in which the seller with the second-highest quality level in does not apply for testing. Therefore, the expected quality of all cheaper untested product models decreases, etc.Combining the above results, it follows that all strategy profiles can be eliminated in which at least one seller in does not apply for testing stating his true quality. - Step 4:
- In this step, we show that, given all remaining strategy profiles, seller may apply to be tested stating his true quality, or he may not apply to be tested, depending on the market parameters.Depending on the joint distribution of qualities, prices and valuations of quality, seller may or may not belong to . If he does not belong to , he would not receive any additional profits if he were tested since he would not be selected by any buyer under CompleteInformation. He would, therefore, also not be selected by any buyer in any strategy profile in which all sellers in are tested since every buyer would select the product model he would have selected under CompleteInformation.If seller does belong to , his equilibrium strategy depends on the joint distribution of qualities, prices and valuations of quality, and his resulting expected quality (if untested). If they are distributed such that seller would not receive any additional demand if tested, he will not apply for testing. If they are distributed such that seller would receive any additional demand if tested, he will apply for testing.
- Step 5:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which at least one of the sellers in (if any) applies to be tested stating his true quality.If seller applied to be tested stating his true quality, he would be tested since
- (i)
- in equilibrium, no seller will apply stating a false quality
- (ii)
- will be locally non-dominated on according to Lemma A1
- (iii)
- there are enough testing slots for all sellers in as
- (a)
- the certifier is assumed to provide at least as many testing slots as there are quality levels (see Section 3.1.1)
- (b)
- there are at most as many sellers in as there are quality levels because we assume there is no pair of sellers offering their product model at the same price (see Section 3.1.1).
However, even if tested, no buyer would select his product model if all buyers’ complete-information-optimal product models are tested.If all buyers’ complete-information-optimal product models except the overall cheapest one (which also belongs to ) are tested, the following strategy profile could not be an equilibrium: a strategy profile in which a seller from applied for testing and buyers who would have otherwise selected the overall cheapest seller would now select the tested seller from . In this strategy profile, they overall cheapest seller would have an incentive to deviate from his not-applying-strategy because the are assumed to be lower than the profit margin of one additional buyer (see Section 3.1.3).Therefore, buyers will select only sellers from or the overall cheapest seller.It follows that would not receive any demand after an applying to be tested stating his true quality, but would have to pay the . Therefore, will not apply.It follows that all strategy profiles can be eliminated in which at least one of the sellers in , applies to be tested stating his true quality. - Step 6:
- In this step, we show that, in equilibrium, all buyers select the same product model as under CompleteInformation.According to Assumption 2, all tested sellers are optimal for the same buyers who would have selected them under CompleteInformation. Also, all untested sellers receive the same demand as under CompleteInformation.All untested sellers in D or in receive zero demand. If does not belong to and is untested, he receives zero demand. If does belong to and is untested, he receives the same positive demand as under CompleteInformation. Otherwise, he would have had an incentive to deviate from his not-applying-strategy because the are assumed to be lower than the profit margin of one additional buyer (see Section 3.1.3).It follows that, in equilibrium, all buyers select the same product model as under CompleteInformation.
Appendix A.8. SellersMayApplyGeneralized
- Sellers (He/His)
- Certifier (It/Its)
- Buyers (She/Hers)
- New Selection Mechanism SellersMayApplyGeneralized
- No Distribution Assumptions
- (i)
- If , i.e., if there are at least as many (regular) testing slots as the number of unique complete-information-optimal product models, consumer surplus is as high as under CompleteInformation.
- (ii)
- If , i.e., if there are fewer (regular) testing slots than the number of unique complete-information-optimal product models, expected consumer surplus is at least as high as the expected consumer surplus under any current mechanism SellersMayNotApply.

- Step 1:
- In this step, we show that all strategy profiles can be eliminated in which at least one seller applies to be tested stating a false quality.If any seller applied to be tested stating a false quality, he would either end up belonging to the set of locally non-dominated applicants (using stated qualities), or he would not. In the latter case, would not be returned the , nor would his application change the set of tested and published product models. Therefore, his profit would be higher if he did not apply for testing.If ended up belonging to the set of locally non-dominated applicants (using stated qualities), we can furthermore distinguish two cases: either he ended up belonging to the subset maximizing aggregate consumer surplus, or he did not. In the former case, would be tested, but his quality would not be published (since detected liars’ qualities are not published). Furthermore, he would not be returned the , he would have to pay the , and an extra testing slot financed through this would be added. Therefore, the set tested and published product models would not be changed by ’s application, and his profit would be higher if he did not apply for testing.If ended up not belonging to the subset maximizing aggregate consumer surplus, he would be returned the , but would not be tested, and his application would not change the set of tested and published product models. Therefore, would be indifferent between applying stating a false quality and not applying, and is assumed to choose not to apply in this case (“indifference assumption 2”).Combining these results, it follows that all strategy profiles can be eliminated in which at least one seller applies to be tested stating a false quality.
- Step 2:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which at least one globally non-dominated seller does not apply to be tested stating his true quality.All globally non-dominated sellers weakly prefer applying stating their true quality over not applying since they would be returned the application deposit when applying. According to the “indifference assumption 1”, all of them will apply (stating their true quality). It follows that all strategy profiles can be eliminated in which at least one globally non-dominated seller does not apply to be tested stating his true quality.
- Step 3:
- In this step, we show that, given all remaining strategy profiles, all strategy profiles can be eliminated in which at least one globally dominated seller applies to be tested stating his true quality.Since all globally non-dominated sellers will apply (stating their true quality), no globally dominated seller would be returned the application deposit when applying (stating his true quality). Therefore, not applying dominates applying (stating their true quality). It follows that all strategy profiles can be eliminated in which at least one globally dominated seller applies to be tested stating his true quality.
- Step 4:
- In this step, we show that, in equilibrium, buyers select their optimal tested product model, or their optimal one from the cheapest untested ones per price range. Consumer surplus depends on the number of (regular) testing slots.
- (i)
- If , i.e., if there are at least as many (regular) testing slots as the number of unique complete-information-optimal product models, buyers can conclude that all unique complete-information-optimal product models are tested (and published) since buyers are assumed to know that . Therefore, each buyer selects the optimal tested product model and consumer surplus is as high as under CompleteInformation.
- (ii)
- If , i.e., if there are fewer (regular) testing slots than the number of unique complete-information-optimal product models, buyers can conclude that not all unique complete-information-optimal product models are tested (and published) since buyers are assumed to know that . Therefore, each buyer selects her optimal tested product model, or her optimal one from the cheapest untested ones per price range, and expected consumer surplus is at least as high as the expected consumer surplus under any current mechanism SellersMayNotApply. (Note that also holds for SellersMayNotApply. Therefore, in the best case, the tested product models would be identical to the ones under SellersMayApplyGeneralized.)
Appendix A.9. Graphical Overview of Experimental Markets
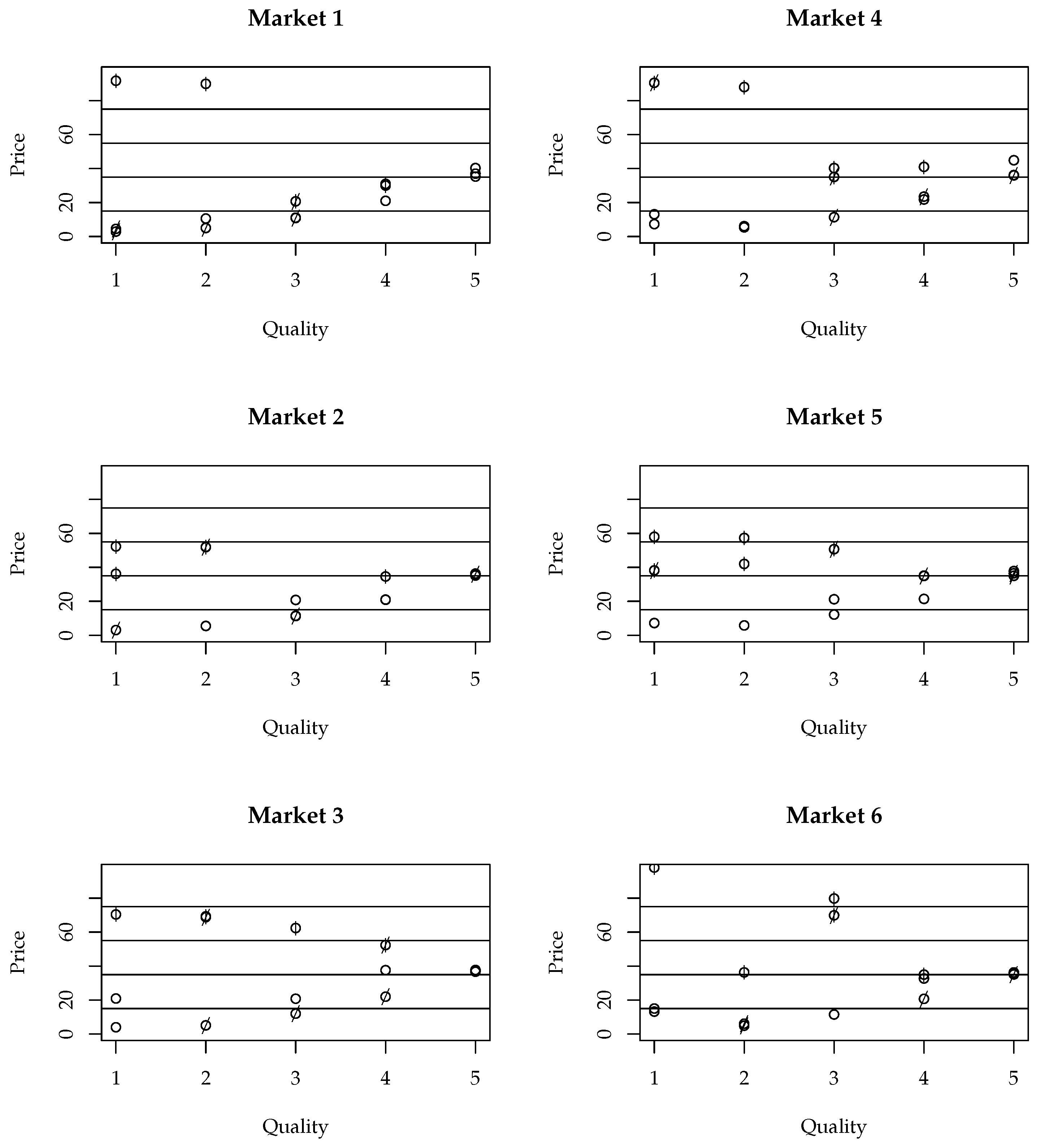

Appendix A.10. Parameters of Experimental Markets
| Market | Experimental Seller ID | Globally Non-Dominated | Tested Under WorstCase | Tested Under Random | |||
|---|---|---|---|---|---|---|---|
| 1 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 4
6 8 11 3 9 10 14 5 1 2 13 12 15 7 | 2.9
4.5 91.7 5 10.6 89.9 10.9 11.1 20.7 21 30 31 35.3 37 40.3 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 1
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
0 1 0 0 1 0 0 1 0 1 1 0 0 0 | 0
0 1 1 0 1 0 1 0 0 1 0 0 0 0 |
| 2 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 3
10 8 15 11 14 2 7 4 13 12 1 5 6 9 | 3.1
36.2 52.3 5.5 51.9 52 11.3 11.5 20.8 20.9 21 34.6 35.2 36.1 36.3 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 1
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
1 1 0 1 1 0 0 0 0 0 1 0 0 0 | 0
0 1 0 0 0 0 1 0 1 1 0 0 0 1 |
| 3 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 3
12 6 4 7 11 2 15 5 14 8 10 9 13 1 | 4
20.9 70.4 5.1 68.8 69.3 12 20.8 62.4 22 37.6 52.4 36.7 37.2 37.7 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 1
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
0 1 0 1 1 0 0 1 0 0 1 0 0 0 | 0
0 1 1 0 1 1 0 0 0 0 1 0 0 0 |
| 4 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 9
1 4 13 15 3 7 8 11 14 12 2 6 5 10 | 7.3
13.1 90.5 5.4 6.1 88 11.4 35.1 40.3 21.8 23.5 41 36 44.9 36.2 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
0 1 0 0 1 0 1 1 0 0 1 0 0 0 | 1
0 0 1 0 0 0 0 1 0 0 0 1 0 1 |
| Market | Experimental Seller ID | Globally Non-Dominated | Tested Under WorstCase | Tested Under Random | |||
|---|---|---|---|---|---|---|---|
| 5 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 4
10 12 15 2 8 5 7 14 1 11 9 6 13 3 | 7.2
38.2 58 5.8 57.3 42 12.2 21.2 50.7 21.4 34.9 35.1 35 36.5 37.8 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
1 1 0 1 1 0 0 1 0 0 0 0 0 0 | 0
1 0 1 0 0 0 0 0 1 0 1 0 0 1 |
| 6 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 10
14 4 5 9 15 11 7 13 1 8 12 6 3 2 | 13.2
15 98 4.9 6.1 36.3 11.5 69.9 79.8 20.7 32.7 35 35.1 35.9 36.3 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 1 0 0 1 0 0 1 0 0 1 0 0 | 0
0 1 0 0 1 0 1 1 0 0 1 0 0 0 | 0
0 0 1 1 0 0 0 1 1 0 0 0 1 0 |
| 7 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 15
6 2 1 3 8 4 10 13 11 12 5 14 9 7 | 13.9
65.6 70.5 14.6 15.8 25.6 10.6 55.6 57.2 18.8 55.4 35.2 30.3 43.5 50.5 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 1 0 0 1 0 0 1 0 0 | 0
1 1 0 0 0 0 1 1 0 1 0 0 0 0 | 1
1 1 0 0 1 0 0 0 0 0 0 0 0 1 |
| 8 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 7
3 11 8 4 12 14 10 6 13 9 1 2 5 15 | 10.7
48.9 57.9 22.3 30.3 42.5 9.7 42.6 45.8 17 34.7 36.7 28.5 40.2 50.7 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 1 0 0 1 0 0 1 0 0 | 0
1 1 0 0 1 0 1 1 0 0 0 0 0 0 | 0
0 1 1 0 0 1 1 0 0 1 0 0 0 0 |
| Market | Experimental Seller ID | Globally Non-Dominated | Tested Under WorstCase | Tested Under Random | |||
|---|---|---|---|---|---|---|---|
| 9 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 4
1 3 13 5 2 15 12 11 6 14 7 8 9 10 | 12
57.3 66.2 14.9 16.9 76.1 11 42.8 81 20.1 35.7 66 32.4 37.5 61.1 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 1 0 0 1 0 0 1 0 0 | 0
1 1 0 0 1 0 0 1 0 0 1 0 0 0 | 1
0 1 1 1 0 0 0 0 0 0 0 1 0 0 |
| 10 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 8
5 6 9 1 3 10 12 14 15 4 13 11 2 7 | 50.3
55.3 59 47 53.5 57.3 29.4 61.9 75 17.6 55.6 79.1 29.3 60.3 77.8 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 0 0 0 1 0 0 1 0 0 | 0
0 1 0 0 0 0 1 1 0 0 1 0 0 1 | 1
0 0 0 1 1 0 1 1 0 0 0 0 0 0 |
| 11 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 5
1 7 14 12 10 11 3 13 9 6 2 8 4 15 | 23.7
26.3 73 26.8 54.5 78.1 36.3 58.4 63.4 21.3 51.8 57.7 33 47.3 58 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 0 0 0 1 0 0 1 0 0 | 0
0 1 0 0 1 0 1 1 0 0 1 0 0 0 | 1
0 0 0 1 0 1 0 0 0 0 1 0 1 0 |
| 12 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 2
12 13 4 15 1 11 6 10 7 9 14 5 8 3 | 30.3
34.6 77 28.9 56.6 80.2 38.4 60.5 65.5 18.5 63.9 79.8 29.9 42.4 72.1 | 1
1 1 2 2 2 3 3 3 4 4 4 5 5 5 | 0
0 0 0 0 0 0 0 0 1 0 0 1 0 0 | 0
0 1 0 0 1 0 0 1 0 1 1 0 0 0 | 0
1 0 1 0 0 0 0 0 0 0 1 1 0 1 |
Appendix A.11. Experimental Instructions
- Welcome to the Experiment
- Participants’ roles
- The experiment consists of twelve rounds. There are two roles: sellers and buyers. First, it will be determined randomly which participants will be sellers and which will be buyers, and which sellers and buyers, respectively, receive which ID. You will keep your role and ID throughout the whole experiment. This means, if you were seller 1 in round 1, for example, you will remain seller 1 in all remaining rounds, or if you were buyer 1 in round 1, you will remain buyer 1 in all remaining rounds. There are 15 sellers an 8 buyers in total.
- Sellers
- Sellers offer identical products each at a certain price, a certain quality and certain unit costs. A product belongs to one of five potential quality levels: 1 (poor), 2 (fair), 3 (satisfactory), 4 (good), 5 (very good); i.e., the higher the number, the higher a product’s quality. Sellers are not able to influence price, quality and unit costs. These will be assigned to them each round.
- Buyers
- Buyers select one seller per round, from whom they can buy at most one product. (They also have the option not to buy a product.) Buyers value the quality of a product differently. You can find the buyers’ individual valuations in the following table. A buyer’s individual valuation is multiplied by the quality of the product purchased, thus influencing the earnings per round (for details, see paragraph “Earnings per round”). It remains the same for each buyer throughout the experiment. Once a buyer has selected a product, it is considered purchased; the seller’s consent is not required. It is possible for multiple buyers to buy from the same seller.
- Available information
- At the beginning of each round, sellers are informed on the screen about their own price, unit costs and quality as well as the prices, unit costs and qualities of the other sellers. At the beginning of each round, buyers are informed about their own valuation of product quality (according to their buyer no. and the information in the table) and the prices of the products offered. It is also known that, in each round, 3 sellers offer products per quality level. This means that there are three sellers with poor product quality, three sellers with fair product quality, three sellers with satisfactory product quality, three sellers with good product quality and three sellers with very good product quality. In no round is it known whether there is a relationship between the price and quality of a product. In each round, assume there are five sellers from whom purchases were made most frequently in the past, but the reasons for this are unknown. At the beginning of each round, you will be informed which these five sellers are.
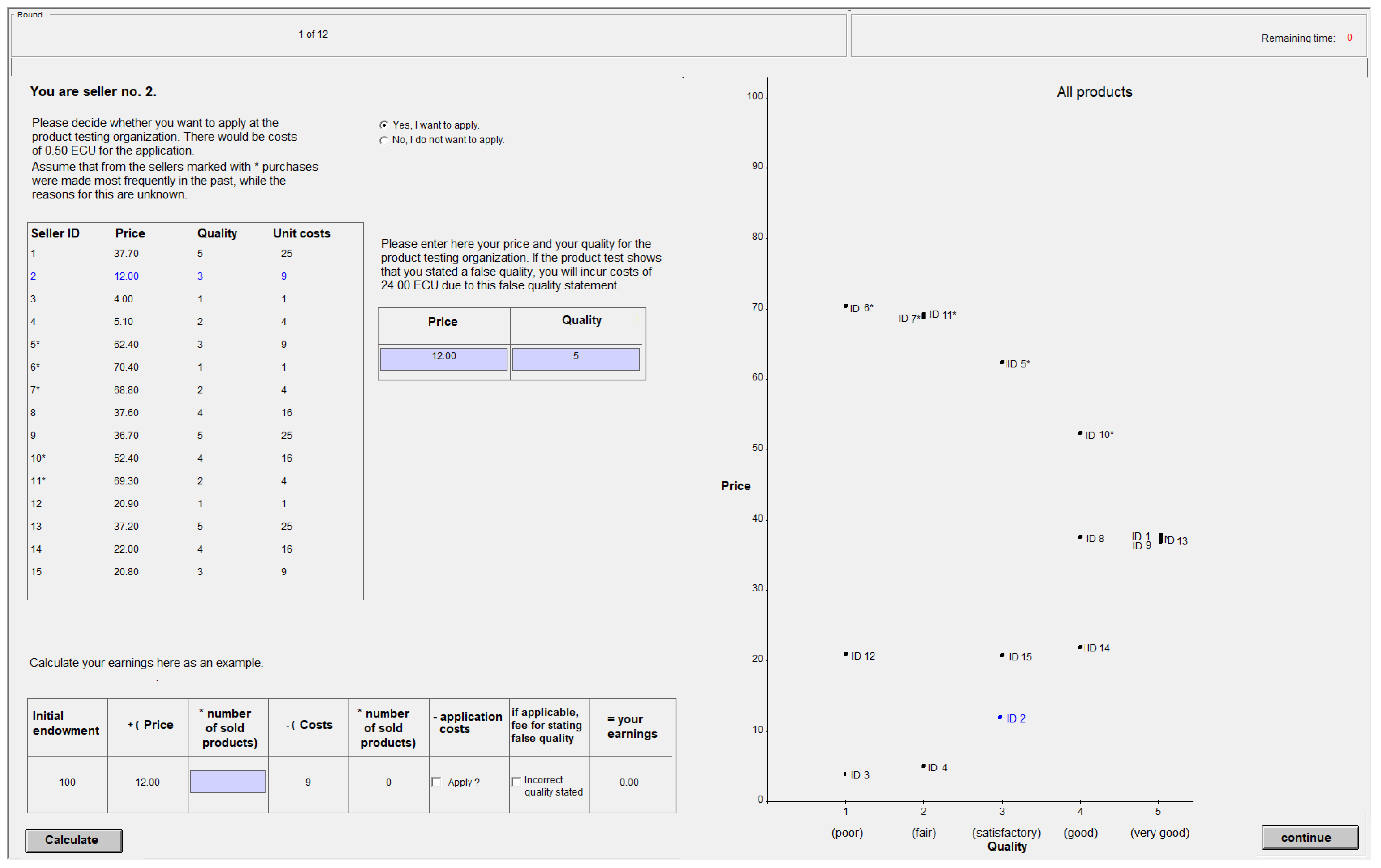
Buyer ID Individual valuation of quality 1 3 2 3 3 7 4 7 5 11 6 11 7 15 8 15 - Product testing
- The sellers are not able to influence price, quality and unit costs, but they have the opportunity to apply to a product testing organization such as Stiftung Warentest each round. The task of the product testing organization is to check the product quality and to disclose it to all buyers. This happens before the buyers decide which products to buy. If applicable, sellers must state the price and quality of their product (it is possible to lie about the quality) when applying, and pay an application fee of 0.50 thalers to the testing organization. Should the product test disclose that a seller stated a false quality, he will have to pay costs of 24.00 thalers for this false quality statement.
- Testing capacity
- The capacity of the product testing organization is limited. Among the applicants, it selects a maximum of five sellers whose products it tests.Step 1: The product testing organization first selects the sellers with the cheapest product per quality level for the test.Step 2: Among these, should there be sellers with products that cost the same or more than a product of a lower stated quality than a product of a better stated quality, these products are excluded again. Only the remaining untested products will be tested. Products that have already been tested will never lose their testing slot.Step 3: If, after the product test, it turns out that in this iteration at least one seller stated a false quality and if the maximum testing capacity has not yet been reached, the testing organization re-starts with step 1. If, after the product test, it turns out that all sellers stated the true quality in this iteration, no further products will be tested.For step 1 and step 2, the testing organization uses the stated qualities of untested products (because their true quality is not yet known). From the second iteration onwards, if applicable, it uses the true qualities of the products already tested (because their true quality is then known). If less than five products are selected by step 1 and step 2, fewer products will be tested accordingly. Should there ever be more applicants selected than the number of remaining testing slots, a random selection will be made among these applicants. The application fee of 0.50 thalers must be paid regardless of whether a product will eventually be tested or not. You can find an overview on page 4.
- Earnings per round
- Each participant receives an initial endowment of 100 thalers. The earnings are determined as follows:Earnings seller per round :initial endowment+(price × number sold products)−(unit costs × number sold products)−if applicable, application fee−if applicable, fee for stating false qualiEarnings buyer per round :initial endowment+(quality × ind. valuation of quality)−priceIn the course of the experiment, sellers will be asked how they think other participants will behave. For each answer that is correct, a seller will receive additional 0.50 thaler in the corresponding round. Sellers only receive feedback on how many of their beliefs were correct for the payoff-relevant round at the end of the experiment.
- Payment
- When all twelve rounds will have been completed, the computer randomly selects one of the twelve rounds to be payoff-relevant for all participants. The other rounds are not taken into account for the payment. At the end of the experiment, each participant will receive the amount of money they have earned in the payoff-relevant round, converted into EUR (4 thalers = 1 EUR). If applicalbe, the amount is rounded up to a multiple of 0.10 EUR.
- Comprehension questions
- Please click on “continue” on the screen when you will have finished reading the instructions and have no further questions until here. The experiment starts on the screen with comprehension questions. These comprehension questions are supposed to make it easier for you to become familiar with the decision-making situation. If you have any questions, please raise your hand. (Participants who are in one of the cubicles with doors today, please open the door so that we can see you raising your hand.) We will then come to you and answer your question at your cubicle. Once all participants will have correctly answered the comprehension questions, round 1 of the experiment will start.
- Technical note
- For technical reasons, please enter a dot instead of a comma to separate decimal places in numbers if applicable.

- Differences to other treatments
- Treatment SellersMayApply-Truth
- Product test
- The sellers are not able to influence price, quality and unit costs, but they have the opportunity to apply to a product testing organization such as Stiftung Warentest each round. The task of the testing organization is to check the product quality and to disclose it to all buyers. This happens before the buyers decide which products to buy. If applicable, sellers must state the price and quality of their product (it is not possible to lie) when applying, and pay an application fee of 0.50 thalers to the testing organization.
- Testing capacity
- The capacity of the product testing organization is limited. Among the applicants, it selects a maximum of five sellers whose products it tests. The testing organization first selects the sellers with the cheapest product per quality level for the test. Among these, should there be sellers with products that cost the same or more than a product of a lower stated quality than a product of a better stated quality, these products will not be tested. If less than five products are selected via this method, fewer products will be tested accordingly. The application fee of 0.50 thalers must be paid regardless of whether a product will eventually be tested or not.
Earnings seller per round :
initial endowment+(price × number sold products)−(unit costs × number sold products)
- Treatments SellersMayNotApply-WorstCase and SellersMayNotApply-Random
- Product testing
- Each round, a product testing organization such as Stiftung Warentest tests certain products. The task of the testing organization is to check the product quality and to disclose it to all buyers. This happens before the buyers decide which products to buy.
- Testing capacity
- The capacity of the product testing organization is limited. It selects five sellers whose products it tests, namely each round the five sellers from whom the most frequent purchases were made in the past.
Earnings seller per round :
initial endowment+(price × number sold products)−(unit costs × number sold products
Appendix A.12. Screenshots of Main Decision Situations in z-Tree



| 1 | Product quality is a multidimensional construct comprising horizontal and vertical dimensions. Horizontal quality dimensions are subjective. More precisely, while it may be possible to objectively specify horizontal quality dimensions, consumers differ in their preferences about them (Hotelling, 1929). For example, horizontal dimensions of a stroller’s quality include its color. While it is possible to objectively specify a certain color, e.g., by using a spectrophotometer, consumers have different preferences over colors. In contrast, vertical quality dimensions are objectively rateable. To illustrate, vertical dimensions of a stroller’s quality include its weight, how waterproof the raincover is, and the level (if any) of toxic substances contained in its materials. Note that these vertical dimensions usually contain search, experience, and credence characteristics (Nelson, 1970; Darby & Karni, 1973). For a stroller, a search characteristic would be its weight since a stroller’s weight can be determined before purchasing it. An experience characteristic would be how waterproof the raincover is since this is usually observable only after use. A credence characteristic would be how many toxic substances are contained in the fabric since consumers are usually not able to observe this amount even after having purchased the stroller. |
| 2 | In our opinion, most products contain some amount of horizontal and some amount of vertical quality dimensions while the relevance of each one may differ. This paper focuses on products whose vertical quality dimensions are at least as relevant for buyers as its horizontal ones, e.g., toothpaste, strollers, or grills. We do not analyze markets for products whose horizontal quality dimensions are more relevant for buyers than its vertical ones, e.g., fiction movies or books. Note that, while online consumer ratings for such products can be found on websites like amazon.com or imdb.com, independent consumer organizations usually do not test fiction movies or books. |
| 3 | See https://www.international-testing.org/members.html?section=icrt_shareholders (accessed on 16 December 2023) for a detailed list of world-wide independent consumer organizations. |
| 4 | We are aware that buyers also use other proxies for quality, e.g., online consumer ratings (Rao & Monroe, 1989 and De Langhe et al., 2016). While online consumer ratings are often readily available, they are problematic since, most importantly, they usually do not include credence characteristics such as toxic substances in food, cosmetics, or clothing, or under which working conditions a product was manufactured. Second, online consumer ratings often include not only vertical, but also horizontal quality dimensions although the latter are, by definition, not objectively rateable. Third, fake ratings constitute a real problem, even among verified purchases (Mayzlin et al., 2014 and Which?, 2023a). Interestingly, online consumer ratings have also been shown to correlate poorly with ratings provided by independent consumer organizations (De Langhe et al., 2016 and Köcher & Köcher, 2018). Some buyers also use price as a proxy for quality. Yet, it seems to be a poor proxy as only moderately positive, zero, or even negative correlations between product quality and price have been found repeatedly (see Ratchford et al., 1996; Olbrich & Jansen, 2014 for overviews, and the following for country-specific studies: Oxenfeldt, 1950 and De Langhe et al., 2016; Diller, 1977, 1988; Yamada & Ackerman, 1984; Bodell et al., 1986; Steenkamp, 1988; Kirchler et al., 2010). We acknowledge that these correlational results are sensitive to the weights of quality dimensions which are, to some degree, arbitrary. Yet, testing results published by Consumer Reports show that more than half of all tested product models are dominated on all quality dimensions (Hjorth-Andersen, 1984). |
| 5 | We use “product” (“product model”) as the more general (specific) term. Usually, several product models belong to one certain type of product, e.g., several smartphone models belong to the product smartphone. Furthermore, we use “game” or “theoretical framework” instead of “theoretical model” in this paper to avoid confusion. Note that independent consumer organizations do not only face capacity constraints as to which product models, but also as to which products to select for testing. This study focuses on the problem of which product models to select. |
| 6 | Professional Sports Authenticator (PSA) is one of the largest card grading services world-wide (for more information, see https://www.psacard.com/services/tradingcardgrading, accessed on 6 December 2023). |
| 7 | USDA organic is a label issued by the US Department of Agriculture (for more information, see https://www.usda.gov/media/blog/2012/03/22/organic-101-what-usda-organic-label-means, accessed on 6 December 2023). Blauer Engel is the ecolabel of the federal government of Germany (for more information, see https://www.blauer-engel.de/en, accessed on 6 December 2023). Note that another difference is that their labels are binary (either USDA organic or Blauer Engel certified, or not) whereas independent consumer organizations provide ordinally scaled ratings which often include at least three to five levels. |
| 8 | Our setting differs from theoretical papers which find that price may signal product quality, e.g., Bagwell and Riordan (1991). We analyze situations in which all buyers have access to quality information about a share of product models. By contrast, Bagwell and Riordan (1991) analyze situations in which a share of buyers is informed about all product models’ quality (see Appendix A.5 for a visual comparison). Moreover, we assume buyers know that producing a higher quality is more expensive, but they do not know the precise production function. By contrast, Bagwell and Riordan (1991) assume the product function is common knowledge. Note that, when starting out from our markets in which quality and price are uncorrelated considering all product models, they will be positively correlated under our new mechanism when considering only the set of tested product models. |
| 9 | Note that there is only one seller in the set of sellers Z since identical prices are ruled out by assumption. |
| 10 | While the literature on certification consistently includes independent consumer organizations in the larger set of “certifiers”, it is less consistent in how a “certified product” is defined. Therefore, unless noted otherwise, we use “tested” when referring to a product model whose quality has been tested and publicly revealed. Note that a “tested product model” may also be of the lowest possible quality, whereas “certified product model” might imply that a certain quality threshold has been reached (see, for instance, Bizzotto & Harstad, 2023). |
| 11 | |
| 12 | See Ispano and Schwardmann (2023) for a model with boundedly rational buyers. |
| 13 | Note that we use an indicator function to describe a buyer’s utility with a single function. If the condition in braces is true, the indicator variable equals one. If the condition is not fulfilled, the indicator variable equals zero. |
| 14 | Note that, from a buyer’s perspective, CompleteInformation is identical to a setting in which a certifier were able to test all existing product models, i.e., . However, from an overall economic perspective, the latter setting would include certifying costs—which we abstract from and do not analyze in this paper. |
| 15 | Importantly, sellers do not send items of their product model to the certifier since these items might be of higher quality than those actually sold to buyers. As mentioned in Section 1, independent consumer organizations usually use their own test-buyers who purchase products anonymously, and this procedure remains unchanged under SellersMayApply. By contrast, sellers of baseball cards do send their actual cards to, e.g., PSA for rating. |
| 16 | Currently, Stiftung Warentest, Consumer Reports and Which? collect the prices of all product models to be tested. If prices vary for a certain product model, Stiftung Warentest calculates the mean price. |
| 17 | Note that the overall cheapest seller is always part of , but he may or may not belong to . More precisely, we would have to write if , and if , respectively. For better readability, we still always write in the following even if . |
| 18 | In Section 3.2.3, we derive how buyers calculate the expected quality of an untested product model under SellersMayApply. |
| 19 | Note that neither contains the qualities of tested sellers, nor quality levels equal to or higher than 4. See Section 3.2.3 for a general explanation of why an untested seller ’s expected quality under SellersMayApply neither contains the qualities of tested sellers, nor quality levels equal to or higher than those of tested sellers in offering higher quality levels than (if any). |
| 20 | See Appendix A.7.2 for details. |
| 21 | More specifically, “no gaps within ” implies that there is one seller for the highest quality level in , one seller for the second highest quality level in , …, one seller for the second-lowest quality level in , and one seller for the lowest quality level in . |
| 22 | Note that only in the third version of the game decisions are interdependent. Therefore, strictly speaking, the first two versions of the game may not be defined as a “game”. |
| 23 | The lowest price range contains all prices lower than the price of the cheapest tested product model. The second-lowest price range contains all prices between those of the cheapest and the second-cheapest tested product model. …The second-highest price range contains all prices between those of the second most expensive and the most expensive tested product model. The highest price range contains all prices higher than the most expensive tested product. |
| 24 | In this case, the unique Nash equilibrium is slightly different: |
| 25 | We are aware that this presents an extreme scenario. However, in this scenario, sellers with the most dominated product models would earn relatively high profits per sold unit given that their prices are highest among product models of the same quality. This relatively greater profit could be spent on advertising to attract more buyers. |
| 26 | More precisely, the share of globally non-dominated product models among all tested product models is 21.7% in this random scenario, while the mean share of globally non-dominated product models in all markets is 23.3%. |
| 27 | Our experiment is conducted in Germany, where Stiftung Warentest uses five different verbal quality ratings (very good, good, satisfactory, fair and poor) for product models; thus, subjects are likely familiar with a five-item rating scale. In addition to these verbal ratings, Stiftung Warentest also publishes more precise numerical ratings ranging from 1.0 to 5.0. |
| 28 | Note that “globally non-dominated” includes sellers with for markets 1 to 3 in which five globally non-dominated product models exist. While we do not expect these sellers to apply for testing, we include them in our analysis to be consistent with markets 4 to 12 in which all sellers with globally non-dominated product models are predicted to apply to be tested. |
| 29 | To the best of our knowledge, this question has not been analyzed again. |
| 30 | For example, two product models rated “good” by Stiftung Warentest were temporarily not available for purchase soon after the ratings had been published: the frying pan “Gastro Sus Diamas Pro Industar” rated in the 01/2021 magazine, and the coffee machine “Philipps EP5447/90” rated in the 01/2022 magazine (see Appendix A.4 for details). |
| 31 | Note that neither contains the qualities of tested sellers, nor quality levels equal to or higher than 3 (2) if seller is untested (tested). See Section 3.2.3 for a general explanation of why an untested seller ’s expected quality under SellersMayApply neither contains the qualities of tested sellers, nor quality levels equal to or higher than those of tested sellers in offering higher quality levels than . |
| 32 | Note that neither contains the qualities of tested sellers, nor quality levels equal to or higher than 3. See Section 3.2.3 for a general explanation of why an untested seller ’s expected quality under SellersMayApply neither contains the qualities of tested sellers, nor quality levels equal to or higher than those of tested sellers in offering higher quality levels than . |
References
- Abeler, J., Nosenzo, D., & Raymond, C. (2019). Preferences for truth-telling. Econometrica, 87(4), 1115–1153. [Google Scholar] [CrossRef]
- Akerlof, G. A. (1970). The market for “lemons”. Quality uncertainty and the market mechanism. The Quarterly Journal of Economics, 84(3), 488–500. [Google Scholar] [CrossRef]
- ALDI Nord Deutschland Stiftung & Co. KG. (2023). Fair & gut tierwohl-weidemilch. Available online: https://www.aldi-nord.de/sortiment/kuehlung-tiefkuehlung/kaese-milch-milchprodukte/milch-milchersatz/tierwohl-weidemilch-5122-0-0.article.html (accessed on 18 December 2023).
- Amazon Europe Core Sàrl. (2023). Bosch staubsauger beutellos serie 6 BGC41XALL. Available online: https://www.amazon.de/Bosch-BGC41XALL-Bodenstaubsauger-Hygiene-Filter-XXL-Polsterd%C3%BCse/dp/B09SZRS8JK/ref=sr_1_9?__mk_de_DE=%C3%85M%C3%85%C5%BD%C3%95%C3%91&crid=1HK4TEZORZ28T&keywords=Staubsauger+testsieger&qid=1702752522&sprefix=staubsauger+testsieger%2Caps%2C107&sr=8-9 (accessed on 18 December 2023).
- Bagwell, K., & Riordan, M. H. (1991). High and declining prices signal product quality. American Economic Review, 81(1), 224–239. [Google Scholar]
- Bahel, E., & Sprumont, Y. (2020). Strategyproof choice of social acts. American Economic Review, 110(2), 596–627. [Google Scholar] [CrossRef]
- Bahel, E., & Sprumont, Y. (2021). Strategy-proof choice with monotonic additive preferences. Games and Economic Behavior, 126, 94–99. [Google Scholar] [CrossRef]
- Barberà, S., Massó, J., & Neme, A. (2005). Voting by committees under constraints. Journal of Economic Theory, 122, 185–205. [Google Scholar] [CrossRef][Green Version]
- Benndorf, V. (2018). Voluntary disclosure of private information and unraveling in the market for lemons: An experiment. Games, 9(2), 23. [Google Scholar] [CrossRef]
- Benndorf, V., Kübler, D., & Normann, H.-T. (2015). Privacy concerns, voluntary disclosure of information, and unraveling: An experiment. European Economic Review, 75, 43–59. [Google Scholar] [CrossRef]
- Bizzotto, J., & Harstad, B. (2023). The certifier for the long run. International Journal of Industrial Organization, 87, 1–19. [Google Scholar] [CrossRef]
- Bizzotto, J., Perez-Richet, E., & Vigier, A. (2021). Communication via third parties. Unpublished.
- Bodell, R. W., Kerton, R. R., & Schuster, R. W. (1986). Price as a signal of quality: Canada in the international context. Journal of Consumer Policy, 9, 431–444. [Google Scholar] [CrossRef]
- Brendel, F. (2021). Limits of information unraveling: A survey on voluntary disclosure. Unpublished.
- Carroll, G. (2019). Robust incentives for information acquisition. Journal of Economic Theory, 181, 382–420. [Google Scholar] [CrossRef]
- Consumer Reports. (2023). What we do. Available online: https://www.consumerreports.org/cro/about-us/what-we-do/media-page/index.htm (accessed on 6 December 2023).
- Darby, M. R., & Karni, E. (1973). Free competition and the optimal amount of fraud. The Journal of Law & Economics, 16(1), 67–88. [Google Scholar]
- De Langhe, B., Fernbach, P. M., & Lichtenstein, D. R. (2016). Navigating by the stars: Investigating the actual and perceived validity of online user ratings. Journal of Consumer Research, 42, 817–833. [Google Scholar] [CrossRef]
- Diller, H. (1977). Der preis als qualitätsindikator. Die Betriebswirtschaft, 37(2), 219–234. [Google Scholar]
- Diller, H. (1988). Die preis-qualitäts-relation von konsumgütern im 10-jahresvergleich. Die Betriebswirtschaft, 48(2), 195–200. [Google Scholar]
- dm-drogerie markt GmbH + Co. KG. (2023). elmex Zahnpasta Kinder, 2 bis 6 Jahre, 50 mL. Available online: https://www.dm.de/elmex-zahnpasta-kinder-2-bis-6-jahre-p8718951271234.html (accessed on 18 December 2023).
- Dranove, D., & Jin, G. Z. (2010). Quality disclosure and certification. Theory and practice. Journal of Economic Literature, 48(4), 935–963. [Google Scholar] [CrossRef]
- Encaoua, D., & Hollander, A. (2007). First degree discrimination by a duopoly: Pricing and quality choice. Berkeley Economic Journal on Theoretical Economics, 7(1), 14. [Google Scholar] [CrossRef]
- Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178. [Google Scholar] [CrossRef]
- Forsythe, R., Isaac, R. M., & Palfrey, T. R. (1989). Theories and tests of “blind bidding” in sealed-bid auctions. The RAND Journal of Economics, 20(2), 214–238. [Google Scholar] [CrossRef]
- GfK SE, Nuremberg. (2017). Point-of-sales-panel Germany: Compact cameras (Nov 15 - Jun 16), Multi-function color printers (Apr 16 - Jun 16), Multi-function black/white printers (Apr 16 - Jun 16), Black/white printers (Apr 16 - Jun 16), Box spring beds, 180x200 cm (Feb 16 - May 16), Tumble dryers with pump (Jan 16 - Feb 16), Tumble dryers without pump (Jan 16 - Feb 16), LED lamps, G9, 230 volt (Jan 16 - Feb 16), Consumer Panel Germany: Tuna in oil (Apr 16 - May 16), Frozen tuna (Apr 16 - May 16), Toothpaste (Mar 16 - Apr 16).
- Greiner, B. (2015). Subject pool recruitment procedures: Organizing experiments with ORSEE. Journal of the Economic Science Association, 1, 114–125. [Google Scholar] [CrossRef]
- Grossman, S. J. (1981). The informational role of warranties and private disclosure about product quality. Journal of Law and Economics, 24(3), 461–483. [Google Scholar] [CrossRef]
- Hagenbach, J., & Perez-Richet, E. (2018). Communication with evidence in the lab. Games and Economic Behavior, 112, 139–165. [Google Scholar] [CrossRef]
- Hjorth-Andersen, C. (1984). The concept of quality and the efficiency of markets for consumer products. Journal of Consumer Research, 11, 708–718. [Google Scholar] [CrossRef]
- Hotelling, H. (1929). Stability in competition. Economic Journal, 39(153), 41–57. [Google Scholar] [CrossRef]
- International Consumer Research & Testing. (2021). Application for membership of international consumer research & testing Ltd. Available online: https://www.international-testing.org/members.html?section=join_icrt (accessed on 16 December 2023).
- Ispano, A., & Schwardmann, P. (2023). Cursed consumers and the effectiveness of consumer protection policies. Journal of Industrial Economics, 71, 407–440. [Google Scholar] [CrossRef]
- Jin, G. Z., Kato, A., & List, J. A. (2010). That’s news to me! Information revelation in professional certification markets. Economic Inquiry, 48(1), 104–122. [Google Scholar] [CrossRef]
- Jin, G. Z., & Leslie, P. (2003). The effect of information on product quality: Evidence from restaurant hygiene grade cards. The Quarterly Journal of Economics, 118(2), 409–451. [Google Scholar] [CrossRef]
- Jin, G. Z., Luca, M., & Martin, D. (2021). Is no news (perceived as) bad news? An experimental investigation of information disclosure. American Economic Journal: Microeconomics, 13(2), 141–173. [Google Scholar]
- Jin, G. Z., Luca, M., & Martin, D. (2022). Complex disclosure. Management Science, 68(5), 3236–3261. [Google Scholar] [CrossRef]
- Kamenica, E., & Gentzkow, M. (2011). Bayesian persuasion. American Economic Review, 101, 2590–2615. [Google Scholar] [CrossRef]
- KantarEmnid & Verbraucherzentrale Bundesverband. (2018). Verbraucherreport: Infografiken Juli 2018. Available online: https://www.vzbv.de/sites/default/files/downloads/2018/10/12/verbraucherreport_2018_-_infografiken.pdf (accessed on 6 December 2023).
- Kirchkamp, O. (2019). Importing z-Tree data into R. Journal of Behavioral and Experimental Finance, 22, 1–2. [Google Scholar] [CrossRef]
- Kirchler, E., Fischer, F., & Hölzl, E. (2010). Price and its relation to objective and subjective product quality: Evidence from the Austrian market. Journal of Consumer Policy, 33, 275–286. [Google Scholar] [CrossRef]
- Köcher, S., & Köcher, S. (2018). Should we reach for the stars? Examining the convergence between online product ratings and objective product quality and their impacts on sales performance. Journal of Marketing Behavior, 3, 167–183. [Google Scholar] [CrossRef]
- List, J. A. (2006). The behavioralist meets the market: Measuring social preferences and reputation effects in actual transactions. Journal of Political Economy, 114(1), 1–37. [Google Scholar] [CrossRef]
- Mathios, A. D. (2000). The impact of mandatory disclosure laws on product choices: An analysis of the salad dressing market. Journal of Law and Economics, 43, 651–678. [Google Scholar] [CrossRef]
- Mayzlin, D., Dover, Y., & Chevalier, J. (2014). Promotional reviews: An empirical investigation of online review manipulation. American Economic Review, 104(8), 2421–2455. [Google Scholar] [CrossRef]
- Milgrom, P. R. (1981). Good news and bad news. Representation theorems and applications. The Bell Journal of Economics, 12(2), 380–391. [Google Scholar] [CrossRef]
- Nelson, P. (1970). Information and consumer behavior. Journal of Political Economy, 78(2), 311–329. [Google Scholar] [CrossRef]
- Olbrich, R., & Jansen, H. C. (2014). Price-quality relationship in pricing strategies for private labels. Journal of Product & Brand Management, 23(6), 429–438. [Google Scholar] [CrossRef]
- Oxenfeldt, A. R. (1950). Consumer knowledge: Its measurement and extent. The Review of Economics and Statistics, 32(4), 300–314. [Google Scholar] [CrossRef]
- Rao, A. R., & Monroe, K. B. (1989). The effect of price, brand name, and store name on buyers’ perceptions of product quality: An integrative review. Journal of Marketing Research, 26, 351–357. [Google Scholar]
- Ratchford, B. T., Agrawal, J., Grimm, P. E., & Srinivasan, N. (1996). Toward understanding the measurement of market efficiency. Journal of Public Policy & Marketing, 15(2), 167–184. [Google Scholar]
- R Core Team. (2023). R: A language and environment for statistical computing [Computer software manual]. R Core Team. Available online: https://www.R-project.org/ (accessed on 18 December 2023).
- Stahl, K., & Strausz, R. (2017). Certification and market transparency. Review of Economic Studies, 84, 1842–1868. [Google Scholar]
- Steenkamp, J.-B. E. M. (1988). The relationship between price and quality in the marketplace. De Economist, 136(4), 491–507. [Google Scholar] [CrossRef]
- Stiftung Warentest. (2019). Statutes. Available online: https://www.test.de/unternehmen/about-us-5017053-0/ (accessed on 6 December 2023).
- Stiftung Warentest. (2020). RAL LOGO LIZENZ—Allgemeine vertragsbedingungen. Available online: https://www.ral-logolizenz-warentest.de/fileadmin/Resources/Public/Pdf/2023/2023-01-02_RAL_Logolizenz_Vertragsbedingungen_Anlagen_01_02.pdf (accessed on 16 December 2023).
- Szalay, D. (2005). The economics of clear advice and extreme options. Review of Economic Studies, 72, 1173–1198. [Google Scholar] [CrossRef]
- Viscusi, W. K. (1978). A note on “lemons” markets with quality certification. The Bell Journal of Economics, 9(1), 277–279. [Google Scholar] [CrossRef]
- Which? (2023a). The facts about fake reviews: Which? Investigators reveal tricks that sellers use to mislead online shoppers. Available online: https://www.which.co.uk/news/2018/10/the-facts-about-fake-reviews/ (accessed on 6 December 2023).
- Which? (2023b). Use our logo. Available online: https://b2b.which.co.uk/work-with-us/use-our-logo (accessed on 16 December 2023).
- Which? (2023c). Who we are. Available online: https://www.which.co.uk/about-which/who-we-are (accessed on 6 December 2023).
- Yamada, Y., & Ackerman, N. (1984). Price-quality correlations in the Japanese market. Journal of Consumer Affairs, 18(2), 251–265. [Google Scholar] [CrossRef]





| CompleteInformation | SellersMayNotApply | SellersMayApply | |
|---|---|---|---|
| Stage 1 | (Sellers are passive.) | Sellers may apply for testing. | |
| Stage 2 | (Certifier is passive.) | Certifier tests subset of product models. | |
| Stage 3 | Buyers decide which product model to buy (if any). | ||
| Treatment | Sellers per Session | Buyers per Session | Number of Sessions/ Independent Observations | Participants |
|---|---|---|---|---|
| SellersMayNotApply-WorstCase | 15 | 8 | 5 | 115 |
| SellersMayNotApply-Random | 15 | 8 | 5 | 115 |
| SellersMayApply-LyingPoss | 15 | 8 | 5 | 115 |
| SellersMayApply-Truth | 15 | 8 | 5 | 115 |
| SellersMayApply-Truth (with beliefs about buyer behavior) | 15 | 8 | 5 | 115 |
| Total | 25 | 575 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vollstädt, U.; Imcke, P.; Brendel, F.; Ehses-Friedrich, C. Test Me If You Can—Providing Optimal Information for Consumers Through a Novel Certification Mechanism. Games 2025, 16, 44. https://doi.org/10.3390/g16050044
Vollstädt U, Imcke P, Brendel F, Ehses-Friedrich C. Test Me If You Can—Providing Optimal Information for Consumers Through a Novel Certification Mechanism. Games. 2025; 16(5):44. https://doi.org/10.3390/g16050044
Chicago/Turabian StyleVollstädt, Ulrike, Patrick Imcke, Franziska Brendel, and Christiane Ehses-Friedrich. 2025. "Test Me If You Can—Providing Optimal Information for Consumers Through a Novel Certification Mechanism" Games 16, no. 5: 44. https://doi.org/10.3390/g16050044
APA StyleVollstädt, U., Imcke, P., Brendel, F., & Ehses-Friedrich, C. (2025). Test Me If You Can—Providing Optimal Information for Consumers Through a Novel Certification Mechanism. Games, 16(5), 44. https://doi.org/10.3390/g16050044






