Cooperative and Non-Cooperative Strategies in Product Warranty Pricing: A Hierarchical Game Approach

Abstract

This paper analyzes the pricing dynamics of product warranties by developing a three-player hierarchical game model involving a manufacturer, an independent service agent, and a consumer. The model provides a scenario where the manufacturer and the agent form a coalition to coordinate pricing strategies, while interacting non-cooperatively with the consumer. In this framework, the manufacturer sets the product’s sale price, including the base warranty, while the agent determines the price of extended maintenance services. The key contribution is the application of the Shapley value to equitably distribute the coalition’s profits based on each member’s contribution—a novel approach in the warranty pricing literature. We detail the characteristic functions that define the coalition’s structure and present computer simulations to estimate the expected costs associated with maintenance services. A comprehensive sensitivity analysis is applied to report how changes in parameters influence equilibrium strategies and players’ payoffs. The results provide strategic insights into how manufacturers and agents can coordinate to optimize pricing, capture consumer surplus, and improve decision-making in warranty service markets.

1. Introduction

Price and warranty are two variables that affect companies’ profitability, as well as consumers’ purchase decisions. Warranty serves as an incentive for the customer to buy a product (Esmaeili et al., 2014; Rahman & Chattopadhyay, 2006), and it can generate additional revenue for companies (Zhou et al., 2025). Consequently, this environment is characterized by the interaction of multiple decision-makers (players) who face several decision problems and pursue different goals (Murthy & Jack, 2014).

The base warranty is an integral part of the sale and is factored into the product’s price (Murthy, 2007). A common type of warranty is the free replacement policy, under which consumers obtain free replacements or repairs for failures within the warranty period (Thomas & Rao, 1999; Rao, 2021). In certain situations, manufacturers may also offer money-back warranty in addition to offering free replacement (Boom, 1998).

Beyond the base warranty provided by the manufacturer, other companies, often referred to as service agents, extend coverage plans by assuming responsibility for post-warranty maintenance under a maintenance service contract (Murthy et al., 2015). This aftermarket warranty is illustrated by third-party plans available for Apple products. For example, Apple1 sells its products with a one-year Limited Warranty, starting from the purchase date. Consumers can then purchase an extended protection plan for their devices through SquareTrade2.

The interaction between these players creates a complex problem. Firstly, the cost of a warranty policy is inherently uncertain. Because failures are modeled as a stochastic process, the future cost of providing this service is not a deterministic event, since it depends on the failure time of the product (Ben-Daya et al., 2016). Given this uncertainty, developing effective pricing models becomes a critical strategic decision for manufacturers and service agents to maximize their profits.

Secondly, under this uncertainty, manufacturers and service agents must anticipate how the consumer will react to this pricing structure, which leads towards a game-theoretic formulation (Singpurwalla & Wilson, 1993). Players’ payoffs are interdependent, that is, the action of one affects the outcome of all (Parilina et al., 2022). For example, if the consumer does not buy the product, the manufacturer and the service agent obtain zero profit. Therefore, manufacturers and service providers must strike a balance between warranty coverage, service quality, and pricing to maximize profitability while ensuring customer satisfaction (Rahman & Chattopadhyay, 2006).

Most research on game theory applied in warranty problems focuses on two-party interactions: a maintenance provider (manufacturer or service agent) and a consumer (Esmaeili et al., 2014; Iskandar et al., 2022). To define the equilibrium strategies, these studies apply Nash equilibrium (Jackson & Pascual, 2008; Taleizadeh & Sherafati, 2019), and, more frequently, Stackelberg (leader–follower) structure (Murthy & Yeung, 1995; Ashgarizadeh & Murthy, 2000; Murthy & Asgharizadeh, 1998, 1999; Rinsaka & Sandoh, 2006; Arabi et al., 2018; Santos et al., 2017; Panda et al., 2020; Iskandar et al., 2022; Li et al., 2023; Zhang et al., 2023).

However, the dynamics of a more complex, three-player market remain largely underexplored. A few studies do consider this three-player view, modeling both non-cooperative and cooperative outcomes (Esmaeili et al., 2014; Gamchi et al., 2013; Taleizadeh & Sherafati, 2019). More importantly, a significant gap persists: these models do not analyze the marginal contribution of each player to the different possible coalitions. This omission prevents a deeper understanding of fair profit allocation and the stability of cooperative agreements.

This paper addresses this gap by developing and comparing solutions from both non-cooperative and cooperative game-theoretic frameworks. Our non-cooperative model is formulated as a sequential game with a two-leader game. At the upper level, the manufacturer and the service agent simultaneously set their prices; at the lower level, the consumer observes these prices and decides whether to purchase the product bundled with the extended maintenance service. The subgame-perfect Nash equilibrium for this interaction is derived.

For the cooperative framework, we introduce a novel coordinated equilibrium concept. Unlike traditional models that simply assume payoff redistribution, our approach models a structured coordination mechanism between the manufacturer and the service agent. This coordinated strategy jointly optimizes the pricing of the product and the maintenance service. To ensure a fair allocation of the gains from this cooperation, we employ the Shapley Value to quantify each player’s marginal contribution (Sun & Sun, 2018; Petrosyan & Zenkevich, 2016). This hybrid approach captures the benefits of both cooperative stability and strategic autonomy, providing a more realistic and implementable framework for warranty pricing. A key methodological aspect of this work is the use of simulation to accurately estimate the maintenance costs for the underlying failure-repair process of the system.

The remainder of this paper is structured as follows. Section 2 details the model formulation, including the equipment’s failure-repair process and the decision problems for the manufacturer, agent, and consumer. This section also formalizes the game-theoretic frameworks, derives the equilibrium strategies, and introduces the Shapley value for payoff allocation. Section 3 presents the computational study, focusing on the simulation model for maintenance cost estimation, followed by equilibrium analysis and a sensitivity analysis to validate the model. Finally, Section 4 concludes the paper by summarizing the main findings, discussing limitations, and suggesting directions for future research.

2. Model Formulation

2.1. Problem Description

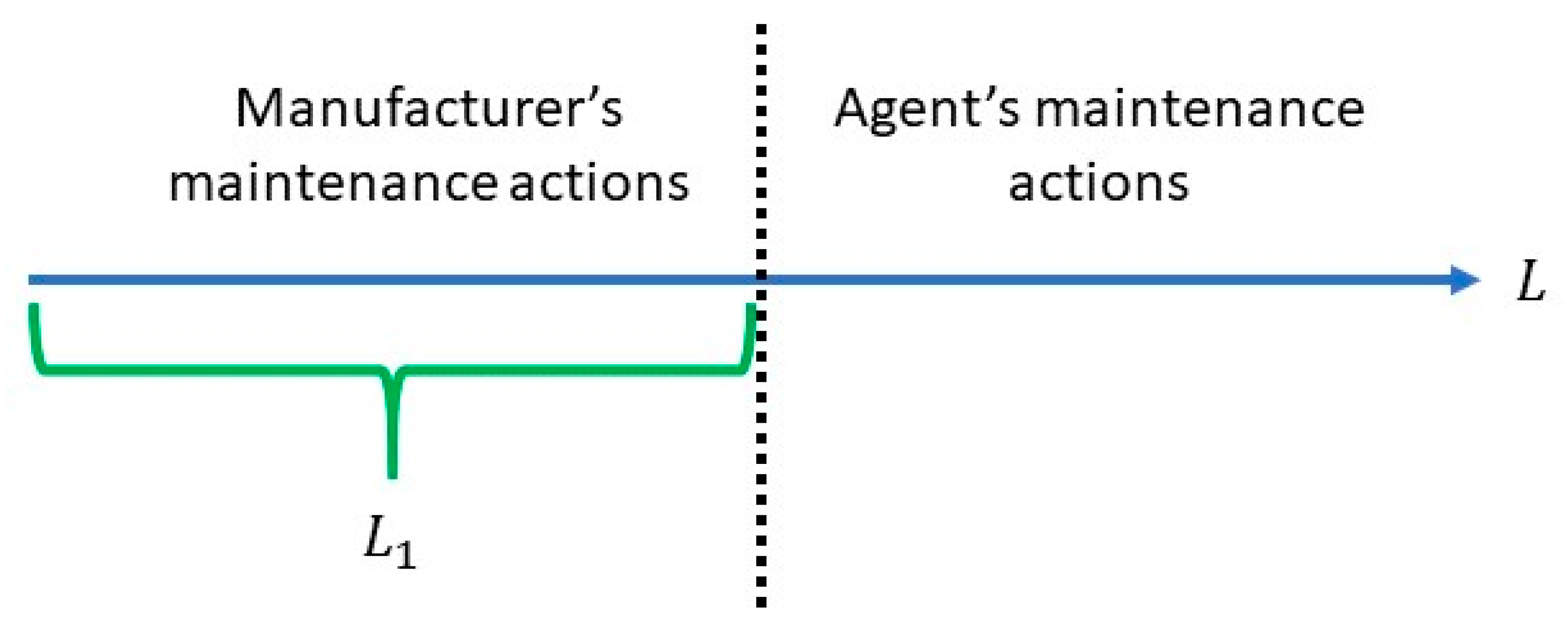
The model is a three-person game, defined between the manufacturer, the agent, and the consumer. The manufacturer sells a durable good (repairable system) that includes the base warranty, and $P_E$ is the price of which is passed on to the consumer. After the base warranty period, the agent provides product maintenance to the residual lifetime of the good, and $P_{MC}$ is the price charged by the agent to the consumer.

During the working state, the product generates revenue R per unit of time to the consumer along with the product’s lifetime $\left(L\right)$. In contrast, in the failed state, the revenue is zero. The item receives maintenance from the manufacturer or the agent, depending on the product’s lifecycle stage. The design of product maintenance differs between the manufacturer and the agent, although both were classified as free replacement warranty policies.

In $L_1\left(<L\right)$, the base warranty period, the manufacturer carries out maintenance. Subsequently, the agent takes over maintenance for the product’s remaining useful life. For a fixed $P_{MC}$, the agent agrees to repair all failures over ($L_1,L$) at no additional cost. If the repair is not finished until time τ, the agent incurs a penalty time. Let Y denote the agent’s repair time, and α denote the penalty cost per time, expressed in monetary units. The penalty design is $\alpha \left(Y-\tau \right)$, if $Y>\tau$, and zero otherwise. In this context, the penalty represents financial compensation that may be received by the consumer related to the downtime to recover the device when the repair time is extensive. Figure 1 summarizes the dynamic of product maintenance, considering who carries out maintenance over $L$.

The failure–repair–failure cycle of the product follows a homogeneous Poisson process considering the failure rate $\left(\lambda >0\right)$, where times between failures are independent, identically exponential random variables (Ushakov, 2012). This model fits when the product is in the second part of the bathtub curve, with random failures and a constant failure rate (Balachandran et al., 1981).

Under a homogeneous Poisson process, the expected value of the number of product failures in the period $\left[0,w\right]$, where $w\left(>0\right)$ is a prefixed time, is $\lambda w$, following a Poisson distribution. We also assume that the agent’s repair time also follows an exponential distribution with repair rate $\mu \left(>0\right)$. Since the failure rate is constant, there is no need for preventive maintenance (Murthy & Asgharizadeh, 1999). Thus, the manufacturer and the agent only provide corrective maintenance. After the failure, repair actions are carried out.

2.2. Manufacturer, Agent and Consumer Decision Problems

The manufacturer’s expected profit is given by

$$\mathsf{{\rm E}}\left[{\mathsf{\Pi }}_M\left(P_E\right)\right]=P_E-C_P-C_{RM}\lambda L_1$$

(1)

where $C_P$ is the manufacturing costs to make the product, and $C_{RM}$ is the manufacturer’s maintenance cost for each intervention in the base warranty period. The agent’s expected profit is given by

$$\mathsf{{\rm E}}\left[{\mathsf{\Pi }}_A\left(P_{MC}\right)\right]=P_{MC}-\alpha {\mathsf{{\rm E}}}_{N\left(L-L_1\right)}\left[{\mathsf{{\rm E}}}_{Y_i-\tau }\left[{\sum }_{i=0}^{N\left(L-L_1\right)}max\left(0,Y_i-\tau \right)|N\left(L-L_1\right)\right]\right]-C_A\lambda \left({L-L}_1\right)$$

(2)

where $N\left(L-L_1\right)$ is a random variable that indicates the number of product failures over $[L_1,L)$, and $C_A$ is the agent’s repair cost for each intervention. The expression $\alpha {\mathsf{{\rm E}}}_{N\left(L-L_1\right)}\left[{\mathsf{{\rm E}}}_{Y_i-\tau }\left[\sum _{i=0}^{N\left(L-L_1\right)}max\left(0,Y_i-\tau \right)|N\left(L-L_1\right)\right]\right]$ represents the expected value of the financial compensation to be received by the consumer related to the penalty time. Formally, this double expectation is the expected value of the penalty time conditional on the number of product failures during the product’s residual life $(L_1,L)$. It is formulated under the concept of the law of total expectation from conditional expectation (Ross, 2014), i.e., the number of product failures affects the penalty time.

The consumer is interested in purchasing a single unit of the good in question. We assume that, after the base warranty period, the consumer does not abandon the item after the failure, i.e., the product owner buys the maintenance services from the agent. Therefore, the consumer’s expected profit is given by

$$\mathsf{{\rm E}}\left[{\mathsf{\Pi }}_C\left({P_E,P}_{MC}\right)\right]=RL+\alpha {\mathsf{{\rm E}}}_{N\left(L-L_1\right)}\left[{\mathsf{{\rm E}}}_{Y_i-\tau }\left[{\sum }_{i=0}^{N\left(L-L_1\right)}max\left(0,Y_i-\tau \right)|N\left(L-L_1\right)\right]\right]-P_E-P_{MC}.$$

(3)

To effectively analyze the decision problems of the manufacturer, agent, and consumer, several key assumptions are established to define the underlying conditions and relationships in the models: (1) All decision-makers seek to maximize their payoff functions (expected profit). Furthermore, the consumer’s satisfaction is maximized by buying the product with maintenance services. (2) Since the players’ payoff functions are profit functions, they are risk-neutral. (3) All elements of the game are known (complete information) by the players. (4) The repair times (manufacturer and agent) are infinitesimal concerning mean times between failures, being negligible compared to the product’s lifetime. Moreover, under the homogeneous Poisson process, the type of repair is perfect. Hence, after each repair, the condition of the repaired item is assumed to be as good as new (Murthy & Blischke, 2006). (5) The repair costs (labor + material) incurred by the manufacturer and the agent do not change over $L$.

Repair times are negligible compared to the equipment’s lifetime. However, these times affect the penalty time incurred by the agent. This assumption is also seen in Ashgarizadeh and Murthy (2000) and Murthy and Asgharizadeh (1998, 1999).

2.3. Game Setting and Equilibrium

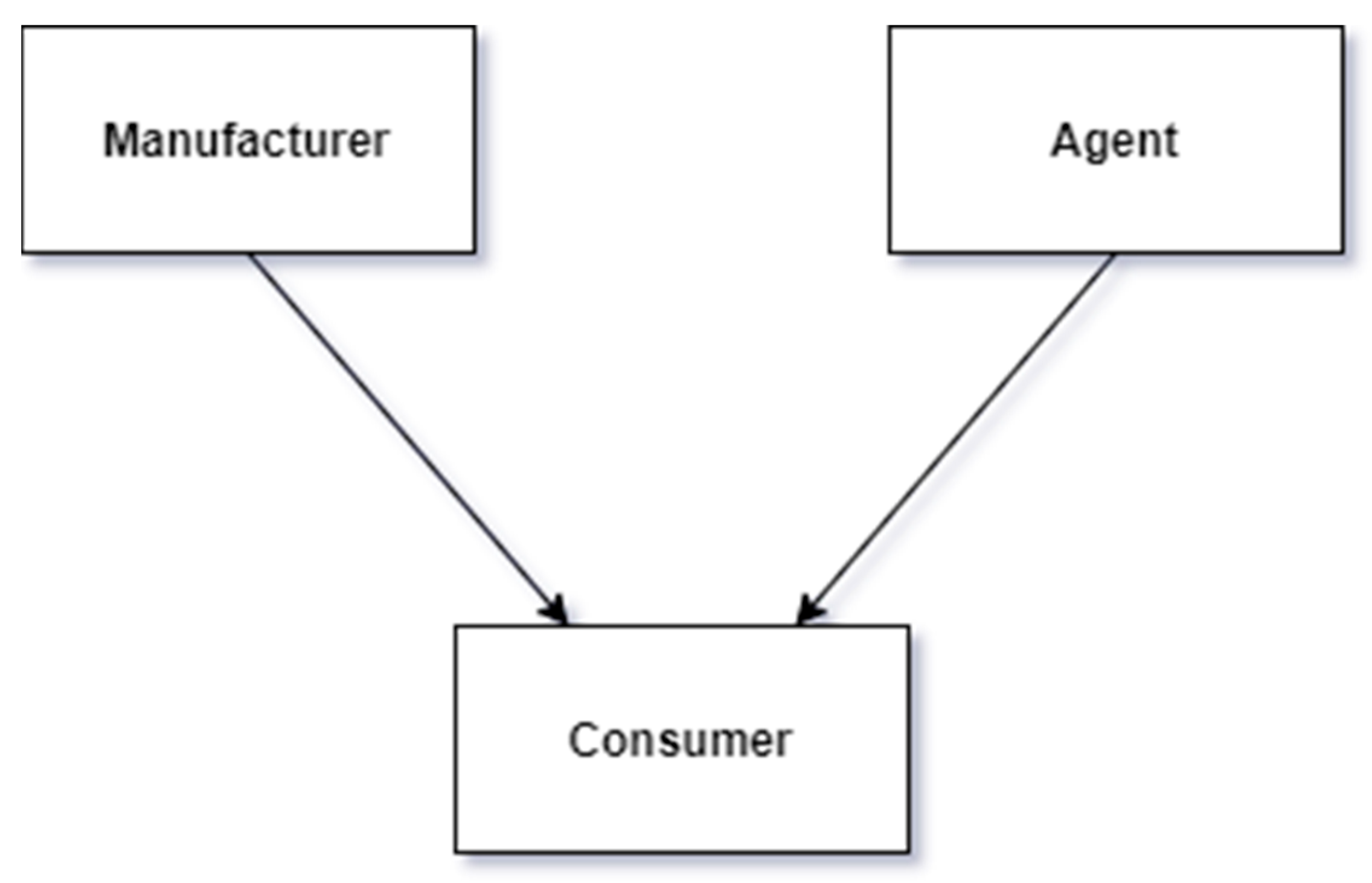
The model is a hierarchical system, a Stackelberg two-leader game, seen in Figure 2. The arrows from the manufacturer and the agent toward the consumer imply the dependence relationship. Formally, the consumer’s strategy is subordinated to the manufacturer’s and the agent’s strategies. The payoff for all decision-makers depends only on the consumer’s decision, which is a function of $P_E$ and $P_{MC}$.

In the upper level, the manufacturer selects a value of $P_E$, and the agent chooses a value of $P_{MC}$. Next, based on these prices, the consumer makes a decision. The consumer does not obtain the item if their expected payoff is negative, indifferent if their expected profit is zero. Finally, if their expected gain is positive, the consumer acquires the product with maintenance services.

The equilibrium is reached via a mix of cooperative and non-cooperative solutions. For every fixed pair $\left(P_E,P_{MC}\right)$, the consumer gives a reply, evaluating their payoff function to decide whether to buy the product with maintenance services or not. For this part, equilibrium strategies can be formulated via the subgame-perfect Nash equilibrium (Mazalov, 2014; Petrosyan & Zenkevich, 2016).

The manufacturer and the agent face a pricing problem. As they operate at the same level, they can form a coalition. The equilibrium prices and the payoffs are computed via the Shapley value: an allocation scheme that provides a unique solution to the coalition, measuring the marginal contribution for each decision-maker with efficiency, symmetry, null player, and additivity properties (Shapley, 1951; Sun & Sun, 2018; Maschler et al., 2020).

Before calculating the Shapley, it is necessary first to set up the characteristic function for each sub-coalition. For two players, there are four sub-coalitions: grand coalition (manufacturer and agent), empty coalition (no player), manufacturer, and agent. The payoff received by the manufacturer is $P_E$. We define their characteristic function as the least price that the manufacturer is willing to sell the product, including warranty costs during period $L_1$, i.e., break-even price (Samuelson et al., 2021). Therefore, the manufacturer’s characteristic function is given by

$$\mathrm{V}\left(M\right)=C_P+C_{RM}\lambda L_1$$

(4)

where $\mathrm{V}\left(M\right)$ is the manufacturer’s characteristic function. The payoff received by the agent is $P_{MC}$. We define their characteristic function as the least price that the agent is willing to offer to the consumer for maintenance services, i.e., the penalty and repair costs. Therefore, the agent’s characteristic function is given by

$$\mathrm{V}\left(A\right)=\alpha {\mathsf{{\rm E}}}_{N\left(L-L_1\right)}\left[{\mathsf{{\rm E}}}_{Y_i-\tau }\left[{\sum }_{i=0}^{N\left(L-L_1\right)}max\left(0,Y_i-\tau \right)|N\left(L-L_1\right)\right]\right]+C_A\lambda \left({L-L}_1\right)$$

(5)

where $\mathrm{V}\left(A\right)$ is the agent’s characteristic function. The characteristic function of the grand coalition is defined when the consumer surplus is zero due to the summation of the manufacturer’s and agent’s prices $\left(P_E,P_{MC}\right)$. As a result, its payoff is the maximum total profit available. The grand coalition’s characteristic function is given by

$$\mathrm{V}\left(M,A\right)=RL-C_P-C_{RM}\lambda L_1-C_A\lambda \left(L-L_1\right)$$

(6)

where $\mathrm{V}\left(M,A\right)$ is the characteristic function of the grand coalition formed by the manufacturer and the agent. Finally, the empty coalition does not include any decision-maker, and its payoff is zero. Through the Shapley value, the marginal contribution for each decision-maker is calculated, representing the equilibrium payoff. Let $S_{HM}$ be the manufacturer’s expected payoff and $S_{HA}$ be the agent’s expected payoff, where

$$S_{HM}={\displaystyle \frac{V\left(M\right)+V\left(M,A\right)-V\left(A\right)}{2}}$$

(7)

and

$$S_{HA}={\displaystyle \frac{V\left(A\right)+V\left(M,A\right)-V\left(M\right)}{2}}$$

(8)

The manufacturer’s and the agent’s equilibrium prices are ${\overline{P}}_E$ and ${\overline{P}}_{MC}$, respectively. ${\overline{P}}_E$ is defined via Equations (1) and (7), and ${\overline{P}}_{MC}$ is given by Equations (2) and (8):

$${\overline{P}}_E=S_{HM}+C_P+C_{RM}\lambda L_1$$

(9)

and

$${\overline{P}}_{MC}=S_{HA}+\alpha {\mathsf{{\rm E}}}_{N\left(L-L_1\right)}\left[{\mathsf{{\rm E}}}_{Y_i-\tau }\left[{\sum }_{i=0}^{N\left(L-L_1\right)}max\left(0,Y_i-\tau \right)|N\left(L-L_1\right)\right]\right]+C_A\lambda \left({L-L}_1\right)$$

(10)

Under this context, the summation of ${\overline{P}}_E$ and ${\overline{P}}_{MC}$ is equal to the consumer surplus. This cooperation (manufacturer and agent) is like a monopolist applying first-degree price discrimination (Varian & Varian, 1992).

3. Simulation Approach and Application

The simulation is applied to estimate the expected value of the penalty time incurred by the agent. It involves two random variables: the number of product failures after $L_1$ and the repair time.

The simulation of the number of product failures follows the approach seen in Ross (2014): failure times are generated after $L_1$, and the number of claims is recorded. For each product failure, a repair time is generated and compared with $\tau$. If the time difference is positive, then it is stored; otherwise zero is assigned. The summation of the penalty times represents the total penalty time. The algorithm reported in Algorithm 1 details the steps of the simulation (pseudocode).

Algorithm 1. Simulation of the penalty time.

Data:  (simulationDuration, λ, μ, τ)    simulationDuration—Total simulation time    λ—Failure rate (Exponential distribution)    μ—Repair rate (Exponential distribution)    τ—Threshold time for penalty   Result: numberOfFailures, totalPenaltyDuration   1  numberOfFailures ← 0 2  totalPenaltyDuration ← 0 3  currentTime ← 0 4  while currentTime ≤ simulationDuration do 5   timeBetweenFailures ← Exponential(λ) 6   currentTime ← currentTime + timeBetweenFailures 7   if currentTime > simulationDuration then 8     break 9   end if 10       numberOfFailures ← numberOfFailures + 1 11       repairTime ← Exponential(μ) 12       if repairTime > τ then 13     penalty ← repairTime - τ 14       else 15     penalty ← 0 16       end if 17       totalPenaltyDuration ← totalPenaltyDuration + penalty 18 end while 19 return (numberOfFailures, totalPenaltyDuration)

The algorithm computes one replica (an individual penalty). Therefore, to estimate the expected value of the penalty time, the Monte Carlo simulation approach (Hillier, 2005) is applied. The following numerical application is carried out to illustrate the game equilibrium. The nominal values for the model’s parameters are as follows: L = 45,000 (hours), $L_1=8500$ (hours), $\lambda =0.0008$ (per hour), $\mu =0.02$ (per hour), $\tau =70$ (hours), $C_P=300\left({10}^3\mathrm{\$}\right)$, $\alpha =0.06\left({10}^3\mathrm{\$}\right)$, $R=0.015$(${10}^3\mathrm{\$}$ per hour), $C_A=5\left({10}^3\mathrm{\$}\right)$, and $C_{RM}=4\left({10}^3\mathrm{\$}\right)$.

Table 1. Expected value of the reliability-related performance measures.

$\mathit{E}\left[\mathit{N}\left({\mathit{L}}_1\right)\right]$	$\mathit{E}\left[\mathit{N}\left(\mathit{L}-{\mathit{L}}_1\right)\right]$	$\mathit{E}\left[\mathit{P}\mathit{e}\mathit{n}\mathit{a}\mathit{l}\mathit{t}\mathit{y}\mathit{T}\mathit{i}\mathit{m}\mathit{e}\right]$
6.8	29.2	357.82 (hours)

presents the expected value of the reliability-related performance measures. The Monte Carlo sample size for simulating the penalty time is 10,000.

Furthermore, the results for ${\overline{P}}_E=507.965\left({10}^3\mathrm{\$}\right)$ and ${\overline{P}}_{MC}=188.504\left({10}^3\mathrm{\$}\right).$ Through these equilibrium prices, the manufacturer’s expected profit is $180.765\left({10}^3\mathrm{\$}\right)$, and the agent’s expected profit is $21.035\left({10}^3\mathrm{\$}\right)$. Based on this price combination, the manufacturer and the agent extract the consumer surplus. In equilibrium, the consumer is indifferent between purchasing and not purchasing the product with maintenance services.

A sensitivity analysis is performed to investigate the equilibrium prices, the average penalty time, the expected value of the number of product failures, and the manufacturer’s and the agent’s expected profit for different values of $\lambda$. The summary of these results can be seen in

Table 2. Effect of $\lambda$ on the model.

Metrics	$\mathit{\lambda }=0.0002$	$\mathit{\lambda }=0.0004$	$\mathit{\lambda }=0.0008$	$\mathit{\lambda }=0.001$
$\mathsf{{\rm E}}\left[N\right(L_1\left)\right]$	$1.7$	$3.4$	$6.8$	$8.5$
$\mathsf{{\rm E}}\left[N\right(L-L_1\left)\right]$	$7.3$	$14.6$	$29.2$	$36.5$
$\mathsf{{\rm E}}\left[Penaltytime\right]$	$90.97$h	$179.82$ h	$357.82$ h	$450.15$ h
${\overline{P}}_E$	$605.071\left({10}^3\$\right)$	$572.705\left({10}^3\$\right)$	$507.965\left({10}^3\$\right)$	$475.496\left({10}^3\$\right)$
${\overline{P}}_{MC}$	$75.387\left({10}^3\$\right)$	$113.084\left({10}^3\$\right)$	$188.504\left({10}^3\$\right)$	$226.514\left({10}^3\$\right)$
$\mathsf{{\rm E}}\left[{\Pi }_M\left(P_E\right)\right]$	$298.271\left({10}^3\$\right)$	$259.105\left({10}^3\$\right)$	$180.765\left({10}^3\$\right)$	$141.496\left({10}^3\$\right)$
$\mathsf{{\rm E}}\left[{\Pi }_A\left(P_{MC}\right)\right]$	$33.429\left({10}^3\$\right)$	$29.295\left({10}^3\$\right)$	$21.035\left({10}^3\$\right)$	$17.005\left({10}^3\$\right)$

.

Table 2 shows that $\mathsf{{\rm E}}\left[PenaltyTime\right]$, $\mathsf{{\rm E}}\left[N\left(L_1\right)\right]$, $\mathsf{{\rm E}}\left[N\left(L-L_1\right)\right]$, and ${\overline{P}}_{MC}$ increase and ${\overline{P}}_E$ decreases as $\lambda$ increases. Furthermore, when the equipment’s reliability decreases ($\lambda$ increases), the manufacturer and the agent’s maximum expected profit also reduces. As a result, when the reliability is low, the players’ payoff decreases since their costs increase. We mention that ${\overline{P}}_{MC}$ increases as $\lambda$ increases since this price includes the cost of the penalty time that also increases with $\lambda$.

4. Conclusions

This paper presented a three-level service contract defined under a hierarchical structure for a manufacturer, an agent, and a consumer. The provision of the base warranty serves to encourage the consumer to purchase the product, and maintenance services provided by the agent after the base warranty period aim to ensure the consumer retains the item throughout its lifetime. The proposed model illustrates how the manufacturer and the agent can collaboratively establish pricing strategies to capture consumer surplus. In this approach, the equilibrium prices for the sale of the product, including base warranty costs and maintenance services, are determined using the Shapley value to provide a unique solution that highlights the marginal contribution of each decision-maker.

The game theory approach was applied due to the presence of many participants with different goals and strategies. The cooperative game established a coalition between the manufacturer and the agent that competes against the consumer (non-cooperative approach). For a given price structure $\left(P_E,P_{MC}\right)$, the consumer replies, buying or not buying the product with maintenance services. As a result, the non-cooperative approach is via a sequential game whose solution is via the subgame-perfect Nash equilibrium. Combining cooperative and non-cooperative game theory elements characterized equilibrium strategies that supported allocating the gains from coalition formation. The results demonstrate how coordination between the manufacturer and the agent can lead to optimized pricing strategies and improved profit-sharing outcomes, offering a useful theoretical contribution to the literature on warranty pricing and service contracts.

Some of the limitations in this work are discussed as follows. First, the model assumes complete and symmetric information. Extending the framework to incorporate asymmetric information on product quality or repair costs can allow for the exploration of screening or signaling contracts. Second, our model assumes a homogeneous consumer with fixed willingness to pay. Future work can introduce consumer heterogeneity and competing service offerings, potentially embedding an endogenous demand function to enrich the pricing dynamics. Third, the current model is static and does not account for dynamic reliability degradation or pricing adjustments over time. A multi-period or repeated game formulation could capture these aspects more realistically.

Moreover, the model employs a simplified reliability structure based on a homogeneous Poisson process. Future research may adopt more advanced reliability models and consider condition-based maintenance strategies. In addition, the sensitivity analysis on individual parameters requires more comprehensive robustness assessments to further strengthen the model’s applicability. Additionally, empirical calibration using real warranty and cost data would be valuable for validating the model and benchmarking predicted outcomes against observed market behaviors. Finally, the policy and welfare implications of coordinated versus competitive pricing regimes remain an open question that can inform regulatory discussions and consumer protection frameworks.

Other interesting extensions can be modeling the manufacturer and the agent interaction with only one warranty option or additional warranty options with different coverage mechanisms and decision variables—such as $L_1$—and considering the risk parameter to model the players’ preferences as seen in Ashgarizadeh and Murthy (2000); Esmaeili et al. (2014); Murthy and Asgharizadeh (1998, 1999). We view these limitations not as shortcomings, but as opportunities to extend the theoretical foundation laid in this paper. Each of these directions would require distinct modeling techniques, richer datasets, and a shift in analytical focus, and are therefore left for future investigation.

The decision-making process can be further enriched by incorporating two distinct maintenance agents, allowing the consumer to select one for the provision of maintenance services following the expiration of the base warranty period. This extension can transform the model into a four-player framework, comprising a manufacturer, two maintenance agents, and a consumer. Such a configuration should offer deeper insights into competitive dynamics between maintenance agents, fostering a more comprehensive understanding of pricing strategies, service quality differentiation, and the resulting consumer behavior, also facilitating the exploration of equilibrium outcomes under varying market conditions and service contracts, contributing to consumer-oriented service policies.