“Anything Goes” in an Ultimatum Game?
Abstract
1. Introduction
- (U.1)
- All logically possible pure strategies (“anything goes”), so that the game is an n-piece Unrestricted UG;
- (U.2)
- Threshold strategies, so that the game is an n-piece Threshold RUG;
- (U.3)
- Singleton strategies where the Recipient accepts only exact offers, so that the game is an n-piece Singleton Restricted Ultimatum Game (hereafter Singleton RUG), and
- (U.4)
- Range strategies where the Recipient accepts only offers lying within a given “connected” range, so that the game is an n-piece Range Restricted Ultimatum Game (hereafter Range RUG).
2. Related Evolutionary Ultimatum Game Studies
3. Ultimatum Game Families


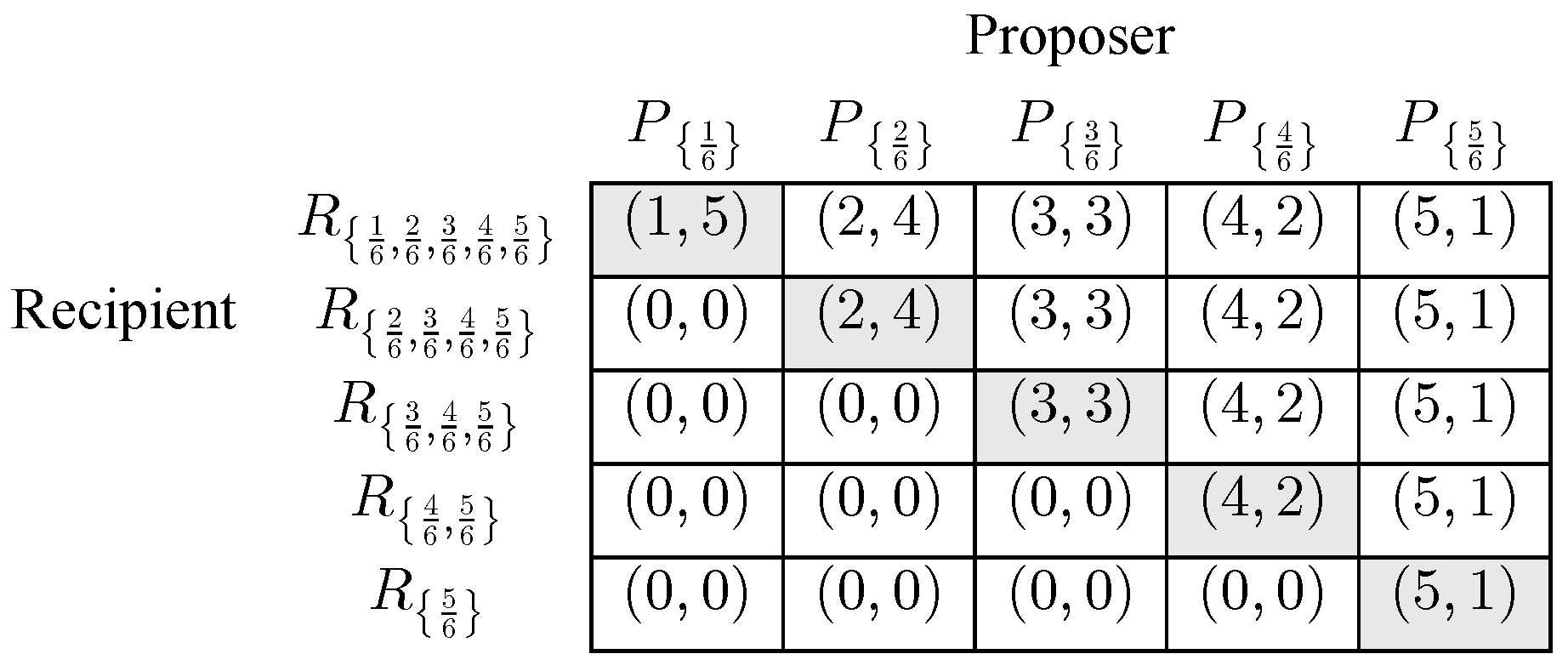
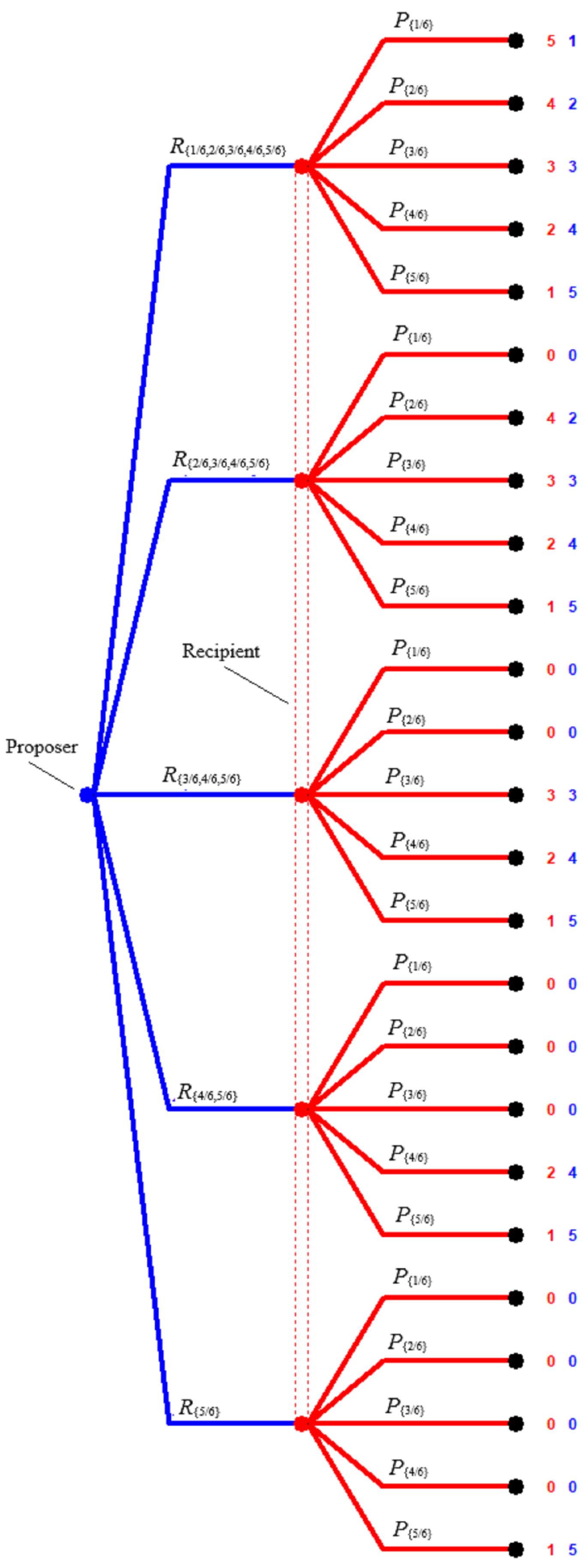

4. Evolutionary Dynamics Applied to -Piece Ultimatum Games
4.1. Description of the Replicator Dynamic Model
4.2. Description of the Computer Simulations
- (U.1)
- The n-piece Unrestricted UG;
- (U.2)
- The n-piece Threshold RUG;
- (U.3)
- The n-piece Singleton RUG; and
- (U.4)
- The n-piece Range RUG.
- (i)
- The deterministic replicator dynamic;
- (ii)
- The -perturbed replicator dynamic;
- (iii)
- The -perturbed replicator dynamic; and
- (iv)
- The -perturbed replicator dynamic.
4.2.1. Five-Piece Ultimatum Games
4.2.2. Ten-Piece Ultimatum Games
5. Discussion
5.1. Relationship of the Section 4 Replicator Dynamic Model to Previous Studies
5.2. The Significance of the Section 4 Simulation Results
6. A Continuum of Ultimatum Games
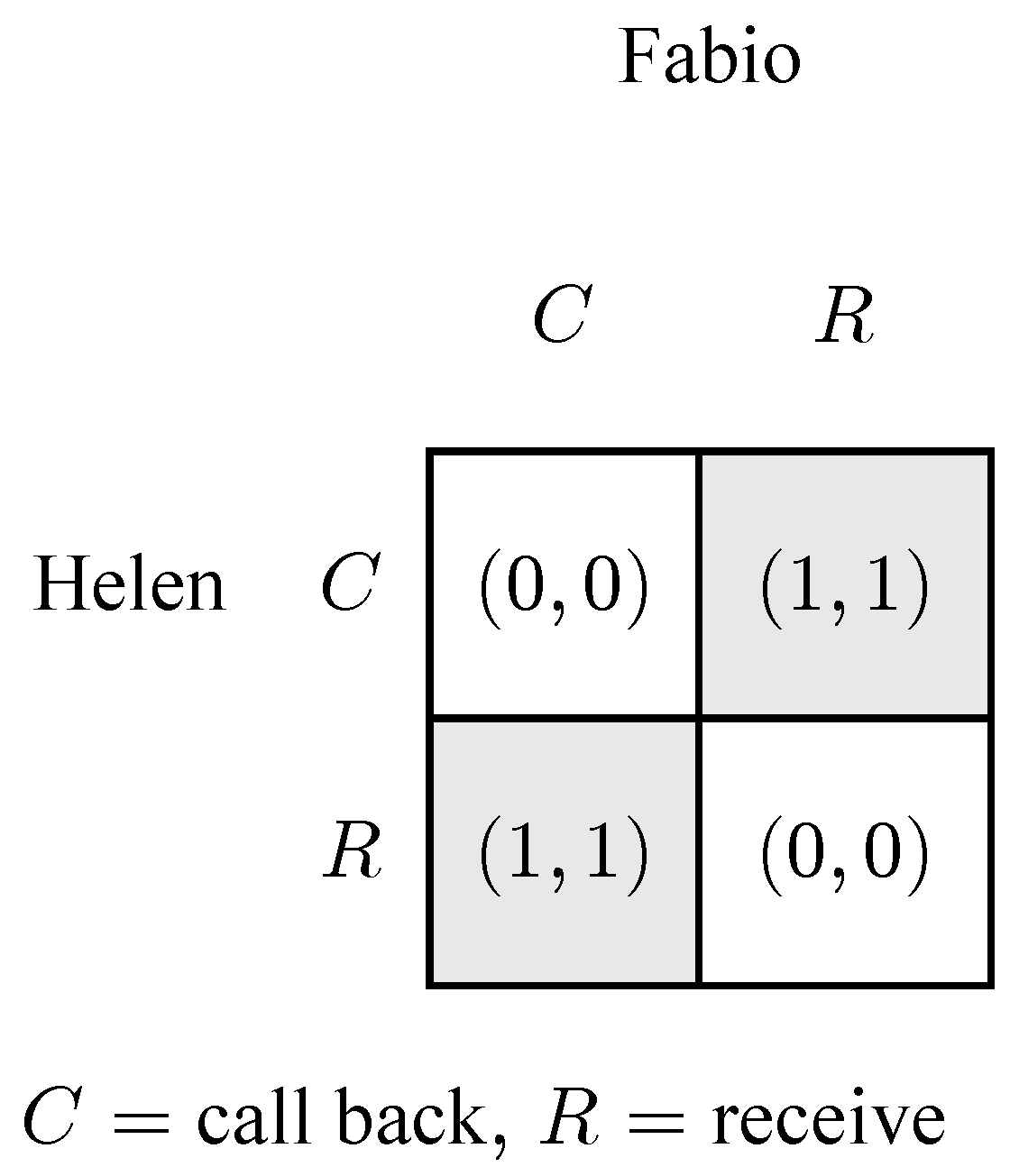
- C when I am the original caller, and R otherwise.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | In this round, all but one Proposer offered or more of the sum at stake, and this share was always at least 1 mark. The exceptional Proposer offered of 5 marks, and the Recipient spurned. Of the five cases where Recipients spurned an offer of at least 1 mark, in four of these cases, the Proposer offered or less. |
| 2 | Camerer (2003, p. 72) reports that market integration is an index that combines the existence of a national language, the existence of a labor market for cash wages, and the existence of farming of crops for cash. |
| 3 | Camerer (2003, p. 49) notes that cueing the subjects this way elicits information regarding likely responses to all offers. |
| 4 | In a survey of recent evolutionary game theory work on Ultimatum Games, Debové, Baumard, and André give a definition of a threshold strategy and then discuss all of the works of this survey in terms of this definition (Debove et al., 2016). |
| 5 | Here, I follow the practice of previous Ultimatum Game studies such as Roth and Erev (1995) and Gale et al. (1995) and refer to a Nash equilibrium where a Recipient accepts any positive offer as subgame perfect. In Section 3, I explain why I think this is a slight but harmless abuse of terminology. |
| 6 | In this paper I will limit my discussion to Ultimatum Games where Z is a finite set, which reflects the conditions of most Ultimatum Game experiments where the good at stake is a sum of money divisible up to only finitely many increments. Of course one can also define Continuous Ultimatum Games where Z = [0, 1] or some infinite proper subset of [0, 1]. |
| 7 | While the Proposer moves first, for strategic form representations, it is convenient to arrange the pure strategy profiles and payoff vectors in this manner, which, following the usual conventions of game theory, makes the Recipient the row player and the Proposer the column player in a strategic form representation of an Ultimatum Game. |
| 8 | If an Agent j in a game has the pure strategy set , then denotes a mixed or partially mixed strategy for Agent j, where Agent j chooses with probability . |
| 9 | denotes the column vector transpose of the ordered n-tuple . |
| 10 | In fact, in (1), one of the n equations is redundant, and in (2), one of the m equations is redundant because and are equivalent to probability distributions and are thus fully determined by of the equations of (1) and of the equations of (2). |
| 11 | The code of these simulators and the simulation data are available from the author upon request. |
| 12 | Some of my own preliminary simulations on Ultimatum Games confirm one of Gale et al.’s (1995) findings in their analysis. Gale et al. (1995) discovered that the Proposers and the Recipients can tend to learn very slowly according to their 2-population replicator dynamic models and only might reach a final limit after many cycles of learning. Similarly, in their reinforcement learning simulations, Roth and Erev (1995) found that Proposers and Recipients can learn only very slowly to reach an equilibrium in an Ultimatum Game, and in their simulations, they allow the reinforcement learning to run for time cycles. In some preliminary simulations, I also found that the Proposers and the Recipients tend to learn slowly according to (1) and (2), which is why I chose the high number of 5000 time cycles for each orbit for the simulations discussed in this paper. |
| 13 | Interestingly, Gale et al. (1995) acknowledge that the full set of possible Recipient strategies are functions of the form , and they note that this is an unmanageably large strategy set. They immediately limit Recipient pure strategies to the 40 threshold strategies, resulting in a Threshold RUG. Indeed, the corresponding Unrestricted UG has pure Recipient strategies. |
| 14 | If one goes even further and considers or , then the results are degenerate games where the Recipient has no strategy option at all. If one sets , then the Recipient rejects all offers, so that there is effectively only one possible outcome where for any . If , then the Recipient can only accept all offers, and the resulting degenerate game is a Dictator Game. Experimental research on Dictator Games complements the experimental research on Ultimatum Games. Camerer (2003, pp. 56–58) summarizes the best-known results of Dictator Game experiments. |
| 15 | A proposition A is common knowledge among the members of a group if each member knows that all know A and knows that all can infer the consequences of this mutual knowledge. Lewis (1969, p. 56–57) presented one of the first analyses of common knowledge. |
| 16 | Note that, for each of these profiles, the Proposer’s and the Recipient’s pure strategies are parts of Nash equilibria. Therefore, each of these profiles is compatible with common knowledge of Bayesian rationality and the payoff structure of the game, the defining conditions of rationalizability. For example, for the nonequilibrium profile , and are corresponding Nash equilibria. Suppose the Proposer’s conjecture is that she believes with probability one that the Recipient will follow his part of and the Recipient’s conjecture is that he believes with probability one that the Proposer will follow her part of . Then is a best response for the Proposer and is a best response for the Recipient; therefore, is rationalizable. |
| 17 | See especially A Treatise of Human Nature (Hume, 1739–1740/2000), Book III, Part I, Sections 1–3 and An Enquiry Concerning the Principles of Morals (Hume, 1751/1998), Section III, Part II and Appendix III. |
| 18 | |
| 19 |
References
- Aumann, R. J. (1974). Subjectivity and correlation in randomized strategies. Journal of Mathematical Economics, 1(1), 67–96. [Google Scholar]
- Aumann, R. J. (1987). Correlated equilibrium as an expression of Bayesian rationality. Econometrica: Journal of the Econometric Society, 55, 1–18. [Google Scholar]
- Bernheim, B. D. (1984). Rationalizable strategic behavior. Econometrica: Journal of the Econometric Society, 52, 1007–1028. [Google Scholar]
- Bicchieri, C. (2005). The grammar of society: The nature and dynamics of social norms. Cambridge University Press. [Google Scholar]
- Camerer, C. (2003). Behavioral game theory: Experiments in strategic interaction. Princeton University Press. [Google Scholar]
- Debove, S., Baumard, N., & André, J.-B. (2016). Models of the evolution of fairness in the ultimatum game: A review and classification. Evolution and Human Behavior, 37(3), 245–254. [Google Scholar]
- Fehr, E., & Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. The Quarterly Journal of Economics, 114(3), 817–868. [Google Scholar]
- Gale, J., Binmore, K. G., & Samuelson, L. (1995). Learning to be imperfect: The ultimatum game. Games and Economic Behavior, 8(1), 56–90. [Google Scholar]
- Gintis, H., Bowles, S., Boyd, R., & Fehr, E. (2005). Moral sentiments and material interests: Origins, evidence, and consequences. In Moral sentiments and material interests: The foundations of cooperation in economic life. The MIT Press. [Google Scholar] [CrossRef]
- Güth, W., & Kocher, M. G. (2014). More than thirty years of ultimatum bargaining experiments: Motives, variations, and a survey of the recent literature. Journal of Economic Behavior & Organization, 108, 396–409. [Google Scholar]
- Güth, W., Schmittberger, R., & Schwarze, B. (1982). An experimental analysis of ultimatum bargaining. Journal of Economic Behavior & Organization, 3(4), 367–388. [Google Scholar]
- Harms, W. (1997). Evolution and ultimatum bargaining. Theory and Decision, 42, 147–175. [Google Scholar]
- Henrich, J., Boyd, R., Bowles, S., Camerer, C., Fehr, E., Gintis, H., & McElreath, R. (2001). In search of homo economicus: Behavioral experiments in 15 small-scale societies. American Economic Review, 91(2), 73–78. [Google Scholar]
- Henrich, J., Boyd, R., Bowles, S., Camerer, C., Fehr, E., Gintis, H., McElreath, R., Alvard, M., Barr, A., Ensminger, J., Henrich, N. S., Hill, K., Gil-White, F., Gurven, M., Marlowe, F. W., & Tracer, D. (2005). “Economic man” in cross-cultural perspective: Behavioral experiments in 15 small-scale societies. Behavioral and Brain Sciences, 28(6), 795–815. [Google Scholar] [PubMed]
- Henrich, J., Ensminger, J., Barr, A., & McElreath, R. (2014). Major empirical results: Markets, religion, community size, and the evolution of fairness and punishment. In Experimenting with social norms: Fairness and punishment in cross-cultural perspective (pp. 89–148). Russell Sage Foundation. [Google Scholar]
- Hume, D. (1998). David hume: An enquiry concerning the principles of morals: A critical edition (T. L. Beauchamp, Ed.). Clarendon Press. (Original work published 1751). [Google Scholar]
- Hume, D. (2000). A treatise of human nature: Being an attempt to introduce the experimental method of reasoning into moral subjects (D. F. Norton, & M. J. Norton, Eds.). Oxford University Press. (Original work published 1739–1740). [Google Scholar]
- Lewis, D. K. (1969). Convention: A philosophical study. Wiley-Blackwell. [Google Scholar]
- Mehta, J., Starmer, C., & Sugden, R. (1992). An experimental investigation of focal points in coordination and bargaining: Some preliminary results. In Decision making under risk and uncertainty: New models and empirical findings (pp. 211–219). Springer. [Google Scholar]
- Mehta, J., Starmer, C., & Sugden, R. (1994a). Focal points in pure coordination games: An experimental investigation. Theory and Decision, 36, 163–185. [Google Scholar]
- Mehta, J., Starmer, C., & Sugden, R. (1994b). The nature of salience: An experimental investigation of pure coordination games. The American Economic Review, 84(3), 658–673. [Google Scholar]
- Pearce, D. G. (1984). Rationalizable strategic behavior and the problem of perfection. Econometrica: Journal of the Econometric Society, 52, 1029–1050. [Google Scholar]
- Roth, A. E., & Erev, I. (1995). Learning in extensive-form games: Experimental data and simple dynamic models in the intermediate term. Games and Economic Behavior, 8(1), 164–212. [Google Scholar]
- Schelling, T. C. (1980). The strategy of conflict: With a new preface by the author. Harvard University Press. [Google Scholar]
- Skyrms, B. (2014). Evolution of the social contract (2nd ed.). Cambridge University Press. [Google Scholar]
- Vanderschraaf, P. (1995). Convention as correlated equilibrium. Erkenntnis, 42(1), 65–87. [Google Scholar]
- Vanderschraaf, P. (2018). Strategic justice: Convention and problems of balancing divergent interests. Oxford University Press. [Google Scholar]
- Young, H. P. (1998). Individual strategy and social structure: An evolutionary theory of institutions. Princeton University Press. [Google Scholar]

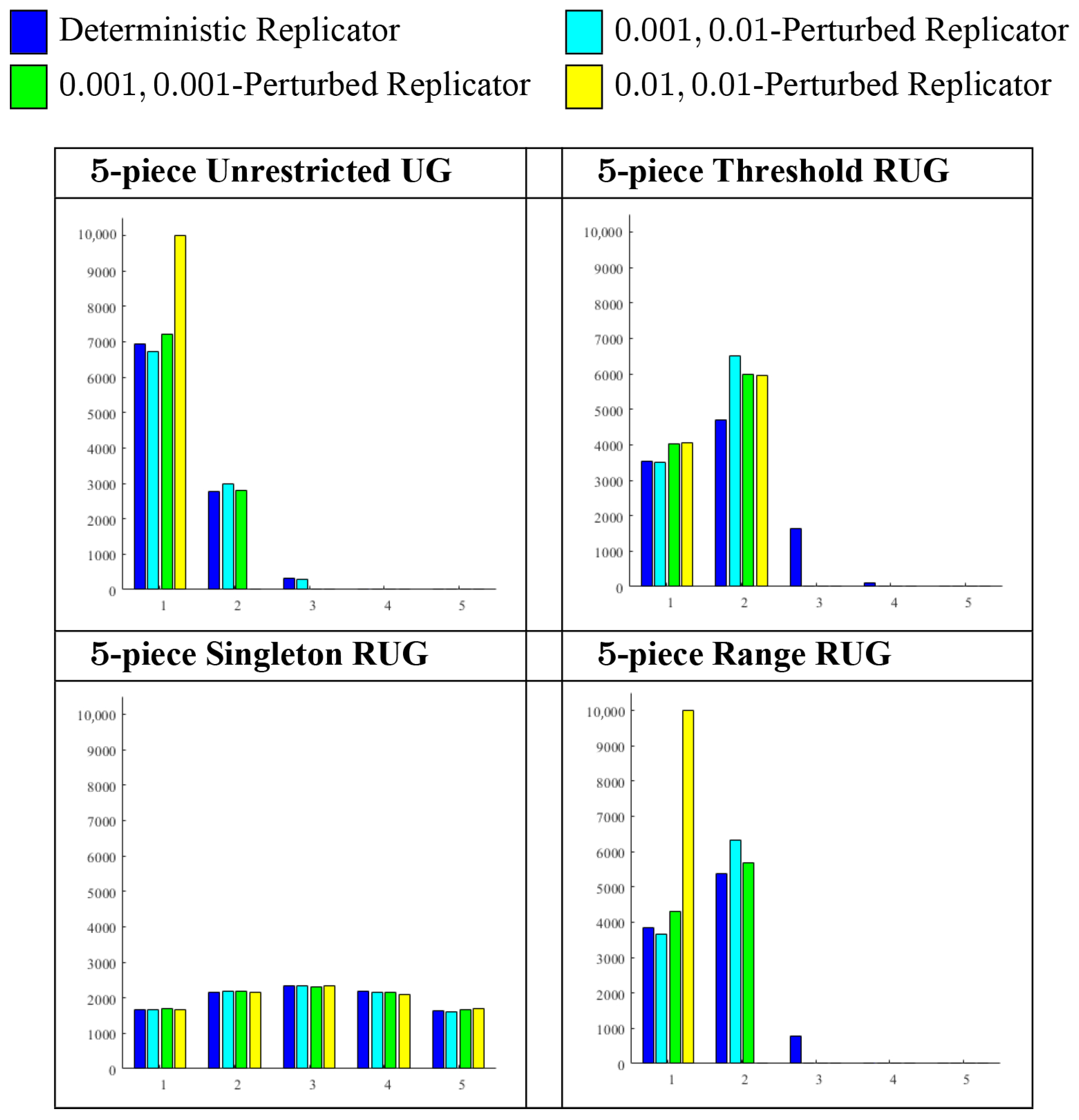

| , -Perturbed Replicator Dynamics | ||||
|---|---|---|---|---|
| Unrestricted UG | 1.0 | 1.0 | 0.9999 | 1.0 |
| Threshold RUG | 1.0 | 1.0 | 1.0 | 0.9999 |
| Singleton RUG | 1.0 | 1.0 | 1.0 | 1.0 |
| Range RUG | 1.0 | 1.0 | 1.0 | 1.0 |
| , -Perturbed Replicator Dynamics | |||||
|---|---|---|---|---|---|
| Proposer | |||||
| Offer | |||||
| Unrestricted UG | 0.6298 | 0.6712 | 0.7206 | 1.0 | |
| 0.2756 | 0.2982 | 0.2793 | 0.0 | ||
| 0.0314 | 0.0306 | 0.0 | 0.0 | ||
| 0.0002 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| Threshold RUG | 0.3540 | 0.3495 | 0.4030 | 0.4095 | |
| 0.4709 | 0.6505 | 0.5970 | 0.5954 | ||
| 0.1643 | 0.0 | 0.0 | 0.0 | ||
| 0.0108 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| Singleton RUG | 0.1637 | 0.1622 | 0.1670 | 0.1706 | |
| 0.2193 | 0.2173 | 0.2147 | 0.2104 | ||
| 0.2328 | 0.2339 | 0.2306 | 0.2355 | ||
| 0.2170 | 0.2187 | 0.2185 | 0.2169 | ||
| 0.1672 | 0.1679 | 0.1692 | 0.1666 | ||
| Range RUG | 0.3851 | 0.3667 | 0.4314 | 1.0 | |
| 0.5363 | 0.6333 | 0.5686 | 0.0 | ||
| 0.0767 | 0.0 | 0.0 | 0.0 | ||
| 0.0019 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| , -Perturbed Replicator Dynamics | ||||
|---|---|---|---|---|
| Unrestricted UG | 0.9996 | 0.9998 | 0.9998 | 0.9999 |
| Threshold RUG | 1.0 | 1.0 | 0.9995 | 1.0 |
| Singleton RUG | 0.9780 | 1.0 | 1.0 | 1.0 |
| Range RUG | 0.9989 | 0.9988 | 0.9995 | 0.9988 |
| , -Perturbed Replicator Dynamics | |||||
|---|---|---|---|---|---|
| Proposer | |||||
| Offer | |||||
| Unrestricted UG | 0.4714 | 0.4515 | 0.4622 | 0.4578 | |
| 0.3448 | 0.3627 | 0.3614 | 0.3609 | ||
| 0.1544 | 0.1501 | 0.1530 | 0.1575 | ||
| 0.0290 | 0.0272 | 0.0231 | 0.0236 | ||
| 0.0 | 0.0005 | 0.0001 | 0.0001 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| Threshold RUG | 0.1050 | 0.1000 | 0.1052 | 0.1076 | |
| 0.3168 | 0.3163 | 0.4139 | 0.8924 | ||
| 0.3464 | 0.3529 | 0.4788 | 0.0 | ||
| 0.1846 | 0.2308 | 0.0016 | 0.0 | ||
| 0.0430 | 0.0 | 0.0 | 0.0 | ||
| 0.0041 | 0.0 | 0.0 | 0.0 | ||
| 0.0001 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| Singleton RUG | 0.0066 | 0.0686 | 0.0672 | 0.0673 | |
| 0.0931 | 0.0986 | 0.0961 | 0.1003 | ||
| 0.1227 | 0.1208 | 0.1218 | 0.1252 | ||
| 0.1332 | 0.1355 | 0.1297 | 0.1377 | ||
| 0.1375 | 0.1367 | 0.1399 | 0.1363 | ||
| 0.1276 | 0.1297 | 0.1357 | 0.1348 | ||
| 0.1188 | 0.1278 | 0.1277 | 0.1218 | ||
| 0.1047 | 0.1084 | 0.1036 | 0.1036 | ||
| 0.0744 | 0.0739 | 0.0783 | 0.0730 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| Range RUG | 0.0231 | 0.0215 | 0.1052 | 0.0220 | |
| 0.4285 | 0.4098 | 0.4139 | 0.9768 | ||
| 0.4412 | 0.4697 | 0.4788 | 0.0 | ||
| 0.0998 | 0.0978 | 0.0016 | 0.0 | ||
| 0.0062 | 0.0 | 0.0 | 0.0 | ||
| 0.0001 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
| 0.0 | 0.0 | 0.0 | 0.0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanderschraaf, P.P. “Anything Goes” in an Ultimatum Game? Games 2025, 16, 36. https://doi.org/10.3390/g16040036
Vanderschraaf PP. “Anything Goes” in an Ultimatum Game? Games. 2025; 16(4):36. https://doi.org/10.3390/g16040036
Chicago/Turabian StyleVanderschraaf, Peter Paul. 2025. "“Anything Goes” in an Ultimatum Game?" Games 16, no. 4: 36. https://doi.org/10.3390/g16040036
APA StyleVanderschraaf, P. P. (2025). “Anything Goes” in an Ultimatum Game? Games, 16(4), 36. https://doi.org/10.3390/g16040036






