Abstract
Herein, we further examine how we can value nonmarket goods and services by considering the costs associated with environmental conflicts. Focusing on two American rules—the asymmetric reimbursement system and the contingent fee contract—we develop a strategic game-theoretic model in which a citizens group engages a delegate through a contingent fee compensation contract, while a polluter engages a delegate through an hourly fee compensation contract. If the citizens group prevails, the polluter is obligated to contribute a portion of the contingent fee. Solving for the subgame perfect equilibrium, two results emerge. First, the 4x-rule can be maintained through the adjustment of the asymmetric reimbursement system. Second, the asymmetric reimbursement system can serve both as a supplementary method to measure nonmarket valuation and to reduce the rent dissipation resulting from environmental conflicts under general circumstances.
Keywords:
asymmetric reimbursement; contingent fee; environmental conflict; nonmarket valuation; rent dissipation JEL Classification:
D72; K41
1. Introduction
The value of nonmarket goods, such as environmental protection and reduced risks to life and well-being, have typically been estimated by using either revealed or stated preference methods (Freeman et al., 2014). Revealed preferences use people’s choices within markets to back out nonmarket values from actual choices, whereas stated preferences use public opinion surveys asking each person to state their value for a nonmarket good directly or indirectly. There is, however, a significant gap between the atomistic person operating in a market and the isolated individual answering questions in their own home that has not been sufficiently addressed—strategic interaction in contests, and how competitors choose to expend valuable resources in fighting over securing the rights to natural resources or defending themselves in natural resource damage lawsuits, can be used to reveal nonmarket values. One exception is Lim and Shogren (2005), who explore how the expenditures of participants in a contest or environmental conflicts can signal preferences for nonmarket goods. In Lim and Shogren (2005), they demonstrated that the baseline costs incurred by the parties in environmental conflicts represent roughly 1/4 of the value of a nonmarket good or service, which they call the 4x-rule. Lim and Shogren (2005) introduced real-world cases, including classic conflicts in the United States such as the Superfund cleanup, the Exxon Valdez natural resource damage, and state tobacco lawsuits over premature deaths, to illustrate the application of the 4x-rule in environmental conflicts (see pp. 254–255). Furthermore, they found that expenditures related to environmental conflicts are unsuitable to measure nonmarket values when differences exist in the abilities of delegates and the values that disputants attribute to the environment.
Herein, we explore the method of using actual choices made within environmental conflicts to estimate the value of nonmarket goods through the ex post revealed preferences method. Our study differs from Lim and Shogren (2005) in two aspects. First, we consider whether the asymmetric reimbursement adopted by the U.S. federal courts can serve as a mechanism to maintain the 4x-rule. The asymmetric reimbursement regime is a system in which, in the case of a successful claim by the victim of pollution, the polluter is required to pay a portion of the victim’s costs. If the polluter prevails, the victim is not obligated to pay the polluter’s costs (Baik & Shogren, 1994; Cherry & Cotten, 2012; Chassé, 2019; Park & Settle, 2023). We find that asymmetric reimbursement can serve as a mechanism to maintain the 4x-rule. Second, we examine whether asymmetric reimbursement, taking into account contingent fees, can mitigate rent dissipation. Baik and Shogren (1994) demonstrated that asymmetric reimbursement increases rent dissipation due to environmental conflicts by encouraging rent-seeking behavior. Our results suggest that the adoption of asymmetric reimbursement in environmental conflicts can reduce rent dissipation in the context of delegate-meditated environmental conflicts.
To establish our results, we examine the prevailing delegate compensation systems in lawsuits in the United States. In this system, the citizens group (a pollution victim) employs their delegate under a contingent fee contract, while the firm (a polluter) hires their delegate under an hourly fee contract (Baik & Kim, 2001; Baik & Kim, 2007; Park, 2022).1 When the citizens group prevails, the firm is obligated to pay the group an asymmetric reimbursement corresponding to a portion of the contingent fee (Park & Settle, 2023).2 We provide a more comprehensive analysis of the effects and implications of the asymmetric reimbursement regime by examining environmental conflicts considering the role of delegates. We contribute to the understanding of how the asymmetric reimbursement regime and the use of delegates can establish the 4x-rule and reduce rent dissipation in environmental conflicts.
The paper proceeds as follows. Section 2 develops the American-style contingent fee contract and asymmetric reimbursement system. In these American rules, the delegate of the citizens group works under a contingent fee, while the delegate of the firm works under an hourly fee. If the citizens group wins, they are reimbursed for a portion of the contingent fee. We demonstrate that the two rules can adhere to the 4x-rule. In Section 3, we examine whether the application of the two American rules can reduce social waste. Total effort level and rent dissipation are used as measures to quantify social waste. Section 4 offers a summary and concluding remarks.
2. Subgame Perfect Equilibrium and the 4x-Rule
Consider an environmental conflict in which two players, 1 (a firm) and 2 (a citizens group), compete for an environmental lawsuit worth v. Player 1 values the lawsuit’s worth as 1 (v = 1), and player 2 evaluates it as k ≥ 1. Each player hires a delegate who represents him in a Tullock-type legal contest. Delegate 1, hired by player 1, works on an hourly fee basis. Delegate 2, hired by player 2, works on a contingent fee basis and earns the contingent fee av (=a) only if player 1 wins the lawsuit worth v = 1, where 0 < a < 1 (Baik & Kim, 2001, 2007; Baumann & Friehe, 2012; Park, 2022; Park & Settle, 2023). Let x1 be delegate 1’s effort level and x2 be delegate 2’s, and let p1 be the probability of player 1 winning the lawsuit worth v = 1 and p2 = 1 − p1 be the probability of player 2 winning k ≥ 1. Now, p1 is defined by the Tullock-type contest success function represented by
where 0 < σ ≤ 1, which implies the contest ability of delegate 1 is at least equal to that of delegate 2 (Tullock, 1980). Let π1 denote the expected payoff for player 1. The expected payoff for the player is
wherein 0 < b < 1 represents the rate of asymmetric reimbursement, δx1 is the hourly fee for delegate 1, and μx1 is the monitoring cost of player 1. To meet delegate 1’s participation requirement, which ensures a non-negative payoff for delegate 1, the hourly fee rate δ should be set at a minimum of 1. The monitoring rate μ > 0 is needed to respond to delegate 1’s moral hazard (Baik & Kim, 2001; Baik & Kim, 2007; Park, 2022). To simplify, we substitute h with the expression δ + μ: h = δ + μ > 1.
p1(x1, x2) = x1/(x1 + σx2) for x1 + x2 > 0
= 1/2 for x1 + x2 = 0,
= 1/2 for x1 + x2 = 0,
π1 = p1(1 − [δ + μ]x1) + p2( − [δ + μ]x1 − abk)
= p1(1 + abk) − [δ + μ]x1 − abk,
= p1(1 + abk) − [δ + μ]x1 − abk,
The expected payoff for the hourly-fee-based delegate 1 is
wherein δ > 1. If delegate 1, who is compensated on an hourly basis, were to choose the effort level himself, he could increase the effort level indefinitely to maximize his expected payoff, or he could falsely report the effort level. Therefore, player 1 chooses and monitors delegate 1’s effort level.
G1 = (δ − 1)x1,
Next, consider the expected payoff for player 2. Let π2 denote the expected payoff for player 2. The expected payoff for the player is assumed to be given by
wherein [1 − b]a < 1, which is the condition for player 2 to participate in the environmental conflict. According to this condition, player 1 can set the contingent fee rate higher than 1 to maximize his expected payoff. Put differently, this implies that the contingent fee rate can be set such that the resulting contingent fee amount exceeds k. The reason is that if player 1 wins, a portion of the contingent fee is reimbursed by player 2. Therefore, Equation (4) raises doubts as to whether an asymmetric reimbursement system could lead to significant rent dissipation in environmental conflicts. This study shows that if a regulator adopts an asymmetric reimbursement system to maintain the 4x-rule, it both leads to a realistic range for the contingent fee rate and reduces rent dissipation.
π2 = p2(k + abk − ak)
= p2(1 − [1 − b]a)k,
= p2(1 − [1 − b]a)k,
The expected payoff for the contingent fee-based delegate 2 is
G2 = p2(ak − x2) + p1( – x2)
= p2ak − x2.
= p2ak − x2.
Park and Settle (2023) assume that player 1 participates directly in environmental conflicts without hiring his own delegate. In contrast, this study assumes that player 1 hires delegate 1 on an hourly basis. Based on this assumption, this study determines the value b corresponding to changes in h, k, and σ to maintain the 4x-rule. This study differs from Baik and Shogren (1994), Cherry and Cotten (2012), and Chassé (2019), in which players 1 and 2 participate directly in environmental conflicts without hiring their own delegates. This study also differs from Baik and Min (2025), in which the winning player receives a portion of his delegate’s effort level from the losing player. We view our model as more appropriate than these previous models in Baik and Shogren (1994), Cherry and Cotten (2012), Chassé (2019), and Baik and Min (2025) that consider reimbursement in two aspects. First, in most lawsuits, players hire delegates, and on an hourly basis, the monitoring costs should be considered. Second, under the asymmetric reimbursement system used in the United States, only the legal fees that citizens pay to their attorneys are eligible for recovery (see Park and Settle (2023)). In our study, the players receive a portion of the legal costs they paid, not a portion of the legal effort levels put in by their delegates.
The game has two stages. In the first stage, player 2 determines the contingent fee fraction a and publicly announces it. In the second stage, player 1 and delegate 2 play simultaneously. Player 1 chooses delegate 1’s effort level, while delegate 2 chooses his own effort level. This study solves for subgame perfect equilibrium using backward induction. We assume this framework is common knowledge among players 1 and 2 and their delegates.
Lemma 1 reports the outcomes in the subgame perfect equilibrium of the game.
Lemma 1.
In the subgame perfect equilibrium,
- (a)
- The contingent fee fraction isa** = (–(1 − b) + ((1 − b)([1 − b] + k[b + σh]))1/2)/(k [1 − b][b + σh]).
- (b)
- Delegate 1 and delegate 2 exertx1** = a**kσ(1 + a**bk)2/(1 + a**k[b + σh])2 and
x2** = (a**k)2σh(1 + a**bk)/(1 + a**k[b + σh])2. - (c)
- The expected payoff for player 1 isπ1** = ((1 + a**bk(2 + a**k[b − 2σh]) − (a**k)3bσh)[2b + σh])/(1 + a**k[b + σh])2.
- (d)
- The expected payoffs for player 2 and delegate 2 areπ2** = a**k2σh(1 − a**[1 − b])/(1 − a**k[b + σh]) and
G2** = (a**k)3(σh)2/(1 + a**k[b + σh])2.
Using Lemma 1, we find the asymmetric reimbursement fraction for maintaining the 4x-rule considering asymmetric abilities, prizes, and delegation contracts (see Table 1, Table 2, Table 3 and Table 4). Note the 4x-rule is set based on the effort level of delegate 1. The effort level of delegate 2 is specified in Table 1, Table 2, Table 3 and Table 4.

Table 1.
Results of asymmetric reimbursement for maintaining the 4x-rule (k = 1).

Table 2.
Results of asymmetric reimbursement for maintaining the 4x-rule (k = 2).

Table 3.
Results of asymmetric reimbursement for maintaining the 4x-rule (k = 3).

Table 4.
Results of asymmetric reimbursement for maintaining the 4x-rule (k = 4).
Next, we examine whether the equilibrium contingent fee in Lemma 1 is realistic. In the United States, the maximum feasible percentage the client can give the delegate is often dictated by legal restrictions on the contingent fee (which prohibit fees exceeding 50 percent). According to early work by Bebchuk and Emons (1996) and Emons (2000), the contingent fee fraction for compensatory damages in the United States in legal disputes regarding accidental injuries ranges from 0.33 to 0.4. However, based on Table 1, Table 2, Table 3 and Table 4, we can infer that cases exist in which a exceeds 0.5 and goes beyond 1 (e.g., a** = 1.619 for k = 1, σ = 0.2, and h = 1). As defined in Equation (4), one key justification for allowing reimbursement when the contingent fee can exceed the prize is that player 2 can receive it if he wins. The detailed explanation is as follows. As shown in (4), if player 2 wins k, his net cost is [1 − b]ak. Therefore, if 1 > [1 − b]a, player 2’s expected payoff is greater than zero (see (4)). Additionally, as seen in (5), the contingent fee for delegate 2 is ak. The higher the value of a, the more effort delegate 2 exerts. Considering this, player 2 can set a value greater than 1 under the condition [1 − b]a to maximize his expected payoff, π2. In the event of player 2 winning, he will obtain a portion of the contingent fee. Even if he sets the contingent fee higher than the prize he receives, he can still earn a positive expected payoff.
A question arises—does an asymmetric reimbursement rate, considering a realistic contingent fee, maintain the 4x-rule? This is difficult to answer directly because there is no available data related to this question. Baik and Kim (2007) and Park (2022) assumed σ to be 1 and h to be between 1.78 and 3, because within that range the plaintiff and the defendant can hire delegates to increase their expected payoffs. Hansler et al. (1991) found that the contingent fee fraction ranges from a low of 0.25 to a high of 0.40 in accidental injury suits in the United States. If we assume σh to be between 1.78 and 3 in this study, the contingent fee fraction corresponds appropriately to 0.249 to 0.410, which is a realistic result (see Table 1, Table 2, Table 3 and Table 4). Although Hansler et al. (1991) did not examine the range of the contingent fee in environmental conflicts, the results of this study are reliable in that the contingent fee rate derived in this study is consistent with that used in the previous study.
Next, we consider the range of the asymmetric reimbursement rate to maintain the 4x-rule. Table 1, Table 2, Table 3 and Table 4 show that the asymmetric reimbursement rate to maintain the 4x-rule satisfies the range between 0 and 1: 0 < b < 1. With our assumption of 0.178 < σh < 3, the reimbursement rate corresponds appropriately to 0.002 to 0.192 (see Table 1, Table 2, Table 3 and Table 4). In the tables, we observe that as the prize k determined by player 2 increases, the corresponding value of b to maintain the 4x-rule also increases.
Finally, Table 1, Table 2, Table 3 and Table 4 demonstrate that the equilibrium delegate 2’s effort level to maintain the 4x-rule can exceed 0.250, but under the assumption of 0.178 < σh < 3, it is shown to be less than 0.250. Proposition 1 reports our key result related to the 4x-rule.
Proposition 1.
The system of asymmetric reimbursement with a contingent fee contract can be used as a supplementary means to measure nonmarket valuation.
Proposition 1 demonstrates that the 4x-rule can be sustained through a system of asymmetric reimbursement combined with a contingent fee contract. For instance, Lim and Shogren (2005) state: “The 4x-rule underestimates value when … the downward bias accentuates as the citizen group’s relative valuation increases” (pp. 256–257). In this system, when σh = 2.8 and k = 1, the 4x-rule holds at b = 0.031 (Table 1). Furthermore, the 4x-rule continues to hold at b = 0.035 even as the citizens group’s relative valuation increases to k = 2 (Table 2).
3. Total Effort and Rent Dissipation
Previous studies considering asymmetric reimbursement have shown that this rule increases social costs. The rationale behind this is that asymmetric reimbursement plays an intermediary role in increasing the size of the citizens group’s and the firm’s prizes (Baik & Shogren, 1994; Cherry & Cotten, 2012; Chassé, 2019). Now, we explore whether asymmetric reimbursement for maintaining the 4x-rule leads to social waste. Social waste can be defined as two types: the total effort level (TE) and rent dissipation (RD). The first is the sum of the effort levels of the two delegates: TE** = x1** + x2**. Using Lemma 1, we obtain
TE** = a**kσ(1 + a**bk)(1 + a**k[b + h])/(1 + a**k[b + σh])2.
In the benchmark model by Lim and Shogren (2005), the equilibrium effort level of each player is 0.250. This effort level defines the 4x-rule. Here, the total effort of the players is 0.5. Table 1, Table 2, Table 3 and Table 4 demonstrate that in most cases, asymmetric reimbursement corresponding to contingent fees can reduce the total effort—and it always decreases the total effort when 0.178 < σh < 3.
Next, we consider rent dissipation (RD), defined as follows:
RD** = (a**bk + hx1** + x2**)/(p1**[1 + a**bk] + p2**[1 + a**b]k).
At the numerator in (7), the expenditure of player 1 corresponds to a**bk + hx1** and the expenditure of delegate 2 corresponds to x2**. At the denominator, the revenue of player 1 is p1**(1 + a**bk), the revenue of player 2 is p2**(1 − a**[1 − b])k, and the revenue of delegate 2 is p2**a**k. The sum of the revenues corresponds to the denominator of rent dissipation. In the benchmark model by Lim and Shogren (2005), rent dissipation is also 1/2. Table 1, Table 2, Table 3 and Table 4 demonstrate that asymmetric reimbursement corresponding to contingent fees reduces rent dissipation when 0.178 < σh < 3.
Proposition 2 summarizes the result.
Proposition 2.
The system of asymmetric reimbursement can reduce the social waste caused by environmental conflicts.
Unlike previous studies by Baik and Shogren (1994), Cherry and Cotten (2012), and Chassé (2019), this study proposes that delegate 2, hired on a contingent fee, does not directly receive asymmetric reimbursement but indirectly receives it through contingent fees (Park & Settle, 2023). That is, asymmetric reimbursement is distributed to player 2 and delegate 2 through contingent fees. In situations in which asymmetric reimbursement is not adopted, the social costs incurred when the players directly engage in environmental disputes can be greater compared to the social costs incurred in disputes in which player 2 hires delegate 2 on a contingent fee contract, as is the case with the adoption of asymmetric reimbursement.
Following the estimation of linear regression models predicting the contingent fee, total expenditures, and rent dissipation (a, TE, and RD) based on the explanatory variables of the rate of asymmetric reimbursement, the value to player 2, and the delegation costs to player 1 weighted by contest ability (b, k, and σh), we conducted a Monte Carlo simulation to examine the potential values of a, TE, and RD under specific conditions (see Table 5 and Table 6). The simulation procedure involved calculating the predicted means of a, TE, and RD using the estimated regression coefficients for given values of the independent variables and adding a random error term. This error term was drawn from a normal distribution with a mean of zero and a standard deviation equal to the estimated root mean squared error (RMSE) of the regression model. In one simulation process, the resulting simulated values for a, TE, and RD were calculated as 0.431, 0.458, and 0.344. We now compare our results to two benchmarked games: no-delegation/no-reimbursement (TENN and RDNN) and yes-delegation/no-reimbursement (TEYN and RDYN).

Table 5.
A: Results of linear regression analysis on the contingent fee, a. B: Results of linear regression analysis on total expenditures, TE. C: Results of linear regression analysis on rent dissipation, RD.

Table 6.
Descriptive statistics of simulated contingent fee, total effort, and rent dissipation (a, TE, and RD).
First, for the no-delegation/no-reimbursement benchmark, Lim and Shogren (2005) and Baik and Kim (2007) estimate that the TENN and RDNN both equal 0.5. Our TE and RD estimated values are lower: 0.458, and 0.344. Second, for the yes-delegation/no-reimbursement, in which players hire delegates with contingent-based compensation without asymmetric reimbursement, Baik and Min (2025) estimate that TEYN = 0.167 and RDYN = 0.5. While this comparison to our estimates suggests a split verdict (0.167 < 0.458 but 0.5 > 0.344), many researchers consider rent dissipation as the more appropriate measure to quantify social costs in contests, since RD accounts for exogenous variables such as prize, contingent fee, and monitoring as well as the probability of success (see Lee and Kang (1998) and Baik and Kim (2007)). If one accepts that RD is a better measure of social cost, our simulation results support the idea that the system of asymmetric reimbursement reduces the social costs induced by the environmental conflicts.
Finally, we examine the effects of changes in the rate of asymmetric reimbursement (b), the size of the prize for player 2 (k), and the cost of the delegate weighted by the contest ability (σh) on rent dissipation, RD. First, note that while the adoption of an asymmetric compensation system designed to maintain the 4x-rule lowers RD, an increase in b raises the contingent fee (a) and consequently increases RD (see Table 5A,C, and Figure 1a,c). This suggests that b should be kept low to maintain the 4x-rule, resulting in less rent dissipation, RD.
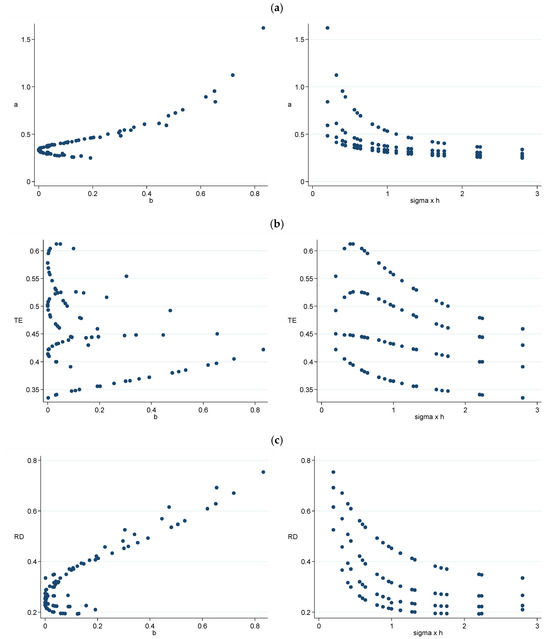
Figure 1.
(a) Changes in a depending on b and . (b) Changes in TE depending on b and . (c) Changes in RD depending on b and .
Second, we estimate that an increase in the prize for player 2 (k) lowers RD (see Table 5C and Figure 1c). In Figure 1c, an increase in k serves to shift RD downward. As the prize for player 2 increases, delegate 2’s prize (ak) also increases, leading to an increase in TE (Table 5B). In Figure 1b, an increase in k serves to shift TE upward. The magnitude of the prize increase is greater, however, which results in a decrease in RD. An increase in k increases the numerator in Equation (7), but the increase in the denominator is larger.
Finally, we estimate that an increase in σh decreases RD (see Table 5C and Figure 1c). In Figure 1c, the change in σh shifts RD downward. Unlike the change in k, an increase in σh reduces TE (Table 5B), thereby decreasing RD. That is, it decreases the numerator in Equation (7), leading to a reduction in RD.
4. Concluding Remarks
Assessing nonmarket values for environmental and natural resources is crucial today because many of nature’s most important benefits—like clean air, biodiversity, scenic beauty, and climate regulation—are not bought or sold in markets. Without proper economic-based valuation, these resources can be overlooked in policy and investment decisions. This leads to under-protection or irreversible damage, or both. Without an estimate of nonmarket values to guide informed and sustainable choices that reflect the full costs and benefits to society, people with differing views will naturally clash over the stringency of environmental regulations and laws. They will spend time, money, and political capital to influence both policy and legal outcomes. Yet, we rarely treat this costly struggle as evidence of the underlying nonmarket values that drive the conflict. Traditional valuation methods rely on markets or surveys, but the effort poured into environmental conflicts tells its own story. Using classic contest theory, we can treat the effort expended in these conflicts as signals of how much the resource is worth to different groups. In a world where the environmental stakes are rising, measuring value through effort offers a new and potentially revealing lens.
Herein, we have further explored the institutional nature of how we can assess the value of environmental goods through the expenditures of disputants in environmental conflicts. This study has examined whether two American rules can be applied to reveal preferences for nonmarket assets based on the expenditures of disputants in environmental conflicts. One of the two American rules is the asymmetric reimbursement regime adopted by the U.S. federal courts, and another is the contingent fee contract that prevails in U.S. civil disputes. Two key results emerge. First, the amalgamation of the two American rules serves as an intermediary in implementing the ex post benchmark 4x-rule, effectively mitigating the convenience disparities stemming from asymmetric contestability and prize sizing. Second, the application of these two rules has the potential to reduce the social waste arising from environmental conflicts.
This study shows how the 4x-rule can be maintained through the adjustment of the rate of asymmetric reimbursement, b. For example, when k or σh increases, the regulator should lower the rate of asymmetric reimbursement (b) to maintain the 4x-rule (see Table 1, Table 2, Table 3 and Table 4). Our study does not argue, however, that a fair-minded regulator should actually set asymmetric reimbursement rates to maintain the 4x-rule. Our work suggests that nonmarket valuation via the strategic effort invested remains a worthwhile topic for further research. One topic would be a study comparing the estimated nonmarket value of the environment based on the costs of disputes arising from a specific environmental conflict that ends up in court relative to parallel studies using the standard revealed and stated preferences methods. This work could take into consideration the asymmetric reimbursement practiced in the U.S. federal courts and the contingent fee arrangement commonly adopted by plaintiffs. This study did not empirically verify its results due to the lack of real-world data on the legal costs incurred in environmental conflicts. Although obtaining and verifying such data would be challenging, it is necessary work to expand our understanding of these approaches.
Author Contributions
Conceptualization, S.-H.P.; methodology, S.-H.P. and J.F.S.; validation, S.-H.P. and J.F.S.; formal analysis, S.-H.P.; investigation, S.-H.P. and J.F.S.; writing—original draft preparation, S.-H.P.; writing—review and editing, S.-H.P. and J.F.S.; supervision, S.-H.P. and J.F.S.; and project administration, S.-H.P. and J.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This paper relies exclusively on the results of the theoretical game-theoretic model. No data was used in any regression. As a result, there is no data to share.
Acknowledgments
We are grateful for the helpful comments provided by two anonymous referees in improving our paper.
Conflicts of Interest
The authors declare no conflicts of interest. Since this research was not funded by external sources, funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Notes
| 1 | In environmental conflicts, it is common for polluters to be large companies that establish contracts with prominent law firms based on hourly fees. In contrast, small citizens group may not have the financial resources to engage high-powered legal representatives under such fee structures. |
| 2 | Baumann and Friehe (2012) considered a model that encompasses both the American-style contingent fee system and the British-style symmetric reimbursement system. In their model, if the plaintiff prevails, the defendant is required to compensate the plaintiff with a portion of the contingent fee that the plaintiff pays his delegate. This aligns with the premise used in our study. Furthermore, they assumed that if the defendant prevails, the plaintiff should compensate the defendant with a portion of the hourly fee that the defendant pays his delegate. |
References
- Baik, K. H., & Kim, I. G. (2001). The political economy of attorneys and human resources. In K. F. Zimmermann (Ed.), Handbook of labor human resources and population economics (pp. 1–20). Springer Nature Switzerland AG. [Google Scholar]
- Baik, K. H., & Kim, I. G. (2007). Strategic decisions on lawyers’ compensation in civil disputes. Economic Inquiry, 45(4), 854–863. [Google Scholar] [CrossRef]
- Baik, K. H., & Min, D. (2025). Reimbursement in contests with bilateral delegation. Economics Letters, 253, 112371. [Google Scholar] [CrossRef]
- Baik, K. H., & Shogren, J. F. (1994). Environmental conflicts with reimbursement of citizen suits. Journal of Environmental Economics and Management, 27(1), 1–20. [Google Scholar] [CrossRef]
- Baumann, F., & Friehe, T. (2012). Contingent fees meet the British rule: An exploratory study. Public Choice, 150, 499–510. [Google Scholar] [CrossRef]
- Bebchuk, L. A., & Emons, A. T. (1996). How would you like to pay for that? The strategic effects of fee arrangements on settlement terms. Harvard Negotiation Law Review, 1(53), 53–63. [Google Scholar]
- Chassé, R. M. (2019). Strategic behavior in environmental contests with asymmetric ability and reimbursement. International Review of Law and Economics, 58, 115–126. [Google Scholar] [CrossRef]
- Cherry, T. D., & Cotten, S. J. (2012). Environmental conflicts with reimbursement: Experimental evidence. Economics Bulletin, 32(4), 3224–3232. [Google Scholar]
- Emons, W. (2000). Expertise, contingent fees, and insufficient attorney effort. International Review of Law and Economics, 20, 21–33. [Google Scholar] [CrossRef]
- Freeman, A. M., III, Herriges, J. A., & Kling, C. L. (2014). The measurement of environmental and resource values: Theory and methods. Routledge. [Google Scholar]
- Hansler, D. R., Marquis, M. S., Abrahamse, A. F., Berry, S. H., Ebener, P. A., Lewis, E. G., Lind, E. A., MacCoun, R. J., Manning, W. G., Rogowski, J. A., & Vaiana, M. E. (1991). Compensation for accidental injuries in the United States. In The institute for civil institute. The RAND Corporation. [Google Scholar]
- Lee, S., & Kang, J. H. (1998). Collective contests with externalities. European Journal of Political Economy, 14(4), 727–738. [Google Scholar] [CrossRef]
- Lim, B. I., & Shogren, J. F. (2005). Valuation by conflict. Ecological Economics, 55(2), 251–262. [Google Scholar] [CrossRef]
- Park, S.-H. (2022). Contingent fees and endogenous timing in litigation contests. European Journal of Law and Economics, 54, 453–473. [Google Scholar] [CrossRef]
- Park, S.-H., & Settle, C. E. (2023). Asymmetric reimbursement and contingent fees in environmental conflicts: Observable vs. unobservable contracts. Games, 14, 55. [Google Scholar] [CrossRef]
- Tullock, G. (1980). Efficient rent seeking. In J. Buchanan, R. Tollison, & G. Tullock (Eds.), Toward a theory of the rent-seeking society (pp. 97–112). Texas A&M University Press. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).