Procedural Information as a “Game Changer” in School Choice

Abstract

This article explores the impact of procedural information on the behavior of students under two school admission procedures commonly used in the US, the EU, and other jurisdictions: the Gale–Shapley mechanism and the Boston mechanism. In a lab experiment, I compare the impact of information about the mechanism, information about individually optimal application strategies, and information about both. I find that strategic and full information increases truth-telling and stability under the Gale–Shapley mechanism. Under the Boston mechanism, however, the adoption of equilibrium strategies remains unaffected. Contrary to the prevailing assumptions in matching theory, the Boston mechanism improves perceived fairness. These results underscore the importance of procedural transparency and suggest that eliminating justified envy may not be sufficient to foster fairness and mitigate litigation risks.

1. Introduction

One of the core challenges in the design of matching markets is to implement mechanisms that achieve stable outcomes and spur market participants to reveal their preferences truthfully. This is a particularly daunting task in matching markets, that is, markets in which prices do not determine how resources are allocated.1 Many of the procedures used in matching markets are not secured against strategic manipulations. Accordingly, many participants have an incentive to manipulate their preferences in order to improve the outcome of the respective allocation procedure.

In the context of school choice, the problem of such mechanisms is that they provide an advantage to sophisticated applicants. Under the Boston mechanism (BOS) used by Boston Public Schools until 2005, for example, applicants could gain by skipping popular schools at the expense of other applicants (Abdulkadiroğlu, 2013).2 Providing a strategic advantage to sophisticated applicants carries the risk of infringing upon equal protection rights and hampering efforts to facilitate social inclusion and promote equal opportunity, especially if these applicants belong to affluent households. While legal scholars have pointed out that school choice is far from being a boon to fairness and autonomous choice (Garnett, 2017; Minow, 2011; Rauch, 2015; Ryan & Heise, 2002), most attempts to design fairer and more efficient assignment procedures have come from market designers. Many public school districts, including Boston (Abdulkadiroğlu et al., 2005b), New Orleans (Abdulkadiroğlu et al., 2017), New York City (Abdulkadiroğlu et al., 2005a), Philadelphia, and Washington, DC, have benefited from the “market design revolution” by adopting assignment procedures that are strategy-proof and produce stable outcomes, thereby dampening the incentives to appeal assignments.

One of the core ideas underlying the adoption of these mechanisms is to create a level playing field by guaranteeing strategy-proofness for parents and students. The problem, however, is that individuals tend to manipulate their preferences even when mechanisms are strategy-proof—often even more so than under manipulable mechanisms (Cerrone et al., 2024). While participants on at least one side of the market can safely reveal their true preferences under the Gale–Shapley (GS) mechanism (Gale & Shapley, 1962) and the Top Trading Cycles (TTC) mechanism (Shapley & Scarf, 1974), evidence for attempts to game these mechanisms has been documented in various lab experiments (Calsamiglia et al., 2010; Chen & Sönmez, 2006; Klijn et al., 2013; Pais & Pintér, 2008). The static GS mechanism, in which applicants make a single decision (by submitting a complete rank-order preference list rather than sequential applications), is particularly vulnerable to preference manipulations, but it remains widely used in practice (Klijn et al., 2019). Accordingly, recent empirical evidence suggests that physicians manipulate their preferences under the National Resident Matching Program (NRMP), one of the most prominent implementations of a strategy-proof assignment procedure in the US (Rees-Jones & Skowronek, 2018).

Considering the substantial efforts put into implementing strategy-proof mechanisms, it is quite remarkable that students attempt to game the system when there is nothing to be gamed.3 One potential explanation is that knowing the rules may not be the same as understanding the rules. On the one hand, cognitive abilities are likely to determine whether students adopt an adequate strategy (see Basteck & Mantovani, 2018). On the other hand, it is far from clear whether the fairness of a mechanism should be assessed based on its allocative or incentive properties (Kamada & Kojima, 2019) rather than on its transparency. Perhaps most importantly, it is not clear whether matching mechanisms can work properly without providing comprehensible procedural information (see Guillen & Hakimov, 2018; Pathak, 2017; Rees-Jones, 2017). Tackling this conundrum, I address the following questions: what kind of procedural information do students exactly need to make better school choices, how do cognitive abilities affect these choices, and what is the impact of procedural information on the perceived fairness of the assignment procedure?

To investigate these questions, I conduct an experiment designed to identify the effects of three different information environments under two of the most commonly used mechanisms: the student-proposing GS mechanism and the BOS mechanism. Under the student-proposing GS mechanism, students are incentivized to reveal their preferences truthfully. Under the BOS mechanism, students are incentivized to adopt two different dropping strategies depending on their type. Students of the first type have an incentive to manipulate their top choice and rank a less-preferred school as the first choice on their rank-order list (skip-the-top). Students of the second type have an incentive to manipulate their second choice and rank a less-preferred school as the second choice on their rank-order list while upholding their top choice (skip-the-middle). In the first environment, students only receive information about the rules of the assignment procedure (baseline). This treatment is designed to increase the salience of the equilibrium strategy and dampen the effect of false inferences about adequate strategies. In the second environment, students only receive information about the equilibrium strategies under the respective mechanism without an explanation of the procedure (strategic information). While students are told that acting strategically will never be beneficial under the GS mechanism, they receive type-specific information about equilibrium strategies under the BOS mechanism. In the third environment, students receive full procedural information both about the procedure and the respective equilibrium strategies (combined information). This treatment mimicks the practice adopted by several US public school districts (that use the GS or the TTC mechanism and tell students not to strategize) and the German clearinghouse in charge of university admissions (that partly uses the BOS mechanism and tells students how to strategize).

I find that the truth-telling rates do not significantly differ between the GS and BOS mechanisms in the baseline treatment. Under the GS mechanism, strategic and combined information strongly increases truth-telling rates as compared to the baseline treatment. The truth-telling rates do not significantly differ between the strategic and combined information conditions. Under the BOS mechanism, the strategic and combined information conditions have a negative effect on truth-telling but no positive effect on the adoption of equilibrium strategies. While the frequency of stable matchings is extremely low (approximately 30%) in the GS baseline treatment, the strategic and combined information conditions significantly and strongly increase stability under the GS mechanism (100% and 87.50%). Moreover, cognitive reflection abilities facilitate sensible strategies only for students facing a particularly complex strategic problem, that is, students who can improve their matching by adopting a skip-the-middle strategy. Finally, my fairness measures yield results that may hint at a conundrum in law and market design: the fairness assessments are not higher under the GS mechanism. Rather, my results suggest that strategic and combined information under the BOS mechanism has a positive impact on perceived outcome fairness.

While this is the first study to investigate the relationship between different kinds of procedural information, cognitive abilities, and fairness, it is closely related to a growing strand in the literature on the impact of advice and simple mechanism descriptions (Gonczarowski et al., 2023; Katuščák & Kittsteiner, 2024; Pycia & Troyan, 2023). There is some evidence that combining a thorough explanation of the mechanism with strategic advice in the German university admission procedure increases truth-telling (Braun et al., 2014). However, the authors of that study use advice as a robustness check under a non-strategy-proof mechanism, whereas my study is intended to isolate the effect of different information environments across different mechanisms, measure the role of cognitive abilities, and evoke fairness assessments. In an investigation of the TTC mechanism, Guillen and Hing (2014) observe higher truth-telling rates when applicants receive correct strategic advice and lower truth-telling rates when the strategic advice is wrong. Similarly, Guillen and Hakimov (2018) find that descriptions of strategy-proofness entail higher truth-telling rates under the TTC mechanism, while descriptions of the mechanism decrease truth-telling rates. Finally, Ding and Schotter (2017, 2019) show that intergenerational advice and chatting through social networks have a positive effect on strategies, welfare, and stability under the GS mechanism and the BOS mechanism. However, none of these studies explore the impact of controlled strategic information on the behavior of different types of applicants, stability, and perceived fairness in a comparison of strategy-proof and non-strategy-proof mechanisms.

My study also relates to other strands in the literature on matching markets. The evidence suggests that truth-telling is sensitive to seemingly innocuous changes in the choice structure. Restricting the admissible number of schools on a rank-order list, for example, may prompt students to manipulate their preferences (Calsamiglia et al., 2010; Haeringer & Klijn, 2009).4 In addition, there is a growing body of experimental literature exploring whether a dynamic implementation of the GS mechanism may improve applicants’ comprehension of the assignment procedure. A dynamic implementation follows a step-by-step procedure in which students sequentially reveal their preferences after each rejection. Exploring a dynamic implementation of the GS mechanism, Echenique et al. (2016) find that proposers do not submit truthful offers (by skipping potential partners) and that less than 50% of the markets yield stable matching. Klijn et al. (2019) show that the dynamic student-proposing GS mechanism slightly outperforms the static implementation in terms of truth-telling, stability, and efficiency. By contrast, the results presented in this article suggest that strategic information may compensate for the weaknesses associated with static mechanism implementations.

Furthermore, evidence indicates that the choices made under matching mechanisms are sensitive to variations in the information structure. While the GS mechanism outperforms the TTC mechanism in truth-telling under incomplete information about the preferences of other applicants (Chen & Sönmez, 2006), the opposite can be observed in complete-information environments (Chen et al., 2016). Truth-telling has been shown to decrease when applicants obtain more information about other students’ preferences (Pais & Pintér, 2008; Pais et al., 2011) or strategies (Guillen & Hakimov, 2017). However, recent experimental evidence also suggests that applicants adopt the truth-telling strategy too frequently when they would be better off adopting a specific truncation strategy under the GS mechanism (Featherstone & Mayefsky, 2011). My study takes a different approach in that I manipulate information about the rules of the respective mechanism rather than information about preferences or strategies.

Finally, there is some evidence that the outcome of a matching mechanism depends on risk preferences and personality traits. For example, Klijn et al. (2013) find evidence that, under the GS mechanism, truth-telling drops as risk aversion increases, while Basteck and Mantovani (2018) show that students with lower cognitive abilities fail to strategize well under the BOS mechanism, which entails lower payoffs and over-representation at low-ranked schools. This article contributes to this literature by showing that the relevance of cognitive abilities depends on the complexity of the strategy required to achieve an individually optimal outcome.

The remainder of this article is organized as follows. In Section 2, I discuss the legal background. Section 3 presents a brief summary of the theory. Section 4 describes my experimental design and predictions. Section 5 reports the results of the experiment. Section 6 concludes.

2. Remedies to Procedural Opacity in School Choice

The remedies to tackle the problem of complex school choice procedures differ across jurisdictions. While many US public school districts have simplified their assignment procedures by adopting the GS mechanism (Section 2.1), other countries, including Germany, cling to assignment procedures based on the BOS mechanism and try to increase the transparency of their deficiencies (Section 2.2).

2.1. Designing Simplicity: The US Example

One of the key problems of the school choice procedures used in the US is the complexity of the admission criteria and assignment procedures. Many parents and applicants, especially those with a less advantaged socio-economic background, do not have the information that is necessary to engage in strategic considerations and make sensible choices (Hitzig, 2019; Minow, 2011; Ryan & Heise, 2002). While access to information and simple assignment procedures is crucial to create a level playing field, courts have avoided taking a clear position on these issues (see Parents Involved v. Seattle School District No. 1 [551 U.S. 701 (2007)]).

The first move to address concerns about transparency and fairness in assignment procedures came from the Boston School Committee in 2005. The Boston Public Schools had previously used the BOS mechanism—a mechanism that involves the immediate acceptance of student applications by schools—which is therefore vulnerable to strategic manipulations (Abdulkadiroğlu et al., 2005b). Students anticipating that they would have low chances of being admitted to their first-choice school could improve their chances of being admitted to their second-choice school by ranking it first. Students who would not strategize, ranking schools according to their true preferences, incurred the risk of losing their priority to strategizing students. This assignment procedure harmed parents who did not strategize well.

In order to eliminate the incentives to game the system and create a level playing field, the Boston Public Schools eventually adopted the student-optimal stable GS mechanism. Many other public school districts, including New York City, Chicago, and Cleveland, followed and abolished assignment procedures based on the BOS mechanism (Pathak & Sönmez, 2013). In England, assignment procedures based on the BOS mechanism—procedures using the first-preferences-first criterion—were first outlawed in 2007 (Pathak & Sönmez, 2013). Under Section 1.9.c of the 2014 School Admissions Code, first-preferences-first remains outlawed as an oversubscription criterion in England.5

The problem of these reforms is that they are incomplete. School choice requires informed decisions. Yet, the mere introduction of strategy-proof mechanisms may be insufficient to create a level playing field if parents and applicants do not understand the incentives set by the assignment procedure. Nudging parents through the default options is not the only solution to this problem (Rauch, 2015). In fact, it is far from clear whether nudges that do not provide specific information actually enable parents to make informed decisions at all. To mitigate the problem of incomplete information, many US public school districts using strategy-proof procedures provide specific information about the strategic implications of the assignment procedures used. More specifically, applicants are told that attempts to game the assignment procedure by not ranking schools according to their true preferences are not individually beneficial.

The Office of the State Superintendent of Education in the District of Columbia, for example, provides the following information:

“Developed specifically for My School DC by the Institute for Innovation in Public School Choice (IIPSC), the lottery is based on the Nobel Prize-winning work of economist Al Roth of Stanford University. (…) The two most important things to know about the program are: (1) Students should rank schools in the order they like most to increase their chances of being matched to their desired school. (2) Students who apply early get no advantage in the matching process. (…) This is why the system is strategy-proof—and why students are best served by ranking schools according to their true choices”.6

The Office of Access and Enrollment in the Chicago Public Schools System provides comparable procedural information:

“The selection process is designed to give you your most preferred option. It places you in line for every program you apply to based on your lottery number or point total. It then looks for the highest ranked program that you’re eligible for and that has open seats. (…) Rank each program according to your honest order of preference. Don’t rank your first choice as number two or three with the belief that the “odds” are better at a “safe” school”.7

Not all public school districts using strategy-proof assignment procedures provide procedural information (an overview of information provided by other public school districts can be found in Appendix A). Moreover, even those that do often do not make it very salient. This is likely to work to the detriment of uninformed or unsophisticated parents and applicants who do not know where to search for procedural information in the first place. It is therefore not clear what the impact of procedural information is, especially when search costs are high. Furthermore, even if parents and applicants end up stumbling upon the information, it is questionable whether they will trust it and rank schools accordingly.8

2.2. Explaining Complexity: The German Example

The German university admission procedure for medical school illustrates the economic and legal problems of non-strategy-proof matching mechanisms (Braun et al., 2010, 2014; Westkamp, 2013). The tools to reduce the adverse impact of complexity and facilitate sensible choices when submitting rank-order lists over universities are therefore quite different from those discussed in the context of school choice in the US. Rather than telling students not to strategize, the university admissions clearinghouse (Stiftung für Hochschulzulassung) tells students how to strategize. The reason for pointing students to the possibility of gaming the admission procedure mainly stems from the implementation of two sequential mechanisms.

The first mechanism is centralized and operated by the university admissions clearinghouse (centralized mechanism). The objective of the centralized mechanism is to provide an advantage to top students and increase their chances of being admitted to a university of their preferred choice. To achieve this objective, university admissions law sets a top student quota.9 According to the Constitutional Court, considering high school grades as the main admission criterion in the centralized mechanism is compatible with freedom of profession and the right to equal protection under Art. 12 Section 1 and Art. 3 Section 1 of the German Constitution (BVerfG, 19 December 2017—1 BvL 3/14, 1 BvL 4/14, paras. 127–138).10 Students are ranked according to their high school grade from best to worst. Eligible students are selected according to their rank on the grade-order list until the number of selected students is equal to the number of seats in the top student quota. Finally, students are assigned to seats using the BOS mechanism.

The second mechanism is decentralized and operated by the universities once the first mechanism has been implemented (university mechanism). The objective of the university mechanism is to increase the chances of all remaining students being admitted to their preferred university. To achieve this objective, each university sets a quota (residual quota). Students are ranked according to the priorities determined by each university. While admission criteria vary across universities, most weight is usually given to high school grades. The pool of eligible students includes both top students who were not assigned a seat in the centralized mechanism and the remaining students. Top students who were assigned a seat in the centralized mechanism do not participate in the second mechanism. All top students are allowed to submit two different rank-order lists (one for each mechanism) since they can be assigned seats both in the centralized and university mechanisms. Eligible students are selected according to university priorities until all the seats available under the residual quota have been assigned. Finally, students are assigned to seats using the university-proposing GS mechanism.11

The problem of this sequential procedure is that it is highly vulnerable to gaming. Since the admission procedure consists of two different mechanisms, top students have to consider their chances of being admitted under each mechanism. If top students submit a long rank-order list in the centralized mechanism, they run the risk of being matched with a university that is low on their rank-order list, while they could have been matched with a more preferred university in the university mechanism (Braun et al., 2010; Westkamp, 2013).12 Therefore, top students can improve their chances of being matched with one of their preferred universities if they truncate their rank-order list for the centralized mechanism by ranking only a few top choices.

To facilitate the strategic considerations that students need to grapple with, the clearinghouse provides explicit information about some of the strategic implications of the procedure by telling top students how they can benefit from manipulating their rank-order lists. More specifically, top students are told that they should consider truncating their rank-order list in the centralized mechanism and only rank the most preferred universities.13 Students who do not strategize accordingly incur the risk of foregoing a preferred seat under the university mechanism. However, it is not clear whether procedural information can effectively compensate for the inequalities between sophisticated and unsophisticated students arising from the use of non-strategy-proof mechanisms. While this article does not explore information about a truncation strategy, it follows the general spirit of the German practice and investigates the impact of information about a dropping strategy.

3. Theory

Consider a school choice problem with a non-empty finite set of students $I=\{i_1,i_2,\dots ,i_n\}$ and a non-empty finite set of schools $U=\{u_1,u_2,\dots ,u_m\}$, where, in general, the number of students and schools need not be equal (i.e., n and m may differ). Each student $i\in I$ has a strict preference ordering ${\succ }_i$ over the set of schools combined with the option of remaining unmatched, that is, over $U\cup \{\varnothing \}$. Define the profile ${\succ }_I:={\left\{{\succ }_i\right\}}_{i\in I}$. Let ${⪰}_i$ be the weak extension of ${\succ }_i$: $a{⪰}_{i}b$ iff $a=b$ or $a{\succ }_{i}b$. Each school $u\in U$ has a weak (i.e., complete, transitive) priority relation ${⪰}_u$ over the set of students I. Its strict and indifferent parts are $i{\succ }_{u}j:\iff i{⪰}_{u}j\wedge \neg \left(j{⪰}_{u}i\right)$ and $i{\sim }_{u}j:\iff i{⪰}_{u}j\wedge j{⪰}_{u}i$. Write ${⪰}_U:={\left\{{⪰}_u\right\}}_{u\in U}$ for the profile of school priorities and let $q_u\in {\mathbb{N}}_{>0}$ be each school’s capacity.

The school choice problem is thus given by $P=({\succ }_I,{⪰}_U,{\left\{q_u\right\}}_{u\in U})$. A matching is a mapping $\mu :I\to U\cup \{\varnothing \}$, which assigns each student to a school or to the unmatched option, with the following feasibility condition: for each school $u\in U$, define $\mu \left(u\right)=\{i\in I:\mu (i)=u\}$. Then, the matching $\mu$ must satisfy $\left|\mu \left(u\right)\right|\le q_u$. That is, no school admits more students than its quota.

A simple—and stylized—representation of a matching is given by the following table, where several students may be assigned to the same school and unmatched students (if any) can be listed separately:

$$\mu =\left(\begin{array}{ccccc}{i}_1& i_2& i_3& ⋮& i_n\\ u_1& u_2& u_1& ⋮& u_n(\mathrm{or}\varnothing )\end{array}\right)$$

In this stylized representation, it is understood that n may be greater than 4 and that some students might remain unmatched. Note that, in the experimental matching market analyzed below, there are five students who can be assigned to four universities, where one university has two available seats. The three core properties that most matching mechanisms seek to achieve are efficiency, stability, and strategy-proofness.

A matching $\mu$ is Pareto-efficient if there exists no alternative matching ${\mu }^{*}$ such that, for every student $i\in I$, ${\mu }^{*}\left(i\right){⪰}_i\mu \left(i\right)$ and for at least one student $j\in I$, ${\mu }^{*}\left(j\right){\succ }_j\mu \left(j\right)$. That is, there is no matching that all students weakly prefer over their current assignment and that at least one student strictly prefers over her current assignment.

A matching $\mu$ is stable if it satisfies the following three conditions. The matching must (i) be individually rational: for each student $i\in I$, $\mu \left(i\right){⪰}_i\varnothing$. This means no student prefers to be unmatched. It must (ii) be non-wasteful: for any student $i\in I$ and school $u\in U$, if $u{\succ }_i\mu \left(i\right)$, then school u must be assigned a full cohort; that is, $\left|\mu \left(u\right)\right|=q_u$. It must (iii) eliminate justified envy: there exists no student–school pair $(i,u)$ such that $u{\succ }_i\mu \left(i\right)$, and, additionally, there is some student $j\in \mu \left(u\right)$ for whom the school’s priority ordering satisfies $i{\succ }_{u}j$. This condition rules out the existence of a blocking pair—a student and a school both preferring to be matched with each other over their current assignments. In summary, a matching is stable if it is individually rational, non-wasteful, and eliminates justified envy.

Let $\mathcal{M}$ be the set of all feasible matchings. Before stating the condition for strategy-proofness, a mechanism can be defined as a function $\phi :({\succ }_I,{⪰}_U,{\left\{q_u\right\}}_{u\in U})⟶\mathcal{M}$. The mechanism $\phi$ is said to be strategy-proof for students if, for every student $i\in I$, every preference profile ${\succ }_I$, every alternative reported preference ${\succ }_i^{\prime }$, and every configuration of the other students’ preferences ${\succ }_{-i}$, the following holds: ${\phi }_i({\succ }_i,{\succ }_{-i}){⪰}_i{\phi }_i({\succ }_i^{\prime },{\succ }_{-i})$. In words, no student can obtain a strictly better outcome by misrepresenting her preferences, regardless of the reports of other students.

Normatively, both stability and strategy-proofness can be conceptualized as criteria of two different types of fairness. On the one hand, stability fosters outcome fairness by eliminating justified envy (Balinski & Sönmez, 1999; Kamada & Kojima, 2019); it ensures that no pair of a student and a school where both would prefer to be matched with each other exists. From a legal perspective, stability is key as it prevents the violation of school priorities and eliminates justified envy among students. In this sense, blocking pairs could be seen as infringing upon equal protection rights if they lead to potential appeals or trigger litigation (Abdulkadiroğlu et al., 2005a; Ehlers & Morrill, 2018). On the other hand, strategy-proofness protects against advantages deriving from differences in strategic sophistication among students, thereby promoting procedural fairness (Pathak & Sönmez, 2008). As such, the final allocation is independent of any initial distribution of strategic abilities in society—aligning the mechanism with egalitarian fairness considerations (Dworkin, 1981; Elster, 1992, pp. 285, 290).

3.1. Gale–Shapley Mechanism

The student-proposing GS mechanism proposed by Gale and Shapley (1962) proceeds as follows:

In the first step, each student applies to her preferred university. Each university tentatively admits students in the order of the university’s priority rankings until the capacity is exhausted or no acceptable students are left. All other students are rejected, the rejection being final.

In the k-th step, each student rejected in k − 1 applies to her most preferred university on the rank-order list of universities that have not rejected her before. If no university is left on the rank-order list, the student applies nowhere. Each university considers the offers on hold from previous steps and new offers. Each university tentatively admits students in the order of the university’s priority ranking until the remaining capacity is exhausted or no acceptable students are left. All other students are rejected, the rejection being final.

The algorithm ends when no more rejections are issued. Each university is matched to the students it is holding.

The student-proposing GS mechanism features two well-known properties. On the one hand, the GS mechanism results in stable matching (Gale & Shapley, 1962). This matching is student-optimal under the stability constraint, that is, efficient among all stable matchings (Dubins & Freedman, 1981). On the other hand, the GS mechanism is strategy-proof for proposing students, with truth-telling being a weakly dominant strategy (Dubins & Freedman, 1981; Roth, 1982).14

3.2. Boston Mechanism

The BOS mechanism (Abdulkadiroğlu et al., 2005b; Abdulkadiroğlu & Sönmez, 2003; Ergin & Sönmez, 2006) proceeds as follows:

In the first step, each student applies to her preferred university. Each university immediately admits students in the order of the university’s priority ranking until the capacity is exhausted or no acceptable students are left. All other students are rejected, the rejection being final. Each admitted student becomes a permanent match. The capacities of each university are adjusted to account for students admitted in this step.

In the k-th step, each student rejected in k − 1 applies to her most preferred university on the rank-order list of universities that have not rejected her before. If no university is left on the rank-order list, the student applies nowhere. Each university immediately admits students in the order of the university’s priority ranking until the remaining capacity is exhausted or no acceptable students are left. All other students are rejected, the rejection being final. Each admitted student becomes a permanent match. The capacities of each university are adjusted to account for students admitted in this step.

The algorithm ends when no more rejections are issued.

In contrast to the GS mechanism, the BOS mechanism can be considered an immediate acceptance mechanism (Featherstone & Niederle, 2016). While acceptance is deferred to the very end of the procedure under the GS mechanism, it is immediate under the BOS mechanism. On the one hand, due to the finality of rejections at each stage, a student may be permanently matched with a university despite the existence of a higher-priority applicant applying later. Such a situation will result in a blocking pair and undermine stability as the priority structure of universities will not be unconditionally respected. On the other hand, this creates strong incentives for students to misrepresent their true preferences. If a university admits a student early in the procedure and exhausts its capacity, it risks later being unable to admit a student with higher priority. As a result, students may benefit from “gaming” the system by ranking less-preferred universities higher in order to avoid being rejected early and avoid wasting their first choice. This is why the BOS mechanism is not strategy-proof.

4. Experimental Design

4.1. Basic Setup

The experiment is designed to identify the effects of three different information environments under the student-proposing GS mechanism and the BOS mechanism (2 × 3 factorial design).15 The setup used in the two baseline treatments of my experiment closely follows the framework used by Featherstone and Niederle (2016).16 There are four universities $u\in U=\{A,B,C,D\}$, five students $s\in S=\{s_1,\dots ,s_5\}$, and two student types $t\in T=\{t_1,t_2\}$. Each student is assigned exactly one type, and the types do not overlap. Students are divided into two mutually exclusive types: three Type-1 students and two Type-2 students.17 According to the quota rule, two seats are available at university A, whereas universities B, C, and D each offer one seat. Notice that the sum of all quotas exactly equals the number of students. Thus, the experimental market is balanced, a configuration known to typically exhibit a richer set of stable matchings compared to unbalanced markets (Ashlagi et al., 2017).

Student preferences over schools are induced exogenously and aligned. Accordingly, each student receives 100 points for being matched with A, 67 points for being matched with B, 25 points for being matched with C, and 0 points for being matched with D (

Table 1. Student preferences.

A

≻

B

≻

C

≻

D

). Preference profiles are common knowledge.

Universities have priority for Type-1 students over Type-2 students (

Table 2. University priorities.

Type 1		Type 2
$s_1,s_2,s_3$	≻	$s_4,s_5$

). These priorities over types are common knowledge. Students of the same type are ordered randomly. The order determines university priorities over students of the same type. Participants are told that priorities over students of the same type will be determined randomly, but the results of the lottery are not revealed to participants.

Students submit a complete rank-order list for universities. Students are neither allowed to truncate their rank-order list nor include the same university more than once in their rank-order list. While the large majority of matching experiments investigate repeated interactions, I conduct a one-shot matching experiment. The reason for this design choice is that many matching markets, such as those for university admissions, involve an important once-in-a-lifetime decision. Students are often unfamiliar with the procedure and may only learn about sensible application strategies from other people in their social network who experienced the procedure in the past (Ding & Schotter, 2017, 2019). Without such intergenerational advice and without the possibility to engage in repeated interactions, however, students are unlikely to fully grasp the strategic properties of the assignment procedure or trust it.

Under the BOS mechanism, in equilibrium, Type-2 students will adopt one strategy (skip-the-top), Type-1 students another (skip-the-middle). Type-2 students know that the two seats at A will be assigned to two Type-1 students. Therefore, they have an incentive to misreport their first preference and rank B first rather than A. This strategy can be referred to as skip-the-top. Conversely, rational Type-1 students will anticipate that the seat at B will already be blocked if they do not obtain a seat at A, their preferred option. They will therefore insure themselves against the risk of foregoing a seat at C and rank it second instead of B. This strategy can be referred to as skip-the-middle.

4.2. Treatments

Under each matching mechanism, I vary the degree of information about the mechanism in three treatments. In the baseline treatment, participants receive detailed information about procedural rules of the respective matching mechanism, including some examples (Base).18 In the strategic information treatment, participants only receive information about the respective equilibrium strategies without an explanation of the procedural rules of the respective matching mechanism (StratInfo). The combined information treatment combines both treatments (Combined). Hence, participants receive both information about the procedural rules of the respective matching mechanism and strategic information.19

The GS StratInfo treatment mimicks the kind of procedural information provided by some public school districts in the US (see Section 2). Accordingly, participants receive specific information that strategizing is not beneficial: “Regardless of what other students do, you will never be better off submitting a rank-order list that does not reflect your true preferences. This means your chances of being admitted to a preferred university (=yielding higher earnings) do not improve if you put a less-preferred university (=yielding lower earnings) at a higher rank on the rank-order list. For example, neither Type-1 students nor Type-2 students can improve their chances of being admitted to a preferred university by ranking university A as their second choice and university B as their first choice”.

The BOS StratInfo treatment approximates the practice of the German clearinghouse in charge of university admissions (see Section 2). Accordingly, participants receive specific information about potentially beneficial strategies for each type: “Depending on what other students do, you might be better off submitting a rank-order list that does not reflect your true preferences. This means your chances of being admitted to a preferred university (=yielding higher earnings) might improve if you put a less-preferred university (=yielding lower earnings) at a higher rank on the rank-order list. Type-2 students might be better off manipulating their first choice, e.g., rank university B as their first choice. In that case, Type-1 students might be better off manipulating their second choice, e.g., rank university C as their second choice. This can increase the chances of Type-1 students being admitted to university C if no seat at university B is available any more”.

4.3. Post-Experimental Tests

After implementing the respective matching mechanism, I first evoked first-order beliefs about other participants’ strategies. The belief evocation task was announced after participants had made their decision under the matching mechanism so as not to trigger strategic considerations based on beliefs. In order to prevent hedging across tasks, the belief evocation stage was not incentivized. Second, I evoked risk preferences using the measure proposed by Holt and Laury (2002). Third, I measured cognitive abilities and heuristics related to intuition using an incentivized version of the cognitive reflection test (Frederick, 2005). The cognitive reflection test is designed to measure the ability to inhibit intuitive responses (System 1 thinking) when the correct response requires conscious reflection (System 2 thinking). Participants in previous studies have been shown to be familiar with the answers from the original version of the cognitive reflection test (Haigh, 2016; Stieger & Reips, 2016). In order to prevent a biased measure due to experience with the test, I used three questions from the original version of the test and three questions from a recent version. Each participant had one minute to answer each test question. Fourth, I measured fairness perceptions using survey questions developed in the literature on procedural fairness (Colquitt & Rodell, 2015; Lind & Tyler, 1988). The experiment ended with a demographics questionnaire to control for gender, age, subject studied, and experience with the German university admission procedure for medical school.

4.4. Procedure

The experiment was programmed using the experimental software z-Tree (Fischbacher, 2007) and the matchingMarkets package in R 1.0-4 (Klein & Giegerich, 2018). The experiment was conducted at the DecisionLab at the Max Planck Institute for Research on Collective Goods in 2018, with a total of 235 participants. Subjects were recruited via ORSEE (Greiner, 2015) and participated in 13 sessions. Each session lasted approximately 60 min. Before the experiment, participants had to answer control questions correctly in order to begin with the actual experiment. At the end of the experiment, participants received the sum of their earnings, including a show-up fee of EUR 5. Participants earned EUR 14.57 on average. In addition, I ran simulations to predict matchings and their stability using the matchingR (Tilly & Janetos, 2018) and matchingMarkets packages in R (Klein & Giegerich, 2018).

4.5. Hypotheses

Under the GS mechanism, using the concept of Bayes–Nash equilibrium, a strategy profile is an equilibrium if and only if Type-1 students rank A first and B second and Type-2 students rank C among the acceptable offers (see Featherstone & Niederle, 2016). Truth-telling is a weakly dominant strategy. In games of incomplete information—where players have private information about their types—a strategy profile $\sigma =({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$ is a Bayes–Nash equilibrium if, for every player i and every type ${\theta }_i$ in the player’s type space ${\Theta }_i$, the strategy ${\sigma }_i\left({\theta }_i\right)$ maximizes player i’s expected utility given their beliefs about the types of the other players and assuming that every other player $j\ne i$ is playing their equilibrium strategy ${\sigma }_j$.20

Under the BOS mechanism, a strategy profile is an equilibrium if and only if Type-1 students rank A first and C second and Type-2 students rank B first (for the formal proof, see Featherstone and Niederle (2016)). It follows that students have an incentive to manipulate their preferences under the BOS mechanism.

Hypothesis 1.

Truth-telling rates are higher under the GS mechanism than under the BOS mechanism.

The strategic information treatment is designed to increase the salience of the equilibrium strategy and dampen strategic considerations as compared to the baseline treatment and the combined information treatment. Under the GS mechanism, strategic information should spur applicants to adopt a truth-telling strategy. Under the BOS mechanism, Type-1 students should be more likely to skip the middle, while Type-2 students should be more likely to skip the top when receiving strategic information. Combined information dampens the salience of the equilibrium strategy; it should trigger strategic considerations and off-equilibrium behavior.

Hypothesis 2.

Students are more likely to adopt the equilibrium strategy in the strategic information treatment than in the combined information treatment and the baseline treatment.

In equilibrium, the GS mechanism will result in unique stable matching, where two Type-1 students (with the two highest ranks among Type-1 students) are matched to A, one Type-1 student is matched to B, one Type-2 student (with the highest rank among Type-2 students) is matched to C, and one Type-2 student is matched to D.

$${\mu }_{GS}=\left(\begin{array}{cccc}{s}_1,s_2& s_3& s_4& s_5\\ A& B& C& D\end{array}\right)$$

Under the equilibrium matching of the BOS mechanism, the Type-1 student with the lowest rank among students of her type will be matched to C or D. It follows that the resulting matching will not be stable: the respective Type-1 student would prefer to be matched to B, and the priority of Type-1 students at B will be systematically violated.

$${\mu }_{BOS}=\left(\begin{array}{cccc}{s}_1,s_2& s_4& s_3& s_5\\ A& B& C& D\end{array}\right)$$

Hypothesis 3.

Stability levels are higher under the GS mechanism than under the BOS mechanism, and higher in the strategic information treatment than in the combined information treatment and the baseline treatment.

In line with previous findings (Basteck & Mantovani, 2018), cognitive abilities should be correlated with strategic abilities and facilitate individually optimal choices regardless of the procedural rules.

Hypothesis 4.

Students with higher cognitive abilities are more likely to adopt the equilibrium strategy under both mechanisms.

The fairness of a public assignment procedure depends both on the outcome it generates and the transparency of its procedural rules (see Section 3). Stability implies that no student prefers another school while a student with lower priority is matched to that school, which should increase perceived outcome fairness (Kamada & Kojima, 2019). Strategy-proofness implies that the mechanism does not provide any advantage to sophisticated students, which should increase procedural fairness.

Hypothesis 5.

Perceived fairness is higher under the GS mechanism than under the BOS mechanism.

5. Results

5.1. Summary

In my data analysis, I use both non-parametric tests and parametric regression models. All p-values are those of Fisher’s exact test if not otherwise reported.

Table 3. Strategic behavior across mechanisms.

	GS	BOS	p-Value
Truth	73.60%	36.36%	<0.001
Skip-the-middle	1.60%	13.64%	$0.001$
Skip-the-top	14.40%	38.18%	<0.001
CABD	4.00%	1.82%	0.453
CBAD	4.80%	6.36%	0.776
N	125	110

presents the summary results for strategic behavior under the GS mechanism and the BOS mechanism.21 In line with Hypothesis 1, I find that the truth-telling rates are significantly higher under the GS mechanism than under the BOS mechanism ($p<0.001$). This result holds both for Type-1 and Type-2 students ($p<0.001$). Conversely, the skip-the-middle rates are significantly higher under the BOS mechanism than under the GS mechanism ($p=0.001$). In line with Hypothesis 2, this effect is driven by Type-1 students. Type-1 students are more likely to skip the middle under the BOS mechanism than under the GS mechanism ($p<0.001$), while I do not find any difference for Type-2 students ($p=0.598$). The skip-the-top rates are significantly higher under the BOS mechanism than under the GS mechanism ($p<0.001$). In line with Hypothesis 2, this effect is mainly driven by Type-2 students. Type-2 students are more likely to skip the top under the BOS mechanism than under the GS mechanism ($p<0.001$), but a similar yet marginally significant effect can be observed for Type-1 students ($p=0.081$). These results corroborate the theoretical prediction that the GS mechanism will yield higher truth-telling rates than the BOS mechanism and that students will adopt type-specific strategies under the BOS mechanism.

Result 1.

The truth-telling rates are higher under the GS mechanism than under the BOS mechanism when aggregating over all information environments (which lends support to Hypothesis 1).

5.2. Treatment Effects on Truth-Telling Strategies

Table 4. Strategic behavior in all treatments.

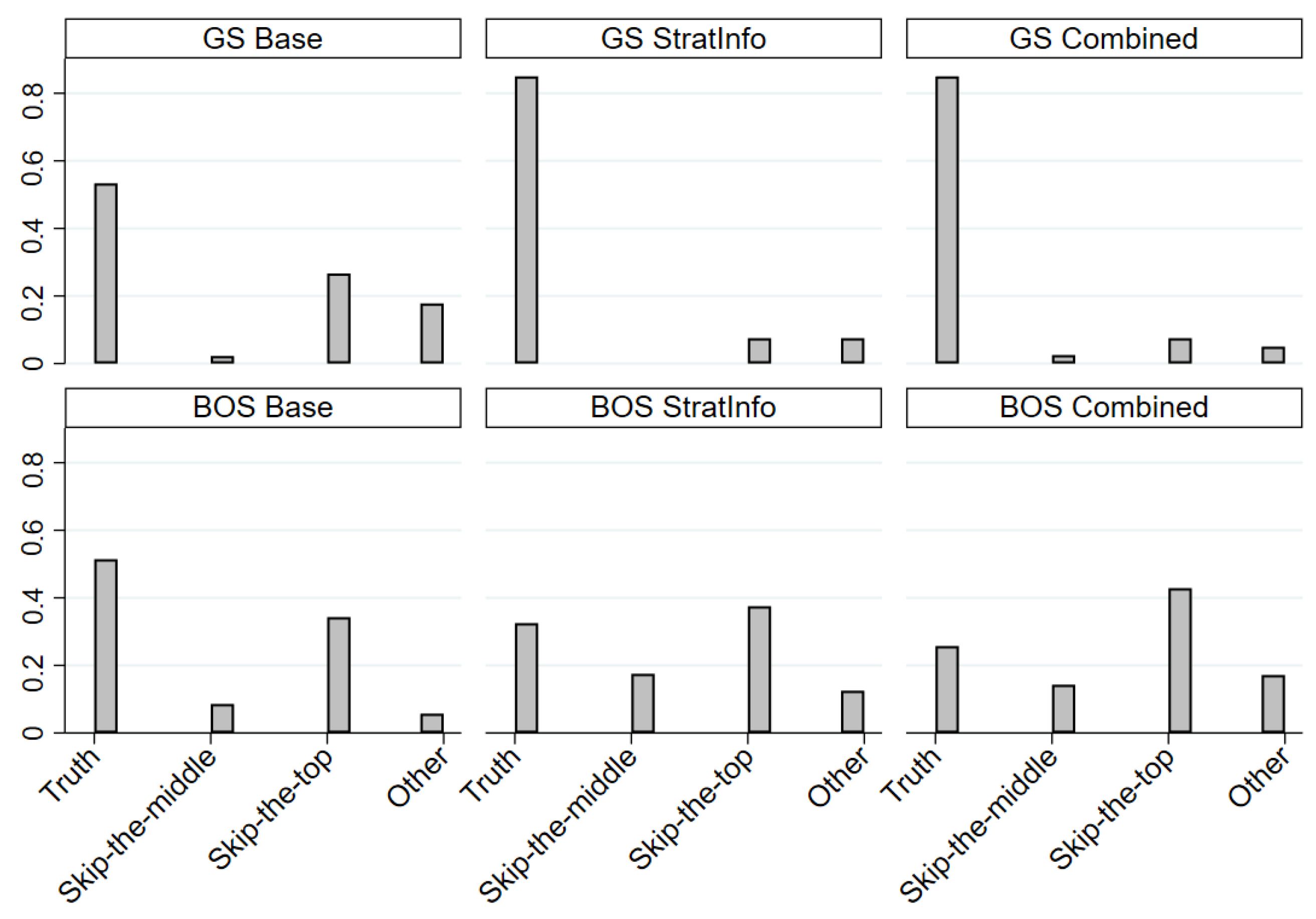
	GS			BOS
	Base	StratInfo	Combined	Base	StratInfo	Combined
Truth	53.33%	85.00%	85.00%	51.43%	32.50%	25.71%
Skip-the-middle	2.22%	0.00%	2.50%	8.57%	17.50%	14.29%
Skip-the-top	26.67%	7.50%	7.50%	34.29%	37.50%	42.86%
N	45	40	40	35	40	35

shows a more nuanced picture of the treatment effects on truth-telling. These nuances are visualized in Figure 1.

First, I analyze the difference in the truth-telling rates across both baseline treatments. Contrary to all the theoretical predictions, the truth-telling rates do not significantly differ across the baseline GS and baseline BOS mechanisms ($p=1.000$). Running a test for the two student types separately, I find no difference for Type-1 students ($p=0.750$) or Type-2 students ($p=0.426$). A multinomial logistic regression corroborates this result (

Table 5. Treatment effects on strategies.

	Truth	Skip-the-Middle	Skip-the-Top	Other
Ref. cat.: GS Base
GS StratInfo	0.317 ***	−0.022 ***	−0.192 **	−0.103
	(0.093)	(0.022)	(0.078)	(0.071)
GS Combined	0.317 ***	0.003	−0.192 **	−0.128 *
	(0.093)	(0.033)	(0.078)	(0.067)
BOS Base	−0.019	0.064	0.076	−0.121 *
	(0.113)	(0.052)	(0.104)	(0.069)
BOS StratInfo	−0.208 **	0.153 **	0.108	−0.053
	(0.105)	(0.064)	(0.101)	(0.077)
BOS Combined	−0.276 ***	0.121 *	0.162	−0.006
	(0.105)	(0.063)	(0.107)	(0.085)

*** $p<0.01$; ** $p<0.05$; * $p<0.1$; multinomial logit regression. Standard errors in parentheses. Treatment coefficients are reported as average marginal treatment effects. All columns report estimates of one and the same multinomial logit regression. Each cell can be interpreted as the difference in the probability of adopting one of the reported strategies (categorical DV: truth, skip-the-middle, skip-the-top, or other) between the respective treatment and GS Base (reference category).

). This suggests that the GS mechanism and the BOS mechanism will not yield different truth-telling rates on average if students receive information about the mechanism only. One potential explanation may be that students fail to fully grasp the strategic implications of the mechanism when only its rules are explained. A comparison with the equilibrium prediction elucidates the intensity of this behavioral effect. The truth-telling rates under the baseline GS mechanism (53.33%) are not even close to the equilibrium prediction (100%). This prompts the conclusion that students strategize excessively under the GS mechanism when they do not receive information about its strategic properties.

Second, I analyze the impact of procedural information on truth-telling within each mechanism. In line with Hypothesis 2, both the strategic information and combined information treatments lead to a strong and significant increase in the truth-telling rates as compared to the baseline under the GS mechanism ($p=0.002$ and $p=0.002$).22 Conversely, the strategic information and combined information treatments trigger decreases in the truth-telling rates as compared to the baseline under the BOS mechanism ($p=0.107$ and $p=0.049$).23 This negative effect is in line with the prediction that truth-telling rates should further decline under the BOS mechanism if students receive information about a potentially beneficial manipulation of preferences.

Result 2.

Strategic information and combined information lead to a strong increase in truth-telling under the GS mechanism, and to a strong decrease in truth-telling under the BOS mechanism (which lends support to Hypothesis 2).

5.3. Treatment Effects on Dropping Strategies

The experiment was also designed to test whether information about the respective equilibrium strategies (dropping strategies) facilitates individually beneficial manipulations of rank-order lists under the BOS mechanism. Accordingly, the data analysis in this subsection only considers observations from the BOS mechanism. Aggregating over all information environments under the BOS mechanism, only 13.64% of the students skip the middle, while 38.18% of the students adopt the skip-the-top strategy (Table 3). The skip-the-top rates are relatively close to the equilibrium (40%), but the skip-the-middle rates are far below the equilibrium prediction (60%). Overall, this suggests that, regardless of the specific information about the assignment procedure, students fail to use individually optimal strategies under the BOS mechanism. This is corroborated by the fact that 36.36% of the students opt for the truth-telling strategy even though a preference manipulation would make them better off.

In line with Hypothesis 2, Type-1 students adopt the skip-the-middle strategy more frequently (19.70%) than Type-2 students (4.55%, $p=0.025$). Conversely, Type-2 students skip the top more frequently (68.18%) than Type-1 students (18.18%, $p<0.001$). This suggest that students have a sense of which strategy to adopt in light of the priorities that universities set for their individual type and the strategic incentives set by the BOS mechanism. The impact of procedural information on both types becomes clear in an analysis that distinguishes between Type-1 and Type-2 students across all the treatments.

On the one hand, only 14.29% of the Type-1 students skip the middle under the baseline BOS mechanism. The skip-the-middle rates increase to 25.00% in the strategic information treatment and to 19.05% in the combined information treatment. Using Fisher’s exact test, however, this tendency towards the equilibrium strategy is not significant ($p=0.469$ and $p=1.000$). Regardless of the specific information environment, Type-1 students fail to skip the middle sufficiently often so as to improve their prospects of obtaining the best possible matching.

On the other hand, 71.43% of the Type-2 students skip the top under the baseline BOS mechanism. The skip-the-top rates drop to 56.25% in the strategic information treatment and increase to 78.57% in the combined information treatment. Yet, none of these changes are significant when using Fisher’s exact test ($p=0.466$ and $p=1.000$). This suggests that Type-2 students are also subject to bounded rationality and fail to adopt the skip-the-top strategy sufficiently often.

A multinomial logistic regression with the baseline GS mechanism as the reference category yields some evidence in support of Hypothesis 2 (

Table 6. Treatment effects on strategies by type.

Strategy	Truth	Skip-the-Middle	Skip-the-Top	Other
Ref. cat.: GS Base
GS StratInfo
Type 1	0.296 ***	−0.0370	−0.222 ***	−0.037
	(0.088)	(0.036)	(0.080)	(0.036)
Type 2	0.347 **	<0.001	−0.146	−0.201
	(0.161)	(<0.001)	(0.148)	(0.151)
GS Combined
Type 1	0.255 ***	−0.037	−0.222 ***	0.005
	(0.097)	(0.036)	(0.080)	(0.055)
Type 2	0.410 ***	0.063	−0.146	−0.326 **
	(0.157)	(0.061)	(0.148)	(0.130)
BOS Base
Type 1	0.058	0.106	−0.127	−0.037
	(0.128)	(0.085)	(0.102)	(0.036)
Type 2	−0.135	<0.001	0.381 **	−0.246 *
	(0.1410)	(<0.001)	(0.164)	(0.148)
BOS StratInfo
Type 1	−0.204	0.213 **	0.028	−0.037
	(0.135)	(0.096)	(0.119)	(0.036)
Type 2	−0.215 *	0.062	0.229	−0.076
	(0.122)	(0.061)	(0.167)	(0.163)
BOS Combined
Type 1	−0.275 **	0.153 *	−0.032	0.153 *
	(0.139)	(0.093)	(0.117)	(0.093)
Type 2	−0.278 ***	0.071	0.452 ***	−0.246 *
	(0.106)	(0.069)	(0.156)	(0.148)

*** $p<0.01$; ** $p<0.05$; * $p<0.1$; multinomial logit regression with interaction between treatment and type. Standard errors in parentheses. Treatment coefficients are reported as average marginal treatment effects. All columns report estimates of one and the same multinomial logit regression. Each cell can be interpreted as the difference in the probability of adopting one of the reported strategies (categorical DV: truth, skip-the-middle, skip-the-top, or other) between the respective treatment and GS Base (reference category) for Type-1 students (top panel) and Type-2 students (bottom panel).

). Type-1 students are more likely to skip the middle when receiving strategic information or combined information under the BOS mechanism. Conversely, Type-2 students are more likely to skip the top when receiving combined information under the BOS mechanism, whereas merely providing strategic information does not seem to facilitate the adoption of the skip-the-top strategy.

However, a multinomial logistic regression with the baseline BOS mechanism as the reference category shows that the treatments under the BOS mechanism have a negative effect on truth-telling but no positive effect on any of the dropping strategies (Appendix B). One potential reason for not observing a treatment effect on skip-the-top rates is that a relatively high fraction of the Type-2 students adopt a skip-the-top strategy under the baseline BOS mechanism (71.43%). In sum, this suggests that it is rather difficult to nudge students to adopt any dropping strategy, be it a simple one (skip-the-top) or a complex one (skip-the-middle). On the one hand, this indicates that information about the strategic properties of the mechanism may not be necessary to push students towards a simple dropping strategy. On the other hand, these results prompt the conclusion that even simple explanations of complex strategies may be too difficult to fathom.

The relatively high skip-the-top rates under the baseline BOS mechanism can be explained by risk aversion. A multinomial logistic regression shows that risk-averse students are more likely to skip the top (Appendix B). These students may be afraid of foregoing a potential seat at university B and thus downrank university A on their rank-order preference list.

Overall, providing procedural information about how to strategize does not seem to facilitate the adoption of equilibrium strategies under the BOS mechanism. Even when provided with strategic and combined information, students do not entirely converge towards the equilibrium. On average, 22% of the Type-1 students skip the middle (equilibrium: 100%), while 67% of the Type-2 students skip the top (equilibrium: 100%) in the strategic information treatment and the combined information treatment.

Result 3.

Strategic information and combined information do not seem to facilitate the adoption of equilibrium strategies under the BOS mechanism (which contradicts Hypothesis 2).

5.4. Stability

A matching is stable if no student can form a blocking pair with a university. A blocking pair exists if a student prefers to be admitted to a university with a seat that has been assigned to a student with lower priority. Under the student-proposing GS mechanism, a student-optimal stable matching is achieved when all students reveal their preferences truthfully.

Table 7. Stable matchings.

GS			BOS
Base	StratInfo	Combined	Base	StratInfo	Combined
33.33%	100%	87.50%	0%	12.50%	0%

reports the fraction of stable matchings across all the treatments and corroborates this hypothesis.

Overall, the results are in line with Hypothesis 3 and show that the GS mechanism yields a higher fraction of stable matchings than the BOS mechanism ($p<0.001$). While I do not observe strong treatment differences under the BOS mechanism, I find stark treatment differences under the GS mechanism. Specifically, the fraction of stable matchings is extremely low under the GS mechanism in the baseline treatment (33.33%) while increasing to 100% in the strategic information treatment ($p<0.001$) and 87.50% in the combined information treatment ($p<0.001$). A logistic regression confirms this result (Appendix B).

This result can again be explained by the high fraction of students who manipulate their preferences under the GS mechanism in the baseline treatment. The results also show that full transparency about both the mechanism and its strategic properties (as implemented in the combined information treatment) may not be the best approach to achieve stability. In fact, the results point to a potential trade-off between transparency and stability.

Result 4.

Strategic and combined information increases the stability of matchings under the GS mechanism while leaving it unaffected under the BOS mechanism (which lends partial support to Hypothesis 3).

5.5. Cognitive Abilities

In line with Hypothesis 4, cognitive reflection abilities partly explain the strategies adopted under both mechanisms. A multinomial logistic regression provides evidence in support of this result (Appendix B). Under the GS mechanism, higher cognitive abilities do not seem to have a positive effect on truth-telling. However, students with higher cognitive abilities are more likely to refrain from a skip-the-top strategy when receiving strategic information, whereas students with lower cognitive abilities are more likely to refrain from a skip-the-top strategy when receiving combined information. Under the BOS mechanism, higher cognitive abilities lead to an increase in skip-the-middle rates with strategic information, whereas lower cognitive abilities lead to an increase in skip-the-middle rates with combined information.

On the one hand, this result suggests that students with higher cognitive abilities are willing to trust strategic information even when the actual procedure is unknown, while students with lower cognitive abilities seem to have a preference for additional information about the assignment procedure. On the other hand, this result stands in contrast to previous findings showing that students with lower cognitive abilities fail to strategize optimally (Basteck & Mantovani, 2018).

One potential reason for only observing an effect on the skip-the-middle strategy is that this strategy is relatively difficult. Type-1 students need to anticipate strategic behavior by Type-2 students and react with a counter-strategy, whereas Type-2 students only need to anticipate the outcome of the procedure conditional on Type-1 students ranking A on top of their rank-order list. Type-2 students can thus adopt a sensible strategy based on first-order beliefs about truth-telling among Type-1 students, while Type-1 students have to form first-order beliefs about preference manipulations among Type-2 students.

Result 5.

Cognitive reflection abilities facilitate the adoption of equilibrium strategies both under the GS mechanism and under the BOS mechanism (which lends support to Hypothesis 4).

5.6. Fairness

Table 8. Treatment effects on perceived fairness.

	Outcome Fairness	Procedural Fairness	Comprehension	Trustworthiness
Ref. cat.: GS Base
GS StratInfo	0.255	0.051	0.529 **	−0.394
	(0.227)	(0.231)	(0.242)	(0.245)
GS Combined	0.127	−0.012	0.202	−0.269
	(0.228)	(0.231)	(0.236)	(0.248)
BOS Base	0.104	0.182	0.310	−0.270
	(0.236)	(0.238)	(0.248)	(0.256)
BOS StratInfo	0.453 **	0.094	0.049	−0.606 **
	(0.226)	(0.230)	(0.235)	(0.243)
BOS Combined	0.605 ***	0.210	0.170	−0.596 **
	(0.235)	(0.238)	(0.242)	(0.250)
N	235	235	235	235

*** $p<0.01$; ** $p<0.05$; * $p<0.1$; ordered probit regression. Standard errors in parentheses. Each column corresponds to a different ordered probit regression. Outcome fairness is an ordinal variable ranging from 1 (very unfair) to 7 (very fair). Procedural fairness is an ordinal variable ranging from 1 (very unfair) to 7 (very fair). Comprehension is an ordinal variable describing the extent to which the explanation of the assignment procedure was comprehensible, ranging from 1 (not at all) to 7 (completely). Trustworthiness is an ordinal variable describing the extent to which the explanation of the assignment procedure was trustworthy, ranging from 1 (not at all) to 7 (completely).

presents the results of an ordered probit regression. The dependent variables stem from a Likert scale survey widely used in procedural fairness studies (Colquitt & Rodell, 2015; Lind & Tyler, 1988).24 On the one hand, I find that the outcomes generated under the BOS mechanism in both the strategic information and the combined information treatments are perceived as fairer than those generated under the GS mechanism. On the other hand, the results show that fairness assessments of the procedure remain unaffected by the treatments in comparison to the baseline GS mechanism.25 At the same time, the information provided in the strategic information and combined information treatments under the BOS mechanism is perceived as less trustworthy. Finally, the results show that providing strategic information under the GS mechanism has a positive impact on the comprehensibility of the procedure.

These results do not provide straightforward evidence in support of Hypothesis 5. Rather, they indicate that strategy-proofness—as a criterion of procedural fairness—and stability—as a criterion of outcome fairness—do not square with the general sentiments about fair assignment procedures (for a theoretical foundation of these fairness concepts, see Section 3). In fact, the results are somewhat opposed to the idea that creating a level playing field through strategy-proofness and eliminating justified envy are indispensable ingredients of fair assignment procedures, an idea that features prominently in matching theory (see Kamada & Kojima, 2019; Pathak & Sönmez, 2008). Not only do these results point to an inherent tension between perceived outcome fairness on the one hand and strategy-proofness on the other hand. They also suggest that strategy-proofness and transparency in assignment procedures embody different—and at times conflicting—fairness notions.

While market designers tend to derive their fairness concepts from strategy-proofness, legal scholars tend to stress the importance of procedural transparency. By contrast, the results presented here indicate that neither strategy-proofness nor transparency entirely translates into any concept of procedural or outcome fairness. On the one hand, the results suggest that, in order to fully deploy the virtues of strategy-proofness, it is crucial to provide salient information about the strategic properties of the mechanism. As the treatment comparisons under the GS mechanism show, sound explanations of the procedural rules alone are not sufficient to prevent attempts to game the assignment procedure, but they do not negatively affect truth-telling if presented in combination with salient strategic information. On the other hand, even when the strategic properties are transparent and salient, neither strategy-proofness nor the transparency of the specific procedural rules seems to be a driving force of the perceived fairness of the procedure. One reason may be that students perceive the GS mechanism as being “mechanic” and imposing strict preferences (Hitzig, 2019), while they may feel that the outcome generated under the BOS mechanism can be improved through behavior perceived as smart. The feeling of being able to exercise process control or “voice” (Thibaut & Walker, 1978) and not simply being a cog in the mechanism designer’s wheel might explain why fairness assessments are higher under the BOS mechanism.

Another possible explanation for why the BOS mechanism with procedural information yields higher outcome fairness ratings yet lower trustworthiness is the way strategic information is framed. While participants were explicitly assured that misrepresenting their preferences would never improve their assignment under the GS mechanism, they were merely told that it might improve under the BOS mechanism. This may have created extra uncertainty under the BOS mechanism—undermining trust—while participants’ experiences showed that their welfare was not significantly worse than under GS, which in turn may have boosted their perceptions of outcome fairness relative to the GS mechanism.

Result 6.

When students are provided with strategic and combined information, the outcomes are perceived as fairer under the BOS mechanism than under the GS mechanism. The procedural fairness assessments do not seem to differ across the mechanisms (which contradicts Hypothesis 5).

6. Conclusions

In this article, I have investigated the impact of different types of procedural information on stability, strategic behavior, and perceived fairness under the GS mechanism and the BOS mechanism. Understanding the impact of procedural information is crucial—for matching theorists who tend to discount potential behavioral effects, for market designers who need to design matching mechanisms in light of bounded rationality, and for lawyers who need to evaluate these mechanisms. To explore the impact of procedural information, I compare three different information environments in a controlled lab experiment: information about the rules of the mechanism, information about individually optimal strategies (strategic properties), and information about both (full transparency).

First, I find no difference in the truth-telling rates (approximately 50%) between the GS mechanism and the BOS mechanism when merely informing applicants about the rules of the respective mechanisms. Second, information about the strategic properties of the mechanism and full transparency significantly increases the truth-telling rates and the fraction of stable matchings under the GS mechanism. Under the BOS mechanism, however, information about the strategic properties of the mechanism and full transparency only reduces truth-telling, without a positive effect on the adoption of equilibrium strategies. Third, I find that cognitive reflection abilities only facilitate the adoption of complex dropping strategies spurred by the BOS mechanism, such as skip-the-middle. Finally, the GS mechanism does not seem to increase fairness perceptions. Contrary to the prevailing assumptions in matching theory, perceived outcome fairness is higher under the BOS mechanism. This indicates that eliminating the incentives to game the system and dampening justified envy do not necessarily square with the actual fairness perceptions.

These results have potentially important implications for the law and the policies applied to matching markets. While the introduction of strategy-proof school choice procedures is an important step towards a level playing field, it is unlikely to mitigate the risk of discrimination between sophisticated and non-sophisticated applicants without additional transparency policies. Rather, parents and students are likely to need specific procedural information about the strategy-proofness of the procedure lest unstable matchings be achieved. Public school districts in New York City and other cities around the world may be able to substantively improve their assignment procedures by urging applicants not to strategize and by increasing the salience of corresponding information about the assignment procedure. Moreover, courts may want to apply stricter scrutiny when assessing the compatibility of assignment procedures with equal protection rights.

From a normative perspective, the adoption of the GS mechanism can be considered as being close to the first-best solution if applicants receive strategic information. Without strategic information, the GS mechanism and the BOS mechanism might be equivalent second-best solutions. In addition to these transparency issues, market designers should consider the possibility of a potential trade-off between strategy-proofness and actual fairness sentiments. A mechanism that incentivizes truthful preference revelation may level the playing field between sophisticated and non-sophisticated applicants, but it might infringe on applicants’ perceived ability of exercising process control or “voice” and on their fairness perceptions. This illustrates that the design of safe, transparent, and fair school choice procedures requires much more than just a strategy-proof matching mechanism (Li, 2017, 2024). It is up to market designers and legal scholars to identify the relevant constraints that matching markets are subject to in practice. This is one of the core challenges of the emerging field of law and market design.