New Categories of Conditional Contribution Strategies in the Public Goods Game
Abstract
1. Introduction
- A free rider is the one who always contributes 0, irrespective of others’ contributions.
- A conditional cooperator is one with a positive and significant (at 1% significance level) Spearman correlation with the investments of others.
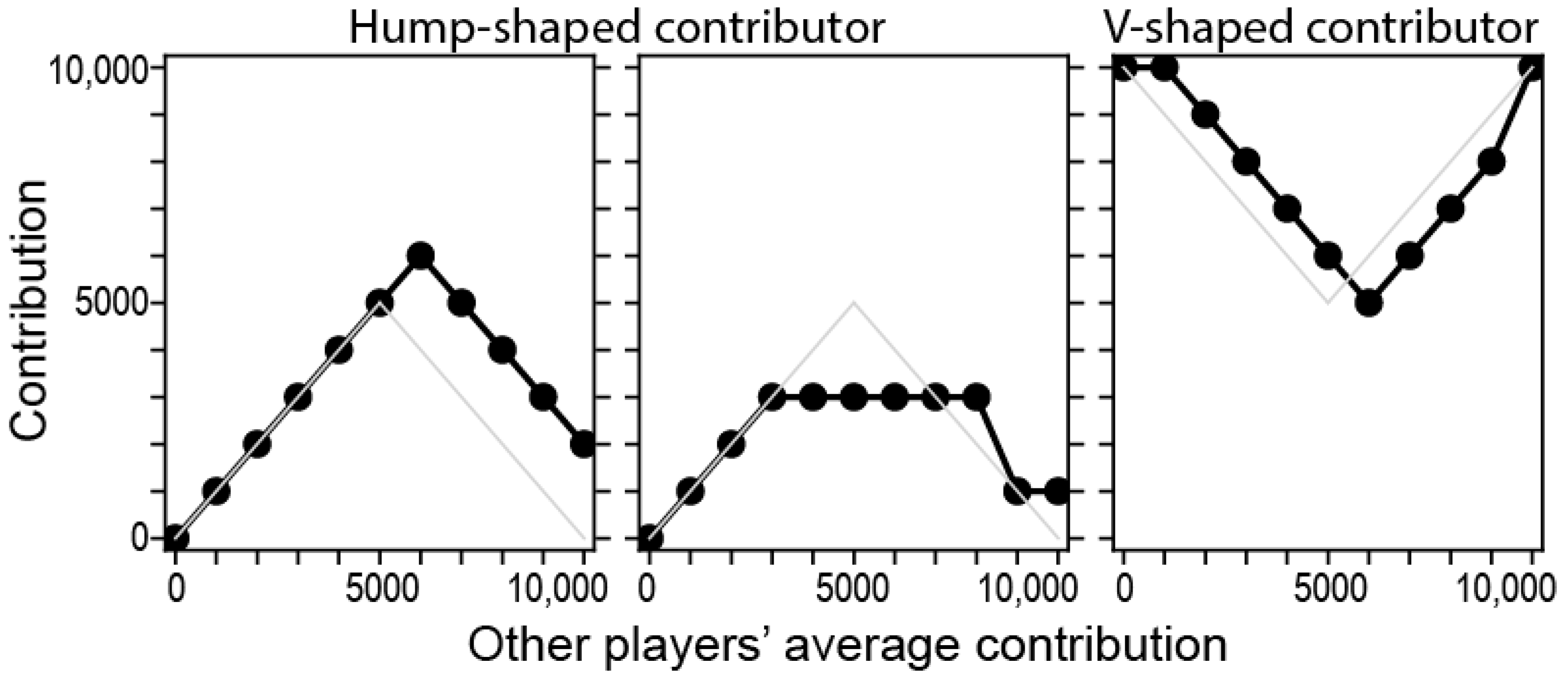
- A hump-shaped or triangular (Fischbacher et al., 2012) contribution is the one that increases to about 50% of the others’ contributions; then, the contribution decreases.
- If an outcome does not fall into any of the above categories, then it is considered “other”.
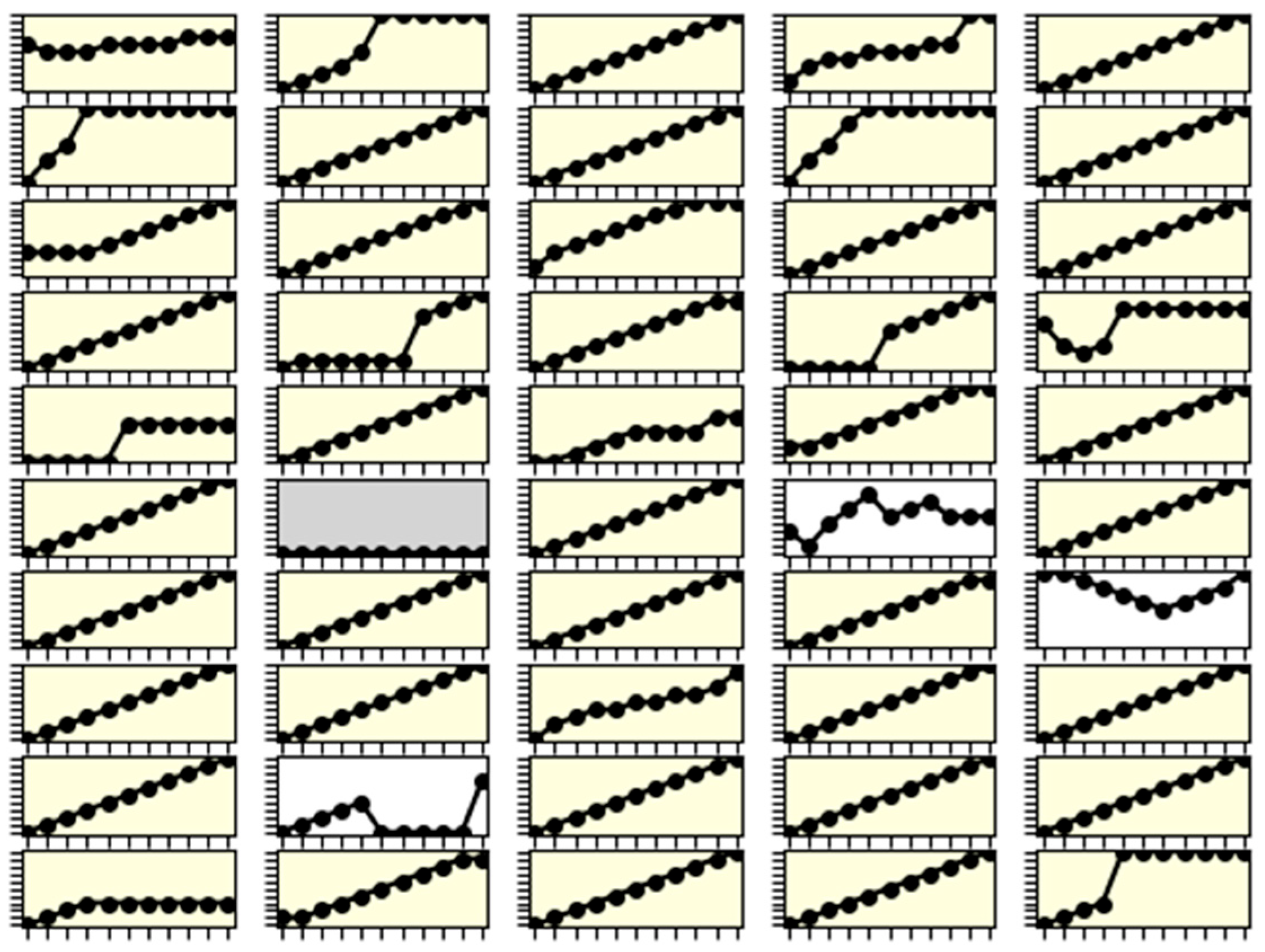
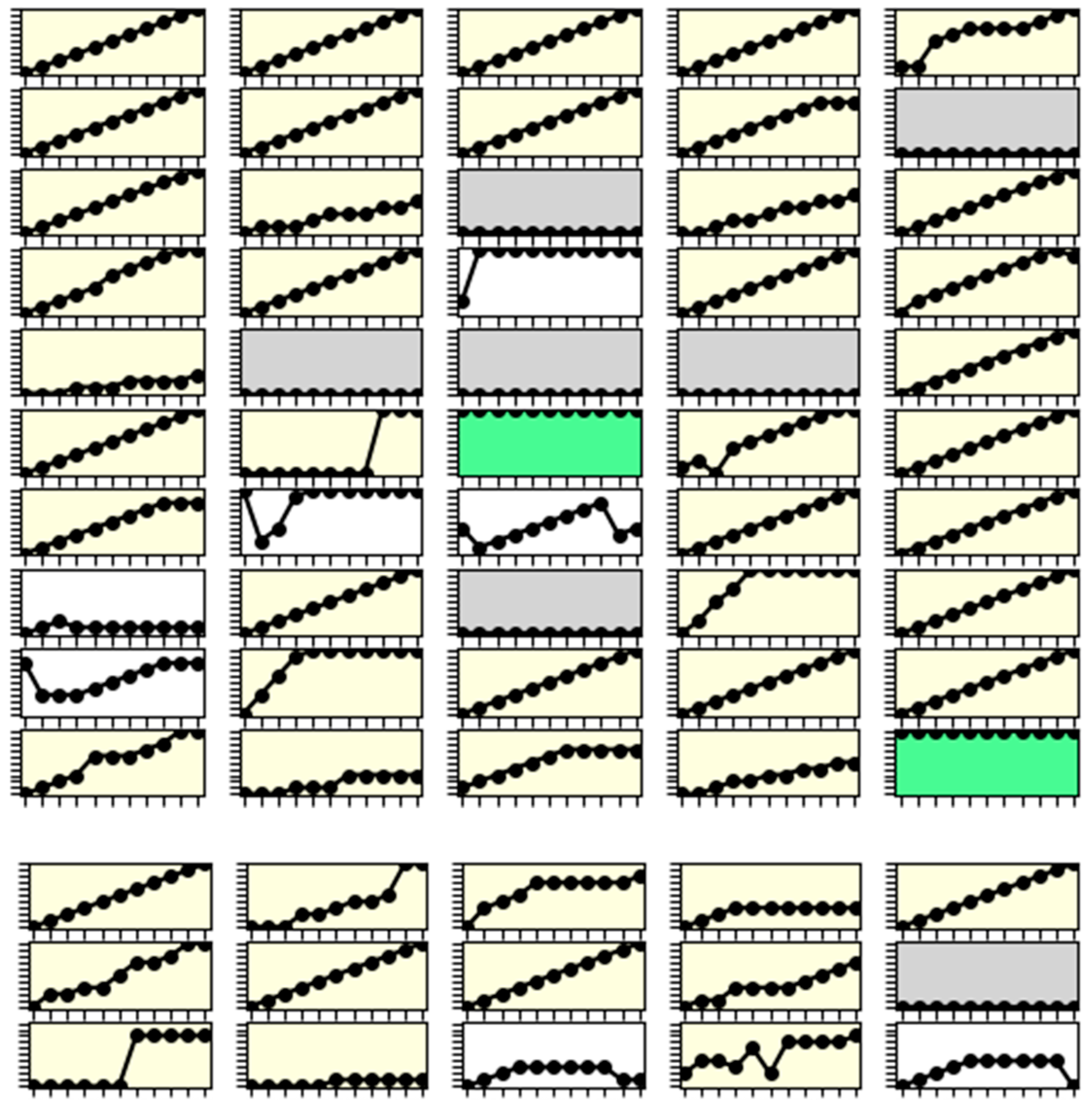
2. Results
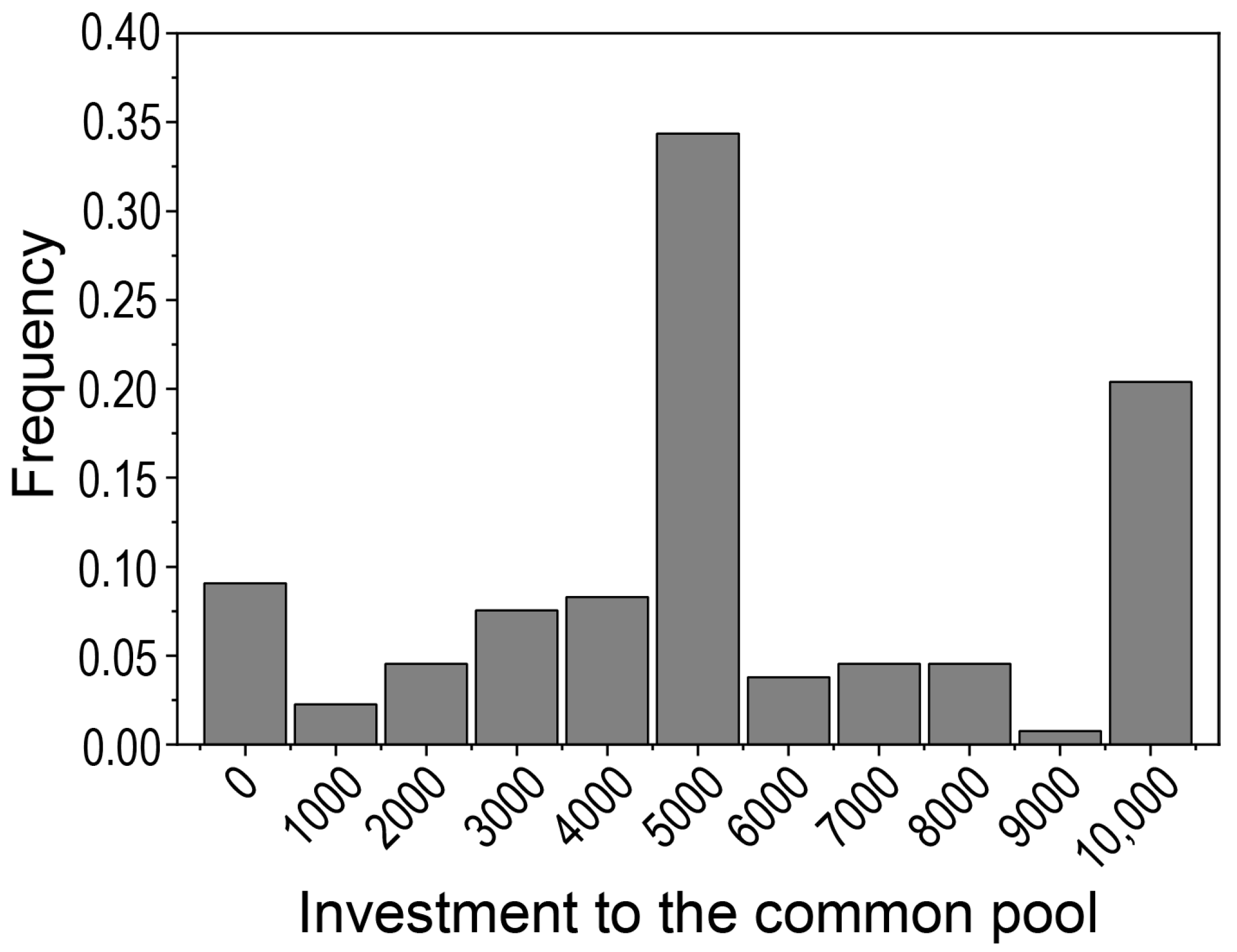
2.1. Unconditional Contribution
2.2. Conditional Contribution
2.3. Recategorization of Conditional Contribution Strategies
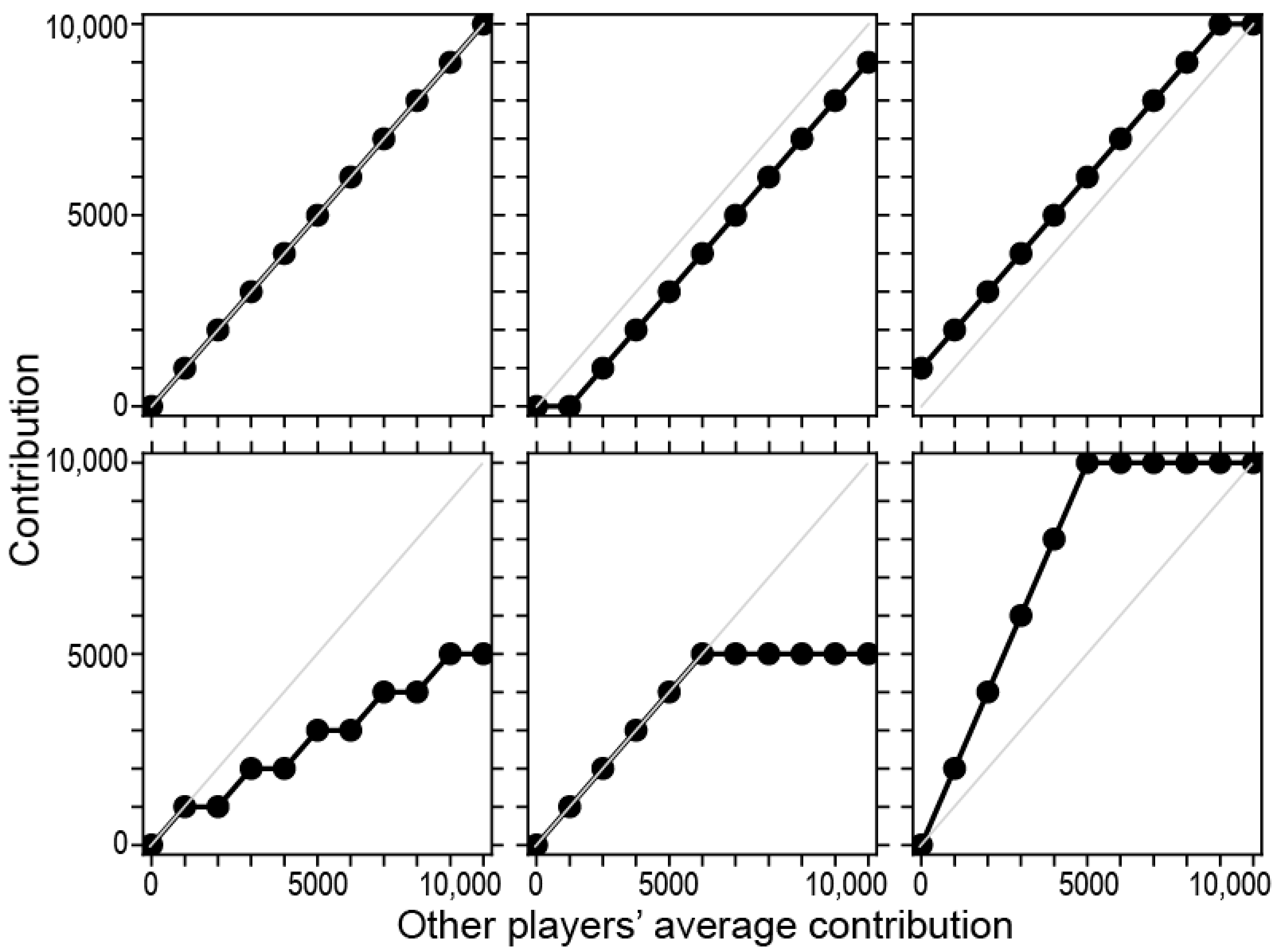
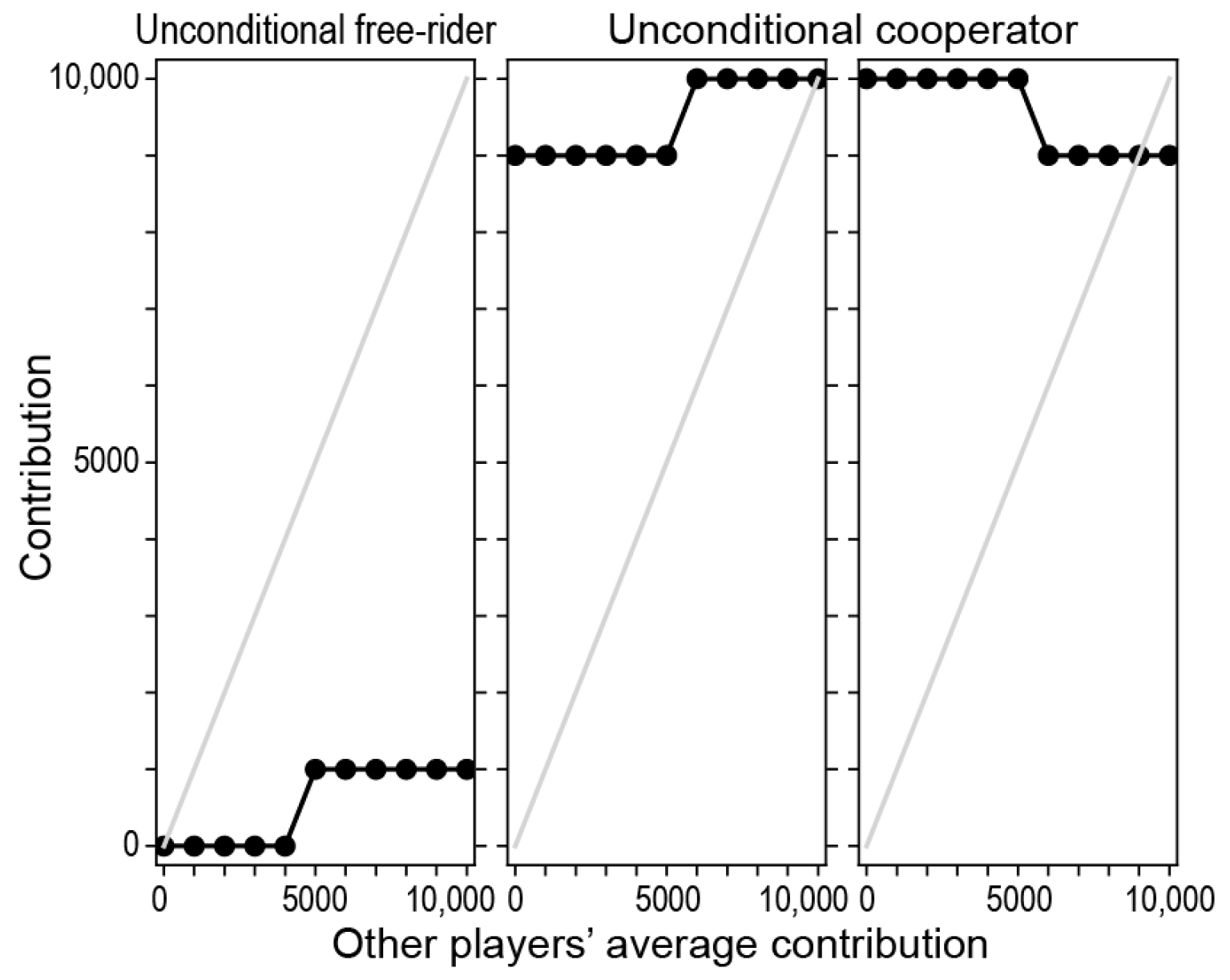
- Unconditional cooperators: contribution is always higher than 75%.
- Unconditional free riders: contribution is always below 25%.
- Perfect conditional cooperators: contributions match the others’ contributions exactly.
- Hump-shaped contributors: the contribution schedule has a maximum contribution that is not at 0 or the maximum contributions of others. The increasing part (from the beginning to the maximum of the contribution) has a positive Spearman correlation, which is significant at the level. The decreasing part has a negative Spearman correlation, which is significant at the level.
- V-shaped contributors: the contribution schedule starts and ends high, but decreases in the middle. The decreasing part (from the beginning to the minimum of the contributions) has a negative Spearman correlation, which is significant at the level. The increasing part has a positive Spearman correlation, which is significant at the level.
- Conditional cooperators: the contribution is always at least as high as the others’ average contributions. The bottom right panel in Figure 1 shows a conditional cooperator.
- Conditional free riders: the contribution is at most as high as the others’ average contributions. The bottom left and bottom center panels in Figure 1 show conditional free riders.
- Conditional contributors: the Spearman correlation between the others’ investments and the contribution of the focal player is positive and significant at . Some investments are above and some are below the others’ average contributions.
- Negative conditional contributors: the Spearman correlation between the others’ investments and the contribution of the focal player is negative and significant at .
- Others: if the contribution pattern does not fit into any of the above categories, it is labeled as “others”.
2.4. Influence of Demographic Characteristics and Personality Traits on Contributions
3. Discussion
4. Materials and Methods
4.1. Participants
4.2. The Main Research Questions
4.3. The Questionnaire
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abeler, J., & Nosenzo, D. (2015). Self-selection into laboratory experiments: Pro-social motives versus monetary incentives. Experimental Economics, 18(2), 195–214. [Google Scholar] [CrossRef]
- Adres, E., Vashdi, D. R., & Zalmanovitch, Y. (2016). Globalization and the retreat of citizen participation in collective action: A challenge for public administration. Public Administration Review, 76(1), 142–152. [Google Scholar] [CrossRef]
- Ahmed, A. M., & Salas, O. (2009). Is the hand of God involved in human cooperation? International Journal of Social Economics, 36, 70–80. [Google Scholar] [CrossRef]
- Aimone, J. A., Iannaccone, L. R., Makowsky, M. D., & Rubin, J. (2013). Endogenous group formation via unproductive costs. The Review of Economic Studies, 80(4), 1215–1236. [Google Scholar] [CrossRef]
- Alencar, A. I., de Oliveira Siqueira, J., & Yamamoto, M. E. (2008). Does group size matter? Cheating and cooperation in Brazilian school children. Evolution and Human Behavior, 29(1), 42–48. [Google Scholar] [CrossRef]
- Andreozzi, L., Ploner, M., & Saral, A. S. (2020). The stability of conditional cooperation: Beliefs alone cannot explain the decline of cooperation in social dilemmas. Scientific Reports, 10(1), 13610. [Google Scholar] [CrossRef]
- Arechar, A. A., Gächter, S., & Molleman, L. (2018). Conducting interactive experiments online. Experimental Economics, 21(1), 99–131. [Google Scholar] [CrossRef]
- Attanasio, O., Pellerano, L., & Reyes, S. P. (2009). Building trust? Conditional cash transfer programmes and social capital. Fiscal Studies, 30(2), 139–177. [Google Scholar] [CrossRef]
- Balliet, D., Wu, J., & De Dreu, C. K. W. (2014). Ingroup favoritism in cooperation: A meta-analysis. Psychological bulletin, 140(6), 1556–1581. [Google Scholar] [CrossRef]
- Barr, A., Packard, T., & Serra, D. (2014). Participatory accountability and collective action: Experimental evidence from Albania. European Economic Review, 68, 250–269. [Google Scholar] [CrossRef]
- Baumard, N. (2011). Punishment is not a group adaptation: Humans punish to restore fairness rather than to support group cooperation. Mind and Society, 10(1), 1–26. [Google Scholar] [CrossRef]
- Belot, M., Duch, R., & Miller, L. (2015). A comprehensive comparison of students and non-students in classic experimental games. Journal of Economic Behavior & Organization, 113, 26–33. [Google Scholar] [CrossRef]
- Bergantino, A. S., Gil-Gallen, S., & Morone, A. (2023). Do risk and competition trigger conditional cooperation? Evidence from public good experiments. Annals of Public and Cooperative Economics, 94(1), 39–73. [Google Scholar] [CrossRef]
- Bigoni, M., Bortolotti, S., Casari, M., & Gambetta, D. (2019). At the root of the north–south cooperation gap in Italy: Preferences or beliefs? The Economic Journal, 129(619), 1139–1152. [Google Scholar] [CrossRef]
- Bigoni, M., Bortolotti, S., Casari, M., Gambetta, D., & Pancotto, F. (2016). Amoral familism, social capital, or trust? The behavioural foundations of the Italian north–south divide. The Economic Journal, 126(594), 1318–1341. [Google Scholar] [CrossRef]
- Bilancini, E., Boncinelli, L., & Celadin, T. (2022). Social value orientation and conditional cooperation in the online one-shot public goods game. Journal of Economic Behavior & Organization, 200, 243–272. [Google Scholar] [CrossRef]
- Björk, L., Kocher, M., Martinsson, P., & Nam Khanh, P. (2016). Cooperation under risk and ambiguity. Working Papers in Economics 683. University of Gothenburg. Available online: https://gupea.ub.gu.se/handle/2077/50814 (accessed on 8 September 2024).
- Bowles, S., & Gintis, H. (2003). The origin of human cooperation. In P. Hammerstein (Ed.), The genetic and cultural origins of cooperation. MIT Press. [Google Scholar]
- Brandts, J., & Charness, G. (2011). The strategy versus the direct-response method: A first survey of experimental comparisons. Experimental Economics, 14(3), 375–398. [Google Scholar] [CrossRef]
- Buisson, M.-C., Das, A., & Mukherji, A. (2013). What determines contribution to a common fund for upkeep of water infrastructures? Evidence from experimental game in coastal Bangladesh. CPWF. [Google Scholar]
- Burlando, R. M., & Guala, F. (2005). Heterogeneous agents in Public Goods experiments. Experimental Economics, 8(1), 35–54. [Google Scholar] [CrossRef]
- Burton-Chellew, M. N., D’Amico, V., & Guérin, C. (2022). The strategy method risks conflating confusion with a social preference for conditional cooperation in Public Goods Games. Games, 13(6), 69. [Google Scholar] [CrossRef]
- Burton-Chellew, M. N., El Mouden, C., & West, S. A. (2016). Conditional cooperation and confusion in public-goods experiments. Proceedings of the National Academy of Sciences, USA, 113(5), 1291–1296. [Google Scholar] [CrossRef]
- Buser, T., & Dreber, A. (2016). The flipside of comparative payment schemes. Management Science, 62(9), 2626–2638. [Google Scholar] [CrossRef]
- Cadsby, C. B., Hamaguchi, Y., Kawagoe, T., Maynes, E., & Song, F. (2007). Cross-national gender differences in behavior in a threshold public goods game: Japan versus Canada. Journal of Economic Psychology, 28(2), 242–260. [Google Scholar] [CrossRef]
- Cardenas, J. C., Rodriguez, L. A., & Johnson, N. (2010). Collective action for watershed management: Field experiments in Colombia and Kenya. Environment and Development Economics, 16(3), 275–303. [Google Scholar] [CrossRef]
- Carpenter, J. P., Daniere, A. G., & Takahashi, L. M. (2004). Cooperation, trust, and social capital in Southeast Asian urban slums. Journal of Economic Behavior & Organization, 55(4), 533–551. [Google Scholar] [CrossRef]
- Cartwright, E. J., & Lovett, D. (2014). Conditional cooperation and the marginal per capita return in Public Good Games. Games, 5(4), 234–256. [Google Scholar] [CrossRef]
- Casler, K., Bickel, L., & Hackett, E. (2013). Separate but equal? A comparison of participants and data gathered via Amazon’s MTurk, social media, and face-to-face behavioral testing. Computers in Human Behavior, 29(6), 2156–2160. [Google Scholar] [CrossRef]
- Chaudhuri, A., Graziano, S., & Maitra, P. (2006). Social learning and norms in a public goods experiment with inter-generational advice. The Review of Economic Studies, 73(2), 357–380. [Google Scholar] [CrossRef]
- Cherry, T. L., McEvoy, D. M., & Sælen, H. (2017). Conditional cooperation and cultural worldviews. Economics Letters, 158, 51–53. [Google Scholar] [CrossRef]
- Colasante, A., García-Gallego, A., Georgantzis, N., Morone, A., & Temerario, T. (2019). Intragroup competition in public good games: The role of relative performance incentives and risk attitudes. Journal of Public Economic Theory, 21(5), 847–865. [Google Scholar] [CrossRef]
- Cox, C. A., & Stoddard, B. (2018). Strategic thinking in public goods games with teams. Journal of Public Economics, 161, 31–43. [Google Scholar] [CrossRef]
- Cubitt, R., Gächter, S., & Quercia, S. (2017). Conditional cooperation and betrayal aversion. Journal of Economic Behavior & Organization, 141, 110–121. [Google Scholar] [CrossRef]
- Czibor, A., & Bereczkei, T. (2010). Ki nyeri meg a versenyt? Egy kompetitív kísérleti játék tanulságai. [Who will win the competition? Personality, strategy and success in a competitive game.]. Magyar Pszichológiai Szemle, 65(1), 165–182. [Google Scholar] [CrossRef]
- Daikeler, J., Bošnjak, M., & Lozar Manfreda, K. (2019). Web versus other survey modes: An updated and extended meta-analysis comparing response rates. Journal of Survey Statistics and Methodology, 8(3), 513–539. [Google Scholar] [CrossRef]
- Dal Bó, P., & Fréchette, G. R. (2011). The evolution of cooperation in infinitely repeated games: Experimental evidence. American Economic Review, 101(1), 411–429. [Google Scholar] [CrossRef]
- Dal Bó, P., & Fréchette, G. R. (2018). On the determinants of cooperation in infinitely repeated games: A survey. Journal of Economic Literature, 56(1), 60–114. [Google Scholar] [CrossRef]
- Dal Bó, P., & Fréchette, G. R. (2019). Strategy choice in the infinitely repeated Prisoner’s Dilemma. American Economic Review, 109(11), 3929–3952. [Google Scholar] [CrossRef]
- Dariel, A., & Nikiforakis, N. (2014). Cooperators and reciprocators: A within-subject analysis of pro-social behavior. Economics Letters, 122(2), 163–166. [Google Scholar] [CrossRef]
- de Oliveira, A. C. M., Croson, R. T. A., & Eckel, C. (2015). One bad apple? Heterogeneity and information in public good provision. Experimental Economics, 18(1), 116–135. [Google Scholar] [CrossRef]
- Diederich, J., Goeschl, T., & Waichman, I. (2016). Group size and the (in)efficiency of pure public good provision. European Economic Review, 85, 272–287. [Google Scholar] [CrossRef]
- Dodou, D., & de Winter, J. C. F. (2014). Social desirability is the same in offline, online, and paper surveys: A meta-analysis. Computers in Human Behavior, 36, 487–495. [Google Scholar] [CrossRef]
- Eckel Catherine, C. (2015). Four classic public goods experiments: A replication study. In H. Harwell (Ed.), Replication in experimental economics (Vol. 18, pp. 13–40). Emerald Group Publishing Limited. [Google Scholar]
- Falk, A., Becker, A., Dohmen, T., Enke, B., Huffman, D., & Sunde, U. (2018). Global evidence on economic preferences. The Quarterly Journal of Economics, 133(4), 1645–1692. [Google Scholar] [CrossRef]
- Falk, A., Becker, A., Dohmen, T., Huffman, D., & Sunde, U. (2023). The preference survey module: A validated instrument for measuring risk, time, and social preferences. Management Science, 69(4), 1935–1950. [Google Scholar] [CrossRef]
- Fallucchi, F., Luccasen, R. A., & Turocy, T. L. (2019). Identifying discrete behavioural types: A re-analysis of public goods game contributions by hierarchical clustering. Journal of the Economic Science Association, 5(2), 238–254. [Google Scholar] [CrossRef]
- Fehr, E., & Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. The Quarterly Journal of Economics, 114(3), 817–868. [Google Scholar] [CrossRef]
- Ferraro, P. J., & Vossler, C. A. (2010). The source and significance of confusion in Public Goods experiments. The B.E. Journal of Economic Analysis & Policy, 10(1), 53. [Google Scholar] [CrossRef]
- Fischbacher, U., & Gächter, S. (2010). Social preferences, beliefs, and the dynamics of free riding in Public Goods experiments. The American Economic Review, 100(1), 541–556. [Google Scholar] [CrossRef]
- Fischbacher, U., Gächter, S., & Fehr, E. (2001). Are people conditionally cooperative? Evidence from a public goods experiment. Economics Letters, 71(3), 397–404. [Google Scholar] [CrossRef]
- Fischbacher, U., Gächter, S., & Quercia, S. (2012). The behavioral validity of the strategy method in public good experiments. Journal of Economic Psychology, 33(4), 897–913. [Google Scholar] [CrossRef]
- Fischbacher, U., Schudy, S., & Teyssier, S. (2014). Heterogeneous reactions to heterogeneity in returns from public goods. Social Choice and Welfare, 43(1), 195–217. [Google Scholar] [CrossRef]
- Fosgaard, T. R., Hansen, L. G., & Wengström, E. (2014). Understanding the nature of cooperation variability. Journal of Public Economics, 120, 134–143. [Google Scholar] [CrossRef]
- Fosgaard, T. R., & Piovesan, M. (2016). Nudge for (the Public) Good: How defaults can affect cooperation. PLoS ONE, 10(12), e0145488. [Google Scholar] [CrossRef] [PubMed]
- Frey, U. J. (2017). Cooperative strategies outside the laboratory—Evidence from a long-term large-N-study in five countries. Evolution and Human Behavior, 38(1), 109–116. [Google Scholar] [CrossRef]
- Gächter, S., & Fages, D. M. (2023). Using the strategy method and elicited beliefs to explain group size and MPCR effects in Public Good experiments. IZA Discussion Paper 16605. IZA—Institute of Labor Economics. [Google Scholar] [CrossRef]
- Gächter, S., Herrmann, B., & Thöni, C. (2004). Trust, voluntary cooperation, and socio-economic background: Survey and experimental evidence. Journal of Economic Behavior & Organization, 55(4), 505–531. [Google Scholar] [CrossRef]
- Gächter, S., Herrmann, B., & Thöni, C. (2010). Culture and cooperation. Philosophical Transactions of the Royal Society B: Biological Sciences, 365(1553), 2651–2661. [Google Scholar] [CrossRef]
- Gächter, S., Kölle, F., & Quercia, S. (2017). Reciprocity and the tragedies of maintaining and providing the commons. Nature Human Behaviour, 1(9), 650–656. [Google Scholar] [CrossRef]
- Gächter, S., Kölle, F., & Quercia, S. (2022). Preferences and perceptions in provision and maintenance public goods. Games and Economic Behavior, 135, 338–355. [Google Scholar] [CrossRef]
- Grandjean, G., Lefebvre, M., & Mantovani, M. (2022). Preferences and strategic behavior in public goods games. Journal of Economic Behavior & Organization, 195, 171–185. [Google Scholar] [CrossRef]
- Granulo, A., Kerschreiter, R., & Kocher, M. G. (2023). Cooperation and confusion in public goods games: Confusion cannot explain contribution patterns. Journal of the Economic Science Association, 9(2), 308–318. [Google Scholar] [CrossRef]
- Griskevicius, V., Delton, A. W., Robertson, T. E., & Tybur, J. M. (2011a). Environmental contingency in life history strategies: The influence of mortality and socioeconomic status on reproductive timing. Journal of Personality and Social Psychology, 100(2), 241–254. [Google Scholar] [CrossRef] [PubMed Central]
- Griskevicius, V., Tybur, J. M., Delton, A. W., & Robertson, T. E. (2011b). The influence of mortality and socioeconomic status on risk and delayed rewards: A life history theory approach. Journal of Personality and Social Psychology, 100(6), 1015–1026. [Google Scholar] [CrossRef] [PubMed Central]
- Guilfoos, T., & Kurtz, K. J. (2017). Evaluating the role of personality trait information in social dilemmas. Journal of Behavioral and Experimental Economics, 68, 119–129. [Google Scholar] [CrossRef]
- Hagen, E. H., & Hammerstein, P. (2006). Game theory and human evolution: A critique of some recent interpretations of experimental games. Theoretical Population Biology, 69, 339–348. [Google Scholar] [CrossRef]
- Hardin, G. (1968). The tragedy of the commons. Science, 162, 1243–1248. [Google Scholar] [CrossRef] [PubMed]
- Hartig, B., Irlenbusch, B., & Kölle, F. (2015). Conditioning on what? Heterogeneous contributions and conditional cooperation. Journal of Behavioral and Experimental Economics, 55, 48–64. [Google Scholar] [CrossRef]
- Hergueux, J., & Jacquemet, N. (2015). Social preferences in the online laboratory: A randomized experiment. Experimental Economics, 18(2), 251–283. [Google Scholar] [CrossRef]
- Herrmann, B., & Thöni, C. (2009). Measuring conditional cooperation: A replication study in Russia. Experimental Economics, 12(1), 87–92. [Google Scholar] [CrossRef]
- Herrmann, B., Thöni, C., & Gächter, S. (2008). Antisocial punishment across societies. Science, 319(5868), 1362–1367. [Google Scholar] [CrossRef]
- Hiraishi, K., Shikishima, C., Yamagata, S., & Ando, J. (2015). Heritability of decisions and outcomes of public goods games. Frontiers in Psychology, 6, 373. [Google Scholar] [CrossRef]
- Isaac, R. M., Walker, J. M., & Williams, A. W. (1994). Group size and the voluntary provision of public goods: Experimental evidence utilizing large groups. Journal of Public Economics, 54(1), 1–36. [Google Scholar] [CrossRef]
- Ishii, K., & Kurzban, R. (2008). Public Goods Games in Japan. Human Nature, 19(2), 138–156. [Google Scholar] [CrossRef]
- Isler, O., Gächter, S., Maule, A. J., & Starmer, C. (2021). Contextualised strong reciprocity explains selfless cooperation despite selfish intuitions and weak social heuristics. Scientific Reports, 11(1), 13868. [Google Scholar] [CrossRef] [PubMed]
- Kamei, K. (2012). From locality to continent: A comment on the generalization of an experimental study. The Journal of Socio-Economics, 41(2), 207–210. [Google Scholar] [CrossRef]
- Kaplan, H. S., Hooper, P. L., & Gurven, M. (2009). The evolutionary and ecological roots of human social organization. Philosophical Transactions of the Royal Society B: Biological Sciences, 364(1533), 3289–3299. [Google Scholar] [CrossRef] [PubMed]
- Katuščák, P., & Miklánek, T. (2023). What drives conditional cooperation in public good games? Experimental Economics, 26(2), 435–467. [Google Scholar] [CrossRef]
- Katuščák, P., & Nikolaychuk, O. (Eds.). (2023). How unconditional is conditional cooperation? Center for Economic Research and Graduate Education. [Google Scholar]
- Keil, J., Michel, A., Sticca, F., Leipold, K., Klein, A. M., Sierau, S., von Klitzing, K., & White, L. O. (2017). The Pizzagame: A virtual public goods game to assess cooperative behavior in children and adolescents. Behavior Research Methods, 49(4), 1432–1443. [Google Scholar] [CrossRef] [PubMed]
- Kocher, M. G., Cherry, T., Kroll, S., Netzer, R. J., & Sutter, M. (2008). Conditional cooperation on three continents. Economics Letters, 101(3), 175–178. [Google Scholar] [CrossRef]
- Kocher, M. G., Martinsson, P., Matzat, D., & Wollbrant, C. (2015). The role of beliefs, trust, and risk in contributions to a public good. Journal of Economic Psychology, 51, 236–244. [Google Scholar] [CrossRef]
- Koopmans, R., & Rebers, S. (2009). Collective action in culturally similar and dissimilar groups: An experiment on parochialism, conditional cooperation, and their linkages. Evolution and Human Behavior, 30(3), 201–211. [Google Scholar] [CrossRef]
- Kumar, P., & Kant, S. (2016). Revealed social preferences and joint forest management outcomes. Forest Policy and Economics, 72, 37–45. [Google Scholar] [CrossRef]
- Lamba, S., & Mace, R. (2011). Demography and ecology drive variation in cooperation across human populations. Proceedings of the National Academy of Sciences, USA, 108(35), 14426–14430. [Google Scholar] [CrossRef]
- Ledyard, J. O. (1995). Public Goods: A survey of experimental research. In J. Kagel, & A. Roth (Eds.), Handbook of experimental economics (pp. 111–194). Princeton University Press. [Google Scholar]
- Leibbrandt, A., Ramalingam, A., Sääksvuori, L., & Walker, J. M. (2015). Incomplete punishment networks in public goods games: Experimental evidence. Experimental Economics, 18(1), 15–37. [Google Scholar] [CrossRef]
- Li, T., & Noussair, C. N. (2024). Conditional cooperation and group size: Experimental evidence from a public good game. Journal of the Economic Science Association, 10(1), 98–112. [Google Scholar] [CrossRef]
- List, J. A. (2004). Young, selfish and male: Field evidence of social preferences. The Economic Journal, 114(492), 121–149. [Google Scholar] [CrossRef]
- Lotito, G., Migheli, M., & Ortona, G. (2013). Is cooperation instinctive? Evidence from the response times in a public goods game. Journal of Bioeconomics, 15(2), 123–133. [Google Scholar] [CrossRef]
- Makowsky, M. D., Orman, W. H., & Peart, S. J. (2014). Playing with other people’s money: Contributions to public goods by trustees. Journal of Behavioral and Experimental Economics, 53, 44–55. [Google Scholar] [CrossRef]
- Markowska-Przybyła, U., & Ramsey, D. M. (2018). Gender as a factor determining declarations to cooperate and cooperative behaviour among Polish students. Economics and Sociology, 11(1), 218–232. [Google Scholar] [CrossRef]
- Martinsson, P., Pham-Khanh, N., & Villegas-Palacio, C. (2013). Conditional cooperation and disclosure in developing countries. Journal of Economic Psychology, 34, 148–155. [Google Scholar] [CrossRef]
- Martinsson, P., Villegas-Palacio, C., & Wollbrant, C. (2009). Conditional cooperation and social group—Experimental results from Colombia. Gothenburg University. [Google Scholar]
- Mertins, V., Schote, A. B., Hoffeld, W., Griessmair, M., & Meyer, J. (2011). Genetic susceptibility for individual cooperation preferences: The role of monoamine oxidase a gene (MAOA) in the voluntary provision of Public Goods. PLoS ONE, 6(6), e20959. [Google Scholar] [CrossRef]
- Muller, L., Sefton, M., Steinberg, R., & Vesterlund, L. (2008). Strategic behavior and learning in repeated voluntary contribution experiments. Journal of Economic Behavior & Organization, 67(3), 782–793. [Google Scholar] [CrossRef]
- Nagatsu, M., Larsen, K., Karabegovic, M., Székely, M., Mønster, D., & Michael, J. (2018). Making good cider out of bad apples—Signaling expectations boosts cooperation among would-be free riders. Judgment and Decision Making, 13(1), 137–149. [Google Scholar] [CrossRef]
- Neal, Z., Neal, J. W., & Piteo, A. (2020). Call me maybe: Using incentives and follow-ups to increase principals’ survey response rates. Journal of Research on Educational Effectiveness, 13(4), 784–793. [Google Scholar] [CrossRef]
- Neugebauer, T., Perote, J., Schmidt, U., & Loos, M. (2009). Selfish-biased conditional cooperation: On the decline of contributions in repeated public goods experiments. Journal of Economic Psychology, 30(1), 52–60. [Google Scholar] [CrossRef]
- Nielsen, U. H., Tyran, J.-R., & Wengström, E. (2014). Second thoughts on free riding. Economics Letters, 122(2), 136–139. [Google Scholar] [CrossRef]
- Nishi, A., Christakis, N. A., & Rand, D. G. (2017). Cooperation, decision time, and culture: Online experiments with American and Indian participants. PLoS ONE, 12(2), e0171252. [Google Scholar] [CrossRef]
- Orosz, G., Tóth-Király, I., Büki, N., Ivaskevics, K., Bőthe, B., & Fülöp, M. (2018). The four faces of competition: The development of the multidimensional competitive orientation inventory. Frontiers in Psychology, 9, 779. [Google Scholar] [CrossRef] [PubMed]
- Ostrom, E. (1990). Governing the commons: The evolution of institutions for collective action. Cambridge University Press. [Google Scholar]
- Oyediran, O. A., Rivas, M. F., Coulson, M., & Kernohan, D. (2018). Cooperation and optimism in a social dilemma. Bulletin of Economic Research, 70(4), 335–340. [Google Scholar] [CrossRef]
- Poynton, T. A., DeFouw, E. R., & Morizio, L. J. (2019). A systematic review of online response rates in four counseling journals. Journal of Counseling & Development, 97(1), 33–42. [Google Scholar] [CrossRef]
- Préget, R., Nguyen-Van, P., & Willinger, M. (2016). Who are the voluntary leaders? Experimental evidence from a sequential contribution game. Theory and Decision, 81(4), 581–599. [Google Scholar] [CrossRef]
- Rand, D. G., Greene, J. D., & Nowak, M. A. (2012). Spontaneous giving and calculated greed. Nature, 489(7416), 427–430. [Google Scholar] [CrossRef]
- Rand, D. G., & Nowak, M. A. (2013). Human cooperation. Trends in Cognitive Sciences, 17(8), 413–425. [Google Scholar] [CrossRef]
- Rand, D. G., Peysakhovich, A., Kraft-Todd, G. T., Newman, G. E., Wurzbacher, O., Nowak, M. A., & Greene, J. D. (2014). Social heuristics shape intuitive cooperation. Nature Communications, 5(1), 3677. [Google Scholar] [CrossRef]
- Rieger, M., & Mata, R. (2013). On the generality of age differences in social and nonsocial decision making. The Journals of Gerontology: Series B, 70(2), 200–212. [Google Scholar] [CrossRef] [PubMed]
- Romano, A., Balliet, D., Yamagishi, T., & Liu, J. H. (2017). Parochial trust and cooperation across 17 societies. Proceedings of the National Academy of Sciences, USA, 114(48), 12702–12707. [Google Scholar] [CrossRef] [PubMed]
- Romano, A., Sutter, M., Liu, J. H., Yamagishi, T., & Balliet, D. (2021). National parochialism is ubiquitous across 42 nations around the world. Nature Communications, 12(1), 4456. [Google Scholar] [CrossRef] [PubMed]
- Romero, J., & Rosokha, Y. (2023). Mixed strategies in the indefinitely repeated Prisoner’s Dilemma. Econometrica, 91(6), 2295–2331. [Google Scholar] [CrossRef]
- Rustagi, D., Engel, S., & Kosfeld, M. (2010). Conditional cooperation and costly monitoring explain success in forest commons management. Science, 330(6006), 961–965. [Google Scholar] [CrossRef]
- Sally, D. (1995). Conversation and cooperation in social dilemmas: A meta-analysis of experiments from 1958 to 1992. Rationality and Society, 7(1), 58–92. [Google Scholar] [CrossRef]
- Sammut, R., Griscti, O., & Norman, I. J. (2021). Strategies to improve response rates to web surveys: A literature review. International Journal of Nursing Studies, 123, 104058. [Google Scholar] [CrossRef]
- Schroeder, K. B., McElreath, R., & Nettle, D. (2013). Variants at serotonin transporter and 2A receptor genes predict cooperative behavior differentially according to presence of punishment. Proceedings of the National Academy of Sciences, USA, 110(10), 3955–3960. [Google Scholar] [CrossRef]
- Schroeder, K. B., Nettle, D., & McElreath, R. (2015). Interactions between personality and institutions in cooperative behaviour in humans. Philosophical Transactions of the Royal Society B: Biological Sciences, 370, 20150011. [Google Scholar] [CrossRef]
- Selten, R. (1967). Die Strategiemethode zur Erforschung des eingeschränkt rationalen Verhaltens im Rahmen eines Oligopolexperimente. In H. Sauermann (Ed.), Beiträge zur experimentellen Wirtschaftsforschung (pp. 136–168). J. C. B. Mohr. [Google Scholar]
- Siva Durga Prasad Nayak, M., & Narayan, K. A. (2019). Strengths and weaknesses of online surveys. IOSR Journal of Humanities and Social Sciences, 24(5), 31–38. [Google Scholar] [CrossRef]
- Soler, M. (2012). Costly signaling, ritual and cooperation: Evidence from Candomblé, an Afro-Brazilian religion. Evolution and Human Behavior, 33(4), 346–356. [Google Scholar] [CrossRef]
- Su, Z., Wei, G., & Binbin, F. (2015). Cognitive ability and cooperation: Evidence from the public goods experiments. Annals of Economics and Finance, 16(1), 43–68. [Google Scholar]
- Teyssier, S. (2012). Inequity and risk aversion in sequential public good games. Public Choice, 151(1), 91–119. [Google Scholar] [CrossRef]
- Thöni, C., Tyran, J.-R., & Wengström, E. (2012). Microfoundations of social capital. Journal of Public Economics, 96(7), 635–643. [Google Scholar] [CrossRef]
- Thöni, C., & Volk, S. (2018). Conditional cooperation: Review and refinement. Economics Letters, 171, 37–40. [Google Scholar] [CrossRef]
- van Hoorn, J., van Dijk, E., Meuwese, R., Rieffe, C., & Crone, E. A. (2016). Peer influence on prosocial behavior in adolescence. Journal of Research on Adolescence, 26(1), 90–100. [Google Scholar] [CrossRef]
- Vásárhelyi, Z., & Scheuring, I. (2018). Behavioral specialization during the Neolithic—An evolutionary model. Frontiers in Sociology, 3, 35. [Google Scholar] [CrossRef]
- Vogelsang, M., Jensen, K., Kirschner, S., Tennie, C., & Tomasello, M. (2014). Preschoolers are sensitive to free riding in a public goods game. Frontiers in Psychology, 5, 729. [Google Scholar] [CrossRef]
- Volk, S., Thöni, C., & Ruigrok, W. (2012). Temporal stability and psychological foundations of cooperation preferences. Journal of Economic Behavior & Organization, 81(2), 664–676. [Google Scholar] [CrossRef]
- Vollan, B., Landmann, A., Zhou, Y., Hu, B., & Herrmann-Pillath, C. (2017). Cooperation and authoritarian values: An experimental study in China. European Economic Review, 93, 90–105. [Google Scholar] [CrossRef][Green Version]
- Weber, T. O., Schulz, J. F., Beranek, B., Lambarraa-Lehnhardt, F., & Gächter, S. (2023). The behavioral mechanisms of voluntary cooperation across culturally diverse societies: Evidence from the US, the UK, Morocco, and Turkey. Journal of Economic Behavior & Organization, 215, 134–152. [Google Scholar] [CrossRef]
- Weber, T. O., Weisel, O., & Gächter, S. (2018). Dispositional free riders do not free ride on punishment. Nature Communications, 9(1), 2390. [Google Scholar] [CrossRef] [PubMed]
- Whitt, S., & Wilson, R. K. (2007). Public goods in the field: Katrina evacuees in Houston. Southern Economic Journal, 74(2), 377–387. [Google Scholar] [CrossRef]
- Wu, M.-J., Zhao, K., & Fils-Aime, F. (2022). Response rates of online surveys in published research: A meta-analysis. Computers in Human Behavior Reports, 7, 100206. [Google Scholar] [CrossRef]
- Yamakawa, T., Okano, Y., & Saijo, T. (2016). Detecting motives for cooperation in public goods experiments. Experimental Economics, 19(2), 500–512. [Google Scholar] [CrossRef]
| Conditional | Free Rider | Hump-Shaped | Unc. Cooperator | Number of Participants | Country | Ref. |
|---|---|---|---|---|---|---|
| 50 | 29.5 | 13.6 | - | 44 | Switzerland | (Fischbacher et al., 2001) |
| 80.6 | 8.3 | - | - | 36 | USA | (Kocher et al., 2008) |
| 41.7 | 36.1 | 11.1 | - | 36 | Japan | (Kocher et al., 2008) |
| 44.4 | 22.2 | 11.1 | - | 36 | Austria | (Kocher et al., 2008) |
| 38 | 35 | 15 | 1.6 | 60 | UK | (Muller et al., 2008) |
| 58.3 | 14.6 | 8.3 | - | 96 | Colombia | (Martinsson et al., 2009) |
| 55.5 | 6.3 | 7.5 | - | 160 | Russia | (Herrmann & Thöni, 2009) |
| 55 | 23 | 12 | - | 140 | Switzerland | (Fischbacher & Gächter, 2010) |
| 34.0 | 11.5 | 2.95 | 2.2 | 679 | Ethiopia | (Rustagi et al., 2010) |
| 58.3 | 25.0 | 13.9 | - | 72 | 4 | (Volk et al., 2012) |
| 55.0 | 22.9 | 12.1 | 1.4 | 140 | Switzerland | (Fischbacher et al., 2012) |
| 69 | 15 | - | - | 1488 | Denmark | (Thöni et al., 2012) |
| 50.0 | 25.7 | 14.0 | - | 350 | USA | (Kamei, 2012) |
| 47.8 | 23.3 | 15.1 | - | 272 | USA | (Aimone et al., 2013) |
| 62.5 | 4.2 | 8.3 | - | 48 | Colombia | (Martinsson et al., 2013) |
| 50.0 | 4.2 | 8.3 | - | 48 | Vietnam | (Martinsson et al., 2013) |
| 63.2 | 22.8 | 9.6 | - | 228 | Germany | (Fischbacher et al., 2014) |
| 66.7 | 2 | - | - | 48 | The Netherlands and Switzerland | (Dariel & Nikiforakis, 2014) |
| 68 | 15 | - | - | 1366 | Denmark | (Fosgaard et al., 2014; Nielsen et al., 2014) |
| 51 | 13.5 | 17.7 | - | 96 | USA | (Makowsky et al., 2014) |
| 71.0 | 6.5 | 3.2 | - | 31 | UK | (Cartwright & Lovett, 2014) |
| 63 | 24 | - | - | 128 | Germany | (Hartig et al., 2015) |
| 43.6 | 24.8 | - | - | 296 | Japan | (Hiraishi et al., 2015) |
| 58.13 | 20.16 | 11.63 | - | 144 | Germany | (Kocher et al., 2015) |
| 67. 8 | 15.5 | 4.0 | - | 174 | UK | (Abeler & Nosenzo, 2015) |
| 54.4 | 6.5 | 6.5 | 15.2 | 46 | Denmark | (Fosgaard & Piovesan, 2016) |
| 50 | 21 | 10 | - | 72 | UK | (Burton-Chellew et al., 2016) |
| 37.5 | 22.5 | 15.0 | - | 40 | France | (Préget et al., 2016) |
| 81.7 | 6.7 | 6.7 | - | 36 | Germany | (Björk et al., 2016) |
| 73.6 | 16.9 | 6 | - | 201 | USA 3 | (Cherry et al., 2017) |
| 49 | 9.5 | 4.5 | 4 | 299 | China | (Vollan et al., 2017) |
| 59.7 | 25.6 | - 1 | - | 592 | UK | (Cubitt et al., 2017) |
| 64 | 17 | - | - | 444 | UK | (Gächter et al., 2017) |
| 48.9 | 26.6 | - | - | 184 | UK | (Weber et al., 2018) |
| 56.4 | 21.6 | - | - | 227 | Denmark | (Nagatsu et al., 2018) |
| 66 | 12 | - | 2 | 134 | Italy | (Bigoni et al., 2019) |
| 67 | 21.6 | 7.5 | - | 134 | Italy | (Andreozzi et al., 2020) |
| 42 | 33 | 9 | - | 88 | Czech Republic | (Katuščák & Nikolaychuk, 2023) |
| 57.4 | 3.1 | - | - | 3653 | UK | (Isler et al., 2021) |
| 50 | 0 | 11.1 | - | 36 | Italy | (Bergantino et al., 2023) |
| 80 | 8 | - | - | 703 | USA | (Gächter et al., 2022) |
| 76 | 10 | - | - | 845 | Switzerland | (Burton-Chellew et al., 2022) |
| 64.4 | 2 | 5.2 | - | 250 | USA/UK | (Bilancini et al., 2022) |
| 50 | 30 | 5.2 | - | 192 | France | (Grandjean et al., 2022) |
| 57.6 | 12.0 | 12.6 | - | 192 | Czech Republic | (Katuščák & Miklánek, 2023) |
| 63.4 | 15.1 | 6.5 | - | 93 | Germany | (Granulo et al., 2023) |
| 55 | 11 | 22.6 | - | 106 | USA | (Weber et al., 2023) |
| 52 | 22 | 18.2 | - | 88 | UK | (Weber et al., 2023) |
| 48 | 8 | 28.7 | - | 80 | Morocco | (Weber et al., 2023) |
| 47 | 20 | 7 | - | 86 | Turkey | (Weber et al., 2023) |
| 47.7 | 20.1 | 15.6 | 1.5 | 66 | USA | (Li & Noussair, 2024) |
| 80.4 | 6.8 | 0.7 | 1.5 | 265 | Hungary | This study |
| Cooperation Type | Number Found | Percentage |
|---|---|---|
| Unconditional cooperators | 4 | 1.5% |
| Unconditional free riders | 28 | 10.6% |
| Perfect conditional cooperators | 113 | 42.6% |
| Hump-shaped contributors | 2 | 0.7% |
| V-shaped contributors | 1 | 0.4% |
| Conditional cooperators | 44 | 16.6% |
| Conditional free riders | 36 | 13.6% |
| Conditional contributors | 17 | 6.4% |
| Negative conditional contributors | 0 | 0.0% |
| Others | 20 | 7.6% |
| Characteristic | Standardized Coefficient Beta | p-Value |
|---|---|---|
| Sex | −0.055 | 0.385 |
| Age | −0.121 | 0.168 |
| Highest completed education | −0.072 | 0.297 |
| Student | −0.044 | 0.664 |
| Worker | 0.061 | 0.479 |
| Size of the residential settlement | −0.101 | 0.102 |
| Self-developmental competitive orientation | 0.145 | 0.116 |
| Anxiety-driven competition avoidance | −0.043 | 0.648 |
| Lack of interest in competition | 0.016 | 0.843 |
| Hypercompetitive orientation | −0.176 | 0.010 |
| Fear of losing competition | 0.115 | 0.162 |
| Past resource availability | −0.030 | 0.654 |
| Present resource availability | 0.112 | 0.116 |
| Risk-taking self-assessment | 0.133 | 0.048 |
| Risk-taking lottery method | −0.113 | 0.077 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schäffer, K.; Král, A.; Kun, Á. New Categories of Conditional Contribution Strategies in the Public Goods Game. Games 2025, 16, 22. https://doi.org/10.3390/g16030022
Schäffer K, Král A, Kun Á. New Categories of Conditional Contribution Strategies in the Public Goods Game. Games. 2025; 16(3):22. https://doi.org/10.3390/g16030022
Chicago/Turabian StyleSchäffer, Klaudia, Adrienn Král, and Ádám Kun. 2025. "New Categories of Conditional Contribution Strategies in the Public Goods Game" Games 16, no. 3: 22. https://doi.org/10.3390/g16030022
APA StyleSchäffer, K., Král, A., & Kun, Á. (2025). New Categories of Conditional Contribution Strategies in the Public Goods Game. Games, 16(3), 22. https://doi.org/10.3390/g16030022






