1. Introduction
Ref. [
1] remarkably shows that, when firms compete on quantity using the [
2] adjustment process
1, the Cournot-Nash equilibrium becomes unstable if the number of firms exceeds two. In fact, with linear demand and constant marginal costs, the Cournot-Nash equilibrium loses stability and bounded but perpetual oscillations arise already for a triopoly. For more than three firms oscillations grow unbounded, but they are limited once the non-negativity price and demand constraints bind.
Whereas [
1] focused only on the homogeneous (Cournot) adjustment process, more recent research extends to models of heterogeneous expectations
2. For instance, Ref. [
3] focus on the Cournot heuristic in competition with rational firms, under replicator dynamics. Ref. [
4] extend the framework in which these heuristics compete in a quantity-setting oligopoly with arbitrary number of firms and for general monotone selection dynamics. Each firm chooses a behavioral rule from a finite set of different rules, which are assumed to be commonly known. When making a choice concerning the behavioral rules, a firm takes the past performance of the rules, i.e., the past realized profit net of the cost associated with the behavioral rules to compare fitness. Both past performance and costs associated with the behavioral rules are publicly available. This implies that successful heuristics will continue to be used, while unsuccessful behavioral rules are dropped.
Experimental evidence for the (in)stability and homogeneous learning in Cournot games, even in linear environments, is rather mixed. Ref. [
5] discuss a linear Cournot oligopoly experiment with four firms. They do not find that quantities explode as the [
1] model predicts, instead the time average quantities converge to the Cournot-Nash equilibrium quantity, although there is substantial volatility of the actual period-by-period around the Cournot-Nash equilibrium quantity. Ref. [
6] run laboratory experiments on two types of linear Cournot oligopolies, the one that displays an unique, stable interior Nash equilibrium (Type I) and a Type II oligopoly for which the interior equilibrium is unstable and two additional, stable boundary Nash equilibria emerge (with one firm acting as a de facto monopolist). Subjects learn to play the Type I, interior stable equilibrium, but not the unstable, or even the stable, boundary ones in the Type II oligopoly. Importantly, on the equilibration path, they reject prediction of homogeneous learning theories such as Cournot adjustment, fictitious play or best-reply to the average of opponents’ entire past play
3. The experimental rejection of the homogeneous learning theories above, naturally leads us to consider alternative heuristics and, more generally, heterogenous learning, with rules updating.
Among the alternative heuristics, there is an increasing interest, both theoretical and experimental, in understanding the performance of imitative players. Ref. [
8] show that Cournot markets with players imitating the past successful strategy of their opponents converge to the Walrasian equilibrium. However, the hypothesis that players actually use the imitate-the-best heuristics in Counot games is invalidated, experimentally, by [
9]. They posit that (naive) imitate-the-best players may realize that past period “success” may be purely drive by a particular realization of opponents’ types. Ref. [
10] adds myopic optimizers (Cournot best-responders) to [
8] population of imitate-the-best players, and finds that in stationary distribution of the stochastic process, the imitators are better off. Moreover, Ref. [
11] prove that imitation can be unbeatable if imitate-the-best heuristic is not subjected to a money pump (i.e., game is not of the circular best-reply, Rock-Scissors-Paper type). Subsequently, Ref. [
12] show that unconditional imitation, of the tit-for-tat variety, is essentially unbeatable in class of potential games. Ref. [
13] analyze a Cournot duopoly, subjects earn on average higher profits when playing against “best-response” computers than against “imitate-the-successful” computers. Ref. [
5] find that a process where participants mix between the Cournot adjustment heuristic an imitating the previous period’s average quantity gives the best description of behavior. Our choice of modelling imitation as imitate-the-average lagged strategy in the population is informed, on the one hand, by this experimental result, and, on the other hand, by the evidence against imitate-the-most successful past period strategy in [
9]. The imitate-the-average heuristic will be tested, firstly, against the standard Cournot heuristic, i.e., firms best-respond to average population past play, and secondly, against ‘rational’ players, i.e., players that understand that they are facing a distribution of updating players types (heuristics) and, consequently, they respond optimally to the expected configuration of types in the market. We show that, even if the imitate-the-average tends to stabilize the Cournot equilibrium (the thresholds for which instability sets in is typically higher, ceteris paribus, in comparison to models of heterogeneous learning without imitation), the differential costs of the more sophisticated heuristic over the simpler one rest critical for the instability threshold number of players, as well as for the non-equilibrium dynamics around Cournot-Nash equilibrium.
Outside the oligopoly realm, learning rules evolution has also been investigated in two-person, strategic games. Ref. [
14] look at the interplay of three heuristics—best-response, imitate-the-majority, imitate-the-minority—and show that it may generate complex, non-Nash equilibrium attractors, such as limit cycles, even in simple,
Coordination games. Ref. [
15] finds that, in a coordination game with endogenous updating of myopic best-response imitate-the best heuristic, the efficient equilibrium is selected. Ref. [
16] also considers
coordination games, but with a threewise ecology of best-reply, better-reply and imitate-the best action among the sample of past play and prove that the risk-dominant equilibrium is selected for small sample sizes. Ref. [
17] studies the evolution of bargaining rules (i.e., pie-sharing demands rules) via an external stability argument, by which incumbent rules should do better than mutant demands, reminiscent of the concept of ESS of [
18]. To this rule evolution literature, we contribute the study of a threewise ecology of heuristics—naive best-reply, equilibrium (rational) play and imitate-the-average past play—which, to the best of our knowledge, has not been investigated before. It would be a direct exercise to apply our methodology to the simple
coordination games that the previous work on heterogenous learning rules has focused on.
A somewhat parallel stream of literature deals with the evolution of preferences
4 as the underlying factor upon which selection acts and which, in turns determines the actual strategy choice in the game played. Pioneered by [
19], who shows that utility-maximization (homo economicus) may be just one among many preferences types selected by evolution in the quest of adaptation to environment, this “indirect evolutionary approach” was developed further in the context of two-person games by, e.g., [
20,
21]. They look at stable configurations of preferences-game equilibria and document the striking possibility that non-Nash outcomes and non-maximizing preferences can be stable, evolutionarily. In the IO literature, Ref. [
22] use this indirect approach to show that owners’ preferences overs managers’ incentives do not always converge to profit-maximization, but may favor sales maximization, in Cournot competition or even sales minimization, in differentiated Bertrand oligopolies. Relatedly, Ref. [
23] prove that oligopolists’ preferences may evolve towards total surplus (producer and consumer) maximization, rather than the (narrow) profit-maximization, assumed by the rational producer theory.
Our approach is largely driven by the quest for understanding the behaviour of boundedly rational players, disciplined by the evolutionary selection operating at the level of behavioral rules. In particular, the question of whether learning converges to the Counot equilibrium, in an environment with competing and costly learning rules. Therefore, we put forth, three ecologies of heterogeneous heuristics (Cournot vs. Imitation, Rational vs. Imitation, Rational vs. Cournot vs. Imitation). Both the fixed fractions and evolutionary switching between heuristics scenarios, are discussed. Our concern is, first and foremost, the role and performance of the imitate-the-average heuristic within a given menu of heuristics, and, secondly, if for a given configuration of heuristics, the Cournot-Nash equilibrium is (un)stable. Unlike, for instance, Ref. [
10], our imitate-the-average rule does not always outperforms Cournot, or sophisticated (rational) play, but may co-exist with other heuristics in equilibrium. In contrast to the strong convergence result in [
8], complicated, non-Cournotian equilibrium limit sets (two-cycles, strange attractors) may emerge once learning heterogeneity is endogenized.
Main findings are that, first, the stability of Cournot equilibrium critically depends on the cost advantage of the ‘stable’ heuristic (imitation) vis-a-vis the unstable one (Cournot myopic best-reply): when the (relatively) cheaper behavioral rule is imitation, the dynamics converge to a situation where most firms use this behavioral rule and all firms produce the Cournot-Nash equilibrium quantity, for market sizes for which homogeneous Cournot play is known to destabilize the interior equilibrium (e.g., triopoly). However, instability eventually sets in, if the number of firms passes a higher threshold . In the case when the relatively cheaper heuristic is unstable, complicated endogenous fluctuations may already occur for in particular, when the evolutionary pressure is high. The nonlinearity causing this erratic behavior comes from the endogenously updating of the fractions, because in our leading example the oligopoly specifications were linear. Secondly, when rational firms compete with imitators, in the particular scenario of linear inverse demand and constant marginal cost, the system is always stable regardless of the game and behavioral parameters. Last, in the case when rational firms, Cournot firms and imitators compete, the stability depends on the differential cost of the rational plays versus the Cournot and imitation heuristics, as well as on the magnitude of the evolutionary pressure. For very large intensity of selection ( and for costly rational choice and costless Cournot and imitation rules, we are able to recover analytically the instability threshold in the pairwise contest Cournot vs. imitation.
The remainder of this paper is organized as follows, in
Section 2 the theoretical framework is introduced, namely the quantity-setting oligopoly, the menu of heuristics and the population evolutionary dynamics. In
Section 3 the evolutionary dynamics will be investigated under exogenous population fractions whereas in
Section 4 the stability of systems made of two learning rules will be investigated, under endogenous population dynamics. In
Section 5 the model extended to a three heuristics environment, with rational players, Cournot and imitators competing and switching learning heuristics, according to their relative performance. Finally, we conclude in
Section 6.
2. Set-Up
Consider a finite population of firms who are competing on the market for a certain good, each discrete-time period all producers have to decide their production plans for the next period. However, instead of simultaneously choosing the supplied quantities directly, the firms act according to behavioral rules that exactly prescribe the quantity to be supplied. Before the evolutionary model is studied a brief review of the traditional, static Cournot model will be given.
Consider a symmetric Cournot oligopoly game, where
denotes the quantity supplied by firm
. Next to that let
be the aggregated production. Furthermore let
denote the twice differentiable, nonnegative and non-increasing inverse demand function and let
denote the twice differentiable non-decreasing cost function, which is the same for all firms. For firm
i the resulting profit function from the above described model is given by
where
. Assume that the profit function of a firm is strictly concave in its own output
. The profit maximizing strategy of firm
i, taking the quantity supplied by the competitors as given, results in the well-known best-reply function for firm
i, which is given by
Due to symmetry, all firms have the same best-reply function
. Moreover, the symmetric Cournot-Nash equilibrium quantity
corresponds to the solution of
In the sequel, we will restrict the analysis to oligopolies displaying an unique, interior Nash equilibrium, the so called Type I oligopoly in [
6]
5. This very general class includes, as special cases, oligopolies with linear demand and (i) constant, (ii) increasing and (iii) even decreasing marginal costs, as long as marginal costs do not decrease too fast, compared to the demand function. In Type I duopolies most learning processes (Cournot best-reply, adaptive dynamics, fictititous play, etc) are known to converge to the unique, interior fixed point. This is not the case for the Type II duopolies
6. It is the main reason why we focus on the Type I oligopolies, as we want to isolate the instability built into the the oligopoly game itself from the destabilizing forces that reside in the heuristics’ of choice and their updating mechanism.
The original Cournot specification of [
1] falls within the class of Type I oligopoly and will be used as leading example: an oligopoly game with linear inverse demand and linear costs, given by
respectively. First, in order to have a strictly concave profit function assume that
. Furthermore, for strictly positive prices we assume that
(so that aggregate output
and
. For these specifications of the inverse demand function and cost function the reaction function is given by
Note that if the other firms produce on average more (less) than the Cournot-Nash equilibrium quantity, firm i reacts by producing less (more) than that quantity.
Straightforward calculations show that in this case the Cournot-Nash equilibrium quantity, aggregated production, price and profit are equal to , , .
Traditional Cournot analysis refers to a static environment. However, in a dynamic setting the reaction function introduced above can be used to study the so called Cournot-dynamics where firms best-reply to their expectations
where
denotes the quantity supplied by player
i in period
t and
stands for player’s
i expectations about her opponents’s total output at time
t. The symmetric Cournot-Nash equilibrium where all firms produce
is stable under the Cournot-dynamics if
.
Main interest is on how firm i decides to play and, more specifically, what does firm i believe about when the production decision has to be made. Our key assumption is that firms are choosing their expectation-formation rule (heuristic) based on its performance.
2.1. Learning Heuristics
In the Cournot oligopoly game the producers have to form expectations about opponents’ production plans. Based on this expectation firms decide how much to produce the next period. One approach is to assume complete information, i.e., rational firms with common knowledge of rationality. This implies that firms have perfect foresight about competitors’ aggregated production plan, i.e.,
This results in the following production plan:
Alternatively one may consider rules that require less information, for example
This results in the following production plan:
where firms expect that aggregated production in the next period equals current aggregated production. This is the so called Cournot adjustment heuristic. It is an straightforward exercice to show that, if all firms use the Cournot heuristic, the Cournot-Nash equilibrium is a locally asymptotically stable
7 fixed point of system (
3) whenever
where
is defined as the largest eigenvalue of the Jacobian, evaluated at the equilibrium.
Leading example. From Equation (
2) it can easily be seen that
, meaning that if others’ aggregated output increases by one unit, the Cournot-Nash firms decrease their output by
units. From stability condition (
4) it follows that the Cournot-Nash equilibrium is stable for this specification only when
and unstable when
(and neutrally stable, resulting in bounded oscillations, for
). The reason for this instability is ‘overshooting’: if aggregated output is above (below) the Cournot-Nash equilibrium quantity, firms react by reducing (increasing) their output. For
this aggregated reduction (increase) in output is so large that the resulting deviation of aggregated output from the equilibrium quantity is larger in the next period than in the current, and so on.
It is a broadly supported idea that not all producers best-reply to their expectations. Experiments [
5] show that people often imitate others’ behavior. A heuristic that possibly seizes this production plan is the so called imitation-the-average heuristic. Imitators believe that “everyone else can’t be wrong” and will therefore produce the average of the other players’ production in the next period, i.e.,
Local stability of the Cournot-Nash equilibrium with only imitation firms depends on the eigenvalues of the Jacobian matrix of the system of Equation (
5) evaluated at that Cournot-Nash equilibrium
. This Jacobian matrix is given by
Imitators only respond to other firms’ production and do not respond to their own production, therefore all diagonal elements are equal to zero. If one competitor increases current production by one unit, an imitator will increase next production with
unit, therefore all off-diagonal elements are equal to
. The Jacobian matrix (
6) thus has
eigenvalues equal to
and one eigenvalue equal to
which is the largest in absolute value. Therefore it follows immediately that the Cournot-Nash equilibrium is neutrally stable independent of
n and game structure (demand and cost function). The reason for this is that if one producer changes his production plan the economy will stabilize to a new equilibrium unequal to
and will remain at this new equilibrium until one producer deviates again. In fact this system has infinitely many neutrally stable equilibria, namely if
the system is neutrally stable for all
2.2. Population Dynamics
In the previous section it was shown how the supplied quantities evolve over time under the Cournot and the imitation heuristic. In this section it will be explained how the population fractions evolve over time. Let us first introduce the vector which has entries equal to , which is the fraction of the population that uses heuristic k at time t. Thus for every time t, denotes the K-dimensional vector of fractions for each strategy/heuristic and belongs to the K-dimensional simplex . We will now describe how the fractions evolve over time. It is assumed that the choice of a behavioral rule is based on its past performance, capturing the idea that more successful rules will be used more frequently.
Evolutionary game theory deals with games played within a (large) population over a long time horizon. Its main ingredients are its underlying game, e.g., the Cournot one-shot game, and the evolutionary dynamic class which defines a dynamical system on the state of the population. The evolutionary dynamical system depends on current fractions
and current fitness
. In general, such an evolutionary dynamic in discrete time, describing how the population fractions evolve, is given by
with
the vector of average utilities and
the factor of fractions. To make sure that the population dynamics is well-behaved in terms of dynamic implications we assume that
is continuous, nondecreasing in
, and such that the population state remains in the
K-dimensional unit simplex
. One widely used evolutionary dynamic in the literature on learning in games is the Logit Dynamics (see, e.g., [
26] for an extensive treatment). It can be derived from discrete choice/random utility models and it specifies that fractions of different heuristics are updated according to
The parameter
represents the intensity of selection, and it captures the idea of boundedly rational play, since individuals do not necessarily select the rule that yields the highest utility. Notice that in the extreme case where
we have completely random behavior: the noise is so large that observed average utility is equal for all behavioral rules. Each behavioral rule is thus chosen with equal probability:
. In the other extreme case, when
, everybody switches to the most profitable strategy each period
8.
In case of equal costs of the heuristics, equilibrium fractions are thus given by , since production is equal and thus profits are equal.
In the leading examples we will focus on the Logit evolutionary dynamics. Firstly, because the Logit rule is a standard tool in economics for modelling boundedly rational choice, and, secondly, because it displays nice regularity/continuity conditions .
4. Evolutionary Competition between Two Heuristics
In this Section we develop an evolutionary version of the model outlined in
Section 3, i.e., relaxing the assumption that
is fixed. As before in ever period
t,
n firms play the
n-player Cournot game. We now assume that the fractions of firms using a heuristic
evolves over time according to a general monotone selection dynamic, capturing the idea that heuristics that perform relatively better are more likely to spread through the population. Under the assumption of random interactions, the fitness of heuristic
k is determined by averaging the payoffs from from each interaction with weights given by the chance of that specific state minus the information cost of using the heuristic. Denoting with
the expected payoff vector in period
t, its entries—individual payoff or fitness in biological terms—of strategy 1 is given by:
and with expected profits for heuristic 2 given by
. If the population of firms and the number of groups of
n firms drawn from that population are large enough, average profits will be approximated well by these expected profits, which we will use therefore as a proxy for average profits from now on.
There might be a substantial difference in sophistication between different heuristics. As a consequence some heuristics may require more information or effort to implement than others. Therefore we allow for the possibility that heuristics involve information cost
,
, that may differ across heuristics. Fitness of a heuristic is then given by the average profits generated in the game minus the information costs of acquiring heuristic
k,
. We only use the realized profit to determine the fitness measure of a behavioral rule. The fitness measure can be generalized by weighting the utility of the past
M periods, yielding similar results [
27]. We assume that the above fitness measures
are publicly observable.
Having the fitness measure we are ready to introduce the population dynamics. Let the fraction of firms using the first heuristic be given by
in period
t. This fraction evolves endogenously according to an evolutionary dynamic which is an increasing function in the difference between the current fitness of the two heuristics and current fraction, that is
The map is a continuously differentiable, monotonically increasing function with , , meaning that it is symmetric around , and .
In the following two subsections we will derive two dynamical versions of the two models discussed in
Section 3 and investigate their stability. First we investigate the stability of the Cournot-Nash equilibrium for the model with endogenous fractions of Cournot and imitation firms and second we investigate the stability of the Cournot-Nash equilibrium for the model with endogenous fractions of rational and imitation firms.
4.1. Cournot vs. Imitation Firms with Endogenous Switching
The dynamics in this section consists of three equations, two equations describing the quantity dynamics: the production of the Cournot firms and the production of the imitation firms. Next to that we need one equation to describe the dynamics of the population fraction. The population and quantity dynamics look like the following system of three equations:
where
Note that this is a 3-dimensional dynamical system which dimensions cannot be reduced. Furthermore, the Cournot-Nash equilibrium quantity
is the unique equilibrium quantity of the complete dynamical system. Let
be the unique equilibrium fraction of Cournot players, such that
, with
the differential cost of the Cournot over the Imitation heuristic. For the general, monotone selection population dynamics
we obtain the result stated in the proposition below.
Proposition 3. For i.e., costlier Cournot than Imitation heuristic, the Cournot-Nash equilibrium along with the equilibrium fractions is a locally asymptotically stable, fixed point for the model with endogenous fractions of Cournot and imitators where all firms produce the Cournot-Nash quantity, firms if and only if Leading example. The equilibrium quantities are given by
. Here
, filling this in Equation (
21) gives the stability condition for the leading example. Thus the equilibrium
is stable when
. In the equilibrium, when all firms produce the same quantity, profits are equal and therefore the equilibrium fraction under Logit dynamics simplifies to
. For
(strictly positive cost differential of Cournot over imitation heuristic) and very large intensity of selection
and, therefore stability threshold becomes
10. The same critical instability threshold
n obtains for
coupled with
any level of the intensity of selection
.
In
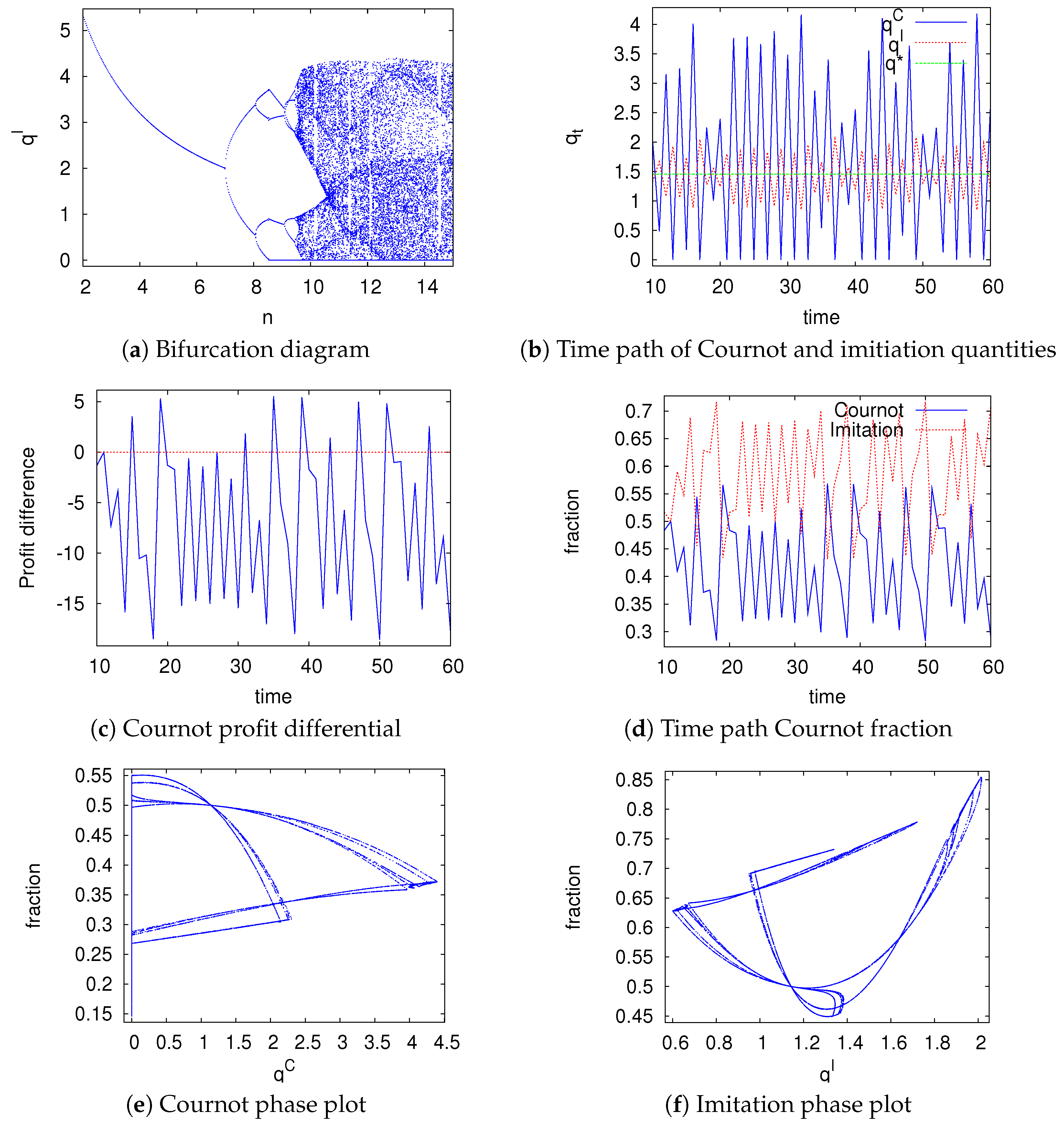
Figure 1 the model is simulated under Logit-dynamics with intensity of choice parameter
, as in [
26]. Panel (a) depicts a period-doubling route to chaotic quantity dynamics as the number of firms
n increases. The first period-doubling bifurcation is for
as calculated analytically. Panel (b) displays oscillating time series of produced quantity by the Cournot and imitation firms and the equilibrium quantity fraction
. As one can see the Cournot quantities are fluctuating more than the imitation quantities. The stabilizing effect of the imitation firms is here clearly visible, when Cournot firms produce more (less) then the Cournot-Nash equilibrium quantity, the imitation firms produce less (more) than the Cournot-Nash equilibrium quantity and therefore decrease the aggregated deviation from the equilibrium. Panel (c) displays the resulting Cournot profit differential
. Panel (d) displays the resulting oscillating time series of the Cournot and imitation fractions. In Panel (e) a phase portrait is shown for the Cournot heuristic whereas in Panel (f) a phase portrait for the imitation heuristic is shown. In Panel (g) the largest Lyapunov exponent for an increasing number of firms is shown. Game and behavioural parameters are equal set to:
,
,
,
,
,
,
. Initial conditions are set equal to:
,
,
When the evolutionary pressure increases, the system evolves to an equilibrium different from the Cournot-Nash equilibrium where the imitation firms produce more than the Cournot-Nash equilibrium whereas the Cournot firms produce less. Imitation profits are therefore much higher and as a consequence the complete population switches to the imitation heuristic.
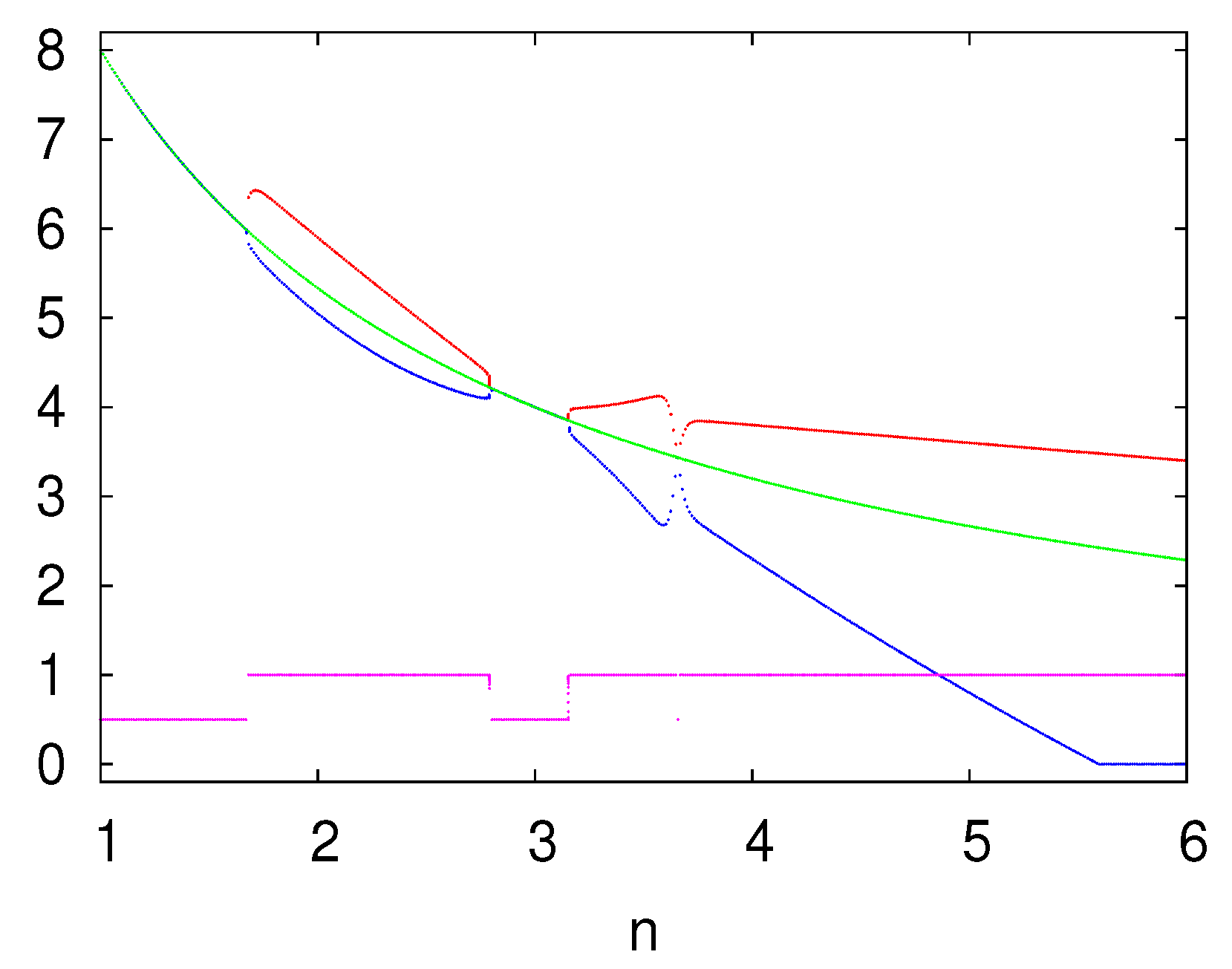
The bifurcation diagram is re-plotted in
Figure 2 under the same game and behavioral parameters and initial conditions, the only difference is that now
. When
the imitation firms produce more then the Cournot-Nash equilibrium quantity while the Cournot firms produce less. This results in higher profits for the imitators and therefore the complete populations switches to imitators
. When
all firms produce the Cournot-Nash equilibrium quantity again, therefore profits and thus fractions are equal. When
the imitation firms produce again more then the equilibrium quantity while the Cournot firms produce less, except when
n is close to
, then all firms produce the Cournot-Nash equilibrium quantity. Finally, when
the imitation firms produce so much that the Cournot firms decide to produce nothing
.
4.2. Rational vs. Imitation Firms with Switching
As in the previous section, we need a 3-dimensional system to describe the dynamics of the model. The rational firms produce each period such that their expected profit is maximized whereas an imitator produces in the next period the currently average played quantity.
The rational quantity dynamics therefore have the following structure
It forms expectations over all possible mixtures of heuristics resulting from randomly drawing
other players from a large population, of which each with chance
is a rational firm too, and with chance
is a imitator. Rational firm
i therefore chooses quantity
such that his objective function, its own expected utility
is maximized given the production of the other players and the population fraction. Here
is the symmetric output level of each of the other rational firms in period
t, and
is the output level of each of the imitator firms in period
t. The first order condition for an optimum is characterized by equality between marginal cost an expected marginal revenue.
Given the value of
and the fraction
, all rational firms coordinate on the same output level
. This gives the first order condition
which equals to
Let the solution to Equation (
23) be given by
, the full system of equations is thus given by
where
. It is easily checked that if the imitators play the Cournot-Nash equilibrium quantity
, or if all firms are rational, then the rational firms will play the Cournot-Nash equilibrium quantity, that is
, for all
and
for all
. Moreover, if a rational firm is certain it will only meet imitation firms (that is
), it plays a best response to the currently average played quantity, that is
, for all
. In the remainder we will denote the partial derivatives of
with respect to
q and
by
and
respectively.
Proposition 4. The Cournot-Nash equilibrium is a locally stable fixed point for the model with endogenous fractions of rational and imitation firms, where all firms produce the Cournot-Nash quantity, if and only if Leading example. Since the stability condition is the similar to the condition derived in
Section 3.2, the equilibrium quantities
and rational play fraction
is stable for all
n in this linear specification.
5. Rational vs. Cournot vs. Imitation with Switching Heuristics
In this section we combine the ideas that we gathered in
Section 4. We will investigate the dynamics when the three heuristics discussed before compete. As before every round
n firms are drawn from a large pool of firms to play the one-shot Cournot game. From this large pool of firms a fraction
plays according to the rational strategy in period
t, a fraction
plays according to the Cournot heuristic in period
t and consequently the fraction of imitators in period
t is determined by
. As in
Section 4 the fitness of a heuristic is determined by the average payoff minus the information cost of using that heuristic. Again the average profits will be approximated by the expected profits but in contrast to
Section 4 the distribution of states now follows a multinomial distribution instead of a binomial distribution. In general the average profit of a firm producing
and competing with other firms that produce either
or
given the fractions
and
is stated below, in this average profit approximation the profit in each state is weighted by the chance of this state.
The summation is over all possible combinations of and , which stand for the number of other firms producing and respectively, that is: Expected profits for heuristic 2 in period t are given by , expected profits for heuristic 3 in period t are given by .
The complete dynamical system consists of five equations, three for the quantity dynamics and two to describe how the fractions evolve. As in all previous sections, the Cournot firms play in the next period a best-response to the current aggregated output of the others, imitators play in the next period the average produced quantity by the others in the current period. Rational players produce every period the quantity that maximizes expected payoff given the fractions and production plans of all other firms (imitators, Cournot players but rational players too). The rational firms produce expectations over all possible mixtures of heuristics resulting from randomly drawing the
other players from the large population of firms. In this setting the rational objective function, its own expected utility is of the following form:
with
denotes the multinomial distribution of three heuristics in the population of firms and
the system’s state variables. The first order condition for an optimum of (
27) is characterized by equality between marginal cost an expected marginal revenue.
Given the value of
, all rational firms coordinate on the same output level
. Differentiating Equation (
27) with respect to
gives the first order condition, which is equal for all rational firms. This first order condition is given by:
which equals to:
Let the solution to this be given by
. The system of quantity dynamics is thus given by
Note that rational player plays such that expected marginal revenue equals marginal cost at
and a Cournot firm plays such that its marginal revenue (of period
t) equals marginal cost (at period
t). Therefore the Cournot heuristic is a lagged version of the rational heuristic if and only if
Thus the Cournot heuristic is only a lagged version of the rational heuristic if the inverse demand is linear. In this specific case the analysis become easier because this gives the possibility to lower the dimension of the dynamical system.
It is easily checked that if the imitation and Cournot firms play the Cournot-Nash equilibrium quantity , or if all firms are rational, the rational firms will play the Cournot-Nash equilibrium quantity, that is , for all and and for all , . In the remainder we will denote by , , , and the partial derivatives of with respect to , , , and respectively, evaluated at the equilibrium , which we will denote by in the remainder of this chapter for notational convenience.
Now that we have the quantity dynamics we can turn to the population dynamics. These are related to the population dynamics from
Section 4 but differ significantly since we are in a three heuristic environment now. The population dynamics, as in
Section 4, depend on relative fitness. Let the fraction dynamics be given by
where
is the fraction of rational firms in period
whereas
is the fraction of Cournot firms in that period. Denoting the rational, Cournot and imitation heuristics’ costs by
respectively, we obtain
, the difference in average fitness of the rational and the Cournot heuristic, and,
the difference in average fitness of the Cournot and the imitation heuristic. Note that
and
are
are continuously differentiable functions where the difference in fitness of the rational and Cournot heuristics and the difference in fitness of the Cournot and imitation heuristic are used as input. The difference in fitness of the rational and imitation heuristic is not used as an input variable since this information is captured implicitly in the other two differences. Note that
is a monotonically increasing function in the first and second element whereas
is decreasing in the first element but increasing in the second element. Furthermore,
. In the remainder of this chapter we denote
and
the partial derivatives of
with respect to the first and the second element respectively and with
and
the partial derivatives of
with respect to the first and the second element respectively.
The full system of quantity and population dynamics is given by:
Since a dynamical system can only depend on lagged variables we substituted
into
. In order to determine the local stability of the unique, interior equilibrium
we need to determine the eigenvalues of the Jacobian matrix evaluated at that equilibrium. The Jacobian of the general oligopoly-general selection dynamic
has very complicated eigenvalues which cannot be expressed in useful functions (see
Appendix A, Proof of Proposition 5, for the full Jacobi matrix), therefore we will restrain the subsequent analysis to the linear-demand, linear-cost oligopoly with Logit Dynamics.
Leading example. We know that the Cournot heuristic is a lagged version of the rational heuristic in this leading example since the inverse demand function is linear, therefore the dimension of the dynamical system can be reduced by one. Note that only the Cournot production is a lagged version of the rational production. The Cournot profits and resulting fractions are in general not lagged rational profits and fractions. Therefore, the restriction of the complete, 5-dim dynamical system to the linear-linear oligopoly with Logit Dynamics becomes 4-dim
This system has one unique equilibrium where all firms produces the Cournot-Nash quantity
. Since production is equal at the equilibrium, profits are equal at the equilibrium. The equilibrium fractions are therefore a function of the information costs and the evolutionary pressure, given by
For general heuristics’ costs—and, therefore, general fractions and —the eigenvalues of the corresponding Jacobian at the rest point are convoluted expressions of model’s parameters, which cannot be meaningfully simplified. Nevertheless, because the rational heuristic is more informationally- and computationally-intensive than the Cournot and the imitation heuristics, it is reasonable to assume a strictly positive cost associated to its use, while setting the costs of the other two heuristics . We obtain the following result:
Proposition 5. For costly, rational heuristic and, costless, Cournot and imitation heuristics the interior, Cournot-Nash equilibrium along with equilibrium fractions is a locally stable fixed point for the model with endogenous fluctuations between of rational, Cournot and imitation firms, if and only if From Equation (
34) we notice first that, when information cost of the rational play
approaches zero, the system is stable for all market sizes
If the cost differential of rational vs. Cournot and imitation play is strictly positive
and intensity of selection
the equilibrium is stable for
For, intermediate, finite
, the equilibrium fractions
, as well as the instability threshold
n are a function of both
and
In the simulations below,
and
, the equilibrium
is stable when
. When
, the system undergoes its first bifurcation. The largest eigenvalue is equal to
at the bifurcation, indicating that the first bifurcation is a period-doubling bifurcation. This is confirmed by the simulations below.
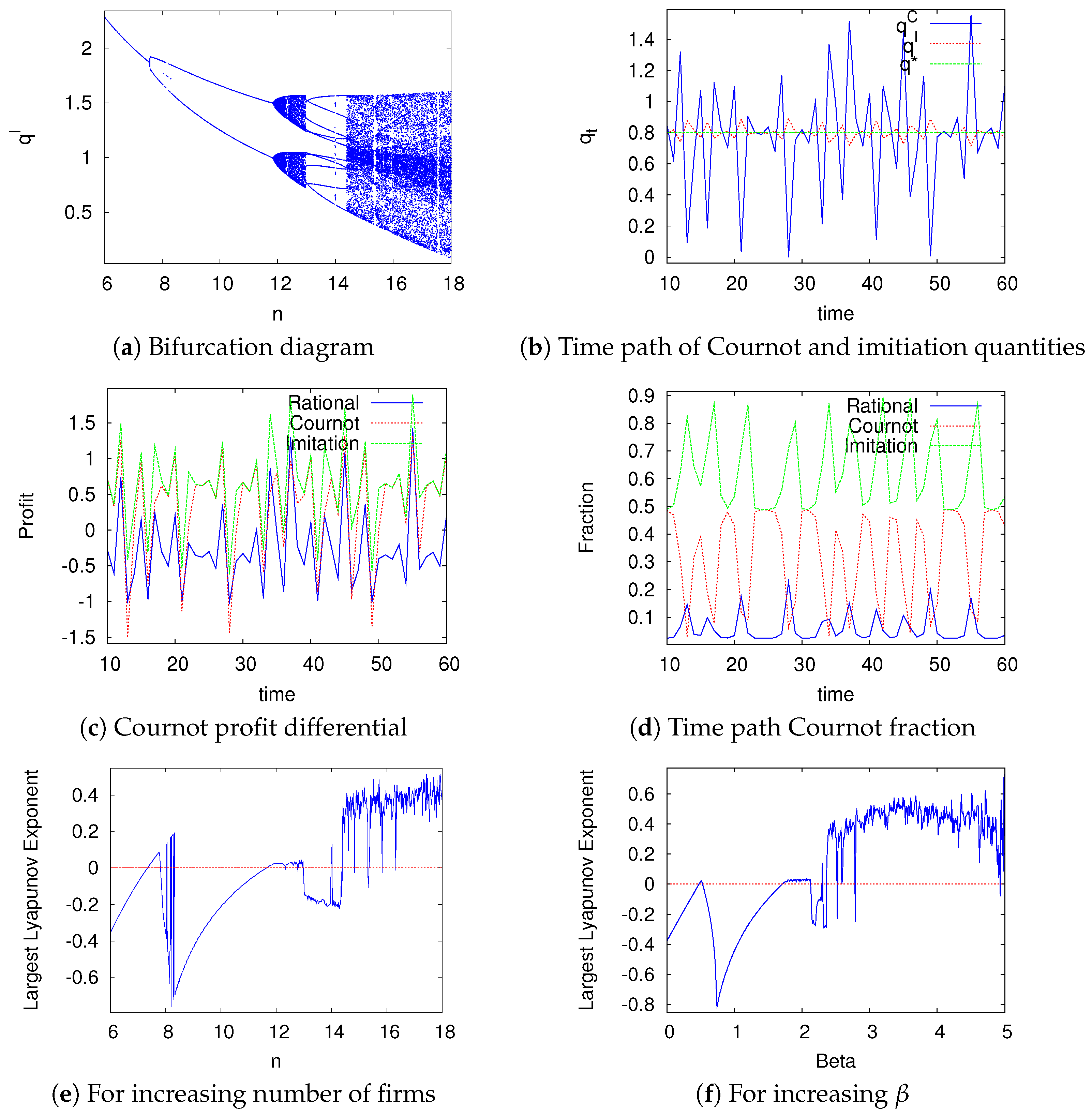
The leading example is simulated in
Figure 3. Panel (a) depicts the bifurcation diagram for increasing number of firms
n. The first period-doubling bifurcation appears, as calculated analytically for
. For
, the system undergoes a Hopf-bifurcation which creates highly non-linear dynamics. For
, the system is in a 10-cycle whereas for
the system becomes chaotic again. Panel (b) displays oscillating time series of produced quantity by the Cournot and imitation firms and the equilibrium quantity fraction
. Since the rational quantity in period
equals the Cournot quantity in period
t this time series is not included. Panel (c) displays the resulting profits. Note that
and
. Panel (d) displays the resulting oscillating time series of the fraction fractions. Due to the information cost the sophisticated rational firms do not perform better than the Cournot and imitation firms resulting in low fractions of rational firms. Moreover, since the imitation profit is at least as high as the Cournot profit, the resulting imitation fraction is at least as high as the Cournot fraction. In Panel (e) the largest Lyapunov exponent for increasing number of firms is shown whereas in Panel (f) the largest Lyapunov exponent for increasing
is shown. Game and behavioural parameters are set equal to:
,
,
,
,
,
,
,
. Initial conditions are set equal to:
,
,
,
,
.
Last,
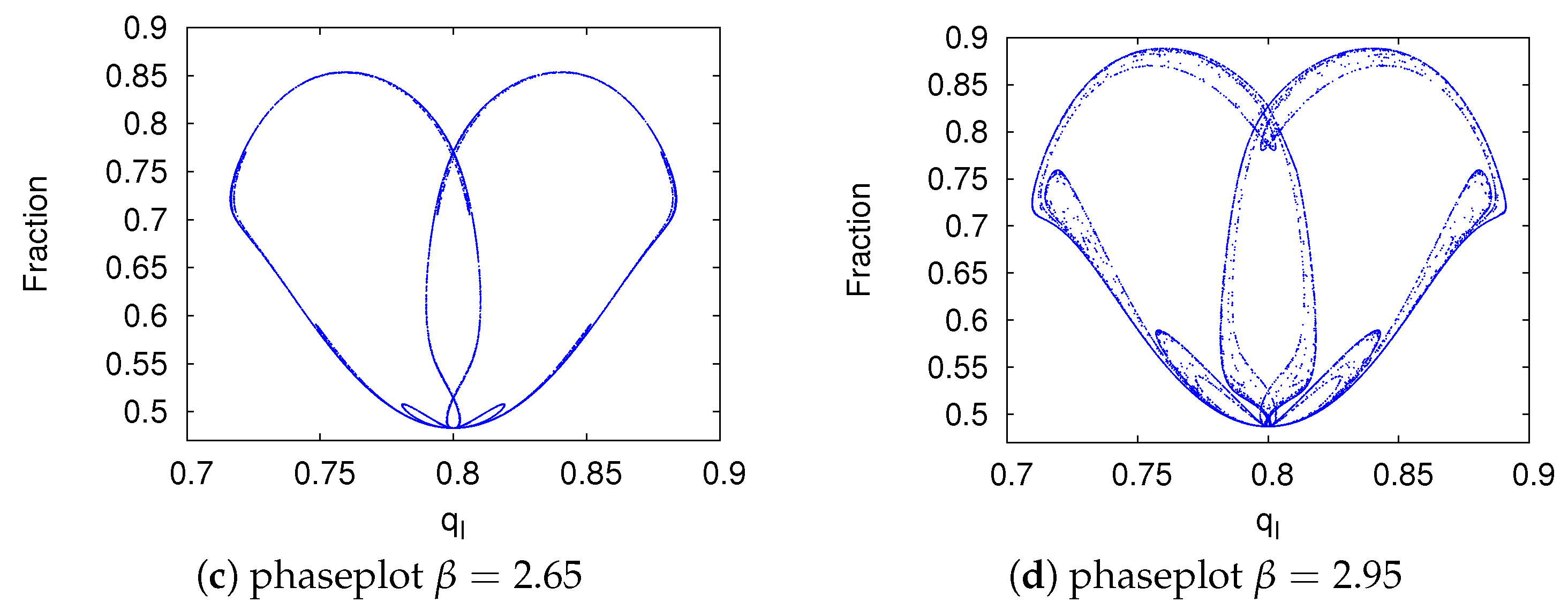
Figure 4 shows some attractors of the evolutionary model for increasing evolutionary pressure, with (quasi-)periodic motion just after the second bifurcation and breaking of the invariant circles into a strange attractor as the number of firms further increases. Similar ‘breaking of the invariant circles’ route to chaos appears for the rational and Cournot series.
6. Concluding Remarks
In this paper we set out to filling a gap in the literature on heterogenous heuristics in a Cournot oligopoly with boundedly rational players. Partly motivated by the experimental evidence for imitate-the-average behaviors in oligopoly games, our focus is on better understanding the role this specific imitation rule plays in a competitive Cournot environment, populated by myopic best-reply and rational (equilibrium) firms. In a population game framework- random re-matching of players, with fitness approximated by the expected payoffs accruing in all possible realizations of opponents’ heuristic types—the interplay between two model’s parameters—differential cost C between heuristics and intensity of evolutionary selection acting upon heuristics -determines the critical market size for which the unique, interior Cournot-Nash equilibrium of the underlying oligopoly loses stability.
For the pairwise, evolutionary contests between heuristics we first showed that in the case when Cournot firms compete with imitators, if (imitation heuristic enjoys a strict cost advantage over the myopic Cournot adjustment) and intensity of selection is very large ( limit), then the Cournot equilibrium is locally stable for Absent the information costs’ differential (i.e., the threshold on the number of firms that changes the system from stable to unstable remains 7, irrespective of the magnitude of the evolutionary pressure In contrast with the model comprising Cournot players only (Cournot equilibrium already unstable for , the addition of players using the relatively cheaper imitate-the-average heuristic, stabilizes the equilibrium. Secondly, in the situation when rational firms compete with imitators, the system is always stable, regardless of the information costs of the more sophisticated, rational choice.
For the full ecology of behavioral rules—rational firms, Cournot firms and imitators—we are able to derive the (in)stability threshold on the number of firms for the linear inverse demand-linear costs oligopoly with Logit Dynamics and for a particular configuration of heuristics costs: costly rational heuristic and costless Cournot and imitation rules . On one hand, if rational plays is costless, the equilibrium is stable, for all possible market sizes . On the other hand, even for small, strictly positive the interior, Cournot equilibrium loses stability for (in the limit) and for larger market sizes (in the case of finite ). Complicated endogenous fluctuations (two-cycles, strange attractors) in the quantities played and the fractions of various heuristics may occur, in particular, when the evolutionary pressure is high.
By deriving the stability conditions for our pairwise and threewise evolutionary model, we conclude that introducing imitators tends to stabilize the dynamics, provided that imitation is the least costly heuristics in the menu of potential learning rules.
At least two avenues seem promising for future research: firstly, our analysis deals with Cournot oligopolies that display an unique, interior Cournot-Nash equilibrium, and, therefore, we conjecture that our local stability analysis also holds globally. This is, of course, not valid for the Type II oligopolies that display multiple—interior and boundary—Nash equilibria. How the (in)stability of these equilibria, along with the relative size of their basins of attraction, vary with the market size n, under the full ecology of three, switching heuristics proposed in this paper, remains an unexplored question.
Secondly, related to the implications of imitative behavior in heterogenous heuristics environments, it would be worth considering alternative models of imitation. Our way of modelling imitation favors the average play (imitate the average behavior in the population) but other imitation rules well-studied in the literature may be envisaged. For instance, a version of the imitation heuristic that copies the past production decision of the most profitable firm from the entire population or one that imitates the successful players only among the m closest neighbors (in a location model, à la Hotelling). In these alternative imitation scenarios, coordination on a non-Cournot equilibrium—for instance, on the Walrasian equilibrium as in [
8] under the homogeneous, imitate-the-best play—may arise.