Quid Pro Quo Diplomacy

Abstract

Political leaders value public demonstrations of support from foreign leaders and frequently make concessions in order to obtain them. We model the bargaining dynamics surrounding these exchanges and their impact on the recipient leader’s political survival, with a focus on top-level diplomatic visits as a means of signaling international support. Our model addresses two interrelated questions; first, we consider how symbolic displays of support from one leader to another can be informative even when they are “purchased” with concessions, and second, we derive the equilibrium price and political impact of a visit under different bargaining protocols. The incentive to make a concession in exchange for a visit generally undermines a visit’s signaling value. We identify a diplomatic resource curse, where the existence of opportunities for diplomatic exchange can force leaders into accepting visit-for-concession deals that leave them worse off than if they were diplomatically isolated. Visits never occur when negotiations are fully transparent. Mutually beneficial quid pro quo diplomacy requires opacity in negotiations.

1. Introduction

Heard from White House—assuming President Z convinces trump he will investigate “get to the bottom of what happened” in 2016, we will nail down date for visit to Washington. Good luck!

—US Special Envoy to Ukraine Kurt Volker, in text message to Ukrainian Presidential Aide Andriy Yirmak, 25 July 2019 [1]

In pursuit of dirt on a political rival, President Trump withheld U.S. support to foreign-occupied Ukraine so as to induce President Volodymyr Zelensky to announce an investigation into the family of then-candidate and former Vice President Joe Biden. Among the forms of support withheld was a White House meeting between the two leaders. For Zelensky, the visit was no small matter: as Deputy Assistant Secretary of State, in the impeachment hearings arising from this exchange, George Kent relayed that leaders like Zelensky “see a meeting with the U.S. President in the Oval Office at the White House as the ultimate sign of endorsement and support from the United States” [2]. Eager for such a public demonstration of diplomatic backing, Zelensky acceded to Trump’s demand, until a whistleblower from within the U.S. government intervened.

Zelensky’s willingness to proffer a concession for a White House visit seems reasonable at first glance but, upon further inspection, a puzzle arises. The value of the visit, according to Kent, was essentially symbolic. But if the Trump administration was selling the White House visit at a price, what exactly would be signaled by the occurrence of the visit, other than Zelensky’s willingness to pay for it? The credibility of a signal is generally thought to depend on its costliness; if the cost of a signal is subsidized, its credibility is undermined. How can a signal of international support be informative when the signal is effectively purchased by its beneficiary?

Recent research has begun to examine the strategic incentives underlying public diplomacy, with a primary focus on the signaling value of top-level diplomatic exchanges and the information that they convey to an international audience [3,4]. Absent from these accounts, however, is consideration of the bargaining that surrounds the exchange and how those bargaining dynamics affect the visit’s signaling value. In public diplomacy, as in all facets of political life, favors are seldom given out freely. To understand the causes and consequences of diplomatic signals, it is essential to understand the bargaining and deal making that accompany them.

This paper presents a formal model of bargaining over diplomatic signals of support. We focus on top-level diplomatic visits as a prominent means of signaling support and we examine the consequences of these exchanges on the recipient leader’s political survival. The analysis addresses two central questions: first, how can symbolic displays of support from one leader to another be informative even when they are “purchased” with concessions, and second, what is the equilibrium price and consequently the political impact of a visit under varying bargaining protocols.

Our model features three players: a foreign leader, a domestic incumbent, and a domestic challenger. The foreign leader and domestic incumbent negotiate over the size of a concession that the domestic leader will provide in exchange for a diplomatic visit. Visiting carries some cost for the foreign leader and the benefit they enjoy from the visit is conditional on the domestic leader being sufficiently secure in office as to be able to deliver the agreed-upon concession. The foreign leader’s decision to visit thus signals their private assessment of the incumbent’s strength. Conversely, the domestic challenger is incentivized to challenge only sufficiently weak incumbents. Upon observing the occurrence (or absence) of a diplomatic visit, the challenger updates her belief of the probability that a challenge will succeed and is deterred from participating in one (or encouraged to do so).

Importantly, the informativeness of the visit depends, among other things, on the size of the negotiated concession: the prospect of a larger (conditional) benefit makes the foreign leader more willing to visit weaker incumbents, who carry a greater risk of “defaulting” on the deal; whereas, a visit granted in exchange for a smaller concession reveals an especially high degree of confidence that the incumbent will be capable of delivering. Thus, in bargaining over the concession, the domestic leader must balance the increased probability of obtaining a visit against the diminished strength of the visit’s signal, as well as the direct costs of the concession.

We vary the bargaining protocol along two dimensions: first, whether the domestic or foreign leader has proposal power, and second, whether the bargaining is “open” or “closed” to the domestic challenger. Consistent with standard bargaining results, we find that each leader obtains a better a deal when she or he has proposal power. Of greater interest are the implications of bargaining transparency. Our first main result is to show that, under fully open bargaining, the domestic leader never stands to benefit from offering a concession that induces a positive probability of a visit occurring (even when they have proposal power). The incumbent is better off leaving the challenger with her prior belief, rather than facing the lottery over good and bad signals that would result from a non-degenerate bargaining outcome.

The open-door bargaining protocol provides a useful analytical benchmark but relies on the substantively questionable assumption that a third party to a diplomatic negotiation can fully observe the bargaining process. In the latter half of the analysis, we relax this assumption and instead assume that bargaining occurs behind closed doors. In this opaque setting, the challenger does not observe negotiations but does observe whether or not a visit occurs; should a visit occur, the challenger probabilistically observes the size of the concession granted. This opacity creates the possibility for quid pro quo diplomacy to occur in equilibrium. These exchanges always benefit the foreign power; their utility to the domestic incumbent, however, depends on the domestic challenger’s prior belief of the likelihood of salient opportunities for concessions. When prior expectations of concession salience are high, the incumbent faces a “diplomatic resource curse”: they are forced into making a large concession in order to induce a visit because they cannot commit to having not made such a concession; this leaves them worse off than if they were fully diplomatically isolated. In contrast, when it seems ex-ante unlikely that the foreign leader is interested in a concession from the incumbent—and thus unlikely that a visit will occur—quid pro quo diplomacy can be mutually beneficial. In this case, the challenger draws a less-negative inference from the absence of a visit, so the incumbent can afford to turn down unfavorable deals and only offers a concession when doing so will improve their survival prospects. We conclude the analysis by examining comparative statistics of the equilibrium price and political impact of the visit with respect to various attributes of the two leaders in the exchange and features of the bargaining protocol.

This paper relates most directly to formal models of diplomatic visits by [4,5] and by [6], which are, to our knowledge, the only game-theoretic approaches to the topic in the extant literature—as well as related empirical research [3,7,8,9,10]. More broadly, our study contributes to a number of other formal pieces of literature as well. Our theory relates to models of bargaining in front of audiences [11,12,13], to models of international bargaining over policy concessions [14,15], and to models of informational channels through which international actors can influence domestic politics [16,17]. Drawing on insights from the diverse literature, our model examines an international bargaining process in which a material concession is exchanged for the revelation of information to a third party. This setup gives rise to some novel strategic considerations and helps makes sense of a broad swath of heretofore unexplained political activity.

2. Bargaining over Symbolic Support

The bargaining over a prospective Trump–Zelensky visit represents, in unusually stark terms, a recurrent pattern in American diplomatic practice of exchanging concessions for diplomatic signals. Here, we present a few more historical cases and consider the insights from existing theoretical and empirical literature which can be leveraged to develop our model of bargaining over symbolic support.

A prospective visit between President Obama and Azerbaijani President Ilham Aliyev unfolded in a manner not entirely dissimilar to the Trump–Zelensky exchange depicted above. Aliyev was slotted to attend a multilateral nuclear security summit in Washington in March 2016 but hoped to leverage the opportunity to elicit an even stronger signal for his domestic audience, in the form of a one-on-one meeting with Obama. According to an Azerbaijani journalist and human rights activist, Aliyev was “eager for that ultimate seal of approval—a few minutes and a photo op with Obama—that would give him the image boost he seeks in the midst of an economic crisis at home” [18]. The Obama administration, aware of the value Aliyev placed on such a signal, demanded a concession in return: the release of political prisoners who were part of the focus of a broader human rights campaign. One US official involved in the negotiations noted that the deal was “made pretty darn explicitly. It was something like, ‘We need the following things to happen…There’s a chance you might get to meet with the President’” 1. Aliyev released two political prisoners, which turned out to be insufficient to earn him a meeting with the President. He instead received a one-on-one with the Vice President [20]; a month later, he effectively revoked the prior concession by imprisoning two other activists on trumped-up charges [21].

Such a transactional approach to the granting or withholding of diplomatic visits can be observed throughout recent American history. Seeking UNSC authorization for a military intervention in Libya earlier in his tenure, Obama turned to Gabonese President Ali Bongo Ondimba for a critical supportive vote. Bongo delivered and, in return, was granted a stay at Obama’s private guest residence later that spring [22]. When President Bush visited Poland shortly after the invasion of Iraq in 2003, “the point of his visit [was] obvious: to thank this country for supporting American policy” and to “signal…that Poland, in the enthusiastic eyes of Washington, has become an important ally, even a special friend” [23]. Despite the fact that a quid pro quo was “obvious”, the occurrence of the visit nonetheless carried some signaling value. Discussing the possibility of a US–Korean visit in 1964, a telegram from the US embassy in Korea advised that “[t]iming of visit should be related to progress [on] ROK-Japan normalization”, an issue the US had been pushing despite domestic difficulties faced by the Korean government 2. A 1955 telegram from the embassy in Cairo likewise recommended delaying a visit with Nasser until a “pendulum in Egyptian-United States relations could by other means be started again toward United States” 3. Generalizing beyond these individual anecdotes, ref. [4] provides large-N evidence that post-war US presidents have systematically reaped concessions from the leaders with whom they conduct diplomatic visits, in the form of closer voting alignment in the UN General Assembly and increased market access for US exporters.

While the discussion thus far has centered around US diplomatic activity, the practice of exchanging visits for concessions is by no means a uniquely American phenomenon. For instance, we see similar tactics employed by both British Prime Minister Tony Blair and French President Nicolas Sarkozy in their dealings with Libyan leader Muammar Gaddafi in 2007. Both European leaders leveraged a high-profile diplomatic visit in exchange for advantageous commercial deals for their own domestic firms [24,25]. These were the publicly known considerations in the deals; the allegation subsequently emerged that Gaddafi illicitly paid EUR 50 million to Sarkozy’s 2007 election campaign in advance of the visit, a crime for which Sarkozy has since been charged by French prosecutors [26].

What does the existing literature tell us about these kinds of international exchanges? In general terms, we are interested in a situation in which two actors are bargaining in front of a third party who draws inferences from the bargaining outcome that they observe. Interactions of this sort have been examined in the previous formal literature, with a particular focus on the incentives for “posturing” that arise and the consequences of transparency and information asymmetry for bargaining outcomes [11,12,13]. Our situation is unique; however, it is unique in that the object of the bargaining is not a division of resources or a policy output. Rather, the object of the bargain is information, in the form of a costly “money-burning” signal sent to a third party. In this sense, the puzzle we present is similar to that considered by [15] in the context of vote-buying in the UN Security Council, where, as the authors describe, “the central political commodity that is bought and sold is legitimacy”. While Vreeland and Dreher’s study is primarily an empirical investigation of aid-for-voting exchanges, we provide a formal theoretical analysis, which highlights the tensions and complexities inherent to the concessions-for-signalling exchanges under examination.

More directly related to our substantive context of analysis is a newly emerging body of quantitative and formal literature on public diplomacy and diplomatic visits [3,4,5]. These studies generally theorize diplomatic visits as public signals of support from one leader to another 4. Ref. [3] conceptualizes visits as tied-hands deterrent signals in the face of threats from foreign adversaries. Refs. [4,5] examine how visits deter domestic challenges against the recipient leader. The present analysis differs substantially from these previous studies in two key respects: first, the model endogenizes the size of the quid pro quo through a bargaining process, and second, the domestic leader is treated as a strategic actor. An implication of these two innovations is that the signal receiver in our model knows that a visit was “purchased” and thus conditions their inference on whatever price was paid. This, in turn, alters the bargaining incentives of both the domestic and foreign leader. As a consequence, our model reveals that the kind of diplomatic exchanges theorized by [4,5] are not generally incentive-compatible for both parties. We instead show that the conditions under which mutually beneficial quid pro quo diplomacy can occur are precisely the conditions under which it would be least expected, as we elaborate in Section 7 below. Furthermore, our analysis uncovers the crucial role of transparency in diplomatic exchange: while the visit itself must be public and visible to third parties, the negotiations surrounding the visit must be conducted out of public view and the degree of transparency has important distributional implications for bargaining outcomes.

3. A Model of Concessions, Visits, and Political Survival

Our model features three players: a domestic incumbent, L; a political challenger, C; and a foreign leader, F. The model has three phases: (1) bargaining; (2) visiting; and (3) domestic political competition. In the bargaining phase, the salience (S) of a concession arises stochastically and L and F bargain (under varying bargaining protocols and informational structures) over the size of the concession, z, that L will provide in exchange for a visit. F then decides whether or not to conduct the visit and reap the concession. Following the bargaining and the occurrence (or not) of a visit, domestic competition occurs, in which C decides whether or not to attempt to remove L from power. We reduce domestic competition to two dimensions: the cost K that C incurs for mounting a challenge against the leader and the probability $\theta$ that the leader can survive a challenge. The challenger fully learns the first factor, while the foreign leader sees a noisy signal of the latter.

3.1. Bargaining

The game begins with a stochastic nature, determining whether a salient opportunity exists for L to provide F a concession. We represent this as a random variable $S\in \{0,1\}$. The realization of S is observed by both L and F. The domestic challenger C has a prior belief that $Pr(S=1)=\sigma \in (0,1)$ and that belief is updated over the course of the game, as discussed below. We refer to $\sigma$ as “expected salience”, that is, C’s expectation that F wants a favor from L.

Absent in such a salient opportunity, the bargaining phase concludes trivially with no concession agreed upon and the game moves directly to the political competition phase. If a salient opportunity arises, then bargaining commences and L and F negotiate the size of the concession that L is to provide F in exchange for a visit. We assume a simple take-it-or-leave-it bargaining framework: one leader, either L or F, proposes a concession z to be proffered upon the completion of a visit and the other leader either accepts or rejects the deal.

We vary the bargaining context along two dimensions: (1) which leader has proposal power and (2) whether the negotiations are “open” or “closed”.

First, with respect to proposal power, if L is the proposer, then they offer a concession of size $z\ge 0$ in return for a visit, which F then either accepts or rejects. If F is the proposer, then the roles are reversed: F makes a demand of z, which L either accepts or rejects. We note that accepting an agreement at this stage does not entail a commitment on F’s part to conduct a visit; rather, it is a commitment on L’s part to provide a concession of size z in the event that F does decide to visit (which we discuss in the next phase).

Second, considering the transparency of negotiations, visits are public events seen by all. However, we vary the extent to which C observes other aspects of the game. Under the “open” bargaining protocol, the first scenario that we examine, C, observes all aspects of the negotiations: that is, C observes the realized salience S, the concession size z that was offered or demanded, and whether the deal was accepted or rejected. In the “closed” protocol, which we believe more closely resembles the reality of diplomatic negotiations, C does not observe concession salience or any aspect of the pre-visit bargaining that occurs between F and L. Within the closed setting, we vary two features of the model setup: first, we vary the expected salience, $\sigma$, and second, we vary the probability $q\in [0,1]$ that, in the event that a visit occurs, the concession value z is revealed to C. We refer to this probability q as “concession transparency”. If C does not observe z, they still infer that a concession was made but must form a conjecture as to the size of the concession 5.

3.2. Visits

Once a deal z is agreed to, F must decide whether to carry out the visit and collect the concession. From F’s perspective, the decision to visit entails balancing costs and benefits, which are conditional on L’s survival in office. Before embarking on the visit, F sees a noisy signal A of L’s strength $\theta$, which captures the likelihood that L can survive a challenge from her domestic rival (described below in detail). For clarity of exposition, we specify the game such that F observes this signal after the negotiations are complete; however, as we discuss in the Appendix A.4, the results are robust to alternative assumptions about the timing of F’s information acquisition.

If F conducts a visit, they incur a fixed cost $\tau$: this includes the opportunity cost of F’s time, as well as any associated transport, security, and administrative costs. F pays this cost regardless of whether or not L survives in office. In the event that L is removed from office following the visit, F pays an additional cost of $\rho$; we refer to this as a reputational cost, following [4]. Weighed against these costs is the benefit F enjoys from the concession z. If L remains in office, this concession is received with certainty; if L is removed, F retains the concession with probability $r\in [0,1]$. Thus, r captures the immediacy with which the concession can be delivered following the negotiation or the difficulty that L’s successor would face in revoking the concession.

3.3. Domestic Political Competition

In the final stage of the game, the challenger, C, may attempt to remove the leader. For expositional purposes, we focus on domestic political competition, though the model readily accommodates a foreign challenger. Many factors shape political contestation. We focus here on two dimensions: $\theta$ and K, which we refer to as the leader’s “strength” and the challenger’s “cost”, respectively. $\theta$ represents the probability that L can withstand a removal attempt by C, while K represents C’s cost for making such an attempt. All actors have common priors about $\theta$ and K. The challenger, C, fully learns their cost K before deciding whether or not to challenge. We assume that F learns nothing about the cost dimension but does see a noisy signal about L’s strength, $\theta$. Thus, while C maintains an informational advantage over F with respect to one dimension of political contestation, he can still learn something about the second dimension from observing F’s decision to visit or not.

C’s payoff from successfully removing L is 1 and we normalize C’s payoff from L remaining in office to 0. Given the regime strength $\theta$, C’s expected payoff from attempting to remove L is

$$(1-\theta )1-K$$

We assume K is uniformly distributed on the internal $[0,1]$.

The domestic leader L receives an office-holding benefit of $\Psi$ if they retain power, while her payoff from being deposed is normalized to 0. If a visit occurs, they incur the cost z for making the concession.

3.4. Signals and Beliefs

Foreign leader F observes a noisy signal of L’s strength $\theta$. This signal A takes values between 0 and n. For intuition (although we do not restrict A to integers), we can think of A as the number of “heads” from n biased coin flips, where the probability of heads in each trial is $\theta$. By this interpretation, each coin flip would represent a new piece of evidence uncovered about L’s strength in office and heads would denote evidence, indicating that L is strong and hence capable of surviving in office to deliver a concession. The number of trials, n, thus provides a convenient metric for the precision of F’s signal.

All players share a common prior belief of $\theta$, which lies between 0 and 1. We specify this prior distribution, $G\left(x\right)=Pr(\theta <x)$, to be the Beta distribution (with parameters $\alpha$ and $\beta$), which is a flexible distribution on the domain [0,1]. The associated probability density is $g\left(\theta \right)=\frac{\Gamma (\alpha +\beta )}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\theta }^{\alpha -1}{(1-\theta )}^{\beta -1}$, where $\Gamma \left(z\right)={\int }_0^{\infty }{x}^{z-1}{e}^{-x}dx$.

We exploit two useful features of the Beta distribution (as have others, for instance [27]). First, the expected value of $\theta$ is $\frac{\alpha }{\alpha +\beta }$. Second, the Beta distribution has a simple Bayesian update. Given regime strength $\theta$, the probability density with which $A=x$ is

$$p\left(x\right|\theta )=\frac{\Gamma (n+1)}{\Gamma (x+1)\Gamma (n-x+1)}{\theta }^x{(1-\theta )}^{(n-x)},$$

the likelihood of x heads from n coin flips where the coin is weighted to come up heads with probability $\theta$ (for integers, the terms involving the Gamma functions simply reduce to the binomial coefficients). Let $p\left(x\right)={\int }_0^{1}p\left(x\right|\theta )g\left(\theta \right)d\theta$ and $P\left(a\right)={\int }_0^{a}p\left(x\right)dx$. Therefore, $Pr(A<a)=\frac{P\left(a\right)}{P\left(n\right)}$ and $Pr(A\ge a)=\frac{P\left(n\right)-P\left(a\right)}{P\left(n\right)}$ 6.

Given the signal A, Bayesian updating yields the posterior belief that $\theta$ is Beta distributed with parameters $\alpha +A$ and $\beta +(n-A)$, so the updated expectation that L can survive a challenge is $E\left[\theta \right|A]=\frac{\alpha +A}{\alpha +\beta +n}$.

3.5. Summary of the Model Setup

To summarize, the sequence of the game form is as follows:

• A stochastic nature determines whether a salient opportunity for a favor arises, $S\in \{0,1\}$, with $Pr(S=1)=\sigma$. Under open bargaining, all players observe S; under closed bargaining, only L and F observe S;
• If $S=1$, then bargaining occurs. Depending on the bargaining protocol, either L offers concession z, which F can accept or reject, or F demands concession z which L can accept or reject;
• F sees signal A and decides whether to visit L;
• Under open bargaining, C observes all aspects of the negotiations. Under closed bargaining, C observes whether a visit occurred and, should a visit occur, C observes the concession granted with probability q;
• Domestic political competition: C either challenges or abstains. If C plays challenge, then L is removed with probability $1-\theta$.

Payoffs and notations are outlined in

Table 1. Payoffs.

F, Foreign Power	$\mathrm{L} \mathrm{Survives}$	$\mathrm{Regime} \mathrm{Change}$
Visit	$Sz-\tau$	$Srz-\tau -\rho$
Non-visit	0	0
L, Leader	$\mathrm{L} \mathrm{Survives}$	$\mathrm{Regime} \mathrm{Change}$
Visit	$\Psi -z$	$-z$
Non-visit	$\Psi$	0
C, Challenger	$\mathrm{Status} \mathrm{Quo}$	$\mathrm{Regime} \mathrm{Change}$
Challenge	$-K$	$1-K$
Abstain	0	n.a.

and

Table 2. Notation.

K∼$U[0,1]$	C’s cost of challenging
$\theta \in [0,1]$	L’s regime strength, with prior distribution $Beta(\alpha ,\beta )$
$A\in [0,n]$	F’s private signal of regime strength
$z\ge 0$	Concession offered in exchange for a visit
$\Psi >0$	L’s valuation of holding office
$S\in \{0,1\}$	Salience of concession for F, with prior $Pr(S=1)=\sigma$
$r\in [0,1]$	Probability that F retains a concession following L’s removal
$\tau >0$	F’s fixed/opportunity cost for visiting
$\rho >0$	F’s conditional/reputational cost for visiting if L is subsequently removed
$\sigma \in (0,1)$	Expected salience: C’s prior belief of $Pr(S=1)$
$q\in [0,1]$	Concession transparency: prob. C observes z after visit under closed bargaining

. We characterize Perfect Bayesian Equilibria under different bargaining protocols.

4. Visit Subgame

We begin with a general characterization of the subgame that follows the negotiation stage, which applies to both open and closed bargaining settings.

4.1. F’s Incentive to Visit

The core incentive is that F wants to visit strong leaders. First, note that in the absence of a salient opportunity for a concession ($S=0$), no bargaining occurs and the game proceeds directly to domestic political competition. Thus, our analysis of F’s visit decision focuses on the case of $S=1$.

Suppose the negotiated concession is z, and F sees signal A, and following a visit the challenger will attempt removal with probability ${\kappa }_v$. Then F’s expected payoff from a visit is

$$\begin{array}{ccc}\hfill V(A,z)& =& Pr\left(L\mathrm{survives}\right|visit,A\left)\right(z-\tau )+Pr(L\mathrm{deposed}|visit,A)(rz-\tau -\rho )\hfill \\ & =& z-\tau -\underset{\mathrm{Pr}\left(\mathrm{challenge}\right)}{\underbrace{{\kappa }_v}}\underset{\mathrm{Pr}(\mathrm{deposed}\left|\mathrm{challenge}\right)}{\underbrace{E[1-\theta |A]}}((1-r)z+\rho )\hfill \end{array}$$

(1)

If C attempts removal, then L is deposed with probability $1-\theta$. The likelihood of a high signal increases in L’s strength $\theta$. Therefore F is more likely to visit as the signal A increases: $E[1-\theta |A]=\frac{n-A+\beta }{\alpha +\beta +n}$, for $A\in [0,n]$. Equation (1) is strictly increasing in z and A. If they refrain from visiting, the foreign leader’s payoff is normalized to 0, so F only visits when $V(A,z)\ge 0$. Thus there is a unique concession size that makes F indifferent between visiting and not.

Let the strictly decreasing function $z\left(a\right)$ characterize the indifference concession associated with each signal a. Conversely, define the inverse function, $a\left(z\right)$, as the signal that makes F indifferent between visiting and not given concession z. Furthermore, define

$$z_0=\frac{\frac{\beta \rho (\beta +n)}{(\alpha +\beta )(\alpha +\beta +n)}+\tau }{1-\frac{\beta (1-r)(\beta +n)}{(\alpha +\beta )(\alpha +\beta +n)}}\mathrm{and}{z}_n=\frac{\frac{{\beta }^2\rho }{{(\alpha +\beta +n)}^2}+\tau }{1-\frac{{\beta }^2(1-r)}{{(\alpha +\beta +n)}^2}}$$

as the extreme concessions that make F indifferent between visiting following the weakest and strongest possible messages, respectively, $V(A=0,z_0)=0$ and $V(A=n,z_n)=0$. Notably, $z_n<z_0$: entails a large concession ($z=z_0$) being necessary to make F indifferent given the lowest signal ($a=0$); a small concession ($z=z_n$) is necessary to make F indifferent given the highest signal ($a=n$).

To summarize, the following can be said:

Lemma 1.

For concessions $z\in (z_0,z_n)$, there is a decreasing monotonic function $a\left(z\right)$ such that $V\left(a\right(z),z)=0$. F visits if and only if they see a signal $A\ge a\left(z\right)$.

4.2. Visits Deter Domestic Political Challenges

In the final move of the game, the challenger C decides whether to challenge or abstain. L survives a removal attempt with probability $\theta$. Given information I, C only challenges when the expectations of success justify the cost of attempting removal.

$$\underset{Pr\left(success\right)}{\underbrace{E[1-\theta |I]}}-\underset{\mathrm{Cost}\mathrm{of}\mathrm{attempt}}{\underbrace{K}}\ge 0$$

There is a critical threshold $k=E[1-\theta |I]$ such that C attempts removal when $K\le k$. The critical threshold depends upon the information revealed by bargaining and visits. To simplify notation, we use $k_0$ to denote C’s challenge threshold given that there was no opportunity for a visit ($S=0$ in open bargaining or $\sigma \to 0$ in closed bargaining). The thresholds $k_v\left(z\right)$ and $k_{nv}\left(z\right)$ indicate C’s critical cost given the occurrence and absence of a visit, respectively, given C’s knowledge (in open bargaining) or conjecture (in closed bargaining) that the agreed-upon concession was of value z.

If C knows that there was no salient opportunity for a visit ($S=0$), then the absence of a visit is uninformative and C cannot update beyond her prior version.

$$k_0=E[1-\theta ]=\frac{\beta }{\alpha +\beta }\mathrm{and}Pr\left(\mathrm{challenge}\right)=Pr(K<k_0)=k_0=E[1-\theta ]$$

Visits affect domestic political competition by altering C’s beliefs about regime strength. The occurrence of a visit reveals that F saw a signal $A\ge a\left(z\right)$. Given this information, C’s expectation of the likelihood of a successful challenge declines, since $E[1-\theta |A\ge a\left(z\right)]\ge E[1-\theta ]$. In contrast, if F forgoes the opportunity to visit (but C knows there was an opportunity), then C infers that L is weaker than initially thought: $E[1-\theta |\mathrm{non-visit}]=E[1-\theta |A\le a(z\left)\right]\le E[1-\theta ]$.

We can now state equilibrium behavior in the visit subgame as follows:

Proposition 1.

Informative equilibrium: Suppose the bargaining phase results in a concession of z that is known to all players. If $z\in (z_n,z_0)$, then F visits if and only if $A\ge a\left(z\right)$ where $a\left(z\right)$ is the implicit function that solves

$$\begin{array}{ccc}\hfill V(a,z)& =& z-\tau -E[1-\theta |A=a\left]E\right[1-\theta |A\ge a]\left(\right(1-r)z+\rho )=0\hfill \end{array}$$

(2)

Following a visit, C attempts removal if and only if $K\le k_v\left(z\right)=E[1-\theta |A\ge a\left(z\right)]$ and following a non-visit, C attempts removal if and only if $K\le k_{nv}\left(z\right)=E[1-\theta |A<a\left(z\right)]$, with $k_v\left(z\right)<k_0<k_{nv}\left(z\right)$.

Consistent with standard refinements [28], we impose the following restriction on out-of-equilibrium beliefs:

Assumption 1.

If $a\left(z\right)\ge n$ (such that no visits occur), then should a visit occur, let $E[1-\theta |\mathit{visit}]=\frac{\beta }{\alpha +\beta +n}$. If $a\left(z\right)\le 0$ (such that visits always occur), then let $E[1-\theta |\mathit{non-visit}]=\frac{\beta +n}{\alpha +\beta +n}$.

Intuitively, if C were to observe a visit when a visit should never have occurred, he draws the most positive inference of L’s strength; and conversely, if C were to observe a non-visit when a visit should necessarily have occurred, they draw the most negative inference of L’s strength. With this restriction in place, the following can be said:

Proposition 2.

Pooling equilibria: If the concession is small, $z\le z_n$, then F never visits and following no visit, C attempts removal if $K\le k_0$. If the concession is large, $z\ge z_0$, then F always visits and, following a visit, C attempts removal if $K\le k_0$.

Notably, Equation (2) is simply Equation (1) with the substitution that ${\kappa }_v=k_v=E[1-\theta |A\ge a]$. For any given z, the equilibrium to the visit subgame is unique.

Corollary 1.

For a fixed concession z, visits become more likely as r increases and as τ and ρ decrease: $\frac{\partial a\left(z\right)}{dr}\le 0$, $\frac{\partial a\left(z\right)}{d\tau }\ge 0$ and $\frac{\partial a\left(z\right)}{d\rho }\ge 0$. The inequalities are strict for $z\in (z_n,z_0)$.

Holding the size of the concession fixed, for a greater risk of default ($1-r$) or greater costs of visiting ($\tau$ and $\rho$), F requires a more favorable signal in order to justify making a visit.

Corollary 2.

For the special case $\alpha =\beta =1$,

$$a\left(z\right)=\frac{3}{2}+n-\frac{1}{2}\sqrt{\frac{8{(n+2)}^2(z-\tau )+\rho +(1-r)z}{\rho +(1-r)z}}$$

(3)

for $z\in (z_n,z_0)$

Alternatively, stated in terms of concessions,

$$z\left(a\right)=\frac{\rho (a-n-2)(a-n-1)+2{(n+2)}^2\tau }{a^2(r-1)-a(2n+3)(r-1)+(n+2)(nr+n+r+3)}$$

(4)

Visits discourage removal attempts ($k_v\left(z\right)<k_0$) and non-visits increase the likelihood of removal attempts ($k_{nv}>k_0$), for $z\in (z_n,z_0)$. However, the likelihood of a visit and the domestic political consequences of a visit depend upon the size of the concession on offer.

Proposition 3.

Effect of Concessions on Occurrence and Impact of Visits: As concessions increase,

1. 

Visits become more likely: $\frac{dPr\left(\mathit{visit}\right)}{dz}\ge 0$;

2. 

The perception of L’s strength following a visit decreases: $\frac{dE\left[\theta \right|\mathit{visit}]}{dz}\le 0$;

3. 

The perception of L’s strength following no visit decreases: $\frac{dE\left[\theta \right|\mathit{non-}\mathit{visit}]}{dz}\le 0$.

These inequalities are strict if $z\in (z_n,z_0)$.

The intuition is straightforward: visits signal regime strength and enhance L’s survival. Hence, L wants to encourage F to visit. However, Proposition 3 shows that making visits more attractive undermines their domestic political value. In the extreme, if C knows that L made a concession of size $z_0$ (which is large enough to induce F to visit even for the worst possible signal), then the visit fails to signal L’s strength. As the concession size decreases, F becomes less likely to visit but the deterrent value of a visit, should it occur, grows stronger. The tension between wanting to increase the likelihood of a visit and undermining the domestic political value of a visit shapes equilibrium bargaining behavior.

5. Open Bargaining

Under open negotiations, C observes all details of the bargaining. In this case, we have the following general result:

Proposition 4.

Under open bargaining, any concession $z\in (z_n,z_0)$ that induces threshold strategy $a\left(z\right)\in (0,n)$ increases L’s risk of deposition relative to no agreement ($z<z_n$).

When the leaders negotiate in the open, the lottery between a survival-improving visit and a deposition-enhancing non-visit reduces L’s aggregate survival prospects relative no information being communicated. This result holds regardless of whether F or L has proposal power.

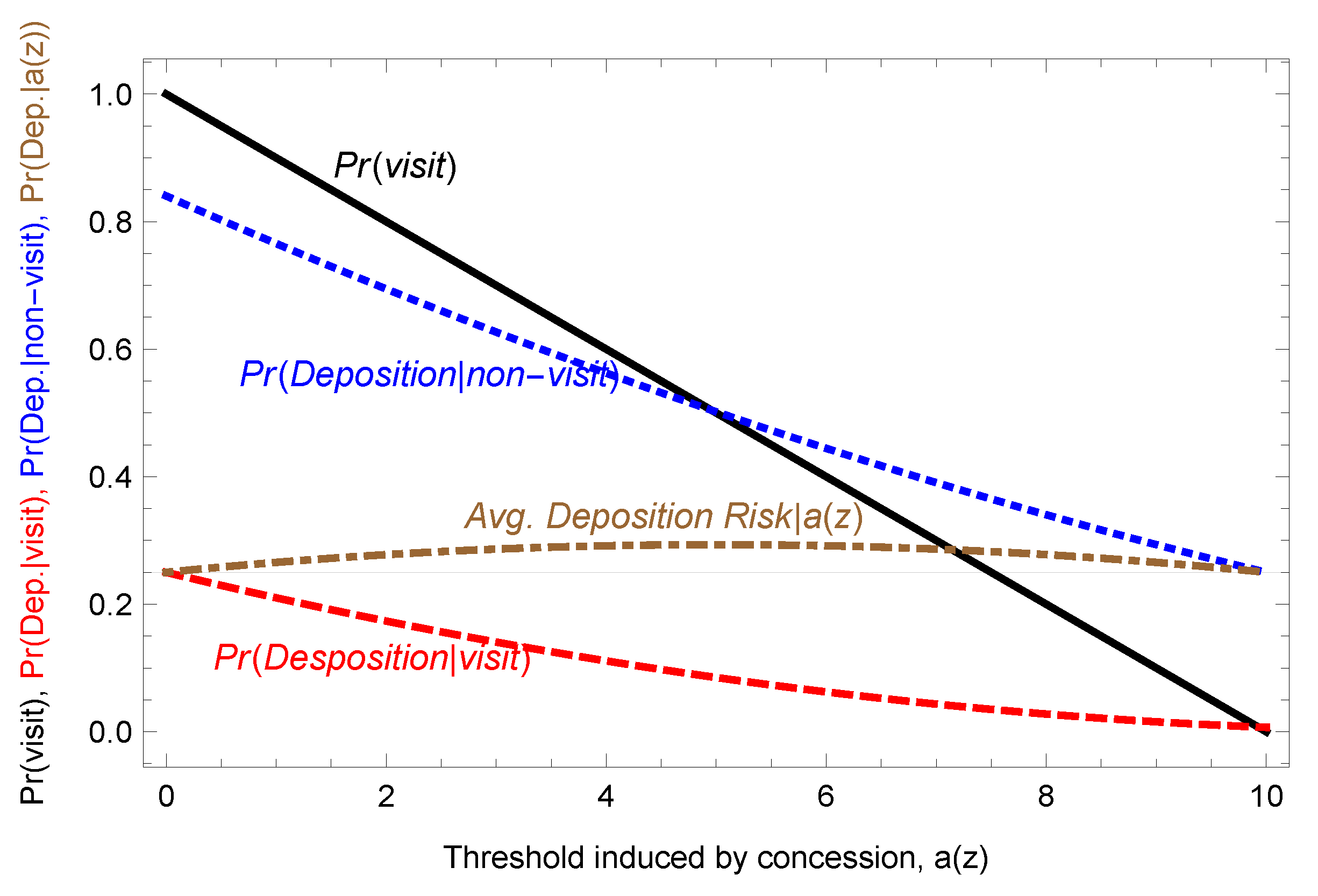
Figure 1 illustrates Proposition 4 for the special case of a uniform prior ($\alpha =\beta =1$). The horizontal axis shows the threshold $a\left(z\right)$ induced by concession z. As z increases, $a\left(z\right)$ decreases and F visits for a greater range of signals. The probability that F visits is shown by the solid line. The figure also shows the probability that L is deposed following a visit (dashed, $Pr\left(Deposition\right|visit)$) and no visit (dotted, $Pr\left(Deposition\right|\mathrm{non-}\mathrm{visit})$). If a bargain is reached ($z\in (z_n,z_0)$), then L’s expected risk of being deposed is:

$$\begin{array}{ccc}\hfill \mathrm{Avg}.\mathrm{Deposition}\mathrm{Risk}\left|a\right(z)& =& Pr\left(visit\right)Pr\left(Deposition\right|a\left(z\right)\left|visit\right)\hfill \\ & +& (1-Pr(visit\left)\right)Pr\left(Deposition\right|a\left(z\right)\left|\mathrm{non-}\mathrm{visit}\right)\hfill \end{array}$$

(5)

This aggregate deposition risk, shown by the dot-dashed hump-shaped curve, is higher than if no additional information were revealed. Thus, it is clear to see that L does not want any deal that could result in a visit; doing so would entail paying a direct cost z in order to decrease personal expected survival prospects. Instead, L would propose $z<z_n$ and reject any deal offered by F in which $z\ge z_n$.

Proposition 5.

Under open bargaining, concessions are never agreed and quid pro quo visits never occur. If L is a proposer, then they propose $z<z_n$. If F is the proposer, then L rejects any offer $z\ge z_n$. C does not revise their beliefs of θ after observing the absence of a visit.

The potential for quid pro quo diplomacy carries only downside risk for L, such that they would prefer to commit to a strategy of never offering a concession in exchange for a visit. Given the fully transparent bargaining protocol, such a commitment strategy is credible: C observes that no concession is on offer and thus does not update negatively upon observing the absence of a visit. As we will see in the next section, removing transparency in negotiations has the effect of removing L’s ability to credibly commit to this no-concession strategy, forcing them into deals which leave them worse off on average.

6. Closed Bargaining

While the open bargain setting provides a useful analytical benchmark, it is substantively unrealistic to assume that domestic actors outside of government have the opportunity to observe all details of diplomatic negotiations. Indeed, observers may not even know that negotiations are occurring. In the closed setting, C does not observe the salience of concession opportunities or the bargaining over concessions. Within this closed setting, we vary expected salience, $\sigma$, and concession opacity, q. See Appendix B.

Recall that C holds a prior belief that $S=1$ with probability $\sigma$ and recall that no visits occur when $S=0$. Upon observing the absence of a visit, C infers that one of two things happened: either $S=0$, so there was no opportunity for a visit, or $S=1$ but F did not observe a strong enough signal to warrant a visit, given the concession z that was on offer. Suppose that in the latter case C conjectures that the size of the negotiated concession was w. Then, her posterior belief of S is given by Bayes’ Rule as follows:

$$Pr(S=1|\mathrm{non-visit},w)=\frac{P\left(a\right(w\left)\right)\sigma }{P\left(a\right(w\left)\right)\sigma +1-\sigma }$$

Following an absent visit, C’s expectation of regime weakness is

$$\begin{array}{ccc}\hfill E_C[1-\theta |\mathrm{non-visit},w]& =& Pr(S=1|\mathrm{non-}\mathrm{visit}\left)E\right[1-\theta |A<a(w\left)\right)]\hfill \\ & & +(1-Pr(S=1|\mathrm{non-}\mathrm{visit}))\frac{\beta }{\alpha +\beta }\hfill \\ & =& \frac{P\left(a\left(w\right)\right)\sigma E[1-\theta |A<a\left(w\right))]+(1-\sigma )P\left(n\right)\frac{\beta }{\alpha +\beta }}{P\left(a\right(w\left)\right)\sigma +(1-\sigma )P\left(n\right)}\hfill \end{array}$$

Observe that this value is increasing in $\sigma$: when it is ex-ante more likely that a salient opportunity exists for a diplomatic exchange, the absence of a visit becomes a more damaging signal ex-post.

6.1. F as Proposer

Closed-door bargaining outcomes vary depending on which leader, F or L, has proposal power. First, let us consider the case where F makes a demand z, which L can accept or reject.

Proposition 6.

If $q\in [0,1]$, $\sigma \in (0,1)$, and F is a proposer, then on the equilibrium path, when $S=1$, F proposes z such that

$$\frac{z}{\Psi }=\frac{\frac{\beta }{\alpha +\beta }P\left(n\right)-E[1-\theta |A<a\left(z\right))]P\left(a\left(z\right)\right)}{P\left(n\right)-P\left(a\right(z\left)\right)}{E}_C{[1-\theta |\mathit{non-}\mathit{visit},z]-E[1-\theta |A\ge a\left(z\right))]}^2,$$

(6)

which L accepts. The concession z is increasing in σ. As office holding becomes the dominant motive ($\Psi \to \infty$), $z\to z_0$.

It is instructive to compare this result against the open-door bargaining result. In the open case, suppose F were to demand some concession $z\in (z_n,z_0)$. As demonstrated above, L prefers that F’s action is uninformative and also prefers not to pay the direct cost of the concession. So, they turn down the deal and C knows that the absence of a visit is uninformative.

Such behavior, however, cannot be supported in equilibrium under closed bargaining. Suppose that C conjectured that L’s strategy was to turn down any offer. Off the equilibrium path, if C were to observe a visit, they would have to infer (by Assumption 1) that F saw a favorable signal of L’s strength and would update their beliefs of $\theta$ accordingly. Then, L has a clear incentive to deviate and accept the lowest-z deals that F would offer. This leads C to update more negatively upon observing a non-visit, which in turn drives up the price L is willing to pay. In equilibrium, L ends up proffering a substantial concession in order to secure an average deposition risk that is at least as large as what they obtained for free under open bargaining. The concession size that L is willing to pay increases in the expected salience $\sigma$ because C’s inference of regime strength (and thus L’s survival prospects) when no visit occurs decreases in $\sigma$ 7.

We characterize this result as a diplomatic resource curse. By virtue of being perceived as having something to offer the foreign power (that is, $\sigma$ being large), the domestic leader faces domestic costs for refraining from diplomatic engagement. They cannot credibly commit to having not offered a concession and so they face a strong incentive to make a large concession that is likely to secure a diplomatic visit. If instead it was thought to be unlikely that L had a salient concession to offer (that is, if $\sigma$ were small), then in the off chance that a salient opportunity did arise, L would come to the diplomatic table with greater bargaining leverage due to her more favorable reservation value for turning down a deal. Though not explicitly allowed in our model, this logic suggests an incentive for some leaders either to isolate themselves diplomatically—making clear to their domestic audiences that foreign powers are not demanding any sort of concession from them—or to make their negotiations more transparent, so that audiences cannot suspect them of having offered a larger concession than they did.

6.2. L as a Proposer

Now, we turn attention to the case of closed-door bargaining with L as a proposer. In the Appendix A.3, we characterize the equilibria in a more general setting. For ease of presentation, here, we focus on the case where office-holding is the dominant motive.

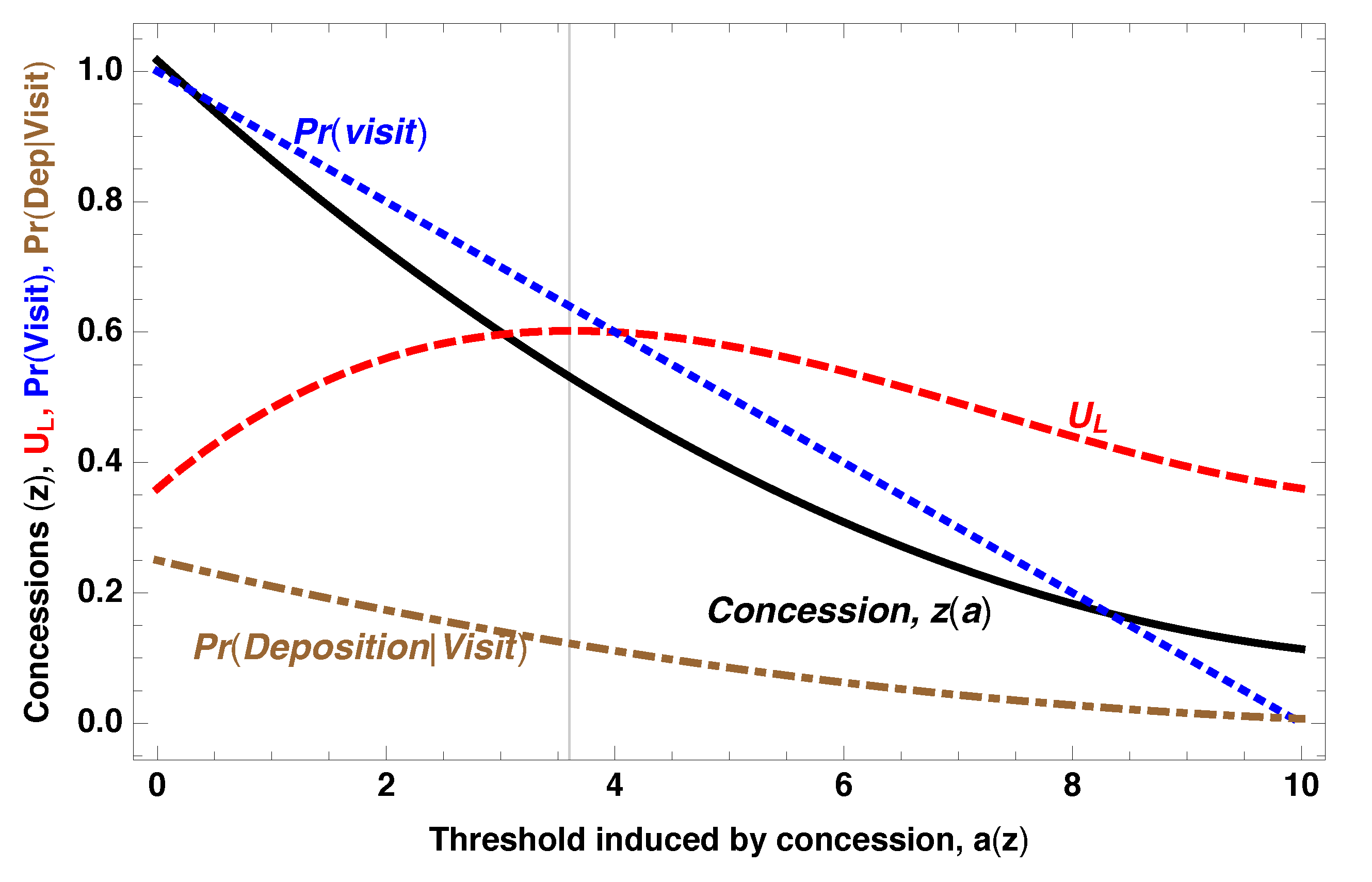
Proposition 7.

If L is a proposer and office holding incentives dominate ($\Psi \to \infty$), then on the equilibrium path, L offers z that solves

$$\begin{array}{cc}\hfill & E[1-\theta |A\ge a\left(z\right)]\left(E[1-\theta |A=a\left(z\right)\left]\right(1+q)-E[1-\theta |A\ge a(z\left)\right]q\right)\hfill \\ \hfill & -\frac{E[1-\theta |A<a\left(z\right)](P\left(n\right)\frac{\beta }{\alpha +\beta }(1-\sigma )+P\left(a\left(z\right)\right)E[1-\theta |A<a\left(z\right)]\sigma )}{P\left(n\right)(1-\sigma )+P\left(a\right(z\left)\right)\sigma }=0\hfill \end{array}$$

(7)

and visits occur if $A\ge a\left(z\right)$.

L trades off the likelihood of receiving a visit against the impact of a visit, should it occur. If L offers a small concession, then F rarely visits, but, if a visit occurs, the visit greatly increases L’s survival prospects. If L offers a large concession, then visits are common but their impact on domestic politics is small. When officeholding motives dominate, L finds the threshold $a\left(z\right)$ that maximizes expected survival and then offers the concession that induces that threshold. The optimal threshold $a\left(z\right)$ represents a compromise between the probability of a visit and domestic political benefits of a visit.

To illustrate the tradeoff between likelihood of a visit and a visit’s impact, we return to the special case of the uniform prior, $\alpha =\beta =1$, with $\sigma \to 0$, $q=1$, and dominant office-holding incentives ($\Psi \to \infty$). This case is depicted visually in Figure 2 8. The threshold $a\left(z\right)$ is the horizontal axis. The solid decreasing line shows the concession z necessary to induce each threshold a. The downward sloping dotted line shows $Pr\left(visit\right)$. The lower dash-dot line shows the probability of regime change given the occurrence of a visit. The dashed line shows L’s (rescaled) expected payoff for the each induced threshold.

A large concession induces a low threshold (LHS of figure, $a\left(z\right)$ close to 0) and so visits become very likely. However, such visits are of little value to L, as they provide only a weak signal of strength. At the opposite extreme, if L offers only a small concession, then the induced threshold is high, meaning visits are unlikely, but visits provide a strong signal of strength when they do occur. L’s payoff is maximized by an intermediate-sized concession, such that visits occur reasonably often and provide a moderate signal of strength.

We can examine how bargaining outcomes depend on concession transparency and expected salience further, as follows:

Corollary 3.

If L is a proposer, as concession transparency q increases, the concession size z becomes smaller and visits become less likely. As expected salience σ increases, the concession z increases and visits become more likely. When office holding is the dominant concern ($\Psi \to \infty$), if either $q\to 0$ or $\sigma \to 1$, then $z\to z_0$.

Expected salience increases the size of concession that L offers, following the resource-curse logic outlined above, and thus makes visits more likely. As C believes it to be increasingly likely that F wants a favor from L, the lack of a visit sends an increasingly negative signal of L’s strength, as follows: $\frac{d{E}_c[1-\theta |\mathrm{non-visit},z]}{d\sigma }>0$. To avoid this negative signal, L offers a large concession that makes F highly likely to visit.

The domestic leader’s equilibrium offer is also determined by concession transparency: the size of the concession is decreasing in the probability that it becomes revealed to C upon delivery. To see why, first note that with full concession transparency, $q=1$, L could set the concession size to optimally balance the likelihood of a visit against the informativeness of a visit; if a visit occurs, C observes the associated concession and draws exactly the inference that L intended. But now consider what happens in the other extreme, $q=0$, so that when a visit occurs, C does not observe the concession that was made. If C conjectures that L has offered the same concession as they had in the $q=1$ case, then L faces the incentive to increase the offer because doing so increases the probability of a visit without undermining the signaling value of the visit. Thus, L will deviate to a larger concession; but, knowing that L faces this incentive, C increases their conjecture of the offered concession in turn. Concession transparency limits the size the concession because without transparency, L cannot resist the temptation to bid up her offer.

As a final consideration, with the uniform prior, we can provide an explicit statement of the equilibrium concession size and corresponding threshold and examine the role of F’s intelligence.

Corollary 4.

For $\alpha =\beta =1$, low expected salience ($\sigma \to 0$) and dominant office incentives ($\Psi \to \infty$), L offers concession

$$z=\frac{\rho \left(\sqrt{n(n+2)+{(q+1)}^2}+n+1\right)\left(\sqrt{n(n+2)+{(q+1)}^2}+n+q+3\right)+2{(n+2)}^2{(q+2)}^2\tau }{(r-1)\left(\sqrt{n(n+2)+{(q+1)}^2}+n+1\right)\left(\sqrt{n(n+2)+{(q+1)}^2}+n+q+3\right)+2{(n+2)}^2{(q+2)}^2}$$

(8)

that induces

$$a\left(z\right)=\frac{(n+1)(1+q)}{2+q}+\frac{\sqrt{n^2+2n+{(1+q)}^2}}{2+q}$$

(9)

As n increases, visits become more likely $\left(\frac{d\frac{a\left(z\right)}{n}}{dn}<0\right)$.

L’s and F’s payoffs both increase in n. The quid pro quo of buying visits is more attractive to both parties as the foreign power has access to better intelligence.

7. The Price of the Quid Pro Quo

Given the results of Propositions 6 and 7, we can now address the question posed at the outset of the paper: what is the price of a diplomatic visit? The preceding analysis produced a number of comparative statics on bargaining outcomes as a function of various features of the bargaining protocol and attributes of the two leaders, which we summarize here.

Transparency vs. Opacity When C is fully aware of salient opportunities and the details of negotiations (as in our “open door” bargaining protocol), then an exchange of concessions for visits is never in the recipient leader’s interest. Quid pro quo diplomacy requires that bargaining occurs behind closed doors. However, our analysis reveals a more nuanced effect of transparency in diplomacy: while the domestic leader benefits from opacity in negotiations, they prefer transparency in the actual delivery of the negotiated concession. When neither the negotiations nor the concessions themselves are observed by the domestic challenger, the size of the concession increases and visits become more frequent but less informative.

Bargaining power: If L makes the proposal, they offer a moderate concession. Their moderate concession balances a desire to increase the likelihood of a visit while maintaining its deterrent value. As bargaining power shifts from L to F, bargaining outcomes shift to favoring F over L. The size of concessions increases, visits become more frequent, and the visits that occur have a decreased impact on L’s survival.

Expected Salience: When F is likely to want a favor, L suffers from a diplomatic resource curse. Because C anticipates that L has something of value to offer F, the fact that F does not make a visit in order to obtain the concession sends a strong negative signal of L’s strength. To avoid this signal of weakness, L pays more for a visit and visits become more likely and less effective. In contrast, when it is seen as unlikely that F wants a favor, the absence of a visit is less politically detrimental to L; this drives the price of the visit down, which in turn implies that any visits that do occur provide an especially powerful signal of L’s strength.

$\mathit{F}$’s cost: As F’s costs of visiting increase, so does the price needed to offset those costs. There are three distinct costs that F must factor into their visit decisions: the material and opportunity costs of travel, $\tau$; the reputational cost of associating with a soon-deposed leader, $\rho$; and the risk that any agreed-upon deal does not become implemented, $1-r$. A stop on a regional tour or a pull-aside at a multilateral summit can be purchased more cheaply than a trip undertaken solely for the bilateral visit. Dictators and human rights abusers will likely see a steeper price for their diplomatic engagements. A policy concession requiring long-term implementation will need to be greater than its cash equivalent, as the policy concession carries the risk that L fails to survive in office long enough to implement it.

Ex-ante survival prospects: Prior expectations of the likelihood that L will survive affect the size of concessions and the likelihood of visits. Intuitively, ex-ante survival prospects affect both the supply and demand of visits. If L is likely to be deposed, then F needs larger concessions to compensate for the risk they assume due to the potential reputational cost as well as the possibility that the concession does not become implemented. When pessimistic about her survival prospects, L values visits highly and is willing to make larger concessions. Thus, when L’s regime is perceived to be unstable, the supply of visits is low and the demand for them is high, so the price is driven upwards. Figure 3 illustrates the impact of survival prospects on concessions when L has proposal power and officeholding incentives are dominant ($\Psi \to \infty$).

The horizontal axis in Figure 3 is $E\left[\theta \right]=\frac{\alpha }{\alpha +\beta }$. The dashed line shows L’s optimal concession and the solid line shows the threshold $a\left(z\right)$ that the concession induces 9. When L is anticipated to be strong, they offers relatively small concessions and F only visits if they see a relatively high signal. The relative rarity of visits means that a visit is a powerful signal of strength. In contrast, when L is perceived to be weak, L makes more generous concessions that induce a lower threshold $a\left(z\right)$, meaning that F visits for a wider range of private signals. L is willing to spend more for a weaker signal of strength when they are perceived to be weak because their precarious situations make any signal of strength valuable. Of course, the increased concession does not necessarily mean visits are more likely to occur, as on average, F’s private signal is likely to be weaker when the prior $E\left[\theta \right]$ is small.

Quality of intelligence The basis of the quid pro quo is that F has some private information about the strength of L’s regime. The number of trials, n, may be interpreted as the quality of F’s intelligence. Both leaders’ payoffs are increasing in n: the visit’s deterrent value is increasing in the precision of the information that guided F’s decision to conduct the visit, enhancing L’s survival prospects, and in turn, L is willing to pay more for the visit, improving F’s payoff. F’s improved intelligence also means that F can better avoid visits with leaders that will be soon be removed and avoid the costs associated with such a diplomatic misstep. An empirical implication is that visits with a US president—whose decisions are informed by USD 80 billion worth of annual intelligence gathering [29]—are far more valuable to recipient leaders than visits are with, for example, a Canadian Prime Minister, who has no formal intelligence apparatus of his own [30]. This relative valuation is not a function of the the countries’ relative prestige or influence but rather of the quality of private information that their leaders have access to. If we suppose that leaders face similar travel and opportunity costs for foreign visits (similar $\tau$ and $\rho$), then US presidents should travel more than Canadian leaders because they can extract larger concessions in return.

8. Discussion and Conclusions

We examine the bargaining that surrounds top-level diplomatic exchanges and the impact of those exchanges on domestic political competition. A symbolic demonstration of support from one leader to another is valuable for the recipient because of the information it communicates to a potential challenger. The fact that visits deter challenges gives the incumbent an incentive to offer a concession to the foreign leader in exchange for a supportive diplomatic signal. Yet such a payment undermines the visit’s signaling value. We show that mutually beneficial quid pro quo diplomacy can occur when negotiations occur behind closed doors. The price of a visit depends on the bargaining structure, the expected likelihood that a foreign leader wants a favor, the transparency of the concession, the recipient leader’s prior regime strength, and the quality of the intelligence informing the foreign leader’s decision. Provided there is a degree of opacity surrounding negotiations, symbolic public diplomacy can be informative even when it is purchased.

A number of interesting substantive implications are suggested by the preceding analysis. A crucial factor identified as shaping the occurrence and impact of diplomatic visits is transparency—regarding the salience of concessions, the bargaining process, and the revelation of the concession size following the completion of a visit. Our model takes these different forms of transparency as exogenous parameters. As a practical matter, however, it is worth considering which actors benefit from more or less transparency and thus which actors are incentivized to try to expose or conceal relevant information.

Suppose that we introduced a third party who was an antagonist to the domestic leader (for instance, a foreign adversary or a domestic opposition leader who sought to motivate our model’s C player to take action against the leader). Intuition would suggest that the antagonist would be incentivized to expose any closed-door deal making that facilitated a visit between L and F, so as to undermine the signaling value of the visit; and that L would conversely wish to maintain secrecy around these aspects of the exchange. Our analysis, however, reaches the opposite conclusion. This counterintuitive result arises from the fact that we take the audience’s ability to learn not only from what they observe directly but also from what they can infer took place out of public view seriously [31]. Without observing the negotiations or the realization of concessions directly, the audience still forms a conjecture as to the size of the concession that was negotiated and delivered in private; this lack of transparency incentivizes the leader to make concessions that exceed the audience’s conjecture, up to the point that they would be better off tying her hands to not negotiating at all. Transparency supports rather than undermines the signaling value of the visit because it enables the leader to commit to conceding less than the audience would have otherwise speculated. Thus, if given the ability to reveal credible information about the bargaining process, the domestic leader would generally prefer to do so, while the antagonist would generally prefer not to.

Finally, this paper presents a model in which the relationship between the domestic leader L and foreign leader F is asymmetric; by assumption, we abstract away from F’s own political concerns and from any signaling value that the visit could provide for F’s own challengers or antagonists. Incorporating these considerations can yield important insights regarding the value and consequences of reciprocal diplomatic exchanges, whereby F visits L in exchange for a “concession” in the form of L’s subsequent visit to F. Speculatively, we can see reasons why this possibility might either strengthen or undermine the signaling value of a visit. On the one hand, the desire to induce L to visit later would make F more willing to visit L now, making the visit a weaker signal of L’s strength; but this would in turn lower the price L has to pay for F’s visit and thus improve the signaling value. It is far from obvious ex-ante what would be the net effect of these competing forces. The potential for reciprocal visits also raises the possibility of some degree of “collusion” between F and L, whereby both agree to visit each other despite unfavorable beliefs of one another’s strength; it also raises the question of the sequencing of visits, how the reciprocity could be enforced, and which party would have an incentive to renege on their commitments. We hope these questions will be taken up in future research.