Abstract
In this paper, we address the problem of fair sharing of the total value of a crowd-sourced network system between major participants (founders) and minor participants (crowd) using cooperative game theory. We use the framework of a Shapley allocation which is regarded as a fundamental method of computing the fair share of all participants in a cooperative game when the values of all possible coalitions could be quantified. To quantify the value of all coalitions, we define a class of value functions for crowd-sourced systems which capture the contributions of the founders and the crowd plausibly and derive closed-form expressions for Shapley allocations to both. These value functions are defined for different scenarios, such as the presence of oligopolies or geographic spread of the crowd, taking network effects, including Metcalfe’s law, into account. A key result we obtain is that under quite general conditions, the crowd participants are collectively owed a share between and of the total value of the crowd-sourced system. We close with an empirical analysis demonstrating the consistency of our results with the compensation offered to the crowd participants in some public internet content sharing companies.
1. Introduction
Many existing and emerging online network systems and services are designed to work semi-autonomously using cloud hardware and secure software created by a small group of founders and enabled by the mass participation of crowds. We refer to (the small number of) the former as major participants and (the large number of) the latter as minor participants. Without the hardware platform and the associated reliability and security provided by the software, there would be no platform and service. But without the participation of the crowd, there would be no data or content to enable the service. Recent examples of such platforms include Waze [1] and Helium [2] and one can count Google and Facebook as older and well-established instances of such services.
There is a large body of literature in the computer science community on the design and operation of such services and a growing number of publications on reliable mechanisms that automatically account for and accumulate rewards for participants (see, for example, [3]). This literature, however, has so far not discussed substantially the concept of fair allocation of the service’s total value to the crowd participants who by constantly feeding data and information to the system are key to its success. As described in [3], one observes a trend toward rewarding crowd participants via automatically counted tokens based on such measures as the number of queries, messages, or packets each participant processes, independently of the total value that the network system and service as a whole generates. This approach particularly obscures the fact that in many such network systems, crowd participants additionally provide critical local or even private information free of charge purely as part of participation which is monetized by the service provider, adding to the total value generated by the service without direct benefit to the participants.
The lack of value-based allocation to participants in large-scale crowd-sourced systems is felt keenly by the general public after over two decades since the emergence of these once novel enterprises (see, for example, [4]), but interestingly, this topic has not been addressed adequately by the research and networking communities; for notable exceptions, see recent articles [5,6] and with respect to the narrower Internet Service Provider settlements, see older articles [7,8,9,10]. Motivated by the interest in revisiting the structural aspects of crowd-sourced systems by the Web 3.0 Foundation (see [11]), and more directly, the new possibilities offered by the enterprise-sourced systems as part of Industry 4.0/5.0 (see [12]), this paper aims to help bridge this gap via a novel and formal methodology for fair allocation of the total value generated by a crowd-sourced system.
Our key result is the derivation of the share of crowd participants as a percentage of the total value generated by the service platform. It is instructive here to draw an analogy between this share (of the participants in a crowd-sourced system) and the share of labor as part of the national income in macroeconomics [13,14]. In the latter, labor is contrasted with capital, and in the former, crowd with the system. Interestingly, we observe essentially the same split: our derivation shows a share for the crowd between and of the total value and macroeconomic data consistently exhibit a labor share between and of the national income; see charts in [13,14] and numerous other national statistical surveys. Thus, additionally, our result may be regarded as a theoretical explanation of the well-known split of shares between labor and capital in large-scale economic systems.
The paper is organized as follows. In Section 2, we describe the role and requirements of value functions that are necessary for the computation of the Shapley value in a cooperative game. Our aim is to make these functions as simple as possible while capturing the key contributions of major and minor participants in crowd-sourced systems.
In Section 3, we consider various models for a single crowd-sourced system consisting of a major participant or founder, and a large number of minor participants or a crowd. We derive close-formed expressions for Shapley allocations to both for a general class of value functions under different regimes. A key result here is that under quite general and plausible conditions, crowd participants collectively receive a payoff of at least of the total value of the crowd-sourced system.
We next consider a broad extension of our methodology to oligopolies of crowd-sourced network systems in Section 4 whereby distinct collections of single-founder crowd-sourced systems agree to cooperate via pair-wise agreements. We show similar results hold in terms of the fair share of participants. Interestingly, and in contrast to the single crowd-sourced system, the ratio of the fair share of major to minor participants now increases with the number of inter-crowd connections each major participant contributes to. In Section 5, we present a model of geographic crowd-sourced systems and obtain closed-form expressions for the Shapley allocation to each community which continues to exhibit the to allocation to the crowd participants. We close with an empirical study of crowd-sourced systems whose public financial statements help estimate the actual revenue share of the crowd which we observe to be consistent with our model’s predictions.
2. Fair Allocation in Cooperative Games
A formal derivation of fair allocation in cooperative games was first introduced by Shapley [15] and numerous extensions of it have been considered since. A good introduction is found in [16]. To summarize the main concept, we consider the setting where a group of participants N are cooperating towards a common goal and generate value as a result, and this value needs to be distributed among all the participants in a fair way. Suppose that there is a value function that takes any subset S of N as input and outputs the value that would have been generated by the coalition formed by only the participants in S, as opposed to all of N. Now, we denote by the payoff that participant i receives as part of the grand coalition, i.e., when .
Fairness. There are a few natural properties that a fair allocation scheme must satisfy:
Property (3) above null player states that any player i that adds no value to any coalition S does not receive any payoff in the grand coalition, while Property (2) symmetry states that any two players i and j that add the same value to every coalition S should receive the same payoff. Participants are rewarded only based on the value they add and no other factors. Property (1) Efficiency states that the total value generated is completely distributed among the participants, and Property (4) linearity says that for two independent games, the fair payoff to each participant must be the sum of the fair payoffs in each independent game.
From these conditions, Shapley derives the following expression for the unique payoff to each participant i:
Here, the expression in brackets on the extreme right hand side is the marginal value that agent i adds to coalition S and this marginal value is averaged out for all possible coalitions. The payoff in (2) is known as the Shapley allocation to participant i.
3. A Single Crowd-Sourced System
We think of a crowd-sourced system ( from here on) as a cooperative game in which one entity (the founder) provides the main infrastructure, which could be physical (hardware) or virtual (software), of a value-generating service that can only succeed if a large number of spatio-temporal agents participate to enable local match of supply and demand for the said infrastructure service. In this setting, we consider a collection of participants denoted by where g is the founder and are the crowd member identities. For a complete list of variables, see the Abbreviation section. There is much symmetry in this setting which we exploit fully in the sequel.
It is assumed that the value of any subset S of N is zero unless it includes the founder, and in the case where the founder is in S, its value is equal to a function of the size of the crowd. This is a restatement of the notion of a (crowd-sourced system) in that it offers much credit to a founder for imagining and initiating a distributed enterprise enabled by a large number of uncoordinated participants who constantly feed the system. This form of the value function also makes it possible to derive closed-form expressions for the Shapley payoff of all participants in various settings, as we observe below. We use a power of the size of the crowd as its value: a linear function corresponds to standard scaling. The quadratic function has been widely discussed in the networking literature as Metcalfe’s law Remark 1, and higher, super quadratic, powers are included for benchmarking purposes.
3.1. Coalition Value Based on Revenue
3.1.1. Case 1 (Identical Participants)
The first situation we consider is one where all the potential participants are identical. Any coalition that does not contain the major participant g is treated as one with no value, while the value of a coalition including g grows as a power of its size. The motivation for this model comes from the network effect, sometimes referred to as Metcalfe’s law, which states that the value of any network grows proportional to the square of its number of participants. This empirical law, originally devised in the context of Ethernet networks [17], seems to also hold remarkably well in many modern situations such as cryptocurrency networks [18] and social networks [19]. The model can be formally written as , and
where is some constant. Metcalfe’s law is simply a special case of our model with .
Here, we list a few key properties of as defined above and explain why we believe this simple form captures the key aspects of a crowd-sourced system valuation. We observe that
- (1)
- (2)
- for any specific crowd participant, there is no special incentive to join any of the numerous coalitions of size S, as the value function only depends on the size of the coalition and not its constitution. This means that the basic assumption in (2), stating that all coalitions of size S are equivalent, is met;
- (3)
- the simple form of we assume—the linear, quadratic or higher powers—does not need a saturation effect, since the more crowd participants, the larger the total value of a coalition. This is in contrast with saturating systems where (say) the first 100 crowd participants provide a higher value than the last 100.
- (4)
- we note that in the analysis in the following pages, relatively small values of S offer us the asymptotic results with respect to the exponent k, which equals one and two, corresponding to linear and quadratic value functions.
Our first result characterizes the Shapley value associated with each participant as a fraction of the value of the total coalition. We now look at a general computation that is useful later as well.
Lemma 1.
Consider the coalition game with the set of agents and value ν given by
The Shapley values of the game satisfy
Proof.
See Appendix A.1. □
Theorem 1.
Consider the coalition game with the set of agents and value ν given by (3). The associated Shapley values satisfy
and
Proof.
Applying the results of Lemma 1 to the value (3), we obtain
□
Remark 1.
The results obtained in Theorem 1 tell us that when , i.e., when the power of a network grows proportional to the number of participants, the value of the grand coalition is shared equally between the major participant and the collection of minor participants. In other words, and .
In the popular case of Metcalfe’s law where , the theorem says that the major participant should receive 1/3 of the value generated while 2/3 should be distributed equally among the minor participants.
3.1.2. Case 2 (Non-Identical Participants)
The assumption that all participants are (nearly) identical might not hold in many settings; for example, when some participants contribute significantly more to the value of the system than others due to their influence in a social network. A slightly more refined model for the value would be
where refers to some notion of the amount of work performed by participant i, e.g., the number of messages routed by i. We denote by the share of total work performed by i.
Theorem 2.
Consider the coalition game with the set of agents and value ν offered by (6) where . The associated Shapley values satisfy
Proof.
See Appendix A.1. □
Remark 2.
The results obtained in Theorem 1 under the identical participant model can be recovered from the above theorem by assuming . In fact, in the case where the workload is more or less uniformly distributed and not too concentrated, as formalized by the condition
the above theorem tells us that and , which is equivalent to dividing the value between the founder and the crowd in the same way as in the identical participant model, and then dividing the value among the crowd proportional to the share of work performed.
Remark 3.
In Theorem 2, we treated the case . However, analogous results hold true for higher values of k as well. It can be shown that
3.2. Coalition Value Based on Profit
A legitimate concern regarding the use of revenue as a proxy for value is that the founder could be incurring significant costs for infrastructure which the minor participants do not. In this case, the resulting profit, revenue minus cost, is a more natural proxy for value. A question which our Shapley allocation derivation answers in the positive is the observable impact of the large infrastructure cost incurred by the founder compared to the small cost incurred by the crowd members.
We modify the model to take into account such costs. We assume that each minor participant incurs a fixed constant cost and the major participant pays a cost of per minor participant with . Formalizing all this, we obtain a new value function
We compute the Shapley values in this case by appealing to Lemma 1 again.
Theorem 3.
Consider the coalition game with the set of agents and value ν given by (8). The associated Shapley values satisfy
for large values of n.
Proof.
Using the results of Lemma 1, the exact same computation in the proof of Theorem 1 delivers this result. □
Remark 4.
Even though in the limit , the results of Theorem 3 collapse to that of Theorem 1, the value of might be large enough that the contribution of cannot be ignored for the moderately large values of n that typically arise.
Remark 5.
In this case, the ratio of the share of the founder to the share of the crowd is
This shows that when , as the cost of the system infrastructure increases, the share of the founder compared to the crowd of participants decrease. This may seem at first counterintuitive or unfair, especially compared to the case of where the share is constant regardless of the cost of the infrastructure. This phenomenon occurs because the revenue should be divided according to and between the founder and the crowd, whereas the total cost is split equally. Thus, the superlinear scaling of revenue and the linear scaling of cost offer a decreasing proportional share to the founder even though the absolute value of the founder share is still increasing.
Another observation regarding (6) is that while the share of the founder is increasing in k, the founder’s profit decreases as a percentage of the total profit. This again is a consequence of the revenue of the network growing as a power of its size.
4. Oligopolies of Crowd-Sourced Systems
We now consider the case of multiple crowd-sourced systems where major participants or founders are willing to cooperate, thus inter-working s for a higher total payoff to all. Let us assume that each major participant v has minor participants in its , crowd-sourced system affiliated with v. The major participants now agree to cooperate for higher payoff by inter-networking their disparate crowds. This is achieved through a series of bilateral agreements between pairs of major players. The key consequence of such cooperation between major participants i and j is joint creation of a payoff which is proportional to for the Metcalfe value model we considered previously, in contrast to for the case i and j do not cooperate. The question we wish to answer is fair allocation to each , and each major and minor participants in each assuming global cooperation represented by a graph G as defined below.
4.1. Shapley Value of an Oligopoly: A Coarse Grain Model
We now assume that major participants form a set of pairwise, bilateral agreements amongst themselves. We represent this by a connected graph whose vertices denote s associated with major participants and each edge in E denotes a bilateral agreement. A natural extension of the notion of Metcalfe value to a graph G is given by
Here, is the Metcalfe law restricted to the system v and each edge adds an additional to the value of G due to the inter-networking between vertices u and w.
We assume that the crowd-sourced systems associated with major participants form the set of agents of a cooperative game. The value of a subset is the Metcalfe value (10) of the subgraph induced by S. This is the graph consisting of vertices S and all edges of G, both ends of which lie in S. This is implicitly an aggregate model that clubs together all the minor participants of a with the major participant, modelling the scenario where each minor participant has already been bound to its major participant, perhaps by means of an agreement or due to some external constraints such as geography that limits the choice of the minor participant. As a result, in the following, denotes the share of the crowd-sourced system associated with major participant u, and not just the share of the major participant u in by itself (which is discussed in Remark 7).
The following result characterizes the Shapley value of each .
Theorem 4.
Consider a graph and a cooperative game with set of agents and value function
The Shapley value of each vertex u is given by
Proof.
See Appendix A.2. □
For example, in the oligopoly shown in Figure 1, we can compute the Shapley values as
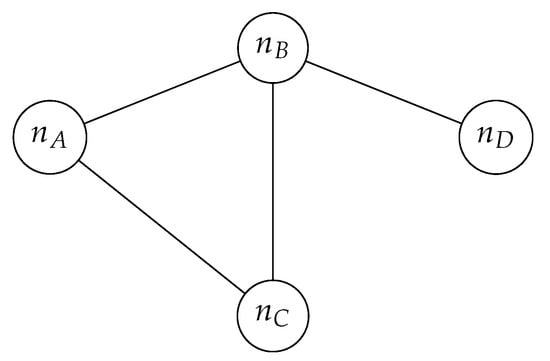
Figure 1.
Graph of four crowd-sourced systems with four bilateral agreements and their Shapley allocations (Theorem 4).
Remark 6.
In the special case where all major participants have an equal number of minor participants within their system, i.e., for all , we obtain
Remark 7.
If we consider , that there is an edge between g and for each , and that and , we obtain a model that is very close to (3) with . The only difference here is that the coalitions that do not contain g have a non-zero value that scales linearly with its size. Unsurprisingly, we obtain
exactly the same as in Theorem 1.
4.2. Shapley Value of an Oligopoly: Fine-Grain Model
Theorem 4 and the Remarks 6 and 7 derive the Shapely value of each crowd-sourced system (CSS) associated with each vertex in the oligopoly game of graph G. What remains is to identify the Shapley fair share of each participant in each associated with each major player . To achieve this, we need to define a new value function on each which takes its size and sizes of its neighboring s explicitly into account.
To this end, we consider a more fine-grained model here. We consider the set of minor participants in the associated with major participant as separate agents, making the total set of agents of the cooperative game
A subset can be partitioned as for each and . The value of the coalition is computed based on two simple principles: each contributes and each contributes to the value of S. That is,
This value function and agent set jointly capture the cooperative game involving all s and their minor and major participants. For , we denote by the size of its set of minor participants.
Theorem 5.
Consider graph where each node has an associated set , and a cooperative game with set of agents and value function
where and for each . The Shapley value of each major participant is the sum of two terms, the intra and inter crowd payoffs, given by
The Shapley value of each minor participant is also the sum of two terms
Proof.
See Appendix A.2. □
Remark 8.
The Shapley share of the major participant u in (vertex of the oligopoly graph G) can be written as
For large enough numbers of minor participants , this ratio can be simplified as
This ratio is greater than and less than , moving closer to as the number of minor participants in the neighbouring grows larger than that in the corresponding to v.
5. Geographic Crowd-Sourced Systems
In this last section, we discuss the extension of the models we have considered so far by considering s which are geographically distributed. More concretely, we consider a collection of agents, and for each agent, the region covered by it. For simplicity, we refer to these regions as “disks”, even though these can be of arbitrary shape. Figure 2 shows five disks associated with five agents.
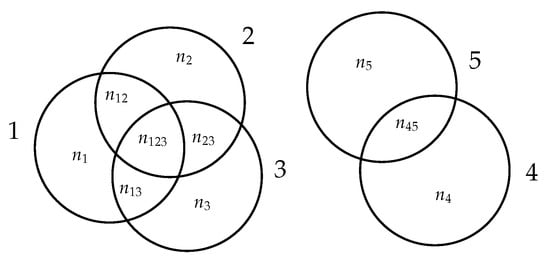
Figure 2.
Geographic with five disks numbered 1 through 5.
In this model, there are m agents , and each agent i has a corresponding disk . There are also users, set U, served by the agents in M. A user u may be served by an agent i only if u is in the region . Notice that a user in may also be in for one or more . We need notation for the number of users in the intersection of disks. For each subset of agents , we denote by the number of users in the geographic area exclusively covered by all for . For example, in Figure 2, is the number of users in that do not belong to any of the other disks, and is the number of users in , etc. More formally, is the number of users in .
In this setting, we define the value functions and as follows. For any ,
With these definitions, the geographic model is equivalent to an oligopoly of s where the underlying graph G is complete and . The Shapley value for each agent under the Metcalfe model is therefore given by Theorem 4 while the linear model is an additive cooperative game where the Shapley value coincides with the value function, namely
Geographic Crowd-Sourced Systems with a Founder
As a conclusion to the discussion of geographic crowd-sourced systems, we consider the contribution of a founder that establishes the infrastructure for the collection of a geographic crowd-sourced system. For example, the agent that provides the software for connecting access points in a distributed wireless network, e.g., [2]. Just to set the notation, we let
As in Section 3.1, we define a macro value function which quantifies the cooperative game involving the founder and any subset of agents .
and
where and are defined in (16).
Theorem 6.
Proof.
Follows from Theorem 2. □
As in Remark 2, notice that and asymptotically approach and as the number of agents increases.
6. Empirical Analysis
Our main thesis in this paper is that many crowd-sourced systems, old or new, do not compensate their crowd participants, and when they do so, the share is a relatively small fraction of their total value (revenue). Our goal is to determine what a reasonable share would be if fair allocation existed. Unfortunately, the information about sharing of the total value (revenue) with crowd participants, if and when this information exists, is hard to come by. Often, data or content from the crowd are collected as part of the service-level agreement signed by the crowd participants in exchange for a service, which may be search, access to social media platforms, use of navigational maps, access to wireless spectrum and other services. In public records, it is often hard to carve out compensation paid to crowd participants directly. In a few instances, however, it is possible to estimate these payouts. Here, we provide three examples: Spotify, Pandora, and YouTube.
- Spotify compensates audio contributors an average of 0.003–0.005 cents per stream which amounts to about 2/3 of its total revenues in 2021 (USD 11.4B); see [20,21].
- Pandora pays an average of 0.00133 cents per stream which translates to 70% of its total revenues to artists and publishers in 2021 (total revenue USD 3.64 B in 2021)) of which 57% goes to artists or record labels, i.e., 2/5 of the total revenue; see [22].
- YouTube is our third example, and here, it is possible to obtain more detailed information from public records which we describe below.
YouTube, an Alphabet subsidiary, has for over a decade awarded its content creators a large share of its advertising revenue. Since 2019, YouTube has disclosed its payments to its crowd content creators. Table 1 below shows the breakout of the total revenues of Alphabet and YouTube in 2017 through 2021. Table 1 offers us the YouTube annual revenues for 5 recent years. But how much of these were paid to content creators in each fiscal year? During August 2021, articles in Fortune [23], Barron’s and numerous other outlets reported that over the previous three years, Alphabet/YouTube paid USD 30B to its content creators. Adding the relevant figures from Table 1, this corresponds to a fraction of 30/(28.8/2 + 19.7 + 15.1 + 11.1/2) = 30/54.75 = 55% share of the total revenues during the second half of 2018, 2019, 2020, and the first half of 2021 to content creators. A more recent article [24] puts this ratio at 68%. Other figures in the same range are also mentioned in various articles in the past 2 years. Putting all of this together, we observe a range of 55–68% of the total YouTube revenues were paid out to content creators in each fiscal year, which is in close agreement with the range we derived under the Shapley allocation using the simple value functions discussed above.

Table 1.
Annual revenues of Alphabet and YouTube in 2017 to 2021.
Other video content crowd-sourced systems, such as TikTok, do not publish corresponding data, although it is believed they also compensate their content creators a substantial share of their revenues. Meta/Facebook has also started compensating its content creators. (https://www.facebook.com/business/learn/lessons/how-make-money-facebook, accessed on 13 July 2023).
7. Conclusions and Future Work
In this paper, we defined value functions that succinctly capture the interplay between the contributions of a small number of infrastructure providers, founders, and a large number of contributors, crowd participants, in cooperative value-generating settings such as crowd-sourced service platforms. We derived closed-form expressions for fair allocation of the total value of such systems between the founders and the crowd participants using the Shapley allocation. We showed that the Shapley allocation offers the crowd participants one half to two third share of the total payoff for the cases of linear and quadratic growth of revenue as a function of crowd size. We further showed that similar results hold in cases of oligopolies of such network systems characterized by bilateral agreements between pairs of independent crowd-sourced systems. We showed that the same holds true for geographic crowd-sourced systems. These results are consistent with the observed share of labor in the setting of the national income but are in contrast to the current practices of numerous existing and emerging crowd-sourced systems whereby participants are awarded tokens of limited value compared to the total payoff of the full system but are in agreement with the practices of a small number of platforms, some of which we documented. A natural next step would be to consider the integration of our proposed value-based allocation in the emerging token-based reward systems which are being actively discussed in standards bodies including the Web3.0 foundation and Industry 4.0/5.0 initiatives. Another avenue for further work is to explore alternative value functions that capture the contributions of the founders and the crowd participants.
Author Contributions
W.K. and I.S. proposed the theme of this research. M.A. and I.S. developed the model and derived the results and did the empirical analysis. Conceptualization, W.K. and I.S.; methodology, M.A. and I.S.; validation, M.A. and I.S.; formal analysis, M.A. and I.S.; writing—original draft preparation, M.A. and I.S.; writing—review and editing, W.K., I.S. and M.A.; supervision, I.S.; project administration, I.S.; internal funding acquisition, W.K. All authors have read and agree to the published version of the manuscript.
Funding
This work was funded by Nokia Bell Labs as part of its core research and summer internship program.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank Glen Weyl for references [5,6] and the macroeconomic parallel mentioned in the introduction.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSS | Crowd Sourced System |
| g | The unique major participant (founder) |
| ith minor participant (crowd) | |
| n | Number of minor participants |
| N | Set containing founder and crowd (grand coalition) |
| S | A coalition of participants, a subset of N |
| Cardinality of S | |
| Value of the coalition S | |
| Shapley payoff to participant | |
| Cost incurred by founder per participant | |
| Cost incurred by each participant | |
| Constant unit in value functions | |
| V | Set of vertices v, each representing a crowd-sourced system, |
| E | Set of edges, each edge denoting an agreement between its ends |
| G | Oligopoly graph of s and their bilateral agreements |
| S | A subset of vertices V |
| Subgraph of G induced by S | |
| v | A vertex/participant in V |
| e | An edge/agreement in E |
| Set of neighbors of the vertex v in graph G | |
| Number of participants(crowd) in v’s crowd-sourced system | |
| g | Main founder of the geographic s |
| Set of agents i, each representing disk | |
| Number of users in disk . |
Appendix A
Appendix A.1. Proofs from Section 3
Proof of Lemma 1.
We can compute the Shapley value of g as
since as . Since is just a function of , we can reduce the computation as
Since the participants are all identical, we derive the Shapley value as
□
Proof of Theorem 2.
The Shapley value of participant i can be computed as
The marginal utility of participant i can be written as
which gives
The first sum can be simplified directly and the second sum maybe rewritten using Fubini’s theorem as follows:
Dividing by the value of the grand coalition , we obtain
It follows that
□
Appendix A.2. Proofs from Section 4
Proof of Theorem 4.
The marginal utility of u to coalition S is
We can then compute
The second term above can be reduced using Fubini’s theorem as we did before to obtain
□
Proof of Theorem 5.
The value function can be split as
where
and
Each of these value functions can be considered as the value function of a cooperative game in its own right. By Linearity of Shapley value,
for any player .
Notice that for any , if , then
which means a is a null player in the game . This implies by the null player axiom of the Shapley value. The game on the remaining set is just the single major player game (3), and the result of Theorem 1 gives us
Similarly, for any ,
which implies by the null axiom of the Shapley value.
All that remains to be computed is the Shapley value of players with the value function . Since we showed that all other players in this game are dummy, we can find the Shapley value of players as their Shapley value in the simplified game whose set of players is and value function . To achieve this, we again split the value function as
where
and compute the Shapley value of the players for each of these value functions separately. We observe that any player or is a null player of the value function , which means
This means we can again reduce the set of players to and value function to , and notice that this value function is symmetric with respect to all four players which implies
We can now compute the original Shapley values as
When or ,
When ,
and when ,
References
- Waze Company. Available online: http://waze.com/company (accessed on 13 July 2023).
- Helium. People-Powered Network. Available online: http://helium.com (accessed on 13 July 2023).
- Voshmgir, S. Token Economy: How the Web3 Reinvents the Internet; Token Kitchen: Berlin, Germany, 2019. [Google Scholar]
- Lanier, J. Who Owns the Future? Simon and Shuster: New York, NY, USA, 2013. [Google Scholar]
- Jia, R.; Dao, D.; Wang, B.; Hubis, F.A.; Hynes, N.; Gürel, N.M.; Li, B.; Zhang, C.; Song, D.; Spanos, C.J. Towards efficient data valuation based on the shapley value. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Okinawa, 16–18 April 2019; pp. 1167–1176. [Google Scholar]
- Li, H.; Vincent, N.; Chancellor, S.; Hecht, B. The Dimensions of Data Labor: A Road Map for Researchers, Activists, and Policymakers to Empower Data Producers. In Proceedings of the 2023 ACM Conference on Fairness, Accountability, and Transparency (FAccT ’23), Chicago, IL, USA,, 12–15 June 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 1151–1161. [Google Scholar] [CrossRef]
- Ma, R.T.; Chiu, D.M.; Lui, J.C.; Misra, V. Internet Economics: The use of Shapley value for ISP settlement. IEEE/ACM Trans. Netw. 2010, 18, 775–787. [Google Scholar] [CrossRef]
- Ma, R.T.; Chiu, D.M.; Lui, J.C.; Misra, V.; Rubenstein, D. On cooperative settlement between content, transit, and eyeball internet service providers. IEEE/ACM Trans. Netw. 2010, 19, 802–815. [Google Scholar] [CrossRef][Green Version]
- Cheung, Y.; Chiu, D.M.; Huang, J. Can bilateral ISP peering lead to network-wide cooperative settlement. In Proceedings of the 2008 IEEE 17th International Conference on Computer Communications and Networks, St. Thomas, VI, USA, 3–7 August 2008; pp. 1–6. [Google Scholar]
- Misra, V.; Ioannidis, S.; Chaintreau, A.; Massoulié, L. Incentivizing peer-assisted services: A fluid Shapley value approach. ACM SIGMETRICS Perform. Eval. Rev. 2010, 38, 215–226. [Google Scholar] [CrossRef]
- Web 3.0 Foundation. Available online: https://web3.foundation/ (accessed on 13 July 2023).
- 4th Industrial Revolution. Available online: https://en.wikipedia.org/wiki/Fourth_Industrial_Revolution (accessed on 13 July 2023).
- Mućk, J.; McAdam, P.; Growiec, J. Will the “True” Labor Share Stand Up? An Applied Survey on Labor Share Measures. J. Econ. Surv. 2018, 32, 961–984. [Google Scholar] [CrossRef]
- Estimating the U.S. Labor Share. Available online: https://www.bls.gov/opub/mlr/2017/article/estimating-the-us-labor-share.htm (accessed on 13 July 2023).
- Shapley, L.S. Notes on the n-Person Game—II: The Value of an n-Person Game; RAND Corporation: Santa Monica, CA, USA, 1951. [Google Scholar]
- Roth, A.E. Introduction to the Shapley value. In The Shapley Value; Cambridge University Press: Cambridge, UK, 1988; pp. 1–27. [Google Scholar]
- Metcalfe, B. Metcalfe’s law after 40 years of ethernet. Computer 2013, 46, 26–31. [Google Scholar] [CrossRef]
- Peterson, T. Metcalfe’s Law as a Model for Bitcoin’s Value. Altern. Invest. Anal. Rev. Q 2018, 2, 9–18. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Liu, J.J.; Xu, Z.W. Tencent and Facebook data validate Metcalfe’s law. J. Comput. Sci. Technol. 2015, 30, 246–251. [Google Scholar] [CrossRef]
- Alexis, M. How Much Does Spotify Pay Per Stream? 2022. Available online: https://twostorymelody.com/spotify-pay-per-stream/ (accessed on 13 July 2023).
- Mulroy, C. Spotify Pays Artists (Sort of), but Not per Stream. 2022. Available online: https://www.usatoday.com/story/life/2022/10/22/how-much-per-spotify-stream/8094437001/ (accessed on 13 July 2023).
- Kormoczi, R. How Much Can an Artist Earn with Pandora Radio? 2020. Available online: https://timesinternational.net/how-much-can-an-artist-earn-with-pandora-radio/ (accessed on 13 July 2023).
- Bergen, M.; Shaw, L. Youtube Has Paid out $30 Billion to Creators as the Competition for Online Content Intensifies? 2021. Available online: https://fortune.com/2021/08/23/youtube-30-billion-ad-sales-online-creators/ (accessed on 13 July 2023).
- How Much Does YouTube Pay Video Creators? 2021. Available online: https://screencast-o-matic.com/blog/how-much-does-youtube-pay-video-creators (accessed on 13 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).