Correlated Equilibrium and Evolutionary Stability in 3-Player Rock-Paper-Scissors

Abstract

In the game of rock-paper-scissors with three players, this paper identifies conditions for a correlated equilibrium that differs from the mixed strategy Nash equilibrium and is evolutionarily stable. For this to occur, the correlation device attaches more probability to three-way ties and solo-winner outcomes than would result from the Nash equilibrium. The correlated equilibrium is evolutionarily stable because any mutant fares worse than a signal-following player when facing two players who follow their own correlated signals. The critical quality of the correlation device is to make this true both for potential mutants who would disobey their signal and instead choose the action which would beat the action signaled to the player, as well as for potential mutants who would deviate to the action that would be beaten by what the device signals to the player. These findings reveal how a strict correlated equilibrium can produce evolutionarily stable strategies for rock-paper-scissors with three players.

1. Introduction

In evolutionary game theory, rock-paper-scissors (RPS) provides an important example of a mixed-strategy Nash equilibrium (MSNE) that is not evolutionarily stable. In classic RPS, each player independently receives a signal from the MSNE distribution (1/3, 1/3, 1/3) over the set of actions (rock, paper, scissors). No player has a profitable unilateral deviation from following the signal they receive from the RPS MSNE, but at the same time, the non-strict nature of the MSNE means that a population of MSNE signal-followers is vulnerable to invasion if any fraction of the population mutates to some strategy where they choose an action different from what was signaled. Any of the pure strategies, “always play rock,” “always play paper,” or “always play scissors,” is the best response to the MSNE strategy, and in a population where the convention is to follow the MSNE, mutants choosing to 100% play some pure strategy will not be driven out of the population. In fact, when a tie results in a payoff that exceeds the average of a winning payoff and a losing payoff, then pure-strategy mutants achieve a higher expected payoff than incumbents who follow the MSNE strategy. The MSNE strategy in RPS is not evolutionarily stable.

In contrast to the Nash equilibrium, a correlated equilibrium (CE) relies on the dependence between the actions that a randomization device recommends to the various players. When a probability distribution over recommended action profiles creates a correlation between the recommendations to different players, it can sometimes be strictly better to obey what the device signaled to a player than to choose any alternative. Strictness lies at the heart of the concept of evolutionary stability, and along these lines, it has been shown that a strict correlated equilibrium strategy is evolutionarily stable [1,2]. I apply this fact to rock-paper-scissors and show that there is an evolutionarily stable strategy, consisting of a strict correlated equilibrium when the game has three players who earn a payoff from three-way ties that exceeds the average of a winning-payoff and a losing-payoff. Unlike two-player RPS, there are three-player conditions, such that a correlated equilibrium exists, that (1) differ from the mixed-strategy Nash equilibrium, (2) achieve higher payoffs than the Nash equilibrium payoffs, and (3) are evolutionarily stable.

With three players, there is an important limitation to the potential harm that a signal-disobeying mutant can cause to non-mutants who follow the randomization device’s signals. The correlated equilibrium probability distribution puts more probability on recommendation profiles where two signal followers cannot suffer the worst possible payoff even if one player chooses an action different than what was recommended. In contrast to the MSNE, the CE distribution puts relatively less probability on each three-way tie signal profile than on each solo-winner signal profile because a three-way tie is a special circumstance where a disobedient mutant can inflict significant damage on two signal followers. These findings build upon previous work by Cripps [1], Mailath et al. [3], Lenzo and Sarver [4], and Metzger [2], who have established the relationship between correlated equilibrium and evolutionary stability. By extending the classic rock-paper-scissors game to include three players, I demonstrate an important new application of correlated equilibrium in evolutionary game theory.

The next section discusses several branches of related research. Section 2 then presents the strategic form of the RPS game with three players. Section 3 defines correlated equilibrium for three-player RPS, establishes conditions for the existence of a strict CE, and analyzes a numerical example. Section 4 establishes the evolutionary stability of a strict CE in three-player RPS and presents an evolutionary perspective on the correlation mechanism.

Related Literature

The concept of correlated equilibrium originates with Aumann [5,6]. The first work that connects correlated equilibrium to evolutionary stability comes from Cripps [1], who shows that the set of strict correlated equilibria is identical to the outcomes from evolutionarily stable strategies. He analyzes so-called simple contests, which are evolutionary games in the spirit of Selten’s work on asymmetric contests [7,8]. An important question is how correlated play can result from the forces of evolution, i.e., how the use of a correlation device can arise for evolutionary game players who are not perfectly Bayes-rational. To answer this question, Mailath et al. [3] and Lenzo and Sarver [4] portray a correlated probability distribution as a matching mechanism in population games. Each player comes from a population where interactions match one member of that population to members of the other player populations. Mailath et al. [3] treat the signals generated by a correlation device as possibilities for meeting other agents arising from the local nature of interactions. In a similar context, Lenzo and Sarver [4] establish the dynamic stability properties of correlated equilibria. They find that every correlated equilibrium is equivalent to a stationary state in the replicator dynamics of a subpopulation model.

Most recently, Metzger [2] explores even deeper connections between evolution and correlated equilibrium. Since players may differ in their preferences over correlation devices, Metzger introduces a selection dynamic where players have the power to suggest that the active distribution over signals be replaced by some new distribution. Such suggestions are accepted only if no player vetoed the suggestion, which would allow the newly proposed correlation device to take over the generation of signals. Metzger’s findings imply that only Pareto efficient states in the set of correlated equilibria are stationary.

Maynard Smith and Price [9] distilled the founding ideas of evolutionary game theory, defining an evolutionarily stable strategy as “a strategy that cannot be overturned once it has become a convention in a population.” Weibull [10] provides a framework for evolutionary stability and invasion barriers that I adopt to understand strategies that are conditional on signals sent by some correlation device. While this paper is the first to analyze evolutionary stability in the particular context of three-player RPS, previous research concerning evolutionary stability has considered generalized situations involving more than two players. Maynard Smith [11] takes this to an extreme in terms of each player interacting with the entire population, in what he calls “playing the field.” Broom et al. [12] extend the evolutionarily stable strategy definition to games with more than two players, with special attention to the three-player, three-strategy case. Accinelli et al. [13] analyze games where an evolutionarily stable strategy does not have a uniform invasion barrier when there are more than two populations. However, just as Broom et al. [12], their players are randomly selected from the population, so these earlier works do not fit with situations where players can choose actions based on correlated signals.

A handful of theoretical models offer nuanced versions of RPS. Loertscher [14] presents a stochastic game with discounting, which results in an evolutionarily stable strategy when the discount factor is less than one. McCannon [15] analyzes biased players who have biased preferences over which action to choose so that their choices balance the tradeoff between achieving a win versus indulging their biased preference. The literature that focuses specifically on RPS games also includes a variety of empirical and experimental work. Friedman and Sinervo [16] provide a comprehensive survey of all such work, including their own research, and how it fits into the larger subject of evolutionary game theory. They define what constitutes classic RPS, which is when pairwise comparisons are intransitive. They portray the potential for cycles in classic RPS using the unit simplex. Again, in contrast to my focus on correlated strategies, this framework is based on random mixing.

Friedman and Sinervo [16] distinguish between the “classic case” where the common type is the second-best response, and the “apostatic case” where the common type is the worst response. Laboratory experiments by Cason et al. [17] reveal cycles that are consistent with learning models such that the population average strategy moves in the direction of the best reply to itself. Their experiments include variation in how ties compare to wins and losses, which is an important determinant of stability or instability in their games’ equilibria. In two unstable games in Cason et al.’s [17] experiments, ties are almost as good as wins, which pushes outwards towards the corners of the strategy simplex. The cycles borne out by actual experimental subjects’ choices fit the theoretical predictions, confirming the importance of the relative magnitudes of wins, losses, and ties. Cason et al.’s [17] work is related to my study in that I also find that how ties compare to wins and losses has important consequences for the existence of correlated equilibria in rock-paper-scissors.

2. The Rock-Paper-Scissors Game with Three Players

The game of rock-paper-scissors with three players is denoted by G = (N, $(A_i{)}_{i\in N}$, $(u_i{)}_{i\in N}$), where the set of players is $N=\left\{1,2,3\right\}$, and the set of actions for each player is $A_i=\left\{r,p,s\right\}$, where r is rock, p is paper, and s is scissors. Each player’s payoff $u_i$ is a function of the action profile $a=\left(a_i,a_j,a_k\right)$, where $i,j,k\in N$ and $i\ne j\ne k$. The set of action profiles (i.e., the set of outcomes) is $A=\left\{a\right\}=A_1\times A_2\times A_3$. The expected payoff $U_i$ expresses i’s preferences concerning lotteries over A.

An outcome resulting in one or more clear winners will be called an unequivocal outcome. Payoffs from unequivocal outcomes reflect the classic rock-paper-scissors rankings: rock beats scissors, paper beats rock, and scissors beats paper. For the unequivocal outcomes $\left(r_i,s_j,s_k\right),\left(p_i,r_j,r_k\right)$, and $\left(s_i,p_j,p_k\right)$, one player beats both of the other players, and the two other players tie for last. In such outcomes, $u_{solo\_first}$ denotes the payoff to the solo winner, and $u_{tie\_last}$ denotes the payoff to either of the players who tie for last. For the other unequivocal outcomes, $\left(r_i,r_j,s_k\right),\left(p_i,p_j,r_k\right)$, and $\left(s_i,s_j,p_k\right)$, two players tie for first and there is a solo loser, resulting in the payoffs $u_{tie\_first}$ for the winners and $u_{solo\_last}$ for the solo loser. I assume that there is a higher payoff from being a solo winner than from beating only one player and tying with the other player. Similarly, there is a lower payoff from being the solo loser than from losing to only one player and tying with the other player. These assumptions concerning unequivocal outcomes imply that $u_{solo\_last}<u_{tie\_last}<u_{tie\_first}<u_{solo\_first}$.

Separate from the unequivocal outcomes are two kinds of outcomes where no player clearly wins. These are three-way ties, $\left(r_i,r_j,r_k\right),\left(p_i,p_j,p_k\right)$, and $\left(s_i,s_j,s_k\right)$, as well as three-way splits, $\left(r_i,p_j,s_k\right)$. For both three-way ties and three-way splits, I assume that the resulting payoff is better than $u_{tie\_last}$ and worse than $u_{tie\_first}$. That is, letting $u_{3way\_tie}$ denote a player’s payoff from a three-way tie and letting $u_{3way\_split}$ denote a player’s payoff from a three-way split, I assume that $u_{tie\_last}<u_{3way\_tie}<u_{tie\_first}$ and $u_{tie\_last}<u_{3way\_split}<u_{tie\_first}$. According to these assumptions, a three-way tie is better than tying with one of the other players and losing to the other, and a three-way tie is worse than tying with one of the other players and beating the other. Additionally, a three-way split (where each player loses to one other player and beats one other player) is better than losing to one of the other players and tying with the other, and a three-way split is worse than beating one of the other players and tying with the other. These assumptions partly reflect preferences where any particular action is the second-best response to itself (what Friedman and Sinervo [16] call the classic case). It is worth noting that “splits” do not arise in two-player RPS because anytime the two players make different choices, one of them will unequivocally win and the other will unequivocally lose.

The assumptions above regarding solo-winner and solo-loser payoffs compared to, respectively, tied-first and tied-last payoffs can be justified with insights from the economic literature on envy. Bosmans and Ozturk [18] survey different measures of envy, including those which take into account “negative elementary envy” which is the extent to which an individual prefers their own bundle to that of another player’s bundle. An RPS solo winner could experience greater negative elementary envy (and greater resulting utility) because they prefer their own outcome over both other players’ outcomes; whereas, a tied-for-first winner has less negative envy (and utility) because they prefer their outcome over only a single other player’s outcome. Similarly, an RPS solo loser envies both rivals; whereas, a tied-last loser envies only one other player. In addition to Bosmans and Ozturk [18], Feldman and Kirmann [19], and Diamantaras and Thomson [20] provide other envy measures that are consistent with the above payoff assumptions concerning solo wins versus tied wins and solo losses versus tied losses.

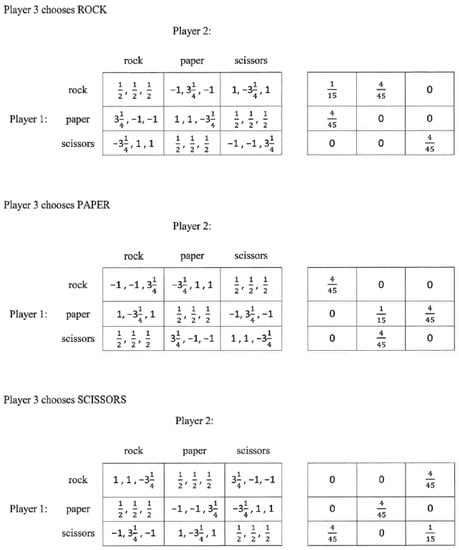
Figure 1 shows the strategic form of G with players 1, 2, and 3 choosing the row, column, and table, respectively. If $u_{solo\_last}=-u_{solo\_first}$ and if $u_{tie\_last}=-u_{tie\_first}$, then G has a unique mixed-strategy Nash equilibrium of $\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$, which produces a payoff of $\left(\frac{1}{9}{u}_{3way\_tie}+\frac{2}{9}{u}_{3way\_split}\right)$ for each player. As is the case with only two players, such a Nash equilibrium is not evolutionarily stable if $u_{3way\_tie}$ is greater than or equal to the MSNE payoff. Then a population with the Nash equilibrium as the incumbent strategy would be vulnerable to invasion if any fraction of the population mutated to playing one of the pure strategies with 100% probability.

Figure 1. Strategic form of G (three-player Rock-Paper-Scissors).

3. Correlated Equilibrium

3.1. Definition of Correlated Equilibrium

The game G can be extended to include communication from some correlation device, consisting of a profile of signals where the device sends one signal to each player. Following Aumann [2,3], let the set of signal profiles be identical to the set of action profiles A. Prior to the players’ action choices, the device selects a signal profile $a=\left(a_i,a_j,a_k\right)$, and each player i receives their signal $a_i$ but is unaware of signals $a_{-i}$ received by the other players. Each player’s strategy is now represented by a function ${\tau }_i:A_i\to A_i$, where ${\tau }_i\left(a_i\right)$ is the action that i chooses when the device sends them the signal $a_i$. The particular strategy, such that i chooses the action that has been signaled to them, is denoted ${\tau }_i$*, i.e., ${\tau }_i$*$\left(a_i\right)=a_i$. This strategy ${\tau }_i$* is called the obedient strategy, or the signal-following strategy.

Let μ denote the correlation device’s probability distribution over A, and the players have common knowledge of μ. For example, $\mu \left(p_i,s_j,r_k\right)$ is the probability that the device sends player i a signal to play p, player j a signal to play s, and player k a signal to play r. Upon receiving their own signal $a_i$, player i can compute the conditional probabilities $\mu \left(a_{-i}│a_i\right).$ In an evolutionary framework, this view can be adapted so that the players are not relying on Bayesian rationality [2,4]. However, I will extend the game G using the language of classical game theory, in order to articulate the general definition of correlated equilibrium for rock-paper-scissors. For a particular probability distribution μ, the extended game is denoted Γ$\left(\mu \right)$. A correlated equilibrium consists of a probability distribution μ and signal-following strategies (τ₁*($a_1$), τ₂*($a_2$), τ₃*($a_3$)) where for every player i:

$${\sum }_{a_{-i}\in A_{-i}}\mu \left(a_i,a_{-i}\right)u_i\left(a_i,a_{-i}\right)\ge {\sum }_{a_{-i}\in A_{-i}}\mu \left(a_i,a_{-i}\right)u_i\left(a_i\prime ,a_{-i}\right)\forall a_i,a_i\prime \in A_i$$

(1)

In other words, a correlated equilibrium involves a probability distribution over signals from the correlation device such that all three players have no expected payoff gains from disobeying the signals they receive. From an evolutionary perspective, a strict correlated equilibrium is of particular interest, where μ is such that the expected payoff from signal-following (the left-hand side of Equation (1)) is strictly greater than the expected payoff from any alternative strategy. It is important to note that the probability distribution μ is not exogenous but is part of the equilibrium. Furthermore, unlike mixed-strategy Nash equilibria, μ is not necessarily a product measure on A.

A strict correlated equilibrium is defined by a set of strategic incentive constraints for the players [6,21]. Each incentive constraint for each player involves how the expected payoff from following a particular signal compares to the expected payoff from choosing some particular alternative action that has not been recommended. Each player has three possible actions and therefore has two alternatives to signal-following for each particular signal that the device could send.

Strategic incentive constraints for player i to follow a signal to play rock:

$$\begin{gathered} \mu \left(r_i,r_j,r_k\right)\left(u_{solo\_first}-u_{3way\_tie}\right)+\mu \left(r_i,p_j,r_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(r_i,s_j,r_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+ \\ \mu \left(r_i,r_j,p_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(r_i,p_j,p_k\right)\left(u_{3way\_tie}-u_{solo\_last}\right)+\mu \left(r_i,s_j,p_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+ \\ \mu \left(r_i,r_j,s_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+\mu \left(r_i,p_j,s_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+\mu \left(r_i,s_j,s_k\right)\left(u_{solo\_last}-u_{solo\_first}\right)<0 \end{gathered}$$

(2a)

$$\begin{gathered} \mu \left(r_i,r_j,r_k\right)\left(u_{solo\_last}-u_{3way\_tie}\right)+\mu \left(r_i,p_j,r_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(r_i,s_j,r_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+ \\ \mu \left(r_i,r_j,p_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(r_i,p_j,p_k\right)\left(u_{solo\_first}-u_{solo\_last}\right)+\mu \left(r_i,s_j,p_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+ \\ \mu \left(r_i,r_j,s_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+\mu \left(r_i,p_j,s_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+\mu \left(r_i,s_j,s_k\right)\left(u_{3way\_tie}-u_{solo\_first}\right)<0 \end{gathered}$$

(2b)

Under a strict correlated equilibrium, player i’s expected payoff would decline if they were to choose paper when the device had signaled to play rock, which is the meaning of (2a). Each bracketed utility differential in (2a) is the change in player i’s payoff that would result from deviating to paper when the correlation device recommended the strategy profile indicated and players j and k followed their recommendations. Similarly, as indicated by (2b), player i’s expected payoff would decline if they were to choose scissors when the device had signaled to play rock. Bracketed utility terms in (2b) are payoff changes that would result from player i deviating to scissors when it was recommended to play rock, while players j and k obeyed what was recommended.

Strategic incentive constraints for player i to follow a signal to play paper:

$$\begin{gathered} \mu \left(p_i,r_j,r_k\right)\left(u_{3way\_tie}-u_{solo\_first}\right)+\mu \left(p_i,p_j,r_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+\mu \left(p_i,s_j,r_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+ \\ \mu \left(p_i,r_j,p_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+\mu \left(p_i,p_j,p_k\right)\left(u_{solo\_last}-u_{3way\_tie}\right)+\mu \left(p_i,s_j,p_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+ \\ \mu \left(p_i,r_j,s_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+\mu \left(p_i,p_j,s_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(p_i,s_j,s_k\right)\left(u_{solo\_first}-u_{solo\_last}\right)<0 \end{gathered}$$

(2c)

$$\begin{gathered} \mu \left(p_i,r_j,r_k\right)\left(u_{solo\_last}-u_{solo\_first}\right)+\mu \left(p_i,p_j,r_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+\mu \left(p_i,s_j,r_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+ \\ \mu \left(p_i,r_j,p_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+\mu \left(p_i,p_j,p_k\right)\left(u_{solo\_first}-u_{3way\_tie}\right)+\mu \left(p_i,s_j,p_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+ \\ \mu \left(p_i,r_j,s_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+\mu \left(p_i,p_j,s_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(p_i,s_j,s_k\right)\left(u_{3way\_tie}-u_{solo\_last}\right)<0 \end{gathered}$$

(2d)

Conditions (2c) and (2d) indicate that player i’s expected payoff would decline if they were to choose, respectively, rock or scissors when signaled to play paper. Each μ identifies how much probability the correlation device assigns to each particular signal profile where paper is recommended to i. Bracketed terms are changes in utility from i disobeying the signal to play paper and instead choosing rock (2c), or instead choosing scissors (2d).

Strategic incentive constraints for player i to follow a signal to play scissors:

$$\begin{gathered} \mu \left(s_i,r_j,r_k\right)\left(u_{3way\_tie}-u_{solo\_last}\right)+\mu \left(s_i,p_j,r_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+\mu \left(s_i,s_j,r_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+ \\ \mu \left(s_i,r_j,p_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+\mu \left(s_i,p_j,p_k\right)\left(u_{solo\_last}-u_{solo\_first}\right)+\mu \left(s_i,s_j,p_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+ \\ \mu \left(s_i,r_j,s_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(s_i,p_j,s_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+\mu \left(s_i,s_j,s_k\right)\left(u_{solo\_first}-u_{3way\_tie}\right)<0 \end{gathered}$$

(2e)

$$\begin{gathered} \mu \left(s_i,r_j,r_k\right)\left(u_{solo\_first}-u_{solo\_last}\right)+\mu \left(s_i,p_j,r_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+\mu \left(s_i,s_j,r_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+ \\ \mu \left(s_i,r_j,p_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+\mu \left(s_i,p_j,p_k\right)\left(u_{3way\_tie}-u_{solo\_first}\right)+\mu \left(s_i,s_j,p_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+ \\ \mu \left(s_i,r_j,s_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(s_i,p_j,s_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+\mu \left(s_i,s_j,s_k\right)\left(u_{solo\_last}-u_{3way\_tie}\right)<0 \end{gathered}$$

(2f)

Finally, choosing rock (2e) or paper (2f) when signaled to play scissors would reduce i’s expected payoff. Any μ satisfying inequalities (2a)–(2f) results in a strict correlated equilibrium of three-player rock-paper-scissors where players’ action choices are obedient to μ. This definition of a strict correlated equilibrium follows Aumann’s Proposition 2.3 [6], p. 6. Due to the symmetry of payoffs in G, the constraints (2a), (2d), and (2e) are identical, as are constraints (2b), (2c), and (2f), so that the system of six constraints could be replaced with just two:

$$\begin{gathered} \mu \left(r_i,r_j,r_k\right)\left(u_{solo\_first}-u_{3way\_tie}\right)+\mu \left(r_i,p_j,r_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(r_i,s_j,r_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+ \\ \mu \left(r_i,r_j,p_k\right)\left(u_{tie\_first}-u_{tie\_last}\right)+\mu \left(r_i,p_j,p_k\right)\left(u_{3way\_tie}-u_{solo\_last}\right)+\mu \left(r_i,s_j,p_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+ \\ \mu \left(r_i,r_j,s_k\right)\left(u_{3way\_split}-u_{tie\_first}\right)+\mu \left(r_i,p_j,s_k\right)\left(u_{tie\_last}-u_{3way\_split}\right)+\mu \left(r_i,s_j,s_k\right)\left(u_{solo\_last}-u_{solo\_first}\right)<0 \end{gathered}$$

(2i)

$$\begin{gathered} \mu \left(r_i,r_j,r_k\right)\left(u_{solo\_last}-u_{3way\_tie}\right)+\mu \left(r_i,p_j,r_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(r_i,s_j,r_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+ \\ \mu \left(r_i,r_j,p_k\right)\left(u_{3way\_split}-u_{tie\_last}\right)+\mu \left(r_i,p_j,p_k\right)\left(u_{solo\_first}-u_{solo\_last}\right)+\mu \left(r_i,s_j,p_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+ \\ \mu \left(r_i,r_j,s_k\right)\left(u_{tie\_last}-u_{tie\_first}\right)+\mu \left(r_i,p_j,s_k\right)\left(u_{tie\_first}-u_{3way\_split}\right)+\mu \left(r_i,s_j,s_k\right)\left(u_{3way\_tie}-u_{solo\_first}\right)<0 \end{gathered}$$

(2ii)

As will be explored further in Section 3.2, the first of these two constraints indicates that player i’s payoff would decline if they were to deviate from any recommendation (regardless of whether itis rock, paper, or scissors in particular) by choosing to play what beats the action that the device recommended. The second of the two constraints above indicates that player i’s payoff would decline if they were to deviate from any recommendation by choosing to play what is beaten by the action that the device recommended.

The full system of six constraints is useful because it defines strict correlated equilibrium for any three-player version of rock-paper-scissors, including versions different from G with asymmetric payoffs. For instance, unlike G, there could be a three-player RPS game where the solo-winner payoff when rock is the solo winner differs from the solo-winner payoff when paper or scissors is the solo winner. Equations (2a)–(2f) define strict correlated equilibrium both for games with symmetric payoffs such as G, which is the focus of this paper, as well as for games with asymmetric payoffs.

3.2. Conditions for a Strict Correlated Equilibrium

Proposition 1.

Let $\underset{\_}{q}=\frac{\frac{1}{3}\left(u_{3way\_tie}-u_{solo\_first}\right)+\frac{2}{3}\left(u_{3way\_split}-u_{tie\_last}\right)}{\frac{4}{3}{u}_{3way\_tie}+\frac{2}{3}{u}_{3way\_split}-\frac{2}{3}{u}_{tie\_last}-\frac{1}{3}{u}_{solo\_first}-u_{solo\_last}}$ and let  $\overline{q}=\frac{\frac{1}{3}\left(u_{solo\_first}-u_{solo\_last}\right)+\frac{2}{3}\left(u_{tie\_last}-u_{tie\_first}\right)}{\frac{4}{3}{u}_{solo\_first}+\frac{2}{3}{u}_{tie\_last}-\frac{2}{3}{u}_{tie\_first}-\frac{1}{3}{u}_{solo\_last}-u_{3way\_tie}}$.

If  $0<\underset{\_}{q}<\overline{q}<1$, then for every  $q\in \left(\underset{\_}{q},\overline{q}\right)$ there is a strict correlated equilibrium with  $\mu \left(r_i,r_j,r_k\right)=\mu \left(p_i,p_j,p_k\right)=\mu \left(s_i,s_j,s_k\right)=\frac{1}{3}q,\mu \left(r_i,s_j,s_k\right)=\mu \left(p_i,r_j,r_k\right)=\mu \left(s_i,p_j,p_k\right)=\frac{1}{9}\left(1-q\right), and \mu \left(a\right)=0\forall a\notin \left\{\left(r_i,r_j,r_k\right),\left(p_i,p_j,p_k\right),\left(s_i,s_j,s_k\right),\left(r_i,s_j,s_k\right),\left(p_i,r_j,r_k\right),\left(s_i,p_j,p_k\right)\right\}.$

Proof 1.

Every strategy ${{\tau }_i}^{\prime }\ne {{\tau }_i}^{*}$ specifies ${{\tau }_i}^{\prime }\left(a_i\right)\ne a_i$ for at least one action $a_i$ that could be recommended to i. Let ${BR}_i\left(a_i\right)$ be the action that beats the action $a_i$ that was recommended and let ${BR}_i^{-1}\left(a_i\right)$ be the action that the recommended action $a_i$ beats. (i) If ${{\tau }_i}^{\prime }\left(a_i\right)={BR}_i^{-1}\left(a_i\right)$, then $U_i\left[{{\tau }_i}^{\prime }\left(a_i\right),{{\tau }_j}^{*}\left(a_j\right),{{\tau }_k}^{*}\left(a_k\right)\right]<U_i\left[{{\tau }_i}^{*}\left(a_i\right),{{\tau }_j}^{*}\left(a_j\right),{{\tau }_k}^{*}\left(a_k\right)\right]$ provided that $q>\underset{\_}{q}$. (ii) If ${{\tau }_i}^{\prime }\left(a_i\right)={BR}_i\left(a_i\right)$, then $U_i\left[{{\tau }_i}^{\prime }\left(a_i\right),{{\tau }_j}^{*}\left(a_j\right),{{\tau }_k}^{*}\left(a_k\right)\right]<U_i\left[{{\tau }_i}^{*}\left(a_i\right),{{\tau }_j}^{*}\left(a_j\right),{{\tau }_k}^{*}\left(a_k\right)\right]$ provided that $q<\overline{q}$. (i) and (ii) $⟹$ (2a)–(2f) hold for all ${{\tau }_i}^{\prime }\ne {{\tau }_i}^{*}$. □

Under a Proposition 1 type of CE, the probability distribution μ only places positive probability on recommendation profiles that would result in two types of outcomes: three-way ties and one-solo-winner/two-tied-last outcomes. The value of q in Proposition 1 is the total amount of probability placed on all three-way ties, with probability $\frac{q}{3}$ on each of the three possible ways that a three-way tie could occur. The value of $\left(1-q\right)$ in Proposition 1 is the total amount of probability placed on all one-solo-winner/two-tied-last outcomes. There are nine different outcomes of this kind, and μ puts probability $\frac{1-q}{9}$ on each such outcome.

To understand the nature of the Proposition 1 type of equilibrium, two particular disobedient strategies are particularly important. First, upon receiving a recommendation from the correlation device, a player must prefer to follow that signal over always choosing the action which would defeat the action that was recommended. Let ${\tau }_i^{BR}$ be the strategy of “always play the action that beats the action $a_i$ that was recommended,” which consists of $\left({\tau }_i^{BR}\left(r_i\right)=p_i,{\tau }_i^{BR}\left(p_i\right)=s_i,{\tau }_i^{BR}\left(s_i\right)=r_i\right)$. When the recommended action profile is a three-way tie and the other two players, j and k, are following their recommendations, the disobedient strategy ${\tau }_i^{BR}$ achieves a higher expected payoff than ${\tau }_i$*. For instance, if the device recommends $\left(r_i,r_j,r_k\right)$, then $u_i\left({\tau }_i^{BR}\left(r\right),{\tau }_j^{*}\left(r\right),{\tau }_k^{*}\left(r\right)\right)=u_i\left(p_i,r_j,r_k\right)>u_i\left(r_i,r_j,r_k\right)$. If the device recommends that everyone plays rock, then by unilaterally deviating to paper, player i would receive the largest possible payoff.

However, the disobedient strategy ${\tau }_i^{BR}$ results in a worse expected payoff than ${\tau }_i$* when the recommended action profile is a one-solo-winner/two-tied-last outcome. Consider, for example, if the device recommends rock to two of the players and paper to the remaining player. If player i uses the disobedient strategy ${\tau }_i^{BR}$ while j and k use the signal-following strategy, then there is a $\frac{1}{3}$ chance that i was designated to be the big winner (i.e., receives the recommendation to play paper) and by playing the ${\tau }_i^{BR}$ strategy, i instead chooses scissors and ends up with the lowest possible payoff $u_{solo\_last}$. At the same time, given that a one-solo-winner/two-tied-last outcome was recommended, there is a probability of $\frac{2}{3}$ that player i was designated to end up tied-for-last (i.e., receives a recommendation to play rock in our example), and by playing the ${\tau }_i^{BR}$ strategy, player i instead chooses paper and ends up tied for first. Thus, when a one-solo-winner/two-tied-last outcome is recommended, there is a $\frac{1}{3}$ chance that ${\tau }_i^{BR}$ delivers a worse payoff to i than $\tau$* and a $\frac{2}{3}$ chance that ${\tau }_i^{BR}$ delivers a better payoff to i than $\tau$*. In expectation, ${\tau }_i^{BR}$ reduces i’s payoff conditional on a one-solo-winner/two-tied-last recommendation. Considering both of these potential consequences (the certain payoff improvement from ${\tau }_i^{BR}$ given a three-way tie recommendation, as well as the expected payoff reduction from ${\tau }_i^{BR}$ given a one-solo-winner/two-tied-last recommendation), the net effect of playing ${\tau }_i^{BR}$ on i’s expected payoff is negative, provided that $q<\overline{q}$.

Secondly, upon receiving a recommendation from the correlation device, a player must prefer to follow that signal over always choosing the action which the recommended action would defeat. Let ${\tau }_i^{BR-1}$ be the strategy of “always play the action that the recommended action beats,” which consists of ${\tau }_i^{BR-1}\left(r_i\right)=s_i,{\tau }_i^{BR-1}\left(p_i\right)=r_i,{\tau }_i^{BR-1}\left(s_i\right)=p_i$. When the recommended action profile is a three-way tie and the other two players are following their recommendations, the disobedient strategy ${\tau }_i^{BR-1}$ achieves the lowest possible payoff $u_{solo\_last}$, which is, of course, worse than the expected payoff from $\tau$*. For instance, if the device recommends $\left(r_i,r_j,r_k\right)$, then $u_i\left({\tau }_i^{BR-1}\left(r\right),{\tau }_j^{*}\left(r\right),{\tau }_k^{*}\left(r\right)\right)=u_i\left(s_i,r_j,r_k\right)<u_i\left(r_i,r_j,r_k\right)$. If the device recommends that everyone plays rock, then by unilaterally deviating to scissors, player i would suffer the solo-last payoff.

If, instead, the recommended action profile is a one-solo-winner/two-tied-last outcome, then the disobedient strategy ${\tau }_i^{BR-1}$ results in a better expected payoff than from playing $\tau$*. Playing ${\tau }_i^{BR-1}$ would hurt i’s payoff if i had been designated to be the solo winner but would improve i’s payoff if i had been designated to be tied for last. If player i was designated to be the solo winner but followed the strategy ${\tau }_i^{BR-1}$, then they would end up with the three-way tie payoff. For instance, if the device recommends rock to players j and k and paper to player i, then the strategy profile $\left({\tau }_i^{BR-1},{\tau }_j^{*},{\tau }_k^{*}\right)$ results in the outcome $\left(r_i,r_j,r_k\right)$, which is worse for i than if they had followed their recommendation and ended up as the solo winner. However, if player i had been designated to be tied for last but followed the strategy ${\tau }_i^{BR-1}$, then they would end up with the three-way split payoff. For instance, if the device recommends rock to i and j and recommends paper to k, then the strategy profile $\left({\tau }_i^{BR-1},{\tau }_j^{*},{\tau }_k^{*}\right)$ results in the outcome $\left(s_i,r_j,p_k\right)$, which is better for i than if they had followed their recommendation. In expectation, ${\tau }_i^{BR-1}$ increases i’s payoff conditional on a one-solo-winner/two-tied-last recommendation. Considering both of these potential consequences (the certain payoff reduction from ${\tau }_i^{BR-1}$ given a three-way tie recommendation, as well as the expected payoff improvement from ${\tau }_i^{BR-1}$ given a one-solo-winner/two-tied-last recommendation), the net effect of playing ${\tau }_i^{BR-1}$ on i’s expected payoff is negative, as long as $q>\underset{\_}{q}$.

In summary of Proposition 1, the critical requirement of a strict correlated equilibrium is to make the obedient strategy $\tau$*’s expected payoff higher than both the “play-what-beats-the-recommendation” expected payoff and the “play-what-the-recommendation-beats” expected payoff. The strict CE distribution μ limits how much probability is on three-way ties so that playing the action that beats the action that was recommended (i.e., the strategy ${\tau }^{BR}$) is worse than the signal-following strategy $\tau$*. In contrast, the MSNE puts an equal amount of probability on any particular three-way tie as on any particular one-solo-winner outcome, which means that ${\tau }^{BR}$ would be just as good as the MSNE strategy. At the same time, the strict CE distribution μ puts more probability on one-solo-winner/two-tied-last outcomes than would occur from the MSNE, but not so much probability that ${\tau }^{BR-1}$ beats $\tau$*. Playing the action that the recommendation beats is worse than the MSNE strategy, and the strict CE exploits this fact but does not raise the probability of one-solo-winner/two-tied-last outcomes so high that ${\tau }^{BR-1}$ becomes a better strategy than $\tau$*.

3.3. Numerical Example of Strict Correlated Equilibrium

Figure 2 presents a numerical example of a strict correlated equilibrium for a game with $u_{solo\_first}=3\frac{1}{4},u_{tie\_first}=1,u_{tie\_last}=-1,u_{sol{o}_{last}}=-3\frac{1}{4}, and u_{3way\_tie}=u_{3way\_split}=\frac{1}{2}$. The probabilities with which the correlation device recommends particular action profiles are shown in the corresponding cells to the right of the game matrix. Each of the strategic incentive constraints are strictly satisfied:

Figure 2. Numerical example of a strict correlated equilibrium.

Strategic incentive constraints for player i to follow a signal to play rock:

$$\left(\frac{1}{15}\right)\left[3\frac{1}{4}-\frac{1}{2}\right]+\left(\frac{4}{45}\right)\left[(1-(-1)\right]+\left(\frac{4}{45}\right)\left[(1-(-1)\right]+\left(\frac{4}{45}\right)\left[-3\frac{1}{4}-3\frac{1}{4}\right]<0$$

(3a)

$$\left(\frac{1}{15}\right)\left[-3\frac{1}{4}-\frac{1}{2}\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-3\frac{1}{4}\right]<0$$

(3b)

Strategic incentive constraints for player i to follow a signal to play paper:

$$\left(\frac{4}{45}\right)\left[\frac{1}{2}-3\frac{1}{4}\right]+\left(\frac{1}{15}\right)\left[-3\frac{1}{4}-\frac{1}{2}\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]<0$$

(3c)

$$\left(\frac{4}{45}\right)\left[-3\frac{1}{4}-3\frac{1}{4}\right]+\left(\frac{1}{15}\right)\left[3\frac{1}{4}-\frac{1}{2}\right]+\left(\frac{4}{45}\right)\left[1-(-1)\right]+\left(\frac{4}{45}\right)\left[1-(-1)\right]<0$$

(3d)

Strategic incentive constraints for player i to follow a signal to play scissors:

$$\left(\frac{4}{45}\right)\left[1-(-1)\right]+\left(\frac{4}{45}\right)\left[-3\frac{1}{4}-3\frac{1}{4}\right]+\left(\frac{4}{45}\right)\left[1-(-1)\right]+\left(\frac{1}{15}\right)\left[3\frac{1}{4}-\frac{1}{2}\right]<0$$

(3e)

$$\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-3\frac{1}{4}\right]+\left(\frac{4}{45}\right)\left[\frac{1}{2}-(-1)\right]+\left(\frac{1}{15}\right)\left[-3\frac{1}{4}-\frac{1}{2}\right]<0$$

(3f)

The symmetry of payoffs in this numerical example makes (3a), (3d), and (3e) identical, with each of those constraints indicating that ${\tau }^{BR}$ results in a lower expected payoff than obeying the signal. Similarly, (3b), (3c), and (3f) are identical, with each of those constraints indicating that ${\tau }^{BR-1}$ is worse than signal-following. Each player’s expected payoff from the CE is 13/30, which exceeds the MSNE payoff of 1/6. The CE achieves a higher expected payoff than the MSNE partly because the CE places more probability on three-way ties, which occur with a probability of 1/5 from the CE and only with a probability of 1/9 from the MSNE. A second contributor to the improvement in the expected payoff is that the CE puts more probability on solo-winner outcomes and zero probability on solo-loser outcomes. Solo-winner outcomes occur with a probability of 4/5 from the CE, and conditional on such an outcome, any given player has a 1/3 chance of being the solo winner with the big payoff of +3¼, and a 2/3 chance of tying for last with the second-worst payoff of −1. This means that, when the correlation device recommends a solo-winner/two-tied-last outcome, each player’s expected payoff is 5/12. Under the MSNE, such outcomes are counter-balanced by equally likely solo-loser outcomes, which have an expected payoff of −5/12, but the CE puts zero probability on solo-loser outcomes. By doing so, the CE achieves higher expected payoffs by giving each player an enhanced chance at the biggest payoff available. Regarding three-way splits, which produce payoffs of ½ for each player, the CE puts zero probability on those outcomes whereas the MSNE puts 2/9 probability on those outcomes. All else equal, this reduces players’ payoffs from the CE compared to the MSNE, but this reduction is overwhelmed by the payoff increases achieved by the CE placing more probability on three-way ties and solo-winner/two-tied-last outcomes.

4. Evolutionary Stability

4.1. Definition of ESS for the Extended Game Γ(μ)

Following Weibull [10], a strategy $\tau$ is evolutionarily stable if, for every mutant strategy ${\tau }^{\prime }$≠$\tau$, there exists an invasion barrier ${\stackrel{-}{\epsilon }}_{\tau \prime }$ such that if ${\tau }^{\prime }$ comes in a smaller dose than ${\stackrel{-}{\epsilon }}_{\tau \prime }$ then the strategy τ does better than ${\tau }^{\prime }$ in the post-entry population. This criterion can be used to determine whether a correlated equilibrium strategy $\tau$* is evolutionarily stable:

Definition 1.

In the extended game Γ(μ) for three-player RPS, the correlated equilibrium signal-following strategy $\tau$* is evolutionarily stable if, for every mutant strategy ${\tau }^{\prime }$≠ $\tau$*, there exists some ${\stackrel{-}{\epsilon }}_{{\tau }^{\prime }}\in (0,1)$ such that for all $\epsilon \in (0,{\stackrel{-}{\epsilon }}_{{\tau }^{\prime }})$:

$$\begin{gathered} \left(1-\epsilon \right)\left(1-\epsilon \right)U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{*}\right)+\left(1-\epsilon \right)\epsilon U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{\prime }\right)+\epsilon \left(1-\epsilon \right)U_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{*}\right)+{\epsilon }^2{U}_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{\prime }\right) \\ >\left(1-\epsilon \right)\left(1-\epsilon \right)U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{*}\right)+\left(1-\epsilon \right)\epsilon U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{\prime }\right)+\epsilon \left(1-\epsilon \right)U_i\left({\tau }_i^{\prime },{\tau }_j^{\prime },{\tau }_k^{*}\right)+{\epsilon }^2{U}_i\left({\tau }_i^{\prime },{\tau }_j^{\prime },{\tau }_k^{\prime }\right) \end{gathered}$$

(4)

for all $i,j,k\in N$ and $i\ne j\ne k$.

The $U_i$ terms on the left-hand side of (4) are the four possible expected payoffs to i from the obedient strategy τ* corresponding to the four kinds of encounters that could occur involving players j and k. When i encounters two fellow signal followers, the resulting expected payoff is $U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{*}\right)$; when i encounters a signal-following player j and a disobedient mutant player k, the resulting expected payoff is $U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{\prime }\right)$; when i encounters a disobedient mutant player j and a signal-following player k, the resulting expected payoff is $U_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{*}\right)$; and, when i encounters two disobedient mutants, the resulting expected payoff is $U_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{\prime }\right)$. The left-hand side of (4) is the expected payoff to a signal-following player i.

The right-hand side is the expected payoff to a mutant playing strategy some strategy ${\tau }^{\prime }$ where i disobeys at least one signal sent by the correlation device. Since there are three possible signals that the correlation device can send (r, p, or s), and three possible actions that a player can choose upon receipt of any given signal, this means that there are a total of 3³ different pure strategies, one of which is the obedient strategy $\tau$*. Thus, there are 26 different ${\tau }^{\prime }$ pure strategies where, for at least one recommendation that could be received, the player chooses an action different from what has been recommended. If Equation (1) holds strictly, or equivalently, if constraints (2a)–(2f) hold, then, for every ${\tau }^{\prime }$≠ $\tau$*, the first payoff term on the left-hand side of (4), $U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{*}\right)$, is greater than the first payoff term on the right-hand side of (4), $U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{*}\right)$. This leads to the following proposition, which restates the results from Cripps [1], Lenzo and Sarver [4], and Metzger [2] that in order to establish the evolutionary stability of strict correlated equilibria in three-player RPS.

Proposition 2.

For any strict correlated equilibrium of the three-player RPS extended game Γ$\left(\mu \right)$, the signal-following strategy $\tau$* is evolutionarily stable.

Proof 2.

We can rewrite (4) as follows:

$$\begin{gathered} \left(1-\epsilon \right)\left(1-\epsilon \right)\left[U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{*}\right)-U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{*}\right)\right]+\left(1-\epsilon \right)\epsilon \left[U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{\prime }\right)-U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{\prime }\right)\right] \\ +\epsilon \left(1-\epsilon \right)\left[U_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{*}\right)-U_i\left({\tau }_i^{\prime },{\tau }_j^{\prime },{\tau }_k^{*}\right)\right]+{\epsilon }^2\left[U_i\left({\tau }_i^{*},{\tau }_j^{\prime },{\tau }_k^{\prime }\right)-U_i\left({\tau }_i^{\prime },{\tau }_j^{\prime },{\tau }_k^{\prime }\right)\right]>0 \end{gathered}$$

(5)

(i) By the definition of a strict CE given by conditions (2a)–(2f), we know $U_i\left({\tau }_i^{*},{\tau }_j^{*},{\tau }_k^{*}\right)>U_i\left({\tau }_i^{\prime },{\tau }_j^{*},{\tau }_k^{*}\right)$ for every mutant strategy ${\tau }^{\prime }$≠ $\tau$*, which guarantees that the first term in (4)’ is positive for all $\epsilon \in [0,1)$. (ii) The left-hand side of (5) is a continuous function of ε. (i) and (ii) imply that, for every mutant strategy ${\tau }^{\prime }$≠ $\tau$*, there exists some invasion barrier $b\left({\tau }^{\prime }\right)$ such that (5) holds, where $b\left(\tau \prime \right)=sup${δ ∈ [0, 1]: (5) holds ∀ε ∈ (0,δ)}. This guarantees the existence of the uniform invasion barrier ${\stackrel{-}{\epsilon }}_{{\tau }^{\prime }}\in (0,1)$, equal to the smallest of all the $b\left({\tau }^{\prime }\right)$ invasion barriers, thus proving the evolutionary stability of the signal-following strategy $\tau$*. □

4.2. The Fate of Constant-Pure-Action Mutants

Suppose that a sufficiently small fraction of the population mutates to a strategy such that they unconditionally choose a particular pure action regardless of what the correlation device recommended. Such a mutant will earn a lower expected payoff when facing two $\tau$*-playing non-mutants, compared to the expected payoff when a $\tau$*-playing non-mutant faces two fellow non-mutants. This fact distinguishes the strict correlated equilibrium from the mixed-strategy Nash equilibrium since a constant-pure-action mutant earns just as high of an expected payoff when facing two MSNE players as an MSNE player does against two fellow MSNE players. Hence, the MSNE is vulnerable to invasion if any fraction of the population mutates to playing some constant-pure-action; whereas, the strict CE is not vulnerable to constant-pure-action mutants in sufficiently small doses.

The evolutionary stability of a three-player RPS strict correlated equilibrium strategy hinges on how the pair of choices of any two $\tau$*-strategy players creates partial protection for themselves. As described in Section 3, the CE distribution μ only places a positive probability on recommendation profiles that would result in two types of outcomes: three-way ties and one-solo-winner/two-tied-last outcomes. Each individual player is therefore designated by the correlation device to either be the recipient of $u_{3way\_tie},u_{solo\_first},$ or $u_{tied\_last}$. If two of the players follow what was recommended, but the third player disobeys their recommendation, then the two signal-following players will not receive what was designated by the correlation device, but it is the disobedient player whose expected payoff suffers more than either of the signal followers. This is because, for any given pair of players following the solo-winner/tied-last recommendations generated by μ, it is impossible for any mutant to ever deliver the worst possible payoff to the obedient two players. When a solo-winner/tied-last outcome is recommended, it will either be the case that (1) both signal followers happened to be designated to receive the tied-for-last payoffs or (2) one signal follower was designated to receive the tied-for-last payoff while the other was designated to be the solo winner. If the third player is a mutant playing some constant pure action, then these designations will not be fulfilled, but in case (1) the signal followers’ payoffs will either improve or remain the same compared to the designated payoffs. In case (2), due to the third player disobeying the recommendation, the payoff would improve for the signal follower who was designated to receive the tied-for-last payoff, while the payoff would decline for the signal follower who was designated to be the solo winner, but it cannot decline to the worst payoff $u_{solo\_last}$ as long as two of the three players are following their recommendations. The net result is that signal-following yields a higher expected payoff than any mutant strategy where the disobedient mutant constantly chooses some pure action instead of following the correlation device’s recommendation.

4.3. Subpopulation Perspective: Bayesian Beliefs as Nature’s Conditional Matching Probabilities

The analysis in Section 3 relied on the language of classical game theory in order to best facilitate the description of correlated equilibrium. In the classic game-theoretic conception of correlated equilibrium, each $a_i$ represents a recommendation that i receives from the correlation device, and then common knowledge of the distribution μ allows i to form beliefs $\mu \left(a_{-i}│a_i\right)$ concerning the recommendations that the other players could be sent. Alternatively, in order to provide a perspective befitting an evolutionary context, it is worthwhile to portray the CE in terms of players who are not necessarily hyper-rational. Relying on the framework suggested by previous authors (Mailath et al. [3]; Lenzo and Sarver [4]; Metzger [2]), we can translate the conditional probabilities $\mu \left(a_{-i}│a_i\right)$ as reflecting the process by which Nature selects members from particular subpopulations of each of the three players in the game. From this evolutionary perspective, each player i can be depicted as consisting of a population that contains a subpopulation of members preprogrammed to play rock, a subpopulation that plays paper, and a third subpopulation that plays scissors. Each action profile $a$ to which $\mu$ assigns positive probability is a possible match that Nature might make by selecting one member from a player-1 subpopulation, one member from a player-2 subpopulation, and one member from a player-3 subpopulation, where $\mu \left(a\right)$ is the probability of a specific match $a$. Conditional on Nature having selected a member from the $a_i$ subpopulation of the player i population, $\mu \left(a_{-i}│a_i\right)$ is the probability that Nature matches that member of player i to interact with a player-j population member and a player-k population member whose subpopulation identities are indicated by $a_{-i}$ in the boxed-in urns. Figure 3 shows the classical extensive form where the correlation device draws a profile of recommendations, and then player i rationally forms beliefs $\mu \left(a_{-i}│a_i\right)$ to quantify the chances of each a_−i at i’s three information sets, having received a signal of rock, paper, or scissors. For example, conditional on player i receiving a signal to play rock, i forms the beliefs $\mu \left(r_j,r_k│r_i\right)$, $\mu \left(s_j,s_k│r_i\right)$, $\mu \left(r_j,p_k│r_i\right)$, $\mu \left(p_j,r_k│r_i\right)$. Each of these is computed by Bayes’ rule:

$$\begin{gathered} \mu \left(r_j,r_k│r_i\right)=\mu \left(r_i,r_j,r_k\right)/\left[\mu \left(r_i,r_j,r_k\right)+\mu \left(r_i,s_j,s_k\right)+\mu \left(r_i,r_j,p_k\right)+\mu \left(r_i,p_j,r_k\right)\right]=\frac{1}{15}/\left[\frac{1}{15}+\frac{4}{45}+\frac{4}{45}+\frac{4}{45}\right]=\frac{1}{5} \\ \mu \left(s_j,s_k│r_i\right)=\mu \left(r_i,s_j,s_k\right)/\left[\mu \left(r_i,r_j,r_k\right)+\mu \left(r_i,s_j,s_k\right)+\mu \left(r_i,r_j,p_k\right)+\mu \left(r_i,p_j,r_k\right)\right]=\frac{4}{45}/\left[\frac{1}{15}+\frac{4}{45}+\frac{4}{45}+\frac{4}{45}\right]=\frac{4}{15} \\ \mu \left(r_j,p_k│r_i\right)=\mu \left(r_i,r_j,p_k\right)/\left[\mu \left(r_i,r_j,r_k\right)+\mu \left(r_i,s_j,s_k\right)+\mu \left(r_i,r_j,p_k\right)+\mu \left(r_i,p_j,r_k\right)\right]=\frac{4}{45}/\left[\frac{1}{15}+\frac{4}{45}+\frac{4}{45}+\frac{4}{45}\right]=\frac{4}{15} \\ \mu \left(p_j,r_k│r_i\right)=\mu \left(r_i,p_j,r_k\right)/\left[\mu \left(r_i,r_j,r_k\right)+\mu \left(r_i,s_j,s_k\right)+\mu \left(r_i,r_j,p_k\right)+\mu \left(r_i,p_j,r_k\right)\right]=\frac{4}{45}/\left[\frac{1}{15}+\frac{4}{45}+\frac{4}{45}+\frac{4}{45}\right]=\frac{4}{15} \end{gathered}$$

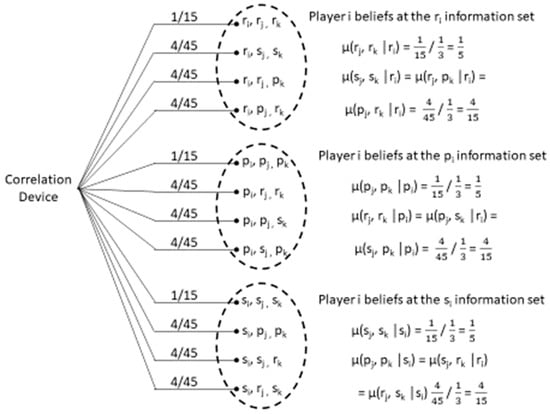
Figure 3. Player i’s beliefs and the correlation device’s distribution over recommendation profiles.

Figure 4 shows the alternative evolutionary perspective, where Nature selects a player-i population member from the rock, paper, or scissors subpopulation, and conditional on that selection, Nature proceeds to select a pair of player-j and player-k members from the subpopulation pairs $a_{-i}$ that are potential matches to the chosen i member. Urns represent specific subpopulations in the Figure 4 representation. Notice that the second stage selection of j- and k- pairs does not draw from all possible j- and k- pairs. This is because, conditional on which subpopulation of player i was drawn from, Nature excludes some j-k pairs from being matched. Given the Proposition 1 type of CE, Nature does not match any particular player i member to a pair of j- and k- members where both j and k would beat that particular i (there is zero probability of solo-loser outcomes). Neither does Nature match a particular i to j- and k- members coming from two different subpopulations than i (there is zero probability of three-way-spit outcomes). Mutations can be represented by a portion of one or more of the subpopulations choosing some action different from what is indicated by their subpopulation identity (shown by the urn labels). As long as the fraction(s) of any of the subpopulation urns, thus, mutating is sufficiently small, then the mutations will be driven out of the populations as long as Nature makes matches according to the distribution μ, and all of the subpopulations will return to contain only members who play their preprogrammed actions that are indicated by their subpopulation identities.

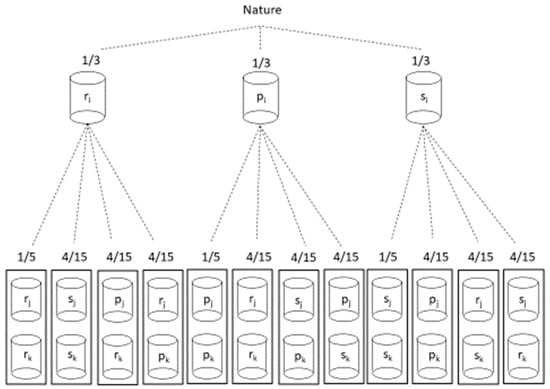
Figure 4. Determination of match probabilities for member subpopulations.

5. Discussion and Conclusions

The kind of probability distribution used by the correlation device to make three players willing to obey recommendations does not have the same power to compel choices if there are only two RPS players. With three players, outcomes arise where there is a solo winner and two tied-for-last losers. Such outcomes are not possible with only two players, since anytime a player loses, they are the solo loser. As a result, with three players, choosing to follow the recommendations from a device that puts sufficient probability on solo-winner/two-tied-last outcomes gives the three players higher expected payoffs than deviating to “play-what-the recommendation-beats” actions. When a player receives a recommendation, it is possible that following the recommendation would lead them to tie for last, but the potential payoff gain from switching to the action that the recommendation beats is muted by the presence of the third player. If i and j have received recommendations to play rock, while k’s recommendation is to play paper, i does improve their payoff somewhat by disobeying the recommendation and instead choosing scissors, but the improvement is less than if player j was not part of the game. In this scenario with three players, i’s deviating to scissors would result only in a three-way split because j chooses rock (provided j follows their recommendation), which compromises i’s payoff from deviating to scissors. This is one of the most important contrasts with two-player RPS. If there were only two players, the only kind of recommendation profile such that player i loses is a solo-last outcome, and this means a greater potential payoff gain from “play-what-the-recommendation-beats.” If the device recommends that I play rock and you play paper, switching to scissors would result in my being the solo winner. There is no third player to dampen my potential gain from disobeying recommendations that would put me in last place.

Rock-paper-scissors holds an important place in the analysis of evolutionary stability in influential textbooks, including Osborne and Rubinstein [22], Weibull [10], and Gintis [23]. In contrast to the two-player results analyzed by those authors, this paper has identified conditions for evolutionarily stable strategies when RPS involves three players who condition their action choices on imperfectly correlated signals. If two of the three players are following their own correlated signals, then the right kind of correlation device can issue recommendations that it is in the third player’s own interest to obey. This allows signal following to be protected against invasions of any potential disobedient mutants. With three players, rock-paper-scissors constitutes an important application of the theoretical linkage between correlated equilibrium and evolutionary stability.