Measuring Price Risk Aversion through Indirect Utility Functions: A Laboratory Experiment
Abstract
1. Introduction
- Holt and Laury design (H&L)—has the advantage of “varying probabilities” (or “probability weighting”), which is an important feature of the expected utility theory (henceforth, the EUT).
- Binswanger design (Bins.)—has the advantage of “varying payoffs” (i.e., weighting payoffs), which is another important feature of the EUT.
- Certainty vs. uncertainty (CvU) design—has the advantage of investigating decision making under both “certainty vs. uncertainty”, which is another important aspect of the EUT.
2. Methodology and Theoretical Considerations
2.1. Measuring Risk Aversion through Three Popular MPL Risk Elicitation Designs
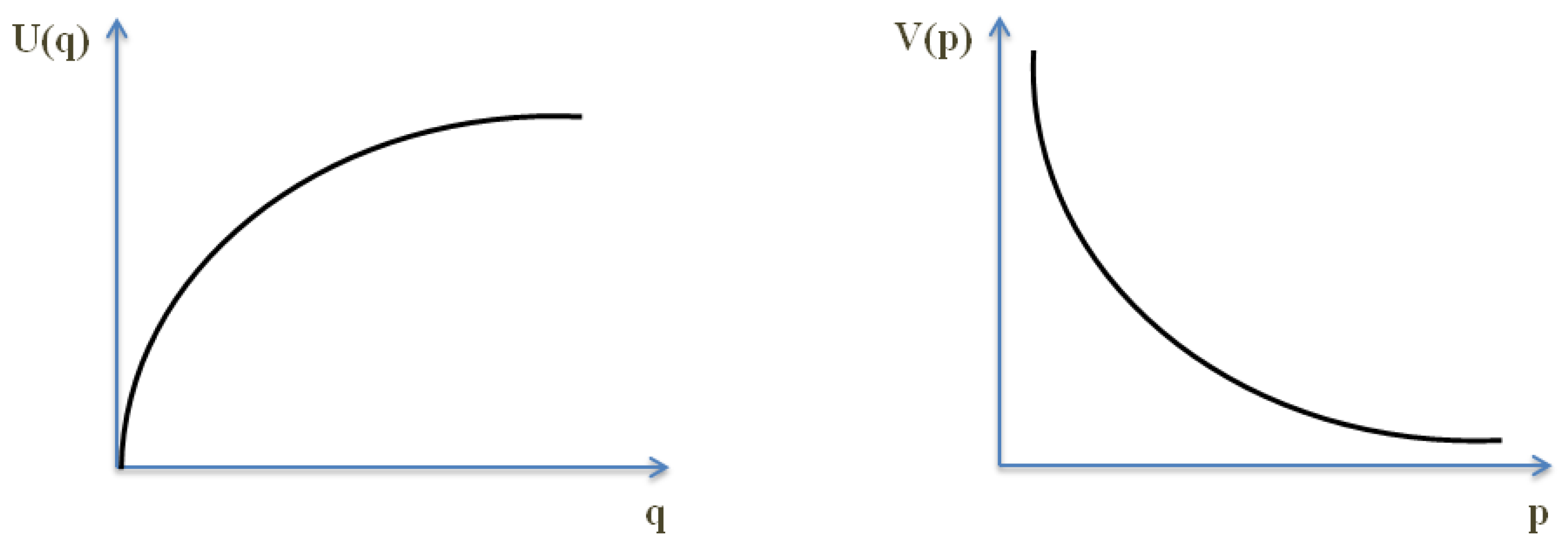
2.2. Risk Aversion in Direct Utility Function vs. Risk Aversion in Indirect Utility Function
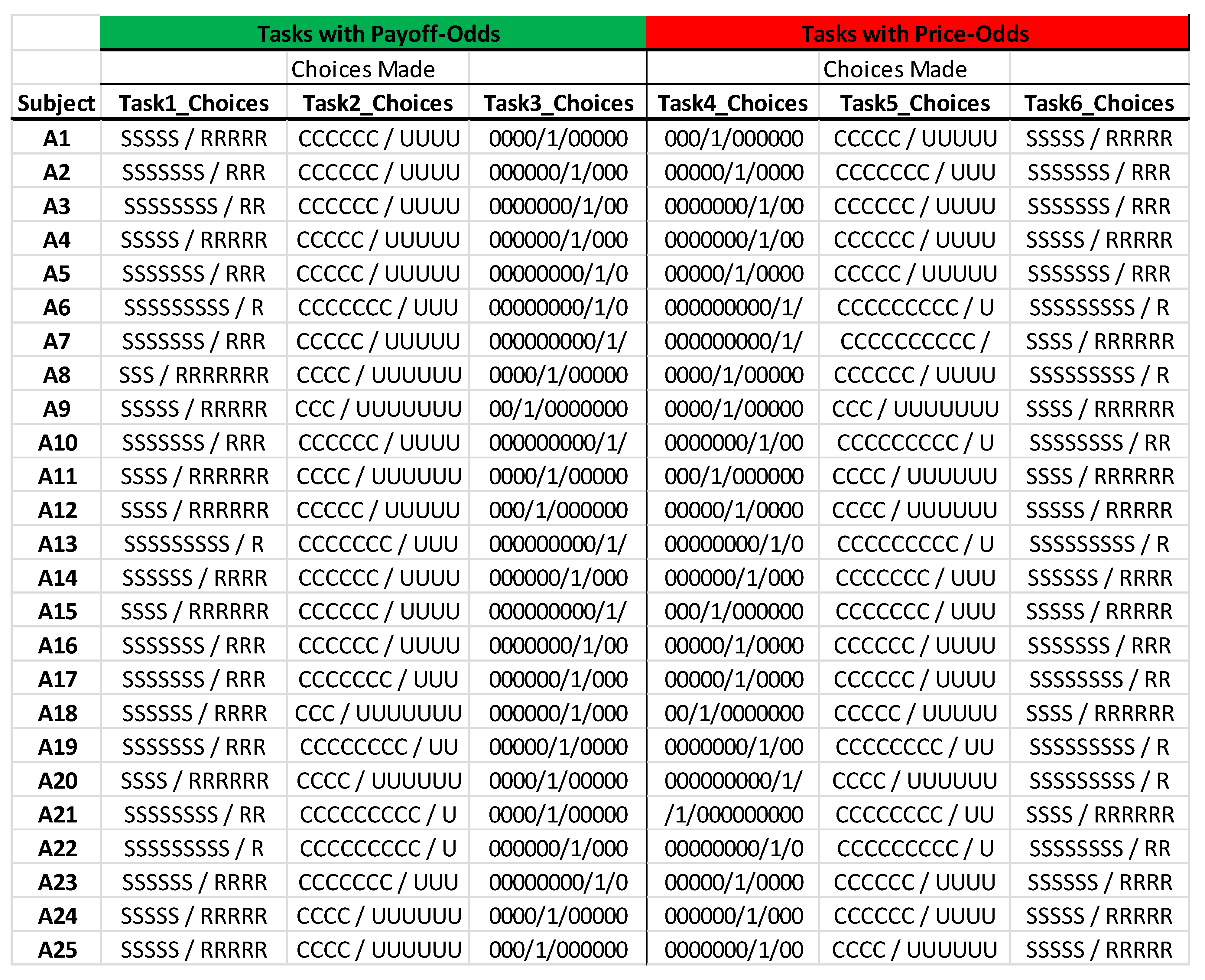
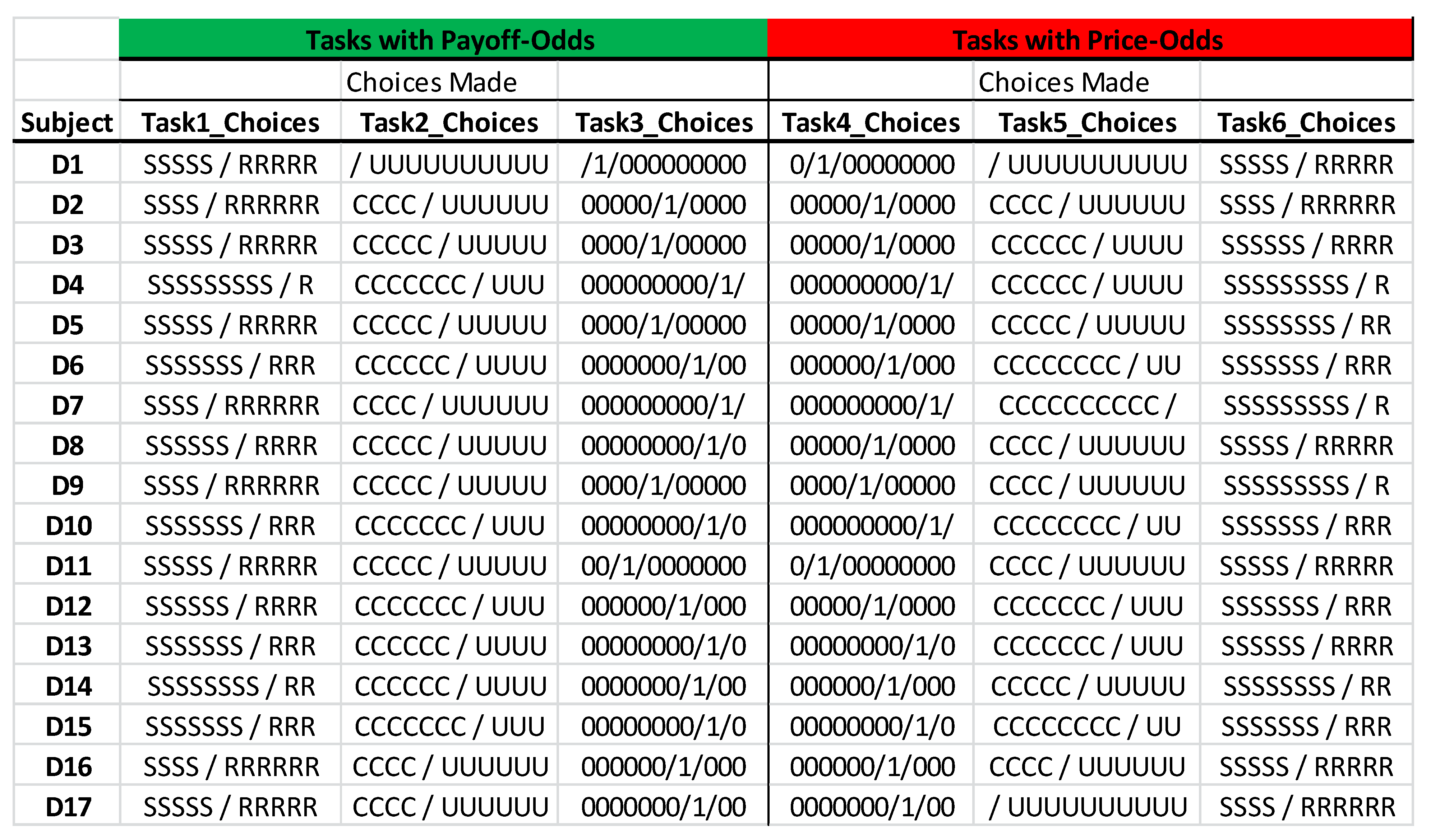
3. Experimental Design and Procedures
3.1. An MPL Design to Elicit Risk Attitudes in the Context of the IUF
3.2. Experimental Design
3.3. The Experiment Procedures
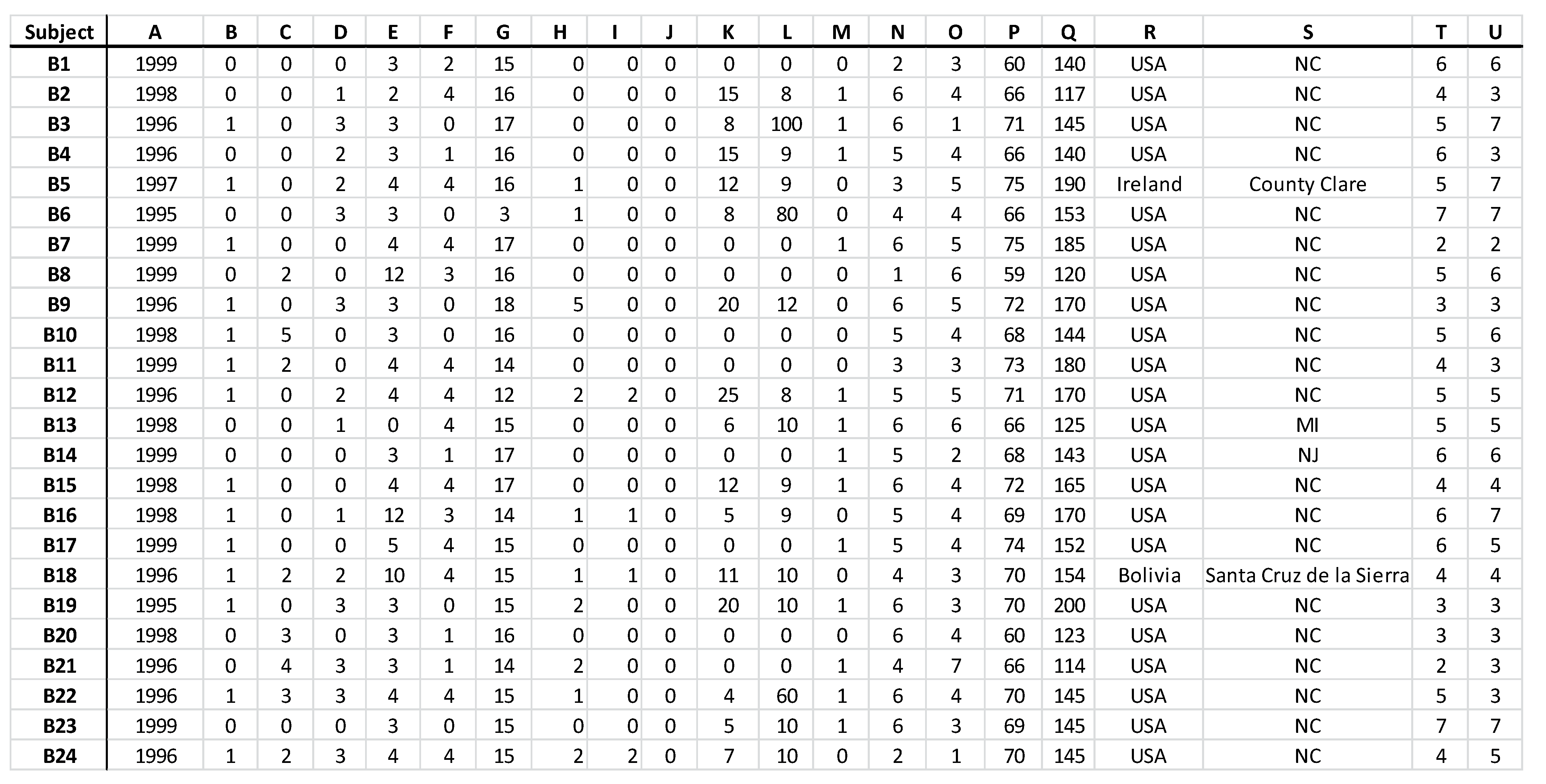
4. Data and Variables
5. Estimation and Results
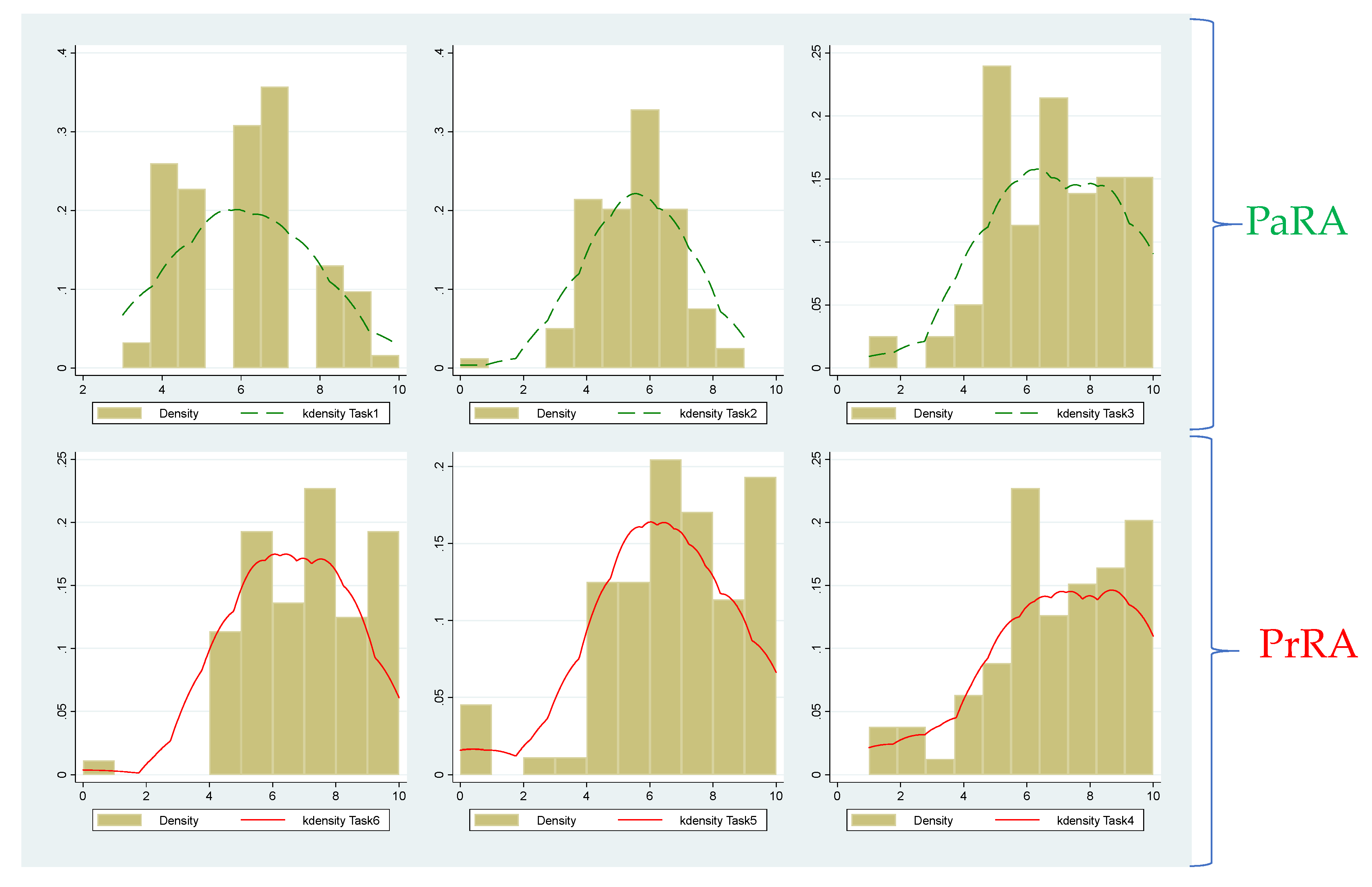
5.1. Payoff Risk Aversion versus Price Risk Aversion
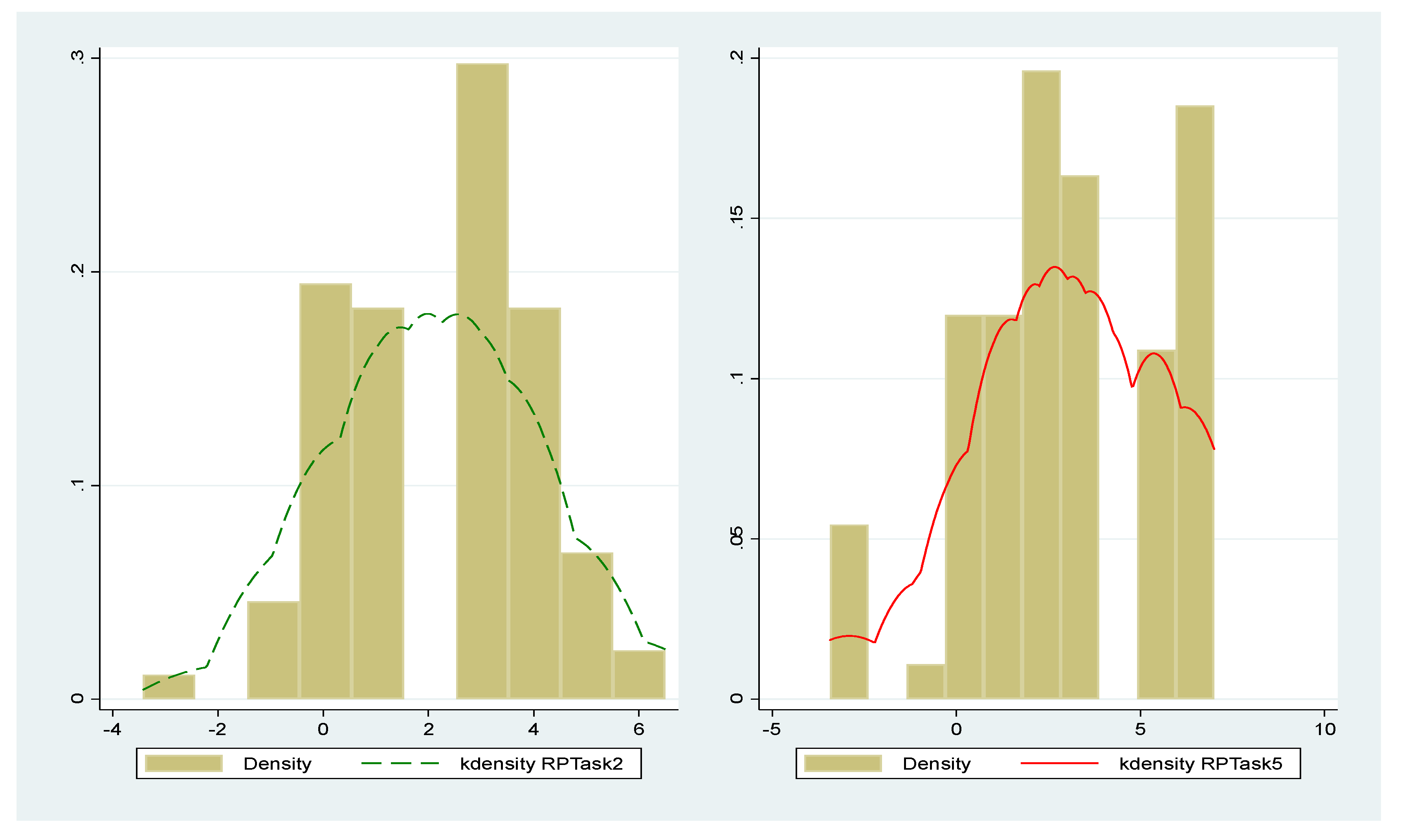
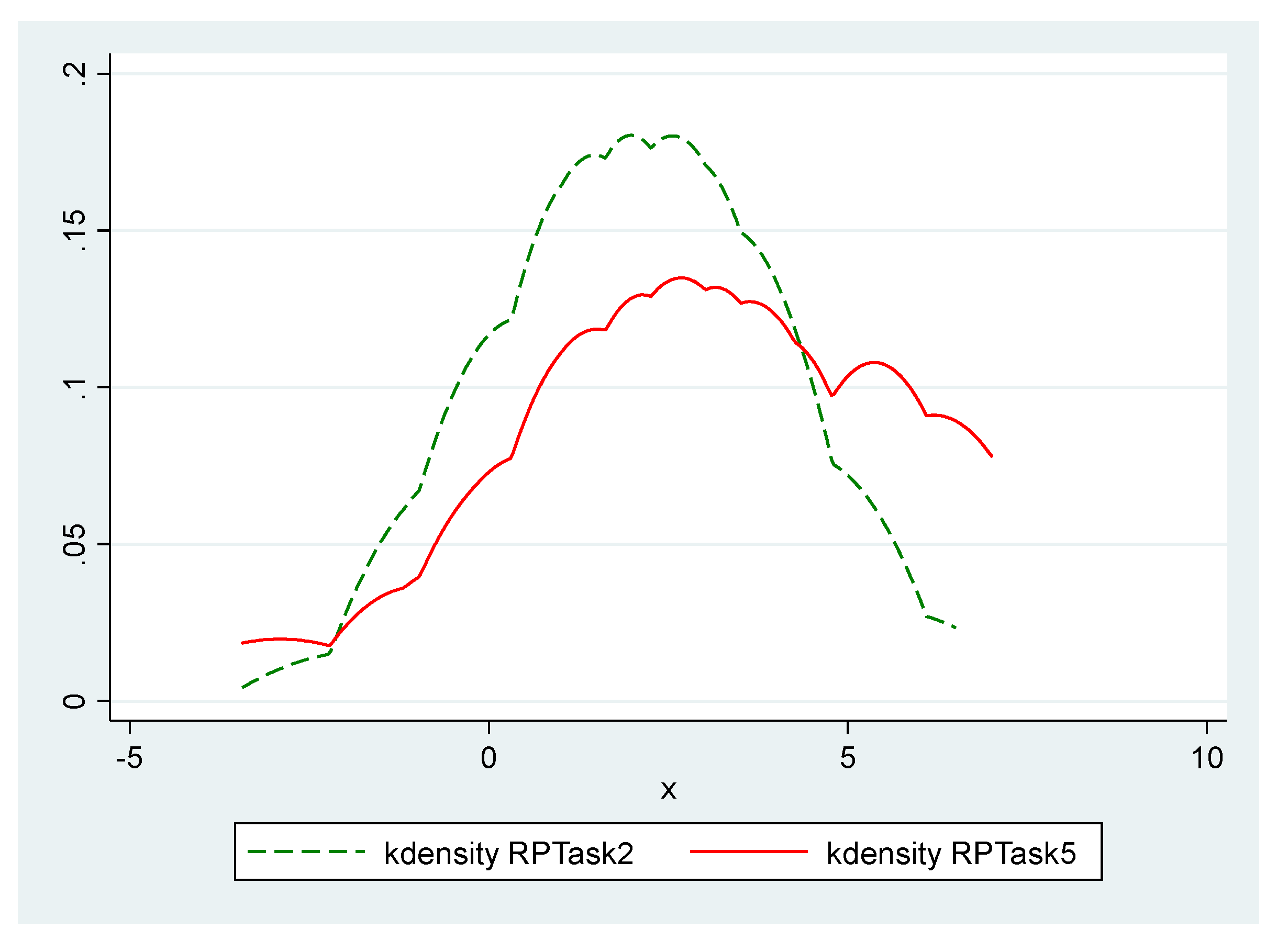
5.2. Estimating Payoff Risk Premiums and Price Risk Premiums Using the CvU Design
6. Summary and Discussion
- The vast majority of subjects are risk-averse, irrespective of whether the elicitation approach is direct (through the DUF) or indirect (through the IUF). In fact, only a few (less than 5%) of them exhibit risk-loving attitudes, and the rest are either risk-neutral (about 12%) or risk-averse (about 83%), averaged across the six tasks.
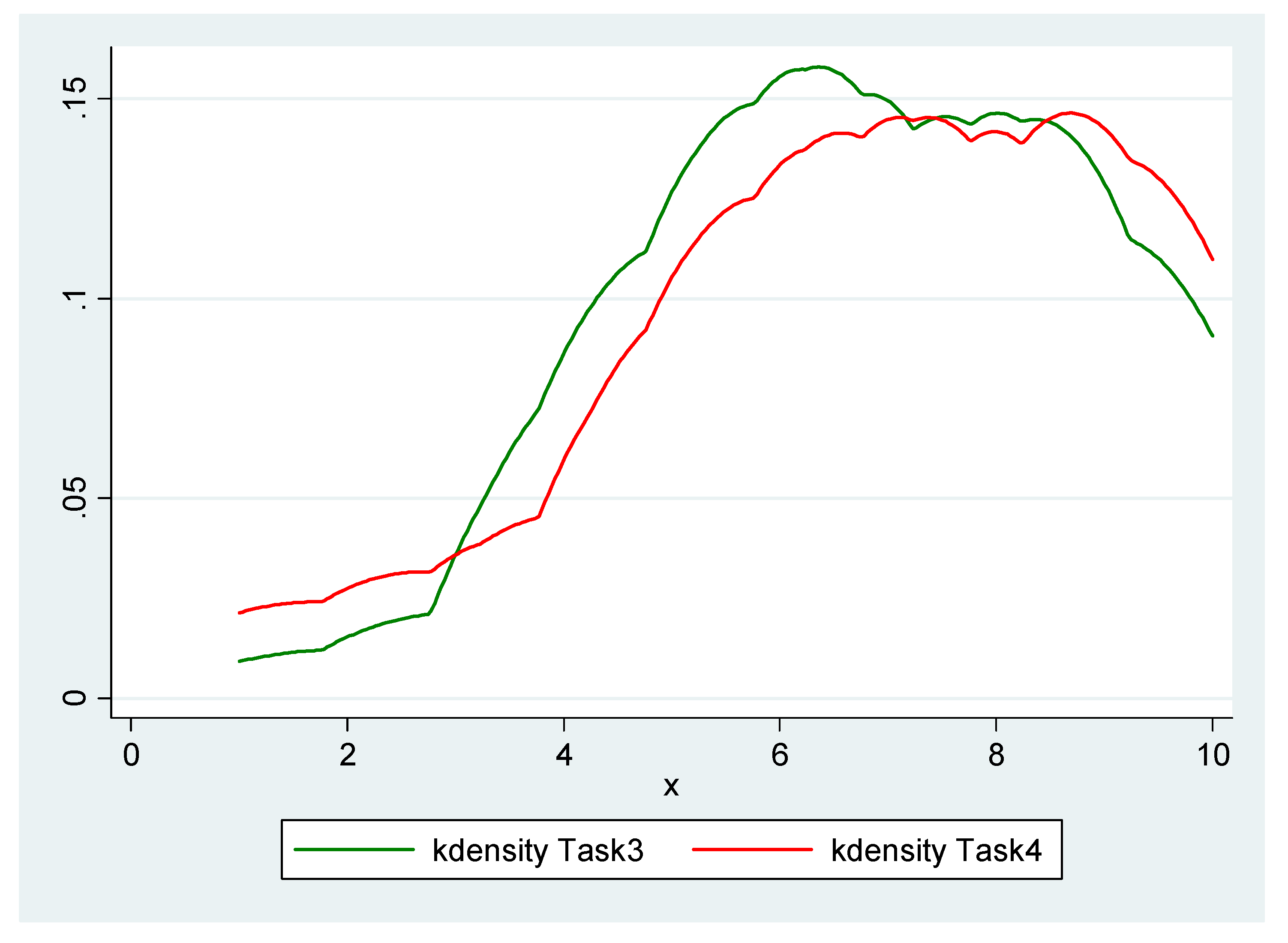
- One clear conclusion that emerges from the results of this research study is that individuals exhibit statistically significantly greater degrees of risk aversion when faced with random prices (PrRA) compared to when they are faced with random payoffs (PaRA). In fact, in all the three pairs of designs, the kernel density representing the degree of PrRA lies to the right of its counterpart that represents the degree of PaRA. This is a remarkable result and a thought-provoking observation. More specifically, the findings indicate that the average of the estimated midpoint CRRAs is equal to 0.597 for PaRA (which implies a ‘risk-averse’ attitude), while it is equal to 0.708 for PrRA (which implies a ‘very risk-averse’ attitude).
- More interestingly, this result (i.e., PaRA < PrRA) is robust across all the three MPL designs that are used, which indicates the fact that the observed anomalies in the degrees of risk aversion exhibited by the subjects are quite systematic; as such, they can sensibly and persuasively be attributed to the nature of each approach (i.e., the inherently different risk preferences that subjects exhibit with respect to random payoffs and random prices). Some scholars have argued that the results of EUT-based elicitations are subject to change with respect to different contextual frameworks. For example, Zhou and Hey (2017) [5] argue that the risk elicitation procedure (i.e., the context) employed in an experiment influences the estimated degrees of risk aversion resulting from the experiment. To account for this possibility and to address this concern, this study considered using three different MPL designs in order to be able to check the sensitivity and robustness of our results to contextual differences. The findings show that the observed anomalies between PaRA and PrRA are systematic; as such, regardless of the MPL designs used, the results of all the designs indicate that PrRA is greater than PaRA. Given the robustness of the results across different contextual designs as well as the existing strong evidence base from different statistical tests, the difference between PaRA and PrRA cannot be attributed to noisy decision making by any means. For the purpose of statistical hypothesis testing, a wide range of relevant statistical tests were used, including the Wilcoxon signed-rank test, the Arbuthnott–Snedecor–Cochran sign test, and the two-sample T test for paired data. The great majority of the above-mentioned statistical tests confirm that PrRA is statistically significantly greater than PaRA.
- This implicitly suggests that individuals, in general, have higher willingness to pay (WTP) for price-guaranteeing insurance premiums than those guaranteeing payoff quantities. It also indicates that risk-preference-related implications of the duality theory (DT) are statistically rejected from a behavioral point of view, since experimental evidence shows that there is a systematic distance from rationality when subjects are exposed to random payoffs versus random prices.
- In addition, our results suggest that although “the degrees of risk aversion” elicited under the EUT are somewhat subject to context (here, the MPL designs) (consistent with the mainstream experimental literature which revealed that context matters when results are produced under the EUT, as discussed by Zhou and Hey (2017) [5]), the broadly defined “risk attitudes” (i.e., risk-loving, risk-neutral, and risk-averse) elicited under the EUT are not subject to as much context. In fact, 41% of the subjects have exhibited different broadly categorized “risk attitudes” across the six designs (i.e., switching their positions back and forth at least once from risk-loving, to risk-neutral, and/or to risk-averse attitudes), among which 23 percentage points have switched back and forth solely around the narrow border of risk neutrality and risk aversion, meaning that only 18% of the subjects have exhibited all the three different broadly defined “risk attitudes” in their six tasks (even in this case, the results from the vast majority of designs are mostly consistent with, and are close to, each other, and only two of the responses are far from the others).
- Additionally, the results of the study show that the extent of being subject to context is greater for PrRA with a standard deviation of 0.451 for its elicited midpoint CRRAs, compared to PaRA with a standard deviation of 0.381 for its elicited midpoint CRRAs.
- These results imply that the MPL elicitation method, referred to as the context of elicitation in this study, does matter to the estimated “degree of risk aversion”, but not much so to the broadly categorized “risk attitudes”. Thus, if one’s concern is only “the general risk attitude” (that is, the broadly defined risk attitude), there is no need to worry much about the MPL design and context of elicitation. However, if “the degree of risk aversion” is of great concern in their studies, then they need to choose the design that greatly resembles the real-world context of their research study. For example, if probability weighting is a crucial aspect of the real-world setting of interest, researchers should choose the H&L design; if payoff weighting is a major facet of the real-world phenomenon under study, then they should choose to work with the Bins. design; and if the confrontation of certain situations and uncertain situations best describes the problem they are studying, then they should select the CvU design. For other general purposes, an average of the three designs may be a good choice that potentially better represents a combination of all the important aspects existing in a more complex real-world situation. Furthermore, it is recommended that researchers and practitioners use multiple designs in their experiments, so that they can gain a better understanding and a more holistic picture of risk aversion characteristics, and also check the robustness of their results with respect to context.
- This finding appears to signal that the degree of risk aversion needs to be elicited in the context within which it is supposed to be interpreted. As Zhou and Hey (2017) [5] state, one should estimate the risk aversion coefficients in its related context, because eliciting these coefficients in an unrelated context could lead to misinterpretations of the data. Additionally, as Loomes and Pogrebna (2014) [16] mention, researchers intending to elicit the degree of risk aversion in their studies should select an elicitation procedure similar to the sort of decisions they are investigating.
- It was also shown that the risk premium (RP), as a measure of willingness to pay for insuring an uncertain situation, is statistically significantly greater for stochastic prices compared to that for stochastic payoffs. The results from all the three statistical tests imply that the PaRP is statistically significantly different from the PrRP. The tests suggest that individuals, in general, demand a larger premium in order to agree playing a lottery with price odds compared to that with payoff odds. This strong experimental evidence base indicates that there is a systematic distance from rationality when subjects are exposed to random payoffs versus random prices. Therefore, behaviorally, we see that individuals are typically more comfortable with uncertain payoffs than uncertain prices.
- Since RPs for lotteries with payoff odds are smaller than those with price odds, it can be inferred that WTPs for price-guaranteeing insurance premiums are greater than those guaranteeing payoff quantities. An implication of this finding is that an insurance company can charge higher premium rates if they frame their insurance coverage around uncertain prices instead of uncertain payoffs, in case there is such a possibility at all in the insurance setting. A fine example of such a situation could be insuring the prices at which farmers buy their inputs or sell their crops (as an indicator of uncertain prices) rather than farmers’ yields (as an indicator of their uncertain payoffs). The results of the present study show that the average subject is willing to pay a RP, even as large as 27.7% of the expected value of payoffs when faced with uncertain prices, and 19.1% when faced with uncertain payoffs. This suggests that if an insurer intends to guarantee a level of revenue for an insured farmer through guaranteeing either a crop quantity or a crop price, each of which exposes the company to exactly the same degree of risk, the insurer will be able to charge higher premiums for guaranteeing the price, since the findings of this study imply that subjects have higher levels of risk aversion with respect to a price change compared to its equivalent payoff quantity change. Moreover, as a result of this higher level of risk aversion, they have higher WTP for price-guaranteeing insurance premiums.
- This result suggests that if a benevolent social planner (e.g., the US Federal Crop Insurance Program) intends to provide insurance services to convince risk-averse agents to produce risky products (e.g., farmers to plant risky crops), it would be more effective for the insurance plan to focus on and more efficient for the program budget to be spent on insuring prices rather than yield quantity. This is because agents typically exhibit higher degrees of risk aversion to random prices than their equivalent random payoffs and quantities. As an example of a piece of evidence outside the laboratory, in the real world, such a tendency and high sensitivity to random prices can be noticed by comparing the share of revenue programs (constituting 77% of the volume of the crop insurance policies sold in the US in 2013) and AHP programs (constituting 23% of the volume of the crop insurance policies sold in the US), according to Shields (2015) [27], while the only major difference between the two types of programs is the inclusion of the insurance coverage on yield prices. This result becomes even more interesting if one pays attention to the fact that the historical data have shown that price changes are responsible only for 7% of the losses paid by the US Federal Crop Insurance Program during the period of 2001–2015, according to Good (2017) [28]. However, farmers have still shown a high degree of risk aversion with respect to price changes. After all, it is important to note that making a claim that this difference can be totally attributed to the relatively higher degree of price risk aversion is not reasonable and needs more investigation, since it can be attributed to some other factors as well, such as the relative availability of insurance plans in different areas and for different crops, as well as the relative price of the insurance plans for different areas and for different crops. However, this example is brought up here to introduce some potential examples of real-world evidence that are worth more attention, although this goes beyond the scope of the present paper to attend to these different aspects here in greater detail.
7. Conclusions and Further Research
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
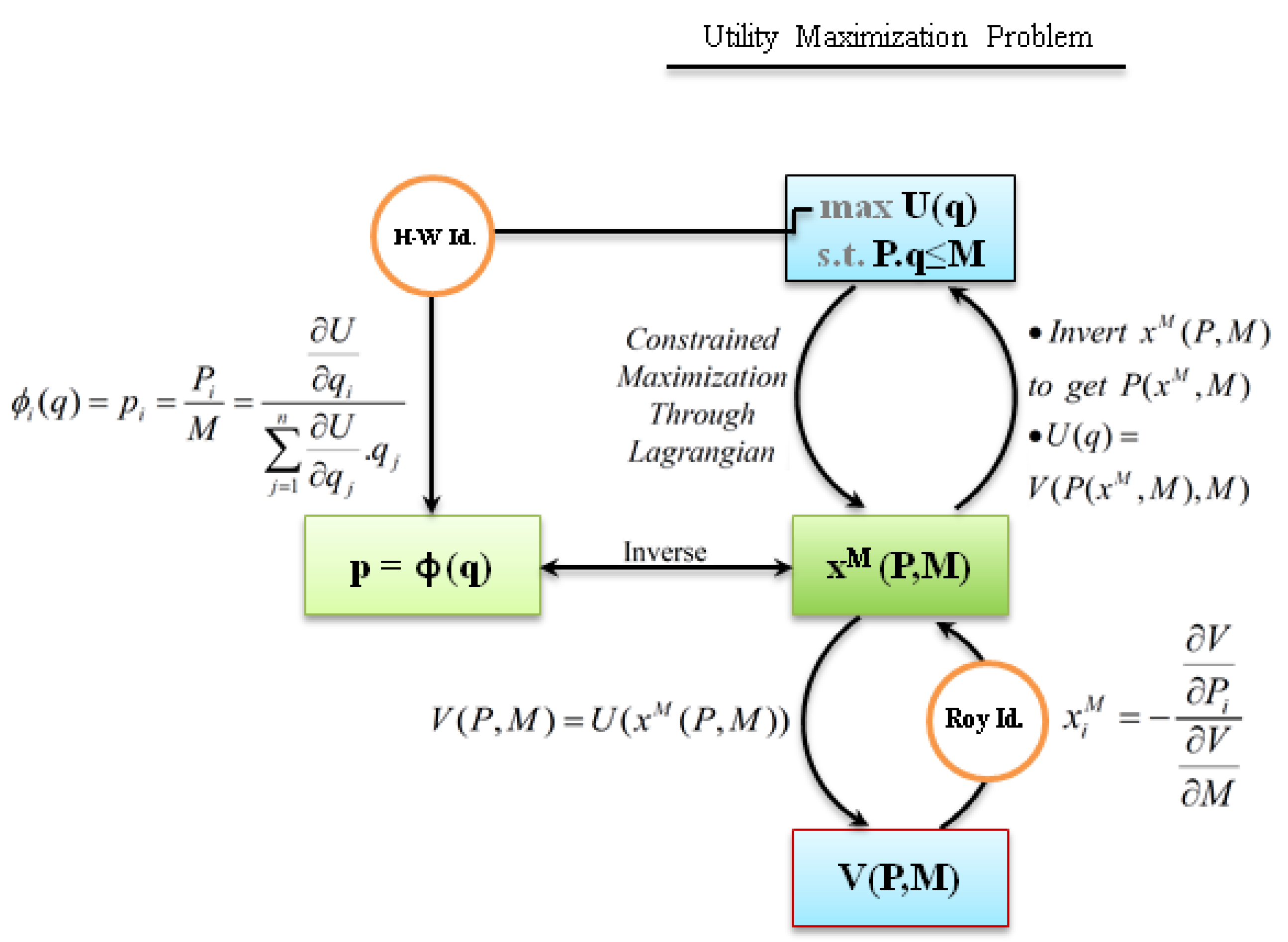
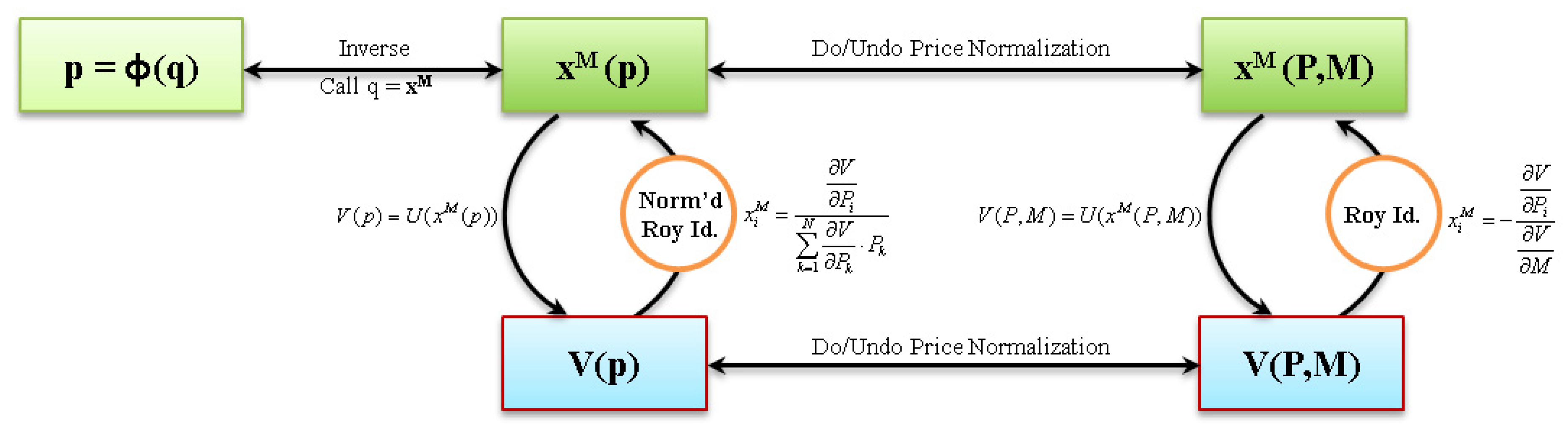
Appendix A. Wheel of Duality (WOD) in the Consumer Theory
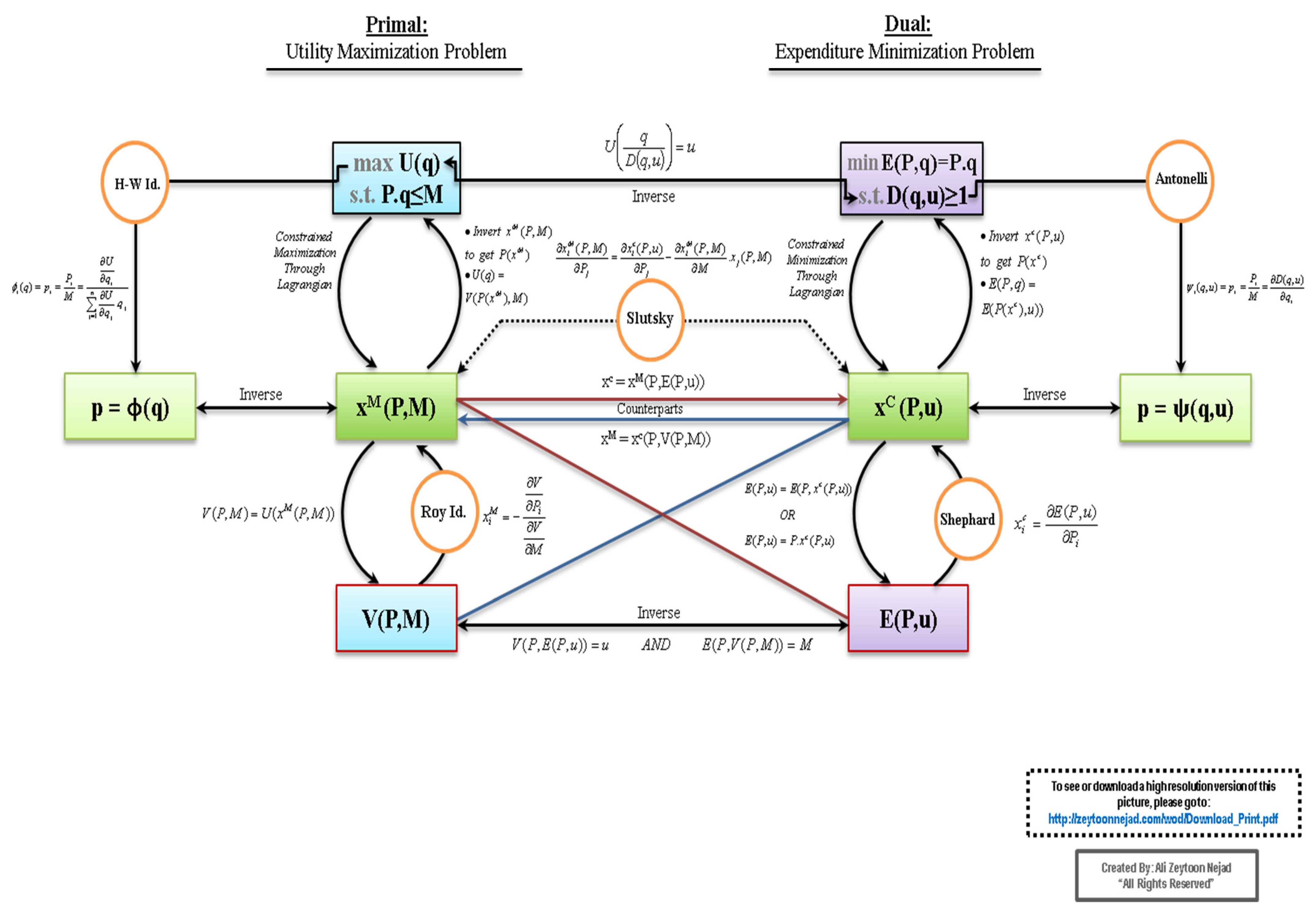
Appendix B. Symbols and Notations in the WOD
- max: maximize
- min: minimize
- s.t.: subject to
- q: vector of quantities consumed
- P: vector of prices
- M: income
- p: vector of normalized prices, i.e., P/M
- U(q): direct utility function (or utility function)
- ≥ P.q: budget constraint
- V(P,M): indirect utility function
- V(p): indirect utility function with normalized prices
- E(P,u): “The” expenditure function
- E(P,q): The amount of expenditures
- D(q,u): The distance function
- xM (P,M): Marshallian (i.e., uncompensated or Walrasian or ordinary) demand function
- xM (p): vector of normalized Marshallian demand function
- p = ϕ(q): vector of Hotelling-style inverse demand function
- xC (P,u): vector of Hicksian-style (i.e., compensated) demand function
- p = ψ(q,u): vector of Antonelli-style inverse demand function
- H-W Id.: Hotelling–Wold identity
- Antonelli: Antonelli equation
- Slutsky: Slutsky equation
- Roy Id.: Roy’s identity
- Norm’d Roy Id.: normalized version of Roy’s identity
- Shephard: Shephard’s lemma
- Norm’d Shephard: Shephard’s lemma with normalized prices
- DUF: direct utility function
- IUF: indirect utility function
- EF: expenditure function
- DF: distance function
- HIDF: Hotelling-style inverse demand function
- MDF: Marshallian demand function
- HDF: Hicksian demand function
- AIDF: Antonelli-style inverse demand function
- EAF: expenditure amount function
- BC: budget constrain
Appendix C. Three Tables Illustrating the Equivalence of the DUF and IUF MPL Designs for H&L
| Option A—(Less Risky) | Option B—(More Risky) | Difference in Final Payoff Expected Values |
|---|---|---|
| 1/10 of (USD 1.25), 9/10 of (USD 1.56) | 1/10 of (USD 0.65), 9/10 of (USD 25.00) | USD 6.99 |
| 2/10 of (USD 1.25), 8/10 of (USD 1.56) | 2/10 of (USD 0.65), 8/10 of (USD 25.00) | USD 4.98 |
| 3/10 of (USD 1.25), 7/10 of (USD 1.56) | 3/10 of (USD 0.65), 7/10 of (USD 25.00) | USD 2.97 |
| 4/10 of (USD 1.25), 6/10 of (USD 1.56) | 4/10 of (USD 0.65), 6/10 of (USD 25.00) | USD 0.96 |
| 5/10 of (USD 1.25), 5/10 of (USD 1.56) | 5/10 of (USD 0.65), 5/10 of (USD 25.00) | -USD 1.05 |
| 6/10 of (USD 1.25), 4/10 of (USD 1.56) | 6/10 of (USD 0.65), 4/10 of (USD 25.00) | -USD 3.06 |
| 7/10 of (USD 1.25), 3/10 of (USD 1.56) | 7/10 of (USD 0.65), 3/10 of (USD 25.00) | -USD 5.07 |
| 8/10 of (USD 1.25), 2/10 of (USD 1.56) | 8/10 of (USD 0.65), 2/10 of (USD 25.00) | -USD 7.08 |
| 9/10 of (USD 1.25), 1/10 of (USD 1.56) | 9/10 of (USD 0.65), 1/10 of (USD 25.00) | -USD 9.09 |
| 10/10 of (USD 1.25), 0/10 of (USD 1.56) | 10/10 of (USD 0.65), 0/10 of (USD 25.00) | -USD 11.10 |
| Option A—(Less Risky) | Option B—(More Risky) | Difference in Final Payoff Expected Values |
|---|---|---|
| 1/10 of (12 units), 9/10 of (9.6 units) | 1/10 of (23.05 units), 9/10 of (0.6 units) | USD 6.99 |
| 2/10 of (12 units), 8/10 of (9.6 units) | 2/10 of (23.05 units), 8/10 of (0.6 units) | USD 4.98 |
| 3/10 of (12 units), 7/10 of (9.6 units) | 3/10 of (23.05 units), 7/10 of (0.6 units) | USD 2.97 |
| 4/10 of (12 units), 6/10 of (9.6 units) | 4/10 of (23.05 units), 6/10 of (0.6 units) | USD 0.96 |
| 5/10 of (12 units), 5/10 of (9.6 units) | 5/10 of (23.05 units), 5/10 of (0.6 units) | -USD 1.05 |
| 6/10 of (12 units), 4/10 of (9.6 units) | 6/10 of (23.05 units), 4/10 of (0.6 units) | -USD 3.06 |
| 7/10 of (12 units), 3/10 of (9.6 units) | 7/10 of (23.05 units), 3/10 of (0.6 units) | -USD 5.07 |
| 8/10 of (12 units), 2/10 of (9.6 units) | 8/10 of (23.05 units), 2/10 of (0.6 units) | -USD 7.08 |
| 9/10 of (12 units), 1/10 of (9.6 units) | 9/10 of (23.05 units), 1/10 of (0.6 units) | -USD 9.09 |
| 10/10 of (12 units), 0/10 of (9.6 units) | 10/10 of (23.05 units), 0/10 of (0.6 units) | -USD 11.10 |
| Option A—(Less Risky) | Option B—(More Risky) | Difference in Final Payoff Expected Values |
|---|---|---|
| 1/10 of (USD 12.00), 9/10 of (USD 9.60) | 1/10 of (USD 23.05), 9/10 of (USD 0.60) | USD 6.99 |
| 2/10 of (USD 12.00), 8/10 of (USD 9.60) | 2/10 of (USD 23.05), 8/10 of (USD 0.60) | USD 4.98 |
| 3/10 of (USD 12.00), 7/10 of (USD 9.60) | 3/10 of (USD 23.05), 7/10 of (USD 0.60) | USD 2.97 |
| 4/10 of (USD 12.00), 6/10 of (USD 9.60) | 4/10 of (USD 23.05), 6/10 of (USD 0.60) | USD 0.96 |
| 5/10 of (USD 12.00), 5/10 of (USD 9.60) | 5/10 of (USD 23.05), 5/10 of (USD 0.60) | -USD 1.05 |
| 6/10 of (USD 12.00), 4/10 of (USD 9.60) | 6/10 of (USD 23.05), 4/10 of (USD 0.60) | -USD 3.06 |
| 7/10 of (USD 12.00), 3/10 of (USD 9.60) | 7/10 of (USD 23.05), 3/10 of (USD 0.60) | -USD 5.07 |
| 8/10 of (USD 12.00), 2/10 of (USD 9.60) | 8/10 of (USD 23.05), 2/10 of (USD 0.60) | -USD 7.08 |
| 9/10 of (USD 12.00), 1/10 of (USD 9.60) | 9/10 of (USD 23.05), 1/10 of (USD 0.60) | -USD 9.09 |
| 10/10 of (USD 12.00), 0/10 of (USD 9.60) | 10/10 of (USD 23.05), 0/10 of (USD 0.60) | -USD 11.10 |
Appendix D. Additional Supplementary Tables of Results

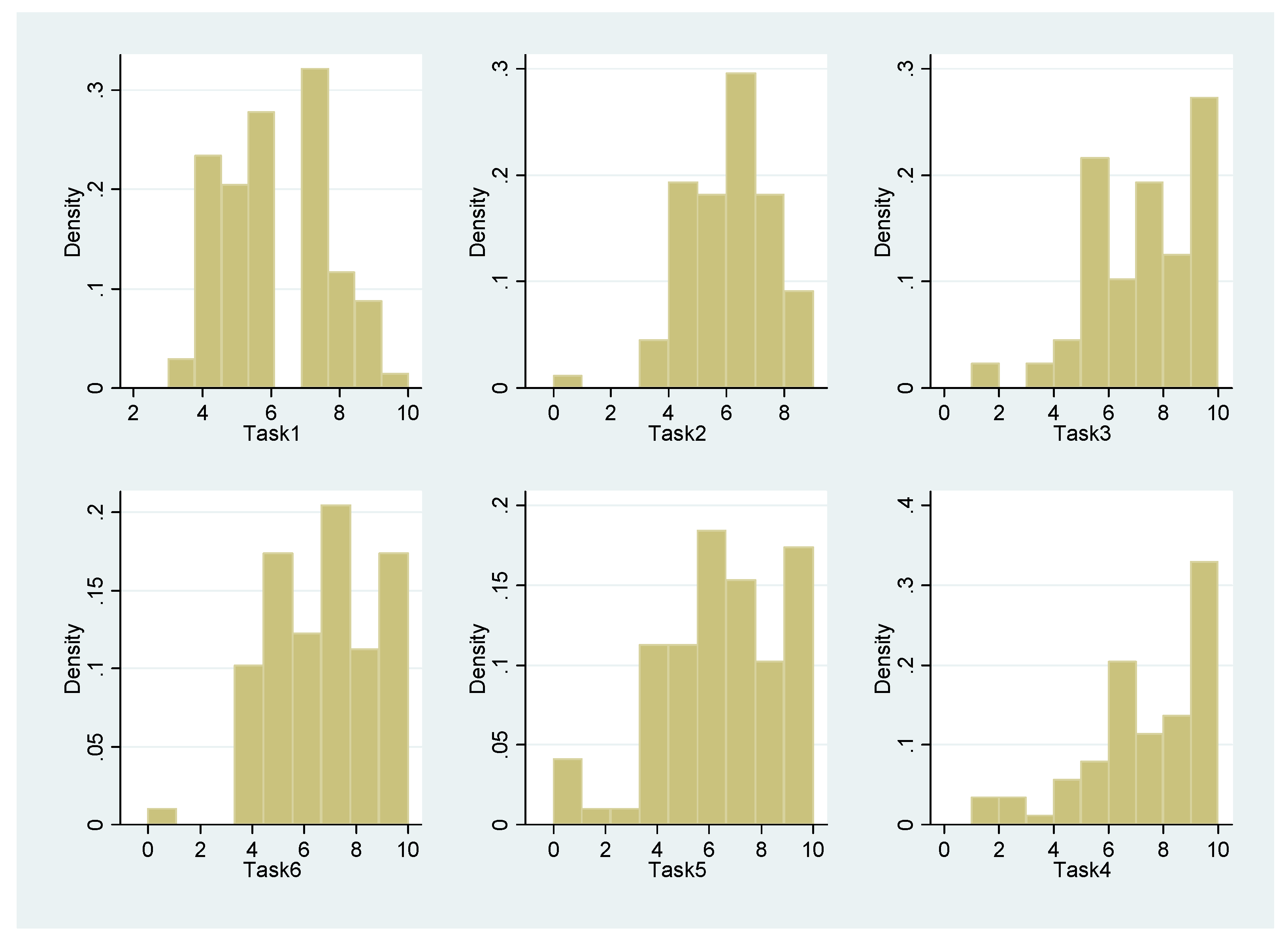
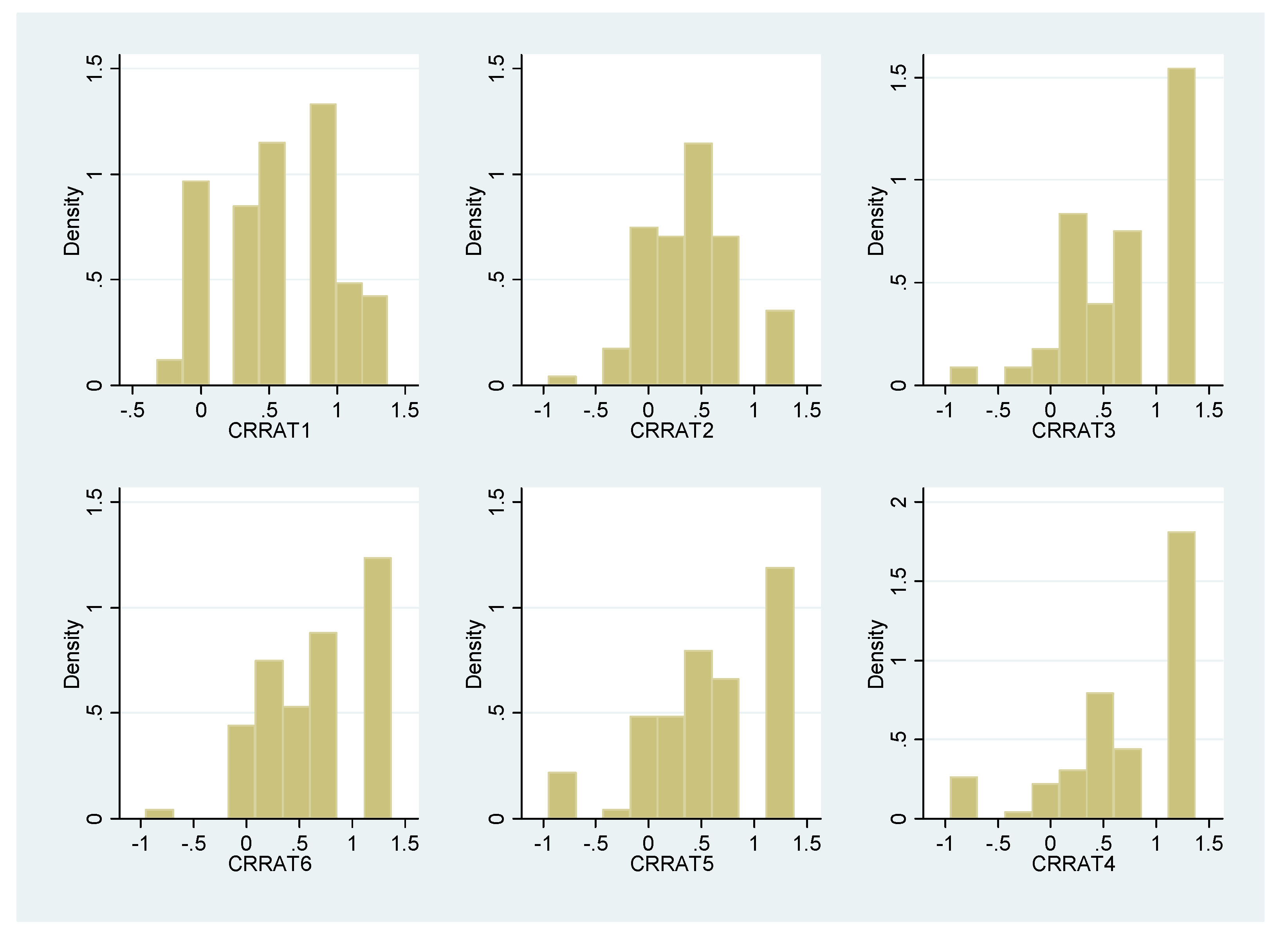
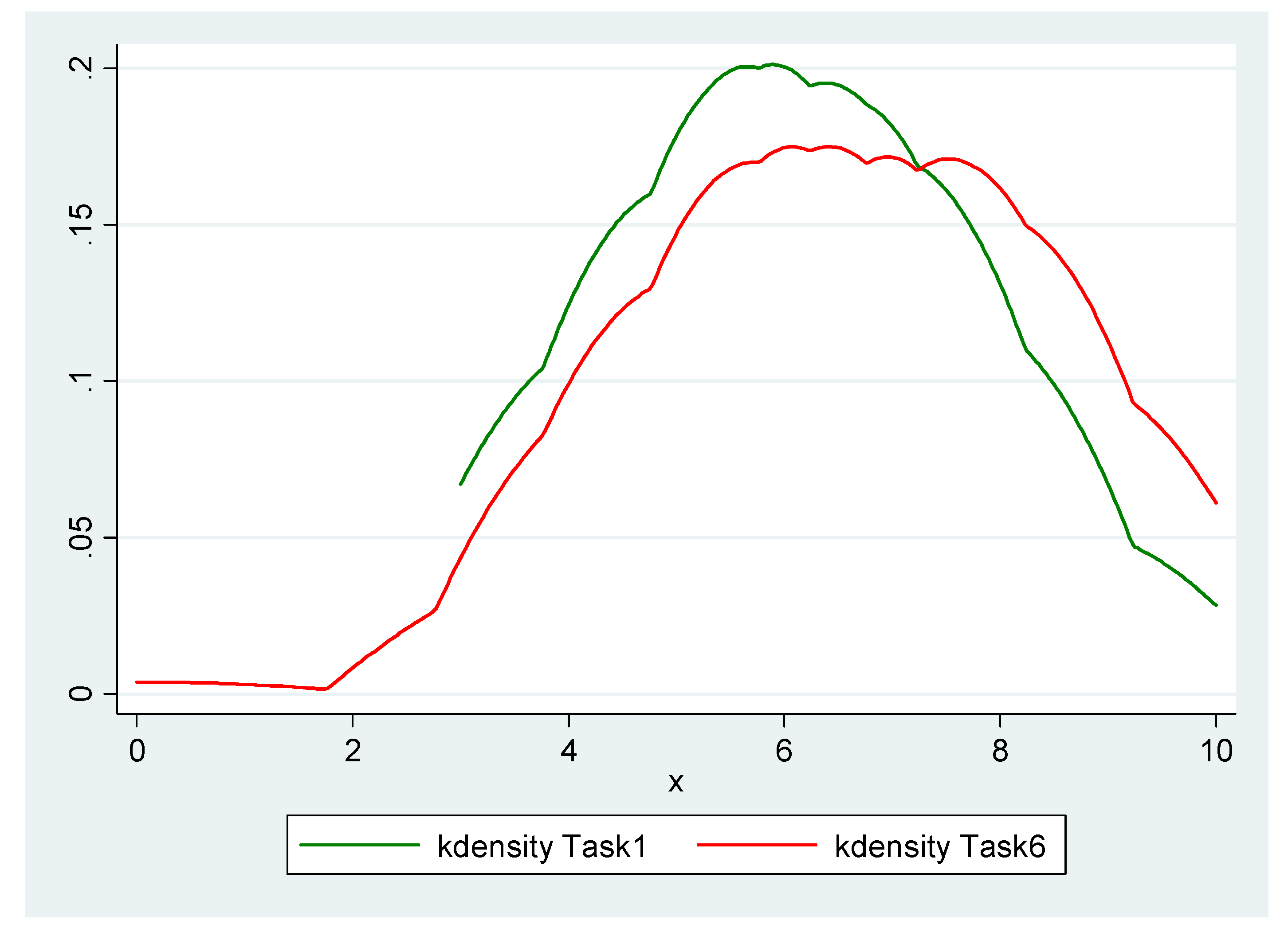


Appendix E. Tables Providing the Details of Statistical Hypothesis Tests
| signrank Task 1 = Task 6 | |||
| Wilcoxon signed-rank test | |||
| sign | obs | sum ranks | expected |
| Positive | 21 | 1189.5 | 1694 |
| Negative | 35 | 2198.5 | 1694 |
| Zero | 32 | 528 | 528 |
| All | 88 | 3916 | 3916 |
| Unadjusted variance | 57761 | ||
| Adjustment for ties | −645.88 | ||
| Adjustment for zeros | −2860 | ||
| Adjusted variance | 54,255.13 | ||
| Ho: Task 1 = Task 6 | |||
| z = −2.166 | |||
| Prob > z = 0.0303 | |||
| signrank Task 2 = Task 5 | |||
| Wilcoxon signed-rank test | |||
| sign | obs | sum ranks | expected |
| Positive | 24 | 1138.5 | 1831.5 |
| Negative | 42 | 2524.5 | 1831.5 |
| Zero | 22 | 253 | 253 |
| All | 88 | 3916 | 3916 |
| Unadjusted variance | 57761 | ||
| Adjustment for ties | −948.88 | ||
| Adjustment for zeros | −948.75 | ||
| Adjusted variance | 55,863.38 | ||
| Ho: Task2 = Task5 | |||
| z = −2.932 | |||
| Prob > z = 0.0034 | |||
| signrank Task 3 = Task 4 | |||
| Wilcoxon signed-rank test | |||
| sign | obs | sum ranks | expected |
| Positive | 28 | 1618.5 | 1755 |
| Negative | 32 | 1819.5 | 1755 |
| Zero | 28 | 406 | 406 |
| All | 88 | 3916 | 3916 |
| Unadjusted variance | 57761 | ||
| Adjustment for ties | −452.13 | ||
| Adjustment for zeros | −1928.5 | ||
| Adjusted variance | 55,380.38 | ||
| Ho: Task 3 = Task 4 | |||
| z = −0.580 | |||
| Prob > z = 0.5619 | |||
| signrank DUF_Task_Mean = IUF_Task_Mean | |||
| Wilcoxon signed-rank test | |||
| sign | obs | sum ranks | expected |
| Positive | 28 | 1368.5 | 1925 |
| Negative | 49 | 2481.5 | 1925 |
| Zero | 11 | 66 | 66 |
| All | 88 | 3916 | 3916 |
| Unadjusted variance | 57761 | ||
| Adjustment for ties | 62.25 | ||
| Adjustment for zeros | −126.5 | ||
| Adjusted variance | 5752.25 | ||
| Ho: DUF_Task_Mean = IUF_Task_Mean | |||
| z = −2.319 | |||
| Prob > z = 0.0204 | |||
| signtest Task 1 = Task 6 | ||
| Sign test | ||
| sign | observed | expected |
| Positive | 21 | 28 |
| Negative | 35 | 28 |
| Zero | 32 | 32 |
| All | 88 | 88 |
| One-sided tests: | ||
| Ho: median of Task 1 - Task 6 = 0 vs. | ||
| Ha: median of Task 1 - Task 6 > 0 | ||
| Pr(#positive >= 21) = | ||
| Binomial(n = 56, x >= 21, p = 0.5) = 0.9780 | ||
| Ho: median of Task 1 - Task 6 = 0 vs. | ||
| Ha: median of Task 1 - Task 6 < 0 | ||
| Pr(#negative >= 35) = | ||
| Binomial(n = 56, x >= 35, p = 0.5) = 0.0407 | ||
| Two-sided test: | ||
| Ho: median of Task 1 - Task 6 = 0 vs. | ||
| Ha: median of Task 1 - Task 6 = 0 | ||
| Pr(#positive >= 35 or #negative >= 35) = | ||
| min(1, 2*Binomial(n = 56, x >= 35, p = 0.5)) = 0.0814 | ||
| signtest Task 2 = Task 5 | ||
| Sign test | ||
| sign | observed | expected |
| Positive | 24 | 33 |
| Negative | 42 | 33 |
| Zero | 22 | 22 |
| All | 88 | 88 |
| One-sided tests: | ||
| Ho: median of Task 2 - Task 5 = 0 vs. | ||
| Ha: median of Task 2 - Task 5 > 0 | ||
| Pr(#positive >= 24) = | ||
| Binomial(n = 66, x >= 24, p = 0.5) = 0.9907 | ||
| Ho: median of Task 2 - Task 5 = 0 vs. | ||
| Ha: median of Task 2 - Task 5 < 0 | ||
| Pr(#negative >= 42) = | ||
| Binomial(n = 66, x >= 42, p = 0.5) = 0.0178 | ||
| Two-sided test: | ||
| Ho: median of Task 2 - Task 5 = 0 vs. | ||
| Ha: median of Task 2 - Task 5 = 0 | ||
| Pr(#positive >= 42 or #negative >= 42) = | ||
| min(1, 2*Binomial(n = 66, x >= 42, p = 0.5)) = 0.0356 | ||
| signtest Task 3 = Task 4 | ||
| Sign test | ||
| sign | observed | expected |
| Positive | 28 | 30 |
| Negative | 32 | 30 |
| Zero | 28 | 28 |
| All | 88 | 88 |
| One-sided tests: | ||
| Ho: median of Task 3 - Task 4 = 0 vs. | ||
| Ha: median of Task 3 - Task 4 > 0 | ||
| Pr(#positive >= 28) = | ||
| Binomial(n = 60, x >= 28, p = 0.5) = 0.7405 | ||
| Ho: median of Task 3 - Task 4 = 0 vs. | ||
| Ha: median of Task 3 - Task 4 < 0 | ||
| Pr(#negative >= 32) = | ||
| Binomial(n = 60, x >= 32, p = 0.5) = 0.3494 | ||
| Two-sided test: | ||
| Ho: median of Task 3 - Task 4 = 0 vs. | ||
| Ha: median of Task 3 - Task 4 = 0 | ||
| Pr(#positive >= 32 or #negative >= 32) = | ||
| min(1, 2*Binomial(n = 60, x >= 32, p = 0.5)) = 0.6989 | ||
| signtest DUF_Task_Mean = IUF_Task_Mean | ||
| Sign test | ||
| sign | observed | Expected |
| Positive | 28 | 38.5 |
| Negative | 49 | 38.5 |
| Zero | 11 | 11 |
| All | 88 | 88 |
| One-sided tests: | ||
| Ho: median of DUF_Task_Mean - IUF_Task_Mean = 0 vs. | ||
| Ha: median of DUF_Task_Mean - IUF_Task_Mean > 0 | ||
| Pr(#positive >= 28) = | ||
| Binomial(n = 77, x >= 28, p = 0.5) = 0.9942 | ||
| Ho: median of DUF_Task_Mean - IUF_Task_Mean = 0 vs. | ||
| Ha: median of DUF_Task_Mean - IUF_Task_Mean < 0 | ||
| Pr(#negative >= 49) = | ||
| Binomial(n = 77, x >= 49, p = 0.5) = 0.0110 | ||
| Two-sided test: | ||
| Ho: median of DUF_Task_Mean - IUF_Task_Mean = 0 vs. | ||
| Ha: median of DUF_Task_Mean - IUF_Task_Mean = 0 | ||
| Pr(#positive >= 49 or #negative >= 49) = | ||
| min(1, 2*Binomial(n = 77, x >= 49, p = 0.5)) = 0.022 | ||
| ttest CRRAT1 = CRRAT6 | ||||||
| Paired t test | ||||||
| Variable | Obs | Mean | Std. Err. | Std. Dec. | [95% Conf. Interval] | |
| CRRAT1 | 88 | 0.5765341 | 0.0467863 | 0.4388945 | 0.4835412 | 0.6695269 |
| CRRAT6 | 88 | 0.7160227 | 0.0526972 | 0.494344 | 0.6112812 | 0.8207642 |
| diff | 88 | −0.1394886 | 0.0630229 | 0.5912076 | −0.2647536 | −0.0142237 |
| mean(diff) = mean(CRRAT1—CRRAT6) | t = −2.2133 | |||||
| Ho: mean(diff) = 0 | Degree of freedom = 87 | |||||
| Ha: mean(diff) < 0 | Ha: mean(diff) = 0 | Ha: mean(diff) > 0 | ||||
| Pr(T < t) = 0.0147 | Pr(|T| >|t|) = 0.0295 | Pr(T > t) = 0.9853 | ||||
| ttest CRRAT2 = CRRAT5 | ||||||
| Paired t test | ||||||
| Variable | Obs | Mean | Std. Err. | Std. Dec. | [95% Conf. Interval] | |
| CRRAT1 | 88 | 0.4475 | 0.0450296 | 0.4224151 | 0.3579988 | 0.5370012 |
| CRRAT6 | 88 | 0.6297159 | 0.639904 | 0.6002836 | 0.502528 | 0.7569039 |
| diff | 88 | −0.1822159 | 0.0591543 | 0.5549168 | −0.2997915 | −0.0646403 |
| mean(diff) = mean(CRRAT2—CRRAT5) | t = −3.0803 | |||||
| Ho: mean(diff) = 0 | Degree of freedom = 87 | |||||
| Ha: mean(diff) < 0 | Ha: mean(diff) = 0 | Ha: mean(diff) > 0 | ||||
| Pr(T < t) = 0.0014 | Pr(|T| >|t|) = 0.0028 | Pr(T > t) = 0.9886 | ||||
| ttest CRRAT3 = CRRAT4 | ||||||
| Paired t test | ||||||
| Variable | Obs | Mean | Std. Err. | Std. Dec. | [95% Conf. Interval] | |
| CRRAT1 | 88 | 0.7665909 | 0.0584238 | 0.5480637 | 0.6504673 | 0.8827145 |
| CRRAT6 | 88 | 0.7779545 | 0.0672888 | 0.6312252 | 0.6442107 | 0.9116984 |
| diff | 88 | −0.0113636 | 0.0647565 | 0.6074701 | −0.1400743 | 0.117347 |
| mean(diff) = mean(CRRAT3—CRRAT4) | t = −0.1755 | |||||
| Ho: mean(diff) = 0 | Degree of freedom = 87 | |||||
| Ha: mean(diff) < 0 | Ha: mean(diff) = 0 | Ha: mean(diff) > 0 | ||||
| Pr(T < t) = 0.4306 | Pr(|T| >|t|) = 0.8611 | Pr(T > t) = 0.5694 | ||||
| ttest DUF_CRRA_Mean = IUF_CRRA_Mean | ||||||
| Paired t test | ||||||
| Variable | Obs | Mean | Std. Err. | Std. Dec. | [95% Conf. Interval] | |
| CRRAT1 | 88 | 0.596875 | 0.0406308 | 0.3811508 | 0.5161169 | 0.6776331 |
| CRRAT6 | 88 | 0.7078977 | 0.0481272 | 0.4514727 | 0.6122398 | 0.8035557 |
| diff | 88 | −0.1110227 | 0.0462402 | 0.4337715 | −0.2997915 | −0.0191153 |
| mean(diff) = mean(DUF_CRRA_Mean—IUF_CRRA_Mean) | t = −2.4010 | |||||
| Ho: mean(diff) = 0 | Degree of freedom = 87 | |||||
| Ha: mean(diff) < 0 | Ha: mean(diff) = 0 | Ha: mean(diff) > 0 | ||||
| Pr(T < t) = 0.0092 | Pr(|T| >|t|) = 0.0185 | Pr(T > t) = 0.9908 | ||||
| sum CETask2 CETask5 | |||||
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| CETask2 | 88 | 8.899204 | 1.895516 | 4.5 | 14.43 |
| CETask5 | 88 | 7.95375 | 2.735412 | 4 | 14.43 |
| sum RPTask2 RPTask5 | |||||
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| RPTask2 | 88 | 2.100796 | 1.895516 | −3.43 | 6.5 |
| RPTask5 | 88 | 3.04625 | 2.735412 | −3.43 | 7 |
| sum RPbyEVTask2 RPbyEVTask5 | |||||
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| RPbyEVTask2 | 88 | 19.09814 | 17.23196 | −31.18182 | 59.09091 |
| RPbyEVTask5 | 88 | 27.69318 | 24.86738 | −31.18182 | 63.63636 |
| signrank RPTask2 = RPTask5 | ||||||
| Wilcoxon signed-rank test | ||||||
| sign | obs | sum ranks | expected | |||
| positive | 24 | 1070.5 | 1831.5 | |||
| negative | 42 | 2592.5 | 1831.5 | |||
| zero | 22 | 253 | 253 | |||
| all | 88 | 3916 | 3916 | |||
| unadjusted variance: 57,761.00 | ||||||
| adjustment for ties: −77.00 | ||||||
| adjustment for zeros: −948.75 | ||||||
| adjusted variance: 56,735.25 | ||||||
| Ho: RPTask2 = RPTask5 | ||||||
| z = −3.195 | ||||||
| Prob > z = 0.0014 | ||||||
| signtest RPTask2 = RPTask5 | ||||||
| Sign test | ||||||
| sign | observed | expected | ||||
| Positive | 24 | 33 | ||||
| Negative | 42 | 33 | ||||
| Zero | 22 | 22 | ||||
| All | 88 | 88 | ||||
| One-sided tests: | ||||||
| Ho: median of RPTask 2 - RPTask5 = 0 vs. | ||||||
| Ha: median of RPTask 2 - RPTask5 > 0 | ||||||
| Pr(#positive >= 24) = | ||||||
| Binomial(n = 66, x >= 24, p = 0.5) = 0.9907 | ||||||
| Ho: median of RPTask2 - RPTask5 = 0 vs. | ||||||
| Ha: median of RPTask2 - RPTask5 < 0 | ||||||
| Pr(#negative >= 42) = | ||||||
| Binomial(n = 66, x >= 42, p = 0.5) = 0.0178 | ||||||
| Two-sided test: | ||||||
| Ho: median of RPTask2 - RPTask5 = 0 vs. | ||||||
| Ha: median of RPTask2 - RPTask5 = 0 | ||||||
| Pr(#positive >= 42 or #negative >= 42) = | ||||||
| min(1, 2*Binomial(n = 66, x >= 42, p = 0.5)) = 0.0356 | ||||||
| ttest RPTask2 = RPTask5 | ||||||
| Paired t test | ||||||
| Variable | Obs | Mean | Std. Err. | Std. Dec. | [95% Conf. Interval] | |
| CRRAT1 | 88 | 2.100796 | 0.2020626 | 1.895516 | 1.699174 | 2.502417 |
| CRRAT6 | 88 | 3.04625 | 0.2915958 | 2.735412 | 2.466672 | 3.625828 |
| diff | 88 | −0.9454544 | 0.2735494 | 2.56612 | −1.489163 | −0.4017455 |
| mean(diff) = mean(RPTask2—RPTask5) | t = −3.4562 | |||||
| Ho: mean(diff) = 0 | Degree of freedom = 87 | |||||
| Ha: mean(diff) < 0 | Ha: mean(diff) = 0 | Ha: mean(diff) > 0 | ||||
| Pr(T < t) = 0.0004 | Pr(|T| >|t|) = 0.0008 | Pr(T > t) = 0.9996 | ||||
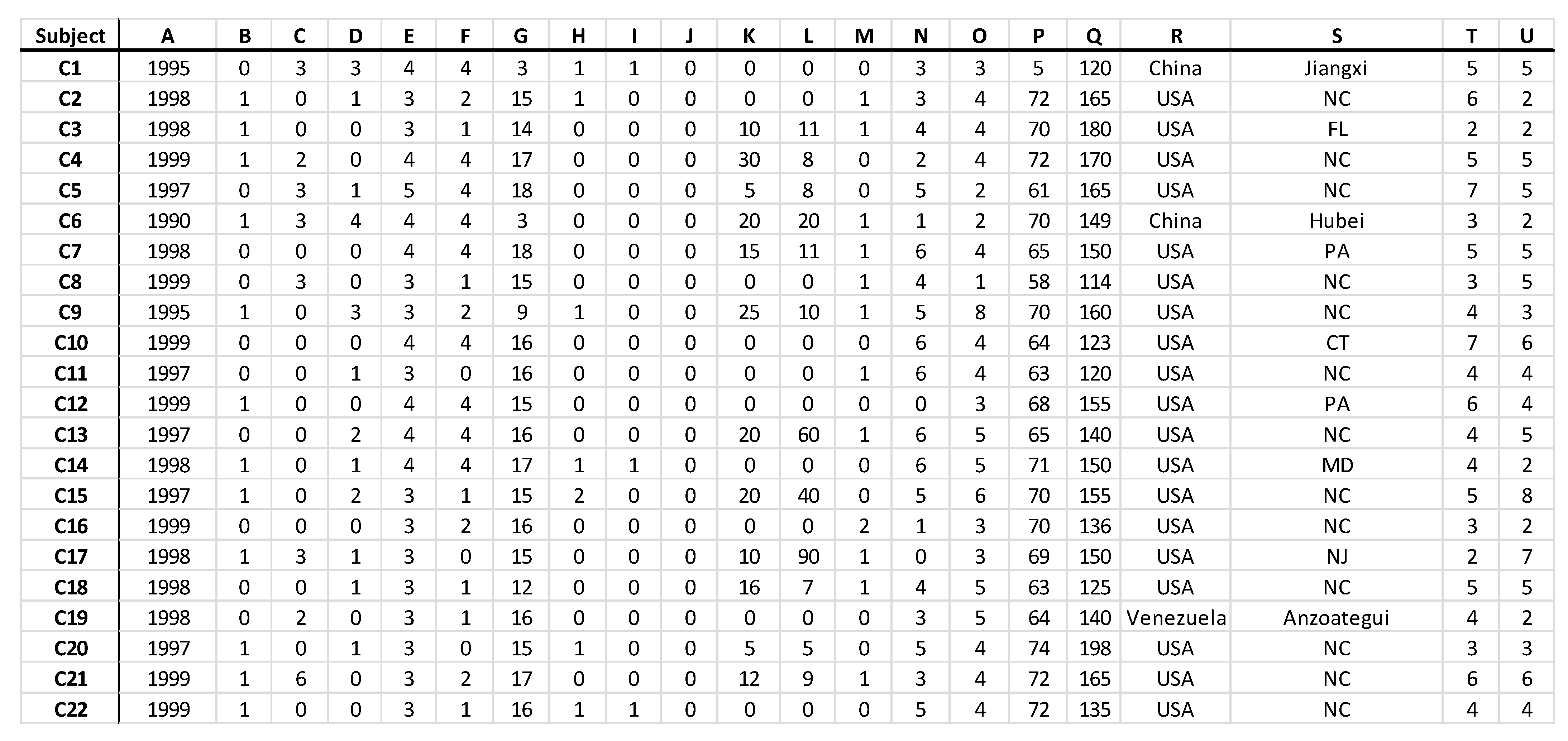
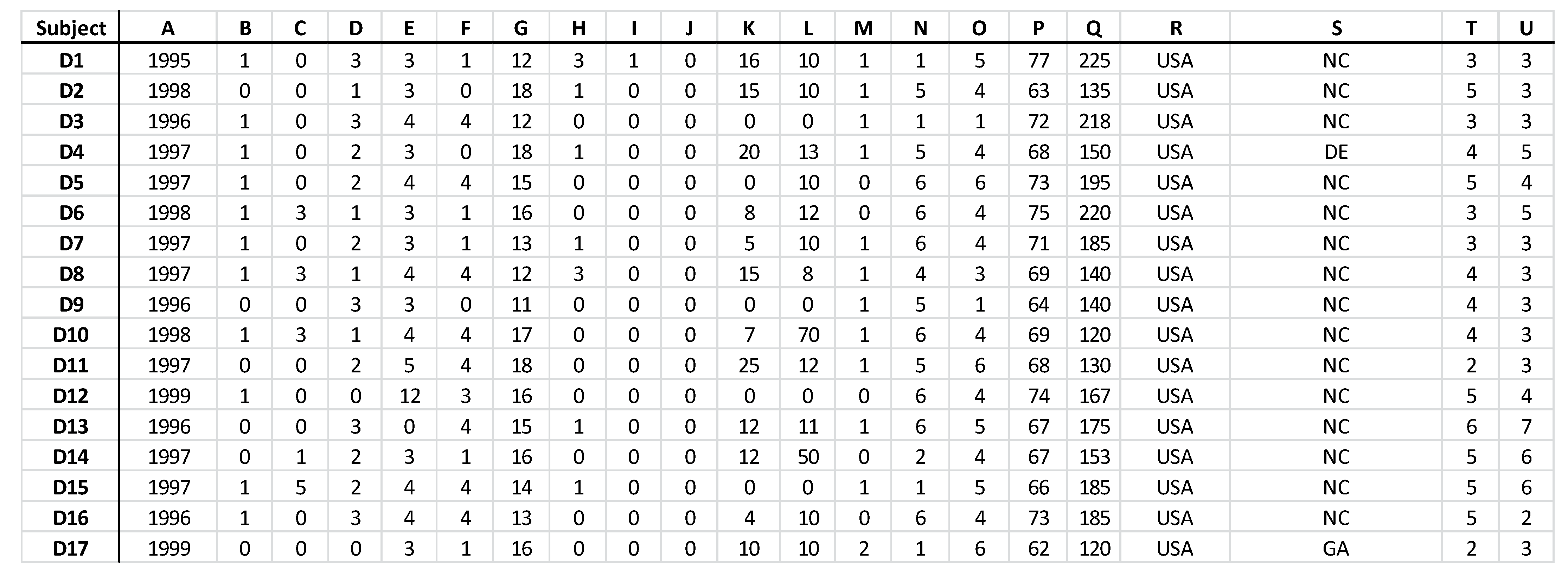
Appendix F. Data Set (Only for Review Purposes)
| Number of Safe Choices (For HL and CVU Designs) | Selected Decision Number (For Bins. Design) | Range of the Implied Coefficients of RRA for the CRRA Utility Function | Risk Attitude Classifications |
|---|---|---|---|
| 0–1 | 1 | r < –0.95 | Highly risk-loving |
| 2 | 2 | –0.95 < r < –0.49 | Very risk-loving |
| 3 | 3 | –0.49 < r < –0.15 | Risk-loving |
| 4 | 4 | –0.15 < r < 0.15 | Risk-neutral |
| 5 | 5 | 0.15 < r < 0.41 | Slightly risk-averse |
| 6 | 6 | 0.41 < r < 0.68 | Risk-averse |
| 7 | 7 | 0.68 < r < 0.97 | Very risk-averse |
| 8 | 8 | 0.97 < r < 1.37 | Highly risk-averse |
| 9–10 | 9 or 10 | r > 1.37 | Stay in bed (extremely risk-averse) |
| Number of Safe Choices (For HL and CVU Designs) | Selected Decision Number (For Bins. Design) | Range of the Implied Coefficients of RRA for the CRRA Utility Function | Risk Attitude Classifications |
|---|---|---|---|
| 0–1 | 1 | r < −0.95 | Highly risk-loving |
| 2 | 2 | −0.95 < r < −0.49 | Very risk-loving |
| 3 | 3 | −0.49 < r < −0.15 | Risk-loving |
| 4 | 4 | −0.15 < r < 0.15 | Risk-neutral |
| 5 | 5 | 0.15 < r < 0.41 | Slightly risk-averse |
| 6 | 6 | 0.41 < r < 0.68 | Risk-averse |
| 7 | 7 | 0.68 < r < 0.97 | Very risk-averse |
| 8 | 8 | 0.97 < r < 1.37 | Highly risk-averse |
| 9–10 | 9 or 10 | r > 1.37 | Stay in bed (extremely risk-averse) |

| Number of Safe Choices (For HL and CVU Designs) | Selected Decision Number (For Bins. Design) | Range of the Implied Coefficients of RRA for the CRRA Utility Function | Risk Attitude Classifications |
|---|---|---|---|
| 0–1 | 1 | r < −0.95 | Highly risk-loving |
| 2 | 2 | −0.95 < r < −0.49 | Very risk-loving |
| 3 | 3 | −0.49 < r < −0.15 | Risk-loving |
| 4 | 4 | −0.15 < r < 0.15 | Risk-neutral |
| 5 | 5 | 0.15 < r < 0.41 | Slightly risk-averse |
| 6 | 6 | 0.41 < r < 0.68 | Risk-averse |
| 7 | 7 | 0.68 < r < 0.97 | Very risk-averse |
| 8 | 8 | 0.97 < r < 1.37 | Highly risk-averse |
| 9–10 | 9 or 10 | r > 1.37 | Stay in bed (extremely risk-averse) |

| Number of Safe Choices (For HL and CVU Designs) | Selected Decision Number (For Bins. Design) | Range of the Implied Coefficients of RRA for the CRRA Utility Function | Risk Attitude Classifications |
|---|---|---|---|
| 0–1 | 1 | r < −0.95 | Highly risk-loving |
| 2 | 2 | −0.95 < r < −0.49 | Very risk-loving |
| 3 | 3 | −0.49 < r < −0.15 | Risk-loving |
| 4 | 4 | −0.15 < r < 0.15 | Risk-neutral |
| 5 | 5 | 0.15 < r < 0.41 | Slightly risk-averse |
| 6 | 6 | 0.41 < r < 0.68 | Risk-averse |
| 7 | 7 | 0.68 < r < 0.97 | Very risk-averse |
| 8 | 8 | 0.97 < r < 1.37 | Highly risk-averse |
| 9–10 | 9 or 10 | r > 1.37 | Stay in bed (extremely risk-averse) |
Appendix G. Data Set (Only for Review Purposes)
- In what year were you born?
- What is your gender? 0 = Female and 1= Male.
- What is your racial or ethnic background? 0 = White or Caucasian, 1 = Black or African American, 2 = Hispanic, 3 = Asian, 4 = Native American, 5 = Multiracial, and 6 = Other.
- What year in school are you? 0 = Freshman, 1 = Sophomore, 2 = Junior, 3 = Senior, 4 = Grad Student, and 5 = Not Listed.
- What is your college? 0 = Agriculture and Life Sciences, 1 = Design, 2 = Education, 3 = Poole College of Management, 4 = Engineering, 5 = Humanities and Social Sciences, 6 = Natural Resources, 8 = Textiles, 9 = College of Veterinary Medicine, 10 = Sciences, 11 = The Graduate School, and 12 = Others.
- What is your major? 0 = Economics, 1 = Business/Management, 2 = Accounting, 3 = Exploratory Studies, and 4 = Others.
- How many credit hours are you enrolled in this semester?
- Not including today, how many previous economics experiments have you participated in? 0, 1, 2, 3, 4, 5, or more(=5).
- Not including today, how many previous economics experiments have you participated in where you made repeated choices between lotteries? 0, 1, 2, 3, 4, 5 or more (=5).
- What is your marital status? 0 = Single and 1 = Married.
- How many hours do you work in a typical week?
- How many dollars per hour do you earn in a typical week?
- Are your financially dependent on your parents? If so, to what extent? 0 = Yes, Fully; 1 = Yes, Partially; and 2 = No, I am independent.
- Please indicate the category that best describes your parents’ income from all sources before all taxes in 2016. 1 = $15,000 and under, 2 = $15,001-30,000, 3 = $30,001-45,000, 4 = $45,001-60,000, 5 = $60,001-75,000, 6 = $75,001-100,000, and 7 = over $100,001.
- How many people are in your household? (Yourself and those who live with you and share your income and expenses)
- What is your weight (in inches)?
- What is your height (in pounds)?
- Please state the country where you were raised.
- Please state the state where you were raised.
- In general, when it comes to making your economic decisions, which of the following items best describes your risk attitude? 1 = Highly risk-loving, 2 = Very risk-loving, 3 = Risk-loving, 4 = Risk neutral, 5 = Slightly risk-averse, 6 = Risk-averse, 7 = Very risk-averse, 8 = Highly risk-averse, 9 = Stay in bed (Extremely risk-averse).
- In today’s experiment, when making your choices over the lotteries, which of the following items you believe best describes your risk attitude? 1 = Highly risk-loving, 2 = Very risk-loving, 3 = Risk-loving, 4 = Risk-neutral, 5 = Slightly risk-averse, 6 = Risk-averse, 7 = Very risk-averse, 8 = Highly risk-averse, 9 = Stay in bed (Extremely risk-averse).
Appendix H

Appendix I. Experiment Instructions
References
- Zeytoon Nejad Moosavian, S.A.; Hammond, R.; Goodwin, B.K. Risk aversion over price variability: Experimental evidence. Appl. Econ. Lett. 2020, 27, 1739–1745. [Google Scholar] [CrossRef]
- Zeytoon-Nejad, A. Price Risk Aversion vs. Payoff Risk Aversion: A Gender Comparison through a Laboratory Experiment; School of Business, Wake Forest University: Winston-Salem, NC, USA, 2022; unpublished work. [Google Scholar]
- Holt, C.A.; Laury, S. Risk aversion and incentive effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Binswanger, H.P. Attitudes toward risk: Experimental measurement in rural India. Am. J. Agric. Econ. 1980, 62, 395–407. [Google Scholar] [CrossRef]
- Zhou, W.; Hey, J. Context matters. Exp. Econ. 2018, 21, 723–756. [Google Scholar] [CrossRef] [PubMed]
- Heinemann, F. Measuring risk aversion and the wealth effect. In Risk Aversion in Experiments; Emerald Group Publishing Limited: Bingley, UK, 2008; pp. 293–313. [Google Scholar]
- Arrow, K.J. Aspects of a Theory of Risk Bearing; Yrjo Jahnsson Lectures: Helsinki, Finland, 1965; reprinted in Essays in the Theory of Risk Bearing; 1971. [Google Scholar]
- Pratt, J.W. Risk aversion in the small and in the large. Econom. J. Econom. Soc. 1964, 32, 122–136. [Google Scholar] [CrossRef]
- Cornes, R. Duality and Modern Economics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Moosavian, S.A.Z.N. The Visual Decoding of the “Wheel of Duality” in Consumer Theory in Modern Microeconomics: An Instructional Tool Usable in Advanced Microeconomics to Turn “Pain” into “Joy”. Appl. Econ. Financ. 2016, 3, 288–304. [Google Scholar] [CrossRef]
- Moosavian, S.A.Z.N.; Hammond, R.; Goodwin, B. Measuring risk aversion using indirect utility functions: A laboratory experiment, a poster presented at the AAEA poster session at the 2018 Agricultural and Applied Economics Association (AAEA) conference. In Proceedings of the AAEA Meeting, Washington, DC, USA, 5–7 August 2018. [Google Scholar]
- Naumenko, A.; Moosavian, S.A.Z.N. Clarifying theoretical intricacies through the use of conceptual visualization: Case of production theory in advanced microeconomics. Appl. Econ. Financ. 2016, 3, 103–122. [Google Scholar] [CrossRef][Green Version]
- Chambers, R.G. Applied Production Analysis; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zeytoon, N.M.S.A. A comprehensive visual “wheel of duality” in consumer theory, Research Note. Int. Adv. Econ. Res. 2016, 22, 357–358. [Google Scholar] [CrossRef]
- Loomes, G.; Pogrebna, G. Measuring individual risk attitudes when preferences are imprecise. Econ. J. 2014, 124, 569–593. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Arbuthnott, J. An argument for divine providence, taken from the constant regularity observed in the births of both sexes. Philos. Trans. R. Soc. Lond. 1710, 27, 186–190. [Google Scholar]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Digital Press: Ames, IA, USA, 1989. [Google Scholar]
- Kahneman, D.; Tversky, A. On the interpretation of intuitive probability: A reply to Jonathan Cohen. Cognition 1979, 7, 409–411. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Loss aversion in riskless choice: A reference-dependent model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]
- Levin, I.P.; Schneider, S.L.; Gaeth, G.J. All frames are not created equal: A typology and critical analysis of framing effects. Organ. Behav. Hum. Decis. Processes 1998, 76, 149–188. [Google Scholar] [CrossRef] [PubMed]
- Levin, I.P.; Snyder, M.A.; Chapman, D.P. The interaction of experiential and situational factors and gender in a simulated risky decision-making task. J. Psychol. 1988, 122, 173–181. [Google Scholar] [CrossRef]
- Tom, S.M.; Fox, C.R.; Trepel, C.; Poldrack, R.A. The neural basis of loss aversion in decision-making under risk. Science 2007, 315, 515–518. [Google Scholar] [CrossRef] [PubMed]
- De Martino, B.; Camerer, C.F.; Adolphs, R. Amygdala damage eliminates monetary loss aversion. Proc. Natl. Acad. Sci. USA 2010, 107, 3788–3792. [Google Scholar] [CrossRef]
- Canessa, N.; Crespi, C.; Motterlini, M.; Baud-Bovy, G.; Chierchia, G.; Pantaleo, G.; Tettamanti, M.; Cappa, S.F. The functional and structural neural basis of individual differences in loss aversion. J. Neurosci. 2013, 33, 14307–14317. [Google Scholar] [CrossRef]
- Shields, D.A. Federal Crop Insurance: Background; Congressional Research Service: Washington, DC, USA, 2015; pp. 7–5700.
- Good, K. USDA-RMA Report: Analysis of the Federal Crop Insurance Portfolio. Farm Policy News. 24 September 2017. Available online: https://farmpolicynews.illinois.edu/2017/09/usda-rma-report-analysis-federal-crop-insurance-portfolio/ (accessed on 10 July 2019).
- Kachelmeier, S.J.; Shehata, M. Examining risk preferences under high monetary incentives: Experimental evidence from the People’s Republic of China. Am. Econ. Rev. 1992, 82, 1120–1141. [Google Scholar]


| Number of Safe Choices (For the HL and CvU Designs) | Selected Decision Number (For the Bins. Design) | Range of the Implied Coefficients of RRA for the CRRA Utility Function | Risk Attitude Classifications |
|---|---|---|---|
| 0–1 | 1 | r < −0.95 | Highly risk-loving |
| 2 | 2 | −0.95 < r < −0.49 | Very risk-loving |
| 3 | 3 | −0.49 < r < −0.15 | Risk-loving |
| 4 | 4 | −0.15 < r < 0.15 | Risk-neutral |
| 5 | 5 | 0.15 < r < 0.41 | Slightly risk-averse |
| 6 | 6 | 0.41 < r < 0.68 | Risk-averse |
| 7 | 7 | 0.68 < r < 0.97 | Very risk-averse |
| 8 | 8 | 0.97 < r < 1.37 | Highly risk-averse |
| 9–10 | 9 or 10 | r > 1.37 | Stay in bed (extremely risk-averse) |
| Test | Test Explanation | Test Hypothesis | Task 1 = Task 6 (PaRA = PrRA) | Task 2 = Task 5 (PaRA = PrRA) | Task 3 = Task 4 (PaRA = PrRA) | PaRA = PrRA (Average of Pa and Pr Tasks) | Overall Conclusion |
|---|---|---|---|---|---|---|---|
| The Wilcoxon matched-pairs signed-rank test | It tests the equality of matched pairs of observations (non-parametric). | H0: Both distributions are the same. | Reject H0 at 5% Prob > |z| = 0.0303 H1: PaRA ≠ PrRA Confirm H1 | Reject H0 at 5% Prob > |z| = 0.0034 H1: PaRA ≠ PrRA Confirm H1 | Fail to reject H0 Prob > |z| = 0.5619 H1: PaRA≠PrRA Cannot Confirm H1 | Reject H0 at 5% Prob > |z| = 0.0204 H1: PaRA ≠ PrRA Confirm H1 | Most of the designs, as well as their average, confirm that PaRA ≠ PrRA. |
| The Arbuthnott–Snedecor–Cochran sign test | It tests the equality of matched pairs of observations (non-parametric). | H0: The median of the differences is zero (the true proportion of positive (negative) signs is one-half.) | Reject H0 at 5% Prob(.) = 0.0407 H1: PaRA < PrRA Confirm H1 | Reject H0 at 5% Prob(.) = 0.0178 H1: PaRA < PrRA Confirm H1 | Fail to Reject H0 Prob(.) = 0.3494 H1: PaRA < PrRA Cannot Confirm H1 | Reject H0 at 5% Prob(.) = 0.0110 H1: PaRA < PrRA Confirm H1 | Most of the designs, as well as their average, confirm that PaRA < PrRA. |
| Two-sample t test for paired data (using mid-point CRRA’s) | It tests if two variables have the same mean, assuming paired data (parametric). | H0: The mean of the difference is zero. | Reject H0 at 5% Prob(T < t) = 0.0147 H1: PaRA < PrRA Confirm H1 | Reject H0 at 5% Prob(T < t) = 0.0014 H1: PaRA < PrRA Confirm H1 | Fail to Reject H0 Prob(T < t) = 0.4306 H1: PaRA < PrRA Cannot Confirm H1 | Reject H0 at 5% Prob(T < t) = 0.0092 H1: PaRA < PrRA Confirm H1 | It shows that most of the designs, as well as their average, confirm that PaRA < PrRA. |
| Test | Test Explanation | Test Hypothesis | RPTask 2 = RPTask 5 (PaRP = PrRP) | Overall Conclusion |
|---|---|---|---|---|
| The Wilcoxon matched-pairs signed-rank test | It tests the equality of matched pairs of observations (non-parametric). | H0: Both distributions are the same. | Reject H0 Prob > |z| = 0.0014 H1: PaRP ≠ PrRP Confirm H1 | It shows that PaRP ≠ PrRP. |
| The Arbuthnott–Snedecor–Cochran sign test | It tests the equality of matched pairs of observations (non-parametric). | H0: The median of the differences is zero (the true proportion of positive (negative) signs is one-half). | Reject H0 Prob(.) = 0.0178 H1: PaRP < PrRP Confirm H1 | It shows that PaRP < PrRP. |
| The two-sample t test for paired data | It tests if two variables have the same mean, assuming paired data (parametric). | H0: The mean of the difference is zero. | Reject H0 Prob(T < t) = 0.0004 H1: PaRP < PrRP Confirm H1 | It shows that PaRP < PrRP. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeytoon-Nejad, A. Measuring Price Risk Aversion through Indirect Utility Functions: A Laboratory Experiment. Games 2022, 13, 56. https://doi.org/10.3390/g13040056
Zeytoon-Nejad A. Measuring Price Risk Aversion through Indirect Utility Functions: A Laboratory Experiment. Games. 2022; 13(4):56. https://doi.org/10.3390/g13040056
Chicago/Turabian StyleZeytoon-Nejad, Ali. 2022. "Measuring Price Risk Aversion through Indirect Utility Functions: A Laboratory Experiment" Games 13, no. 4: 56. https://doi.org/10.3390/g13040056
APA StyleZeytoon-Nejad, A. (2022). Measuring Price Risk Aversion through Indirect Utility Functions: A Laboratory Experiment. Games, 13(4), 56. https://doi.org/10.3390/g13040056





