A Game-Theoretic Model of Voluntary Yellow Fever Vaccination to Prevent Urban Outbreaks

Abstract

Yellow fever is a vector-borne acute viral hemorrhagic disease. It is endemic in tropical areas of Africa and Latin America but demonstrated the potential for international spread during the 2016 outbreak in Luanda, Angola. Yellow fever can be prevented by vaccination, vector control, and avoiding mosquito bites. To account for human behavior in disease dynamics, we add a game-theoretic component to a recent compartmental model of yellow fever transmission. The self-interested individuals evaluate the risks of contracting yellow fever and choose to vaccinate or avoid the bites to minimize the overall costs. We find the Nash equilibria, the optimal levels of vaccination and bite protections if the individuals can decide on the use of only one of the prevention methods as well as when they can decide on the use of both of them. In the later case, we show that vaccination is the preferred method of protection from the individual standpoint and, in the Nash equilibrium, individuals use vaccination only. Our model predicts the vaccination coverage in Angola to be around 65%, which is in reasonable agreement with the empirical value of 68%. We also study whether voluntary prevention can lead to the elimination of the disease in endemic areas. We show that voluntary vaccination alone is not enough to mitigate the risks of outbreaks, suggesting that a mandatory vaccination policy is necessary.

1. Introduction

Yellow fever is a life-threatening acute viral hemorrhagic disease that is endemic in tropical areas of Africa and Latin America and difficult to distinguish from dengue and other hemorrhagic fevers [1]. It is transmitted by the bites of infected female mosquitoes Aedes aegypti [2].

Symptoms, including fever, muscle pain, headache, and nausea or vomiting, usually appear 3 to 6 days after the bite. For most patients, the symptoms disappear after 3 to 4 days. However, 15% of patients enter a second, more toxic phase affecting several body systems, including the kidneys [1]. There is no specific drug to treat yellow fever [3] but good and early supportive treatments for dehydration, liver and kidney failure, and fever improve survival rates [4].

Yellow fever can be prevented by vaccination, vector control, and by avoiding mosquito bites [4]. Vaccination is the most important preventive measure against yellow fever. The single dose vaccine is affordable (costs about $2), 99% effective (within 30 days), and offers life-long protection [1,5].

Climate changes and shifting mosquito habitats may be behind the recent rise in yellow fever and other Aedes-borne infections [6,7,8]. After the 2016 outbreak of yellow fever in Luanda, Angola and a linked outbreak in Kinshasa, Democratic Republic of the Congo [9], the Eliminate Yellow Fever Epidemics (EYE) strategy was developed to respond to the increased threat of urban outbreaks with international spread [10]. The strategy is guided by three strategic objectives: (1) protect at-risk populations, (2) prevent international spread of yellow fever, and (3) contain outbreaks rapidly.

Mathematical modeling is now a standard tool for modeling epidemics and disease elimination efforts [11,12]. There used to be very few mathematical models of yellow fever [13,14] although the 2016 outbreak sparked an increased modeling activity [15,16,17,18,19]. Several modeling studies further estimated the basic reproduction number [20,21,22].

The previous models neglect the impact that human behavior can have on infectious disease dynamics. Ref. [23] introduced vaccination games and incorporated voluntary disease prevention into standard epidemics modeling. These new types of models study complex scenarios in which self-interested individuals take actions based on the decisions of the rest of the population. As argued in [24], by incorporating human behavior, mathematical models provide more insight and better predictions. Thus, it is not surprising that the vaccination game theory is now a vibrant and growing field [25]. The game-theoretical models are now predictive tools in populations for extracting an optimal decision-making strategy [26]. They have been applied to study the prevention and elimination of many different diseases, including Ebola [27], COVID-19 [28,29,30], monkeypox [31], chikungunya [32], Hepatitis B [33] or cholera [34].

In this paper, we adapt the mathematical model from [18] that was developed and calibrated based on the 2016 outbreak in Angola. We incorporate voluntary vaccination and mosquito bite prevention as two strategies that individuals can take to reduce their risk of contracting the disease. We show that due to the relatively low vaccination cost, vaccination is the preferred protection strategy. Moreover, the current vaccination coverage in Angola is in agreement with our theoretical predictions. Thus, the model suggests that a mandatory vaccination policy is needed to mitigate the threat of yellow fever outbreaks.

2. Mathematical Model

In this section, we build a mathematical model for voluntary protection against yellow fever. We first introduce a compartmental ODE model of yellow fever transmission. Then, we add the game-theoretic component that allows us to investigate individuals’ optimal decisions regarding vaccination and bite protection. Finally, to make quantitative predictions, we describe how we picked the values for the model parameters.

2.1. Compartmental Model

We adapt the model from [18]. We distinguish the human population (subscript H) and mosquito/vector population (subscript V).

The human population is subdivided into susceptible ($S_H$), exposed ($E_H$), symptomatic infectious ($I_H$), asymptomatic infectious ($A_H$), toxic fever ($T_H$) and recovered ($R_H$). The vector population is divided into susceptible ($S_V$), exposed ($E_V$) and infectious ($I_V$).

The human individuals are born at rate ${\Lambda }_H$. A fraction $\overline{p}$ of the individuals is vaccinated, becomes permanently protected against yellow fever (YF) and enters the compartment $R_H$. The remaining fraction, $(1-\overline{p})$, remains susceptible and enters a compartment $S_H$. The susceptible individuals become exposed after a bite by an infectious mosquito. The per capita rate is given by $(1-\overline{e})ab\frac{I_V}{N_H}$, where $\overline{e}\in [0,1]$ is the level of bite protection in the population, a is the mosquito biting rate (without any protection), b is the probability of a transmission of yellow fever virus (YFV) from a mosquito to a human, and $\frac{I_V}{N_H}$ is the number of infected mosquitoes per human. The most common interpretation of $\overline{e}$ is the level of repellent usage, but one can also consider other measures, such as avoiding being outside when mosquitoes are active or avoiding traveling to parts of the town where YF is more prevalent. After an incubation period ${\sigma }_H^{-1}$, the exposed individuals move either to a symptomatic stage $I_H$ with a probability $\delta$ or to the asymptomatic stage, $A_H$, with probability $1-\delta$. Either one of those stages lasts for a period ${\gamma }_H^{-1}$. The asymptomatic individuals fully recover and become permanently immune to YFV and enter $R_H$. The symptomatic individuals enter a toxic stage $T_H$ that lasts for a period ${\kappa }_H^{-1}$. For simplicity, we assume that all cases fully recover and enter $R_H$. All individuals can die at the natural mortality rate ${\mu }_H$.

The vectors are born at rate ${\Lambda }_V$ as susceptible. They become exposed after they bite a symptomatic or asymptomatic individual. The force of infection is given as $(1-\overline{e})ac\frac{I_H+\psi A_H}{N_H}$, where c is the probability of a transmission of YFV from symptomatic cases, and $\psi c$ is the transmission probability from asymptomatic cases. The incubation period is ${\sigma }^{-1}$ after which mosquitoes become infectious. All vectors die at the natural mortality rate ${\mu }_V$.

We also assume that there are m mosquitoes per human, i.e., the total number of mosquitoes, $N_V$, is given by $\frac{\Lambda }{{\mu }_V}=m{N}_H$.

The schematic diagram of the model is shown in Figure 1 and the model parameters are summarized in

Table 1. Model parameters. The per capita rates are per day. The times are in days.

Symbol	Description	Value	Source
${\Lambda }_H$	Human birth rate (per 1000)	$0.04/365$	[35]
${\mu }_H$	Human natural death rate	${(61\ast 365)}^{-1}$	[36]
a	Mosquito biting rate	$0.5$	[37]
b	Transmission probability from vector to host (per bite)	$0.4$	[37]
c	Transmission probability from host to vector (per bite)	$0.5$	[38]
${\sigma }_H^{-1}$	Duration of the latent period in host	4	[39]
${\sigma }_V^{-1}$	Duration of the latent period in vector	10	[40]
${\gamma }_H^{-1}$	Duration of the infectious period (host)	4	[41]
${\kappa }_H^{-1}$	Duration of the toxic case	8	[41]
${\mu }_V^{-1}$	Vector life span	20	[37]
$\delta$	Proportion of the severe cases	$0.15$	[1]
$\psi$	Non-severe case relative infectivity	$0.2$	estimated
$\overline{p}$	Proportion of vaccinated individuals	variable in $[0,1]$
$\overline{e}$	Bite prevention strategy	variable in $[0,1]$
$C_V/C_{YF}$	Cost of vaccination relative to the cost of YF	2/30	[5,42]
$C_B/C_{YF}$	Cost of bite prevention	3/30	estimated
${\Lambda }_V$	Vector birth rate	$m\frac{{\Lambda }_H}{{\mu }_H}{\mu }_V$

. The model yields the following differential equations:

$$\begin{array}{cc}\hfill \frac{d{S}_H}{dt}& =(1-\overline{p}){\Lambda }_H-\left({\mu }_H+(1-\overline{e})ab\frac{I_V}{N_H}\right)S_H\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{d{E}_H}{dt}& =(1-\overline{e})ab\frac{I_V}{N_H}{S}_H-({\mu }_H+{\sigma }_H)E_H\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \frac{d{A}_H}{dt}& =(1-\delta ){\sigma }_H{E}_H-({\mu }_H+{\gamma }_H)A_H\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \frac{d{I}_H}{dt}& =\delta {\sigma }_H{E}_H-({\mu }_H+{\gamma }_H)I_H\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{d{R}_H}{dt}& =p{\Lambda }_H+{\gamma }_H{A}_H+{\kappa }_H{T}_H-{\mu }_H{R}_H\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \frac{d{T}_H}{dt}& ={\gamma }_H{I}_H-({\mu }_H+{\kappa }_H)T_H\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{d{S}_V}{dt}& ={\Lambda }_V-\left((1-\overline{e})ac\frac{I_H+\psi A_H}{N_H}+{\mu }_V\right)S_V\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \frac{d{E}_V}{dt}& =(1-\overline{e})ac\frac{I_H+\psi A_H}{N_H}{S}_V-({\mu }_V+{\sigma }_V)E_V\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \frac{d{I}_V}{dt}& ={\sigma }_V{E}_V-{\mu }_V{I}_V.\hfill \end{array}$$

(9)

2.2. Game-Theoretic Component

We add a game-theoretic component to study individual vaccination and bite prevention strategies and introduce the following game inspired by the framework introduced in [23].

The players of the game are susceptible individuals. The individuals can (a) choose to vaccinate against YF or not, and (b) choose to protect themselves against mosquito bites. Their strategy is given by a pair $(p_{ind},e_{ind})$ where $p_{ind}$ specifies if they vaccinate ($p_{ind}=1$) or not ($p_{ind}=0$), and $e_{ind}\in [0,1]$ specifies the bite prevention (with $e_{ind}=0$ being no prevention and $e_{ind}=1$ being a complete prevention). We will also consider cases when individuals can choose only to vaccinate or only to prevent bites.

There is a cost associated with vaccination and bite prevention. We assume the vaccine costs $C_V$ and, for simplicity, the bite prevention costs $C_B{e}_{ind}$. We assume that the cost of contracting YF and proceeding to the symptomatic and toxic stage is $C_{YF}$, while the cost of asymptomatic stage is assumed to be 0.

The solution of the game, called the Nash equilibrium, is the population-level value $(p_{\mathrm{NE}},e_{\mathrm{NE}})$ at which no individual can increase their own benefits by deviating from the population strategy.

The individual’s benefit depends on the individual’s strategy but also on the prevalence of YF in the population, i.e., on the strategies of other players. Following [23], we assume that all individuals are provided with the same information and that they all use the information in the same and rational way to assess costs and risks.

2.3. Model Calibration

Most of the specific model parameter values were taken from [18], and the original sources are shown in Table 1. The birth and death rates in Angola were found in [35,36].

We estimated the relative infectivity of asymptomatic cases as $\psi =0.2$ as opposed to $\psi =0.1$ used in [18]. This value brought the basic reproduction number in line with other models as discussed in the model validation section.

The cost of the vaccine was estimated as $C_V=$$2 [5], while the cost of yellow fever disease was estimated as $C_{YF}=$$30 [42]. We could not find reliable estimates for the cost of bite protection, but since the protection must be ongoing rather than one time, we used $C_B=$$3 to indicate a slightly bigger cost than the cost of the vaccine.

3. Analysis of the ODE System

Because we assume no disease-induced death, the population size remains constant at $N_H=\frac{{\Lambda }_H}{{\mu }_H}$ and $N_V=m{N}_H=\frac{{\Lambda }_V}{{\mu }_V}$. There are two equilibria of the dynamics.

3.1. Disease-Free Equilibrium

The disease-free equilibrium ${\mathcal{E}}^0=(S_H^0,E_H^0,A_H^0,I_H^0,T_H^0,R_H^0,S_V^0,E_V^0,I_V^0)$ is given by $S_H^0=(1-\overline{p})N_H$, $R_H^0=\overline{p}{N}_H$, $S_V^0=N_V$ and $E_H^0=A_H^0=I_H^0=T_H^0=E_V^0=I_V^0=0$. Similarly as in [18], the effective reproduction number is

$$\mathcal{R}={(1-\overline{p})}^{1/2}(1-\overline{e}){\mathcal{R}}_0,$$

(10)

where

$${\mathcal{R}}_0=\sqrt{\left(\psi (1-\delta )+\delta \right)a^{2}bcm\left(\frac{{\sigma }_V}{{\sigma }_V+{\mu }_V}\right)\left(\frac{{\sigma }_H}{{\sigma }_H+{\mu }_H}\right)\left(\frac{1}{{\gamma }_H+{\mu }_H}\right)\left(\frac{1}{{\mu }_V}\right)}$$

(11)

is the basic reproduction number in the population without vaccination ($\overline{p}=0$) and without any bite prevention ($\overline{e}=0$).

The disease-free equilibrium is locally asymptotically stable if $\mathcal{R}<1$ and unstable if $\mathcal{R}>1$ [43]. It follows that the population will reach the disease-free equilibrium if $\overline{p}\ge p_{\mathrm{HI}}\left(\overline{e}\right)$ where

$$p_{\mathrm{HI}}\left(\overline{e}\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}(1-\overline{e}){\mathcal{R}}_0\le 1,\hfill \\ 1-\frac{1}{{(1-\overline{e})}^2{\mathcal{R}}_0^2},\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(12)

or if $\overline{e}\ge e_{\mathrm{HI}}\left(\overline{p}\right)$ where

$$e_{\mathrm{HI}}\left(\overline{p}\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{(1-\overline{p})}^{1/2}{\mathcal{R}}_0\le 1,\hfill \\ 1-\frac{1}{{(1-\overline{p})}^{1/2}{\mathcal{R}}_0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(13)

This is illustrated in Figure 2.

3.2. Endemic Equilibrium

The endemic equilibrium ${\mathcal{E}}^{*}=(S_H^{*},E_H^{*},A_H^{*},I_H^{*},T_H^{*},R_H^{*},S_V^{*},E_V^{*},I_V^{*})$ is stable if $\mathcal{R}>1$. To highlight the dependence on $\overline{p}$ and $\overline{e}$, we express $I_V^{*}$ as

$$I_V^{*}(\overline{p},\overline{e})=N_H\frac{(1-\overline{p}){(1-\overline{e})}^2{\mathcal{R}}_0^2-1}{\frac{(1-\overline{e})ab}{{\mu }_H}+(1-\overline{p}){(1-\overline{e})}^2{\mathcal{R}}_0^2\frac{{\mu }_V+{\sigma }_V}{m{\sigma }_V}}.$$

(14)

Furthermore,

$$\begin{array}{cc}\hfill E_V^{*}& =\frac{{\mu }_V}{{\sigma }_V}{I}_V^{*}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill S_V^{*}& =N_V-I_V^{*}-E_V^{*}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill S_H^{*}& =(1-\overline{p})\frac{{\Lambda }_H}{{\mu }_H+ab\frac{I_V^{*}}{N_H}}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill E_H^{*}& =\frac{(1-\overline{p}){\Lambda }_H-{\mu }_H{S}_H^{*}}{{\mu }_H+{\sigma }_H}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill A_H^{*}& =(1-\delta )\frac{{\sigma }_H}{{\mu }_H+{\gamma }_H}{E}_H^{*}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill I_H^{*}& =\delta \frac{{\sigma }_H}{{\mu }_H+{\gamma }_H}{E}_H^{*}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill T_H^{*}& =\frac{{\gamma }_H}{{\mu }_H+{\kappa }_H}{I}_H^{*}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill R_H^{*}& =\overline{p}{N}_H+\frac{{\gamma }_H{A}_H^{*}+{\kappa }_H{T}_H^{*}}{{\mu }_H}.\hfill \end{array}$$

(22)

Note that by (14), $I_V^{*}(\overline{p},\overline{e})$ is decreasing in $\overline{p}$ and $\overline{e}$.

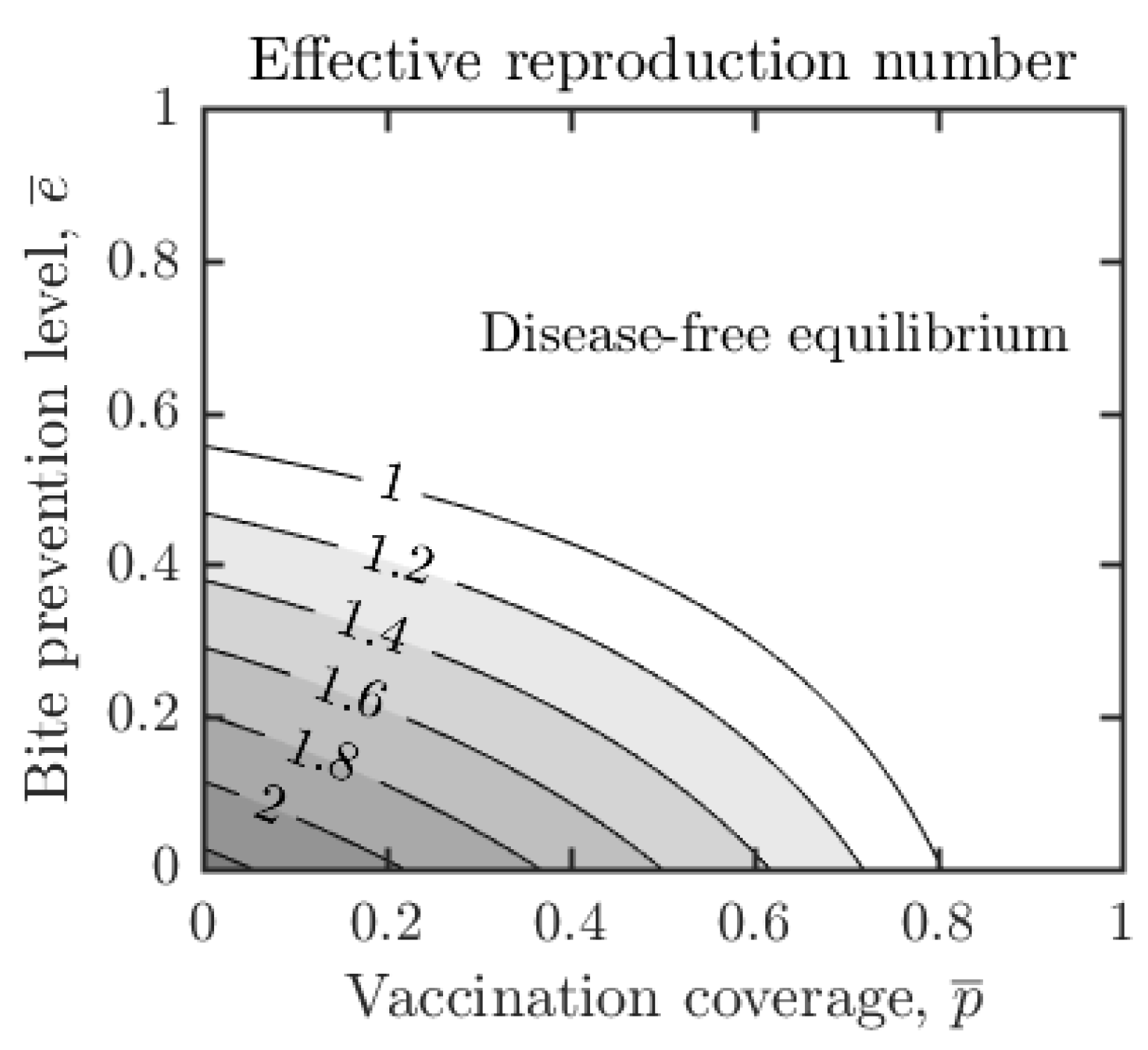
4. Results

Our overall aim is to understand what the individuals would choose if they can decide about about the optimal use of vaccination and bite prevention simultaneously. To achieve this, we will first consider a game when the individuals only decide whether to vaccinate or not, assuming the bite prevention level is fixed. Then, we will consider the game when the individuals decide on the bite protection, assuming the vaccination level is fixed. We will then combine these two results and derive optimal actions when the individuals can use both preventive options at the same time. We validate the model by comparing our reproduction number to previous studies. We also compare the predicted vaccination coverage at Nash equilibrium with the actual coverage in Angola. We conclude this section by sensitivity analysis to see how different parameters influence the predictions of our model.

4.1. Optimal Vaccination Decisions

Let us first assume that individuals can only decide whether or not to vaccinate; all other model parameters including $\overline{e}$ are fixed.

In the disease-free equilibrium, the optimal decision is not to vaccinate. Therefore, for the rest of the section, we assume that the population is, or at least can be, in the endemic equilibrium, i.e., ${\mathcal{R}}_0>1$.

For a moment, assume that the rest of the population uses a strategy $\overline{p}$ and the focal individual is still making a choice whether to vaccinate or not. When the focal individual decides to vaccinate, they will pay the cost $C_V$. If they do not vaccinate, they will remain susceptible. In this case, they can become exposed and eventually proceed to the symptomatic stage with probability

$$\pi =\frac{(1-\overline{e})ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{(1-\overline{e})ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}$$

(23)

where $I_V^{*}(\overline{p},\overline{e})$ is given by (14). Thus, the expected cost of not getting vaccinated is given by $\pi C_{YF}$. Note that, $I_V^{*}(\overline{p},\overline{e})/N_H$ is decreasing in $\overline{p}$. Thus, $\pi$ is decreasing in $\overline{p}$. Moreover, when $\overline{p}=1$, $\pi =0$. Thus, as in [23], the Nash equilibrium is unique and given by

$$p_{\mathrm{NE}}=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{C}_V>\pi C_{YF}\mathrm{for}\overline{p}=0,\hfill \\ \overline{p},\hfill & \mathrm{which}\mathrm{solves}{C}_V=\pi C_{YF}.\hfill \end{array}\right.$$

(24)

In particular, $p_{\mathrm{NE}}<1$ regardless of $\overline{e}$. Additionally, $p_{\mathrm{NE}}$ is a convergent stable Nash equilibrium (CSNE). If $\overline{p}<p_{\mathrm{NE}}$, then the best response is to vaccinate. Conversely, when $\overline{p}>p_{\mathrm{NE}}$, then the best response is to not vaccinate. In either case, the vaccination coverage in the population will tend toward $p_{\mathrm{NE}}$.

Furthermore, as $\overline{e}$ increases, $I_V^{*}(\overline{p},\overline{e})$ does not increase and so the risk of infection $\pi$ is non-increasing in $\overline{e}$. Consequently, the equilibrium value of $p_{\mathrm{NE}}$ is non-increasing in $\overline{e}$. This is shown in Figure 3a.

When $\overline{e}=1$, there is no disease in the population and thus $p_{\mathrm{NE}}=0$. Similarly, when $C_V>0$ is fixed and $\overline{e}<1$ is close enough to 1, $p_{\mathrm{NE}}=0$. Thus, there are only two possibilities as illustrated in Figure 3, depending on the relation of $C_V/C_{YF}$ to

$$\begin{array}{cc}\hfill C_{crit}& =\frac{ab\frac{I_V^{*}(0,0)}{N_H}}{ab\frac{I_V^{*}(0,0)}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H},\hfill \end{array}$$

(25)

where $I_V^{*}(0,0)$ is an equilibrium value of $I_V^{*}$ when $\overline{e}=\overline{p}=0$. We have

(1)

If $C_V/C_{YF}>C_{crit}$, then vaccination is too expensive and the Nash equilibrium is to not vaccinate, even if $\overline{e}=0$, i.e., to not vaccinate for any $\overline{p}$ and thus $p_{\mathrm{NE}}\left(\overline{e}\right)=0$ for all $\overline{e}$.

(2)

When $C_V/C_{YF}<C_{crit}$, then $0<p_{\mathrm{NE}}\left(0\right)<1$ and $p_{\mathrm{NE}}\left(1\right)=0$, i.e., the individuals should vaccinate (but not always) when $\overline{e}=0$ and not vaccinate at all when $\overline{e}\approx 1$.

This is illustrated in Figure 4a.

Figure 4b shows the incidence rate of new YF infections in the population where individuals use the voluntary vaccination at the optimal (from the self-interest point of view) levels.

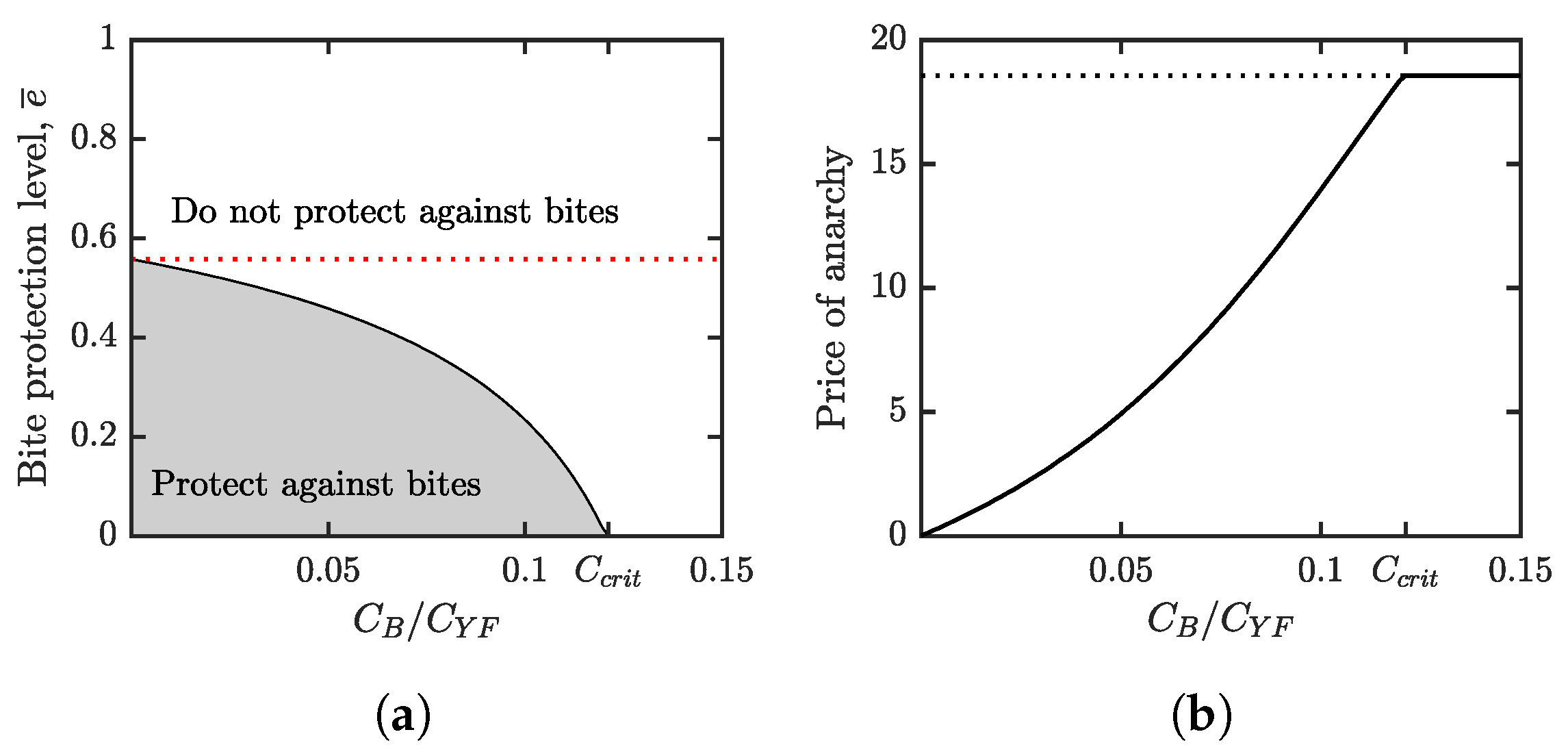
4.2. Optimal Bite Prevention

Here, we consider a game in which the individuals can only decide how much they prevent the vector bites. All other model parameters including $\overline{p}$ are fixed.

Assume that the rest of the population is using $\overline{e}$, while the focal individual uses $e_{ind}$. The risk of infection for the focal individual is given by

$$\pi \left(e_{ind}\right)=\frac{(1-e_{ind})ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{(1-e_{ind})ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}.$$

(26)

The individual will choose $e_{ind}\in [0,1]$ that minimizes the overall costs, i.e., minimizes the function $h\left(e_{ind}\right)=C_B{e}_{ind}+\pi \left(e_{ind}\right)C_{YF}$. We have

$$h^{\prime }=C_B-\frac{{\mu }_{H}ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{{\left((1-e_{ind})ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H\right)}^2}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}{C}_{YF},$$

(27)

and thus $h^{″}<0$. Hence, the minimum of h must occur either at $e_{ind}=0$ or $e_{ind}=1$. The condition $h\left(1\right)<h\left(0\right)$ is equivalent to

$$\frac{C_B}{C_{YF}}<\frac{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}.$$

(28)

Thus, the optimal choice for the focal individual is

$$e_{ind}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\left(28\right)\mathrm{is}\mathrm{true},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(29)

Additionally, as $\overline{e}$ increases, the right-hand side of (28) decreases. Thus $e_{ind}$ is a non-increasing function of $\overline{e}$. Hence, as in the previous section, NE is unique and given by

$$e_{\mathrm{NE}}=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{\displaystyle \frac{C_B}{C_{YF}}<\frac{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}}\mathrm{for}\overline{e}=0,\hfill \\ \overline{e},\hfill & \mathrm{which}\mathrm{solves}{\displaystyle \frac{C_B}{C_{YF}}=\frac{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}}{ab\frac{I_V^{*}(\overline{p},\overline{e})}{N_H}+{\mu }_H}\frac{\delta {\sigma }_H}{{\sigma }_H+{\mu }_H}}.\hfill \end{array}\right.$$

(30)

Additionally, the right-hand side of (28) is decreasing in $\overline{p}$ and thus $e_{ind}$ and consequently $e_{\mathrm{NE}}$ is a non-increasing function of $\overline{p}$. This is shown in Figure 3b.

Similarly to the analysis in the previous section, the $e_{\mathrm{NE}}$ is CSNE.

The outcomes depend on the relationship between $C_B/C_{YF}$ and the critical value $C_{crit}$ defined in (25).

(1)

If $C_B/C_{YF}>C_{crit}$, then $e_{\mathrm{NE}}\left(\overline{p}\right)=0$ for all $\overline{p}$, i.e., the cost of bite prevention is too high no matter what is the vaccination coverage in the population.

(2)

If $C_B/C_{YF}<C_{crit}$, then $1>e_{\mathrm{NE}}\left(0\right)>0$ and $e_{\mathrm{NE}}\left(1\right)=0$, i.e., the individuals should somewhat prevent vector bites (but never fully) if the vaccination coverage is relatively low, but do not prevent them at all once the vaccination coverage is above a certain threshold.

This is illustrated in Figure 5a.

Figure 5b shows the incidence rate of new YF infections in the population where individuals use the voluntary vaccination at the optimal (from the self-interest point of view) levels.

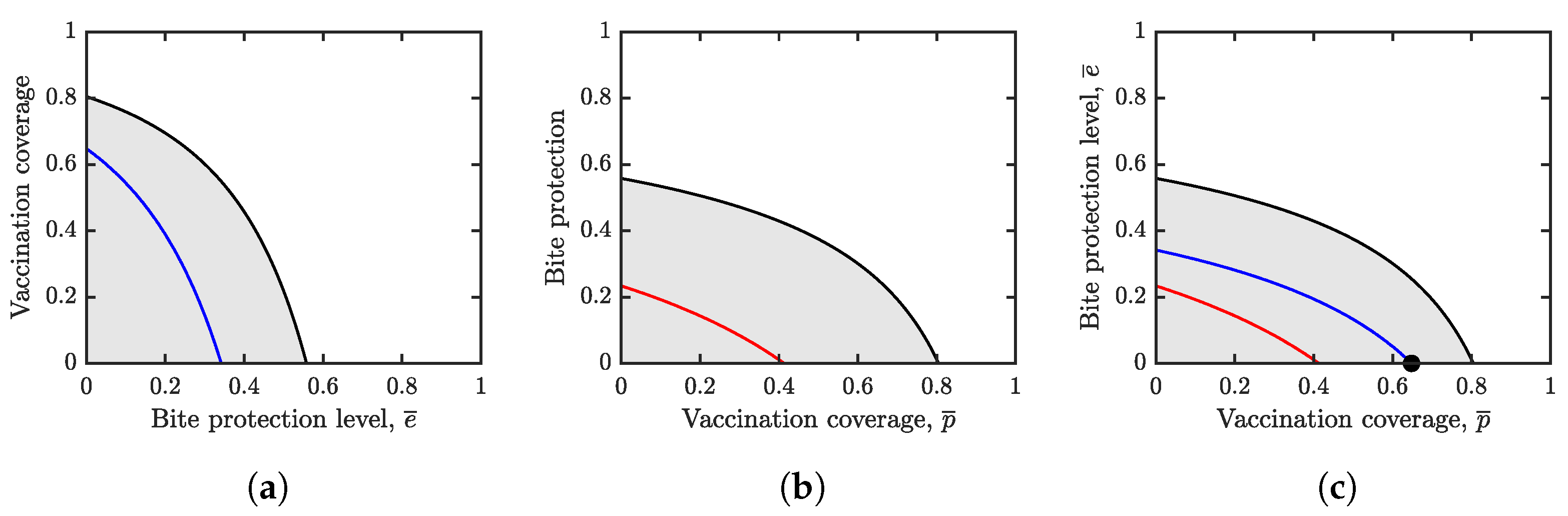
4.3. Optimal Vaccination and Bite Prevention

Here, we assume that individuals decide whether to vaccinate as well as whether to prevent the bites. The strategy is thus given by a pair $(p,e)$ and the NE $(p_{\mathrm{NE}},e_{\mathrm{NE}})$ must satisfy that $p_{\mathrm{NE}}$ is a NE of the game when $\overline{e}=e_{\mathrm{NE}}$ is fixed (as discussed in Section 4.1) and $e_{\mathrm{NE}}$ is a NE of the game when $\overline{p}=p_{\mathrm{NE}}$ is fixed (as discussed in Section 4.2). As demonstrated in Figure 3c, only the equilibrium $(p_{\mathrm{NE}},0)$ is possible, although there is a relatively narrow region of $C_B$ values for which up to three NEs are possible. A similar situation is discussed in more detail in [44].

4.4. Validation

For the parameter values given in Table 1, Formula (11) yields ${\mathcal{R}}_0\approx 2.26$, i.e., a single infectious case results in ${\mathcal{R}}_0^2\approx 5.1$ secondary infections [43]. This is reasonably close to previous modeling studies estimating the number of secondary infections around 5 or more [18,21,22].

Our model also predicts that one needs about 80% of people to be vaccinated for $\mathcal{R}<1$, which is in agreement with [10].

Finally, the game theoretical analysis predicts the NE to be around 65%. This is in a reasonable agreement with about 68% in Angola overall [45]. Additionally, following the 2016 YF outbreak, the vaccination coverage in Luanda province shot up from 57.9% to 92.9% in 2017 and has been on a slow but steady decline to 89.1% in 2022, while the overall vaccine coverage in Angola has been slowly rising. This may demonstrate the voluntary choice of new individuals in Luanda province to not get vaccinated, given the already high vaccination coverage there.

4.5. Sensitivity Analysis

We performed a sensitivity analysis based on [46]. The sensitivity index of $p_{\mathrm{NE}}$ on parameter x is calculated as $\left(\frac{x}{p_{\mathrm{NE}}}\right)·\left(\frac{\partial p_{\mathrm{NE}}}{\partial x}\right)$. The sensitivity index $-0.5$ means that 1% increase in a parameter value x will result in a 0.5% decrease in $p_{\mathrm{NE}}$. The calculations of the sensitivity of $e_{\mathrm{NE}}$ are analogous. The results are shown in Figure 6.

We can see that the sensitivities of $p_{\mathrm{NE}}$ and $e_{\mathrm{NE}}$ on various parameter values are similar, although the sensitivity indices of $e_{\mathrm{NE}}$ are roughly three to four times as much as those for $p_{\mathrm{NE}}$. The NE values increase most with the increase in the mosquito biting rate a, but are also quite sensitive to the transmission probabilities b and c, and the number of mosquitoes per human. On the other hand, the equilibrium values decrease with the increased mortality of mosquitoes, ${\mu }_V$ and the shortening of the human incubation period. In all of these instances, the more likely it is to contract the disease, the higher the value of NE will be.

Similarly, decreasing the cost of vaccination or the bite protection (relative to the cost of the disease) also increases the NE values and lowers the incidence rates at this voluntary equilibrium.

5. Conclusions and Discussion

In this paper, we adapted the compartment model of yellow fever transmission developed by [18]. We added the game-theoretic component and used the model to study the voluntary prevention strategies by vaccination or bite protection. We calibrated the model based on the values from the literature and mostly in agreement with the parameter values used in [18]. We validated the model prediction based on the current vaccination coverage and trends in Angola.

The model shows that vaccination, as opposed to bite protection, should be a preferred way to protect against the disease. In agreement with previous studies [10], our model predicts that one needs about 80% vaccination coverage to contain the outbreaks of yellow fever in urban areas. This is in agreement with previous models of YF without the game theoretical component. Our model indicates that from the individual perspective, the optimal vaccination coverage is about 65%, which is in a reasonable agreement with the actual coverage in Angola. Thus, we show that voluntary vaccination alone is not enough to eliminate yellow fever from endemic areas and to mitigate the risks of outbreaks. These predictions are in line with similar studies on other vector borne diseases [47,48,49] or diseases when the cost of protection is relatively high, such as typhoid [50].

Studies on the prevention of other vector-borne diseases such as chagas disease [51] suggest that individuals behave rationally and that the actual level of protective action depends on the cost of the protection. Thus, from the policy making perspective, the vaccine should be made available for the population at as little cost as possible. This will align the selfish optimal voluntary vaccination coverage with the societal optimum of herd-immunity coverage.

Our model has several limitations. We assumed a homogeneous, well-mixed population and, as a result, we obtained a single Nash equilbrium. To model real-world populations, complex networks provide a better platform [24,52]. Heterogeneity in the population yields heterogeneity in vaccinating actions [53]. The individuals with many contacts may have higher inclination to voluntarily vaccinate than individuals with fewer contacts, and this can largely inhibit the outbreaks [54]. At the same time, we note that YF is transmitted by mosquitoes rather than directly from a person to another person. Thus the usual social network methodology may not apply in a straightforward way. The use of the multi-agent-simulation (MAS) methodology [55,56,57,58,59,60,61] would possibly allow for much higher flexibility and realism in the modeling approach, taking into account both geographical and social heterogeneity. This approach could also capture the qualitative difference between vaccination, which is a one-time decision, and bite protection, which is a repeated action.

Our model can be extended in several ways. Vector control is another preventative measure that could be considered. The control is closely linked to the social structure and living conditions. We focused on urban transmission and thus ignored the sylvanic cycle with non-human primates acting as alternative hosts for yellow fever. Incorporating the primates into the model is, thus, the next natural step which will account for the fact that as cities grow, they become increasingly connected to areas with YF potential. Additionally, the model should account for intensified population movement to the cities from rural areas [10].