Invitation Games: An Experimental Approach to Coalition Formation

Abstract

This paper studies how to form an efficient coalition—a group of people. More specifically, we compare two mechanisms for forming a coalition by running a laboratory experiment and reveal which mechanism leads to higher social surplus. In one setting, we invite the subjects to join a meeting simultaneously, so they cannot know the other subjects’ decisions. In the other setting, we ask them sequentially, which allows each subject to know his or her predecessor’s choice. Those who decide to join the meeting form a coalition and earn payoffs according to their actions and individual preferences. As a result, we obtain the following findings. First, the sequential mechanism induces higher social surplus than the simultaneous mechanism. Second, most subjects make choices consistent with the subgame-perfect Nash equilibrium in the sequential setting and choose the dominant strategy in the simultaneous setting, when a dominant strategy exists. Finally, when the subjects need to look further ahead to make a theoretically rational choice, they are more likely to fail to choose rationally.

1. Introduction

Coalition formation is a fundamental issue discussed in a wide range of economic, social, and political fields because the formation of a coalition provides the coalition members with the opportunity to engage in collective actions that have a stronger impact and may lead to more effective and efficient results than solo actions. A typical example of the importance of coalition formation is international organizations among nations, such as the United Nations and the World Health Organization. For example, ref. [1] conducts an empirical study of coalition formation in the UN Security Council. Moreover, climate change must be another example that is discussed in a framework of international cooperation. Climate contracts, negotiations and agreements have been a prolific topic in the field of coalition formation and have also been analyzed in terms of game theory.1 In addition, designing a mechanism or procedure to manage momentum in climate negotiations is also an issue studied intensively.2

From a theoretical viewpoint, refs. [14,15] offer a game-theoretic analysis of coalition formation. Despite the importance of coalition formation, the potential members of a coalition must resolve a difficulty before enjoying the fruit of cooperation: conflicting preferences among those members. For example, in forming an international organization with three nations, nation A may decline to join the organization if nation B participates, but might be very eager to join if nation C participates. An additional example could be the relationship between a startup firm that plans to launch a new service and the large companies that plan to invest financial support in that startup: the startup has to invite many large companies to obtain financial support, while some of those companies may either hesitate or become more eager to support the startup if certain rival companies also invest in the startup.

As depicted in the preceding examples, a central concern for the organizers of a group or coalition, namely, the startup firm and the (leader of) international organizations, is to resolve conflicting preferences among potential participants, such as large companies and nations. The main purpose of this paper is to depict these situations as a non-cooperative game among participants with conflicting preferences and address the following question: how should organizers lead coalition formation by reconciling the conflicts among potential participants in order to maximize social welfare? To answer this question, we propose and compare two procedures for coalition formation in this paper.

As formally introduced later, the players, namely, the potential participants in a coalition, receive an invitation to join that coalition. Each player is interested in who participates in the coalition and therefore has preferences over the possible members of the coalition.3 Each player chooses to either “join” or “not join”. The organizer is not a player and “designs” the game by choosing either a simultaneous procedure or a sequential procedure. Below, we briefly describe the games generated through these two procedures through the startup-firm example. In the simultaneous procedure, the startup, i.e., the organizer, invites all companies at once, and each company independently makes its decision about whether to invest. In the sequential procedure, the startup now sends an invitation to the companies one by one and informs each company about which other companies have already decided to support the startup. In this sense, the organizer can be seen as a game “designer”. The purpose of the organizer is to maximize the social welfare of the participants.4

These two procedures yield large differences in terms of strategies. For simplicity, we now suppose that three players, A, B and C, each receive an invitation to join a coalition. Moreover, we assume that each player $i\in \{A,B,C\}$ has their list $L_i$ of coalitions in which he/she is willing to participate. For example, player A will accept the invitation if he/she is the only member of the coalition. Player B will accept the invitation if A joins and C declines. Player C will accept it if both A and B join. Their preferences are summarized as follows: $L_A = \left\{A\right\}, L_B = \left\{AB\right\}, L_C = \left\{ABC\right\}$. A player i obtains a high payoff if he/she accepts the invitation and the resulting coalition is an element in their list $L_i$, a low payoff if he/she accepts the invitation and the resulting coalition is not in $L_i$, and a moderate payoff if he/she declines the invitation. For convenience, we suppose that the high payoff is 30, the moderate payoff is 15, and the low payoff is 0. Therefore, for example, player C obtains a payoff of 30 if the strategy profile is (Accept, Accept, Accept), 15 if it is (Accept/Decline, Accept/Decline, Decline), and 0 otherwise. If the organizer designs this game as a simultaneous game, then clearly, this game has no Nash equilibrium. On the other hand, if the game is a sequential game with ordering ABC, then the strategic configuration changes drastically. Player A first has to consider the actions of B and C: If A decides to join, then B has an incentive to decline because if B also joins, then C will join to create coalition ABC. However, in view of B’s preferences, B prefers to obtain a payoff of 15 by declining the invitation over obtaining a payoff of 0 in coalition ABC by accepting the invitation. Therefore, (A expects that) B will decline the invitation. Hence, taking this expectation as given, A accepts the invitation. Note that the equilibrium path induced from the unique subgame-perfect Nash equilibrium is (Accept, Decline, Decline), which results in coalition A and matches A’s preferences. Clearly, (Accept, Decline, Decline) is not a Nash equilibrium if their moves are simultaneous, as player B will change their decision to Accept.5

As this example illustrates, these two procedures yield different strategic interactions and may lead to different coalition formation results. Therefore, the selection of the procedure plays a key role for organizers who facilitate coalition formation and wish to maximize the social welfare of potential participants. In this paper, we conduct a laboratory experiment for the main purpose of comparing the performance of the two procedures.

There have been some previous experimental studies to compare the simultaneous procedure and the sequential procedure. For example, refs. [21,22,23,24] compare the two procedures in the context of a public good game experiment. Especially, ref. [24] utilizes a step-level public good experiment where the public good is provided only when some minimum threshold of provision is exceeded. The experimental subjects in their study choose a level of contribution simultaneously in one treatment and sequentially in the other treatment. Under their settings, the public good is not provided in all equilibria with the simultaneous procedure, while there is a unique subgame perfect equilibrium in which the public good is provided with the sequential procedure. As a result, they find that the sequential procedure actually increases the public good provision, i.e., improves efficiency in their context. We would like to know if the sequential procedure also brings more social surplus than the simultaneous one does in our context of coalition formation.

There have also been several previous laboratory experiment studies on coalition formation. For example, ref. [25] conducts a three-person bargaining experiment with majority votes. Ref. [26] utilizes a sequential move game for a three-person bargaining experiment. However, the experimental subjects in these studies negotiated not only about coalition formation but also about how to share the payoff from the formed coalition, i.e., the payoff distribution. The payoff from each coalition was given by the experimenter, and the subjects could arbitrarily split the payoff if they agreed on the distribution. On the other hand, in our experiment, the subjects do not negotiate about coalition formation and the payoff distribution. They simply choose to join or not join, and those who choose to join become members of the coalition. Their payoff is automatically decided according to their choice and the coalition formed, so there is no room for negotiations about the payoff. Therefore, the protocol in our experiment can be described as a simple non-cooperative game: either a strategic form game or an extensive form game. We analyze the subjects’ behavior by comparing the results of our experiment with those predicted by theory.

The rest of this paper is organized as follows. In Section 2, we provide a formal introduction of the framework of the invitation game and some concepts from non-cooperative game theory, such as a Nash equilibrium and a subgame-perfect Nash equilibrium. In Section 3, we show how we conducted the experimental sessions and provide a detailed explanation of the experimental protocol. In Section 4, we examine the result by focusing on a comparison of the two procedures and the individual choices made in each. In Section 5, we finally summarize the results and provide their interpretation and implications and possibilities for future work.

2. Theoretical Model

In this section, we formally introduce the framework for the invitation game. Let N be the set of players. A subset S of N is called a coalition of players. For an arbitrary set X, we denote the number of elements in X by $\left|X\right|$. For example, $\left|S\right|$ means the number of members in S. Let $n = \left|N\right|$ for simplicity.

On the basis of the motivation given in the introduction, each player is invited to join a group or coalition. Each player chooses either Yes or No: Yes (No) means that the player joins (does not join). Let $A = \left\{\mathrm{Yes},\mathrm{No}\right\}$. An outcome is the set of players who chose Yes. Let $\Omega$ be the set of all possible outcomes. Clearly, $\Omega$ is equal to the set of all subsets (including the empty set) of N, namely, $2^N$.

Each player $i\in N$ has complete transitive preferences ${⪰}_i$ over $\Omega$. For each $i\in N$, let $D_i = \{S\in \Omega |i\notin S\}$ and assume that $S{\sim }_{i}T$ for every $S,T\in D_i$. Let $L_i = \{S\in \Omega |S{\succ }_{i}T\mathrm{for}\mathrm{some}T\in D_i\}$ and $R_i = \{S\in \Omega |T{\succ }_{i}S\mathrm{for}\mathrm{some}T\in D_i\}$. Therefore, $L_i$, $D_i$ and $R_i$ are mutually disjoint and $L_i\cup D_i\cup R_i = \Omega$. In the same manner as for $D_i$, we assume that $S{\sim }_{i}T$ for every $S,T\in L_i$ and $S^{\prime }{\sim }_i{T}^{\prime }$ for every $S^{\prime },T^{\prime }\in R_i$. Intuitively, $L_i$ represents the set of coalitions player i is willing to join, and $R_i$ is the set of coalitions i wants to avoid joining. If player i chooses No, the choice must lead to a coalition in $D_i$, while if i chooses Yes, that choice results in a coalition in either $L_i$ or $R_i$.

In a simultaneous game, every player simultaneously chooses a strategy in $A = \left\{\mathrm{Yes},\mathrm{No}\right\}$. Therefore, there is a one-to-one mapping $m:A^N\to \Omega$ between strategy profiles and outcomes, $m\left(a\right) = \{i\in N|a_i=\mathrm{Yes}\}$. A strategy profile $a\in A^N$ is a Nash equilibrium (NE) if for every $i\in N$ and every $a_i^{\prime }\in A$, $m(a_1,\cdots ,a_i,\cdots ,a_n){⪰}_{i}m(a_1,\cdots ,a_i^{\prime },\cdots ,a_n)$. Note that a simultaneous game may have multiple or no Nash equilibria. A player i’s strategy $a_i$ strongly dominates strategy $a_i^{\prime }$ if for every $j\in N\backslash \left\{i\right\}$ and every $a_j\in A$, $m(a_1,\cdots ,a_i,\cdots ,a_n){\succ }_{i}m(a_1,\cdots ,a_i^{\prime },\cdots ,a_n)$.

In a sequential game, each player chooses their action in A in a specific order after observing all preceding players’ actions. Note that an action is different from a strategy in a sequential game. An action is simply choosing either Yes or No. We now call a sequence of actions played by players a path. For example, if the first player A chooses Yes and the second player B chooses No, then (Yes, No) is a path. For convenience, we also consider the sequence that consists of no actions to be a path. In a sequential game, a strategy for a player i is a mapping that assigns an action to all possible paths that consist of the actions taken by the players preceding i.6 In a sequential game, let ${\alpha }_i$ be the set of player i’s strategies. Every path yields a unique subgame: A subgame is a part of the entire sequential game that is played by the players whose actions are not contained in the path. A strategy profile $a\in {\times }_{i\in N}{\alpha }_i$ is said to be a subgame-perfect Nash equilibrium (SPNE) if a generates a Nash equilibrium in every subgame. Note that every sequential game has exactly one SPNE because if player i chooses Yes for their move, the resulting outcome is in either $L_i$ or $R_i$, while if he/she chooses No, then the result is $D_i$. Moreover, each player i has a strict preference between $L_i$ and $D_i$ (and similarly between $D_i$ and $R_i$). Therefore, for every decision to be made, the player is not indifferent between a choice of Yes and a choice of No, which generates exactly one SPNE.

In our experiment, each player must choose an action instead of a strategy, even in the sequential game. There are two reasons behind this choice of design. First, if each player chooses a strategy, their decisions are no longer comparable between the two types of games. We avoid this incompatibility by requiring players to choose either Yes or No in both types of games. Second, choosing a strategy, namely, assigning Yes or No to all possible paths, including those that may not be realized, is not representative of actual coalition formation procedures: If one is invited to join a coalition, then he/she should simply say Yes or No instead of fully mapping out all possible outcomes. Therefore, note that the path chosen by the players and the resulting coalition are observable in our experiment, whereas a strategy profile is not.

In addition to the notion of an SPNE, we now introduce the concept of Pareto optimality. A strategy profile a is said to be Pareto optimal if there is no strategy profile $a^{\prime }$ such that $m\left(a^{\prime }\right){⪰}_{j}m\left(a\right)$ for every $j\in N$ and $m\left(a^{\prime }\right){\succ }_{i}m\left(a\right)$ for some $i\in N$. In a simultaneous game, the Pareto optimality of a strategy profile is neither necessary nor sufficient for being a NE. An outcome is said to be Pareto optimal if the strategy profile which induces the outcome is Pareto optimal. The Pareto optimality of an outcome depends only on players’ preferences and is independent of the selection of simultaneous and sequential procedures.

Finally, we review these settings by revisiting the example given in Section 1. Let $N = \{A,B,C\}$ and $L_A = \left\{A\right\}, L_B = \left\{AB\right\}, L_C = \left\{ABC\right\}$, where we write, for example, coalition $AB$ instead of $\{A,B\}$ for simplicity. It immediately follows that $D_A = \{B,C,BC,\varnothing \}$, $D_B = \{A,C,AC,\varnothing \}$, $D_C = \{A,B,AB,\varnothing \}$ and $R_A = \{AB,AC,ABC\}$, $R_B = \{B,BC,ABC\}$, $R_C = \{C,AC,BC\}$.7 As briefly mentioned in Section 1, there is no Nash equilibrium in a simultaneous game, while in a sequential game, strategy profile $(a_A,(a_B^Y,a_B^N),(a_C^{YY},a_C^{YN},a_C^{NY},a_C^{NN})) = (\mathrm{Yes},(\mathrm{No},\mathrm{No}),(\mathrm{Yes},\mathrm{No},\mathrm{No},\mathrm{No}))$ is the unique Pareto optimal SPNE. For example, $a_C^{YN}$ represents C’s action after A’s action Yes and B’s action No here. The realized path is $(\mathrm{Yes},\mathrm{No},\mathrm{No})$, and the resulting outcome is the one-person coalition A.

3. Experimental Settings

We utilize two treatments in one experimental session. One treatment employs the simultaneous mechanism (SIM), in which the subjects simultaneously choose Yes or No and do not know the others’ choice of action when they make their own decision. The other treatment employs the sequential mechanism (SEQ), in which the subjects choose Yes or No in turn and do know their predecessors’ choice of action when they make their decision. In both treatments, each subject makes a choice with knowing not only their preferences, but also the other subjects’ preferences. The subjects participate in both treatments.

We designed and ran three experimental sessions, Session 1 in February 2018, Session 2 in June 2018 and Session 3 in June 2021. We recruited 32 students from Waseda University, mainly undergraduates, from several faculties for each session. Although the capacity for each session was 30, we recruited two extra participants in case some recruits dropped out of the study. Recruitment was performed through the portal website for Waseda University students, named MyWaseda. First, the students who were interested in the experiment sent us their personal information, such as their name, student ID, and email address. After receiving each application, we checked for duplication: no one was allowed to join multiple sessions. Those who passed the check received an email from us and participated in the study.

On the day of the session, we had the participants come to the laboratory just before the starting time. Each participant randomly picked a plastic number plate when entering the laboratory and took a seat according to the number selected. Each seat was in a cubicle surrounded by high partitions so that the subjects could not see each other. When more than 30 participants arrived, we paid a show up fee to the extra participants, and they returned home.8 A total of 58 male students and 32 female students participated.9

Each session consisted of the two treatments and we examined two orders of the treatments: we employed SIM as the first treatment and SEQ as the second in Sessions 1 and 2, while SEQ was the first and SIM was the second in Session 3. After entering the laboratory, the subjects first read and signed a consent form that discussed the protection of their private information. Then, computer software read the instructions for the first treatment SIM (in Sessions 1 and 2)/SEQ (in Session 3) aloud; see Appendix A. They completed a comprehension test (see Appendix C) to check their understanding of the experiment after receiving the instructions. The first treatment started after all subjects passed all questions on the comprehension test. After the first treatment, we distributed the instructions for the second treatment SEQ (in Sessions 1 and 2)/SIM (in Session 3) to the subjects (see Appendix B), and the software again read the instructions aloud. After the second treatment was finished and while the subjects were completing the post-experiment questionnaires, we calculated the subjects’ payoffs and paid them in cash according to their performance. After that, they checked the payment amount and filled out receipts, and the session ended.

This experiment was designed and run on z-Tree by [27]. Both treatments consisted of 10 rounds, and the subjects played one game per round. At the beginning of each round, the subjects were randomly divided into 10 groups of three.10 Additionally, each subject was randomly assigned a role: A, B or C. In addition to their role, lists were shown to the subjects. These lists were common among the subjects and consisted of A’s list, B’s list and C’s list, and all subjects in the same group could see each list. The subjects’ sole requirement in each round was to choose Yes or No. The time limit for choosing an action was 60 s. After all members of the group made their choice, the outcome was fixed. Then, one of three payoffs was given according to the subjects’ actions and the outcome.11 First, if an individual’s action was Yes and if the resulting outcome was on that individual’s own list, he/she received 30 points. Second, if an individual’s action was Yes and if the resulting outcome was not on that individual’s own list, he/she received 0 points. Finally, if an individual’s action was No, he/she received 15 points with certainty, regardless of the outcome. After choosing their own action, the subjects were shown the actions of the other subjects in the same group, the outcome of their group and their own payoff from the round, and the round ended. The members of each group and the roles assigned were shuffled by the computer, and the subjects moved to the next round. In addition to the shuffle of the group member and the roles, the subjects faced a different game from one round to another, which is explained later. We believe that these settings make it possible for us to regard that each observation from each round is independent. The final payment was the sum of the participation fee and the payoffs accumulated across all rounds in both treatments.12^,13 The points the subjects earned were exchanged at a rate of 3 JPY per point. We paid the subjects in cash at the end of the session. Each session took approximately 60 min, and the average payment was approximately 1300 JPY.14

The difference between the two treatments SIM and SEQ was the receipt of information about the others’ actions and the timing of the actions. In SIM, the subjects simultaneously chose an action without knowing the other subjects’ choice of action. On the other hand, in SEQ, each subject chose an action in turn while knowing their predecessor’s action. The order of choosing was fixed as A first, B second and C third in every game.15 In other words, A did not know B or C’s action when choosing their own action, while B knew A’s choice of action and C knew both A and B’s choice of action. The subjects knew that the order was fixed to A, B, C; that they could see their predecessor’s choice of action; and that their successor could see their choice of action.

Note that the subjects participated in both SIM and SEQ. This setting results in a within-subject study. This means that it is possible that their experiences and results in the first half of the session affected their actions and results in the second half. In other words, there might have been a learning effect. However, we believe that the learning effect was weakened because the members of the groups and the roles were shuffled at the beginning of each round. Moreover, as previously explained, the subjects had a short break between the first treatment and the second one to receive the instructions for the second treatment. We believe that this break also weakened the learning effect. In order to eliminate the possibility of the learning effect completely, we examined two orders of the treatments: SIM in the first half of the session and SEQ in the second half in Sessions 1 and 2; SEQ first and SIM second in Session 3.

Table 1. Lists, maximum-payoff outcome, Nash equilibrium outcome, subgame-perfect Nash equilibrium outcome, games with * are implemented only in Sessions 2 and 3.

Game	${\mathit{L}}_{\mathit{A}}$	${\mathit{L}}_{\mathit{B}}$	${\mathit{L}}_{\mathit{C}}$	MPO	NE Outcome	SPNE Outcome
1 *	ABC, A	ABC, B	ABC, C	ABC	ABC, A, B, C	ABC
2	ABC	ABC	ABC, AC, BC, C	ABC	ABC, C	ABC
3	ABC	ABC	ABC	ABC	ABC, ∅	ABC
4 *	ABC, AB, AC, A	BC, B	ABC, C	ABC, A, B, C	A	A
5 *	AB, AC, A	AB, BC, B	AC, BC, C	AB, AC, BC	AB, AC, BC	AB
6 *	ABC, AB, AC	B	C	B, C	no NE	B
7	A	B	C	A, B, C	A, B, C	A
8	A	AB	ABC	A	no NE	A
9	AB, AC	AB, BC	AC, BC	AB, AC, BC	AB, AC, BC, ∅	AB
10 *	ABC, AB, AC, A	ABC, AB	AC	AB, AC	AB	AB

shows each player’s list, the maximum-payoff outcome (defined in the next section), the NE outcome and the SPNE outcome for each game. The order of the games and that of the rounds was the same in both treatments: the subjects played game 1 in the first round through to game 10 in the tenth round in the first treatment, and then they again played from game 1 to game 10 in the second treatment. Note that the NE is a profile of strategies and the NE outcome is the resulting coalition, and similarly, the SPNE is a profile of strategies and the SPNE outcome is the resulting coalition.16 In game 4, for example, the NE is the strategy profile (Yes, No, No), which corresponds to the NE outcome coalition A. Likewise, the SPNE outcome is coalition A induced by executing the SPNE $(a_A,(a_B^Y,a_B^N),(a_C^{YY},a_C^{YN},a_C^{NY},a_C^{NN})) = (\mathrm{Yes},(\mathrm{No},\mathrm{Yes}),(\mathrm{Yes},\mathrm{No},\mathrm{No},\mathrm{Yes}))$.

Since we do not employ the strategy method introduced by [28], we cannot observe the subjects’ actions in any subgame that was not reached in our experiment. In the strategy method, the subjects choose an action for every possible subgame, while in our experiment, the subjects chose an action only at the subgame reached. Hence, the strategy method enables the experimenter to observe not only each subjects’ choice of action, but also their strategy profile. On the other hand, in our experiment, we could not observe whether the SPNE was reached, but we could observe whether the SPNE outcome was achieved. Although we later analyze consistency of the subjects’ actions with the SPNE, we did not employ the strategy method since the main purpose of this study is not an analysis of the SPNE itself, but the comparison of the two mechanisms. Therefore, as argued in the previous section, we did not employ the strategy method in order to avoid incomparability in the results between SIM and SEQ.

Now, we describe the ten games analyzed in the experiment. First of all, we avoid the games in which each player has an empty list, and the games of which the results are straightforward enough without the experiment. The odd-numbered games, namely, games 1, 3, 5, 7, and 9 can be thought of as symmetric games, in which the preferences of the three players are symmetric. For example, A’s list can contain (i) either coalition ABC or no three-person coalition, (ii) either both of coalitions AB and AC or no two-person coalitions, and (iii) either coalition A or no one-person coalition. Then, there are potentially eight lists (=$2 \times 2 \times 2$) for A. We remove the following three cases from the eight lists: the empty list, the list containing all coalitions, and the list containing the three-person coalition and all two-person coalitions, which results in the five lists on Table 1. These games are removed because No is a dominant strategy for every player in the first case, Yes is a dominant strategy for every player in the second case, and the list leads the players to choose Yes in the third case.

We next focus on the even-numbered games, namely, games 2, 4, 6, 8, and 10, which can be thought of as asymmetric games. Since the games in which two or more players have a dominant strategy end up with an obvious outcome, we analyze the games in which only one player has a dominant strategy, and the games in which none of the players have a dominant strategy. To be more specific, C has a dominant strategy in game 2, and A has a dominant strategy in games 4 and 10. In game 2, given that C chooses the dominant strategy, this game is a coordination game between A and B. Then there are two NEs based on the coordination by A and B. On the other hand, in games 4 and 10, given that A chooses the dominant strategy, B also has a dominant strategy. Likewise, given that A and B choose the dominant strategies, C also has a dominant strategy. Hence, there is only one NE between A and B in these games. The difference between games 4 and 10 is that B’s dominant strategy is No in game 4 and Yes in game 10. Detailed analysis on the dominant strategies is provided in Section 4.2, where we focus on individual choices in the experiment. In games 6 and 8, no players have a dominant strategy and there is no NE. In these games, the first player A in SEQ faces the difficulty of complex speculation about the actions of the other players, which decreases the efficiency of SEQ. This is elaborated in Section 4.1, where we compare SIM and SEQ in terms of efficiency. Note that we alternate between symmetric and asymmetric games to weaken an effect of the order of the games.

Although we conducted three sessions, some of the games were played only in Sessions 2 and 3. The 5 games marked with an asterisk (*) were included only in Sessions 2 and 3, while the other games were included in all sessions. In Session 1, 5 different games were played instead of including the games marked with an asterisk. However, the results of those games were almost identical to what we had predicted before the session, so we concluded that the results would not change even if we ran further sessions. Hence, we replaced those games with the games marked with an asterisk. Note that each session generated 10 observations for each game, so we collected 20 observations for the games marked with an asterisk and 30 observations for the other games.

4. Results

This chapter consists of two sections: the first section compares the performance of the two mechanisms, SIM and SEQ, and the second section focuses on individual actions. Here, we summarize the results in advance. First, a comparison of the two mechanisms shows that SEQ was more efficient than SIM in terms of social surplus. Second, when we look at individual actions, most subjects chose the action that was consistent with the SPNE outcome in SEQ and that was their dominant strategy in SIM, when such a strategy existed. Finally, the rate at which these actions were chosen decreased when the subjects needed to look further ahead to choose the action corresponding to the theoretically rational action.

Table 2. Coalition formation in SIM, * corresponds to the NE outcome.

Game	ABC	AB	AC	BC	A	B	C	∅	Obs.
1	13 *	1	3	1	1 *	1 *	0 *	0	20
2	18 *	0	5	7	0	0	0 *	0	30
3	19 *	3	3	3	1	0	1	0 *	30
4	1	0	4	0	12 *	1	0	2	20
5	10	2 *	4 *	1 *	2	1	0	0	20
6	0	0	0	0	4	3	3	10	20
7	3	2	3	3	5 *	3 *	3 *	8	30
8	0	0	2	0	11	3	3	11	30
9	4	4 *	9 *	5 *	1	3	1	3 *	30
10	0	16 *	0	0	3	1	0	0	20

and

Table 3. Coalition formation in SEQ, * corresponds to the SPNE outcome.

Game	ABC	AB	AC	BC	A	B	C	∅	Obs.
1	15 *	1	0	0	0	1	3	0	20
2	27 *	1	0	0	0	0	2	0	30
3	27 *	0	1	0	0	0	0	2	30
4	2	0	0	0	16 *	2	0	0	20
5	0	17 *	1	1	0	0	1	0	20
6	0	0	1	0	6	11 *	2	0	20
7	0	0	0	1	24 *	4	1	0	30
8	1	0	0	0	7 *	0	0	22	30
9	2	25 *	1	2	0	0	0	0	30
10	1	19 *	0	0	0	0	0	0	20

show the number of coalitions formed under each mechanism in the laboratory experiment.

4.1. Efficiency

The main goal of this research is to clarify which mechanism is more efficient. We regard a mechanism as being more efficient than the other when the sum of the payoffs of the subjects is higher. To compare the efficiency of the two mechanisms, we first define the maximum-payoff outcome (MPO). We calculate the sum of the payoffs for all members of the group, which we regard as the social surplus, from each possible outcome for each game; the MPO is the outcome that gives the highest sum. For example, in game 1, coalition ABC gives 30 points to each subject and 90 points in total. This is the largest sum across all possible outcomes, so coalition ABC is the MPO here. Note that an MPO exists in all games, but is not always unique. Consider another example: In game 4, coalition ABC results in 30 points for A and C and 0 for B. On the other hand, coalitions A, B and C each result in 30 points for those who chose Yes and 15 for those who chose No. Hence, these four coalitions give 60 points in total, and all are MPOs for this game. Additionally, note that the MPO is always Pareto optimal, but the opposite is not always true. We first compare the two mechanisms with respect to which resulted in the MPO more frequently.

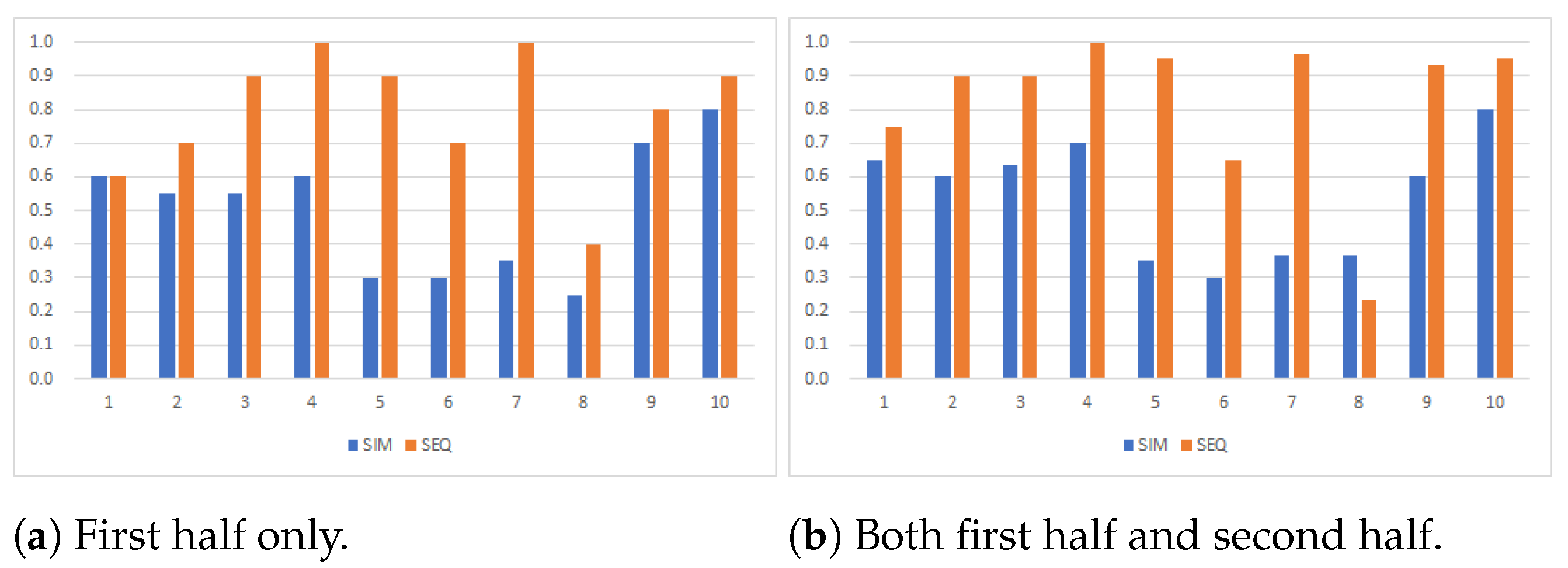
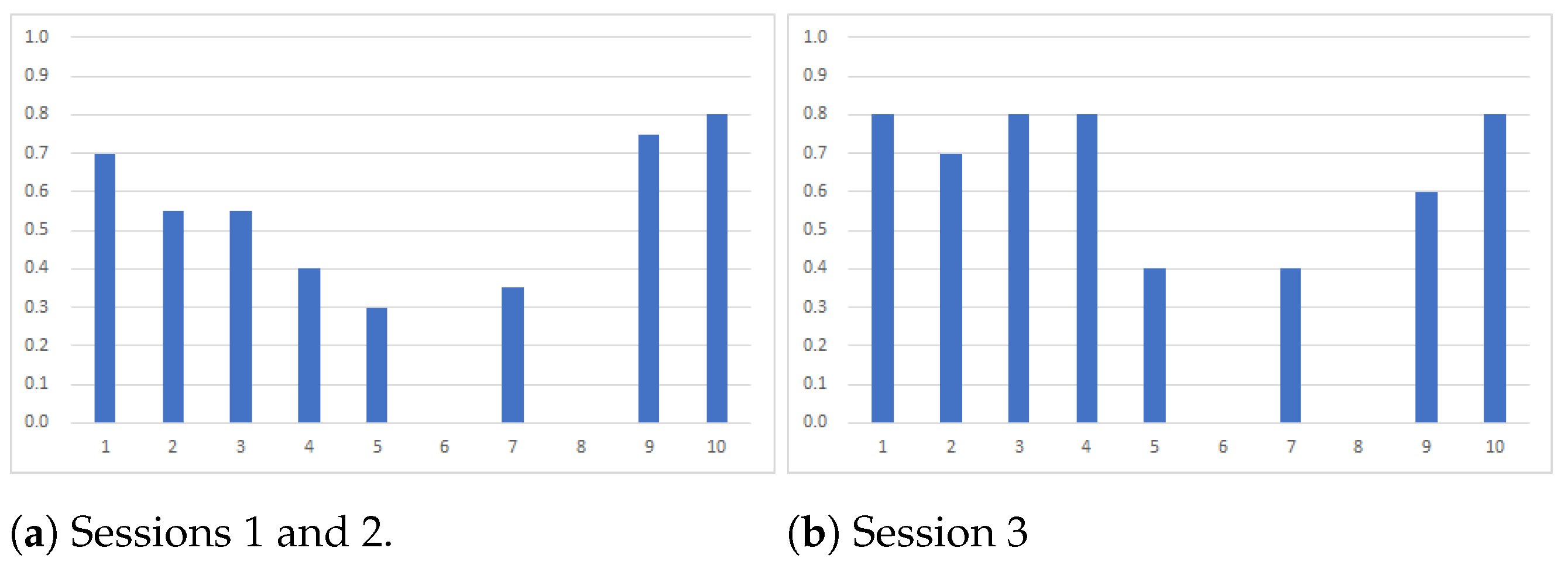
Figure 1 shows the frequency with which the MPO is reached under each mechanism game by game. Figure 1a includes only the observations in the first treatment, i.e., SIM in Sessions 1 and 2, and SEQ in Session 3. With this restriction of the observations, we compare the two mechanisms without the learning effect since the subjects in the observations had not experienced the other treatment yet. On the other hand, Figure 1b includes the observations in both the first treatment and the second one, so the numbers of the observations in Figure 1b are larger than those in Figure 1a.

From both figures, the comparison between the two mechanisms shows that SEQ performed better than SIM except in game 8. Why is this so? First, the subjects in SEQ have more information about the other players’ actions than those in SIM. While the subjects in SIM cannot see the other subjects’ actions, those in SEQ can see their predecessors’ actions. Additionally, the subjects in SEQ make their choice of action while knowing that their successor(s) will see their actions. Second, even if one subject in SEQ chooses an off-equilibrium path, their successor can still choose an action consistent with the SPNE. On the other hand, when one subject in SIM deviates from the MPO, the other subjects cannot know about it. Let us take a simple example, game 3, in which each subject has only coalition ABC on their list. If A chooses No in SEQ, then successors B and C know that coalition ABC cannot be formed and that they should choose No. On the other hand, if A chooses No in SIM, B and C might still choose Yes, believing that the others would also choose Yes since they cannot see the other subjects’ choice of action. If A chooses Yes in SEQ, B should choose Yes, believing that C will also choose Yes in order to form coalition ABC since B knows that C will see A and B’s choice of action. On the other hand, even if A chooses Yes in SIM, it could still happen that B and C choose No if either of them believes that the others chose No.

SEQ basically achieved the MPO at a high rate though the rate at which the MPO was reached was relatively low in games 6 and 8. What caused this? In game 8, under SEQ, the SPNE outcome is coalition A, which is the MPO. In theory, A should choose Yes; by looking ahead, A can see that B will choose No. This is because from B’s point of view, if B chooses Yes, C will also choose Yes to obtain 30 from coalition ABC. Then, B gets 0 from the coalition; thus, it is better for B to choose No. However, in the laboratory experiment, the subjects who played the role of A did not reason in this way, and only 8 out of 30 subjects successfully chose Yes. This is why the MPO was rarely reached in game 8 under SEQ. Likewise, a similar misunderstanding by A occurred in game 6. If A were to choose Yes, then neither B nor C would choose Yes because they each have only a single-person coalition on their list. Then, coalition A would be formed and A would get 0. Hence, in theory, it is better for A to choose No. However, in the laboratory experiment, 35% of the subjects playing role A chose Yes, and the frequency with which the MPO was reached was relatively low. This kind of difficulty and failure to think about their successors’ future actions is supported by some previous studies, for example, ref. [20].

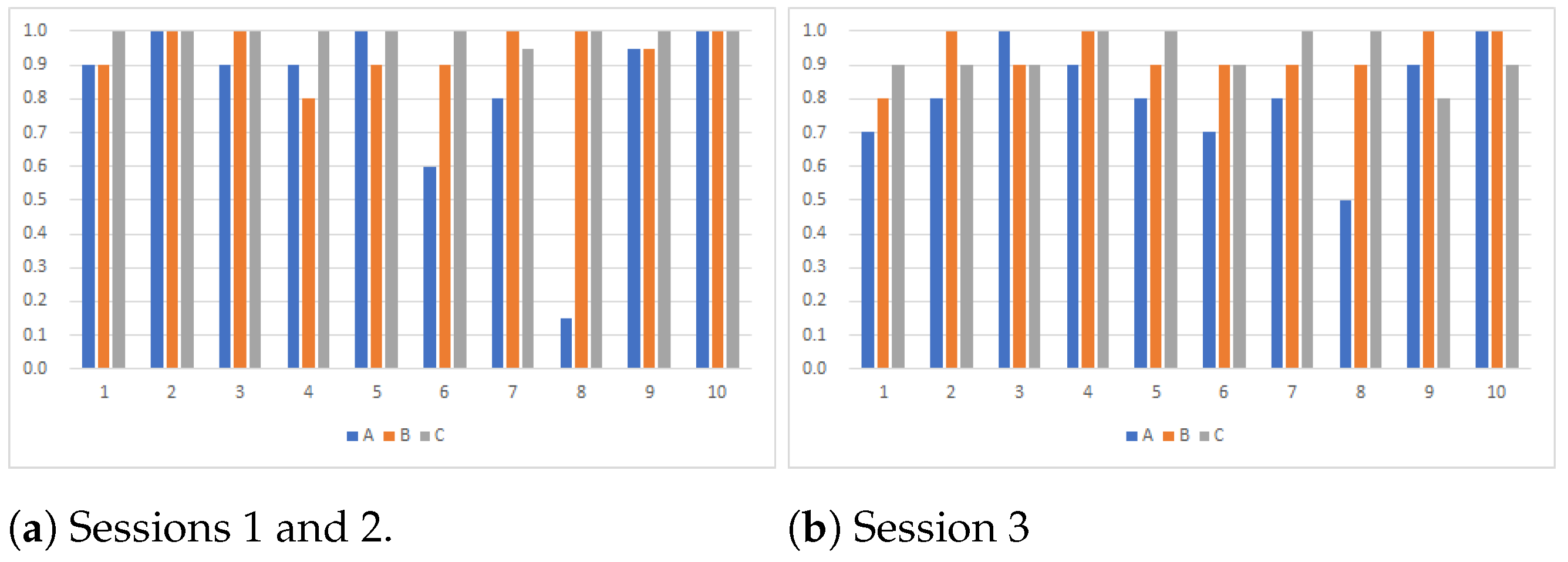
When we compared the two mechanisms with respect to the frequency with which the MPO was reached, we considered binary results: we considered the worst case, in which everybody earns 0 points, and the middle case, in which everybody chooses No and earns 15 points, to be equal. However, the finding that SEQ basically performed better than SIM, but worse in some games might not hold if we evaluate the two cases differently. Hence, we define and calculate the social surplus rate (SSR) as another measurement of the performance of each mechanism. The SSR is defined for each game as follows: SSR = [the average of the sum of the payoffs of all members in each group in the experiment]/[the sum of the payoffs of all members in each group at the MPO of each game]. By employing the SSR, we can evaluate the two mechanisms differently: social surplus is 0 in the worst case and 45 in the middle case. Again, we compare the two mechanisms with respect to the SSR.

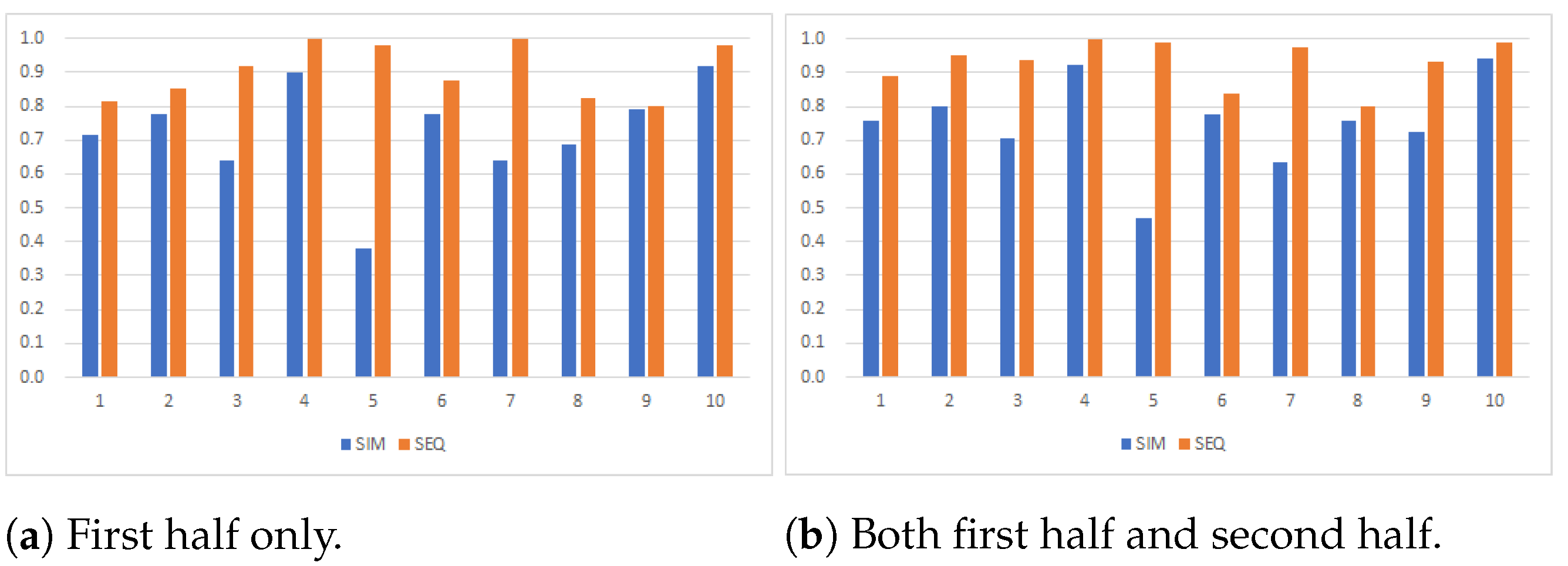
Figure 2 shows each mechanism’s SSR game by game. The difference between Figure 2a,b is the same as that between Figure 1a,b. From both figures, even though the two graphs are close for some games, SEQ performed better than SIM in all games. SEQ performed worse than SIM in game 8 in terms of reaching the MPO, but this result is reversed when using the SSR to evaluate the outcomes. Therefore, we can conclude that SEQ performs better than SIM. Note that this conclusion does not change even when we totally eliminate the possibility of the learning effect by restricting the observations as depicted by Figure 2a.

4.2. Individual Actions

Hereafter, we focus on the individuals’ decisions. First, we look at their actions in SIM. Figure 3 shows the frequency with which the NE outcome, which is usually referred to as a bundle of rational actions, was reached in SIM. Figure 3a represents the frequency in Sessions 1 and 2 where SIM was played in the first half of the session, while Figure 3b represents the frequency in Session 3 where SIM was played in the second half. Note that games 6 and 8 have no NE outcome. Additionally, note that several games have multiple NE outcomes (see Table 1), and we count the NE outcome as being achieved if one of those outcomes is reached. However, it is difficult for us to judge whether a given subject’s action is rational by looking at whether a NE outcome was reached. For example, in game 3, the NE outcomes are coalition ABC and ∅. In this game, we cannot tell whether a subject who chose action Yes acted rationally or irrationally. Hence, we employ an action-related concept from simultaneous games, the dominant strategy. We define one’s action as rational when it is a dominant strategy, conditional on the dominant strategy existing. The games that have a dominant strategy for one of the players are games 2, 4 and 10. First, in game 2, C has a dominant strategy of choosing Yes because every possible outcome including C is on their list. In this game, all 30 out of 30 subjects chose Yes, so we can conclude that they identified this dominant strategy and behaved rationally.

While only one player has a dominant strategy in game 2, all players had dominant strategies in games 4 and 10, given the following consideration. First, in game 4, A has the dominant strategy Yes, so B and C should realize that A will choose Yes. Given this forward thinking, B’s action No dominates their action Yes because neither coalition BC nor B on their list can be formed, so C should realize that B will choose No. Given that A chooses Yes and B chooses No, C’s action No dominates Yes because neither coalitions ABC nor C on their list can be formed. If all subjects follow this line of reasoning, then in theory, their actions should be uniquely determined: (Yes, No, No).17 In this sense, this game is dominance-solvable through forward thinking even though it is played in SIM.18 The result of the laboratory experiment is that 17 out of 20 subjects who played role A were rational and chose the dominant strategy Yes, 18 out of 20 subjects who played role B were rational, and 15 out of 20 subjects who played role C were rational.

Likewise, game 10 can be solved as follows. First, A has a dominant strategy, Yes, so B and C should look ahead and see that in theory, A will choose Yes. Given this forward thinking, B’s action Yes dominates their action No because either coalition ABC or AB on their list will be formed and B can obtain their highest payoff regardless of C’s action, so C should look ahead and see that both A and B will choose Yes. Finally, given that both A and B choose Yes, C’s action No dominates Yes because coalition AC on their list cannot be formed. If all subjects follow this line of reasoning, their actions should be uniquely determined: (Yes, Yes, No). The result of the laboratory experiment is that 19 out of 20 subjects who played role A were rational and chose the dominant strategy Yes, 17 out of 20 subjects who played role B were rational, and all the 20 subjects who played role C were rational.

Previous studies such as [20] have revealed that thinking about others’ actions becomes difficult when the number of steps to consider increases. For example, in game 4, C has to think about what B will choose. This requires looking ahead one step. Additionally, B has to think about what A will choose. This induces C to think about what B will think about what A will choose. This requires looking ahead two steps. If the subjects in the experiment follow this principle, the rate at which rational actions are chosen should decrease from A to B to C. However, while the actual experimental result for game 4 follows this principle, that of game 10 does not. Why do these results differ? One possible explanation is that in game 10, it is easier for C to look ahead than in game 4 because both A and B should choose Yes in game 10, while A should choose Yes and B should choose No in game 4. We might be able to say that the subjects tended to notice that the other subjects would choose Yes when the coalition including them is on their list in this framework. This is because the coalitions on the lists show who should choose Yes. A game in which the subject who needs to look many steps ahead has to think about another player’s No in order to choose a theoretically rational action should be difficult, which leads to the irrational actions in game 4 in SIM.

Next, we focus on the individual actions in SEQ. As mentioned in the previous sections, we can observe only each player’s choice of action, not their strategy, to avoid incomparability between SIM and SEQ. We checked whether A, B and C’s actions were consistent with an SPNE. A subject’s action is said to be consistent with an SPNE if their action is in the SPNE of the subgame that the action initiates. Let us take game 3 as an example. The strategy profile $(a_A,(a_B^Y,a_B^N),(a_C^{YY},a_C^{YN},a_C^{NY},a_C^{NN})) = (\mathrm{Yes},(\mathrm{Yes},\mathrm{No}),(\mathrm{Yes},\mathrm{No},\mathrm{No},\mathrm{No}))$ is the SPNE in this game and we judge the consistency of each player’s action according to this outcome.19 Suppose that the chosen actions are (No, No, Yes). First, we note that A’s action No is not consistent with the SPNE because A should have chosen Yes. Second, we note that B’s action No is consistent in the subgame starting from B’s action, given A’s No. Note that if A’s action was Yes, B’s No would not be consistent. Finally, in a similar manner, we note that C’s action Yes is not consistent because C should have chosen No in the subgame starting from C’s action, given A’s No and B’s No.

Figure 4 shows the frequency with which consistent actions were chosen. Figure 4a represents the frequency in Sessions 1 and 2 where SEQ was employed in the second half of the session, while Figure 4b represents the frequency in Session 3 where SEQ was employed in the first half. From both figures, the result of the experiment is that the subjects in role C consistently chose actions consistent with the SPNE, while some of their predecessors in roles A and B failed to choose consistent actions.20 An important point is that the frequency with which A chose consistent actions changed most sharply from game to game. Again, this makes sense because of the three players, A needs to look the furthest ahead to choose the consistent action. It is also important to note that even though A needs to look two steps ahead, this does not necessarily lead to a decrease in the frequency of choosing the action consistent with the SPNE. For example, in game 10, all of the subjects in role A successfully chose the consistent action Yes. This is because A has all possible outcomes that include A on their list, so A does not need to look ahead to B and C’s actions in this game. On the other hand, in games 6 and 8, many subjects in role A failed to choose the action consistent with the SPNE, as explained regarding the MPO in Section 4.1. This is for the same reason that C failed to act rationally in game 4 in SIM: it is difficult for the subjects in role A to look ahead to B and C’s No actions.

5. Discussion and Concluding Remarks

When people form their cooperative coalitions, internal conflicts of interest among members often matter. In this paper, we propose two procedures that induce strategic games in which the subjects, namely, the players, form a coalition. One of the procedures is a simultaneous procedure: The players simultaneously choose to “join” or “not join” the coalition. The other procedure is a sequential procedure in which the players choose to “join” or “not join” one by one, following a given ordering of the players. The main purpose of this study is to reveal which procedure brings more efficient outcomes. Our experiment shows that the sequential procedure results in higher social surplus than the simultaneous procedure. This makes sense because the experimental subjects in the sequential setting had more information about the other players’ action than did those in the simultaneous setting. The subjects in the sequential setting were able to see their predecessors’ choice of actions and knew that their successors would see their action. On the other hand, in the simultaneous setting, the subjects could not see the other players’ actions. We conclude that this difference in the amount of information available about the other subjects’ choice of action affected the subjects’ ability to look ahead and led to the differences in the performance of the two procedures.

We can also think that there could be two effects that caused the difference of the performance of the two mechanisms. One is information about the predecessors’ actions, and the other is the possibility of the games for forward thinking. Let us discuss the two effects. When we look at information about the predecessors’ actions, the subjects in the simultaneous mechanism do not have it while the ones in the sequential mechanism have it in all games. On the other hand, when we focus on the possibility of forward thinking, all games are possible in the sequential mechanism while it is divided into three classes in the simultaneous mechanism. The first class is “possible” games the same as the ones in the sequential mechanism, which include games 4 and 10 where each player has a dominant strategy. The second class is “partially possible” games, which include game 2, where one player has a dominant strategy. Finally, the other games are classified to “non-possible”, games where no player has a dominant strategy. When we again take a look at Figure 2b, in the possible games, the sequential mechanism induces higher social surplus rate (SSR) than the simultaneous mechanism does by 0.075 in game 4 and 0.050 in game 10. Since these games are possible to think forward in both the simultaneous and the sequential mechanisms, we can regard these efficiency gaps originate only in information about the predecessors’ actions. In the partially possible game, the efficiency gap is 0.150 in game 2. Furthermore, in the non-possible games, some games generate a relatively small efficiency gap; 0.134 in game 1; 0.063 in game 6; 0.042 in game 8. In contrast, other games generate a large efficiency gap; 0.233 in game 3; 0.520 in game 5; 0.342 in game 7; 0.206 in game 9. In these games, we should think that both effects are simultaneously working because there are larger gaps than in the possible games. However, we should also think that separating the two effects completely is difficult, because when we give the subjects information about the predecessors’ actions, the games become possible for forward thinking at the same time.

This paper also focuses on individual actions, revealing two findings. First, most subjects in the sequential setting chose actions consistent with the SPNE, and those in the simultaneous setting chose actions corresponding to their dominant strategy, when such a strategy existed. Here, information on others’ preferences over outcomes played a key role: it enabled the subjects to look ahead to the other players’ actions. Second, it was more difficult for the subjects to look two steps ahead than one step. This result is consistent with [20] and is caused by the subjects’ limited cognitive skills. However, we also reveal that the subjects did not necessarily fail to look two steps ahead in all games. It seems that it was easier for the subjects to predict another player’s Yes than No in some games. In this sense, we can say that the difficulty of looking ahead depends on how information about the other subjects’ preferences is listed.

Our experimental settings assume that the players have perfect information about not only their own preferences but also the other players’ preferences over outcomes. We also assume that this is common knowledge among the players. However, in the real world, it is often the case that some players know the other players’ preferences only partially or even do not know those preferences at all.21 In this case, will the sequential procedure still perform better than the simultaneous procedure? Let us consider an example. Suppose that the players do not know the other players’ preferences at all and only know their own preferences in the sequential setting. When the order of actions is A, B, C, as in our experiment, it should be difficult, or even impossible, for A and B to look ahead to their successors’ choice of action. For example, when B tries to look ahead to C’s action, B knows that C’s choice will depend on A and B’s action and C’s preferences. Therefore, it is impossible for B to choose an action through forward thinking.22 On the other hand, from C’s point of view, the problem is not the same because he/she has no successor. Hence, in this example, C will be able to choose an action in the same way as the subjects in our experiment. From this argument, we expect that the performance of the sequential procedure will be worse in the setting described in this example. Let us take another example. Suppose that the players know their own and their successor’s preferences but do not know their predecessor’s preferences in the sequential procedure. In other words, A knows A, B and C’s preferences, B knows B and C’s preferences, and C knows only C’s preferences. In this case, it will remain possible for A and B to look ahead to their successor’s choice of action, which means we can derive the SPNE outcome without complete information and even without common knowledge. An important point is that information on one’s predecessor’s preferences is not necessary to engage in forward thinking. Hence, we can expect that the performance of the sequential procedure will not be worse in the setting described this example. In this discussion, information is very important for predicting outcomes. There is little theory on this, so it is important to check the behaviors of experimental subjects in this incomplete information setting. This will be done in future work.

What about performance of the simultaneous mechanism? We can expect a similar decrease in performance among the dominance-solvable games such as games 4 and 10 when there is a lack of information on the other players’ preferences. This is because these games are solved by looking ahead to the other players’ choice of the dominant strategy. Note that whether this decline occurs depends on what kind of information is lacking. For example, in game 4, suppose that A knows only A’s preferences, B knows A and B’s preferences, and C knows all preferences. In this case, the game is still dominance-solvable, just as we could derive the SPNE outcome in the sequential procedure even though there is a lack of information. On the other hand, for games that are not dominance-solvable, we cannot clearly predict the change in performance. We expect that individual actions will be affected by the lack of information since the subjects should choose their action by referring not only to their own preferences, but also to the preferences of the other players. Conducting a simultaneous procedure experiment with incomplete information will also be completed in future research.

In addition to the above two procedures, other variants may also be employed, for example, a procedure in which players are free from following an order, can make their decision at any time, and can see their predecessors’ choice of action (if any). We can regard this procedure as a variant of the sequential procedure, and the main difference is that the order of action is endogenous. Can we say that acting quickly is advantageous for a player? Let us suppose that game 7 is played following this procedure, where the lists are $L_A = \left\{A\right\}, L_B = \left\{B\right\}, L_C = \left\{C\right\}$. In this game, acting quickly is advantageous: if B chooses Yes first, A and C should choose No, and B will obtain the highest payoff while A and C will obtain a moderate payoff. However, if all players understand this situation and rush to act first, it could happen that they all choose Yes almost simultaneously, without seeing the others’ choice of action, and they all obtain the low payoff from forming coalition ABC. As this example shows, we need to incorporate the timing of the choice of action in each player’s strategy, which requires a complicated theoretical analysis of the induced game. More theoretical and experimental research should be done to examine this procedure.

Other settings regarding the number of the players or the players’ preferences can also be applied. We started this study with simple settings, three players in a group without externality. The number of the players can be extended to four or more, but one difficulty is related with subjects’ cognitive skills. In this study, the maximum number of the outcomes in each list is four. However, the maximum number exponentially increases as the number of the players increases: eight for four-player games, 16 for five-player games and so on. When each list becomes longer, it rapidly gets difficult for subjects to not only take into account the whole list but engage in forward thinking. We can also introduce externality to the players’ preferences. For example, in reality, the utility of the person who decided not to attend a party might differ when the other two attended the party and when they did not. Such cases are equally evaluated in this study, so introducing such externality is also one interesting possibility for future work. However, as the number of the players expands, we must be careful that the lists become too complicated by introducing externality. We have to add payoffs from each outcome to the lists, not only the cases where a subject chooses Yes, but also the cases where the subject chooses No. Then, the lists will get complicated again even in three-player games: the number of the outcomes in each list increases from four to eight at maximum. We need to elaborate how to show the subjects’ preferences for such extensions in order to avoid the complication, but the elaboration should be difficult.

Finally, as mentioned in the first section, we assume that the organizer of the coalition takes a “neutral” stance and maximizes the social welfare of the players. This paper reveals that the organizer should employ a sequential mechanism rather than a simultaneous mechanism to maximize social welfare. However, if we consider the organizer’s point of view, it is important that he/she knows the players’ preferences and what the order of action is. Let us take an example in which the lists are $L_A = \left\{ABC\right\}, L_B = \left\{BC\right\}, L_C = \left\{BC\right\}$ and the order of action is A, B and C. In this game, the SPNE outcome is coalition BC, and this is the MPO. However, suppose that the organizer mistakenly sets the order to be C, B and A. Now, the SPNE outcome is ∅, and this is not the MPO. Such loss of social welfare can be caused by incorrectly ordering the choice of action, and such incorrect ordering can arise not only from the organizer’s mistake, but also from their ignorance of the players’ preferences. Therefore, one question arises: is there any procedure that can maximize social welfare even if the organizer does not know the players’ preferences? The answer to this question requires more research, but the procedure we proposed above is a candidate because the order of action is decided by the players themselves.

Moreover, it is often the case that the organizer also has preferences over the resulting coalitions and might choose the mechanism that is most likely to facilitate the formation of the coalition the organizer prefers. In other words, the organizer also joins the game as a player instead of a neutral designer. This additional setting can be applied to both the simultaneous and sequential procedures; more research on this setting is needed. This extension is also left for future work.