Abstract
We explore how an incremental change in complexity of strategies (“an inch of memory”) in repeated interactions influences the sets of Nash equilibrium (NE) strategy and payoff profiles. For this, we introduce the two most basic setups of repeated games, where players are allowed to use only reactive strategies for which a probability of players’ actions depends only on the opponent’s preceding move. The first game is trivial and inherits equilibria of the stage game since players have only unconditional (memory-less) Reactive Strategies (RSs); in the second one, players also have conditional stochastic RSs. This extension of the strategy sets can be understood as a result of evolution or learning that increases the complexity of strategies. For the game with conditional RSs, we characterize all possible NE profiles in stochastic RSs and find all possible symmetric games admitting these equilibria. By setting the unconditional benchmark as the least symmetric equilibrium payoff profile in memory-less RSs, we demonstrate that for most classes of symmetric stage games, infinitely many equilibria in conditional stochastic RSs (“a mile of equilibria”) Pareto dominate the benchmark. Since there is no folk theorem for RSs, Pareto improvement over the benchmark is the best one can gain with an inch of memory.
MSC:
91A05; 91A20; 91A10
1. Introduction
In the theory of repeated games, restrictions on players’ strategies are not usually imposed (see, for example, [1]). However, an interest in bounded rationality and strategic complexity [2] has led to the study of repeated games where players’ strategies are assumed to be finite automata or to have finite memory (bounded recall). This paper falls into the strategy-restrictions framework: we make an extensive study of the Nash equilibrium in infinitely repeated games where payoffs are determined by Reactive Strategies (RSs) and players’ payoffs are evaluated according to the limit of means. A player’s reactive strategies are strategies that, for each move of the opponent in the previous round, prescribe stationary probabilities to the player of playing his/her own pure actions.
One may naturally think of two-by-two classification of RSs. The first aspect is related to information. Players may ignore the available information about the action of the opponent in the previous round; hence, we distinguish between unconditional and conditional RSs. The second aspect is related to predictability of actions. Deterministic and semi-deterministic RSs allow deterministic responses (probabilities 1 or 0) to actions in the previous rounds, while for stochastic RSs, all responses have non-degenerate probabilities.
The paper explores how an incremental change of complexity of strategies in repeated interactions influences the sets of Nash equilibrium (NE) strategy and payoff profiles. For this, we introduce, perhaps, the two most basic setups of repeated games. In the first game, which is trivial and inherits equilibria of the stage game, players have only memory-less RSs. In the second game, players in addition have conditional stochastic RSs. This extension of the strategy sets can be understood as a result of evolution or learning, resulting in increased complexity of strategies. For the game with conditional RSs, we answer the following questions:
- (Q1)
- What are all possible NE profiles in stochastic RSs?
- (Q2)
- What are all possible symmetric games admitting NE in stochastic RSs?
- (Q3)
- Do equilibrium profiles in conditional stochastic RSs Pareto improve over equilibrium profiles in unconditional RSs?
Surprisingly, the answers to (Q1)–(Q3), the most basic results for equilibria in reactive strategies, are still missing in the literature, while similar questions were studied for 1-memory (aka memory-one) strategies with discounted payoffs.
Before we proceed to more technical elements of the paper, let us give a simple example where reactive and 1-memory strategies meet together.
Example 1.
A textbook example of repeated games is the iterated Prisoner’s Dilemma, where the stage game has two strategies for both players, C (cooperate) and D (defect). Any round ends with a possible action profile: or . As profile i of the previous round is known, player 1 chooses C with probability (hence, D with probability ). Then a 4-tuple, say would define a 1-memory strategy of player 1. A reactive strategy of player 1 is a 1-memory strategy that only depends on the opponent’s action, i.e., and ; this reduces 4-tuples to ordered pairs. By omitting the issue of opening moves, one derives 1-memory form for the strategies that were found to be the most popular in experimental study [3]. These strategies are Tit-for-Tat, ; Always Defect, ; both are reactive ones, while Grim, , is not.
1.1. Related Literature
Reactive strategies were introduced by Karl Sigmund and Martin Nowak (see [4,5]) as an abstraction of bounded rationality. However, while their research has never been focused directly on the Nash equilibrium, we should note that the authors’ comprehensive study of evolutionary stable strategies is indeed relevant to (Q1), as the definition of these strategies requires a symmetric Nash equilibrium to be formed. This is why, for the infinitely repeated Prisoner’s Dilemma in [4], a full characterization of symmetric Nash equilibria in the class of reactive strategies was obtained for the limit-of-means payoff. Note that these symmetric equilibria are equilibrium points (see [6]) of adaptive dynamics on the set of all reactive strategies. The concept of adaptive dynamics was introduced in [7] to describe evolution in continuous sets of strategies. In this paper, we significantly extend the results from [4] related to the Nash equilibrium by considering arbitrary stage games and by characterizing both symmetric and non-symmetric equilibria, with non-symmetric equilibria prevailing over symmetric ones.
For the discounted Prisoner’s Dilemma, subgame perfect equilibria in the class of deterministic reactive strategies were studied in [8]. In [9], Appendix 5.5, a brief analysis can be found of equilibrium refinements in the class of deterministic reactive strategies (referred to as “memory zero” strategies) for a repeated Prisoner’s Dilemma. In [9], R. Aumann considered eight pure strategies for each player (four stationary reactions multiplied by two actions for the initial round). Note that the concepts of reactive strategies and 1-memory strategies in repeated games with a continuum of pure strategies are related to stationary “reaction functions” [10,11], “immediately reactive strategies” [12], and stationary “single-period-recall strategies” [13]. In contrast to the studies mentioned in this paragraph, we consider limit-of-means payoffs and reactive strategies mixing over (two) pure actions, that is, reactive strategies mapping the previous opponent’s moves into distributions over pure actions.
We also study the problem of the existence of a Nash equilibrium. Note that Kryazhimskiy [14] obtained conditions sufficient for the existence of a Nash equilibrium within subsets of the players’ 1-memory strategies in repeated bimatrix games with the limit-of-means payoff. The conditions require the sets of players’ strategies to have a convexity property and all strategies to be strictly randomized, so the Kakutani fixed-point theorem becomes applicable.
There is evidently much more literature available on the topic of 1-memory strategies than on the topic of reactive strategies. The recent spike of interest in 1-memory strategies was stimulated by the discovery of Zero-Determinant (ZD) strategies, a special class of 1-memory strategies enabling linear relationships between players’ payoffs, irrespective of opponent’s strategies (see [15] for the case of the limit-of-means payoff). Remarkably, ZD strategies can fix the opponent’s payoff or guarantee some surplus that outperforms the opponent’s surplus by the chosen constant factor. Hilbe et al. [16] extended the theory of ZD strategies to the case of the discounted payoff; see [16] for the most recent review of the topic.
Within the literature dealing with 1-memory strategies, one of the most relevant studies for our research was conducted by Dutta and Siconolfi [17]. In that study, the ideas, which were independently proposed in the seminal paper [18] to derive a robust folk theorem for the discounted Prisoner’s Dilemma, were extended to generic repeated games. In other words, Dutta and Siconolfi explored a Strong Mixed Equilibrium (SME) in the class of 1-memory strategies. This equilibrium is formed by completely mixed 1-memory strategies and has the salient property that both players are indifferent between their actions after every history. Specifically, in [17], conditions were obtained that are necessary and sufficient for a game to have an SME, and the set of all equilibria payoffs was described. The latter result allowed us to demonstrate that SMEs generally lead to a continuum of equilibrium payoffs but still do not generate a folk theorem. To summarize, Dutta and Siconolfi [17] studied subgame perfect equilibria formed by completely mixed (stochastic) strategies in repeated games with discounted payoffs and 1-memory strategies.
An analysis of subgame perfect equilibria (SPE) in 1-memory strategies focused on the Prisoner’s Dilemma was presented in [19]. In particular, SPEs formed by zero-determinant strategies were characterized and the corresponding upper bound for all NE and SPE payoffs was obtained (it is equal to the mutual cooperation payoff).
Moving from 1-memory to finite memory strategies, we should mention finite automata as a common abstraction of bounded rationality; see [2,20,21].
Following [22], we observe different natural levels of complexity, motivating us to distinguish between deterministic and Stochastic Reactive Strategies (SRSs). In this paper, we focus on SRSs as the simplest ones. The higher complexity of some deterministic strategies is due to the fact that the probability of the first action should be a part of the strategy to correctly define expected payoffs, while the payoffs for stochastic strategies do not depend on the first action.
To summarize, the field of finite-memory strategies (and, in particular, reactive strategies) has been studied for the last 30 years. Especially comprehensive results were obtained for 1-memory strategies but even the most basic facts for generic stage games are still missing for equilibria in RSs. The research not only delivers the missing piece of theory but also demonstrates that even an inch of memory in repeated interactions translates into a mile of new equilibria.
1.2. Results and Structure of the Article
First, we provide an expository geometrical representation to draw contrasts between unconditional and conditional SRSs in the repeated games; see Section 2.1. An example of the Prisoner’s Dilemma with equal gains from switching is considered in Section 2.2 to illustrate how the representation will be applied to study the Nash equilibrium.
Second, in Section 2.3, we derive a characterization of all Nash equilibria in the class of reactive strategies in terms of solutions to a system of equations and inequalities; see Theorem 1.
Third, in Section 2.4, Theorem 2, we present a characterization of all symmetric games admitting Nash equilibria in the class of reactive strategies; Appendix A contains all related proofs.
Fourth, we elaborate on equilibrium payoff profiles in conditional SRSs; see Section 3. Namely, we demonstrate that:
- If there exists an NE formed by a profile of conditional SRSs, then there are infinitely many NE profiles generated by conditional SRSs that, in general, have distinct payoffs, but we do not have a folk theorem.
- If there exists an NE formed by a profile of unconditional SRSs, then NE profiles in conditional SRSs either Pareto improve over it or provide the same payoff profile.
For symmetric games, the complete analysis of equilibrium payoff profiles becomes feasible in Section 3.2 and Appendix B. In our setting, an NE in unconditional RSs always exists. Among equilibrium payoff profiles in unconditional RSs, we select the symmetric one with the lowest payoffs as the benchmark. We then check if there exists an equilibrium payoff profile formed by conditional stochastic RSs that Pareto dominates this benchmark. Only in the very special games where both players (by choosing the dominating pure strategy) get the highest possible individual payoff are payoff profiles in conditional SRSs dominated by the benchmark unconditional payoff profiles. This means that it is possible to get new equilibria with lower payoffs while the strategies become more advanced; see an example in Section 3.3. In the remaining cases, if equilibrium profiles in SRSs exist and result in distinct payoff profiles, then there exists an NE profile in SRSs dominating the benchmark. In some cases, all NE profiles in conditional SRSs dominate the benchmark.
Fifth, with the extensive use of examples, we highlight some interesting properties of NE profiles in stochastic RSs; see Appendix C.
In this paper, some reactive strategies are excluded from players’ strategy sets. In Section 2.5, we discuss how this decision influences the results.
1.3. Definitions of Repeated Games
Consider an arbitrary one-shot game

The first player chooses rows (possible strategies are T and B); the second player chooses columns (possible strategies are L and R); stand for top, bottom, left, right, respectively. A mixed strategy of player 1 is a probability of playing action similarly, a mixed strategy of player 2 is a probability of playing action Mixed strategies defined by non-degenerate probabilities are called completely mixed strategies. Let us introduce payoff functions for the one-shot game in mixed strategies by the rules:
where
1.3.1. Strategies
In the following, we study a game that is a repeated modification of To define in normal form, we first introduce reactive strategies [4,5,23].
Definition 1.
We define reactive strategies of player 1 (player 2) as arbitrary maps of (maps of ) into sets of all mixed strategies of player 1 (player 2); players’ mixed strategies in the current round are completely defined by the preceding opponent’s action. To simplify the notation, we understand any reactive strategy of player 1 as an ordered pair such that the conditional probability of action T and action B is and given that the second player’s previous move was L, and the conditional probability of T and B is and given that the second player’s previous move was In a similar way, a reactive strategy of player 2 is a pair such that the conditional probability of action L and action R is and given that the first player’s previous move was T, and the conditional probability of L and R is and given that the first player’s previous move was
Reactive strategies form a subset of 1-memory strategies (see [15,16,17,18]). Figure 1 shows the classification of RSs that we follow in this paper.
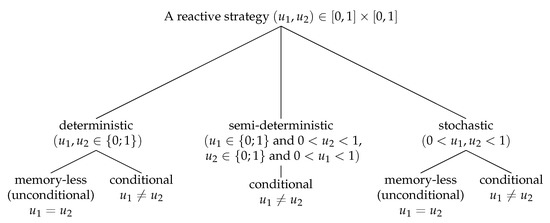
Figure 1.
A possible classification of reactive strategies.
To avoid ambiguity, we denote an open interval as . For player 1 (player 2), we introduce the set of Stochastic Reactive Strategies (SRSs): ( ).
We start with the repeated setting where players use only unconditional strategies (both deterministic and stochastic), game Game is basically memory-less infinite repetition of the stage game. Then we slightly increase the complexity of players’ behavior; i.e., we allow players to use also SRSs. This changes into Thus, the set of all possible strategies of player 1 (of player 2) in game is defined as (as ).
1.3.2. Payoffs
Given any initial action profile corresponding to the first round and a profile of stochastic RSs, we obtain an infinite discrete-time Markov stochastic process (hence the name for strategies) defined on four possible states: and (states 1, 2, 3, and 4, correspondingly). For every actual l-step trajectory of actions the average payoffs are random variables. According to [14], for the limits of expected l-round average payoffs are well defined for all SRSs and initial profiles. As usual, we call these limits limit-of-means payoffs.
The paper studies equilibrium profiles formed only by SRSs due to two reasons:
- 1.
- In contrast to semi-deterministic and deterministic RSs, the payoffs for profiles of SRSs do not depend on the opening move;
- 2.
- SRSs capture non-deterministic behavior that is the most natural for the domain of evolutionary game theory, where RSs originated to model real-life processes.
Every profile of SRSs ensures nice properties for the induced Markov process with the transition probability matrix
That is, there exists a stationary distribution (a row vector) such that note that depends on u and v but not on the initial profile. In [4,5,23], it was proven that stationary distribution allows the following representation:
where mappings are defined by the rules
Note that the trajectories of actions for profiles of deterministic RSs contain a deterministic cycles (hence the name of the strategies) of action profiles that may depend on the opening moves.
In what follows, we omit arguments of where it is possible. We also refer to as a stationary distribution, since the original stationary distribution can be easily recovered.
For a profile of SRSs, the limit-of-means payoffs are determined by the stationary distribution that is independent from the initial actions. Hence, for a profile of SRSs, players’ payoffs in are the exact same payoffs as in if player 1 uses mixed strategy and player 2 uses mixed strategy This helps to specify and that denote the first and second player’s payoff function in respectively:
See the summary for all introduced games in Table 1.

Table 1.
Summary for two-player games considered in the paper.
1.3.3. Equilibria
To summarize, we study a game with two players; the sets of strategies are and the payoff functions are and
Definition 2.
A profile is called a Nash equilibrium (NE) in if the following conditions hold:
In what follows, a pure (completely mixed) Nash equilibrium stands for a Nash equilibrium in a one-shot game formed by pure (completely mixed) strategies. In the stationary distribution generated by an NE is called an Equilibrium Stationary Distribution (ESD).
2. Characterization of Nash Equilibria
2.1. Geometric Intuition and Attainable Sets
Our immediate goal is to illustrate for the difference between conditional and unconditional SRSs. First, let us introduce the concept of attainable sets.
Definition 3.
The set of all stationary distributions feasible for a fixed opponent’s reactive strategy is called an attainable set for a player. To be precise,
Here, is an attainable set for player 1 if player 2 chooses strategy see Figure 2b. Similarly, is an attainable set for player 2 if player 1 chooses see Figure 2a. Obviously, see Figure 2c. Using (4), we obtain
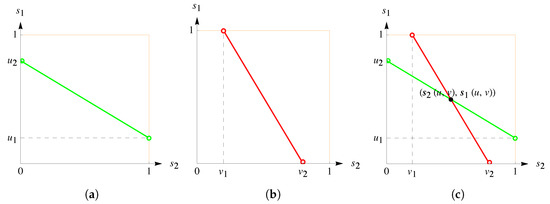
Figure 2.
Let Then, plot (a) corresponds to attainable set plot (b) corresponds to Plot (c) depicts the corresponding stationary distribution as the intersection of the attainable sets.
Lemma 1.
The following representations hold true
Proof.
We will check only the first representation, as, using similar arguments, it easy to demonstrate the second one. Fix an arbitrary let
Take then Let be the reactive strategy of player 1 such that It follows from (7) that and Thus, Then therefore,
Remark 1.
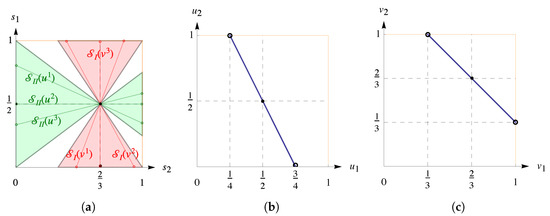
Equation (7) implies that for player 1 to achieve any element of say she may use the corresponding unconditional RS ; for player 2, the similar statement holds true. Figure 3a shows us the corresponding example.

Figure 3.
For stationary distribution plot (a) shows the range of all possible attainable sets generating it. Namely, the green region (the red region) is a ‘combination’ of all possible attainable sets of player 2 (player 1), which are lines similar to Figure 2a (to Figure 2b). Notice that all profiles result in the same stationary distribution but different attainable sets here are unconditional RSs. Plots (b,c) depict all SRSs of players that joined in profiles generate this stationary distribution.
We now see the key difference between unconditional and conditional SRSs. For a memory-less strategy of the first player (i.e., ), the attainable set of the second player is a horizontal line. Similarly, for a memory-less strategy of the second player (i.e., ), the attainable set of player 1 is a vertical line; this is similar for mixed strategies in one-shot games. Hence, memory-less strategies only allow intercepts to be chosen. By contrast, conditional SRSs (i.e., and ) also allow slopes of attainable sets to be set. Thus, conditional SRSs have more flexibility in adjusting slopes of attainable sets to gradients of payoff functions at the stationary distributions (the points where players’ attainable sets intersect). This flexibility provides significantly more opportunities for equilibria to emerge (compared to memory-less mixed strategies).
Proposition 1.
For a one-shot game , any NE profile in mixed strategies becomes the corresponding NE profile in both and .
Proof.
Fix the memory-less RS of player 1 corresponding to an equilibrium in a one-shot game . We will show that is a best response to in . By Remark 1, for player 2, deviations in unconditional strategies are “operationally equivalent” to deviations in conditional strategies – that is, if player 2 can deviate, then he can deviate with a strategy of the form . If player 2 picks an unconditional RS we arrive at the stationary distribution Combining the last fact with (5), we obtain that
From the definition of NE in mixed strategies in , it follows that as a function defined on attains its maximum at By (10) and the above argument on the operational equivalence,
Thus, unconditional RS which emerges from the stage game NE, “remains” the best reply to in (and hence in ). Symmetrically, is a best response to and hence the profile is an NE in (hence, in ). □
Remark 2.
Note that players are free to move within their attainable sets from one point (stationary distribution) to another in a variety of ways. Moreover, for a stationary distribution within an attainable set of one player, there are infinitely many strategies leading to this stationary distribution for the given opponent’s strategy. In turn, the choice among these strategies leads to distinct attainable sets for the opponent. For example, Figure 3 shows the set of all possible strategy profiles leading to the stationary distribution Figure 3a depicts all possible slopes of players’ attainable sets. Note that the lines circumscribing the shaded regions have simple analytic representations. This allows us to infer all possible players’ strategies generating this stationary distribution. Namely, any pair of u from Figure 3c and v from Figure 3c leads to the same stationary distribution . All such that the stationary distribution equals induce the attainable sets inside the shaded regions.
2.2. Prisoner’s Dilemma with Equal Gains from Switching
We consider , a Prisoner’s Dilemma with equal gains from switching (see [4]),

Equal gains from switching implies that clearly, we have For the repeated version of we have (see (1) and (5))
Lemma A2 tells us that every pair of well-defined SRSs such that and forms a Nash equilibrium. Figure 4 illustrates that for player 1, curves-of-equal-payoff coincide with attainable sets if player 2 uses the above equilibrium strategies, meaning that equilibrium strategies fix the opponent’s payoff:
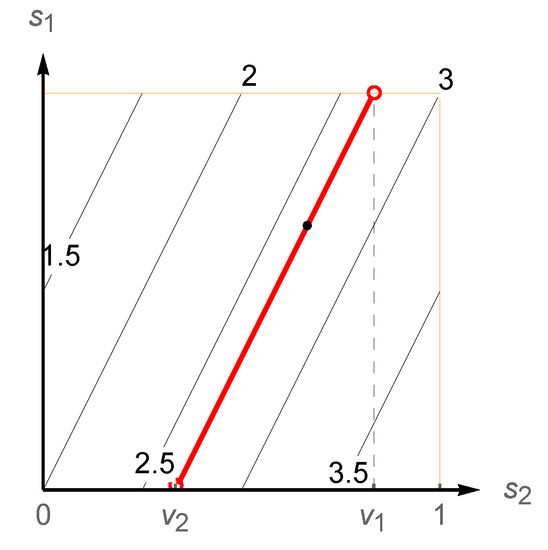
Figure 4.
Thin lines correspond to curves-of-equal-payoff for player 1. As before, the red line corresponds to the attainable set of player 1 for Here, coincides with the curve of payoffs equal to Strategies form a Nash equilibrium with the ESD .
The reactive strategy is known as generous tit-for-tat [24]; it leads to the most cooperative symmetric equilibrium.
Note that an equilibrium can only be sustained if both players choose strategies u and v such that and Value directly encourages player 1 to cooperate. Specifically, if then player 1 has an incentive to climb the attainable set by choosing more cooperative strategies increasing and . If then player 1 has an incentive to step down the attainable set; this decreases and . Clearly, memory-less SRSs can not support Nash equilibria. For example, the attainable sets of player 1 become vertical lines, giving her clear incentives to defect since her payoff increases moving from top to bottom of the attainable sets. Note that, generally, curves-of-equal-payoff are non-linear; see the example in Appendix C.1.
2.3. Characterization of Nash Equilibria in
Since every NE is formed by strategies that are best responses to each other, we proceed further with a standard analysis using derivatives. Let stand for the derivative of a function w.r.t.
Lemma 2
(The necessary condition). If form a Nash equilibrium and is the corresponding ESD, then the following holds true:
Proof.
Define the functions by the rules:
We now obtain the first and second derivatives of these functions:
Theorem 1
(Characterization of all Nash equilibria). The set of all Nash equilibria coincides with the set of all solving the following system:
Proof.
Let denote the set of all Nash equilibria in stands for the set of all solving (18). Let us prove that
Take As (v) in (18) holds, is a pair of reactive strategies; . Obviously, (iv) ensures that is the corresponding stationary distribution; As (iii) in (18) holds true, we have three cases:
- 1.
- and
- 2.
- and (or, symmetrically, and ),
- 3.
- and
All cases are composed from similar elements: equalities and strong inequalities. We consider only two of these elements. The analysis for the others is similar. Suppose Then is a concave quadratic function (see (13)). Conditions (i) and (iii) ensure that is a local maximum of see (14), (15). As local maxima of concave functions are also global maxima, we have
Assume Thus, and/or If then player 2 uses the repeated version of her mixed Nash equilibrium strategy. If then it follows from (13) and (i) in (18) that We have already observed this effect in the example of Section 2.2. Thus, in all cases, player 1 has a payoff independent of her strategy.
Consequently, and are the best responses to each other, meaning that
2.4. Existence of Nash Equilibria in Symmetric Games
In this section, we obtain conditions for the existence of NE when players are identical (one-shot games are symmetric). We fix a symmetric game

This allows us to introduce the following convenient definitions:
If then
To reach the goal of the section, we must derive conditions on and c that ensure the existence of a solution of (18). Taking into account inequality (iii) in (18), in Appendix A, we study three possible cases: The next theorem combines Lemmas A1, A7 and A10 (see Appendix A.1, Appendix A.2 and Appendix A.3, respectively).
Theorem 2.
For repeated symmetric games, there exists a reactive Nash equilibrium iff one of the following conditions holds true:
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
In this paper, we focus on symmetric stage games due to tractability of the corresponding results. Appendix C.2 shows an example of a non-symmetric stage game.
2.5. If All RSs Are Available
In this paper, players’ strategy sets do not include conditional deterministic and semi-deterministic RSs, and we focus only on equilibria generated by SRSs. Thus, in , the set of all possible profiles was instead of the set of all profiles in RSs. Let us discuss how this decision influences the NE profiles in SRSs.
Recall that for the premises of the Kakutani fixed-point theorem do not hold, as the strategy set is not compact, although payoff functions are continuous. Thus, the existence of an NE in an arbitrary game is not guaranteed. By simply allowing all RSs, the strategy set becomes compact, but the payoff functions become dependent on initial action profiles, making payoff functions no longer continuous and properly defined. The last fact is due to payoff-relevance of the initial round for some strategy profiles. Thus, one may decide to complement strategies with one extra variable, an initial action, leading to more complicated analysis. There are two approaches that can be used to avoid the complication. The first approach, the one used for discounted payoffs, is to assume that nature draws initial actions. In this case, one may consider only equilibria that hold independently of initial moves (see [17,18]); actual equilibrium payoffs may depend on the initial actions. The second approach, which is possible for the-limit-of-means setting and is used in this article, is to restrict the strategy set such that players’ payoffs are independent of initial actions. Both approaches ensure that any equilibrium holds for all opening moves.
Starting with the restricted strategy sets, one may ask, what if we extend the set of strategies to include all RSs? How would it influence the set of all equilibria? One straightforward aspect is that new equilibria may form. The second (less obvious) aspect is that we increase players’ abilities to deviate; this may erase some existing equilibria.
Regarding the first aspect, the precise answer requires a thorough analysis that can not be included in this paper since, as we mentioned above, the results will depend on initial actions. More importantly, the value of such results is not obvious.
Regarding the second aspect, the characterization of all Nash equilibria generated by SRSs remains valid independently of initial moves, even if one considers the setting where all RSs are available for players. Let us show this. Consider player 1. If player 2 picks an SRS , then the corresponding stationary distribution is well defined by (4) for all RSs of player 1 and does not depend on initial actions. For player 1, in terms of payoff-relevant deviations, the set of RSs is equivalent to
3. Equilibrium Payoffs in Conditional SRSs
In this section, we compare equilibrium payoffs in conditional SRSs versus unconditional RSs in the following simple way. First, we fix a stage game such that Theorem 2 gives us an NE in SRSs. The repeated version inherits all equilibrium payoff profiles from that are generated by the corresponding unconditional RSs. Among these payoff profiles, we select the symmetric one with the lowest payoffs as the benchmark. We then compare the best symmetric NE payoff profile in formed by SRSs against this benchmark. Since we have existence results only for symmetric games, the complete analysis is only feasible for this special case. Nevertheless, the existence of an NE in memory-less SRSs implies the existence of an NE in conditional SRSs that allows us to compare the corresponding payoffs even for non-symmetric games. The next subsection presents this partial result; afterwards, we complete analysis for symmetric games.
3.1. Payoffs for NE Profiles of Unconditional and Conditional SRSs
From (4) and Theorem 1, it follows that any admitting solutions of the system
forms a NE. Note that (22) is a system of six equations with eight variables. We consider or as free parameters to express the remaining variables; x and y are introduced to simplify the notation. We omit the rather simple case and start solving the system under the assumption that
Assume that a completely mixed NE exists in a one-shot game . Then is the corresponding NE profile since . Furthermore, and form an NE in by Proposition 1. Indeed (see (5)),
The next proposition shows that for both players, equilibrium payoffs in conditional SRSs are at least equilibrium payoffs in memory-less SRSs.
Proposition 2.
Suppose that and there exists an NE profile of memory-less SRSs in (hence in ); then, for any NE profile of conditional SRSs in , the following holds true
Let us outline the proof. From (1) and (5), we have as a function of stationary distributions. Since we deal with ESDs, we use formulas for and from (23). Hence, become functions of only x and y that are defined by the NE profile these equilibrium profiles exists by our assumption. Using (24) and (25), it remains only to perform some algebra and to recall that (see the last line in (23)).
3.2. Symmetric Games
For symmetric games, results in Section 2.4 allow us to gain more understanding on how equilibrium payoffs in conditional SRSs compare to the benchmark payoffs in memory-less RSs. Note that a generic one-shot symmetric game with distinct payoffs on the leading diagonal is strategically equivalent to
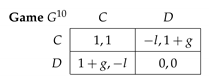
Generic one-shot symmetric games with identical payoffs on the leading diagonal are considered in Appendix B. Using these generic games, we study equilibrium payoffs for games satisfying the conditions of Theorem 2. For , Figure 5 shows all pairs of such that there exists an equilibrium according to Theorem 2. For example, the first condition results in trivial stage games that cannot be. The second condition (region 2) restricted to Quadrant I, includes prisoner’s dilemmas with equal gains from switching. Quadrant I contains all prisoner’s dilemmas and the entire region 5 that embodies the ones where cycles are more profitable than cycles
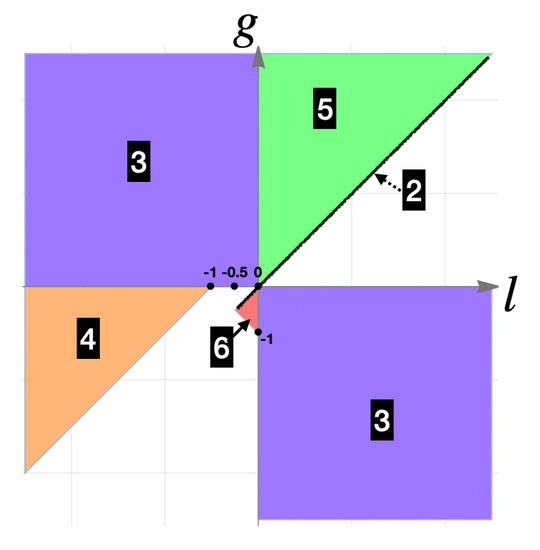
Figure 5.
The numbered regions are derived from the conditions of Theorem 2 that ensures existence of NE for the repeated modification of generic game for possible values of l and g.
Region 3 completely covers Quadrant II and IV where all stage games with two pure equilibria are located; here, we have completely mixed NE for stage games and, hence, an equilibrium profile in memory-less SRSs for the repeated versions. If by Proposition 2, there exists an NE profile of conditional SRSs that Pareto dominates the benchmark of NE payoffs for memory-less SRSs; else all ESDs (hence, NE payoff profiles) for conditional and unconditional SRSs coincide.
Quadrant III contains all deadlock games, which have one dominant strategy with the equilibrium payoff being Pareto optimal. This property makes deadlock games of the least interest for theory since self-interest and mutual benefit are fully compatible. The repeated versions of games from region 4 have NE payoff profiles Pareto dominating this unconditional benchmark. Thus, in all cases considered up to this point, an equilibrium profile in conditional SRSs provides greater or equal payoffs than the benchmark equilibrium profile in memory-less RSs. The exceptions to this rule are region 2, restricted to Quadrant III, and region 6 that contain very special deadlock games: both players (by choosing dominating pure strategy) get the highest possible individual payoff. Because of this unique property, the repeated versions of these one-shot games are the only cases when all NE profile in conditional SRSs are Pareto dominated by any equilibrium profile in memory-less RSs. We provide an example of such game in Section 3.3. Finally, all one-shot games in region 6, after we swap strategies for both players, comply with condition 7 in Theorem 2; i.e., conditions 6 and 7 cover strategically equivalent deadlock games.
Appendix B provides the similar analysis for generic symmetric games with identical payoffs on the leading diagonal, where we conclude that in the cases when payoffs of the stage game are not diverse enough, and payoffs of NE profiles in SRSs coincide with the memory-less benchmark. Otherwise, there exists an NE profile in SRSs that Pareto dominates the benchmark.
Let us summarize both cases of the generic games. Only in the very special deadlock games where both players (by choosing dominating pure strategy) get the highest possible individual payoff, payoff profiles in conditional SRSs are dominated by the benchmark unconditional payoff profiles; see the next subsection for an example. In the remaining cases, if distinct ESDs do exist, then there exists an NE profile in SRSs dominating the benchmark.
3.3. A Game with Pareto-Efficient Equilibrium and Dominant Strategies
The following example highlights one counterintuitive property of NE in SRSs by showing that it is possible to establish equilibria with lower payoffs by introducing a more complex class of strategies. Consider the following symmetric game .
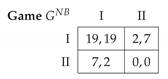
Once we scale all payoffs into the range , the stage game falls into region 6 of Figure 5. Here and According to Theorem 2, a NE in SRSs exists; we depict the set of all ESDs in Figure 6. A mixed NE in the stage game does not exist since . The profile of the memory-less RSs forms an NE and corresponds to the Pareto-efficient pure NE in the stage game. This equilibrium is excluded from our characterization as we are focusing on equilibria in SRSs. Remarkably, there is a noticeable gap between this equilibrium payoff, serving as memory-less benchmark, and payoffs corresponding to ESDs in the repeated game. For any , there exists a Nash equilibrium such that is the ESD. For example, equilibrium strategies and generate the ESD with payoffs (compare with 19). Thus, the example shows that it is possible to establish equilibria with lower payoffs by introducing a more complex class of strategies.
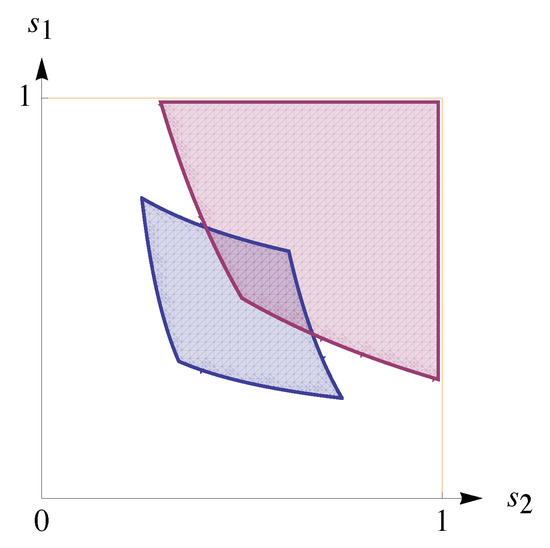
Figure 6.
The blue set is the set of all ESDs for the red set is the set of all stationary distributions such that both players get payoffs greater than 7 (the second-highest payoff in the one-shot game).
4. Conclusions
We show analytically that even an incremental change of complexity of strategies (an inch of memory) in repeated interactions has a huge influence on the sets of equilibrium payoff profiles for some classes of stage games that are circumscribed by Theorem 2. The first thing to note is that except for some trivial cases, payoff-relevant indeterminacy holds true [17]; i.e., there now exists a continuum of equilibria in “new” conditional strategies with distinct payoff profiles. Clearly, there is still no folk theorem (see the example in Appendix C.1); this still holds [17] for the next incremental improvement, 1-memory strategies. It is also now evident that one should not expect some consistency while incrementally increasing the memory of strategies. For example, in RSs, there exist equilibria with higher payoffs than the upper bound obtained independently of the discount factor in [17] (see the example in Appendix C.1) and the reverse dominance condition [17], which is important for the 1-memory case, does not influence the existence of NE in RSs.
In this paper, we focused on symmetric stage games due to tractability of the corresponding results. Appendix C.2 shows the example of a non-symmetric stage game where the set of all ESDs looks like a special combination of the corresponding sets for two symmetric stage games derived from the payoff matrix. This may be a way to study a broad class of non-symmetric stage games. An alternative approach may be to study specific classes of non-symmetric stage games, e.g., strategically zero-sum games [25].
In all examples considered so far, the region of all ESDs was a connected set. Appendix C.3 demonstrates the example with disconnected regions of equilibria. A branch of literature assumes that we may have some local dynamics on the set of all Nash equilibria, e.g., in the spirit of adaptive dynamics [4] or local cooperation patterns [26]. This example calls for new models to tackle the issue of disconnectedness that may be an obstacle on the way to higher equilibrium payoffs.
As for future work, we note that the idea of a reactive strategy was recently generalized to “reactive learning strategy” [27] allowing a player to gradually change the probability of actions depending on the past actions of the opponent. It is not known how the change from reactive strategies to reactive learning strategies would influence the equilibrium outcomes.
Funding
The study was supported by a grant from the Russian Science Foundation (project No. 20-71-00034). Note: all results were obtained at HSE University according to the tasks of the project (grant proposal) except for numerical simulations of sets of ESDs with Wolfram Mathematica, Appendix C.2 and Appendix C.3 that were not specified as tasks or deliverables in the project and were done during my visits in IIASA.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The author would like to thank all referees and my colleagues, especially Daniel T. Jessie and Egor Ianovski, for their valuable comments. The author would like to express his deepest gratitude to academician Arkady Kryazhimskiy and Elena Rovenskaya for encouraging this research.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ESD | Equilibrium stationary distribution |
| NE | Nash equilibrium |
| RS (SRS) | Reactive strategy (stochastic reactive strategy) |
| SME | Strong mixed equilibrium |
| SPE | Subgame perfect equilibrium |
| ZD | Zero-determinant (strategies) |
Appendix A. Existence of Equilibria in Symmetric Games
Let us derive conditions for (see (20)) that ensure the existence of solutions in (18). Inequalities (iii) in (18) lead to three possible cases:
Appendix A.1. Case a = 0
Assuming we obtain the specific version of (18):
Recall that solutions of this system generate the set of all Nash equilibria.
If then If and then Trivially, any pair of reactive strategies is a Nash equilibrium. If then we simplify (A1)
The recent statements lead us to the following lemma.
Lemma A1.
Suppose that in a symmetric game Then, there exists a reactive Nash equilibrium iff or
Note that in this case, a mixed Nash equilibrium exists only if
Lemma A2.
Suppose that in a symmetric game If and then any pair of reactive strategies is a Nash equilibrium. If then the set of all Nash equilibria coincides with the set of all pairs such that
where
If and then we have the following game:
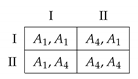
Here Trivially, in this case any stationary distribution is an ESD; the Nash equilibrium is formed by the strategies and which are repeated mixed strategies. These equilibria are not strict.
The set of all Nash equilibria from Lemma A2 generates the parallelogram of ESDs; see Figure A1. The area of the shaded regions tends to 1 as this is the idea behind the following propositions.
Proposition A1.
Every pair of reactive strategies such that forms Nash equilibria in symmetric games with and
Proposition A2.
For every stationary distribution , there exists such that is an ESD in all symmetric games with and
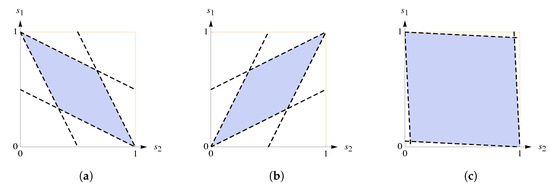
Figure A1.
The case The shaded regions in (a–c) depict the set of all ESDs for the games with respectively.
Though the case is degenerate, it is of interest in connection with ZD strategies [15]. These strategies are 1-memory ones. Since reactive strategies can also be treated as 1-memory strategies, we investigate the relationship between equalizer ZD and reactive strategies.
Lemma A3.
For symmetric games with a first player’s reactive strategy u is an equalizer ZD strategy if and
The proof is based on [15], (8). Here, for the 1-memory strategy , one has to substitute by the reactive one , and for the payoff profile one has to substitute This gives the system
Subtracting the first equation from the second one, we obtain The final part of the proof is trivial.
Proposition A3.
In symmetric games with , all reactive Nash equilibria are generated by equalizer ZD strategies.
Appendix A.2. Case a < 0
We now proceed with the case As before, we derive conditions (on ) that ensure the existence of solutions of (18). Before we proceed, let us express (22) for the symmetric games in terms of . If , and is an ESD, then the corresponding NE profile is defined by the following system:
From Theorem 1 we derive that for any equilibrium pair , the following holds true:
Since and we rewrite (i) and (ii) in (18)
First, we pay attention to a degenerate case. Suppose that there exists a solution to (A3) such that This is only possible if Assuming this, we get
Since a solution of (A4) may exist only if Assuming this, we get
Then there exists a solution iff this corresponds to the existence of the mixed Nash equilibrium. Clearly, the strategies and form a Nash equilibrium. We stress that this is not a unique solution to (A5) under the assumptions. However, all Nash equilibria lead to the same ESD and payoffs. Let us now combine our findings in the following:
Lemma A4.
If in a symmetric game and there is an ESD such that
then and the strategies and form a Nash equilibrium. Moreover, is the only possible ESD for the game.
For the remainder of this section, we suppose that We define the useful functions by the rules motivated by (A2)
Lemma A4 implies that if then are well defined for any ESD. Obviously,
Lemma A5.
In a symmetric game with for , there exists a Nash equilibrium with the corresponding ESD iff
Proof.
Assume that strategies lead to the ESD . Combining (A6) with (i) and (ii) in (A3), we get that Since are well defined strategies, it follows from (iii) in (A3) that
Suppose that for a stationary distribution recall that . To show that is an ESD, one has to ensure validity (i)–(v) in (A3) by demonstrating well-defined strategies and generating such that Let us recall the geometric representation of attainable sets; the difference between the first and second component of reactive strategies completely determines the slopes of the opponent’s attainable set (see Figure 2 and Figure 3). We see that it is always possible to draw an attainable set of player 1 (straight line) through the point with the slope defined by if As a result we obtain the well-defined reactive strategy . In the same way, we derive well-defined such that By construction, and generate □
Lemma A6.
Suppose that in a symmetric game with a Nash equilibrium exists with the ESD Then, and are ESDs too.
Proof.
There are two cases: and The proof is trivial in the first case. In the second case, by using the symmetry of the game, it is easy to prove the existence of ESD As corresponds to some Nash equilibrium and , for and , we have (see (A2)). Let us now consider such that It is easy to show that in this case,
Straightforwardly, Moreover, Thus, Combining this with Lemma A5, we obtain that is an ESD. □
Corollary A1.
In symmetric games with there exists a Nash equilibrium iff there exists a pair of identical reactive strategies forming a Nash equilibrium. The last is equivalent to the existence of an ESD for some
The next theorem provides a necessary and sufficient condition for the existence of a Nash equilibrium.
Theorem A1.
In symmetric games with there exists a Nash equilibrium iff there exists a stationary distribution such that
The proof is a combination of Lemma A5, Lemma A6, and the last corollary. Further, we derive conditions such that there exists a solution in (A8). By definition, put
We stress that if then and sign of a completely characterize Nash equilibria in symmetric games. The solution of (A8) is the union of two regions:
Lemma A7.
For symmetric games with there exists a Nash equilibrium iff
Remarkably, some symmetric games allow to be an ESD for every
Proposition A4.
In a symmetric game, is an ESD for all if and
Appendix A.3. Case a > 0
An analysis in this case is more involved, but quite similar. It follows from Theorem 1 that for every equilibrium the following holds: For the remainder of this section, we suppose that as Lemma A4 was obtained independently of the sign of We start with an analog of Lemma A5; see also (A7).
Lemma A8.
In symmetric games with for there exists an ESD iff
In symmetric games with for there exists an ESD iff
We omit the proof based on the inference of analytic formulas for tangents (slopes) of border lines similar to the ones in Figure 3a. These formulas provide the lower bounds for in (A14) and (A15). The next step is to derive an analog of Lemma A6.
Lemma A9.
If in symmetric games with a Nash equilibrium exists with the ESD then and are ESDs too.
Proof.
There are two cases: and The proof is trivial in the first case. In the second case, by using symmetry, it is easy to prove the existence of a Nash equilibrium with the ESD We consider three cases: and Analyses of the cases are similar; therefore, we proceed only with case Without loss of generality, we assume that Since is a Nash equilibrium, there exists the pair such that and We infer analytic formulas for the tangents of border lines similar to those in Figure 3a to derive the following restriction:
We stress that any pair of reactive strategies leading to complies with
Let us now consider value we have Straightforwardly, Moreover, Thus, In contrast to Lemma A6, the last statement is insufficient to apply Lemma A8. We also need to prove a stronger result (see (A15)):
First, we obtain derivatives of w.r.t. :
For all functions and are monotonically nondecreasing on Thus, attains minimum on at
Recall that we are proving (A16). Since and we obtain that
It follows from Lemma A8 that is an ESD. □
Corollary A2.
In symmetric games with there exists a Nash equilibrium iff there exists a pair of identical reactive strategies forming a Nash equilibrium. The latter is identical to the existence of an ESD for some
The next theorem provides a necessary and sufficient condition for the existence of a Nash equilibrium.
Theorem A2.
In symmetric games with there exists a Nash equilibrium iff there exists an ESD such that
The proof is a combination of Lemma A8, Lemma A9, and the last corollary. Let us derive conditions ensuring the existence of a solution in (A17). As before, we use the notation We decompose (A17) into two systems of the inequalities:
We begin with (A18). Arguing as in the case we obtain that the conditions
admit solutions of (A18). We proceed to (A19). First, (A19) can be transformed in
(an instance of (A18)) by applying the following rules:
Substituting , and in (A21), we get
Simplifying, we have this chain of inequalities is identical to (A19). Thus, bijective rules (A22) provide an easy way for one-to-one transformation of problem (A19) into problem (A18), which was solved in (A20). Using (A20), we solve the problem for (A21):
Lemma A10.
If then there exists a reactive Nash equilibrium iff
Appendix B. Theorem 2 for Symmetric Games with Equal Payoffs on the Leading Diagonal
A generic one-shot symmetric game with identical payoffs on the leading diagonal is strategically equivalent to
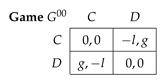
Figure A2 shows all pairs of such that there exists an equilibrium in the repeated version of in SRSs by Theorem 2.
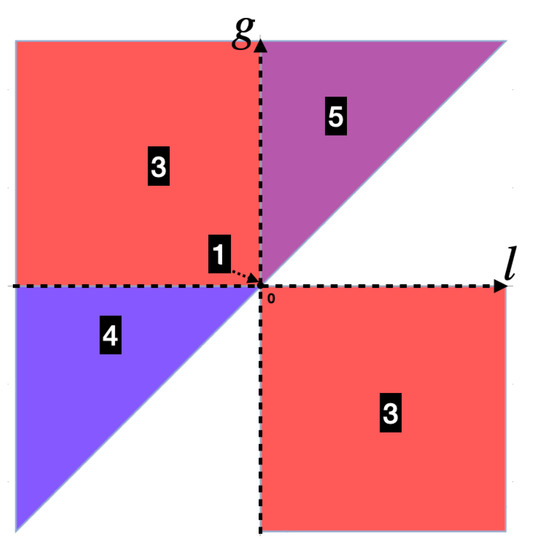
Figure A2.
The numbered regions are derived from the corresponding conditions of Theorem 2. The regions specify all l and g such that there exists an NE profile in SRSs for the repeated modification of .
Table A1 contains the corresponding case analysis. In general, there exists an NE profile in conditional SRSs that Pareto dominates a benchmark NE profile in memory-less reactive strategies. Thus, an inch of memory for players (upgrading memory-less RSs to conditional SRSs) brings new equilibria where they both better off. Only a very special type of this one-shot games is the exception to this rule, i.e., games with

Table A1.
Summary for Theorem 2 for symmetric games with equal payoffs on the leading diagonal.
Table A1.
Summary for Theorem 2 for symmetric games with equal payoffs on the leading diagonal.
| Condition of the Theorem | One-Shot Game Description | The Benchmark in Memory-Less RSs | NE Payoffs in Conditional SRSs |
|---|---|---|---|
| 1 | A trivial stage game with identical payoffs | Any profile of memory-less RSs forms a NE with payoffs | Any profile of conditional RSs forms an NE with payoffs |
| 2, 6, and 7 | Can not hold for | ||
| 3 | Coordination and anti-coordination stage games with two pure equilibria | There is an NE profile in memory-less SRSs with payoffs | If then there exists an NE profile of conditional SRSs Pareto dominating the memory-less benchmark. If then there is an unique ESD ; all payoff profiles of equilibria in SRSs coincide. |
| 4 and 5 | Stage games having one dominant pure strategy; any symmetric profile of mixed strategies Pareto improves the NE payoffs | Payoff profile of dominant strategies | Any NE profile of conditional SRSs Pareto dominates the memory-less benchmark. |
Appendix C. Additional Examples
In this section, we provide examples illustrating properties of reactive Nash equilibria. In what follows, we use definitions given in (2), (3), and (20). Recall that for symmetric games, if
Appendix C.1 presents two examples of the Prisoner’s Dilemma to demonstrate non-symmetric equilibria. In the first example we observe equilibrium strategies leading to payoffs that are higher than the mutual cooperation payoff. In the second example, one can see that there exist equilibria that admit any level of mutual cooperation. We then consider an example of non-symmetric games admitting equilibria that may be incorrectly recognized as symmetric ones; see Appendix C.2. Finally, in Appendix C.3, we highlight the example that makes it possible to observe disconnected regions of equilibria. Assume that we have some dynamics on the set of all Nash equilibria in the spirit of adaptive dynamics [4] or local cooperation patterns [26]. This disconnectedness becomes an obstacle on the way to higher equilibrium payoffs.
Appendix C.1. Non-Symmetric Equilibria in Prisoner’s Dilemma and Folk Theorem
Reactive strategies were introduced to study the evolution of cooperation in the repeated Prisoner’s Dilemma. Recall that in [4,5] symmetric equilibria in the repeated Prisoner’s Dilemma were characterized. The following examples illustrate an abundance of non-symmetric equilibria in repeated Prisoner’s Dilemmas. Consider two games:
A mixed Nash equilibrium does not exist in both games.
Game . Here This Prisoner’s Dilemma is different from the standard versions since Hence, contrary to the standard setting, infinite cycles like are more profitable for both players than the infinite mutual cooperation. As a result, in some equilibria, both payoffs are strictly better off than the mutual cooperation payoff; see Figure A3a. For example, equilibrium strategies and lead to the ESD with the payoffs which are greater than the mutual cooperation payoff 5.
Game . Here, We depict the set of all ESDs in Figure A3b. It follows from Proposition A4 that for any there exists a Nash equilibrium such that is the ESD. Therefore, there are equilibria admitting any level of mutual cooperation. For example, equilibrium strategies lead to the ESD
Figure A3.
The blue sets in (a,b) depict the sets of all ESDs for and respectively. The red region corresponds to all stationary distributions such that both players get more than the mutual cooperation payoff (this is possible only in ).
Figure A4 shows that to ensure an equilibrium, player 2 must choose and not the other way round. For an equilibrium with a higher rate of cooperation, player 2 must increase even further. Generally, the greater the difference the less attractive the defection for player 1. In (a), the strategy sets the attainable set of player 1 (the straight line) to be a tangent to the curve of payoffs equal to at the ESD In (b), the strategy incentivizes player 1 to descend in the attainable set (the straight line) to the unconditional defection.
Figure A4.
For plots (a,b) depict the first player’s attainable sets (the straight lines) for and respectively. The thin lines correspond to the payoff levels equal to .
The range of all possible payoffs for SMEs was obtained in [17] proving that there is no folk theorem (see [17], Corollary 2, Theorem 4). For example, for game , all SME payoffs are in for any discount factor. In [28], Section 4, the repeated Prisoner’s Dilemma was considered as an example of a game with non-rich action spaces. It was rigorously shown that there are no efficient payoff vectors corresponding to subgame perfect equilibria in deterministic 1-memory strategies, even if the discount factor is close to one. However, by introducing an additional pure action, it becomes possible to obtain an efficient outcome, which is higher than the upper bound for SME payoffs.
Figure A5 shows that there are Nash equilibria in with payoffs higher than would be ensured by the mutual cooperation, although not all individually rational payoffs are supported by reactive equilibria. First, this means that there are ESDs with payoffs for both players that are higher than the upper bound shown in [28] (for equilibria in deterministic 1-memory strategies) and in [17] (for SMEs). Second, similarly to [17], in our case there is no folk theorem.
Figure A5.
The blue set corresponds to all ESD. The brown set corresponds to distributions with individually rational payoffs (greater or equal to 0); the red set corresponds to distributions such that both payoffs are in range .
Appendix C.2. Symmetric ESD in Non-Symmetric Games
Consider the non-symmetric game 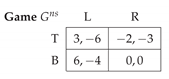 admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.
admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.
 admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.
admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.It is easy to see that Note that this is impossible for symmetric games. Figure A6c depicts the set of all ESDs; we see an abundance of symmetric ESDs. One can also see a clear connection between the non-symmetric game and two symmetric games (see Figure A6a,b) constructed directly from players’ payoff matrices.
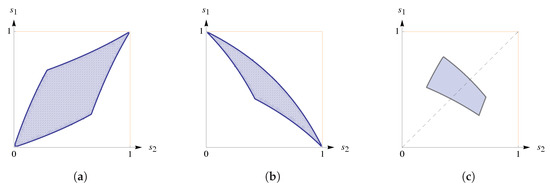
Figure A6.
Plots (a–c) depict the set of all ESDs for the symmetric game with , , for the symmetric game with and non-symmetric respectively.
Appendix C.3. Games with Disconnected Regions of ESDs
Let us demonstrate that in the case it is possible to observe disconnected regions of ESDs. Consider the stage game

Note that there exists a mixed NE in the stage game. For , we have , , We depict the set of all ESDs in Figure A7a and all possible symmetric equilibria in Figure A7b.
Assume that we have some dynamics on the set of all Nash equilibria in the spirit of the adaptive dynamics [4] or local cooperation patterns [26]. This disconnectedness then becomes an obstacle on the way to higher equilibrium payoffs.
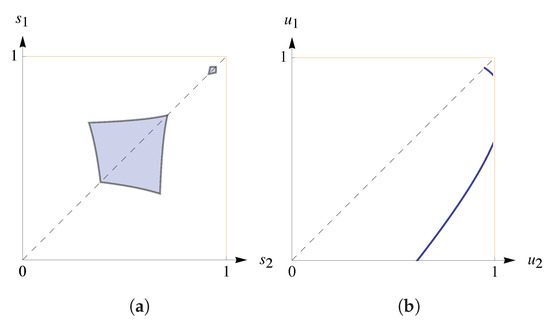
Figure A7.
Plots (a,b) depict all ESDs and all symmetric equilibria for respectively.
References
- Mailath, G.J.; Samuelson, L. Repeated Games and Reputations: Long-Run Relationships; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kalai, E. Bounded Rationality and Strategic Complexity in Repeated Games. In Game Theory and Applications; Academic Press, Inc.: San Diego, CA, USA, 1990; Chapter V; pp. 131–157. [Google Scholar]
- Dal Bó, P.; Fréchette, G.R. Strategy Choice in the Infinitely Repeated Prisoner’s Dilemma. Am. Econ. Rev. 2019, 109, 3929–3952. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. The evolution of stochastic strategies in the Prisoner’s Dilemma. Acta Appl. Math. 1990, 20, 247–265. [Google Scholar] [CrossRef]
- Nowak, M. Stochastic strategies in the Prisoner’s Dilemma. Theor. Popul. Biol. 1990, 38, 93–112. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sigmund, K. Adaptive dynamics and evolutionary stability. Appl. Math. Lett. 1990, 3, 75–79. [Google Scholar] [CrossRef]
- Kalai, E.; Samet, D.; Stanford, W. A note on reactive equilibria in the discounted prisoner’s dilemma and associated games. Int. J. Game Theory 1988, 17, 177–186. [Google Scholar] [CrossRef]
- Aumann, R.J. Repeated Games. In Issues in Contemporary Microeconomics and Welfare; Feiwel, G.R., Ed.; Palgrave Macmillan: London, UK, 1985; Chapter 5; pp. 209–242. [Google Scholar] [CrossRef]
- Friedman, J.W. Reaction Functions and the Theory of Duopoly. Rev. Econ. Stud. 1968, 35, 257–272. [Google Scholar] [CrossRef]
- Stanford, W.G. Subgame perfect reaction function equilibria in discounted duopoly supergames are trivial. J. Econ. Theory 1986, 39, 226–232. [Google Scholar] [CrossRef]
- Kamihigashi, T.; Furusawa, T. Global dynamics in repeated games with additively separable payoffs. Rev. Econ. Dyn. 2010, 13, 899–918. [Google Scholar] [CrossRef][Green Version]
- Friedman, J.W.; Samuelson, L. Continuous Reaction Functions in Duopolies. Games Econ. Behav. 1994, 6, 55–82. [Google Scholar] [CrossRef]
- Kryazhimskiy, A. Equilibrium stochastic behaviors in repeated games. In Abstracts of International Conference Stochastic Optimization and Optimal Stopping; Steklov Mathematical Institute: Moscow, Russia, 2012; pp. 38–41. [Google Scholar]
- Press, W.H.; Dyson, F.J. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, C.; Traulsen, A.; Sigmund, K. Partners or rivals? Strategies for the iterated prisoner’s dilemma. Games Econ. Behav. 2015, 92, 41–52. [Google Scholar] [CrossRef]
- Dutta, P.K.; Siconolfi, P. Mixed strategy equilibria in repeated games with one-period memory. Int. J. Econ. Theory 2010, 6, 167–187. [Google Scholar] [CrossRef]
- Ely, J.C.; Välimäki, J. A Robust Folk Theorem for the Prisoner’s Dilemma. J. Econ. Theory 2002, 102, 84–105. [Google Scholar] [CrossRef]
- D’Arcangelo, C. Too Much of Anything Is Bad for You, Even Information: How Information Can Be Detrimental to Cooperation and Coordination. Ph.D. Thesis, University of Trento, Trent, Italy, 2018. [Google Scholar]
- Abreu, D.; Rubinstein, A. The Structure of Nash equilibrium in Repeated Games with Finite Automata. Econom. J. Econom. Soc. 1988, 56, 1259–1281. [Google Scholar] [CrossRef]
- Marks, R. Repeated games and finite automata. In Recent Developments in Game Theory; Edward Elgar Publishing: Cheltenham, UK, 1992; pp. 43–64. [Google Scholar]
- Baek, S.K.; Jeong, H.C.; Hilbe, C.; Nowak, M.A. Comparing reactive and memory-one strategies of direct reciprocity. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M. An evolutionarily stable strategy may be inaccessible. J. Theor. Biol. 1990, 142, 237–241. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Moulin, H.; Vial, J.P. Strategically zero-sum games: The class of games whose completely mixed equilibria cannot be improved upon. Int. J. Game Theory 1978, 7, 201–221. [Google Scholar] [CrossRef]
- Kleimenov, A.; Kryazhimskiy, A. Normal Behavior, Altruism and Aggression in Cooperative Game Dynamics; IIASA: Laxenburg, Austria, 1998. [Google Scholar]
- McAvoy, A.; Nowak, M.A. Reactive learning strategies for iterated games. Proc. R. Soc. A 2019, 475, 20180819. [Google Scholar] [CrossRef]
- Barlo, M.; Carmona, G.; Sabourian, H. Repeated games with one-memory. J. Econ. Theory 2009, 144, 312–336. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).