Nudging Climate Change Mitigation: A Laboratory Experiment with Inter-Generational Public Goods
Abstract
1. Introduction
2. A Game of Multi-Level Conflict in Climate Change Mitigation
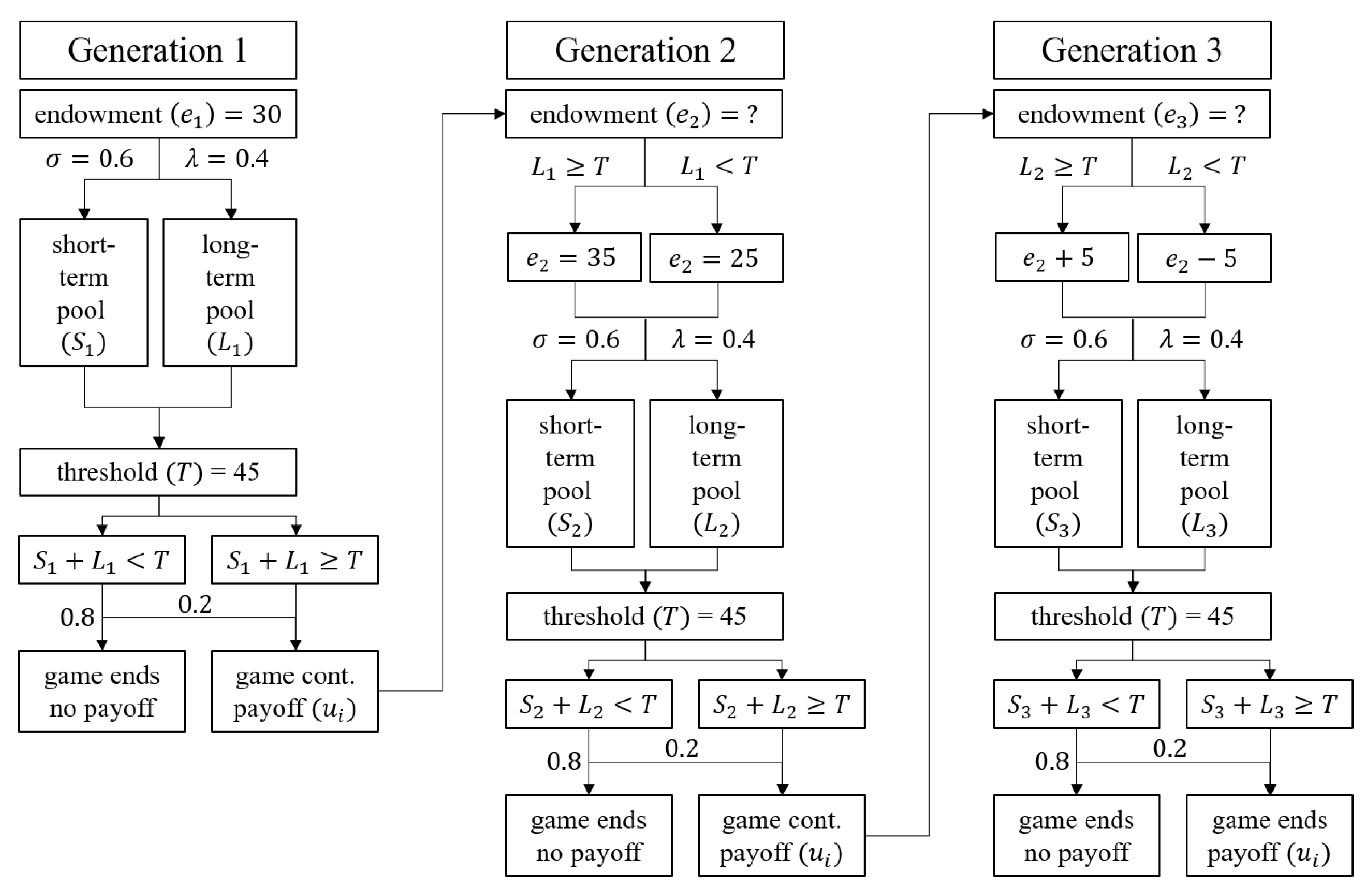
2.1. Players and Generations
2.2. Intra-Generational Conflict
2.3. Inter-Generational Conflict
2.4. Game Predictions
2.5. Game Parameters
3. Related Literature
3.1. Conflict Structure of Climate Change Mitigation
3.2. Nudges toward Climate Change Mitigation
4. Treatments and Hypotheses
5. Materials and Methods (Experimental Procedures)
6. Results
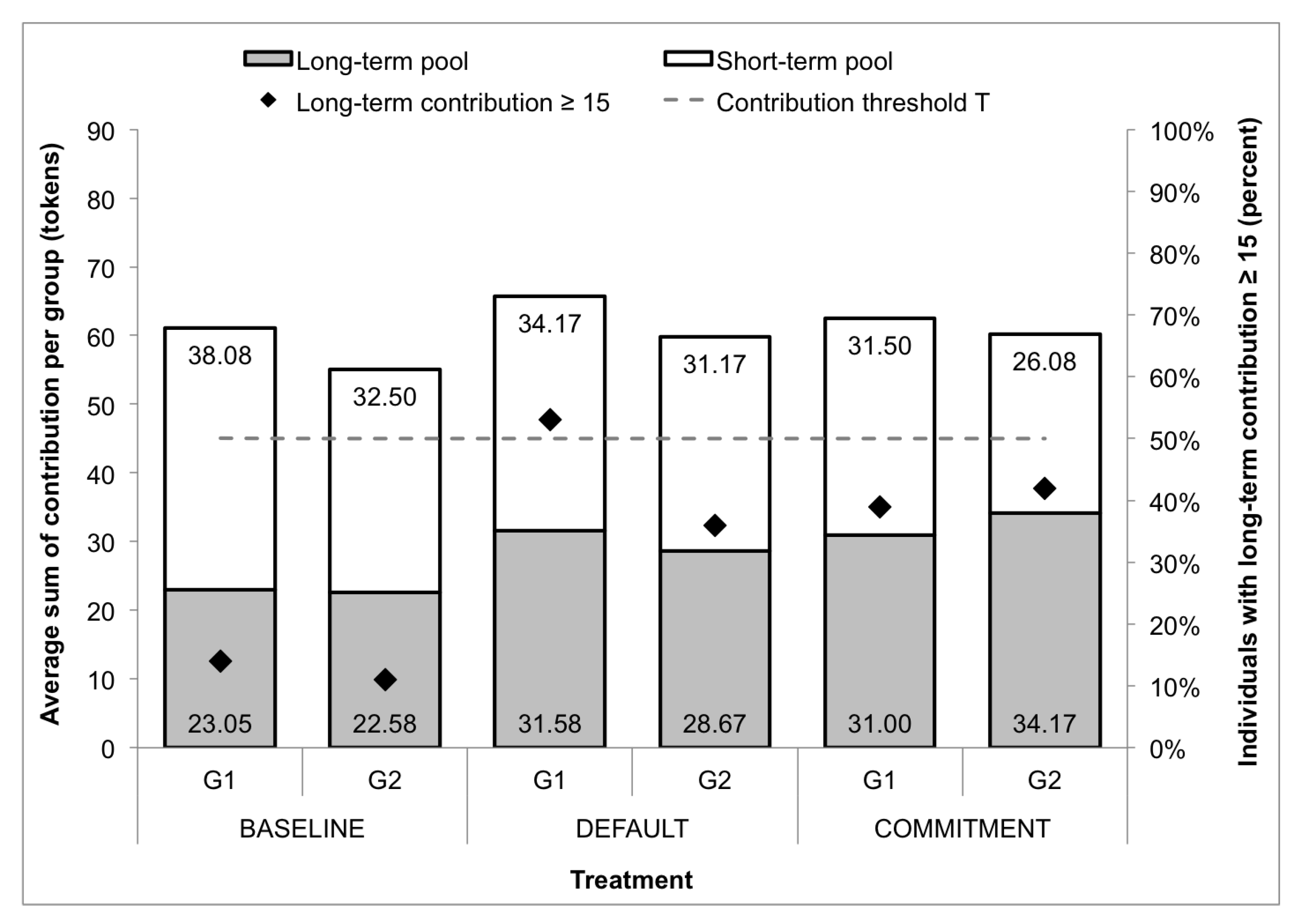
6.1. Contributions in the baseline Treatment
6.2. Contributions in the default Treatment
6.3. Contributions in the default+commitment Treatment
6.4. Regression Analysis
7. Discussion
7.1. Limitations and Outlook
7.2. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
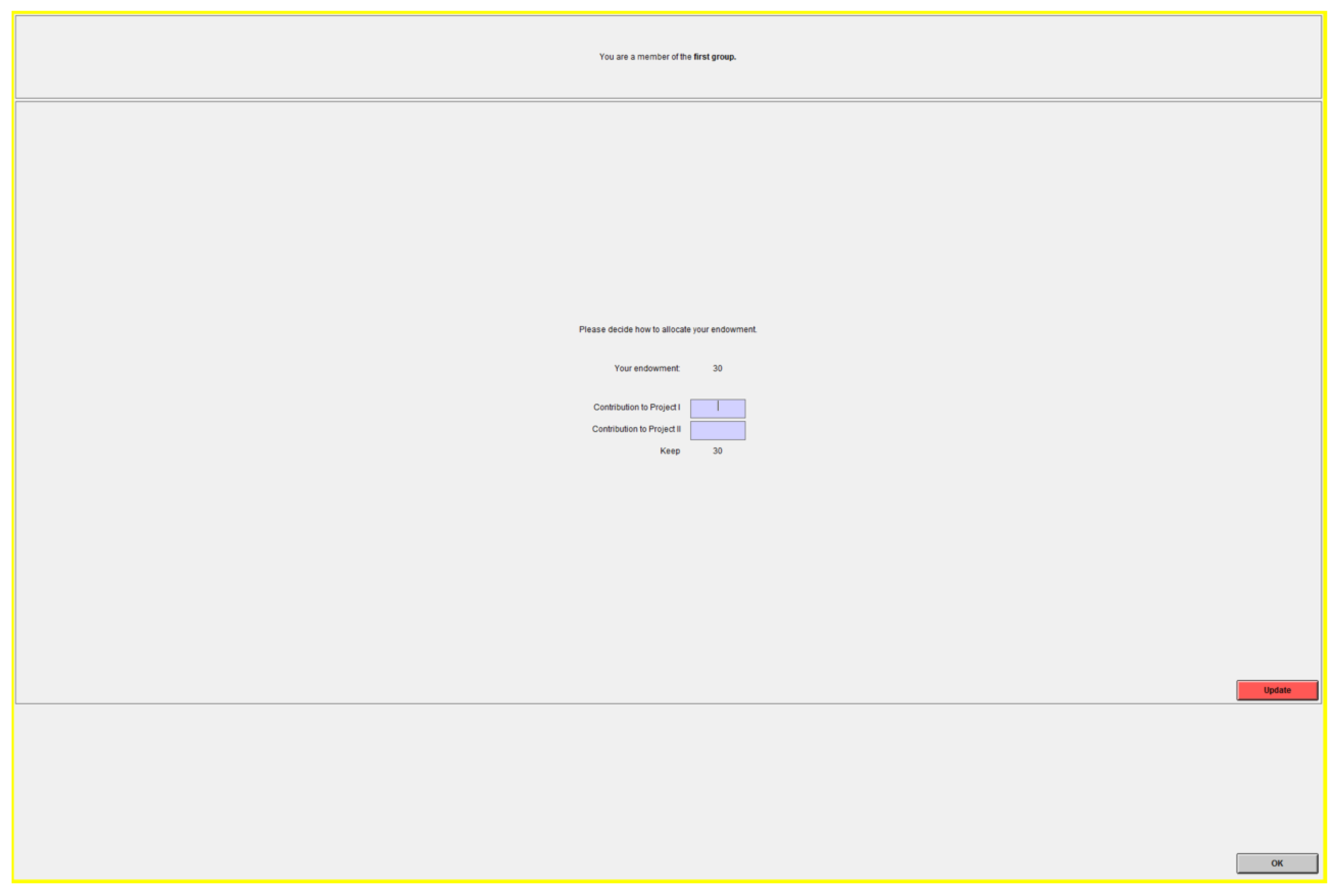
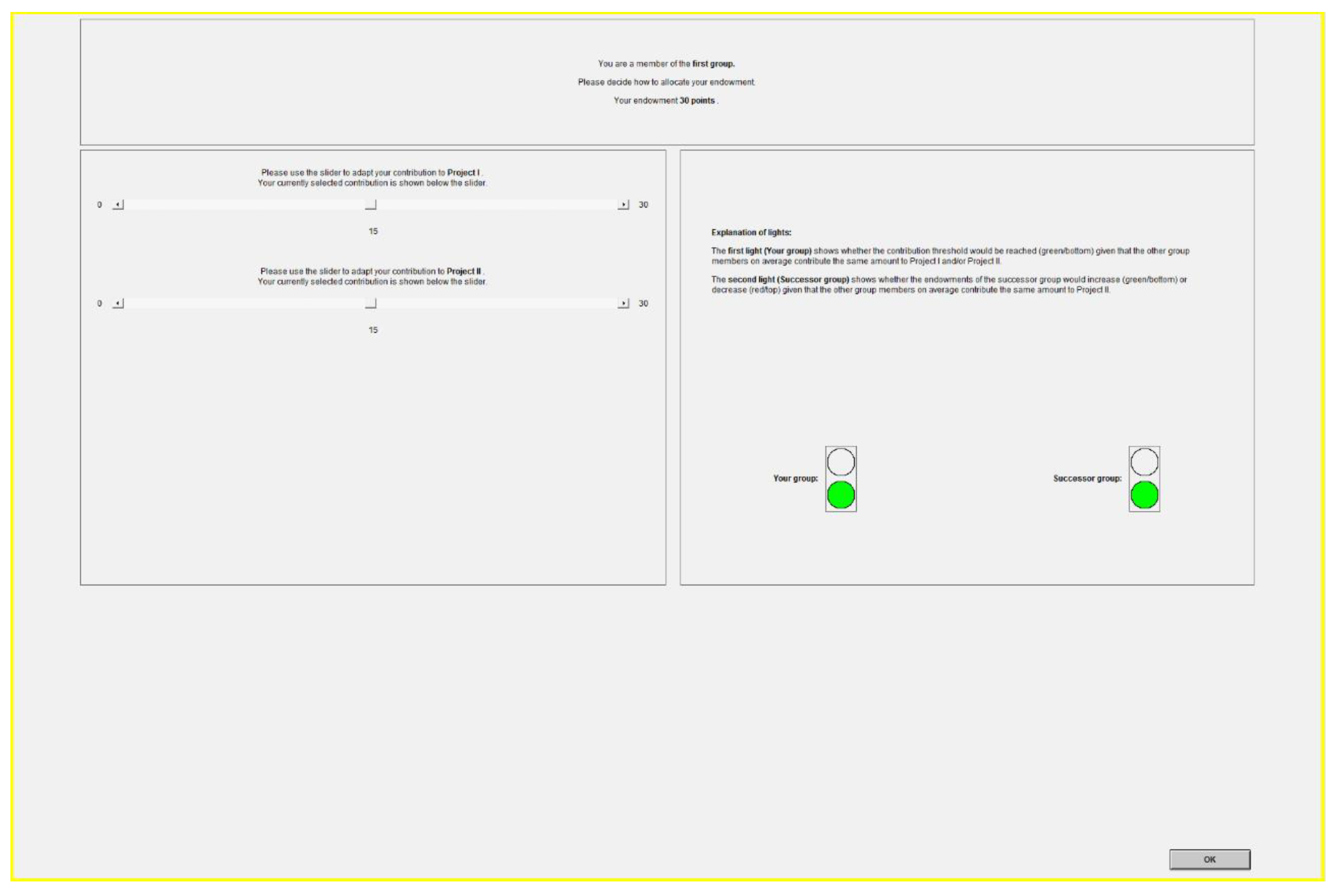
Appendix B
- Participation fee: Each participant in this experiment will receive 5 Euros. This remuneration is independent of the decisions and the earnings of the experiment.
- Earnings from the experiment: During the experiment, your income is first calculated in points. The total number of points that you score during the experiment will be converted into Euros at the end of the experiment, using the following conversion scheme: 10 points = 1.50 Euros.
- You are part of a group of 3 members. Throughout the experiment, you will interact exclusively with the members of your group.
- Your group belongs to a series with a total of 3 groups, each also consisting of 3 members. The groups of one series will take part in the experiment in succession. That is, the first group in the series has a successor group, the second one has a predecessor and a successor group, and the third group has only a predecessor group.
- Your group’s position in the series will be communicated to you on the screen before the start of the experiment.
- Your task in this experiment is to make a contribution decision.
- All members of the first group in a series will receive an initial endowment of 30 points.
- All participants of a group will make their contribution decisions simultaneously and independently of each other.
- There are two projects available for the contribution decision, to which each member of the group can contribute any number of points of his/her initial endowment. You have to decide how many points you will contribute to each of the two projects.
- You will keep any points that you do not contribute to the projects in your private account.
- Each point contributed to Project I will be multiplied by 1.8 and distributed evenly to all group members.
- This means that for each contributed point, each of the 3 group members will receive 0.6 points from the project, regardless of which group member contributed that point.
- Each point contributed in Project II will be multiplied by 1.2 and distributed evenly to all group members.
- This means that for each contributed point, each of the 3 group members will receive 0.4 points from the project, regardless of which group member contributed that point.
- For each of the 3 groups, a contribution threshold applies, which is reached if the sum of all contributions of a group is at least 45 points. In order to reach this threshold, it does not matter whether the points were only contributed to Project I, Project II, or both.
- If the contribution threshold is reached in a group, the experiment will continue and the successor group will make its contribution decision.
- If the contribution threshold in a group is not reached, the game will terminate with a probability of 80%. All members of the active group and all members of the successor group(s) will lose their payoff from both projects and their initial endowment. In this case, the experiment will be over for you.
- With a probability of 20%, the game will not terminate if the contribution threshold has not been reached, but will continue, and the successor group will make their contribution decisions.
- In the first group of a series, the initial endowment available to each group member is 30 points.
- For the second and third group, the initial endowment is determined by the relationship between the contribution threshold and the sum of contributions in Project II from the predecessor group.
- If, in the predecessor group, the number of points invested in Project II equals or exceeds the contribution threshold of 45 points, the initial endowment increases by 5 points for each member of the successor group. If, in the predecessor group, the number of points invested in Project II falls below the contribution threshold of 45 points, the initial endowment for each member of the successor group is reduced by 5 points.
- Sum of the contributions of the members of the currently playing group to Projects I and II,
- Information on whether the contribution threshold has been reached. If it has not, information on whether the game will terminate or not,
- If the game is not over, then information about whether the initial endowment of the successor group is increasing or decreasing (except for the third group).
| Group | First Group | ||
| Member | 1-1 | 1-2 | 1-3 |
| Endowment | 30 | 30 | 30 |
| Contribution to Project I | 15 | 5 | 0 |
| Sum of the contributions to Project I | 20 | ||
| Earnings from Project I | 20 × 0.6 = 12 | ||
| Contribution to Project II | 10 | 8 | 3 |
| Sum of the contributions to Project II | 21 | ||
| Earnings from Project II | 21 × 0.4 = 8.4 | ||
| Keep in private account | 5 | 17 | 27 |
| Total earnings | 12 + 8.4 + 5 = 25.4 | 12 + 8.4 + 17 = 37.4 | 12 + 8.4 + 27 = 47.4 |
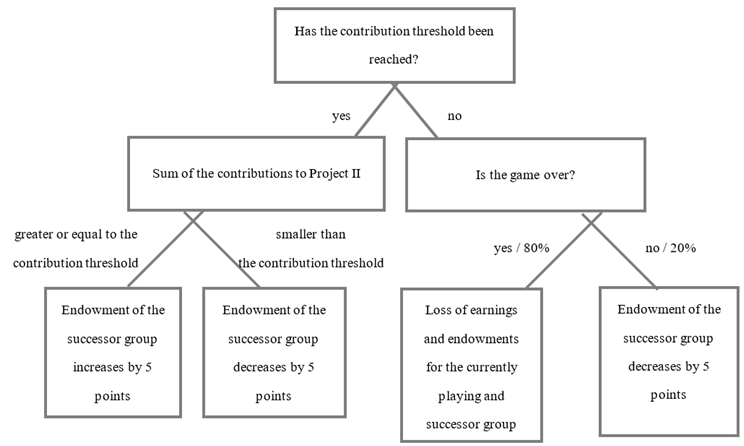
- If termination of the game occurs, your earnings from the experiment will be as follows:Your earnings from the experiment = Your endowment − your contribution to Project I − your contribution to Project II + 0.6 × Sum of the points in Project I + 0.4 × Sum of the points in Project II
- If a termination occurs in your group or predecessor group, your earnings from the experiment will be zero.
- Regardless of a possible termination, each participant will receive 5 Euro as a participation fee.
Appendix C
| Dependent Variable: Contribution to Long-Term Pool | Coefficient | Robust Standard Error | p-Value | 95% Confidence Interval |
|---|---|---|---|---|
| Independent variables: | ||||
| default+commitment treatment | −3.810 | 1.612 | 0.018 | −6.970–0.650 |
| Committed player | 5.555 | 1.707 | 0.001 | −2.210–8.901 |
| Player in G2 | 0.578 | 0.601 | 0.336 | −0.600–1.756 |
| Endowment | 0.254 | 0.067 | 0.001 | 0.124–0.384 |
| Constant | 2.533 | 2.286 | 0.268 | −1.947–7.014 |
| Dependent Variable: Relative Contribution to Long-Term Pool | Coefficient | Robust Standard Error | p-Value | 95% Confidence Interval |
|---|---|---|---|---|
| Independent variables: | ||||
| default treatment | 7.359 | 2.735 | 0.007 | 1.999–12.719 |
| default+commitment treatment | −5.490 | 5.843 | 0.347 | −16.941–5.962 |
| Committed player | 19.764 | 6.149 | <0.001 | 7.695–31.797 |
| Player in G2 | 4.113 | 2.396 | 0.086 | −0.584–8.810 |
| Constant | 26.054 | 2.025 | <0.001 | 22.085–30.024 |
References
- Burke, E. Reflections on the French Revolution, 24th, ed.; Part 3; P.F. Collier & Son: New York, NY, USA, 1909. [Google Scholar]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Hsiang, S.M.; Burke, M.; Miguel, E. Quantifying the influence of climate on human conflict. Science 2013, 341. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Bhattachan, A.; Davis, K.F.; Ravi, S.; Runyan, C.W. Global desertification: Drivers and feedbacks. Adv. Water Resour. 2013, 51, 326–344. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/SYR_AR5_FINAL_full.pdf (accessed on 7 October 2020).
- Stern, N.H. Why Are We Waiting? The Logic, Urgency, and Promise of Tackling Climate Change, 1st ed.; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Hardin, G. The tragedy of the commons. Science 1968, 162, 1243–1248. [Google Scholar]
- Lenton, T.M. Early warning of climate tipping points. Nat. Clim. Chang. 2011, 1, 201–209. [Google Scholar] [CrossRef]
- Barrett, S.; Dannenberg, A. Climate negotiations under scientific uncertainty. Proc. Natl. Acad. Sci. USA 2012, 109, 17372–17376. [Google Scholar] [CrossRef]
- Milinski, M.; Sommerfeld, R.D.; Krambeck, H.-J.; Reed, F.A.; Marotzke, J. The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 2291–2294. [Google Scholar] [CrossRef]
- Tavoni, A.; Dannenberg, A.; Kallis, G.; Löschel, A. Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proc. Natl. Acad. Sci. USA 2011, 108, 11825–11829. [Google Scholar] [CrossRef]
- Chermak, J.M.; Krause, K. Individual Response, Information, and Intergenerational Common Pool Problems. J. Environ. Econ. Manag. 2002, 43, 47–70. [Google Scholar] [CrossRef]
- Jacquet, J.; Hagel, K.; Hauert, C.; Marotzke, J.; Röhl, T.; Milinski, M. Intra- and intergenerational discounting in the climate game. Nat. Clim. Chang. 2013, 3, 1025–1028. [Google Scholar] [CrossRef]
- Fischer, M.-E.; Irlenbusch, B.; Sadrieh, A. An intergenerational common pool resource experiment. SSRN Electron. J. 2004, 48, 811–836. [Google Scholar]
- Hauser, O.P.; Rand, D.G.; Peysakhovich, A.; Nowak, M.A. Cooperating with the future. Nature 2014, 511, 220–223. [Google Scholar] [CrossRef]
- Sherstyuk, K.; Tarui, N.; Ravago, M.-L.V.; Saijo, T. Intergenerational Games with Dynamic Externalities and Climate Change Experiments. J. Assoc. Environ. Resour. Econ. 2016, 3, 247–281. [Google Scholar] [CrossRef]
- Thaler, R.H.; Sunstein, C.R. Nudge: Improving Decisions about Health, Wealth and Happiness; Yale University Press: London, UK, 2008. [Google Scholar]
- Peth, D.; Mußhoff, O.; Funke, K.; Hirschauer, N. Nudging Farmers to Comply With Water Protection Rules —Experimental Evidence From Germany. Ecol. Econ. 2018, 152, 310–321. [Google Scholar] [CrossRef]
- Schubert, C. Green nudges: Do they work? Are they ethical? Ecol. Econ. 2017, 132, 329–342. [Google Scholar] [CrossRef]
- Dannenberg, A.; Tavoni, A. Collective action in dangerous climate change games. In The WSPC Reference on Natural Resources and Environmental Policy in the Era of Global Change; Botelho, A., Ed.; Word Scientific Publishing: Singapore, 2016; pp. 95–2016. [Google Scholar]
- Milinski, M.; Röhl, T.; Marotzke, J. Cooperative interaction of rich and poor can be catalyzed by intermediate climate targets. Clim. Chang. 2011, 109, 807–814. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; May, R.M.; West, S. Combined inequality in wealth and risk leads to disaster in the climate change game. Clim. Chang. 2013, 120, 815–830. [Google Scholar] [CrossRef]
- Grolleau, G.; Sutan, A.; Vranceanu, R.M. Do people contribute more to intra-temporal or inter-temporal public goods? Res. Econ. 2016, 70, 186–195. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Graziano, S.; Maitra, P. Social Learning and Norms in a Public Goods Experiment with Inter-Generational Advice. SSRN Electron. J. 2004, 73, 357–380. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Schotter, A.; Sopher, B. Talking Ourselves to Efficiency: Coordination in Inter-Generational Minimum Effort Games with Private, Almost Common and Common Knowledge of Advice. Econ. J. 2008, 119, 91–122. [Google Scholar] [CrossRef]
- Putterman, L.; Tyran, J.-R.; Kamei, K. Public goods and voting on formal sanction schemes. J. Public Econ. 2011, 95, 1213–1222. [Google Scholar] [CrossRef]
- Bornstein, G. Intergroup Conflict: Individual, Group, and Collective Interests. Pers. Soc. Psychol. Rev. 2003, 7, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Blackwell, C.; McKee, M. Only for my own neighborhood? J. Econ. Behav. Organ. 2003, 52, 115–131. [Google Scholar] [CrossRef]
- Wit, A.P.; Kerr, N.L. ‘Me versus just us versus us all’ categorization and cooperation in nested social dilemmas. J. Pers. Soc. Psychol. 2002, 83, 616–637. [Google Scholar] [CrossRef] [PubMed]
- Buchan, N.R.; Brewer, M.B.; Grimalda, G.; Wilson, R.K.; Fatas, E.; Foddy, M. Global Social Identity and Global Cooperation. Psychol. Sci. 2011, 22, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Buchan, N.R.; Grimalda, G.; Wilson, R.K.; Brewer, M.; Fatas, E.; Foddy, M. Globalization and human cooperation. Proc. Natl. Acad. Sci. USA 2009, 106, 4138–4142. [Google Scholar] [CrossRef]
- Campbell, D.J. Task Complexity: A Review and Analysis. Acad. Manag. Rev. 1988, 13, 40. [Google Scholar] [CrossRef]
- Hughes, K.K.; Young, W.B. The relationship between task complexity and decision-making consistency. Res. Nurs. Health 1990, 13, 189–197. [Google Scholar] [CrossRef]
- Payne, J.W.; Bettman, J.R.; Johnson, E.J. Behavioral decision research: A constructive processing perspective. Annu. Rev. Psychol. 1992, 43, 87–131. [Google Scholar] [CrossRef]
- Barr, S. Are we all environmentalists now? Rhetoric and reality in environmental action. Geoforum 2004, 35, 231–249. [Google Scholar] [CrossRef]
- Kollmuss, A.; Agyeman, J. Mind the Gap: Why do people act environmentally and what are the barriers to pro-environmental behavior? Environ. Educ. Res. 2002, 8, 239–260. [Google Scholar] [CrossRef]
- How Do Consumers Respond When Default Options Push the Envelope? Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3050562 (accessed on 7 October 2020).
- Choi, J.J.; Laibson, D.; Madrian, B.C.; Metrock, A. For Better or for Worse: Default Effects and 401(k) Savings Behavior. In Perspectives on the Economics of Aging; Wisse, D.A., Ed.; University of Chicage Press: Chichago, IL, USA, 2004; pp. 81–125. [Google Scholar]
- Johnson, E.J.; Goldstein, D.G. Do Defaults Save Lives? Science 2003, 302, 1338–1339. [Google Scholar] [CrossRef] [PubMed]
- Pichert, D.; Katsikopoulos, K.V. Green defaults: Information presentation and pro-environmental behaviour. J. Environ. Psychol. 2008, 28, 63–73. [Google Scholar] [CrossRef]
- Egebark, J.; Ekstrrm, M.; Ekström, M. Can Indifference Make the World Greener? SSRN Electron. J. 2013, 76, 1–13. [Google Scholar] [CrossRef][Green Version]
- Brounen, D.; Kok, N. On the Economics of Energy Labels in the Housing Market. SSRN Electron. J. 2010, 62, 166–179. [Google Scholar] [CrossRef][Green Version]
- Cappelletti, D.; Mittone, L.; Ploner, M. Are default contributions sticky? An experimental analysis of defaults in public goods provision. J. Econ. Behav. Organ. 2014, 108, 331–342. [Google Scholar] [CrossRef]
- Carlsson, F.; Johansson-Stenman, O.; Pham, N. Funding a new bridge in rural Vietnam: A field experiment on social influence and default contributions. Oxf. Econ. Pap. 2015, 67, 987–1014. [Google Scholar] [CrossRef]
- Ariely, D.; Wertenbroch, K. Procrastination, deadlines, and performance: Self-control by precommitment. Psychol. Sci. 2002, 13, 219–224. [Google Scholar] [CrossRef]
- Breman, A. Give more tomorrow: Two field experiments on altruism and intertemporal choice. J. Public Econ. 2011, 95, 1349–1357. [Google Scholar] [CrossRef]
- Schwartz, J.; Mochon, D.; Wyper, L.; Morabe, J.; Patel, D.; Ariely, D. Healthier by Precommitment. Psycextra Dataset 2014, 25, 538–546. [Google Scholar] [CrossRef]
- Freytag, A.; Güth, W.; Köppel, H.; Wangler, L. Is regulation by milestones efficiency enhancing? An experimental study of environmental protection. Eur. J. Polit. Econ. 2014, 33, 71–84. [Google Scholar] [CrossRef]
- Cadsby, C.B.; Maynes, E. Voluntary provision of threshold public goods with continuous contributions: Experimental evidence. J. Public Econ. 1999, 71, 53–73. [Google Scholar] [CrossRef]
- Dal Bó, E.; Dal Bó, P. ‘Do the right thing:’ The effects of moral suasion on cooperation. J. Public Econ. 2014, 117, 28–38. [Google Scholar] [CrossRef]
- Greiner, B. Subject pool recruitment procedures: Organizing experiments with ORSEE. J. Econ. Sci. Assoc. 2015, 1, 114–125. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Del Ponte, A.; Delton, A.W.; Kline, R.; Seltzer, N.A. Passing It Along: Experiments on Creating the Negative Externalities of Climate Change. J. Polit. 2017, 79, 1444–1448. [Google Scholar] [CrossRef]
- Kline, R.; Seltzer, N.; Lukinova, E.; Bynum, A. Differentiated responsibilities and prosocial behaviour in climate change mitigation. Nat. Hum. Behav. 2018, 2, 653–661. [Google Scholar] [CrossRef]
- Lohse, J.; Waichman, I. The effects of contemporaneous peer punishment on cooperation with the future. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
| 1 | These parameters imply a discount rate of 0.33 from one generation to the next generation. |
| 2 | Note that in Milinski et al. [10], players know the exact probability of losing their endowment if they fail to reach the contribution threshold. In contrast, Barrett and Dannenberg [9] consider the scientific uncertainty by modeling both the threshold level as well as the probability of losing as an uncertain value with a uniform distribution. They show that uncertainty about the threshold level reduces contributions considerably. |
| 3 | The second light was only shown to participants in generations with a subsequent generation, i.e., generations 1 and 2. |
| 4 | Note, that the term “contract” is strictly speaking not correct, since future generations take part without their consent. Therefore, a more precise term would be “agreement”. |
| 5 | In the default+commitment treatment, we had two sessions with only 9 participants each. With respect to the main variables of interest (overall contributions, short-term and long-term contributions), there were no significant differences between the 9-person and 18-person sessions. |
| 6 | Note that in G3, as could be expected, the average sum of tokens contributed to the short-term pool significantly exceeds the sum of tokens contributed to the long-term pool, irrespective of treatment (Wilcoxon-signed-rank tests; baseline: Z = 3.5, p < 0.001; default: Z = 4.7, p < 0.001; default+commitment: Z = 5.1, p < 0.001). Interestingly, in all treatments, the majority of participants in G3 contributed a positive amount to the long-term pool. Unless otherwise stated, we report two-sided p-values for all tests. |
| 7 | When considering contributions relative to the individual endowment instead of absolute contributions, results remain qualitatively similar (see Appendix C Table A2). |
| Dependent Variable: Contribution to Long-Term Pool | Coefficient | Robust Standard Error | p-Value | 95% Confidence Interval |
|---|---|---|---|---|
| Independent variables: | ||||
| default treatment | 2.130 | 0.759 | 0.005 | −0.643–3.616 |
| default+commitment treatment | −1.665 | 1.591 | 0.297 | −4.795–1.466 |
| Committed player | 5.536 | 1.683 | <0.001 | −2.237–8.835 |
| Player in G2 | 0.682 | 0.540 | 0.207 | −0.377–1.741 |
| Endowment | 0.247 | 0.063 | <0.001 | 0.123–0.370 |
| Constant | 0.560 | 1.872 | 0.765 | −3.110–4.230 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böhm, R.; Gürerk, Ö.; Lauer, T. Nudging Climate Change Mitigation: A Laboratory Experiment with Inter-Generational Public Goods. Games 2020, 11, 42. https://doi.org/10.3390/g11040042
Böhm R, Gürerk Ö, Lauer T. Nudging Climate Change Mitigation: A Laboratory Experiment with Inter-Generational Public Goods. Games. 2020; 11(4):42. https://doi.org/10.3390/g11040042
Chicago/Turabian StyleBöhm, Robert, Özgür Gürerk, and Thomas Lauer. 2020. "Nudging Climate Change Mitigation: A Laboratory Experiment with Inter-Generational Public Goods" Games 11, no. 4: 42. https://doi.org/10.3390/g11040042
APA StyleBöhm, R., Gürerk, Ö., & Lauer, T. (2020). Nudging Climate Change Mitigation: A Laboratory Experiment with Inter-Generational Public Goods. Games, 11(4), 42. https://doi.org/10.3390/g11040042






