Evolution of Cooperation in Social Dilemmas with Assortative Interactions
Abstract
1. Introduction
2. Models
2.1. Discrete Games
2.1.1. Replicator Dynamics with Assortative Interactions
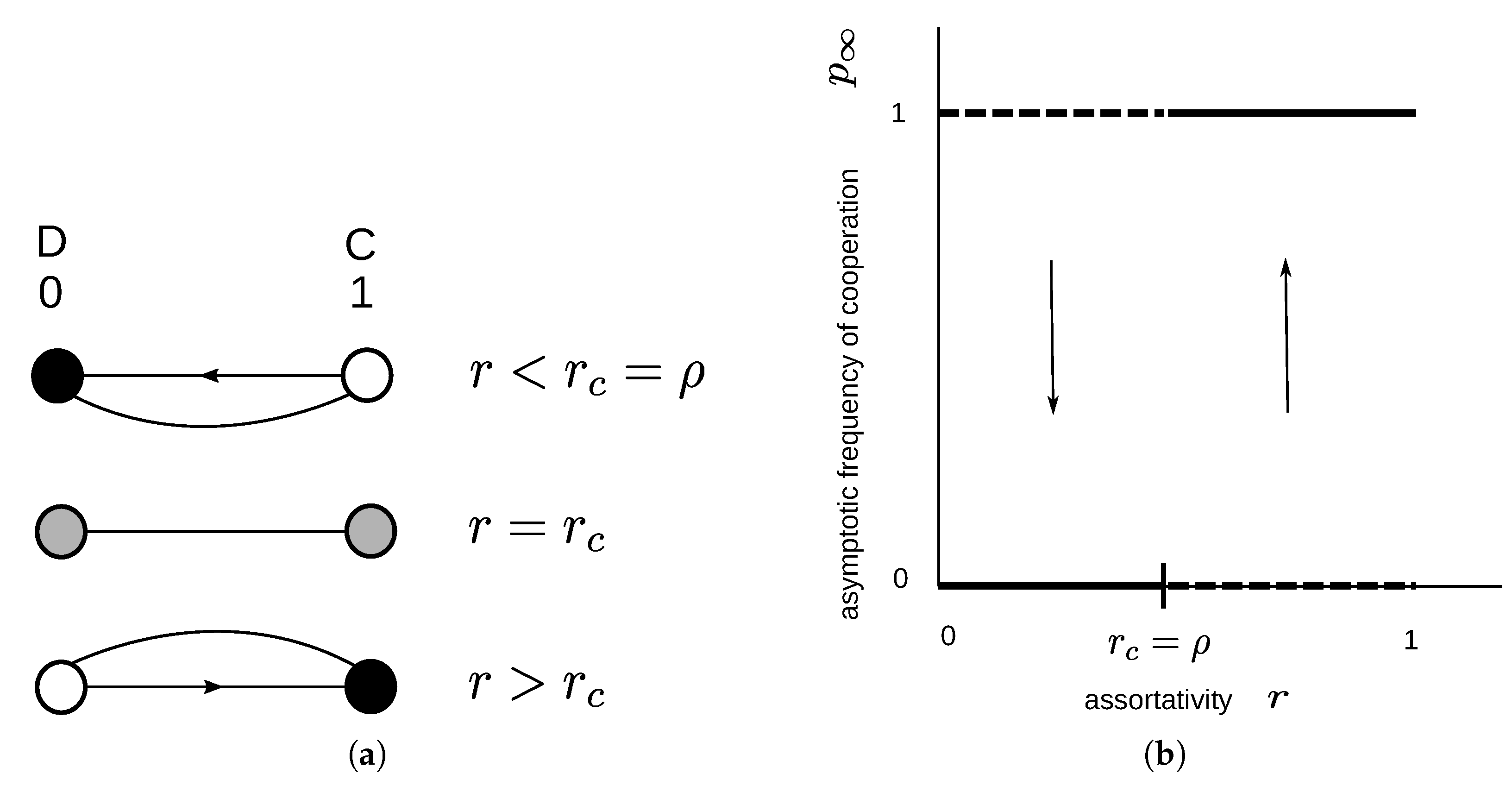
2.1.2. Donation Game
2.1.3. Snowdrift Game
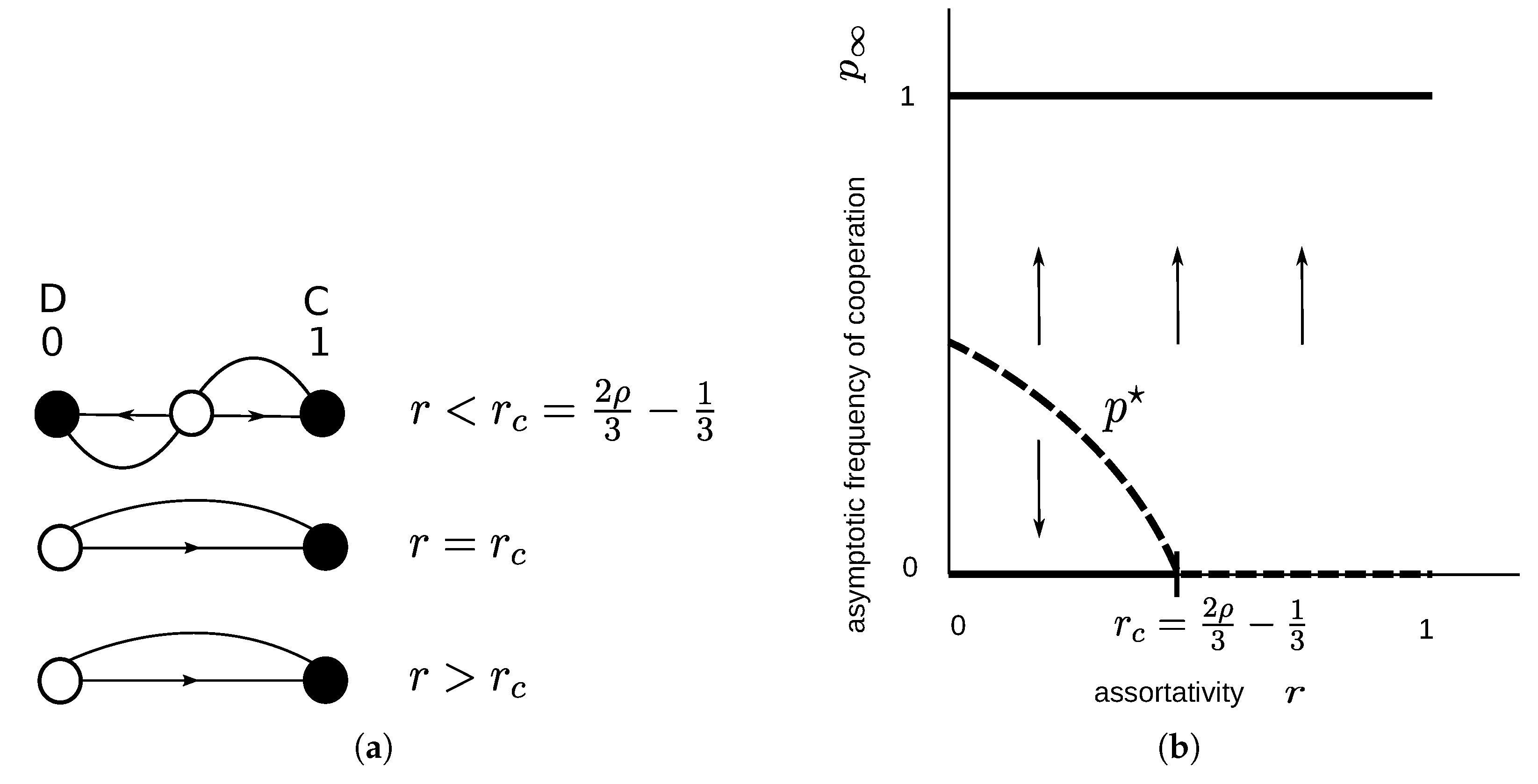
2.1.4. Sculling Game
2.2. Continuous Games
2.2.1. Adaptive Dynamics with Assortative Interactions
2.2.2. Continuous Donation Game
Linear Cost and Benefit Functions
Convex Cost and Concave Benefit Functions
2.2.3. Continuous Snowdrift Game
Concave Cost and Benefit Functions
2.2.4. Continuous Tragedy of the Commons Game
Convex Cost and Sigmoidal Benefit Functions
2.3. Individual-Based Model
2.3.1. Discrete Games
2.3.2. Continuous Games
3. Results from Individual-Based Simulations
3.1. Discrete Games
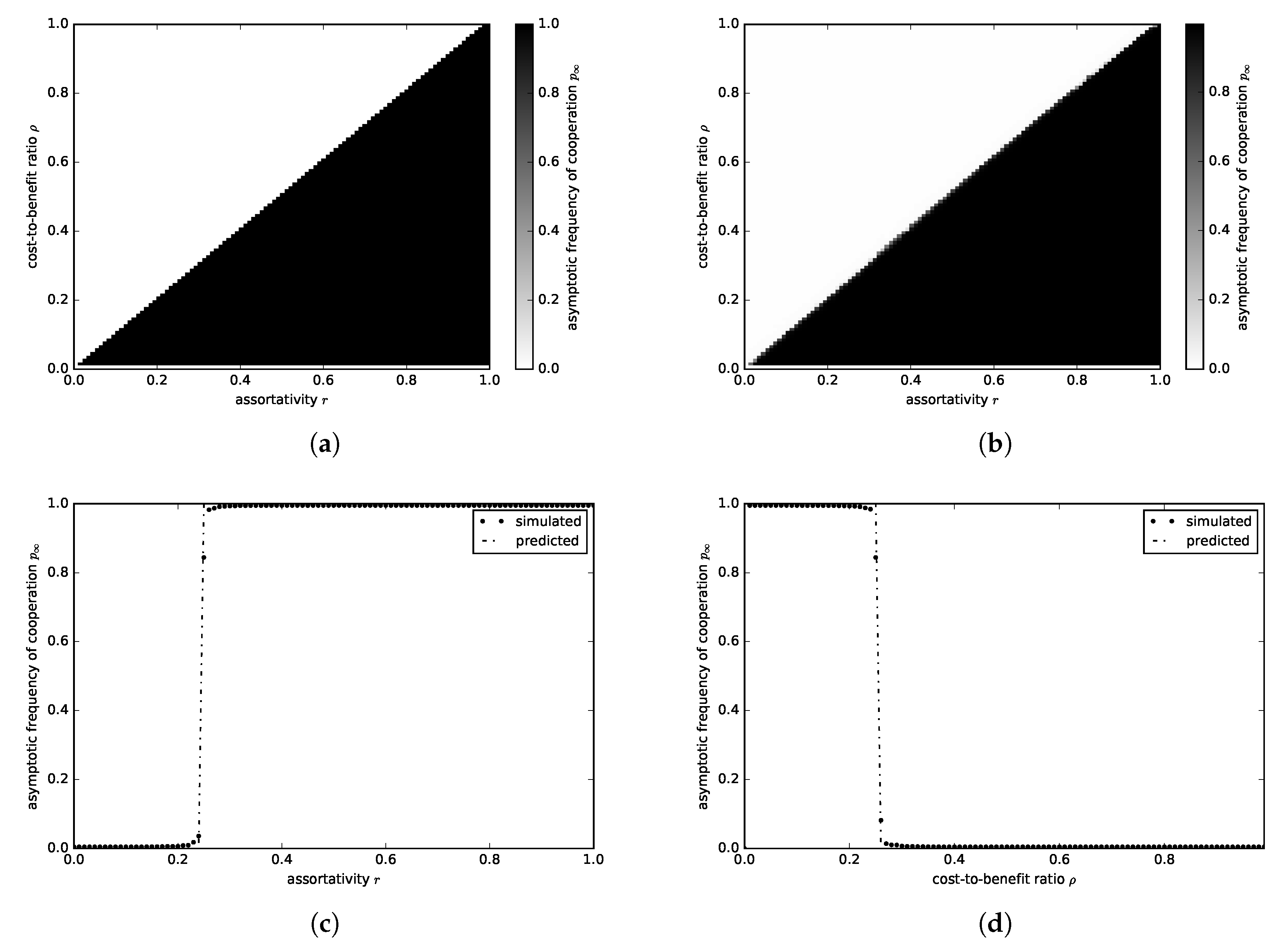
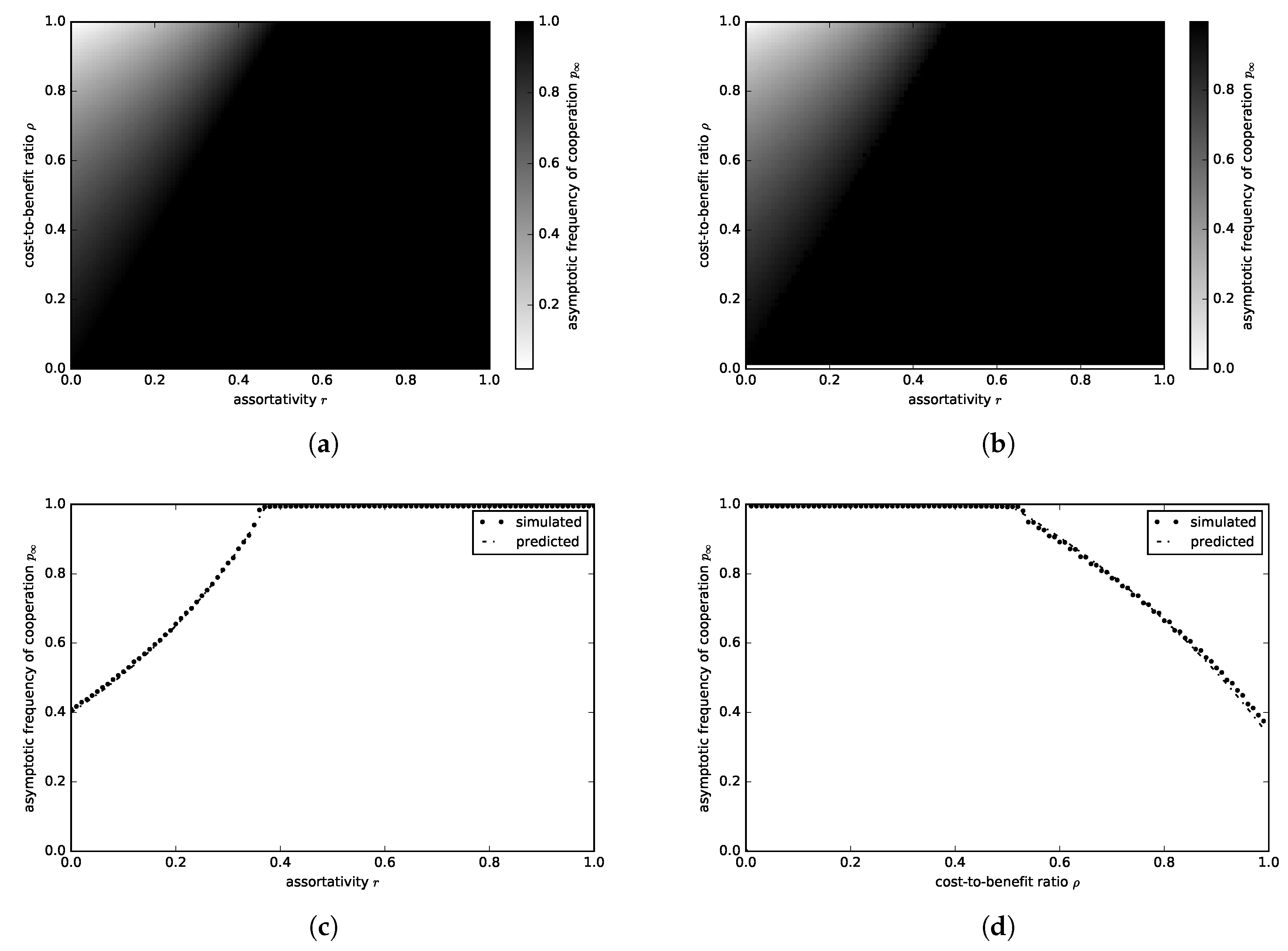
3.1.1. Donation Game
3.1.2. Snowdrift Game
3.1.3. Sculling Game
3.2. Continuous Games
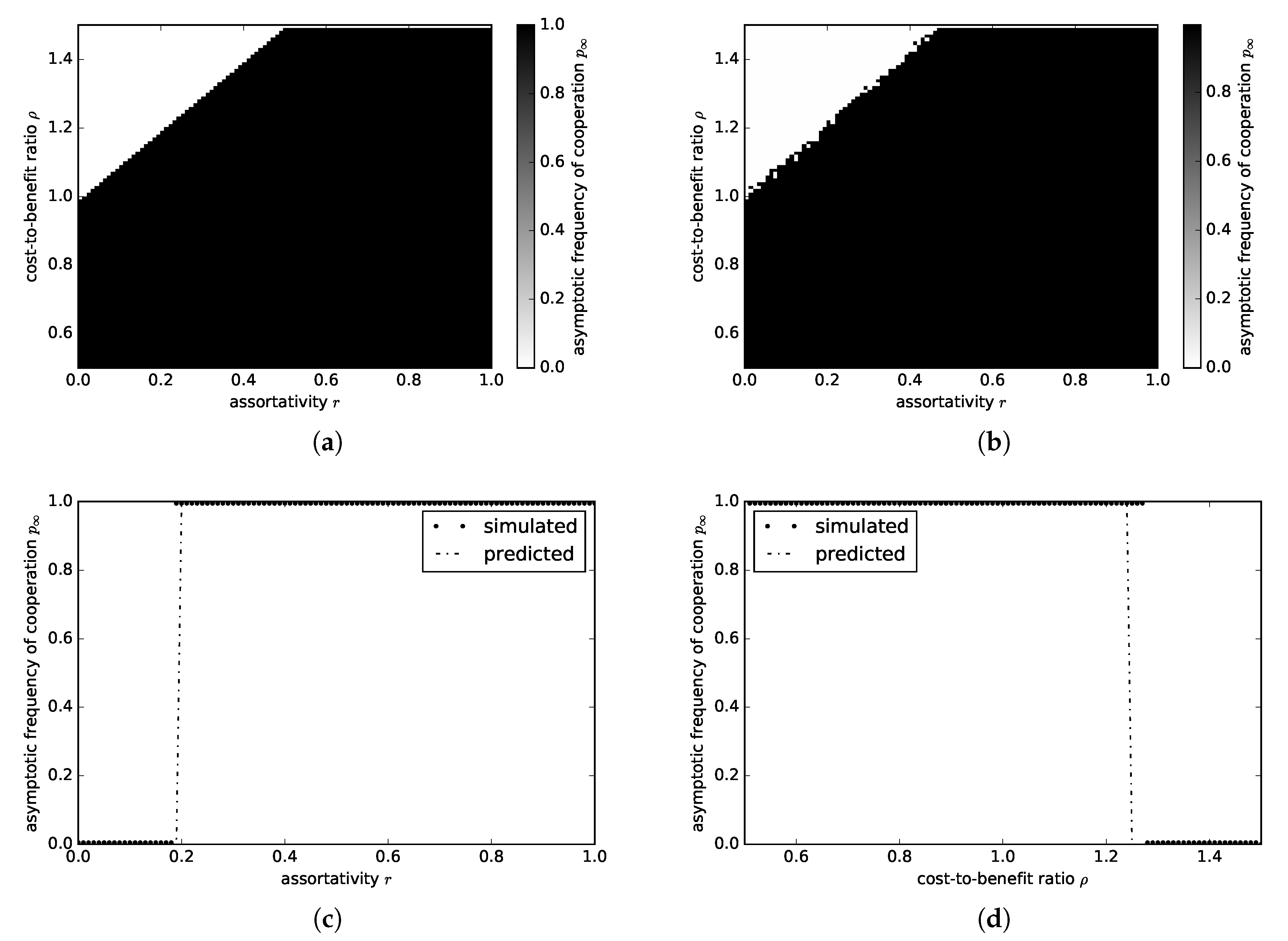
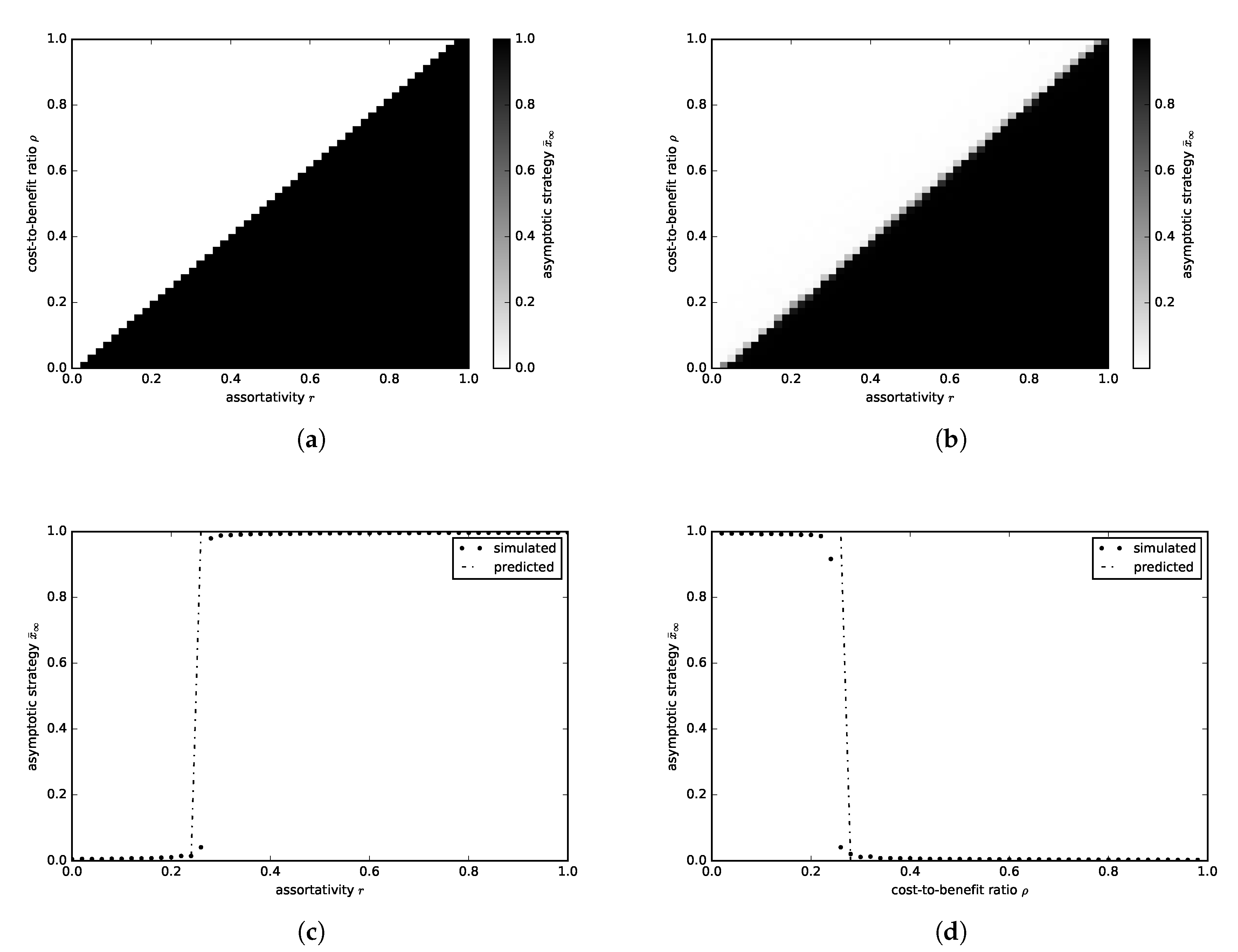
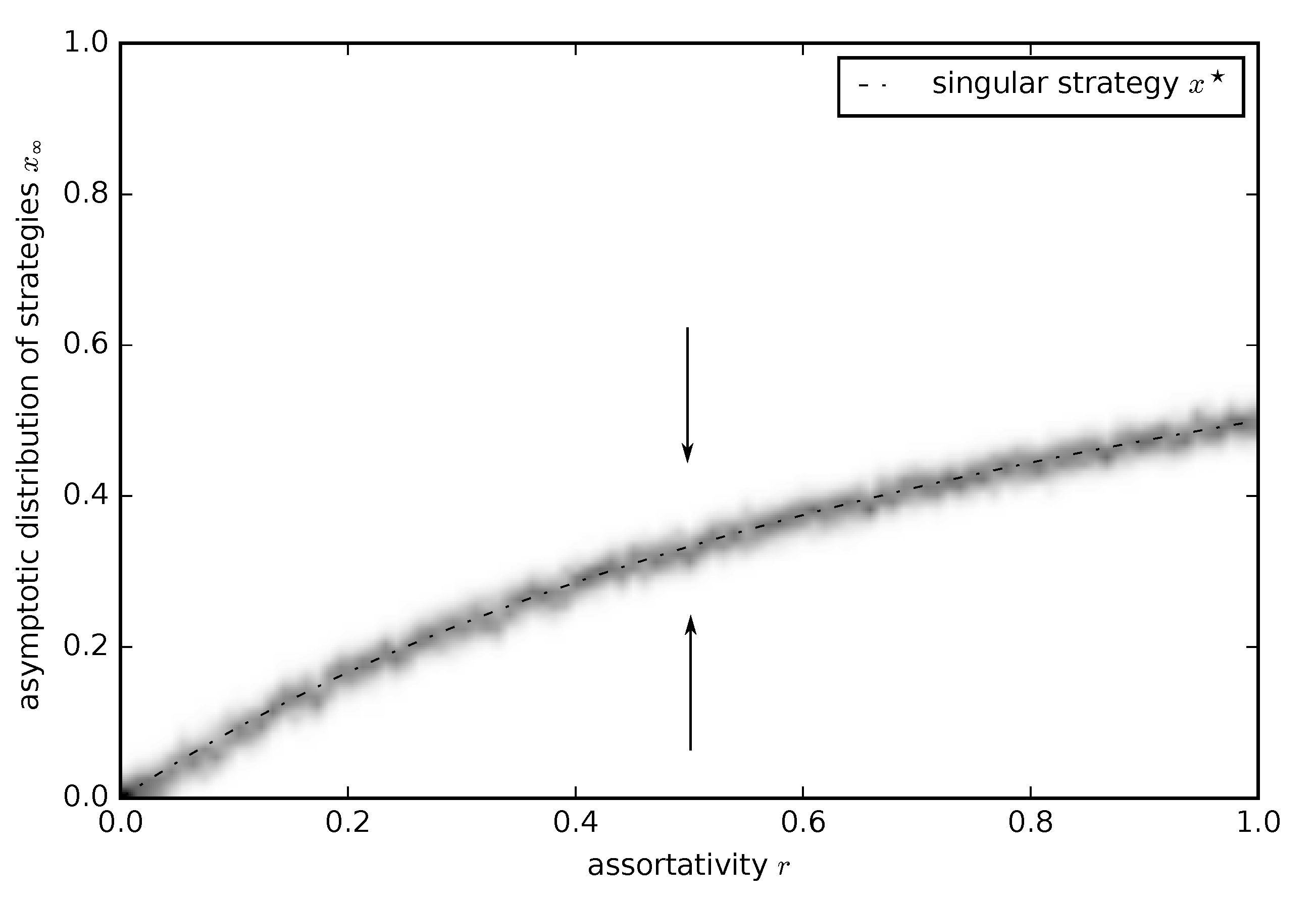
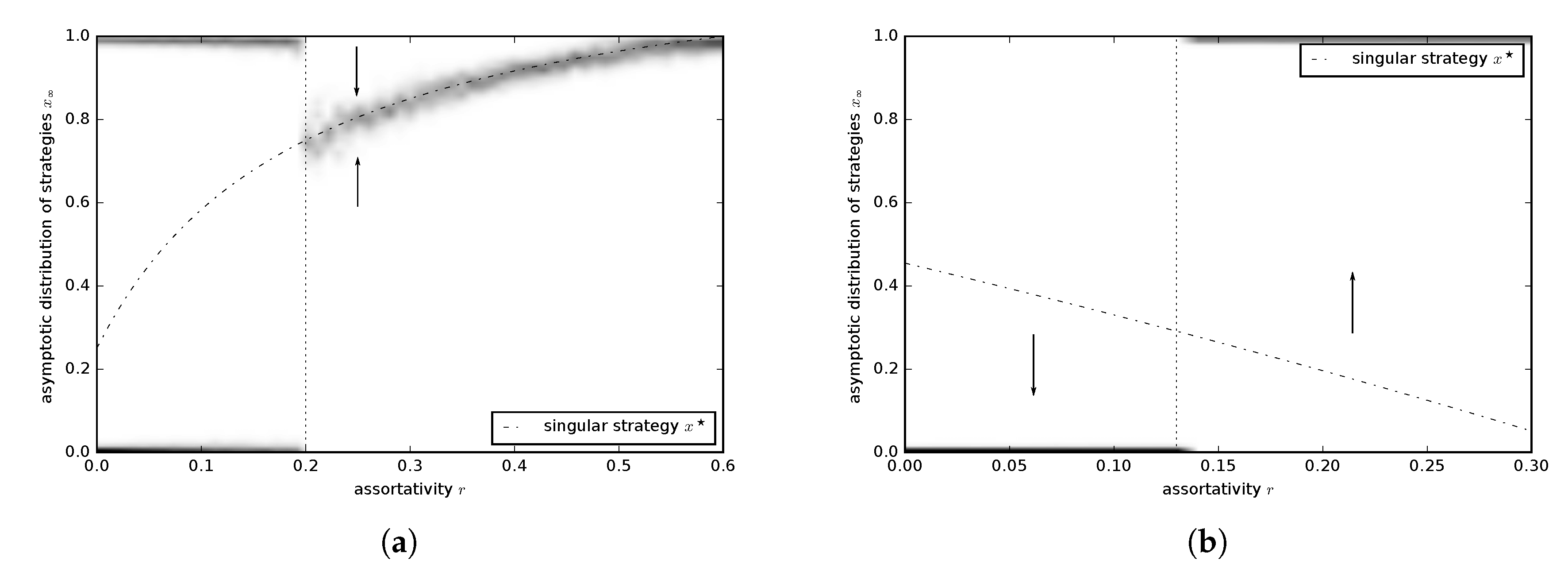
3.2.1. Continuous Donation Game
3.2.2. Continuous Snowdrift Game
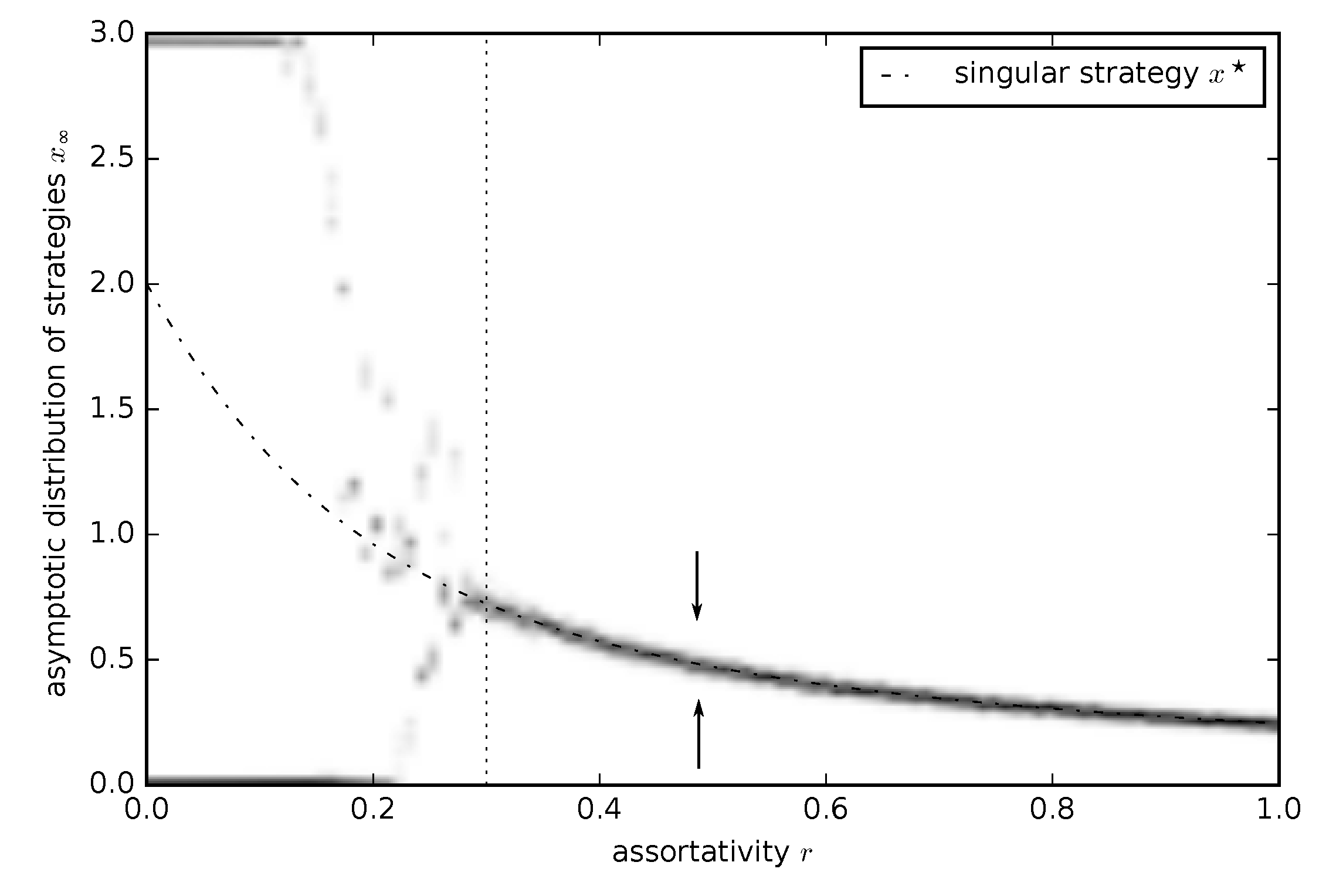
3.2.3. Continuous Tragedy of the Commons Game
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Eigen, M.; Schuster, P. The hypercycle: A principle of natural self-organization. Naturwissenschaften 1977, 64, 541–565. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J.; Szathmary, E. The Major Transitions in Evolution; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Turner, P.; Chao, L. Prisoner’s dilemma in an RNA virus. Nature 1999, 398, 441. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, G. Food sharing in vampire bats. Sci. Am. 1990, 262, 76–82. [Google Scholar] [CrossRef]
- Milinski, M. Tit for tat in sticklebacks and the evolution of cooperation. Nature 1987, 325, 433–435. [Google Scholar] [CrossRef] [PubMed]
- Mooring, M.; Hart, B. Reciprocal allogrooming in wild impala lambs. Ethology 1997, 103, 665–680. [Google Scholar] [CrossRef]
- Seyfarth, R.; Cheney, D.; Marler, P. Vervet monkey alarm calls: Semantic communication in a free-ranging primate. Anim. Behav. 1980, 28, 1070–1094. [Google Scholar] [CrossRef]
- Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef]
- Hardin, G. The tragedy of the commons. Science 1968, 162, 1243–1248. [Google Scholar]
- Ostrom, E. Governing the Commons: The Evolution of Institutions for Collective Action; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Leyton-Brown, K.; Shoham, Y. Essentials of Game Theory: A Concise, Multidisciplinary Introduction; Synthesis Lectures on Artificial Intelligence and Machine Learning; Morgan & Claypool Publishers: San Rafael, CA, USA, 2008. [Google Scholar]
- Adar, E.; Huberman, B. Free Riding on Gnutella. First Monday 2000, 5. Available online: https://firstmonday.org/ojs/index.php/fm/article/download/792/701?inline=1 (accessed on 19 September 2020).
- Hamilton, W. The genetical evolution of social behavior I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Sugden, R. The Economics of Rights, Cooperation and Welfare; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Kollock, P. Social dilemmas: The anatomy of cooperation. Annu. Rev. Sociol. 1998, 24, 183–214. [Google Scholar] [CrossRef]
- Nowak, M. Evolutionary Dynamics: Exploring the Equations of Life; Belknap Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Iyer, S.; Killingback, T. Evolution of cooperation in social dilemmas on complex networks. PLoS Comput. Biol. 2016, 12, e1004779. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J.; Price, G. The logic of animal conflict. Nature 1973, 246, 15. [Google Scholar] [CrossRef]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Taylor, P.; Jonker, L. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Metz, J.; Geritz, S.; Meszéna, G.; Jacobs, F.; Van Heerwaarden, J. Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction. Stoch. Spat. Struct. Dyn. Syst. 1996, 45, 183–231. [Google Scholar]
- Geritz, S.; Meszéna, G.; Metz, J. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 1997, 12, 35–57. [Google Scholar] [CrossRef]
- Doebeli, M.; Hauert, C.; Killingback, T. The evolutionary origin of cooperators and defectors. Science 2004, 306, 859–862. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M.; Hauert, C. Cooperation and defection in the tragedy of the commons. Biol. Theory 2010, 5, 3–6. [Google Scholar] [CrossRef]
- Kandori, M.; Mailath, G.; Rob, R. Learning, mutation, and long run equilibria in games. Econom. J. Econom. Soc. 1993, 61, 29–56. [Google Scholar] [CrossRef]
- Young, H. The evolution of conventions. Econom. J. Econom. Soc. 1993, 61, 57–84. [Google Scholar] [CrossRef]
- Kaniovski, Y.; Young, H. Learning dynamics in games with stochastic perturbations. Games Econ. Behav. 1995, 11, 330–363. [Google Scholar] [CrossRef]
- Nowak, M.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef]
- Manapat, M.; Rand, D.; Pawlowitsch, C.; Nowak, M. Stochastic evolutionary dynamics resolve the Traveler’s Dilemma. J. Theor. Biol. 2012, 303, 119–127. [Google Scholar] [CrossRef]
- Rand, D.; Nowak, M. Evolutionary dynamics in finite populations can explain the full range of cooperative behaviors observed in the centipede game. J. Theor. Biol. 2012, 300, 212–221. [Google Scholar] [CrossRef]
- Cornforth, D.M.; Sumpter, D.J.; Brown, S.P.; Brännström, Å. Synergy and group size in microbial cooperation. Am. Nat. 2012, 180, 296–305. [Google Scholar] [CrossRef]
- Nowak, M. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Frank, S. Foundations of Social Evolution; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Nowak, M.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 2006. [Google Scholar]
- Nowak, M.; Sigmund, K. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.; May, R. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Lindgren, K.; Nordahl, M. Evolutionary dynamics of spatial games. Phys. D Nonlinear Phenom. 1994, 75, 292–309. [Google Scholar] [CrossRef]
- Nowak, M.; Bonhoeffer, S.; May, R. Spatial games and the maintenance of cooperation. Proc. Natl. Acad. Sci. USA 1994, 91, 4877–4881. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M. Spatial evolutionary game theory: Hawks and Doves revisited. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1996, 263, 1135–1144. [Google Scholar]
- Nakamaru, M.; Matsuda, H.; Iwasa, Y. The evolution of cooperation in a lattice-structured population. J. Theor. Biol. 1997, 184, 65–81. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M. Self-organized criticality in spatial evolutionary game theory. J. Theor. Biol. 1998, 191, 335–340. [Google Scholar] [CrossRef]
- Szabó, G.; Tőke, C. Evolutionary prisoner’s dilemma game on a square lattice. Phys. Rev. E 1998, 58, 69. [Google Scholar] [CrossRef]
- Van Baalen, M.; Rand, D. The unit of selection in viscous populations and the evolution of altruism. J. Theor. Biol. 1998, 193, 631–648. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M.; Knowlton, N. Variable investment, the continuous prisoner’s dilemma, and the origin of cooperation. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1999, 266, 1723–1728. [Google Scholar] [CrossRef]
- Brauchli, K.; Killingback, T.; Doebeli, M. Evolution of cooperation in spatially structured populations. J. Theor. Biol. 1999, 200, 405–417. [Google Scholar] [CrossRef]
- Szabó, G.; Antal, T.; Szabó, P.; Droz, M. Spatial evolutionary prisoner’s dilemma game with three strategies and external constraints. Phys. Rev. E 2000, 62, 1095. [Google Scholar] [CrossRef]
- Ifti, M.; Killingback, T.; Doebeli, M. Effects of neighbourhood size and connectivity on spatial Continuous Prisoner’s Dilemma. J. Theor. Biol. 2004, 231, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.; Pacheco, J. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 2005, 95, 98–104. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.; Pacheco, J.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ren, J.; Chen, G.; Wang, B. Memory-based snowdrift game on networks. Phys. Rev. E 2006, 74, 056113. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef]
- Tang, C.; Wang, W.; Wu, X.; Wang, B. Effects of average degree on cooperation in networked evolutionary game. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 53, 411–415. [Google Scholar] [CrossRef]
- Szabo, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Wu, C. Evolution of prisoner’s dilemma strategies on scale-free networks. Phys. A Stat. Mech. Its Appl. 2007, 385, 379–384. [Google Scholar] [CrossRef]
- Du, W.; Zheng, H.; Hu, M. Evolutionary prisoner’s dilemma game on weighted scale-free networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 3796–3800. [Google Scholar] [CrossRef]
- Gómez-Gardeñes, J.; Poncela, J.; Floría, L.; Moreno, Y. Natural selection of cooperation and degree hierarchy in heterogeneous populations. J. Theor. Biol. 2008, 253, 296–301. [Google Scholar] [CrossRef]
- Lee, K.; Chan, C.; Hui, P.; Zheng, D. Cooperation in N-person evolutionary snowdrift game in scale-free Barabási–Albert networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 5602–5608. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M.; Danku, Z. Towards effective payoffs in the prisoner’s dilemma game on scale-free networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 2075–2082. [Google Scholar] [CrossRef]
- Alonso-Sanz, R. Memory versus spatial disorder in the support of cooperation. BioSystems 2009, 97, 90–102. [Google Scholar] [CrossRef] [PubMed]
- Floría, L.; Gracia-Lázaro, C.; Gómez-Gardenes, J.; Moreno, Y. Social network reciprocity as a phase transition in evolutionary cooperation. Phys. Rev. E 2009, 79, 026106. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; Rong, Z.; Zhang, Z.; Zhou, S. The prisoner’s dilemma in structured scale-free networks. J. Phys. A Math. Theor. 2009, 42, 245002. [Google Scholar] [CrossRef]
- Newth, D.; Cornforth, D. Asynchronous spatial evolutionary games. BioSystems 2009, 95, 120–129. [Google Scholar] [CrossRef]
- Pacheco, J.; Santos, F.; Souza, M.; Skyrms, B. Evolutionary dynamics of collective action in N-person stag hunt dilemmas. Proc. R. Soc. Lond. B Biol. Sci. 2009, 276, 315–321. [Google Scholar] [CrossRef]
- Perc, M. Evolution of cooperation on scale-free networks subject to error and attack. New J. Phys. 2009, 11, 033027. [Google Scholar] [CrossRef]
- Roca, C.; Cuesta, J.; Sánchez, A. Promotion of cooperation on networks? The myopic best response case. Eur. Phys. J. B 2009, 71, 587–595. [Google Scholar] [CrossRef]
- Yang, D.; Shuai, J.; Lin, H.; Wu, C. Individual’s strategy characterized by local topology conditions in prisoner’s dilemma on scale-free networks. Phys. A Stat. Mech. Its Appl. 2009, 388, 2750–2756. [Google Scholar] [CrossRef]
- Débarre, F.; Hauert, C.; Doebeli, M. Social evolution in structured populations. Nat. Commun. 2014, 5, 3409. [Google Scholar] [CrossRef]
- Allen, B.; Lippner, G.; Chen, Y.; Fotouhi, B.; Momeni, N.; Yau, S.; Nowak, M. Evolutionary dynamics on any population structure. Nature 2017, 544, 227. [Google Scholar] [CrossRef]
- Traulsen, A.; Nowak, M. Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. USA 2006, 103, 10952–10955. [Google Scholar] [CrossRef]
- Killingback, T.; Bieri, J.; Flatt, T. Evolution in group-structured populations can resolve the tragedy of the commons. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2006, 273, 1477–1481. [Google Scholar] [CrossRef]
- Hamilton, W. Innate social aptitudes of man: An approach from evolutionary genetics. Biosoc. Anthropol. 1975, 53, 133–155. [Google Scholar]
- Grafen, A. The hawk-dove game played between relatives. Anim. Behav. 1979, 27, 905–907. [Google Scholar] [CrossRef]
- Grafen, A. A geometric view of relatedness. Oxf. Surv. Evol. Biol. 1985, 2, 28–89. [Google Scholar]
- Maynard Smith, J. Evolutionary Genetics, 2nd ed.; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Fletcher, J.; Doebeli, M. A simple and general explanation for the evolution of altruism. Proc. R. Soc. Lond. B Biol. Sci. 2009, 276, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Price, G. Selection and covariance. Nature 1970, 227, 520–521. [Google Scholar] [CrossRef] [PubMed]
- Henrich, J. Cultural group selection, coevolutionary processes and large-scale cooperation. J. Econ. Behav. Organ. 2004, 53, 3–35. [Google Scholar] [CrossRef]
- Russell, B. Common Sense and Nuclear Warfare; Simon & Schuster: New York, NY, USA, 1959. [Google Scholar]
- Young, H. Individual Strategy and Social Structure: An Evolutionary Theory of Institutions; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Skyrms, B.; Pemantle, R. A dynamic model of social network formation. Proc. Natl. Acad. Sci. USA 2000, 97, 9340–9346. [Google Scholar] [CrossRef] [PubMed]
- Skyrms, B. The Stag Hunt and the Evolution of Social Structure; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bergstrom, T. On the evolution of altruistic ethical rules for siblings. Am. Econ. Rev. 1995, 85, 58–81. [Google Scholar]
- Bergstrom, T. The algebra of assortative encounters and the evolution of cooperation. Int. Game Theory Rev. 2003, 5, 211–228. [Google Scholar] [CrossRef]
- Taylor, C.; Nowak, M. Evolutionary game dynamics with non-uniform interaction rates. Theor. Popul. Biol. 2006, 69, 243–252. [Google Scholar] [CrossRef]
- Van Veelen, M. The replicator dynamics with n players and population structure. J. Theor. Biol. 2011, 276, 78–85. [Google Scholar] [CrossRef]
- Alger, I.; Weibull, J. Homo moralis—Preference evolution under incomplete information and assortative matching. Econometrica 2013, 81, 2269–2302. [Google Scholar]
- Bergstrom, T. Measures of assortativity. Biol. Theory 2013, 8, 133–141. [Google Scholar] [CrossRef]
- Allen, B.; Nowak, M. Games among relatives revisited. J. Theor. Biol. 2015, 378, 103–116. [Google Scholar] [CrossRef] [PubMed]
- Cooney, D.; Allen, B.; Veller, C. Assortment and the evolution of cooperation in a Moran process with exponential fitness. J. Theor. Biol. 2016, 409, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.; Rigos, A. Assortativity evolving from social dilemmas. J. Theor. Biol. 2016, 395, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M.; Allen, B.; Hoffman, M.; Simon, B.; Veller, C. Hamilton’s rule. J. Theor. Biol. 2017, 414, 176–230. [Google Scholar] [CrossRef] [PubMed]
- Killingback, T.; Doebeli, M. The continuous prisoner’s dilemma and the evolution of cooperation through reciprocal altruism with variable investment. Am. Nat. 2002, 160, 421–438. [Google Scholar] [CrossRef]
- Allen, B.; Nowak, M.; Dieckmann, U. Adaptive dynamics with interaction structure. Am. Nat. 2013, 181, 139–163. [Google Scholar] [CrossRef] [PubMed]
- Coder Gylling, K.; Brännström, Å. Effects of relatedness on the evolution of cooperation in nonlinear public goods games. Games 2018, 9, 87. [Google Scholar] [CrossRef]
- Zeeman, E. Population dynamics from game theory. Glob. Theory Dyn. Syst. 1980, 819, 471–497. [Google Scholar] [CrossRef]
- Meszéna, G. Adaptive dynamics: The continuity argument. J. Evol. Biol. 2005, 18, 1182–1185. [Google Scholar] [CrossRef]
- McGill, B.; Brown, J. Evolutionary game theory and adaptive dynamics of continuous traits. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 403–435. [Google Scholar] [CrossRef]
- Brännström, A.; Johansson, J.; Von Festenberg, N. The hitchhiker’s guide to adaptive dynamics. Games 2013, 4, 304–328. [Google Scholar] [CrossRef]
- Dieckmann, U.; Law, R. The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 1996, 34, 579–612. [Google Scholar] [CrossRef]
- Hamilton, W. The evolution of altruistic behavior. Am. Nat. 1963, 97, 354–356. [Google Scholar] [CrossRef]
- Altmann, S. Altruistic behaviour: The fallacy of kin deployment. Anim. Behav. 1979, 27, 958–959. [Google Scholar] [CrossRef]
- Weigel, R. The distribution of altruism among kin: A mathematical model. Am. Nat. 1981, 118, 191–201. [Google Scholar] [CrossRef]
- Schulman, S.; Rubenstein, D. Kinship, need, and the distribution of altruism. Am. Nat. 1983, 121, 776–788. [Google Scholar] [CrossRef]
- Sibly, R.; McFarland, D. On the fitness of behavior sequences. Am. Nat. 1976, 110, 601–617. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef]
- Iyer, S.; Killingback, T. Evolutionary dynamics of a smoothed war of attrition game. J. Theor. Biol. 2016, 396, 25–41. [Google Scholar] [CrossRef]
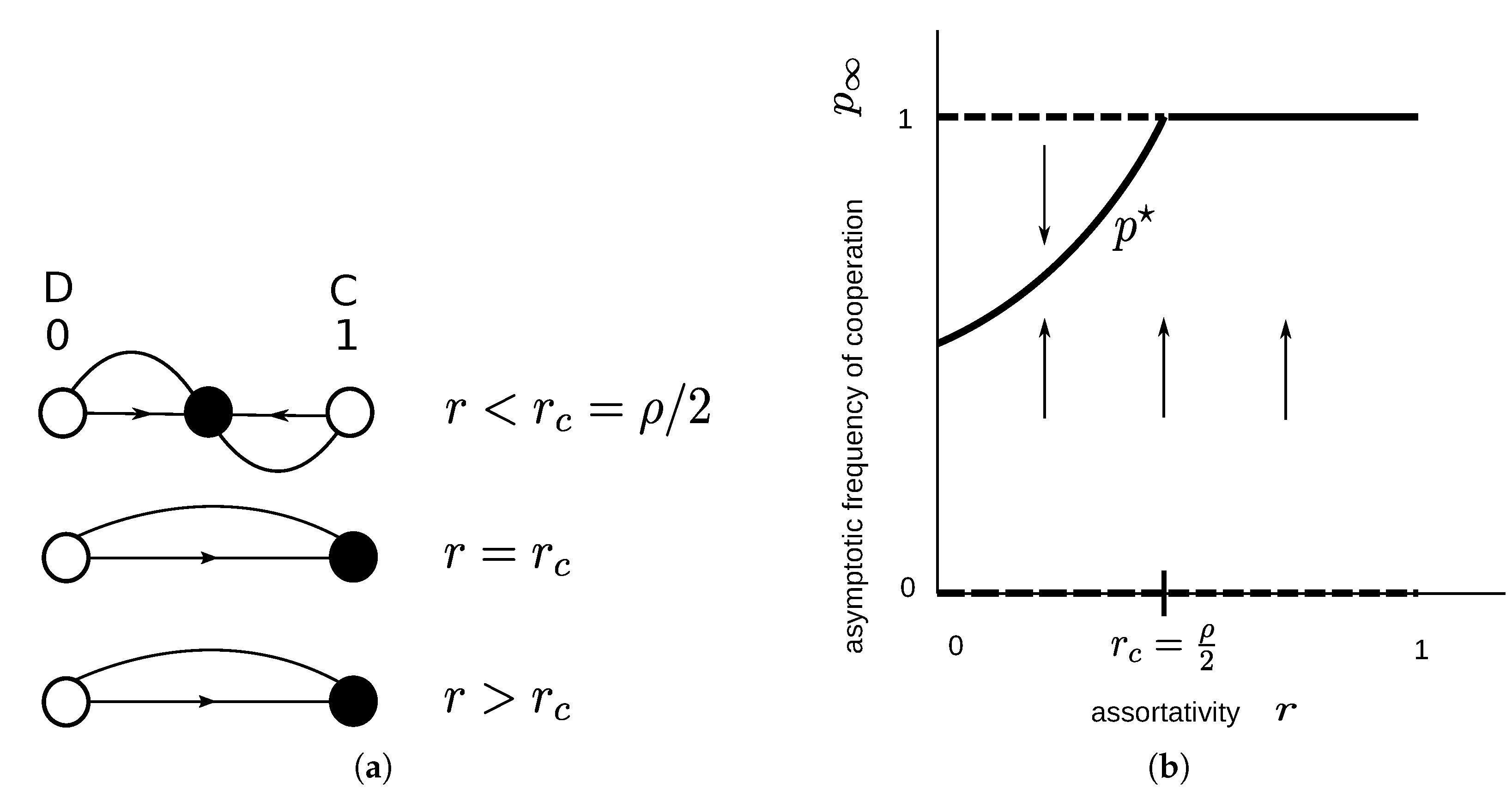
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iyer, S.; Killingback, T. Evolution of Cooperation in Social Dilemmas with Assortative Interactions. Games 2020, 11, 41. https://doi.org/10.3390/g11040041
Iyer S, Killingback T. Evolution of Cooperation in Social Dilemmas with Assortative Interactions. Games. 2020; 11(4):41. https://doi.org/10.3390/g11040041
Chicago/Turabian StyleIyer, Swami, and Timothy Killingback. 2020. "Evolution of Cooperation in Social Dilemmas with Assortative Interactions" Games 11, no. 4: 41. https://doi.org/10.3390/g11040041
APA StyleIyer, S., & Killingback, T. (2020). Evolution of Cooperation in Social Dilemmas with Assortative Interactions. Games, 11(4), 41. https://doi.org/10.3390/g11040041




