Thankful or Thankless: Does the Past’s Altruism Increase the Present’s Public Good Contributions?
Abstract
1. Introduction
2. Methodology
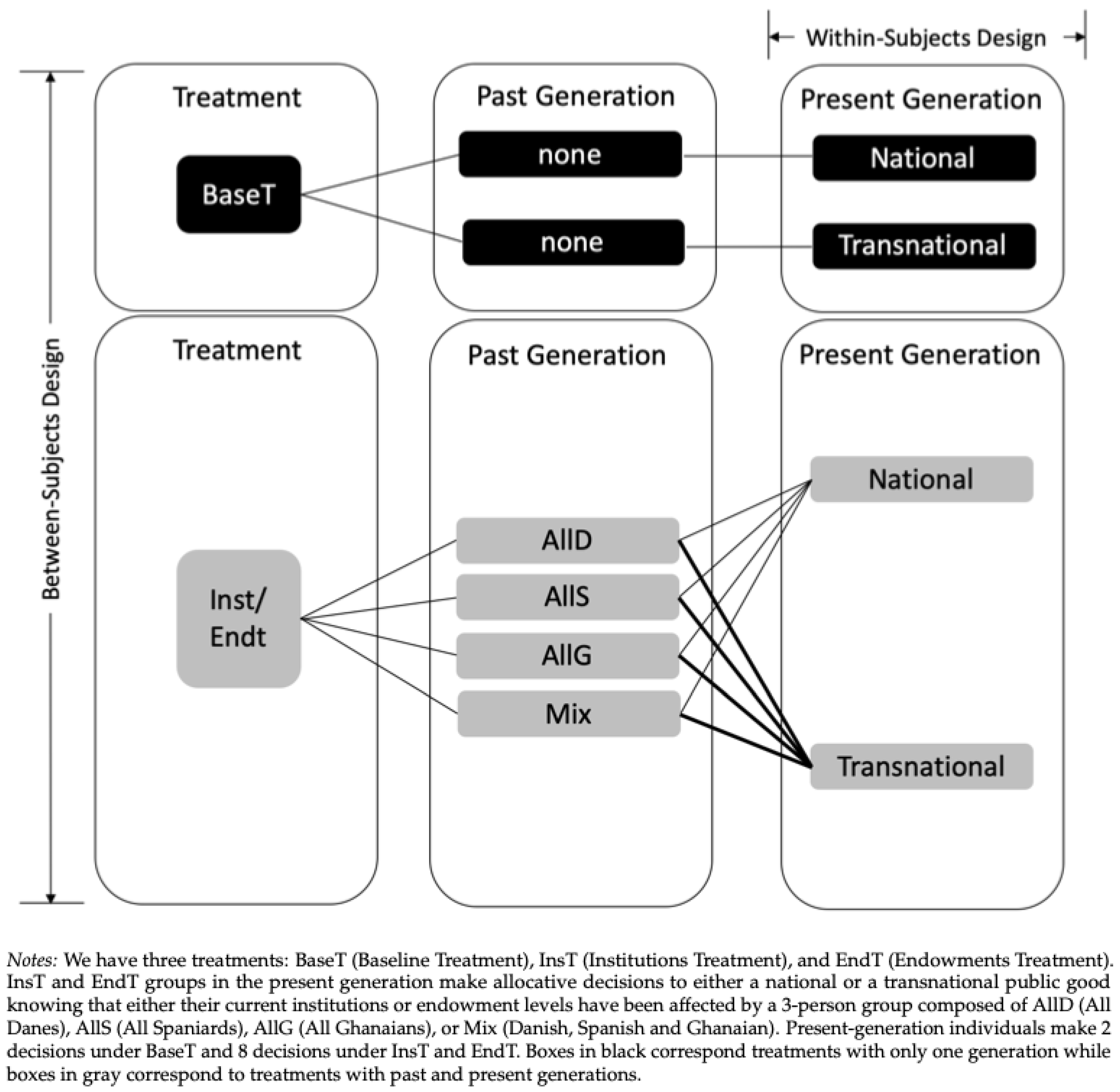
2.1. Experimental Design
2.2. Game and Predictions
3. Hypotheses
Procedures
4. Results
4.1. Main Results
4.2. Other Results
5. Discussion
5.1. Intergenerational and Transnational Effect
5.2. Experimental Design Caveats
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Instructions
Appendix A.1. Experiment Instructions (PG-T0G)
- The total group investment in the Group Account?
- Your earnings from the Group Account?
- Your total earnings?
Appendix A.2. Experiment Instructions (PG-T1G)
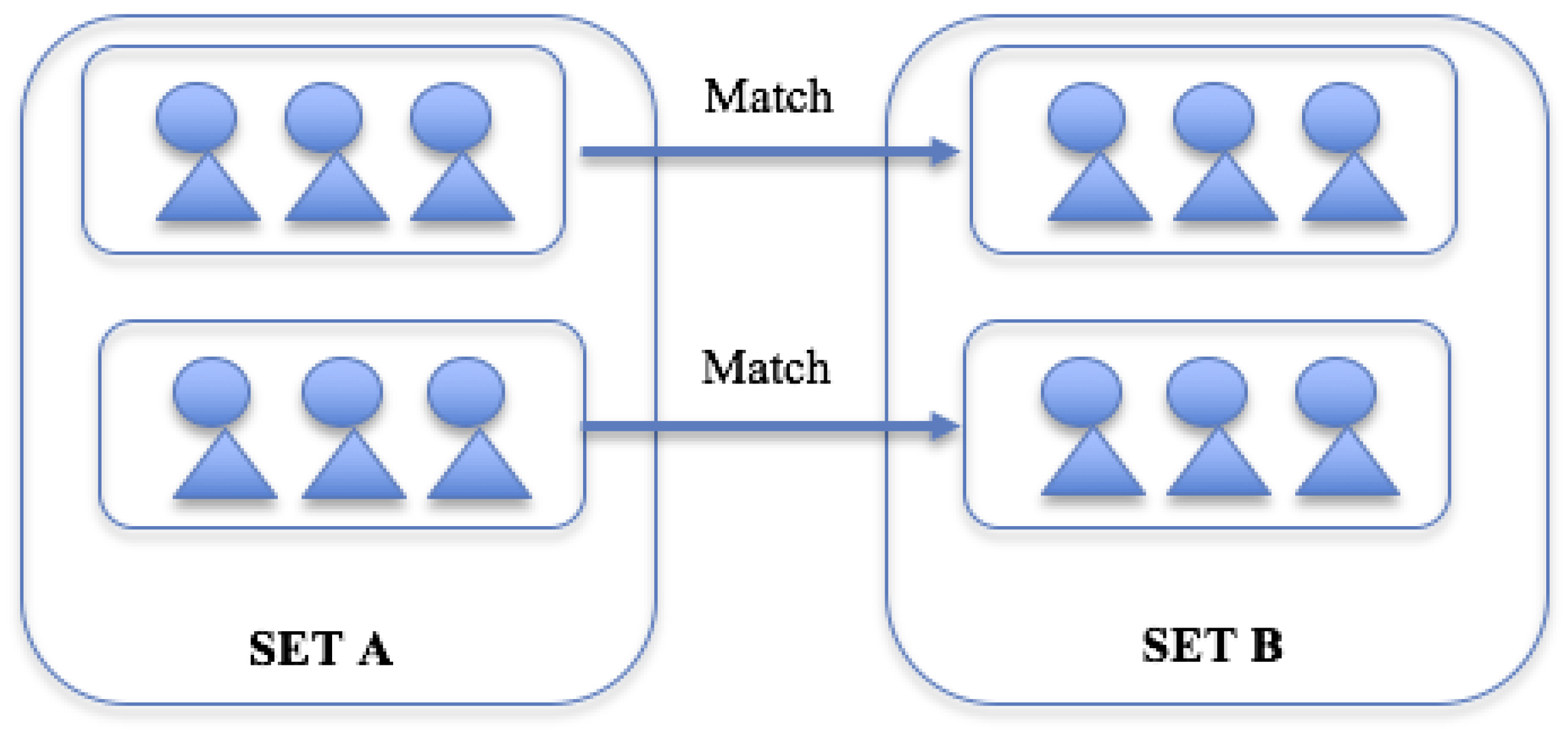
- Which set are you assigned to?
- Suppose you kept 6 tokens and your other group members invested 32 tokens in the Group Account. What is:
- (a)
- The total group investment in the Group Account?
- (b)
- Your earnings from the Group Account?
- (c)
- Your total earnings?
- If a group in SET A invested all their tokens to the Group Account, what is for the matched group in SET B?
Appendix A.3. Experiment Instructions (PG-T2G)
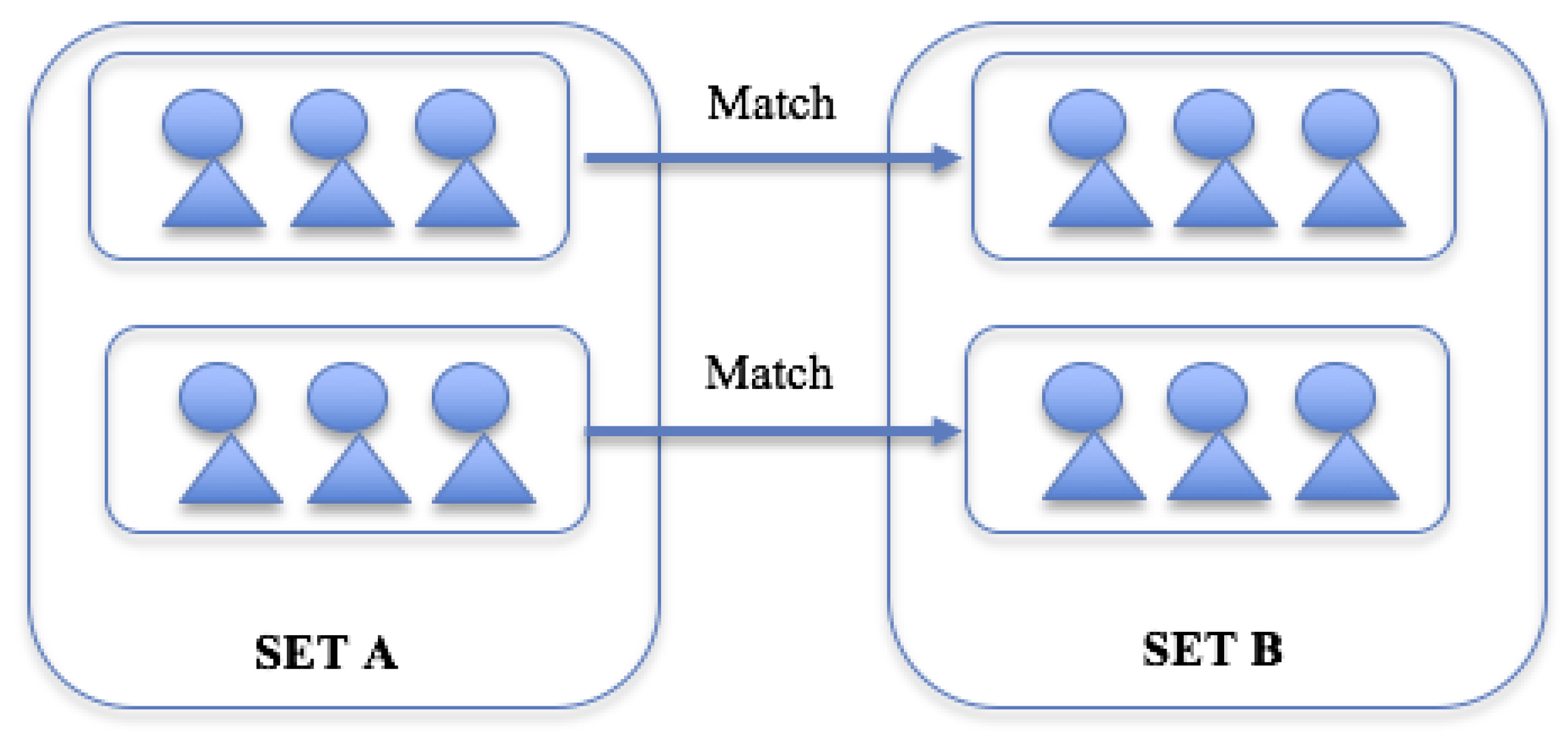
- Which set are you assigned to?
- Suppose you kept 6 tokens and your other group members invested 32 tokens in the Group Account. What is:
- (a)
- The total group investment in the Group Account?
- (b)
- Your earnings from the Group Account?
- (c)
- Your total earnings?
- If a group in SET A invested all their tokens to the Group Account, what is for the matched group in SET B?
Appendix B. Decision Sheets
Appendix B.1. Baseline Treatments


Appendix B.2. Set A: Institutions and Endowments Treatments


Appendix B.3. Set B: Institutions Treatment


Appendix B.4. Set B: Endowments Treatment


Appendix C. Survey Questionnaire
- Subject ID Number:
- Age:
- Gender:
- □
- Female
- □
- Male
- Are you a student?
- □
- Yes
- □
- No
- Field of Study:
- Highest Educational Attainment:
- Marital Status
- □
- Single
- □
- Co-habiting
- □
- Married
- □
- Widowed
- Number of Children:
- Do you believe that individuals in Denmark and Spain had the same experiment you had?
- □
- Yes
- □
- No
| Not at all willing to take risks | Very willing to take risks |
| 0 | 10 | ||||||||
| □ | □ | □ | □ | □ | □ | □ | □ | □ | □ |
| Strongly agree | Kind of agree | Kind of disagree | Strongly disagree | I don’t know | |
| I like the Danes | □ | □ | □ | □ | □ |
| I think Danes can be trusted | □ | □ | □ | □ | □ |
| I think Danes are not very cooperative | □ | □ | □ | □ | □ |
| I think Danes care for nature | □ | □ | □ | □ | □ |
| I think Danes will not protect the habitats of migratory birds | □ | □ | □ | □ | □ |
| I think Danes are quite wealthy | □ | □ | □ | □ | □ |
| I think Danes do not care what happens to my country and my people | □ | □ | □ | □ | □ |
| Strongly agree | Kind of agree | Kind of disagree | Strongly disagree | I don’t know | |
| I like the Spaniards | □ | □ | □ | □ | □ |
| I think Spaniards can be trusted | □ | □ | □ | □ | □ |
| I think Spaniards are not very cooperative | □ | □ | □ | □ | □ |
| I think Spaniards care for nature | □ | □ | □ | □ | □ |
| I think Spaniards will not protect the habitats of migratory birds | □ | □ | □ | □ | □ |
| I think Spaniards are quite wealthy | □ | □ | □ | □ | □ |
| I think Spaniards do not care what happens to my country and my people | □ | □ | □ | □ | □ |
| Strongly agree | Kind of agree | Kind of disagree | Strongly disagree | I don’t know | |
| I like the Ghanaians | □ | □ | □ | □ | □ |
| I think Ghanaians can be trusted | □ | □ | □ | □ | □ |
| I think Ghanaians are not very cooperative | □ | □ | □ | □ | □ |
| I think Ghanaians care for nature | □ | □ | □ | □ | □ |
| I think Ghanaians will not protect the habitats of migratory birds | □ | □ | □ | □ | □ |
| I think Ghanaians are quite wealthy | □ | □ | □ | □ | □ |
| I think Ghanaians do not care what happens to my country and my people | □ | □ | □ | □ | □ |
References
- The New York Times. World’s Richest Little Isle. 1982. Available online: https://www.nytimes.com/1982/03/07/magazine/world-s-richest-little-isle.html (accessed on 30 December 2019).
- Chaudhuri, A.; Graziano, S.; Maitra, P. Social learning and norms in a public goods experiment with inter-generational advice. Rev. Econ. Stud. 2006, 73, 357–380. [Google Scholar] [CrossRef]
- Duffy, J.; Lafky, J. Birth, death and public good provision. Exp. Econ. 2014, 19, 317–341. [Google Scholar] [CrossRef]
- Engel, C.; Rockenbach, B. We are not alone: The impact of externalities on public good provision. MPI Collect. Goods Prepr. 2011. [Google Scholar] [CrossRef]
- Schotter, A.; Sopher, B. Social learning and coordination conventions in intergenerational games: An experimental study. J. Polit. Econ. 2003, 111, 498–529. [Google Scholar] [CrossRef]
- Sherstyuk, K.; Tarui, N.; Ravago, M.-L.V.; Saijo, T. Intergenerational games with dynamic externalities and climate change experiments. J. Assoc. Environ. Resour. Econ. 2016, 3, 247–281. [Google Scholar] [CrossRef]
- Van der Heijden, E.C.; Nelissen, J.H.; Potters, J.J.; Verbon, H.A. Transfers and the effect of monitoring in an overlapping-generations experiment. Eur. Econ. Rev. 1998, 42, 1363–1391. [Google Scholar] [CrossRef]
- Offerman, T.; Potters, J.; Verbon, H.A. Cooperation in an overlapping generations experiment. Games Econ. Behav. 2001, 36, 264–275. [Google Scholar] [CrossRef]
- Anderson, L.R.; Mellor, J.M.; Milyo, J. Inequality and public good provision: An experimental analysis. J. Soc.-Econ. 2008, 37, 1010–1028. [Google Scholar] [CrossRef]
- Isaac, R.; Walker, J. Communication and free-riding behavior: The voluntary contribution mechanism. Econ. Inq. 1988, 26, 585–608. [Google Scholar] [CrossRef]
- Kachelmeier, S.J.; Shehata, M. Internal auditing and voluntary cooperation in firms: A cross-cultural experiment. Acc. Rev. 1997, 72, 407–431. [Google Scholar]
- Nitta, K. The Effect of Income Heterogeneity in An Experiment with Global and Local Public Goods; Working Paper No. 14-3; University of Hawaii at Manoa, Economics Department: Honolulu, HI, USA, 2015. [Google Scholar]
- Oxoby, R.J.; Spraggon, J. A clear and present minority: Heterogeneity in the source of endowments and the provision of public goods. Econ. Inq. 2013, 51, 2071–2082. [Google Scholar] [CrossRef]
- Fellner, G.; Iida, Y.; Kröger, S.; Seki, E. Heterogeneous Productivity in Voluntary Public Good Provision: An Experimental Analysis; Working Paper Series 133; University of Vienna, Department of Economics: Vienna, Austria, 2011. [Google Scholar]
- Fisher, J.; Isaac, R.M.; Schatzberg, J.W.; Walker, J.M. Heterogenous demand for public goods: Behavior in the voluntary contributions mechanism. Public Choice 1995, 85, 249–266. [Google Scholar] [CrossRef]
- Cappelen, A.W.; Moene, K.O.; Sørensen, E.Ø.; Tungodden, B. Needs versus entitlements—An international fairness experiment. J. Eur. Econ. Assoc. 2013, 11, 574–598. [Google Scholar] [CrossRef]
- Chuah, S.-H.; Hoffmann, R.; Jones, M.; Williams, G. Do cultures clash? Evidence from cross-national ultimatum game experiments. J. Econ. Behav. Org. 2007, 64, 35–48. [Google Scholar] [CrossRef]
- Carpenter, J.; Cardenas, J.C. An intercultural examination of cooperation in the commons. J. Confl. Resolut. 2011, 55, 632–651. [Google Scholar] [CrossRef]
- Castro, M.F. Where are you from? Cultural differences in public good experiments. J. Soc.-Econ. 2008, 37, 2319–2329. [Google Scholar] [CrossRef]
- Buchan, N.R.; Grimalda, G.; Wilson, R.; Brewer, M.; Fatas, E.; Foddy, M. Globalization and human cooperation. Proc. Natl. Acad. Sci. USA 2009, 106, 4138–4142. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The Strategy Method: A Survey of Experimental Evidence; Technical Report, Mimeo; Department of Business Economics, Autònoma de Barcelona and Department of Economics: Santa Barbara, CA, USA, 2009. [Google Scholar]
- Ledyard, J. Public Goods: A Survey of Experimental Research in Handbook of Experimental Economics; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Heap, S.P.H.; Ramalingam, A.; Stoddard, B.V. Endowment inequality in public goods games: A re-examination. Econ. Lett. 2016, 146, 4–7. [Google Scholar] [CrossRef]
- Buckley, E.; Croson, R. Income and wealth heterogeneity in the voluntary provision of linear public goods. J. Public Econ. 2006, 90, 935–955. [Google Scholar] [CrossRef]
- Hofmeyr, A.; Burns, J.; Visser, M. Income inequality, reciprocity and public good provision: An experimental analysis. S. Afr. J. Econ. 2007, 75, 508–520. [Google Scholar] [CrossRef]
- Greiner, B. Subject pool recruitment procedures: Organizing experiments with ORSEE. J. Econ. Sci. Assoc. 2015, 1, 114–125. [Google Scholar] [CrossRef]
- Levitt, S.D.; List, J.A. What do laboratory experiments measuring social preferences reveal about the real world? J. Econ. Perspect. 2007, 21, 153–174. [Google Scholar] [CrossRef]
- Tanaka, T.; Camerer, C.F.; Nguyen, Q. Risk and time preferences: Linking experimental and household survey data from vietnam. Am. Econ. Rev. 2010, 100, 557–571. [Google Scholar] [CrossRef]
- Gneezy, U.; Leibbrandt, A.; List, J.A. Ode to the sea: Workplace organizations and norms of cooperation. Econ. J. 2015, 126, 1856–1883. [Google Scholar] [CrossRef]
- Henrich, J.; Boyd, R.; Bowles, S.; Camerer, C.; Fehr, E.; Gintis, H.; McElreath, R. In search of homo economicus: Behavioral experiments in 15 small-scale societies. Am. Econ. Rev. 2001, 91, 73–78. [Google Scholar] [CrossRef]
| 1. | Tests show no statistically significant order effect in our results. |
| 2. | In our design, our participants made decisions as both “Set A” and “Set B” individuals. This introduces the possibility of a self-serving bias, where one could imagine that the same individual when deciding to contribute in “Set A” thinks that this might benefit her/himself in “Set B”. We made sure to inform participants that this would never be the case; however, one cannot exclude this as a possible motivational bias in the observed public good contributions. |
| 3. | To limit the complexity of the experimental design, we chose only to examine the influence of a positive feedback from a past generation. We acknowledge that this is a limitation of our design, as a negative feedback mechanism is a realistic possibility in the real world, which also have been studied previously in the literature [4]. |
| 4. | Two participants in Denmark, five participants in Spain and 3 participants in Ghana were no longer students at the time of the experiment. |
| 5. | Instructions were originally written in English, translated to Danish and Spanish and then re-translated to English by a different translator. |
| 6. | Contributions are also statistically significantly different between InsT and EndT. One-sided t-Tests show that past-generation individuals under InsT contributed more than past-generation individuals under EndT, . |
| Denmark | |||
|---|---|---|---|
| Code | Treatment Name | # Sessions | # Participants |
| BaseT | Baseline | 6 | 72 |
| InsT | Institutions Treatment | 6 | 72 |
| EndT | Endowments Treatment | 5 | 60 |
| Spain | |||
| Code | Treatment Name | # Sessions | # Participants |
| BaseT | Baseline | 6 | 72 |
| InsT | Institutions Treatment | 6 | 72 |
| EndT | Endowments Treatment | 5 | 60 |
| Ghana | |||
| Code | Treatment Name | # Sessions | # Participants |
| BaseT | Baseline | 6 | 72 |
| InsT | Institutions Treatment | 6 | 72 |
| EndT | Endowments Treatment | 5 | 60 |
| Dependent Variable: Tokens Contributed | ||
|---|---|---|
| Simple (1) | Controls (2) | |
| InsT | 1.1424 ** (0.4158) | 0.7229 ** (0.3261) |
| EndT | 0.4979 (0.3837) | 2.2572 *** (0.4214) |
| Constant | 7.6458 *** (0.2561) | −3.2526 (2.7702) |
| R-squared | 0 | 0.06 |
| N | 3600 | 3536 |
| Controls | no | yes |
| Dependent Variable: % Tokens Contributed | ||||||||
|---|---|---|---|---|---|---|---|---|
| Pooled | Transnational Only | National Only | Pooled with Interaction | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| InsT | 0.0477 *** | 0.0397 ** | 0.0568 *** | 0.0453 ** | 0.0385 ** | 0.0335 | ||
| (0.0147) | (0.0151) | (0.0154) | (0.0164) | (0.0167) | (0.0233) | |||
| EndT | −0.027 | −0.0327 | −0.0175 | −0.0271 | −0.0365 ** | −0.0388 | ||
| (0.0152) | (0.0170) | (0.0173) | (0.0202) | (0.0142) | (0.0211) | |||
| BaseT * Trans | −0.0206 ** | −0.0206 ** | ||||||
| (0.0083) | (0.0083) | |||||||
| InsT * Nat | 0.0385 ** | 0.0303 | ||||||
| (0.0167) | (0.0187) | |||||||
| InsT * Trans | 0.0362 ** | 0.0285 | ||||||
| (0.0123) | (0.0132) | |||||||
| EndT * Nat | −0.0365 ** | −0.0415 ** | ||||||
| (0.0142) | (0.0173) | |||||||
| EndT * Trans | −0.0381 ** | −0.0445 ** | ||||||
| (0.0146) | (0.0184) | |||||||
| Constant | 0.3823 *** | −0.1249 | 0.3720 *** | −0.1057 | 0.3926 *** | −0.1435 | 0.3926 *** | −0.1146 |
| (0.0128) | (0.1201) | (0.0141) | (0.1186) | (0.0128) | (0.1243) | (0.0128) | (0.1196) | |
| R-Squared | 0.01 | 0.07 | 0.01 | 0.08 | 0.01 | 0.08 | 0.01 | 0.07 |
| N | 3600 | 3536 | 1800 | 1768 | 1800 | 1768 | 3600 | 3536 |
| Controls | no | yes | no | yes | no | yes | no | yes |
| Dependent Variable: % Tokens Contributed | |||||
|---|---|---|---|---|---|
| Pooled | Transnational Only | National Only | |||
| (1) | (2) | (3) | (4) | (6) | |
| MPCR | 0.2141 *** | 0.2464 ** | 0.1875 ** | 0.1824 ** | 0.1381 |
| (0.0686) | (0.0806) | (0.0630) | (0.0769) | (0.0889) | |
| Constant | 0.3050 *** | 0.2845 *** | −0.3501 ** | 0.3251 *** | −0.3738 ** |
| (0.0318) | (0.0388) | (0.1553) | (0.0369) | (0.1648) | |
| R-squared | 0 | 0.01 | 0.12 | 0 | 0.12 |
| N | 2160 | 1080 | 1072 | 1080 | 1072 |
| Controls | no | no | yes | no | yes |
| Pooled | Transnational Only | National Only | |||
| (7) | (8) | (9) | (10) | (11) | |
| Endowment | −0.003 | −0.0024 | −0.0029 | −0.0035 ** | −0.0036 |
| (0.0017) | (0.0020) | (0.0022) | (0.0014) | (0.0018) | |
| Constant | 0.4392 *** | 0.4221 *** | 0.1402 | 0.4561 *** | 0.0883 |
| (0.0436) | (0.0527) | (0.1285) | (0.0380) | (0.1252) | |
| R-squared | 0 | 0 | 0.04 | 0 | 0.05 |
| N | 1872 | 936 | 912 | 936 | 912 |
| Controls | no | no | yes | no | yes |
| Dependent Variable: % Tokens Contributed | ||||||
|---|---|---|---|---|---|---|
| Denmark | Denmark | Spain | Spain | Ghana | Ghana | |
| (1) | (2) | (3) | (4) | (5) | (6) | |
| BaseT * Trans | −0.0361 ** | −0.0369 *** | −0.0243 *** | −0.0243 *** | −0.0243 *** | −0.0021 |
| (0.0116) | (0.0099) | (0.0065) | (0.0074) | (0.0065) | (0.0222) | |
| InsT * Nat | 0.0536 | 0.0571 | 0.0281 | 0.0282 | 0.0281 | −0.0025 |
| (0.0511) | (0.0393) | (0.0212) | (0.0226) | (0.0212) | (0.0458) | |
| InsT * Trans | 0.058 | 0.0616 | 0.0389 | 0.0392 | 0.0389 | −0.0191 |
| (0.0443) | (0.0354) | (0.0216) | (0.0243) | (0.0216) | (0.0471) | |
| EndT * Nat | −0.0943 | −0.0877 | 0.0152 | 0.0141 | 0.0152 | −0.0616 |
| (0.0432) | (0.0446) | (0.0289) | (0.0354) | (0.0289) | (0.0422) | |
| EndT * Trans | −0.0995 ** | −0.0927 ** | 0.0071 | 0.0058 | 0.0071 | −0.0557 |
| (0.0384) | (0.0400) | (0.0251) | (0.0319) | (0.0251) | (0.0453) | |
| Constant | 0.4743 *** | 0.3047 | 0.2236 *** | 0.193 | 0.2236 *** | 0.1288 |
| (0.0280) | (0.1962) | (0.0208) | (0.1248) | (0.0208) | (0.3385) | |
| R-Squared | 0.05 | 0.21 | 0 | 0.1 | 0 | 0.09 |
| N | 1200 | 1174 | 1200 | 1168 | 1200 | 1014 |
| Controls | no | yes | no | yes | no | yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abatayo, A.L.; Svenningsen, L.S.; Thorsen, B.J. Thankful or Thankless: Does the Past’s Altruism Increase the Present’s Public Good Contributions? Games 2020, 11, 6. https://doi.org/10.3390/g11010006
Abatayo AL, Svenningsen LS, Thorsen BJ. Thankful or Thankless: Does the Past’s Altruism Increase the Present’s Public Good Contributions? Games. 2020; 11(1):6. https://doi.org/10.3390/g11010006
Chicago/Turabian StyleAbatayo, Anna Lou, Lea Skræp Svenningsen, and Bo Jellesmark Thorsen. 2020. "Thankful or Thankless: Does the Past’s Altruism Increase the Present’s Public Good Contributions?" Games 11, no. 1: 6. https://doi.org/10.3390/g11010006
APA StyleAbatayo, A. L., Svenningsen, L. S., & Thorsen, B. J. (2020). Thankful or Thankless: Does the Past’s Altruism Increase the Present’s Public Good Contributions? Games, 11(1), 6. https://doi.org/10.3390/g11010006






