Perceptions of Farm Size Heterogeneity and Demand for Group Index Insurance
Abstract
1. Introduction
2. Dairy Farmers in the Dominican Republic
3. Dry-Run Satellite Vegetation Index Product
4. Methods
4.1. Experimental Task
4.2. Experimental Treatments
4.2.1. Monthly Compared to Seasonally Cumulative Index Option
4.2.2. Groups versus Individual Contracts
4.3. Perceptions of Farm Size
4.4. Procedures
5. Empirical Results
5.1. Who Participated
5.2. Demand for Insurance
5.3. Group Distance
6. Comprehension
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| (1) | (2) | |
|---|---|---|
| First Stage | Second Stage | |
| VARIABLES | Distance | Insurance |
| High–Low | 13.42 * | |
| (8.272) | ||
| Monthly | 10.10 | 0.137 |
| (9.584) | (0.561) | |
| Age | −0.216 | −0.0116 |
| (0.194) | (0.0113) | |
| Total Own Cows | −0.335 *** | −0.0105 ** |
| (0.128) | (0.00420) | |
| Distance | −0.0278 *** | |
| (0.00524) | ||
| Constant | 33.55 ** | 1.540 |
| (13.44) | (1.069) | |
| Observations | 125 | 125 |
| F-Stat | 3.26 | |
| (Prob > F ) | (0.0192) |
| (1) | (2) | |
|---|---|---|
| First Stage | Second Stage | |
| VARIABLES | Distance | Insurance |
| High–Low | 25.27 * | |
| (14.26) | ||
| Monthly | 6.320 | 1.122 |
| (12.55) | (39.44) | |
| Age | −0.0282 | 0.389 |
| (0.276) | (0.709) | |
| Total Own Cows | −0.137 | 0.477 |
| (0.124) | (0.464) | |
| Distance | 2.388 * | |
| (1.389) | ||
| Constant | 12.83 | 219.2 *** |
| (16.25) | (49.26) | |
| Observations | 82 | 82 |
| R-squared | −0.940 | |
| F-Stat | 3.99 | |
| (Prob > F ) | (0.0095) |
| (1) | (2) | |
|---|---|---|
| First Stage | Second Stage | |
| VARIABLES | Total Perceived Cows | Insurance |
| High–Low | −17.90 *** | |
| (5.403) | ||
| Monthly | 0.607 | 18.26 |
| (6.608) | (29.02) | |
| Age | 0.167 | 0.885 * |
| (0.107) | (0.492) | |
| Total Own Cows | 0.291 | 1.132 |
| (0.278) | (1.067) | |
| Total Perceived Cows | −3.371 ** | |
| (1.341) | ||
| Constant | 16.94 | 306.9 *** |
| (10.45) | (47.15) | |
| Observations | 82 | 82 |
| F-Stat | 7.46 | |
| (Prob > F) | (0.0002) |
References
- Cai, J.; de Janvry, A.; Sadoulet, E. The Impact of Insurance Provision on Household Production and Financial Decisions. Am. Econ. J. Econ. Policy 2016, 8, 44–88. [Google Scholar] [CrossRef]
- Cole, S.; Giné, X.; Vickery, J. How Does Risk Management Influence Production Decisions? Evidence from a Field Experiment. Rev. Financ. Stud. 2017, 30, 1935–1970. [Google Scholar] [CrossRef]
- Karlan, D.; Osei, R.; Osei-Akoto, I.; Udry, C. Agricultural decisions after relaxing credit and risk constraints. Q. J. Econ. 2014, 129, 597–652. [Google Scholar] [CrossRef]
- Norton, M.; Osgood, D.; Madajewicz, M.; Holthaus, E.; Peterson, N.; Diro, R.; Mullally, C.; Teh, T.L.; Gebremichael, M. Evidence of Demand for Index Insurance: Experimental Games and Commercial Transactions in Ethiopia. J. Dev. Stud. 2014, 50, 630–648. [Google Scholar] [CrossRef]
- Cai, J. The impact of contract design on insurance uptake. In Proceedings of the 2014 Symposium on Economic Experiments in Developing Countries (SEEDEC), Bergen, Norway, 10–11 December 2014. [Google Scholar]
- Clarke, D.J. A Theory of Rational Demand for Index Insurance. Am. Econ. J. Microecon. 2019, 8, 283–306. [Google Scholar] [CrossRef]
- Takahashi, K.; Barrett, C.; Ikegami, M. Does Index Insurance Crowd In or Crowd Out Informal Risk Sharing? Evidence from Rural Ethiopia. Am. J. Agric. Econ. 2019, 101, 672–691. [Google Scholar] [CrossRef]
- Jensen, N.; Barrett, C.; Mude, A. Index Insurance Quality and Basis Risk: Evidence from Northern Kenya. Am. J. Agric. Econ. 2016, 98, 1450–1469. [Google Scholar] [CrossRef]
- Cai, J.; Song, C. Do disaster experience and knowledge affect insurance uptake decisions? J. Dev. Econ. 2017, 124, 83–94. [Google Scholar] [CrossRef]
- Cai, J.; de Janvry, A.; Sadoulet, E. Social networks and the decision to insure. Am. Econ. J. Appl. Econ. 2015, 7, 81–108. [Google Scholar] [CrossRef]
- Cole, S.; Giné, X.; Tobacman, J.; Topalova, P.; Townsend, R.; Vickery, J. Barriers to Household Risk Management: Evidence from India. Am. Econ. J. Appl. Econ. 2013, 5, 104–135. [Google Scholar] [CrossRef]
- Vasilaky, K.; Diro, R.; Norton, M.; McCarney, G.; Osgood, D. Can Education Unlock Scale? The Demand Impact of Educational Games on a Large-Scale Unsubsidised Index Insurance Programme in Ethiopia. J. Dev. Stud. 2018, 48. [Google Scholar] [CrossRef]
- Gaurav, S.; Cole, S.; Tobacman, J. Marketing complex financial products in emerging markets: Evidence from rainfall insurance in India. J. Mark. Res. 2011, 48, 150–162. [Google Scholar] [CrossRef]
- Dercon, S.; Hill, R.V.; Clarke, D.; Outes-Leon, I.; Seyoum Taffesse, A. Offering rainfall insurance to informal insurance groups: Evidence from a field experiment in Ethiopia. J. Dev. Econ. 2014, 106, 132–143. [Google Scholar] [CrossRef]
- de Janvry, A.; Dequiedt, V.; Sadoulet, E. The Demand for insurance against common shocks. J. Dev. Econ. 2014, 106, 227–238. [Google Scholar] [CrossRef]
- Janssens, W.; Kramer, B. The social dilemma of microinsurance: Free-riding in a framed field experiment. J. Econ. Behav. Organ. 2016, 131, 47–61. [Google Scholar] [CrossRef]
- Boucher, S.; Delpierre, M. The impact of index-based insurance on informal risk-sharing networks. SSRN Electron. J. 2014. [Google Scholar] [CrossRef][Green Version]
- Lenel, F.; Steiner, S. Insurance and Solidarity: Evidence from a Lab-in-theField Experiment in Cambodia. J. Econ. Behav. Organ. 2020. forthcoming. [Google Scholar]
- Vroege, W.; Dalhaus, T.; Finger, R. Index insurances for grasslands—A review for Europe and North-America. Agricultural systems. Sci. Rep. 2019, 168, 101–111. [Google Scholar]
- Dalhaus, T.; Musshoff, O.; Finger, R. Phenology information contributes to reduce temporal basis risk in agricultural weather index insurance. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Farrin, K.; Javier Miranda, M.; O’Donoghue, E. How Do Time and Money Affect Agricultural Insurance Uptake? A New Approach to Farm Risk Management Analysis. Econ. Res. Rep. 2016, ERR-212, 128–132. [Google Scholar]
- Sherrick, B.J.; Barry, P.J.; Ellinger, P.N.; Schnitkey, G.D. Factors Influencing Farmers’ Crop Insurance Decisions. Am. J. Agric. Econ. 2004, 86, 103–114. [Google Scholar] [CrossRef]
- Attanasio, O.; Rios-Rull, J.V. Consumption smoothing in island economies: Can public insurance reduce welfare? Eur. Econ. Rev. 2000, 44, 1225–1258. [Google Scholar] [CrossRef]
- McPherson, M.; Smith-Lovin, L.; Cook, J. Birds of a Feather: Homophily in Social Networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef]
- De Weerdt, J. Risk-Sharing and Endogenous Network Formation. In Insurance Against Poverty; Dercon, S., Ed.; Oxford University Press: Cambridge, UK, 2005. [Google Scholar]
- Fafchamps, M.; Lund, S. Risk-sharing networks in rural Philippines. J. Dev. Econ. 2003, 71, 261–287. [Google Scholar] [CrossRef]
- Johnson, T.; Smirnov, O. Inequality as information: Wealth homophily facilitates the evolution of cooperation. Sci. Rep. 2018, 8, 1225–1258. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.; Johns, T.; Krinner, G.; et al. Chapter 12—Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013: The Physical Science Basis; IPCC, Ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [CrossRef]
- Leblois, A.; Quirion, P. Agricultural insurances based on meteorological indices: Realizations, methods and research. Meteorol. Appl. 2012, 20, 1–9. [Google Scholar] [CrossRef]
- Brahm, M.; Vila, D.; Martinez, S.S.; Osgood, D. Can disaster events reporting be used to drive remote sensing applications? A Latin America weather index insurance case study. Meteorol. Appl. 2019, 92, 1–10. [Google Scholar] [CrossRef]
- Osgood, D.; Powell, B.; Diro, R.; Farah, C.; Enenkel, M.; Brown, M.; Husak, G.; Blakeley, S.L.; Hoffman, L.; McCarty, J. Farmer Perception, Recollection, and Remote Sensing in Weather Index Insurance: An Ethiopia Case Study. Remote Sens. 2019, 10, 1887. [Google Scholar] [CrossRef]
- Carter, M.R.; Barrett, C.B.; Boucher, S.; Chantarat, S.; Galarza, F.; Mcpeak, J.; Mude, A.; Trivelli, C. Insuring the Never Before Insured: Explaining Index Insurance. SSRN Electron. J. 2008, 1–8. [Google Scholar] [CrossRef][Green Version]
- Gelman, A.; Carlin, J. Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors. Perspect. Pscychol. Sci. 2014, 9, 641–651. [Google Scholar] [CrossRef] [PubMed]
- Szucs, D.; Ioannidis, J. Empirical assessment of published effect sizes and power in the recent cognitive neuroscience and psychology literature. PLoS Biol. 2017, 15, e2000797. [Google Scholar] [CrossRef] [PubMed]
- Carpena, F.; Cole, S.; Shapiro, J.; Zia, B. Unpacking the Causal Chain of Financial Literacy; World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2012. [Google Scholar]
- Duflo, E.; Kremer, M. Using Randomization in Development Economics Research: A Toolkit. In Handbook of Development Economics; Schultz, T.P., Strauss, J.A., Eds.; Elseiver: Amsterdam, The Netherlands; New York, NY, USA, 2008; Volume 4, Chapter 61; pp. 3935–3940. [Google Scholar]
- Fréchette, G.R. Session-effects in the laboratory. Exp. Econ. 2012, 15, 485–498. [Google Scholar] [CrossRef]
- Bertrand, M.; Duflo, E.; Mullainathan, S. How Much Should We Trust Differences-In-Differences Estimates? Q. J. Econ. 2004, 119, 249–275. [Google Scholar] [CrossRef]
- Cameron, A.C.; Gelbach, J.B.; Miller, D.L. Bootstrap-Based Improvements for Inference with Clustered Errors. Rev. Econ. Stat. 2008, 90, 414–427. [Google Scholar] [CrossRef]
- MacKinnon, J.G.; Webb, M.D. The wild bootstrap for few (treated) clusters. Econometr. J. 2018, 21, 114–135. [Google Scholar] [CrossRef]
- Roodman, D.; Nielsen, M.; MacKinnon, J.G.; Webb, M.D. Fast and wild: Bootstrap inference in Stata using boottest. Stat J. 2019, 19, 4–60. [Google Scholar] [CrossRef]
- Wooldridge, J. Introductory Econometrics: A Modern Approach; Southwestern Cengage Learning: Mason, OH, USA, 2008. [Google Scholar]
- Syngenta Foundation. New Routes to Smallholder Prosperity: Unlocking the Potential for Farm Insurance and Finance. In Syngenta Foundation Conference 2018; Syngenta Foundation for Sustainable Agriculture: Basel, Switzerland, 2018. [Google Scholar]
- Food and Agriculture: Key to Achieving the 2030 Agenda for Sustainable Development; Technical Report; Food and Agriculture Organization of the United Nations: Rome, Italy, 2016.
| 1. | While our study focuses on the developing country context, our setup could also extend to developed country contexts as well, where farmers have cooperatives and experience contemporaneous covariate risk. Vroege et al. [19] and Dalhaus et al. [20] cover index insurance in the developed country context. |
| 2. | The first dry season, typically with a widespread impact across the region, runs from December to March. The second dry season begins in July and lasts until September, usually affecting the coastal zones more dramatically. |
| 3. | On average, according to 2014 data, dairy producers receive 18 Dominican Pesos (DOP), or 0.42 USD, per liter of milk after accounting for handling fees. Production costs per cow each month range between 2175 and 3045 DOP (50 and 70 USD) during the dry season and rainy season, respectively. These costs typically include: supplementary feed, labor, veterinary costs, and pasture packs. |
| 4. | The raw NDVI image files from eMODIS were sourced via http://www.fews.net/, a USAID-supported drought and famine early warning program implemented by several US Federal agencies. |
| 5. | NDVI is a spectral transformation of the visible (red) and near-infrared (NIR) bands. |
| 6. | To estimate the land extent significant to the dairy farmers for the index, the USAID DR CRII modeling partner extracts the NDVI pixels that correspond with grassland data from The Food and Agriculture Organization land cover dataset (GLC-SHARE). The pentads are averaged at a municipal or district level, using the boundaries provided by the Dominican National Statistics Office. The pentads are then accumulated into months and payouts are defined at a threshold value based on normalized historical values, calibrated against yield data. For this study, the normal conditions for each pentad and geographical area are established for the reference period 2000 to 2014. |
| 7. | For the validation of the index and evaluation of the basis risk, we performed a product assessment exercise across four sample villages, funded by USAID, throughout 2013 and 2014. This exercise consisted of a series of focus group workshops with dairy farmer associations to discuss farmers’ perception of historical droughts compared to the historical years the index would have triggered. The exercise is based on the participatory processes used in the R4 project, https://www.wfp.org/r4-rural-resilience-initiative, and studied by Brahm et al. [31] and Osgood et al. [32]. The assessment shows that the model agreed with most of the historical drought years mentioned by the farmers. It also confirmed that the NDVI-based index design captured the severe drought events with more accuracy than the available yield data or previous index iterations based on rainfall data. |
| 8. | Community funds were used to implement community level risk management measures, which were not announced until game payments were made, to benefit only those who did contribute. |
| 9. | Note that the choice was not between allocating funds either into savings or into insurance, as the expected return to insurance in any given year would not exceed the returns to our savings account. However, conditional on the probability of drought being positive, it is always in the farmer’s interest to purchase some insurance. |
| 10. | Farmers receive approximately 20 DOP (before accounting for handling fees) for each liter of milk sold, and yield an average of 10 L per day during the rainy season. |
| 11. | The interest rates do not reflect the real market rates in the Dominican Republic. Further, a 3× payout reflected an index that would pay a full payout approximately once every six years, mimicking several active index insurance projects in the developing world and the expectations for the expected commercial implementation in the Dominican Republic. |
| 12. | Participants given the monthly index option could choose the particular months to be insured during the dry run period of February to September. Participants could allocate their tokens (425 DOP, 10 USD) to one month or allocate their tokens throughout all or some months. For example, if participants invested one token (25 DOP) in one month and another token to a different month, and, if both months were dry enough to trigger the index, producers would receive a three-token (75 DOP) insurance payout for each month that triggered. In the seasonally cumulative index insurance, participants were free to allocate their game endowment across three different periods: (1) February and March; (2) April, May, and June; and (3) July, August, and September. (January was excluded as the games took place from 28 to 31 January 2014.) For example, if participants put one token on Period 1 and another token on Period 2, and both three-month periods were dry enough to trigger the index, then producers would receive a three-token insurance payout for each of the different periods. |
| 13. | It is likely that group uptake would change with group size—a question we do not address here. |
| 14. | Note that farmers could defer this decision to the time of any eventual payouts in the season, although the majority (79%) chose to make this decision upfront. |
| 15. | The sample size was determined using power calculation for a two treatment arm study with = 0.8, = 0.05, effect size of 30, and = 80, and approximately 30 observations per cluster, which resulted in a required sample size of 84 in the control group and 168 for both treatment groups, with a minimum of nine clusters for the two treatment groups. sampsi 0 30, sd(80) ratio(2) power(.8) and sampclus, obsclus(30) were the commands used in Stata. We powered the group treatment sessions comparing high and low distance with = 0.8, = 0.10, effect size of 40, and = 80, and approximately three observations per cluster, with an ICC = 0.5, which resulted in a required sample size of 76 in each group and a minimum of 60 clusters. sampsi 0 40, sd(80) power(.8) and sampclus, obsclus(3) rho(0.10) were the commands used in Stata. Note that the ex-post intra-class correlation coefficient that we find in the data are higher than 0.1, ranging 0.25–0.5 for the session and group level, respectively. Therefore, we should be cautious in interpreting the magnitude of our results given that under-powered studies have a greater likelihood of overstating the magnitude of the effect size [34,35]. |
| 16. | For example, the overall insurance uptake in the game, and amounts of insurance purchased might be higher than would be observed commercially, particularly because farmers were given cash in the form of tokens alleviating any liquidity constraints, which typically hinder demand [11]. |
| 17. | The majority of participants were literate. In a few cases, we had an additional facilitator assisting illiterate farmers in recording their choices. |
| 18. | Due to concerns about contagion effects, discussions between farmers in sessions were discouraged. Farmers were not allowed to speak to one another during the framing and experimental choice process. The only time farmers were allowed to speak to one another was during the group insurance sessions within the assigned groups. |
| 19. | The upcoming season occurred between February and September 2014. Unlike the practice round, the insurance outcome in the final round was determined by the upcoming season’s pasture conditions and was not based on the outcome of a hypothetical draw. |
| 20. | Only 3 out of the 354 participants did not allocate any of their endowment to insurance. |
| 21. | We could also compare the amount of group insurance purchased in group sessions to the amount of insurance purchased in individual sessions, which would capture the treatment-on-the-treated (TOT). This estimate, however, would suffer from selection bias, given that only certain types individuals self-select into purchasing group insurance ([37], p. 3935). |
| 22. | While we did not design the study to be powered to test for interaction effects between the monthly index treatment and the group insurance treatment, the interaction effect of the two treatments is neither statistically nor economically significant when adding it as an additional term. |
| 23. | Instruments are significant at the first stage but not reported here. |
| 24. | In some instances for the instrumental variable approach, our models return a negative R-squared, which is feasible and does not detract from the estimators’ validity. As Wooldridge [43], p. 516 discusses, a R-squared statistic from an instrumental variable model is neither very useful nor has a natural interpretation as it does in OLS. |
| 25. | 0.05 × 20 cows = 1 cow; (0.59 − 0.56/0.56) = 0.053. |

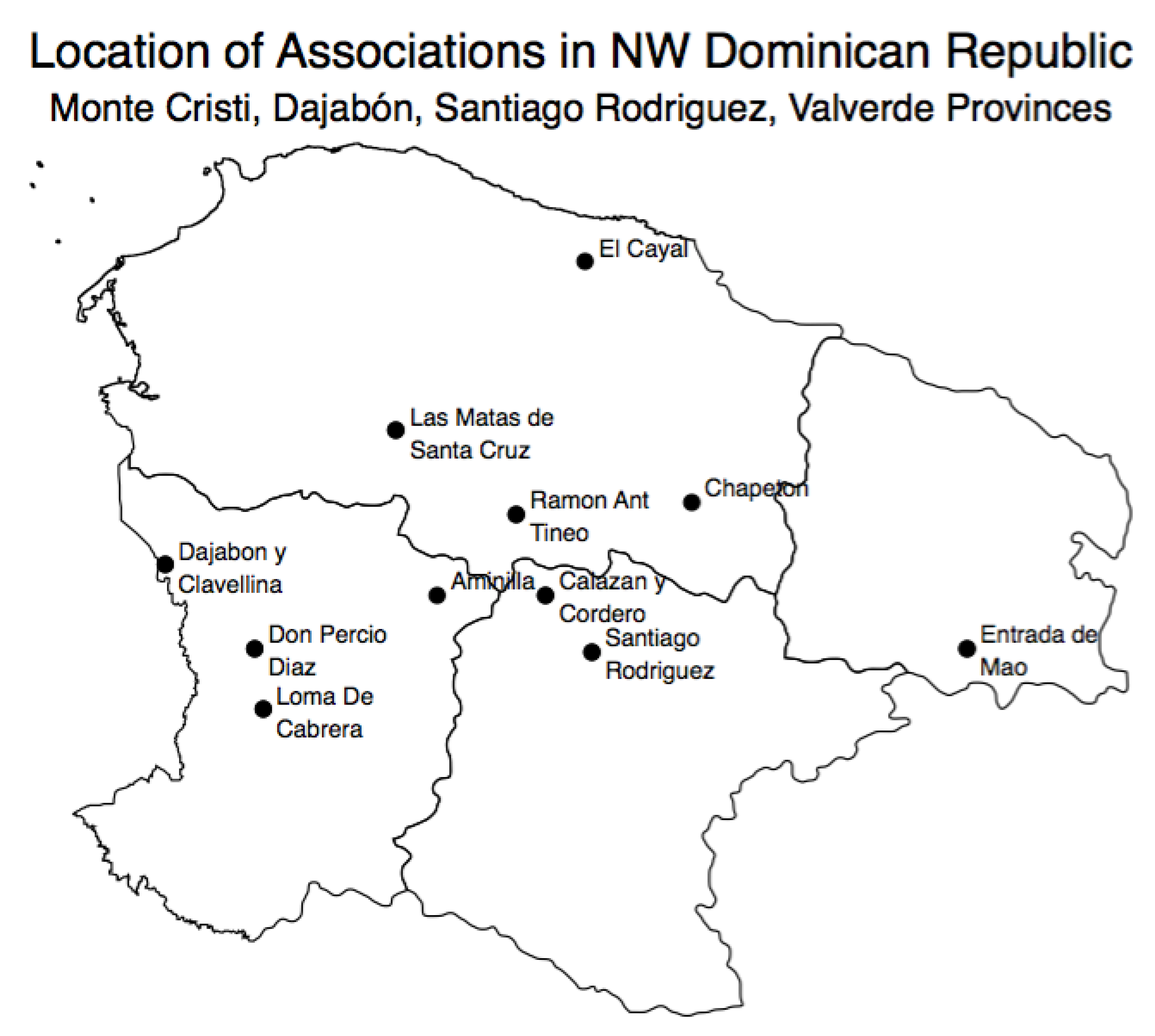
| Association Name | N |
|---|---|
| Aminilla | 44 |
| Calazan y Cordero | 45 |
| Chapeton | 28 |
| Dajabon and Clavellina | 39 |
| Don Percio Diaz | 34 |
| El Cayal | 24 |
| Entrada de Mao | 36 |
| Las Matas de Santa Cruz | 21 |
| Loma De Cabrera | 27 |
| Ramon Ant Tineo | 32 |
| Santiago Rodriguez | 24 |
| Total | 354 |
| Variable | IND | GRP | IND SD | GRP SD | Pval | N |
|---|---|---|---|---|---|---|
| Age | 57.9 | 52.99 | 12.93 | 13.67 | 0.0029 *** | 341 |
| Male | 1.93 | 1.93 | 0.25 | 0.26 | 0.82 | 355 |
| Education * | 1.92 | 2.12 | 1.44 | 1.64 | 0.22 | 350 |
| No. Cows 2013 | 20.96 | 21.65 | 24.08 | 20.34 | 0.78 | 320 |
| No. Cows 2014 | 19.18 | 20.58 | 21.82 | 19.74 | 0.54 | 333 |
| Pasture (acre) | 35.24 | 34.42 | 38.94 | 50.86 | 0.87 | 338 |
| Irrigated pasture (acre) | 3.99 | 3.36 | 8.52 | 11.36 | 0.58 | 319 |
| Projected Labor Costs 2014 (DR Pesos) | 180,893 | 133,579 | 516,002 | 185,437 | 0.27 | 309 |
| Knows of insurance | 0.53 | 0.5 | 0.5 | 0.5 | 0.53 | 341 |
| Knows of index insurance | 0.2 | 0.17 | 0.4 | 0.37 | 0.39 | 326 |
| Variable | Low | High | Low Distance | High Distance | Pval | N |
|---|---|---|---|---|---|---|
| Age | 54.35 | 50.46 | 11.3 | 15.53 | 0.1 | 133 |
| Male | 1.93 | 1.9 | 0.26 | 0.31 | 0.57 | 135 |
| Education * | 2.21 | 2.22 | 1.78 | 1.63 | 0.98 | 134 |
| No. Cows 2013 | 24.22 | 18.58 | 22.32 | 18.5 | 0.14 | 119 |
| No. Cows 2014 | 20.51 | 17.55 | 14.84 | 22.17 | 0.38 | 127 |
| Pasture (acre) | 29.34 | 27.82 | 29.37 | 50.05 | 0.84 | 127 |
| Irrigated pasture (acre) | 2.61 | 2.2 | 4.71 | 3.86 | 0.61 | 117 |
| Projected Labor Costs 2014 (DR Pesos) | 121,615 | 129,261 | 103,957 | 212,156 | 0.8 | 119 |
| Knowledge of insurance | 0.46 | 0.54 | 0.5 | 0.5 | 0.38 | 126 |
| Knowledge of index insurance | 0.14 | 0.21 | 0.35 | 0.41 | 0.29 | 125 |
| Variable | IND | GRP | p-Value |
|---|---|---|---|
| Insurance Purchased | 330.29 | 296.03 | 0.0001 *** |
| Savings | 58.33 | 79.90 | 0.0008 *** |
| Community Savings | 18.11 | 21.11 | 0.01 ** |
| Take Home | 18.268 | 27.94 | 0.09 * |
| (1) | (2) | |
|---|---|---|
| VARIABLES | OLS | OLS |
| Group | −38.81 * | −38.32 * |
| (21.59) | (21.43) | |
| Monthly | 25.61 | 25.65 |
| (21.64) | (21.66) | |
| Age | 0.115 | |
| (0.304) | ||
| Constant | 321.7 *** | 315.1 *** |
| (22.15) | (24.43) | |
| Observations | 354 | 354 |
| R-squared | 0.067 | 0.068 |
| Variable | Low Distance | High Distance | p-Value |
|---|---|---|---|
| (Similar) | (Dissimilar) | ||
| Distance | 5.26 | 15.95 | 0.0026 *** |
| Purchased in Group | 80% | 56% | 0.0058 *** |
| Premium Purchased | 281 | 321 | 0.0003 *** |
| Total Reported No. Group Cows | 51.59 | 32.31 | 0.0017 *** |
| Marginal Effects, Group Sessions | ||
|---|---|---|
| (1) | (2) | |
| VARIABLES | Probit | IV Probit |
| Monthly | −0.173 | 0.142 |
| (0.136) | (0.554) | |
| Age | −0.00675 ** | −0.0110 |
| (0.00266) | (0.0110) | |
| Total Own Cows | −0.00139 | −0.0103 ** |
| (0.00220) | (0.00407) | |
| Distance | −0.0279 *** | |
| (0.00472) | ||
| High–Low | −0.173 | |
| (0.141) | ||
| Observations | 125 | 125 |
| Group Sessions | ||
|---|---|---|
| (1) | (2) | |
| VARIABLES | OLS | IV Reg |
| Monthly | 16.21 | 1.122 |
| (18.31) | (39.44) | |
| Age | 0.322 | 0.389 |
| (0.424) | (0.709) | |
| Total Own Cows | 0.150 | 0.477 |
| (0.242) | (0.464) | |
| Distance | 2.388 * | |
| (1.389) | ||
| High–Low | 60.34 *** | |
| (17.96) | ||
| Constant | 249.8 *** | 219.2 *** |
| (25.78) | (49.26) | |
| Observations | 82 | 82 |
| R-squared | 0.266 | −0.940 |
| Group Sessions | |
|---|---|
| (1) | |
| VARIABLES | IV |
| Monthly | 18.26 |
| (29.02) | |
| Age | 0.885 * |
| (0.492) | |
| Total Own Cows | 1.132 |
| (1.067) | |
| Perceived Cows in Group | −3.371 ** |
| (1.341) | |
| Constant | 306.9 *** |
| (47.15) | |
| Observations | 82 |
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Variable | Premium | After Rain | Basis Risk | Satellite |
| Group | −0.0232 | −0.0370 | 0.0392 | 0.108 |
| (0.0919) | (0.0701) | (0.0695) | (0.0838) | |
| Monthly | −0.0266 | −0.0798 | −0.156 * | −0.120 |
| (0.0940) | (0.0750) | (0.0749) | (0.0759) | |
| Age | 0.00395 *** | 0.000640 | 0.000671 | 0.00115 |
| (0.00126) | (0.00164) | (0.00183) | (0.00198) | |
| Constant | 0.00633 | 0.208 * | 0.688 *** | 0.770 *** |
| (0.0990) | (0.103) | (0.127) | (0.138) | |
| Observations | 254 | 265 | 268 | 260 |
| R-squared | 0.022 | 0.017 | 0.026 | 0.033 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilaky, K.; Martínez Sáenz, S.; Stanimirova, R.; Osgood, D. Perceptions of Farm Size Heterogeneity and Demand for Group Index Insurance. Games 2020, 11, 15. https://doi.org/10.3390/g11010015
Vasilaky K, Martínez Sáenz S, Stanimirova R, Osgood D. Perceptions of Farm Size Heterogeneity and Demand for Group Index Insurance. Games. 2020; 11(1):15. https://doi.org/10.3390/g11010015
Chicago/Turabian StyleVasilaky, Kathryn, Sofía Martínez Sáenz, Radost Stanimirova, and Daniel Osgood. 2020. "Perceptions of Farm Size Heterogeneity and Demand for Group Index Insurance" Games 11, no. 1: 15. https://doi.org/10.3390/g11010015
APA StyleVasilaky, K., Martínez Sáenz, S., Stanimirova, R., & Osgood, D. (2020). Perceptions of Farm Size Heterogeneity and Demand for Group Index Insurance. Games, 11(1), 15. https://doi.org/10.3390/g11010015





