1. Introduction
Some of the most difficult judgment calls humans have to make concern not just how to act but when to do so. These judgment calls are not always predetermined by policies but are made in near-real time by decision-makers who are helped and hindered by individually varying preferences and systematic cognitive biases (e.g., [
1,
2]). In this paper, we present two exploratory studies that show how an individual’s personality characteristics of risk propensity and need for cognition influence behavior over increasing task experience in a game that models safety and security decisions. Our paper benefits from earlier conference presentations of this data [
3,
4]. Here, we add context and an analysis of timing bias in addition to the analysis of the payoff bias we observed.
Timing decisions are important in many contexts and timescales. In computer security, users might, for example, decide when to conduct backups, when to patch, when to update passwords, or when to check the correctness of personal financial account information. Many decisions maintain safety in highly dynamic environments, for instance, in traffic, where drivers periodically direct attention to various locations to update their mental situation model. These decisions mitigate external risks at the cost of attentional resources. While existing studies in judgment and decision-making cover such risk management, they concern decisions between discrete choices. Here, we address decisions along a continuous scale: time. Furthermore, a reward may progressively increase with time up until a point, when it suddenly falls to zero or becomes negative. We can relate this theoretical argument to a more naturalistic situation in the context of security and safety. Consider the case of a decision such as purchasing a motor club membership that provides insurance against break-downs. The membership costs a small fee: saving it, adds up over time. But as one’s car ages, problems become more likely, and sooner or later, we can expect to break down. At that point, calling a tow truck can be free or very costly. We operationalize this class of situations into a game of timing called FlipIt [
5], in which a human player is asked to choose several points in time in order to quickly react to the future actions of a stochastic opponent. In the game, the human player chooses time-points at which to check on the presence of a hidden external, stochastic event. Early checks, before the event, come with a moderate, constant cost, while late checks, after the event, result in a benefit that declines linearly with temporal distance to the event. The game has a defined rational norm [
6], which defines temporal checkpoints that maximize expected utility (see [
2] for the rational model). This allows us to examine timing decisions in relation to this normative model.
In two behavioral experiments, following an observational methodology, we determine how individuals’ general risk-taking propensity interacts with their ability to act successfully in FlipIt. Risk propensity may be a measure that aggregates more stable personality traits [
7], but it can be summarized in that risk-seeking individuals prefer the rare, highly advantageous outcome, while risk-avoiders prefer a steady but potentially lower payoff—provided these are the two available options. In addition, we study the impact of the need for cognition, which is a measure of “relative proclivity to process information” and “tendency to...enjoy thinking” [
8]. Both individual variables were assessed with established psychometric scales [
9,
10]. We provide a detailed discussion of the measures in
Section 2.6. We start with the following hypotheses: (1) Individuals apply their risk-taking preferences systematically. (2) However, the degree to which they are willing to take risks varies with task familiarity and with the perceived amount of available information.
We have known for a while that time factors into the perceived value of rewards: A reward is more desirable if it is expected sooner rather than later [
11,
12]. Economic-behavioral models of such decision-making ascribe a hyperbolic discount function that translates rewards and temporal delays to a perceived value (e.g., [
13]). Indeed, FlipIt players can exhibit a preference for earlier action [
2]. However, we want to make it clear that in the experiments presented here, we keep the wait for the reward constant and decouple reward from action timing.
Games of timing like FlipIt are not new (e.g., [
14,
15]). The economic literature has considered a range of games of timing under many different names that include preemption games [
16], wars of attrition [
17], clock games [
18], and stealing games [
19]. Furthermore, human behavior exhibits general systematic biases in the domain of security [
20,
21,
22,
23].
2. Two Timing Studies: Methods
2.1. Overview
Our analysis in this paper relies on the data from two studies. The studies elicit timing decisions from subjects across several rounds of a task that allows for learning. They also obtain, in a between-subject design, measures of personality differences, which are then correlated with the timing decisions. We will first describe the FlipIt game, before introducing participants, survey measures, the general procedure, and then the individual experiments.
2.2. The FlipIt Game: A Timing Task
The FlipIt game was designed to represent the trade-offs involved in the kinds of decisions described in the introduction [
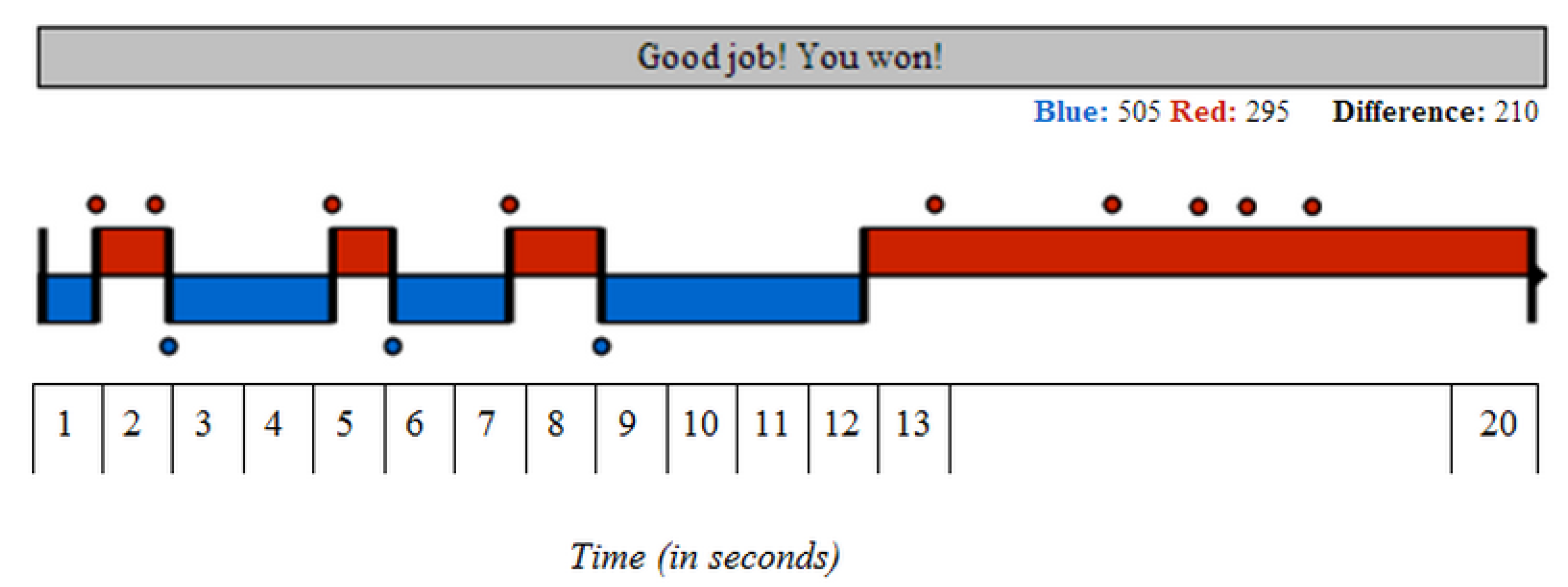
5]. FlipIt players decide on the timing of their actions, and their choices reveal related preferences and biases. Consider a card that is red on one side and blue on the other. It can be flipped to either side, representing the state of the game and ownership of a shared resource for which players compete in the game. The longer the card is flipped to the red side, the more payoff is generated for the red player, and vice versa for the blue player. Players can pay to flip the card over to their own color (i.e., “flips”); however, they have to make these moves with incomplete information about the current state of the card: They do not know which color it shows at the time, and they do not know if and when the other player has flipped the card. Thus, the goal of each player is to predict the timing of the covert move of the opponent and to follow it as closely as possible with their own move. After each move, players see whether it was a wasted expense (because the card was already showing the player’s color), or if not, how long ago the other player had flipped it. Thus, they can learn about their opponent’s strategy. (
Appendix A gives the detailed instructions given to the experimental participants, which may be helpful in understanding the game.)
At an abstract level, the question is when to take investigative action and to reset the resource to a secure state (if compromised). We find that the principles of FlipIt transfer to a range of shorter-term decisions as outlined in the Introduction. Resources and payoffs in these cases may be cognitive, such as limited attentional resources that need to be divided between different stimuli. The element of FlipIt that transfers is the forecasting of external, stochastic events and the making of timing decisions under such uncertainty.
The rules of the FlipIt game can be formalized as follows. Our implementation is a finitely long game with two competing players who each aim to maximize ownership duration of an indivisible resource (i.e., the game board). Two players compete for ownership of the board, which stands for a resource that one player always occupies or a strategy that they pursue. Hence, the board’s current state is two-valued. Its state is covert: Who owns the board is not immediately visible to the players, but players can attempt to take over the board at any time.
Each player has a single constant-cost move (i.e., the flip), which has the effect of taking/re-taking control (if the other player has ownership) or merely maintaining control over the board (if the other player does not have ownership). That means that if a player already owns the board at the time, that cost is wasted; if however, the opponent owns the board, the player takes over ownership at that time.
The original FlipIt study concerned equilibria and dominant strategies for simple cases of interaction [
24,
25]. In addition, the usefulness of the FlipIt game has been investigated for various application scenarios [
5]. We have, in some working papers, suggested that participant performance improves over time [
26], although older participants improve less than younger ones. The same experiment found significant performance differences with regards to gender and the need for cognition. (In Study 1 of the present paper, we describe and analyze these data.) In other work, we determine the rational strategies and begin to develop a model backed by a cognitive architecture, which describes human heuristics that practically implement risk-taking preference in timing decisions [
2,
3,
27].
2.3. This Instantiation of FlipIt
This version of FlipIt reflects a number of design choices. First, the individual payoff of the players increases linearly with the time they have ownership of the resource. This choice is suitable if we are considering compromise of a networked resource for the purpose of sending spam, but alternative scenarios are plausible as well. Second, we reveal information about the past state of the resource to the player after each flip. That is, at the time of each flip the defender learns whether the resource has been compromised since her previous flip (and she then also learns the exact payoff since the previous flip). However, the current state forward will again be covert. This design choice reflects a middle-ground; we defer to future work the experiment in which defenders only receive feedback about their payoff performance and the state of the resource after the experiment has ended. Furthermore, we would consider the opposite case (i.e., a game without any covert state) less relevant for the security context. Third, our experimental setup focuses on relatively fast-paced games with a length of 20 s. With this initial set of experiments, we explore the challenges of timing security decisions that require quick reactions and fast information processing [
28].
Each human participant played a relatively fast-paced version of the FlipIt game. However, we expected that the round length of 20 s would provide participants with enough time to develop an appropriate strategy against the computerized opponent. We used the series of rounds to create increasing familiarity with the game.
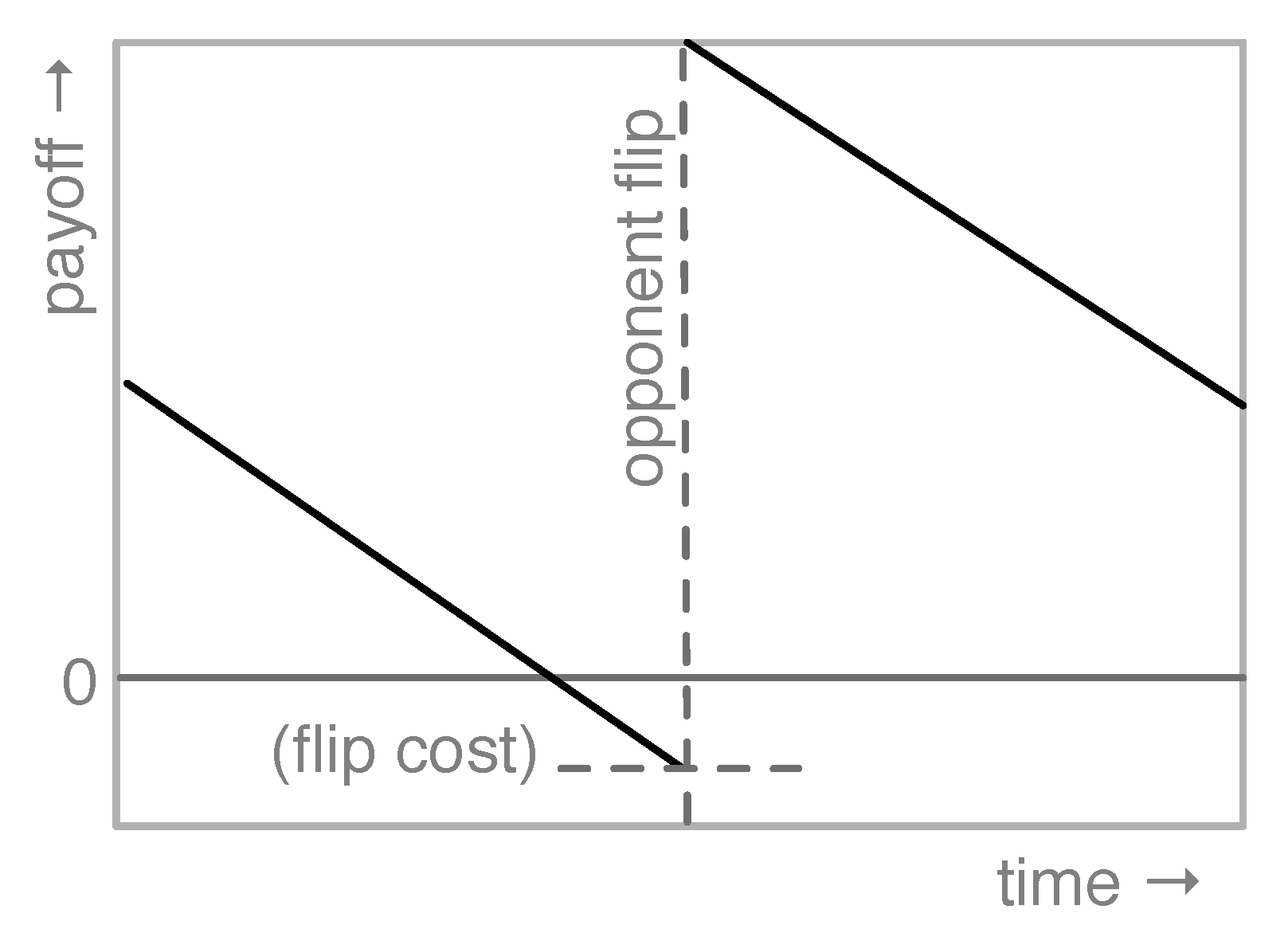
Participants were incentivized as follows to estimate the next opponent flip, follow it with one flip of their own as soon as possible, and not to flip more often than necessary. Their incentive payment decreased linearly with time after the opponent’s flip, and each flip they issued reduced their payment by the equivalent of one second of lateness. The payments were cast as a deduction from an initial endowment, similar to a realistic security decision. Participants were given 50 cents, minus an amount proportional to the time that the opponent owned the FlipIt board, minus a multiple of the number of participant flips. We visualize the payoff structure in
Figure 1. (See
Appendix B for a more exact incentive description.)
2.3.1. Strategy of the Computer Opponent
In both studies, participants faced the same type of computerized opponent that played a fixed (non-adaptive) periodic strategy. The opponent’s flip spacing (i.e, tick) and time of first flip (i.e., anchor) changed in every round of the game, but the overall strategy of the opponent did not. (The human participants always owned the board at the beginning of each round. The computerized player would first act based on the randomly determined anchor value.) Both values were drawn from uniform distributions before a new round started. Flip rates ranged from 1 to 5 s, and the anchor ranged form 0.1 to 4.1 s. Flip rates remained constant within each round.
In the instructions, human participants were given no information about the nature of their opponent.
1 2.3.2. Variability of Available Information
With ecological validity in mind, we covered different degrees of uncertainty in our materials. We gave participants information about the opponent’s strategies, either by pointing out the regularity of spacing, the actual spacing, and/or the time of the initial move. Subjects were randomly assigned to one of these information treatments. For the purpose of the analysis in this paper, we do not distinguish the data across the materials.
2.4. Hypotheses
For the player behavior in FlipIt, we had certain expectations. A participant’s performance likely depends on her individual ability to produce an accurate estimate and her understanding of the task. We address these two sources of variance in two ways. First, we studied the impact of individual differences between subjects (as measured by the psychometric scales) on performance in the game, described in
Section 2.6. We expect that a higher psychometric risk propensity affects the outcome (payment per round) for the participants. Second, we modeled the role of experience and task learning explicitly by allowing the participants to engage in multiple rounds of the game. We generally expect a greater influence of risk propensity at the beginning of the familiarization process, that is, that high risk propensity primarily hurts the untrained decision-makers. This would be compatible with results of risk propensity in the context of impatience [
27].
2.5. Participants
Participants were recruited via the Amazon Mechanical Turk platform and compensated for their participation. The platform allows researchers to post tasks to a diverse audience of potential participants who previously chose to sign up for the platform and who can select from the available posted tasks. Research comparing performance in a variety of well-studied economic experiments (with incentives) showed comparable task performance to classical laboratory experiments [
30]. The pool of participants was restricted to include only United States members with a 90% or better approval rate. We applied settings to prevent repeat entries.
A total of 310 participants completed the first study, and 151 participants completed the second study. We excluded 5 subjects from Study 1 due to repeat participation. In total, the two studies include data for 456 participants who played 2736 rounds of the FlipIt game (see
Section 2.2). As per a survey (see
Section 2.6), the mean age of the participants was
(
), with less than 15% of the participants being older than 40 years. Of the participants, 320 (70%) were male, 45% of the participants had completed “some college”, and an additional 45% had obtained at least a four-year college degree.
2.6. Survey Measures of Individual Differences
We investigate the role of individual difference variables in security decision-making. In particular, we determine how their general risk-taking propensity interacts with their ability to act successfully in the security scenario [
9]. In addition, we study the impact of need for cognition, which is a measure of “relative proclivity to process information” and “tendency to...enjoy thinking” [
8]. Both individual variables were assessed with established psychometric scales [
9,
10].
The survey consisted of four parts. The first part of the survey asked participants basic demographic information, including their age, gender, level of education, and country of origin. The next three parts of the survey were presented in randomized order. One part was a set of integrity check questions to verify participants’ attention to the details of the survey.
The other two sections in the survey were psychometric scales that assessed the level of risk propensity (from [
9]) and need for cognition (from [
10]) of participants.
Psychometric scales measure psychological constructs, usually with regard to individual differences. The scales that were used in this paper were a series of Likert-style questions that were aggregated to yield a measure of the construct desired (here, risk propensity and need for cognition). While there are a number of other ways to measure these constructs (such as the Iowa Gambling Task; [
31] for risk propensity), the survey is a less time-consuming, yet reliable, standardized instrument.
Below, we briefly present the two psychometric scales we selected.
The scale for risk propensity (RP) that we utilized consists of 7 questions. RP is a measure of general risk-taking tendencies [
9]. Note that the RP measure does not define an absolute measure of risk-neutrality with respect to a rational task analysis. Instead, risk taking is measured within its sample distribution.
To measure need for cognition (NFC), we used a five-question scale. This shortened scale has been tested and verified to be usable as an alternative for the original long scale [
10].
2 NFC is a measure of “relative proclivity to process information” and “tendency to...enjoy thinking” [
8]. That is, individuals with low NFC are typically not motivated to engage in effortful, thoughtful evaluation and analysis of ideas. As a result, they will be more likely to process information with low elaboration, i.e., heuristically [
32]. Individuals with a high NFC may also still be guided by intuition, emotions, and images, but they will use these factors “in a thoughtful way” [
33]. Therefore, the assumption that one can equate a high NFC with fully rational reasoning has to be treated with caution [
33]. As a result, the exact impact of high NFC is an empirical question that we investigate in the context of security games of timing.
Studies 1 & 2: Visual vs. Temporal Estimation
The two studies examined timing decisions in two different modalities.
In Study 1, the visual modality task, subjects saw all past moves (until their most recent flip) on a single timeline (i.e., they had a partial history of the game available). See
Figure 2. For the benefit of the reader, we include the instructions page for Study 1 in
Appendix A.
In Study 2, the temporal modality task, we showed participants only the results of their most recent move. That is, they had no visual representation of the history of the game available to them.
Figure 3 shows the subject’s screen after the round.
The additional information available in Study 1 allowed participants to visually extrapolate distances rather than having to decide on an optimal time to flip without this additional information. In addition, Study 2 places higher demands on individuals’ working memory, i.e., they need to try to remember when the opponents’ actions happened.
It is reasonable to assume that Study 2 requires an initially higher degree of system-1-type decision-making because individuals have to take intuitive actions to gather data under the more difficult regime with only temporal feedback and without visual access to the game history.
2.7. Procedure
Participants were informed in writing of the rules and procedures of the game as well as the structure of payments. Furthermore, they were shown an example game. They were then administered a survey questionnaire (see
Section 2.6), which was followed by the main stage of the studies.
In the main stage, the screen showed the actions and results of the FlipIt game, a button to start a new game round, and a button to “flip” the board. Additionally, participants were given the option to revisit the rules of the game in another portion of the window.
Each participant then played six rounds of the FlipIt game that lasted 20 s each. The first round was introduced as a “practice” round during which no bonus payment was awarded. The start of the five experimental rounds was signaled with a pop-up message.
3. Results
3.1. Timing Bias
In the following analysis, data points represent individual subjects’ flips. The subject population and the fact that we investigate early-stage, untrained behavior necessitates more filtering for motivated and able subjects than would be adequate in a controlled laboratory setting. To study timing choices, we will first focus on the subset of subjects () that performed better than the simplistic computer opponent. A second analysis will focus on payoff (the objective given to the participants) and will include all data.
We report two dependent measures. The round payment reflects a subject’s bonus payment per round. We see it as indicative of comprehending the overall game and of performing well in the core risk management and estimation task. The timing bias quantifies performance at the more precise task of estimating the opponent’s flip time and triggering a flip in relation to it. The timing bias is defined as the temporal distance between a subject’s flip and the nearest opponent flip (negative values indicate that the subject flipped shortly before the opponent). The theoretically optimal subject flip occurs immediately after an opponent’s flip (timing bias ). We normalize the error by the periodicity of the opponent’s flips, so that −0.5/+0.5 would describe a flip that occurred halfway between two opponent flips.
Histograms of the timing bias for those subjects who earned at least a break-even bonus payment show a peak following 0. (Subjects who lost all or part of their bonus endowment of $0.50 exhibit a peak before 0, i.e., before the opponent’s flip.)
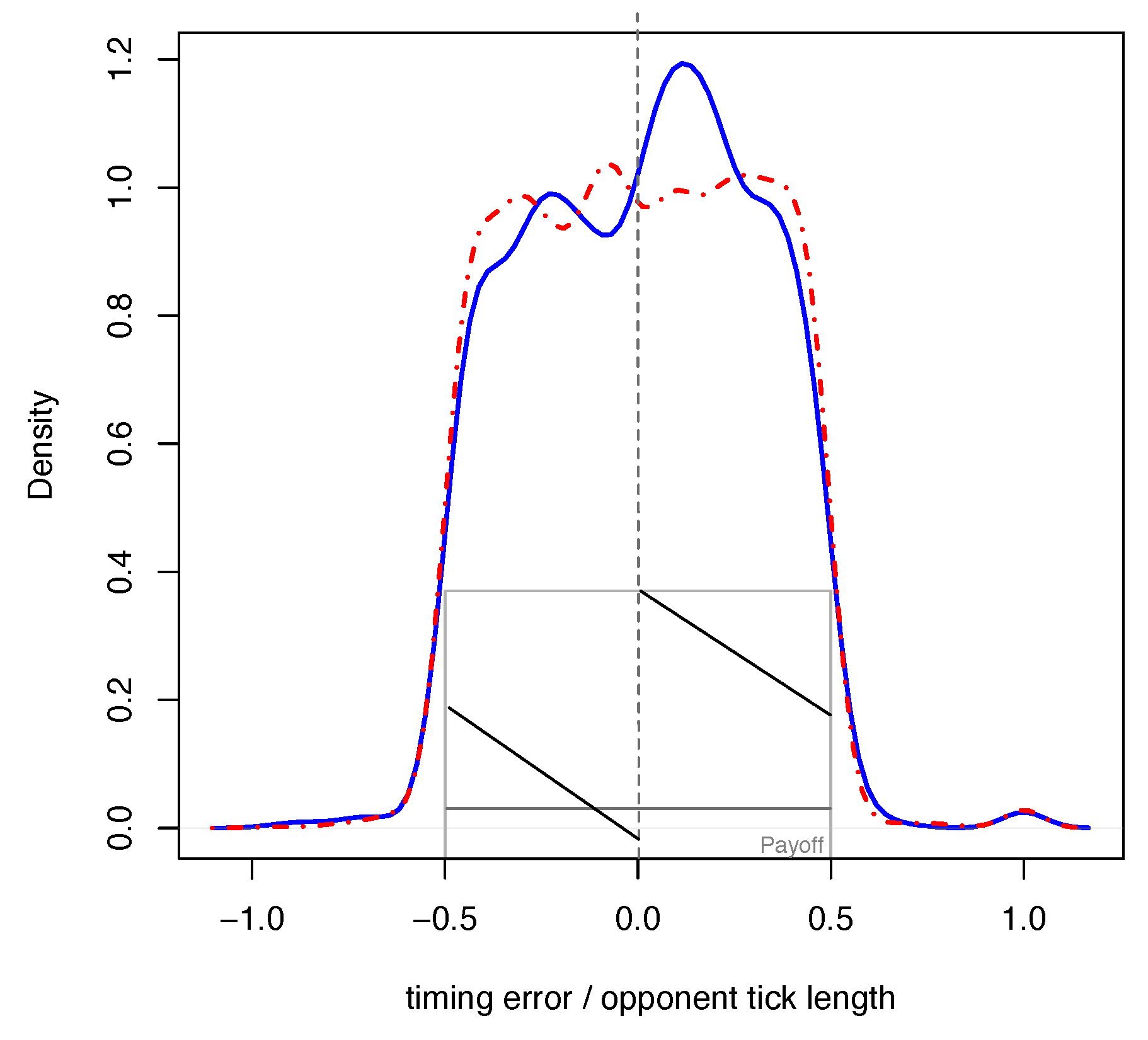
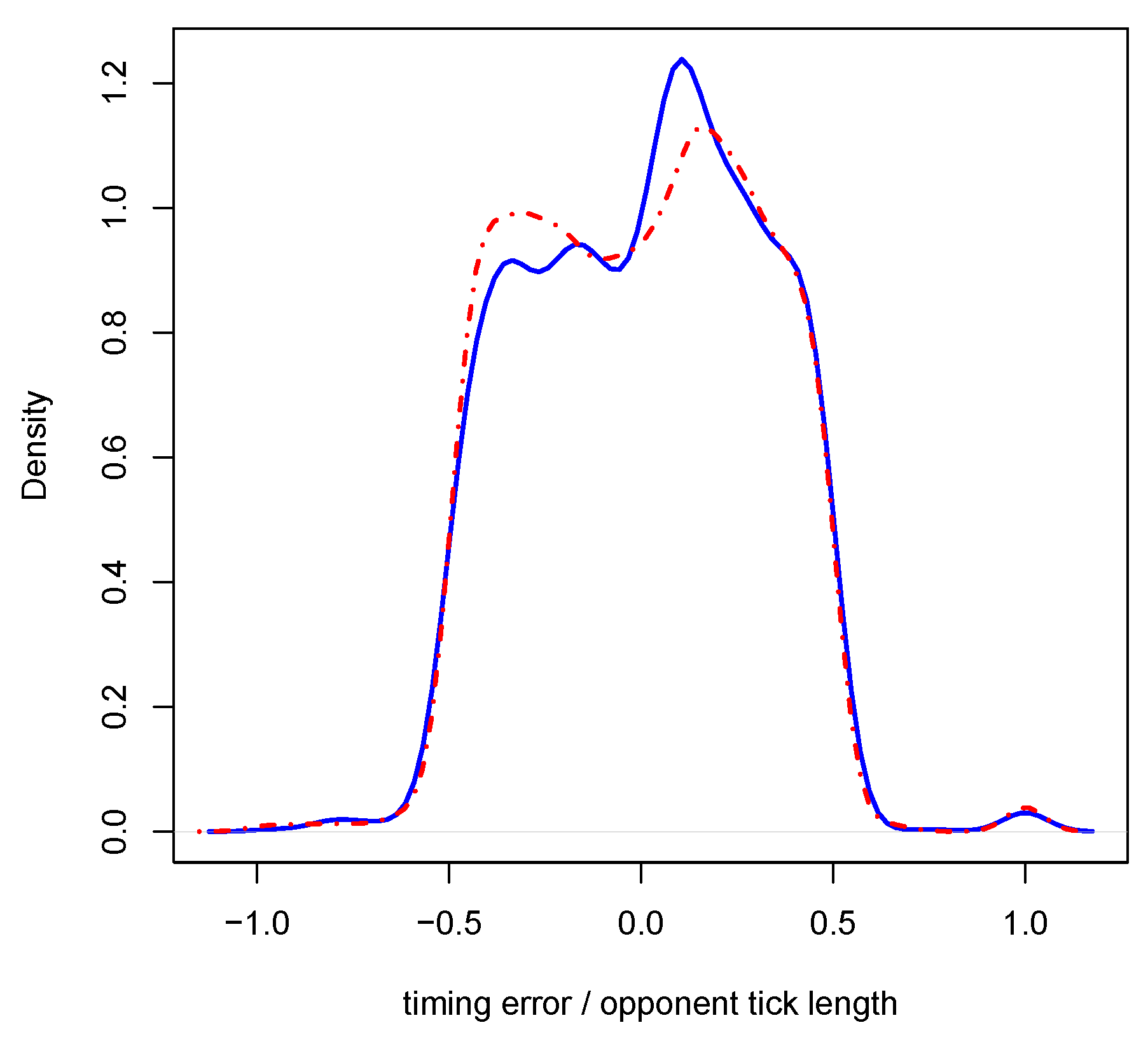
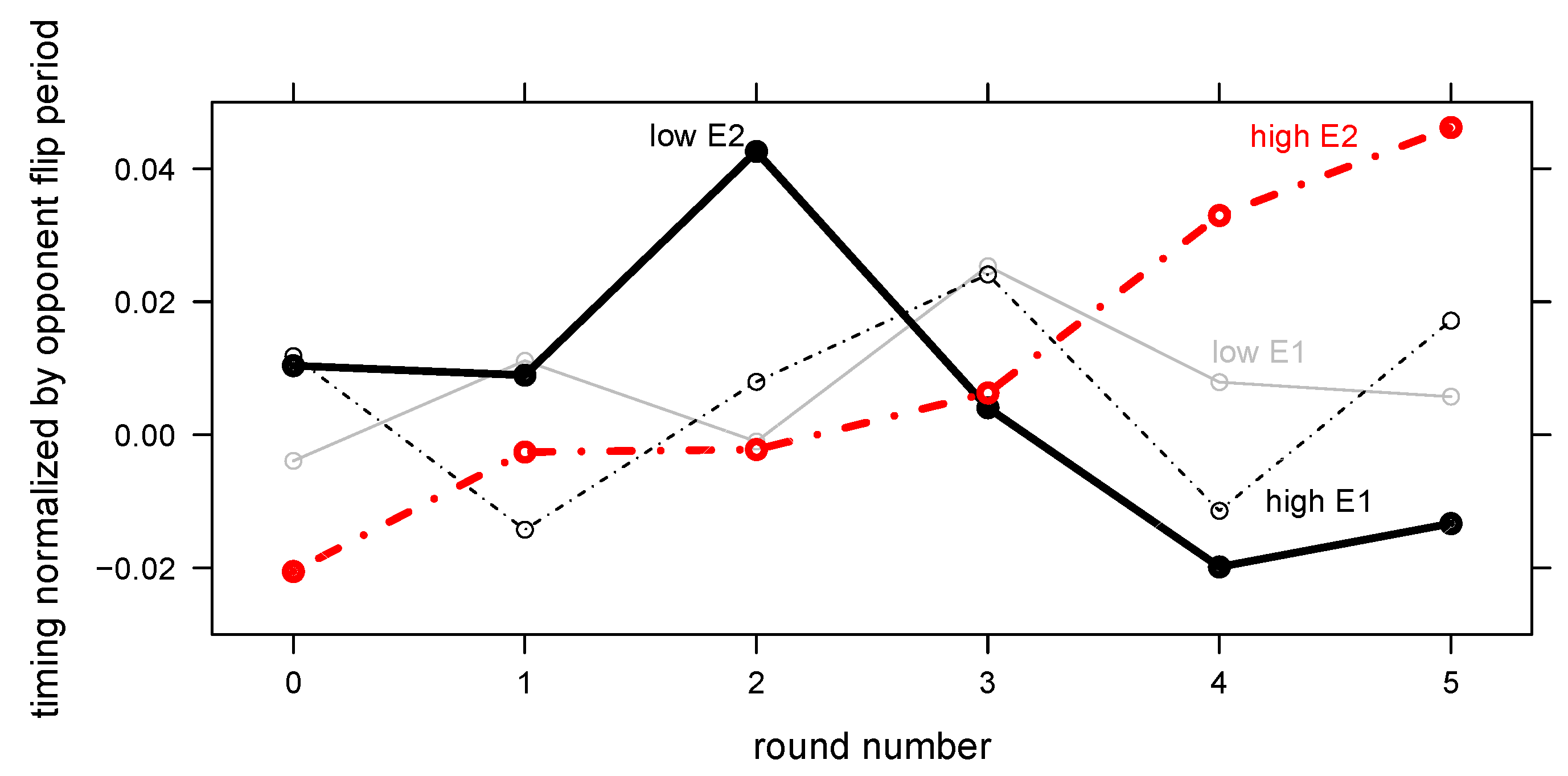
Risk propensity affects people’s behavior in the FlipIt game. We contrast participants of lower-than-mean and higher-than-mean risk propensity (as evaluated by the survey instrument). Subjects with low risk propensity (
Figure 4) show different behavior in Study 1, where the full flip history is available visually: they do not concentrate their flips in the optimal zone. Participants with high risk propensity (
Figure 5), on the contrary, exhibit a peak shortly after the opponent’s flip. This is consistent with subjects more reliably reliably predicting the opponent’s future flips. In Study 2, both participant groups show the peak at the correct time, although participants with high risk propensity concentrate their flips near the opponent’s flip, which is compatible with the explanation that risk-seekers are better at this task.
Do people adapt to the underlying payoff structure of the task? For the qualitative payoff structure, the answer is “yes”: participants understand the basic implications of the rules. However, for the quantitative payoff function (see subgraph in
Figure 4), the answer is more complex. It appears that only individuals with high risk propensity show flip preferences congruent with payoff potential: they mostly flip shortly after the opponent, tapering off slowly afterwards, but strictly avoid the penalty zone right before the opponent’s flip. Conservative individuals show a symmetrical Gaussian peak after the opponent’s tick. The following explanation is consistent with the data: risk-seeking individuals have learned to manage risk better.
The distributions show an aggregate over all rounds, i.e., over all stages of learning. The linear mixed-effects regression model reveals a more detailed picture (see
Table 1). Predicting the bonus payment gained by participants in each round shows that overall, in Study 1, low- and high-risk individuals fare similarly on average, but that high-risk propensity individuals achieve higher gains as time goes on (see also next section).
Figure 6 visualizes the reasons for this effect: in Study 2, risk-seeking individuals start with an overly early timing (before the opponent’s flip), but then shift their timing to be later as they learn to do the task. Risk-avoiding individuals begin with a low bias away from the flip and then adjust their timing as they learn. A linear mixed effects model predicting timing shows a significant, positive interaction effect of experience and risk propensity in Study 2 on timing (
).
3.2. Payoff Model
In this subsection, we investigate the aggregate data across both studies (i.e., the column marked “Combined”) and for the individual studies. We fitted three regression models to understand the impact of the key variables on the payoff earned by the individuals (see
Table 1, which shows the minimized, final model after stepwise regression; with significance threshold
).
As expected, we find that Study 2 came with lower monetary prospects for participants, likely due to its increased difficulty. Age had a small negative impact on performance in the studies (see effect for ), primarily in the later rounds (see interaction effect for (Round): ).
A higher tick and a larger anchor increased the payoff for the human participants.
3 The former finding is intuitive since the human participants have to flip less often to maintain control of the board. The latter finding is straightforward since participants maintain longer control of the board at the start of the game.
Increased experience with the game (as measured by round) improved performance, i.e., participants gained approximately an additional 2 cents in each subsequent round.
We include terms for need for cognition. This variable (abbreviated to NFC) is, like others, centered around 0 (mean) with a standard deviation of 7.09 and range . Based on an exploratory analysis, risk propensity was first centered around 0 (mean), then transformed by taking the absolute to provide a measure of deviation from the mean and log-transformed. We abbreviate this measure as . The standard deviation of this transformed measure is 1.02, with a mean 1.72 and range of .
In the combined data for both studies, we find a main effect for NFC, indicating improved performance by participants with higher need-for-cognition characteristics. The combined model finds no main effect for . However, we discuss interaction effects for NFC and in the following sections.
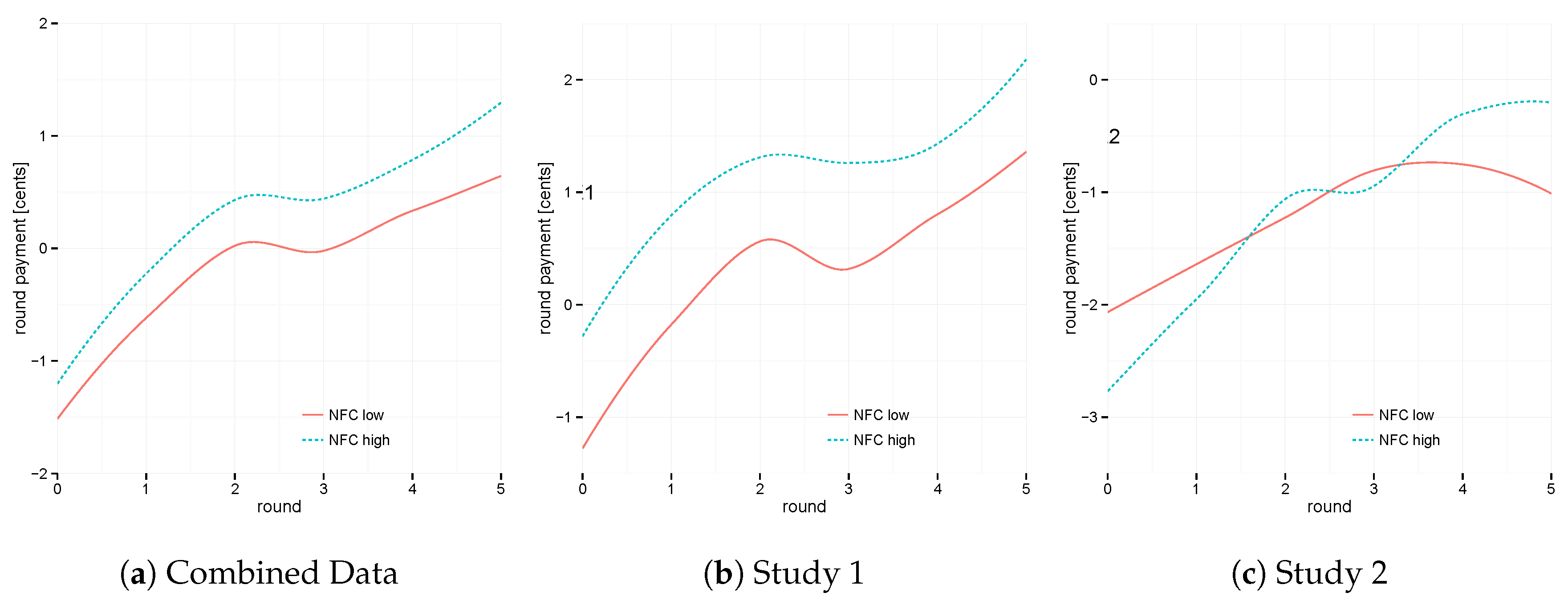
3.3. Interaction Effect of Need For Cognition and Task Experience on Performance
Aggregated across both studies, we find that a higher NFC benefits individuals irrespective of the level of experience (see
Figure 7a). This observation is primarily driven by data from Study 1 (see
Figure 7b). (Note that for all graphical representations, we classified the population of subjects as higher-than-average and lower-than-average NFC and RP levels, respectively.) Concretely, a participant with a need-for-cognition characteristic of one standard deviation above the norm (
) achieved 0.8 cents more in payoff per round. This applies to the situation of average task experience. Task experience mattered more in Study 2 (see
Figure 7c). Here we find that initially, a high NFC is associated with lower payoffs numerically. Only with increased task experience do we observe the superiority of an increased tendency for thinking. While the round is reliably correlated with a higher performance in all models (
), this performance improvement appears to steepen with higher NFC in Study 2 (
,
Table 1, and
Figure 7c).
Accordingly, NFC has a nuanced impact. We observe that a tendency to think deeply about the game and to arrive at strategy choices through system-2 thinking is often, but not always, helpful (see
Figure 7a–c). The interaction effect of NFC and task experience may have been influenced by general task difficulty and the visual feedback that participants received. In the visual modality of Study 1 (i.e., the easier game), participants generally benefit from higher NFC levels, both in early and late stages of the task (see
Figure 7b). In the temporal modality of Study 2, this benefit, if any, may be increased with greater task experience.
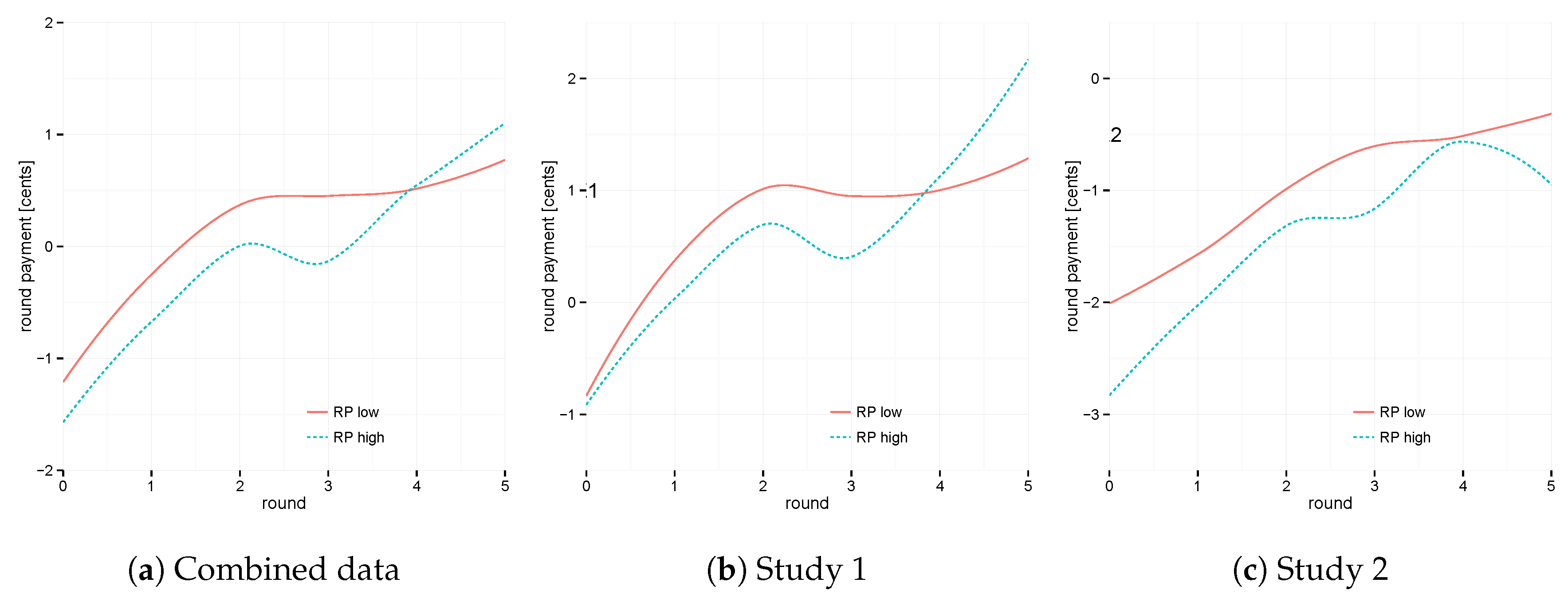
3.4. Interaction of Risk Propensity and Task Experience
In both experimental modalities, risk propensity affects performance in a similar way (see
Figure 8a–c). After applying post-hoc controls for age, tick, and anchor, risk-seeking subjects appear to benefit from a tendency to seek risks not initially but in the final two rounds.
Over the full set of rounds, the full regression model indicates an interaction effect between risk deviation and experience of about
cents per unit of log-transformed risk deviation. If it were visualized in
Figure 8a, the slope of very-high or very-low-RP subjects would steepen compared to that of normal-RP subjects. The regression model describes an additional round profit of
cents per round played for a participant whose risk propensity is one standard deviation higher or lower than average.
3.5. Interaction Effect of Risk Propensity and Need For Cognition
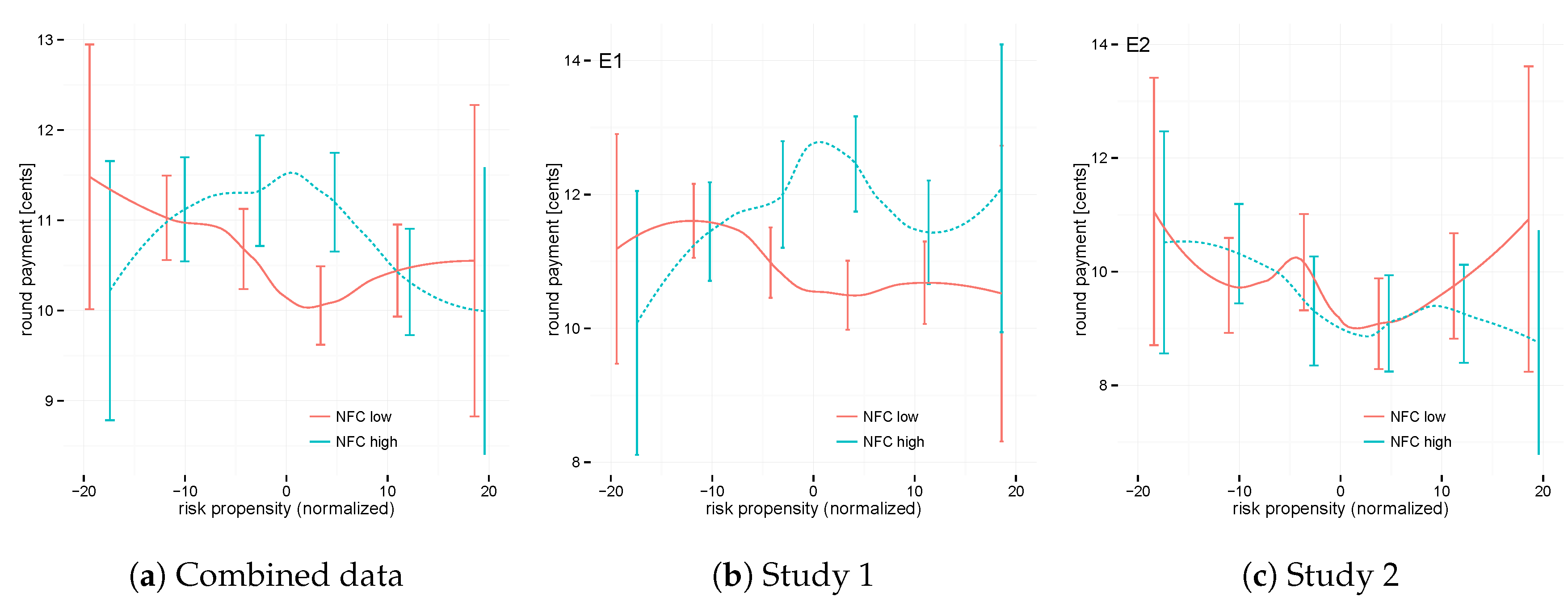
Finally, we study the interaction effect between the two individual difference variables on task performance (see
Figure 9a–c). The exploratory (unplanned) analysis suggests that individuals’ NFC preferences dictate whether they benefit from risk biases. In the aggregate data and in Study 1, we observe that for very risk-averse and highly risk-seeking individuals, there is no observable correlation between task performance and NFC. In contrast, average risk-seeking individuals benefit strongly from a high NFC and suffer considerably from a low NFC.
4 This effect is particularly strong for Study 1 (see
Figure 9b).
The risk deviation captures the interaction with NFC. The models show a reliable interaction effect for the combined data and in Study 1 alone. The associated main effect was not significant. Thus, risk propensity does not help participants immediately. Instead, risk propensity different from the average may reduce the effect of NFC (interaction NFC, ) and it appears to increase learning (interaction round, ).
4. Discussion
The first set of analyses concerned risk-seeking and risk-avoiding participants, who nonetheless did well in the task. We saw that risk-seeking preferences are correlated with strategy choice at the beginner’s level. Once individuals gain experience, risk seekers appear to shift their aggressive timing to be more rational, while risk avoiders start late. Thus, risk taking quite sensibly interacts with task experience.
The cognitive mechanism of this shift in timing may lie in differences in how confident subjects are about their own estimates. If they are less confident about their abilities due to noisy estimates or the unavailability of information (as in Study 2), they will resort to their preferred default and seek higher or lower risks. Even short training can invert the effect due to a change in one’s metacognitive assessment of task ability. (A dynamic model that sees decision-makers adjust their “goals” over time has been proposed but not empirically verified—see [
35].) The modality of estimation (time vs. space) would, sensibly, influence confidence in a decision-maker’s situational awareness.
The experimental task requires implicit, system-1 type decision-making. In particular, we believe that Study 2 requires an initially higher degree of system-1 type decision-making because individuals have to take intuitive actions to gather data under the more difficult regime with only temporal feedback and without visual access to the game history. Need for cognition (NFC) is a metric that allows us to assess whether subjects like to engage in system-2 reasoning. Thus, it makes sense that a high NFC is beneficial particularly in Study 1, with partial history availability, and less so (or later in the game) in Study 2. With this relationship, we show that the survey-based measure of NFC can be predictive of payoff performance.
This becomes even more relevant when considering the role of risk propensity as participants learn to do the task. Risk-seeking personalities fare well once they are ready to analyze the task (Rounds 4 and 5,
Figure 8a,b). Before task experience is acquired, this is not the case.
Subjects can at times make up for their risk propensity or moderate their risk taking in relation to task experience. As we show elsewhere in a psychological experiment [
27] using a different—but comparable—timing game, subjects with a range of risk propensities can play at a comparable level. There, risk-seeking participants took increased risks primarily in fast games and while inexperienced. In an analysis of the timing in Study 2, we show that risk-seekers play early (and riskily) at the beginning of the game but late (and conservatively) towards the end. Risk-avoiders do the opposite. We argue that risk-taking preferences can provide a behavioral default whose influence reduces as more experience with the task is acquired.
Risk propensity leads to different outcomes for individuals who have different psychometric scores for need for cognition.
Figure 9a,b show that average risk propensity may help those with a high need for cognition and hurt those with a low need for cognition. The strength of this effect may be moderated somewhat by the nature of the task and the availability of information used in explicit reasoning. In contrast, in the aggregate data and in Study 1, we observe that for very risk-averse and highly risk-seeking individuals there is no appreciable correlation of task performance and NFC.
Performance in the game is impacted by each participant’s estimate of the timing of the actions of the opponent (i.e., primarily the observations about the computerized player’s flip rate). According to the design of the task, there are two variables that should reduce the noise in this estimation task that induces risk: familiarity with the task, but also precision of the estimates of opponent’s actions. Both of these commonly occur in security scenarios. However, to understand the cognitive process involved and to draw conclusions about policy, it is necessary to differentiate between these two influences. Participants consistently earn higher payoffs with task experience (round number). High need for cognition, as well as particularly high or low risk propensity intensify learning.
As the plots (
Figure 8a and
Figure 9c) show, the interaction between the two individual-difference properties we examine is non-linear. The underlying cognitive processes will be better reflected in more complex process models than the presented mixed-effects models, which were designed to determine the relevant variables. From a theory perspective, the observed data would be consistent with a cognitive model that shifts the optimal risk taking for system-2 thinking in accordance with the task (see [
27] for models that contrast risk taking and patience in a similar task). Risk-seeking facilitates exploration of new strategies, while risk-avoidance leads to exploitation of the best strategy learned so far. Which one is most appropriate depends on the availability of task-related information. For instance, an optimal decision-maker would take into account the distribution of the opponent’s actions and, more simply, the payoffs, in order to gauge whether exploration is likely to yield a better strategy than the best-known one.
The stratified results we found suggest an approach to a cognitive psychology of decision-making that does not average over individual differences but rather embraces them. With a better theory of how individual predispositions interact with task familiarity and other meta-cognitive insights, we will be able to analyze biases that affect groups of subjects rather than everybody. Applications may lie in industrial and organizational psychology as well as in decision-making environments such as security and safety.
5. Conclusions
Differences in individuals’ cognitive predispositions lead to significant and non-obvious biases during timing decisions.
Our experiments apply to a range of, but not all, behavioral timing decisions. We focus on rapid choices made by individual human decision-makers in real-time. Naturally, the risk/reward structure chosen may affect decision-makers, as well as the framing of the task. (Our design included no framing.) Provided the scope of these results are understood, they lend evidence to a model of metacognitive assessment of task difficulty or the reliability of available information, which influence a risk-seeking person’s willingness to take risks.
The remarkable effect we observe is that risk-seeking individuals benefit more from familiarity with the task. Thus, risk propensity may be thought of as a behavior that facilitates or coincides with improved learning. A similar picture emerges for need for cognition in the more difficult task of Study 2, where figuring out the optimal strategy takes longer. There, participants with a high need for cognition perform better once they are experienced.
Individuals who prefer to make thoughtful, deliberate decisions generally fare better over the range of task experience we studied. Other individuals, i.e., those that prefer intuitive decision-making, seem to benefit from clear risk-avoidance or even risk-seeking. The experiments show that individuals of a range of risk propensities can make successful timing decisions in principle, even if the task comes with asymmetric risk–reward distributions, where risk-seeking or risk-avoiding is discouraged. As could be expected, tasks with enough information available to reason carefully are suited to deliberate thinking—but in particular if risk preferences are average. Tasks requiring more working memory and perhaps intuitive decision-making may not benefit from average risk preferences. Levels of risk propensity that maximize the outcome for some tasks can be thought of as those that are risk-neutral, maximizing utility in the security context. Interestingly, however, these “useful” amounts of risk taking happen to be near the population average.
Our results are compatible with a theoretical view that posits the following. Cognitive predispositions vary between individuals, but some of them interact in ways that suggest that there are more or less fortunate combinations when it comes to decision-making. This appears to be the case for risk propensity and need for cognition. We hypothesize that some combinations of traits can even increase predictability. The two traits we examine are fortuitous in that, as we propose on the basis of the data, they help individuals learn to manage external risks in a general way (a lifelong process) and they help them learn to understand a new task (within the experiment). Note that, as in any study involving personality traits, we can only observe correlations between such characteristics, task experiments, and game outcomes. Correlations obviously do not necessarily indicate causal effects. A second caveat is that the FlipIt game was chosen to mimic dynamic security and safety situations; it introduces variability that requires many participants to be sufficiently powered.
The attendant question from a cognitive science perspective—and one to explore next—is how the cognitive predispositions actually combine in people. That is, do they typically occur in advantageous ways? The second question we are exploring is whether we can develop cognitive models of decision-making in security that incorporate such preferences.
The results presented in this paper illustrate an important lesson for security system design and policy: individual differences bias decision-making in predictable ways. From a cyber-security perspective, we ask whether security managers can utilize data about cognitive predispositions and begin adapting policies to individual users or begin addressing the observed biases through intervention strategies. Finally, we call for follow-up studies with behavioral experiments—specifically in the timing context—to better understand the tremendous variety and complexity of practical security decision-making scenarios.