1. Introduction
This paper illustrates how conflict between two parties could possibly arise as a result of rational decision-makers endogenously processing information—that is, without any exogenous changes to the fundamentals of the environment. Consequently, an agent may choose to initiate a conflict for no apparent reason: without instigation or provocation; without observing a change in the behavior of the rival party; without any changes in the costs or benefits of engaging in conflict.
The forces at play in the present model are quite similar to those identified by Hart and Tauman [
1] (2004), where a market environment between two potential traders is examined. An early paper in this field that predates Hart and Tauman is Geanakoplos and Polemarchakis [
2] (1982). Several researchers in the field of finance have since extended this literature to investigate the cause of market crashes. Examples of such papers are Barlevy and Veronesi [
3] (2003), Yuan [
4] (2005), etc. This literature is related to our work. We are, however, not aware of any application of this idea in the analysis of conflicts.
In Hart and Tauman [
1] (2004), agent behavior eventually changes as a result of the gradual processing of information and updating of beliefs. In a market setting, trade will occur when one party wants to be a buyer and one party wants to be a seller. A “crash” will occur when both want to be sellers; a “bubble” will occur when both want to be buyers. A market setup is fairly symmetrical, in that each party wants to buy when they believe the value is high and sell when they believe the value is low. Transactions occur when agents have different beliefs, but the market collapses once beliefs converge.
In the game-theoretic model of conflict presented and analyzed below, there are two agents who are opposed to one another (“Adversary A,” denoted as , and “Adversary B,” denoted as ). Each wants to act (i.e., initiate an attack) if, and only if, he believes that the probability that he possesses the upper-hand is sufficiently high. Thus, as beliefs converge, an agent may choose to attack after not doing so in previous periods. Within the present framework (depending upon the true state of the world), we can ultimately have: (i) eventually initiating an attack without regret; (ii) eventually initiating an attack with regret; (iii) eventually initiating an attack without regret; (iv) eventually initiating an attack with regret; or (v) neither agent choosing to initiate an attack (indefinite stability).
Numerous scholars within the field of international relations have broadly examined the causes of conflict. Levy [
5] (1998) provides an extensive overview of the literature, assessing multiple explanations including balance of power theories, economic interdependence and war, domestic coalition theories, and decision-making under risk and uncertainty. Academics such as Bueno De Mesquita [
6] (1985) and Fearon [
7] (1995) have put forth ideas that treat the decision to engage in conflict as a rational choice. In contrast, Levy [
8] (1983) highlights how misperceptions—about an adversary’s capabilities, adversary’s intentions, or third-party interests—can essentially serve as the root cause of conflict. Such formulations are directly compatible with traditional economic and game-theoretic analyses of behavior. Consistent with this rationality-based approach, van Evera [
9] (1998) argues that conflict is more likely to arise when parties view conquest to be easy or low cost. Also in this vein, Ohlson [
10] (2008) argues that, “people take to arms because they have
Reasons in the form of grievances and goals, they have
Resources in the form of capabilities and opportunities, and they have
Resolve because they perceive of no alternative to violence in order to achieve their goals” (page 134). From here it follows that an adversary would be more inclined to initiate conflict if one of these factors were to change exogenously. For example, if a rival country enters a time of political turmoil, leading to an economic downturn and corresponding decline in military capacity, an adversary might very well choose to launch an opportunistic attack. Identifying such a change in external circumstances as the cause of conflict is often quite natural and consistent with a view of conflict as a rational decision.
But, the main point of the present study is that an easily identifiable external cause of a conflict might not be present, even when a rational agent chooses to initiate conflict. Instead, it may possibly be the case that an agent chooses to rationally initiate a conflict (after multiple periods of peace) for no apparent reason, as a consequence of refining his beliefs about the true state of the world. If this occurs, then any attempt to identify the changed external factor that caused the conflict would be a search in vain. Recognizing the potential for information processing and the dynamic updating of beliefs to essentially be a cause of conflict is important for both academics and practitioners in the fields of international relations and conflict economics.
The remainder of the paper is structured as follows. In
Section 2, we outline the general framework of the game that is considered throughout. A very simple example is analyzed in
Section 3 to illustrate the main point of the paper described in the previous paragraph (i.e., that observing the action “not attack” can be informative and make an adversary update his beliefs in such a way that he rationally chooses to initiate an attack in a subsequent period). A more complex example is presented and analyzed in
Section 4 to more precisely highlight the driving force behind this phenomenon and to illustrate the qualitatively different outcomes that can arise for different true states of the world. A generalization of this more complex example is specified and analyzed in
Section 5 to show that conflict may eventually be initiated after an arbitrarily long number of periods of initial tranquility.
Section 6 concludes.
2. Framework of Game
Consider a simple game in which there are two parties to a potential conflict: “Adversary A” (denoted as
) and “Adversary B” (denoted as
). These two parties could be two sovereign nations, a sovereign nation and a terrorist organization, (for an overview of the literature analyzing terrorism using tools of game theory, see Sandler and Arce M. [
11] (2003)), or, more generally, any two parties that could possibly be engaged in conflict with one another. In each period, each player must decide to either attack or wait (i.e., initiate or not initiate conflict). A period is a duration of time over which each player must make a decision. It is assumed that the period length is common knowledge between the players. If either party chooses attack, conflict ensues in the present period. If both parties choose wait, no conflict ensues in the present period and the decision process repeats itself in a subsequent period. Assume each player makes this decision to maximize his expected payoff, taking into account the costs of engaging in conflict, coupled with the expected gain from, and assessed probability of, “winning” the conflict.
Let the continuous interval
denote the set of possible states of the world. Each state of the world is characterized as one of two environments: “favorable to
” (
) or “favorable to
” (
). Engaging in a conflict costs
resources of
and costs
resources of
, regardless of the outcome. (Assuming specific values for costs and benefits (as well as a specific partition of the state space into the different environments of “favorable to A” and “favorable to B”) are acceptable, since the aim of the entire analysis is to illustrate qualitatively different outcomes that can possibly arise.) Separate from these costs, if the true environment is
, then
expects to gain and
expects to lose
from a conflict. If instead the true environment is
, then (again, separate from these costs)
expects to gain and
expects to lose
from a conflict. Assuming a baseline payoff of zero from no conflict,
will want to attack if and only if he believes that the probability of
, denoted
, is such that:
Similarly,
will want to attack if and only if he believes
is such that:
Suppose that the prior probability assessments of and are such that they both accurately believe that each point on the interval is equally likely. The private information of each agent can be summarized by a partition of the state space. This serves to specify the framework of the game to be played between to the adversaries.
3. Simple Example to Illustrate How Updating of Beliefs Can Lead to Initiation of Attack
Within this section we present an example, with the simplest possible initial private information partitions, to illustrate how the updating of beliefs following an observation of “no attack” can lead to an adversary choosing to initiate an attack in a subsequent period.
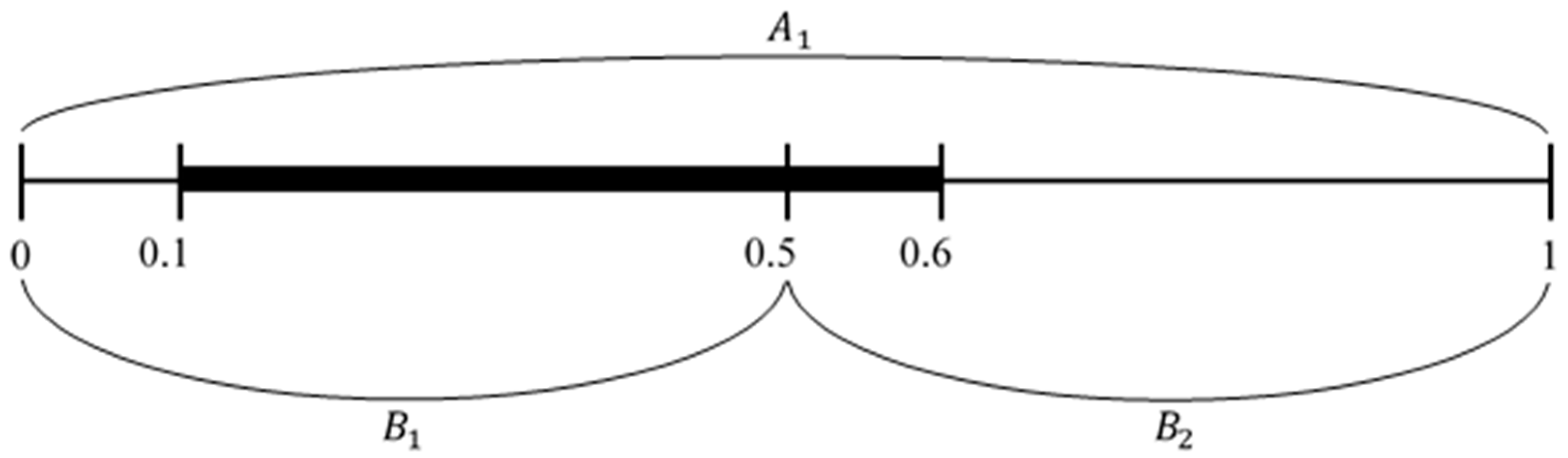
Suppose, as illustrated in
Figure 1, that Adversary A’s single information partition is:
And that Adversary B’s two information partitions are:
To understand the interpretation of these information partitions, suppose that the true state of the world is . The players do not observe the actual value of the true state of the world; rather, they only observe the information partition in which it is contained. So, when the true state of the world is , knows that the true state is , but cannot distinguish between the points within this subset. Similarly, knows that the true state is , but cannot distinguish between the points within this subset.
The set
is illustrated by the shaded interval in
Figure 1.
When analyzing agent behavior in any period, it is critical to correctly determine the probability assessment of each agent over each possible environment (
and
) given the agent’s knowledge regarding what states of the world are possible. For the simplistic information structure illustrated in
Figure 1, this is straightforward. (As will be seen from the analysis of the more complex example in
Section 4, to correctly determine the probability assessment of each agent over each possible environment in each period, it is necessary to recognize what information is common knowledge—as defined by Aumann [
12] (1976)—between the two agents at any point in time.) In Period 1,
simply knows that
, regardless of the actual state of the world. Thus, based upon his knowledge,
computes the probability that the true state of the world is “favorable to
” (
) to be
. Consequently,
does not want to attack in Period 1.
In contrast, the initial probability assessment by in Period 1 critically depends upon the actual state of the world. For any , computes the probability that the true state of the world is “favorable to ” () to be . Similarly, for any , computes the probability that the true state of the world is “favorable to ” () to be . Thus, in Period 1 will choose to stage an attack if and only if the true state of the world is .
If no attack is staged by either adversary in Period 1, then the game transitions to Period 2. But this only occurs if the true state of the world is . Therefore, if the game reaches this stage (which occurs only as a consequence of choosing to not attack in Period 1), then now knows that . Based upon his updated beliefs, now computes the probability that the true state of the world is “favorable to ” () to be . For this probability assessment, rationally chooses to stage an attack in Period 2. As a result of updating of beliefs after observing “no attack” by his rival in Period 1, an adversary has chosen to initiate an attack in a later period of interaction. Thus, conflict is initiated in Period 2 after an initial period of tranquility. This conflict results without any observed impetus—there are no new events or apparent provocations, there are no changes in the costs or benefits of engaging in conflict. Rather, the stimulus is simply the updating of information undertaken by an agent after observing the action chosen by his rival.
Within the next section, we present and analyze a more complex example to illustrate that the driving force which can give rise to this possibility (of an attack being staged after initial periods of tranquility) is the evolution of the states of the world that are common knowledge—as defined by Aumann [
12] (1976)—after both adversaries choose to “not attack.”
4. More Complex Example to Illustrate Importance of Updated Beliefs and Common Knowledge
Observing that a rival has chosen to “not attack” in any particular period conveys information which allows a player to update his beliefs about the true state of the world. In the example analyzed in the previous section, we saw how an observation by . that did not attack in Period 1 reveals to that the true state of the world must be . Consequently, rationally chooses to stage an attack in Period 2 (after the initial tranquility in Period 1). More precisely, this change in behavior by is a result of a dynamic updating of beliefs about the true state of the world, based upon the information conveyed by the observed chosen action of . Analysis of a more complex example will serve to illustrate this driving force more precisely and will also allow us to see the qualitatively different types of outcomes which can arise in this framework. From this more complex example we will see that (depending upon the true state of the world) after multiple initial periods of initial tranquility, we can then have: (i) choose to initiate an attack without regret (i.e., when the true environment is ); (ii) choose to initiate an attack with regret (i.e., when the true environment is ); (iii) choose to initiate an attack without regret (i.e., when the true environment is ); (iv) choose to initiate an attack with regret (i.e., when the true environment is ); or (v) perpetual stability (with neither agent ever choosing to attack in any period).
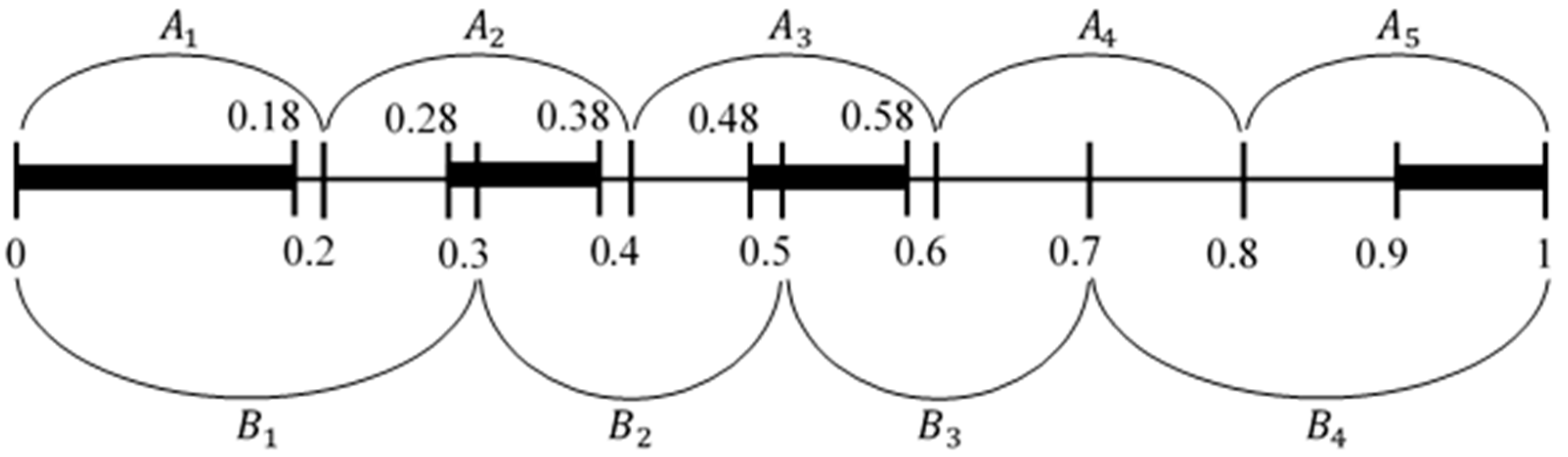
Suppose, as illustrated in
Figure 2, that Adversary A’s partitions are:
And that Adversary B’s partitions are:
Assume that
The set
is illustrated by the four shaded intervals in
Figure 2.
As noted in the previous section, when analyzing agent behavior in each period, it is critical to correctly determine the probability assessment of each agent over each possible environment ( and ) given the agent’s knowledge regarding what states of the world are possible. To formally do so, it is important to recognize what information is common knowledge between the two agents at any point in time. Let denote the different periods of interaction between the agents, and let denote the set of information that is common knowledge between the two agents at the start of Period (before they choose to either wait or attack in Period ).
Because of the way in which the information partitions in
Figure 2 overlap one another, regardless of the true state of the world in Period 1 we have
. That is, at the start it is not common knowledge that any particular value of
did not occur. For example, suppose the true state of the world is
.
knows
, and
knows
. Thus, while it is mutual knowledge that the true state of the world is neither
nor
, these facts are not common knowledge. As defined by Aumann [
12] (1976), something is common knowledge between
and
if and only if:
knows it;
knows it;
knows that
knows it;
knows that
knows it;
knows that
knows that
knows it; ad infinitum. There are several researchers who extend Aumann [
12] (1976). Some examples are Cave [
13] (1983), Morris [
14] (1995) and Ozkaya [
15] (2012).
To understand why neither
nor
are common knowledge in Period 1, let
denote the smallest subset
for which it can be stated that “
knows that the true state of the world is within
.” Likewise, let
denote the smallest subset
for which it can be stated that “
knows that
knows that the true state of the world is within
,” and so on. This hierarchical description of layers of knowledge is described in Aumann [
16] (1999). Given the information structure as summarized by
Figure 2:
That is, when the true state of the world is , in Period 1 it is not the case that knows that knows that knows that knows that the true state of the world is not any particular value of . Similarly, . More generally, regardless of the actual true state of the world, we quickly reach a point where both and .
4.1. Realized States for Which B Ultimately Chooses to Initiate an Attack
Suppose the true state of the world is
—that is, somewhere on the interval between
and
. At the start of Period 1,
knows
, and
knows
. Consequently,
computes the probability of the true environment being
to be
, and
computes the probability of the true environment being
to be
. The agents base their actions in Period 1 (and in each subsequent period) upon these computed probabilities over this interval which they know to be the true state of the world (denoted by
and
, as in
Table 1). Thus,
will choose to wait (i.e., not attack) since
, and
will choose to wait (i.e., not attack) since
.
But to comprehend how an observation of “no attack” is informative and leads to a dynamic updating of beliefs, it is necessary to compute each agent’s perceived probability of
in each distinct information set (in order for agents to be able to infer how their rival would have behaved in other states of the world). To this end, in Period 1:
,
,
, and
for
; and
,
, and
for
. These probabilities are summarized in the top row of
Table 1.
At the start of Period 2, it is common knowledge that neither agent chose to attack in Period 1. As an immediate consequence, it is common knowledge that the true state of the world is not within
, since if it were, then
would have chosen to attack in Period 1. As a further result of no attack occurring in Period 1, it becomes common knowledge that the true state of the world is not within
, since this segment of the state space is now cutoff from the information sets that overlap one another starting at the true state of the world. Thus, at the start of Period 2, the common knowledge information set is reduced to
. To understand this, recognize that at the start of Period 2:
For this new common knowledge information set of
:
and
. Consequently,
,
, and
would be meaningless to compute. Further,
Each of the other five assessed probabilities are effectively unchanged from Period 1. These probabilities are summarized in the second row of
Table 1. In Period 2
again chooses to wait since
, and
again chooses to wait since
.
Now, at the start of Period 3, it is common knowledge that neither agent chose to attack in Period 2. Thus, it is common knowledge that the true state of the world is not within
, since if it were then
would have chosen to attack in Period 2. The common knowledge information set becomes
. For this refined information set,
would be meaningless to compute and
. The other assessed probabilities are effectively unchanged from Period 2. These probabilities are summarized in the third row of
Table 1. In Period 3
again waits since
, and
again waits since
.
At the start of Period 4 it is now common knowledge that the true state of the world is not within , since if it were then would have chosen to attack in Period 3. The common knowledge information set is now further refined to . Consequently, . In Period 4 neither nor will attack since and .
At the start of Period 5 it is common knowledge that the true state of the world is not within (since if it were, would have chosen to attack in Period 4). Thus, and . Again, both agents choose to wait.
After
chooses to wait in Period 5, it becomes common knowledge that the true state of the world is not within
. Accordingly,
. But this refinement alters
’s perception of the true state of the world in a meaningful way. Agent
now knows that the true state of the world is
not in
, but rather must be in
. As a result,
computes the probability of the true environment being
to be
. Since
, agent
will choose to attack in Period 6. Thus, conflict is initiated in Period 6 after five initial periods of calm. As was the case in the simpler example in
Section 3, this conflict results without any observed impetus. Rather, it resulted from the updating of information (i.e., the refinement of the common knowledge information set) undertaken by the agents after observing the actions chosen by their rival.
In this case, when chooses to initiate the attack, the information set partitions of the two agents have converged and both agents agree that the true state of the world is . However, within this range both and are possible, the former being true for and the latter being true for . Thus, this example illustrates how (i) could choose to initiate an attack without regret (i.e., if the true environment is ) and (ii) could choose to initiate an attack with regret (i.e., if the true environment is ).
4.2. Realized States for Which A Chooses to Initiate an Attack
Within this subsection we illustrate that it is also possible for A to eventually initiate an attack after multiple periods of not doing so. Recognize that, even though we have already shown that B may choose to do so, showing that A may also choose to do so for the same initial information structure and costs/benefits from conflict does, in fact, provide additional insights. Only after obtaining these results will we have shown that with the information structure and costs/benefits from conflict fixed, depending upon the true state of the world, either one of the two potential adversaries may ultimately choose to initiate conflict after multiple initial periods of tranquility.
Instead suppose the true state of the world is
—that is, somewhere on the interval between
and
. At the start of Period 1,
knows
, and
knows
. Consequently, the agents base their actions upon the computed probabilities
and
. Both agents choose to wait (i.e., not attack) since
and
. Since in Period 1 we have
, all nine of the computed probabilities (i.e., five for
and four for
) are equal in value to what they were in the example from
Section 4.1, as reported in the top row of
Table 2.
As a first step, we again have that, at the start of Period 2—after both agents observe that no attack occurred in Period 1—it becomes common knowledge that the true state of the world is not in or . Thus, . Again, , , and would be meaningless to compute, and . In Period 2 both agents again choose to wait, since and .
After observing no attack in Period 2, in Period 3 we have
. As reported in
Table 2, this results in
, for which
will choose to attack. Similar to the example in
Section 4.1, conflict is initiated in Period 3 after multiple initial periods of calm.
In contrast to the example in
Section 4.1, when the true state of the world is
, conflict is initiated before the information set partitions of the agents have converged. When
chooses to attack, he knows that the true state of the world is
, but
more broadly believes that the true state of the world could be anywhere in the larger set
. Nonetheless, in this example both
and
are possible, the former being true for
and the latter being true for
. This example illustrates how (iii)
could choose to initiate an attack without regret (i.e., if the true environment is
) and (iv)
could choose to initiate an attack with regret (i.e., if the true environment is
).
4.3. Realized States for Which Neither Agent Ever Chooses to Initiate an Attack
Finally, suppose the true state of the world is
—that is, somewhere on the interval between
and
. At the start of Period 1,
knows
, and
knows
. Since in Period 1 we have
, all nine of the initial computed probabilities are again equal in value to what they were in the two previous examples presented in
Section 4.1 and
Section 4.2, as reported in the top row of
Table 3. In Period 1 both agents choose to not attack since
and
. As an immediate consequence of observing that no attack occurred in Period 1, it becomes common knowledge that the true state of the world is not within
. Furthermore, it becomes common knowledge that the true state is not within
(since this portion of the state space is now cutoff from the information sets that overlap one another starting at the true state of the world). Thus, at the start of Period 2, the common knowledge information set is reduced to
.
For we have and (all other probabilities would be meaningless to compute), for which neither agent chooses to attack. No current or future actions lead to any further refinement of the common knowledge information set or the subsequent assessed probabilities. Beliefs and assessed probabilities have converged and are equal to , , and for all . Consequently, neither agent ever chooses to attack in any future period. This illustrates a situation wherein we realize (v) indefinite stability, in which neither agent ever chooses to initiate an attack.
Note that an outcome of this nature could not be realized in the model of market trade analyzed by Hart and Tauman [
1]. This is because within their model the two agents had a common probability cutoff upon which behavior was based. Once a sufficient number of periods transpire, the agents’ beliefs converge and both parties will either agree that the better action is buy or that the better action is sell. Eventually the agents agree and want to behave in the same manner, causing the market to collapse (with either a crash or a bubble occurring).
In contrast, in the model of conflict presented here, the interests of an individual agent are diametrically opposed to those of their rival. An agent only wants to “act” (i.e., initiate an attack) when he believes that the probability with which he possesses the upper-hand is sufficiently high. Given the negative constant sum nature of the payoffs realized if either agent initiates an attack (as described in
Section 2, the gain/loss of
or
sums to zero across the two players, so that the positive valued costs result in a combined loss of
when conflict occurs) it is clearly possible for the behavioral cutoffs for the two agents to differ from one another. That is, the probability of
below which
will want to initiate an attack can be strictly less than the probability of
above which
will want to initiate an attack. If this is the case and the true state of the world is such that beliefs converge to the point where the common assessed probability of
is between these two cutoffs, then the agents can realize the harmonious outcome of indefinite stability.
5. Illustration of Conflict Initiated after Arbitrarily Long Period of Initial Tranquility
The aim of this section is to show how the more complex example from
Section 4 can be generalized so that conflict is initiated by either party after any arbitrarily large number of periods of tranquility. Suppose
has a total of
information sets. Let
and
. Divide the interval from 0.2 to 0.8 into
information sets of equal length, so that
for
. Each intermediate segment has length of
, with a midpoint of
. for
. Suppose
has a total of
X − 1 information sets. Let
,
, and
for
. Further define the following
intervals:
,
, and
. for
. Let
, and let
. Note that
. Recognize that the example from
Section 4 is a special case of this environment with
.
Observe that for each information set
,
j = 2, …,
X − 2, the lower boundary is the midpoint of
and the upper boundary is the midpoint of
. Consequently, because of the manner in which the information sets of the two agents overlap one another, regardless of the true state of the world in Period 1 we have
.
Table 4 summarizes each agent’s perceived probability of
in each distinct information set when
(which is true at the start of Period 1, no matter the true state of the world).
To see that might choose to initiate conflict after an arbitrarily large number of periods of tranquility, consider . At the start of Period 1, knows and knows . Thus, and . Neither agent chooses to attack. For each period we have , so that the relevant probability upon which each agent bases his behavior remains unchanged. However, after chooses to not attack in Period , . Consequently, , prompting to attack in Period . Since can be arbitrarily large, this example illustrates how might eventually choose to stage an attack after arbitrarily many periods of tranquility. Recognize that since both and are possible within , we have that may either regret or not regret initiating this attack.
Next, to see that might choose to initiate conflict after an arbitrarily large number of periods of tranquility, consider . At the start of Period 1, knows and knows . Thus, and . Neither agent chooses to attack. For each period we have , so that the relevant probability upon which each agent bases his behavior remains unchanged. However, after chooses to not attack in Period , . Accordingly, , prompting to attack in Period . Since can be arbitrarily large, this example illustrates how might eventually choose to stage an attack after arbitrarily many periods of tranquility. Again, since both and are possible within , we have that may either regret or not regret initiating this attack.
Finally, to see that this general example can lead to indefinite stability, consider . In Period 1, knows and knows . Consequently, and . For these probabilities, neither agent chooses to attack. After chooses not to attack in Period 1, it becomes common knowledge that . That is, , for which and . Neither agent chooses to attack in Period 2. The common knowledge information set and relevant probabilities remain unchanged in all future periods—that is, and for every . Neither agent ever chooses to attack, and therefore, indefinite stability results.
6. Concluding Remarks
The game presented and analyzed here illustrates how it is possible for an agent to rationally choose to initiate conflict without instigation or provocation, without observing a change in the behavior of his rival, or without any changes in the costs or benefits of engaging in conflict. Rather, conflict may result when rational decision-makers endogenously process information—that is, without any exogenous changes to the fundamentals of the environment. This occurs because an observation that an adversary has chosen to not stage an attack conveys information that allows a player to update his beliefs regarding the true state of the world.
The forces at play are very similar to those identified by Hart and Tauman [
1] (2004) in a trading environment. But, the model itself and the ultimate results are qualitatively different. In the present model the state space is continuous, not discrete. Further, because of the negative constant sum nature of the payoffs realized when an attack occurs, the probabilities which serve as behavioral cutoffs for the two agents can differ in value from one another. Sebenius and Geanakoplos [
17] (1983) analyze the updating of beliefs in a gamble game between two players in which the state space is continuous. However, their setup is qualitatively different from that considered here in numerous ways, one of which is the fact that—like in Hart and Tauman—both players ultimately share a common valued behavioral cutoff. Consequently, it is possible for the system to reach an equilibrium in which an attack is never initiated. The parallel outcome in Hart and Tauman would be for the market to never collapse (that is, never realize a crash or a bubble), but this cannot occur since the traders are symmetric and have the same common cutoff dictating whether they want to buy or sell.
In the present model, as beliefs converge, we will ultimately have: (i)
eventually initiating an attack without regret; (ii)
eventually initiating an attack with regret; (iii)
eventually initiating an attack without regret; (iv)
eventually initiating an attack with regret; or (v) neither agent choosing to initiate an attack (indefinite stability). It is important to note (as illustrated by the presentation and analysis of the more complex example in
Section 4) that we can realize all five of these different outcomes for a single example, depending upon what the actual true state of the world happens to be. However, this does not imply that the indefinite avoidance of conflict can ever be expected (even if the true state of the world at the onset is
) or that all conflicts that do arise are the result of information processing. After all, over time there clearly could be exogenous changes to the system (e.g., changes of types, changes of cost/benefits that lead to changes in cutoff probabilities, changes in fundamental information partitions) which lead to rational agents choosing to initiate an attack.