Abstract
For cancer, we develop a 2-D agent-based continuous-space game-theoretical model that considers cancer cells’ proximity to a blood vessel. Based on castrate resistant metastatic prostate cancer (mCRPC), the model considers the density and frequency (eco-evolutionary) dynamics of three cancer cell types: those that require exogenous testosterone (), those producing testosterone (), and those independent of testosterone (). We model proximity to a blood vessel by imagining four zones around the vessel. Zone 0 is the blood vessel. As rings, zones 1–3 are successively farther from the blood vessel and have successively lower carrying capacities. Zone 4 represents the space too far from the blood vessel and too poor in nutrients for cancer cell proliferation. Within the other three zones that are closer to the blood vessel, the cells’ proliferation probabilities are determined by zone-specific payoff matrices. We analyzed how zone width, dispersal, interactions across zone boundaries, and blood vessel dynamics influence the eco-evolutionary dynamics of cell types within zones and across the entire cancer cell population. At equilibrium, zone 3’s composition deviates from its evolutionary stable strategy (ESS) towards that of zone 2. Zone 2 sees deviations from its ESS because of dispersal from zones 1 and 3; however, its composition begins to resemble zone 1’s more so than zone 3’s. Frequency-dependent interactions between cells across zone boundaries have little effect on zone 2’s and zone 3’s composition but have decisive effects on zone 1. The composition of zone 1 diverges dramatically from both its own ESS, but also that of zone 2. That is because cells (highest frequency in zone 1) benefit from interacting with cells (highest frequency in zone 2). Zone 1 cells interacting with cells in zone 2 experience a higher likelihood of encountering a cell than when restricted to their own zone. As expected, increasing the width of zones decreases these impacts of cross-boundary dispersal and interactions. Increasing zone widths increases the persistence likelihood of the cancer subpopulation in the face of blood vessel dynamics, where the vessel may die or become occluded resulting in the “birth” of another blood vessel elsewhere in the space. With small zone widths, the cancer cell subpopulations cannot persist. With large zone widths, blood vessel dynamics create cancer cell subpopulations that resemble the ESS of zone 3 as the larger area of zone 3 and its contribution to cells within the necrotic zone 4 mean that zones 3 and 4 provide the likeliest colonizers for the new blood vessel. In conclusion, our model provides an alternative modeling approach for considering density-dependent, frequency-dependent, and dispersal dynamics into cancer models with spatial gradients around blood vessels. Additionally, our model can consider the occurrence of circulating tumor cells (cells that disperse into the blood vessel from zone 1) and the presence of live cancer cells within the necrotic regions of a tumor.
1. Introduction
As ecosystems, tumors exhibit both spatial and temporal variability in the types and densities of cancer cells, immune cell composition, stroma (architecture created by normal cells), and environmental factors such as pH, oxygen and glucose [1,2,3,4,5]. Heterogeneity tends to increase with cancer progression, and it influences patient prognosis, therapy, and subsequent treatment outcomes [6,7,8,9,10]. Understanding, measuring and modeling within-tumor heterogeneity permits the integration of clinical practices, spatial data generated from biopsies and radiomics, and mathematical modeling [11,12]. Here, we are interested in advancing models of within-tumor spatial and temporal variability, extending our previous work in [13,14,15].
The dynamics of blood vessels (angiogenesis) within the tumor must be a primary driver of within-tumor heterogeneity. Blood flow provides the majority of resources to cancer cells. Hence, resource availability likely declines and toxins likely increase with distance from blood vessels [16]. For breast cancer, Lloyd et al. [17] showed that the ratio of estrogen positive to estrogen negative cancer cells increases in biopsy samples with greater densities and sizes of blood vessels. Furthermore, within a tumor, estrogen positive cells are generally closer to blood vessels than estrogen negative cells. The decline in estrogen availability with distance from vasculature may influence the outcome of competition between cell types or phenotypes. Here, we are interested in modeling competition between cancer cell types where competitive interactions vary with blood vessel size and distance from a blood vessel.
In addition to influencing the evolution, diversity, and distribution of cancer cells, blood vessels are not fixed entities within a tumor. They too exhibit dynamics. Blood vessels as living tissue undergo destruction and renewal. Cancer cells influence the presence of VEGF (vascular endothelial growth factor), which directs and stimulates the growth of blood vessels. As blood flow to one neighborhood of cancer cells increases, it may be diverted from another [18]. Furthermore, the proliferation and crowding of cancer cells may inadvertently block or destroy blood vessels. To a neighborhood of cancer cells, the appearance, growth and disappearance of blood vessels may occur stochastically or fairly regularly, but it will likely be universally haphazard and quite unlike that of normal tissue. Here, we incorporate blood vessel dynamics in a spatially explicit model of cancer cell dynamics.
Several mathematical models have considered angiogenesis and within-tumor heterogeneity [19,20]. The authors of [2,21,22] modeled progression from a normal tissue to one occupied by cancer cells as the tumor grows. The appearance and disappearance of blood vessels change with tumor progression. Traits defining the cancer cells can include acid production (glycolosis) and acid resistance. As the tumor grows, the models predict increasingly acid producing and acid tolerant cells that outcompete the normal cells and reduce vascularity. Shirinifard et al. [23] adopted a spatially explicit three-dimensional model of tumorigenesis and angiogenesis to show how diffusion of nutrients influences both processes. The authors of [24,25] modeled cancer cells growing on a lattice. Cancer cells have a birth–death process that is influenced by oxygen and resource availability, which is often related to proximity to blood vessels. In these models, there is frequently an implicit or explicit evolutionary game between cancer cells mediated by vasculature. It may, for example, take the form of a public goods game where the combined actions of cancer cells contribute blood flow to all [26,27,28]. Conversely, the game may occur implicitly, as the frequencies and densities of cell types influence cancer cell fitness via feedbacks on resource availabilities [29].
Our goal is to embed an evolutionary game within a spatially-explicit, agent-based model. The model complements and builds upon existing approaches. Similar to the authors of [30,31], we use a matrix game to determine the fitness of different cell types as they interact with each other. Following You et al. [13], we imagine that this game is played between nearby cancer cells that are distributed as discrete entities across a continuous space.
Here, we expand on these approaches by explicitly including blood vessel dynamics where the game played between nearby cancer cells is a function of the distance from a blood vessel. Specifically, we are interested in the scales at which cancer cells depress each other’s growth rates (density-dependent radius), engage in evolutionary games (frequency-dependent radius), and disperse (dispersal radius). In terms of a static blood vessel, we ask how these scale-dependent interactions influence the spatial distributions, densities and frequencies of different cell types including the likelihood of entering the blood stream and becoming a circulating tumor cell associated with metastases. We can compare the spatial model’s output with the evolutionary stable strategies (ESSs) of the non-spatial matrix games. By considering a blood vessel that occludes and reappears within a given site of the tumor, we ask how the size of the blood vessel, death rate of cancer cells, and disturbance frequency of the blood vessel influence whether the cancer cells can persist at all; and, if they can, how this affects the distribution and abundances of different cancer cell types. For instance, the probability that the cancer cells go locally extinct should decline with the size of the vessel, and increase with the death rates of cancer cells and the disturbance frequency of blood vessel disappearance and reappearance.
2. Modeling Metastatic Prostate Cancer in the Vicinity of a Blood Vessel
Prostate cancer typically metastasizes to the bone and/or lymph nodes [5,32,33,34]. The metastatic tumors are heterogeneous in the genetic and phenotypic composition of the cancer cells. There can be at least three cancer cell types in metastatic prostate cancer. We consider these in our model: (1) cells possess androgen receptors and require an exogenous source of testosterone to be able to survive and proliferate; (2) cells have androgen receptors and produce their own testosterone that as a public good is also available to other and cells; and (3) cancer cells lack androgen receptors and have evolved to be entirely independent of testosterone [13,14,15]. By way of hormone therapy, cells by themselves can be suppressed by androgen deprivation therapy, and by therapies that target the androgen receptors, while there is no targeted therapy for cells, which are usually treated by chemotherapy [35]. We extend work from three prior papers [13,14,15]. Aspects of the interactions between the three cell types were framed by a matrix game where the inequality relations between payoffs represent hypotheses regarding the known biology of the cancer [13].
Zhang et al. [14] and Cunningham et al. [15] introduced a non-spatial model of adaptive therapy where the biology suggests various interaction matrices. Around blood vessels, one may expect the coexistence of , and cells as the blood provides abundant of nutrients, and cells and the blood become sources of androgens ( cells become free-riders in a public-goods game with cells). The community near the blood may favor the highest frequency of . Farther from the blood, nutrients will be somewhat reduced, the community of cancer cells may favor cells as the sole source of androgens, and there may be a near absence of cells because of intense competition from the other two cell types. At still greater distances, resource delivery from the blood is much reduced and the resulting community may favor a predominance of less proliferative but otherwise androgen-independent cells.
Beyond a certain distance from the blood vessel, cells may persist temporarily while unable to proliferate because of few to no resources. These are the assumed elements for our spatial, agent-based model. We imagine a blood vessel surrounded by zones of nutrient and androgen availability (Figure 1). We let zone 0 represent the space within the blood vessel itself. Cells that disperse into the blood are immediately swept away and become what are known as circulating tumor cells (CTCs) [36]. While not directly relevant to the present model, they are of empirical interest as CTCs become the source of metastases. Hence, in our model, we track the number and frequency of cells that become CTCs. Zones 1–3 (Figure 1) represent the successive distances from the blood vessel where the successive payoff matrices favor the predominance of , then and finally cells, respectively. The three matrices for zones 1–3 are shown in Table 1. The details of their derivation is given in Appendix A. In a non-spatial game where the three zones do not interact, these matrices each generate unique ESSs where the frequencies of , and are for zone 1, for zone 2, and for zone 3. Of interest is how the spatial game results in deviations from these non-spatial ESSs in each of the zones.
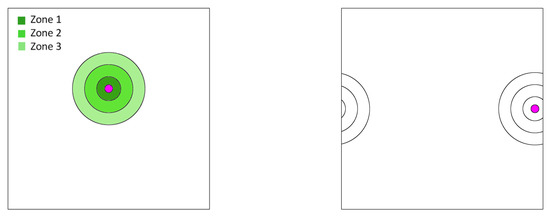
Figure 1.
Schematic representation of a blood vessel and its ring-shaped zones 1–3. The area inside a blood vessel is called zone 0, and the rest of the torus is called zone 4.

Table 1.
Payoff matrices and for zone (left), zone 2 (middle), and zone 3 (right), respectively.
3. The Agent-Based Continuous-Space Model with Frequency- and Density-Dependent Interactions and Dispersal
For our agent-based spatial model, we used a two-dimensional torus with periodic boundary conditions. The units of spatial scale are set relative to the radius of a putative blood vessel that we set equal to one unit. Cells may exist at any point of For all simulations and scenarios, we placed a single blood vessel with radius 1 within the two-dimensional space defined by its center in the -spatial coordinates. Since tumors are 3-D, a 2-D cross section of a tumor leaves a blood vessel appearing as a disc (Figure 2). For scenarios with a static blood vessel, the single blood vessel remains fixed at the chosen location for the entire simulation. For scenarios with dynamic blood vessels, the single randomly placed blood vessel has some probability of elimination during each time step. Upon elimination, a new blood vessel appears at a new random location of the torus.
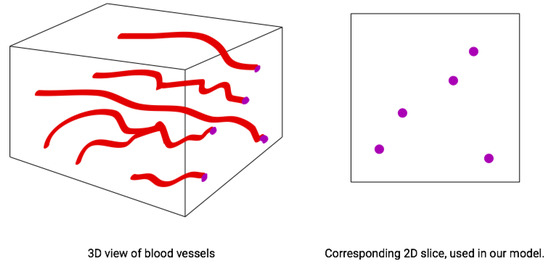
Figure 2.
Cancer cells and blood vessels in a 3D space (left); and its 2D cross-section (right).
We assume that cells need to be close enough to a blood vessel to proliferate. Zones 1–3 form concentric rings around the blood vessel. Each of these rings has width 1. Zone consists of those points for which the distance to the center of the blood vessel is between i and and is associated with a zone-specific payoff matrix as discussed above and a density-dependent limit. The density-dependent limit indicates the maximum number of cells that can exist per unit area while still permitting cell proliferation. We assume that this limit is greatest in zone 1 (=20 per unit area), intermediate in zone 2 (=10) and least in zone 3 (=5). We have two other relevant zones. The first we refer to as zone 0; and this is the area inside a blood vessel. Any cell that disperses into the blood vessel (zone 0) is swept away and enters the bloodstream as a circulating tumor cell (CTC). Such cells are eliminated from the simulation and the torus. We keep count of them as a means of modeling the number and types of cancer cells that become CTCs. CTCs are of clinical relevance as the source for metastases. Zone 4 describes the area of the torus beyond zone It represents the remaining area of the torus that is too far from the blood vessel to allow for cell proliferation. Cells that find themselves in zone 4 can persist but they cannot proliferate. They have the same death rate as cells in zones 1–3. Hence, zone 4 represents a sink population that is maintained either through dispersal or from the loss of a blood vessel and a newly appearing blood vessel elsewhere in the torus.
We initialized each simulation by placing the initial blood vessel at the middle of the torus at position We then seeded the torus with 33 cells of each type placed randomly within a square of the torus centered on the blood vessel. Each simulation was run for 5000 generations. To determine the outcome and general tendency of each simulation, we averaged the state of the system for the last 1000 generations. Averages included the population sizes of each of the three cell types within zones 1–4, and the number of cells that dispersed into Zone 0 and became CTCs. To complete a generation, all living cells were selected in a random order to undergo the following actions as the focal cell:
Cell death: Each focal cell, regardless of its zone, has a mortality probability of If the focal cell dies, it does not undergo any further actions. Following death, the cell remains visible in the torus for five more generations. If the focal cell is in zone 4, then it undergoes no further actions. Cells in zone 4 can survive but they cannot proliferate. If the focal cell remains alive and is in zone 1, 2 or 3, then it undergoes the next action.
Density-dependent cell interactions: We imagine that available space and resources are necessary for successful cell proliferation. We define the density-dependence neighborhood as a disc around the focal cell with a pre-specified radius, called the density-dependence radius (Figure 3a). If the number of cells (itself and dead cells included) within this density-dependence neighborhood is greater than or equal to the density-dependence limit for the zone of the focal cell, then the focal cell cannot proliferate and it does not move onto additional actions in the current generation. If the density of cells within the density-dependence neighborhood is less than the limit specified for the zone of the focal cell, then the focal cell moves on to the next action.
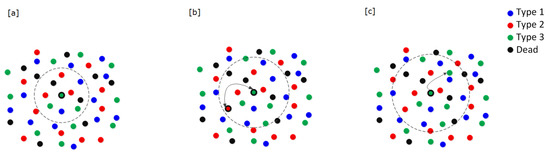
Figure 3.
A focal cell and its three neighborhoods (here we assume there are three cell types). (a) Density-dependence neighborhood: A focal cell can only proliferate if the density of cells within the disc defined by the density-dependence radius is below a threshold. (b) Frequency-dependence neighborhood: The focal cell’s likelihood of proliferating will be determined from an interaction between it and a randomly selected cell from within the frequency-dependence radius. (c) Dispersal neighborhood: If a focal cell proliferates, its daughter cell is placed randomly within the disc defined by the dispersal radius. Adapted from [13]. All the radii may vary with blood-vessel zone.
Frequency-dependent cell interactions: We imagine that the focal cell engages in the matrix game within its frequency-dependence neighborhood, which is a disc around the focal cell with a prespecified radius, called the frequency-dependence radius (Figure 3b). Two scenarios in this frequency-dependence neighborhood are considered: (1) the focal cell randomly selects a neighbor cell from the living cells occurring within this neighborhood; or (2) the focal cell has no living neighbor. While a focal cell may interact with all of the cells within its frequency-dependence neighborhood, we have chosen to derive the cell’s payoff from an interaction with a single cell of the neighborhood instead of letting it “play the field” with the entire set of cells. With a large number of cells, eventually these one-on-one interactions will get averaged over time and space in a manner that becomes functionally equivalent to averaging across all of the cells in the neighborhood.
Cell proliferation: For the focal cell of type i in zone , which selects a living neighbor of type j, the probability of it undergoing cell division and producing a daughter cell is determined by the payoff matrix assigned to the focal cell’s zone. The payoff matrix assigns the probability of the focal cell proliferating when it is of type i and the randomly selected neighbor is of type If a focal cell within zones 1–3 has no living neighbor within its frequency-dependence radius, then we evaluate two alternatives. Either the neighborless cell cannot proliferate (); or it proliferates with probability (). As shown below, whether a neighborless cell can proliferate or not has little consequence for simulations involving a fixed blood vessel, but big consequences when the blood vessel dynamically disappears and reappears within the torus.
Dispersal: If the focal cell reproduces, it will always be of the same type (cell types breed true), and it is randomly placed within the focal cell’s dispersal neighborhood (Figure 3c). The dispersal neighborhood is a disc around the focal cell with pre-specified radius, called the dispersal radius. Daughter cells are only placed within their respective dispersal neighborhoods at the end of the generation after all living cells have been evaluated as the focal cell. This insures that daughter cells produced early in the generation do not influence events later in the generation. When a daughter cell lands in zone 0, it is counted as a CTC and it is removed immediately from the torus.
In the following section, we explore our model by modeling interactions of cancer cells in metastatic castrate-resistant prostate cancer. We analyze spatial games with one blood vessel. The blood vessel either stays in throughout the entire game (called a static blood vessel) or follows a stochastic birth–death process (called a dynamic blood vessel), where a blood vessel may die at the end of each generation with a pre-specified probability, and reappears at a random location in .
4. Observations and Hypotheses
The density-dependent, frequency-dependent and dispersal radii result in a variety of interactions between cells across the four zones. These interactions or cross-zone spill-over effects should result in deviations of a zone’s cell type frequencies from the non-spatial ESS of the zone’s payoff matrix. These deviations should increase with the frequency-dependent radius and the dispersal radius as individuals will now interact with cells from other zones as well as disperse from zone to zone. Deviations of the spatial model from a zone’s ESS should decline with increasing the width of that zone as there will be more intra-zone rather than cross zone interactions. We might expect zone 2 to be distorted most from cross-zone interactions because it has boundaries with both zones 1 and Zone 3 should experience little distortion from cells in zone 4 as they must originate from zone 3, and cells in zone 4 cannot produce daughter cells. The frequency of cell types in zone 4 should match those in zone Zone 1 has just one boundary and the only additional dynamic is the loss of daughter cells to the blood stream. This will cause a slight if not imperceptible drop in the abundance of cells in zone
Density-dependent radius: The density-dependent radius should enhance proliferation rates and hence overall densities of cells in zone 1 over zone 2 and zone 2 over zone This is because the density limit is set by the focal cell’s zone which is highest in zone 1 and lowest in zone On average, cell densities will rank according to: Zone 1’s density > zone 2’s density > zone 3’s density. Thus, a focal cell in zone 1 near the boundary with zone 2 will experience a lower number of cells within its density-dependent neighborhood as the frequency of zone 2 within its neighborhood increases. This same logic applies across all boundaries but sometimes in reverse. Cells in zone 2 will suffer and benefit from being near the zone 1 and zone 2 boundaries, respectively. Cells in zone 3 will suffer and benefit from being near the zone 2 and zone 4 boundaries, respectively.
Effects of the frequency-dependent radius: There is some likelihood that a focal cell’s opponent in the matrix game comes from a different zone. This might have subtle and interesting consequences. In zone 1, a focal cell interacting with the ESS community favored by zone 2 will benefit (relative to the ESS community of zone 1) if it is (zone 2 favors a higher frequency of ), and be hurt if it is (zone 2 has no at the ESS). Cells in zone 2 face sometimes countervailing effects from cross boundary interactions with zones 1 and However, cells in zone 2 should be favored as the ESSs of zones 1 and 3 are both more favorable to than that of zone Finally, for cells in zone 3, the ESS of zone 2 is favorable to and cells. For zone 3, the frequency-dependent radius may reduce the frequency of cells below their ESS.
Effects of the dispersal radius: Dispersal creates mixing between the populations of cells within each of the zones. Zone 1 becomes a source population for zone 2, zone 2 for zone 3, and zone 3 for zone This happens for two reasons. The zone nearer the blood vessel has the higher cell density; and it has the higher boundary length to area ratio. This means that on average more cells will migrate from the zone nearer the blood vessel into the zone farther from the blood vessel than vice-versa. Dispersal should have little effect on zone 1’s frequency of cell types. Dispersal means that zone 2 will come to resemble more the ESS of zone 1; and zone 3’s composition more like the ESS composition of zone Based on the payoff matrices, dispersal should increase the frequency of cells in zone 2, and decrease the frequency of cells in zone Reducing the width of a zone will amplify these effects.
Blood vessel dynamics: If the blood vessel remains static and in the same place for the duration of the simulation, then we expect a dynamic equilibrium of cell numbers and cell type frequencies to emerge. This equilibrium should apply both within and across all four zones. Hence, the means of separate runs should vary little in their last 1000 generations; and there should be relatively little variance in cell densities and cell-type frequencies during the last 1000 generations. Furthermore, whether neighborless cells can proliferate or not ( versus ) should matter little as very few, if any, cells in zones 1–3 will be neighborless. This all changes if the blood vessel has some probability each generation of disappearing and then re-appearing elsewhere. There should be sharp crashes in total cell counts as cells that had been in zones 1–3 find themselves in zone 4. Simply by virtue of overall zone area, zone 4 is most likely to provide “colonists” for the new blood vessel, followed by zone 3. Hence, the recovery of the cancer cells around the new blood vessel will start with cell frequencies closer to those of zone 3 than of zones 1 and However, recovery is not assured and the local cancer cell population of the torus may go extinct. Extinction will be likelier if the width of zones 1–3 are small, if the rate of blood vessel shift is higher, and if neighborless cells cannot proliferate.
5. Results
A single fixed blood vessel: Here, the blood vessel was static and remained in the center of the torus. The density-dependent, frequency-dependent and dispersal radii were all set to A representative simulation of this case study is shown in Figure 4.
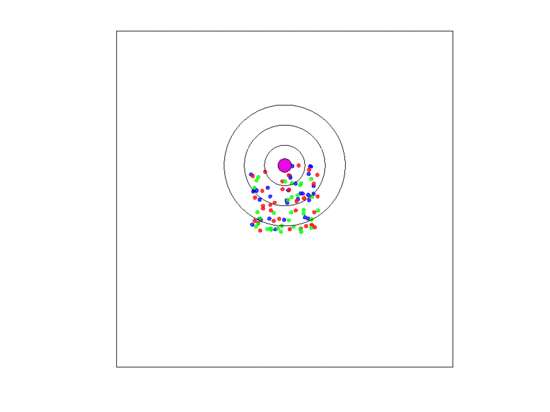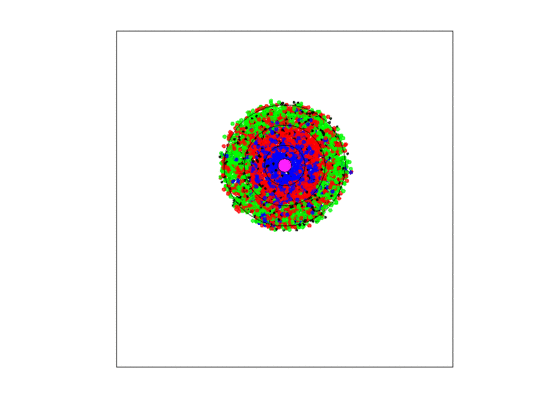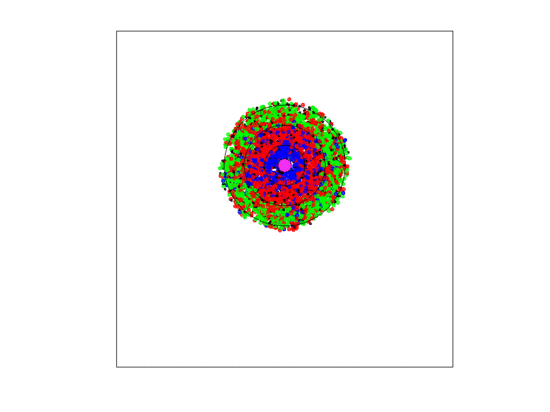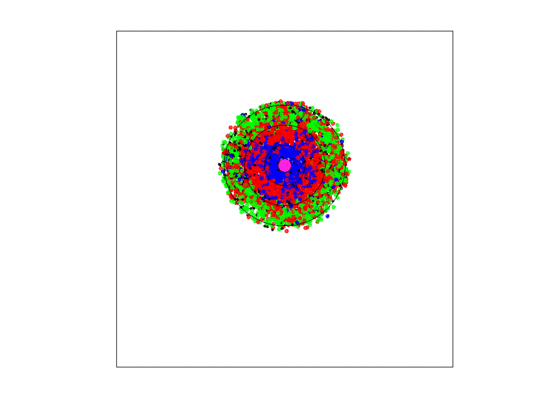
Figure 4.
A video simulation when the blood vessel has a fixed location and each zone has a width of three units. Neighborless cells cannot prolifereate: The blue, red, and green represent and cells, respectively.
We examined cases when a neighborless cell could not proliferate () and when it proliferated with probability . We ran each case ( and ) five times and each simulation for 5000 generations. Table 2 and Table 3 give the outcome of a single run for the cases when and , respectively. The table entries report the average frequency and cell number (per type) over the last 1000 generations. Comparing Table 2 and Table 3, we see very little difference between and for neighborless cells.

Table 2.
Mean frequencies and population sizes of the three cell types averaged over the last 1000 generations. The final three columns provide the non-spatial ESS frequencies for the three zones. Results are from a single run where neighborless cells cannot proliferate: Replicate runs provide very similar outcomes.

Table 3.
Mean frequencies and population sizes of the three cell types averaged over the last 1000 generations. The final three columns provide the non-spatial ESS frequencies for the three zones. Results are from a single run where neighborless cells can proliferate: Replicate runs provide very similar outcomes regardless of whether neighborless cells can proliferate or not (Table 2).
Figure 5 presents the frequency dynamics of a representative run for the full 5000 generations and for zones 1– Figure 6 presents the population dynamics of this same representative run.
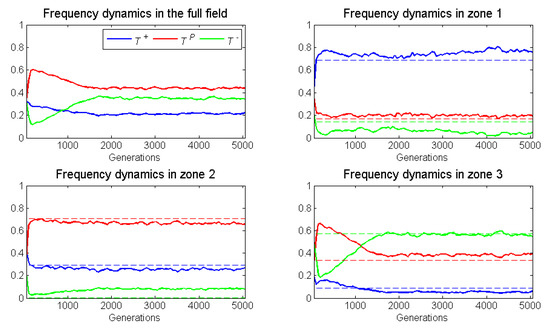
Figure 5.
Frequency dynamics (of a single run) of the spatial game in across the entire torus (top, left). For the other three panels, the dotted lines show the ESS frequencies of the respective matrices , , and In this case, an isolated cell cannot proliferate and the blood vessel remains fixed in its location.
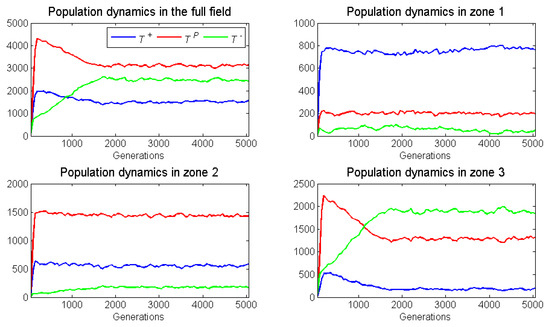
Figure 6.
The population dynamics for the simulation shown in Figure 4. The four panels show the population sizes of the three cell types across the entire torus, zone 1, zone 2 and zone 3. In this case, an isolated cell cannot proliferate and the blood vessel remains in a fixed location.
Examination of the five replicate runs for and revealed that the standard deviations of cell frequencies and population sizes are small over the last 1000 generations (see Appendix B). Within-run variation (last 1000 generations) was greater than between-run variation. Therefore, even a single run provided a good representation for the spatial game dynamics when the blood vessel remains static. The same equilibrium frequencies were achieved when the total population reached saturation, and those equilibrium frequencies were repeatable across the five replicate simulations.
As expected, the proliferation rate of neighborless cells had no effect on outcomes. With a frequency-dependent radius of 1, there were too few neighborless cells to be relevant. Relative to its ESS, zone as expected, had a substantial increase in the already high frequency of . This increase in came at the expense of cells, which presumably were also losing individuals to zone 2. While not expected, there was a small increase in the frequency of in zone due to immigration from zone In conclusion, for zone 1, we observed frequency-dependent dynamics elevating , and dispersal dynamics depressing and elevating .
Zone 2 had a large increase in the frequency of cells, even though its ESS would have none. This occurred at the expense of and cells that stabilizd at frequencies below their ESS. We expected cross-boundary frequency dynamics to elevate , but this was not so. It seemed that dispersal dynamics dominated deviations from the ESS as cells migrated into zone 2 from both zones 1 and
Zone 3 experienced an increase in , and a decrease in and frequencies from the zone’s ESS. As expected, frequency dynamics and dispersal dynamics contributed to a modest decline in the frequency of cells. Dispersal of cells from zone 2 explained their increase in frequency.
Overall, we observed deviations from the ESSs occurring in all zones. These deviations showed the impact of cross-boundary frequency and dispersal dynamics. Thus, either increasing or decreasing the width of a zone should diminish or amplify these effects.
Effects of varying the widths of zones 1, 2 or 3: For the following set of simulations, we retained a static blood vessel in the middle of the torus but varied the width of each zone among and 5 while holding the width of the remaining two zones at For these conditions, we only examined the case where a neighborless cell has a probability of of proliferating each generation. Varying the width of a zone influences the cross-boundary density-dependent, frequency-dependent and dispersal interactions. With a width of 1, essentially every cell would interact across boundaries. Furthermore, in zones 2 and 3, most cells would interact with cells across two boundaries. With a width of approximately a third of the cells would not interact across boundaries (for zones 2 and 3) and a cell can only interact across one boundary. With a width of 5, the majority of cells within any of the three zones (zones 1–3) would not interact across boundaries.
For the cases where we varied the width of a given zone, Figure 7, Figure 8 and Figure 9 report the eco-evolutionary outcomes (averaged over five runs) for zones 1– respectively. Changing the width of a zone had large effects on the total cell counts. When zone 1’s width increased, increased cell counts occurred in all three zones as each now became larger. When zone 2’s width increased, little happened to cell counts in zone 1 (its size remains the same), while cell count increases occurred in zones 2 and Finally, an increase in the width of zone 3 only increased its cell count as the other zones experienced no increase in area. The number of cells that became CTCs remained relatively constant regardless of the width of various zones with between and (means of five runs for a particular treatment) CTCs per generation. This was a tiny fraction of the total number of cells. The frequency of cell types comprising the CTCs corresponded roughly to the frequency of cell types in zone 1 (mostly ).
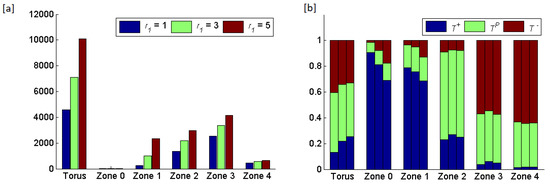
Figure 7.
Results of increasing the radius of zone from 1 to 5, while keeping the radii of the other zones ( and ) at 3. (a) The total number of cells in the torus and in each zone. The average rates at which cells land in zone 0 and become circulating tumor cells are , , and cells per generation, respectively, for equal 1, 3 and 5. (b) The frequencies of the three cell types per zone shown as triplets of stacked bars where the order of bars per triplet shows
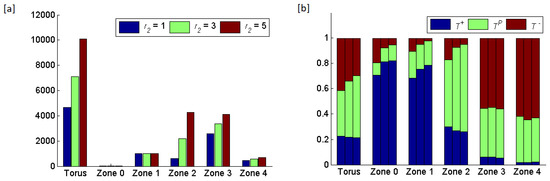
Figure 8.
Results of increasing the radius of zone from 1 to 5, while keeping the radii of the other zones ( and ) at 3. (a) The total number of cells in the torus and in each zone. The average rates at which cells land in zone 0 and become circulating tumor cells are , , and cells per generation, respectively, for equal 1, 3 and 5. (b) The frequencies of the three cell types per zone shown as triplets of stacked bars where the order of bars per triplet shows from left to the right.
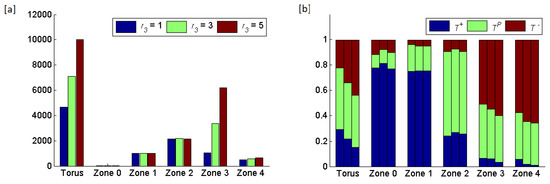
Figure 9.
Results of increasing the radius of zone from 1 to 5, while keeping the radii of the other zones ( and ) at 3. (a) The total number of cells in the torus and in each zone. The average rates at which cells land in zone 0 and become circulating tumor cells are , , and cells per generation, respectively, for equal 1, 3 and (b) The frequencies of the three cell types per zone shown as triplets of stacked bars where the order of bars per triplet shows from left to the right.
Increasing the width of zone 1 caused the frequency of to decline towards its ESS. Hence, a width of 1 saw the largest deviation of cell type frequencies from their ESS values. With a width of there were many fewer cross-boundary interactions and the community of cells resembles closely the ESS for zone Changing the width of zone 1 had little effect on the frequencies of cell types in zones 2 and
Increasing the width of zone 2 caused a decline in frequency and convergence of and frequencies on zone 2’s ESS. This was unsurprising as the cells in zone 2 appearred as a result of cross-boundary interactions with zones 1 and Cross-boundary effects from zone 2 meant that increasing the width of zone 2 influenced zones 1 and 2 via the convergence of zone 2 on its ESS that having a much higher frequency of and lower frequency of relative to the ESSs of zones 1 and Curiously, in zone 1, this resulted in a steady increase in and decline in frequencies as the width of zone 2 increased. Unsurprisingly, in zone 3, the increase in the width of zone 2 resulted in large increases and large declines in and frequencies, respectively.
Increasing the width of zone 3 resulted in an increase in the frequency of cells at the expense of and This change in frequency also spilt over into the composition of zone 4 (the area unsupportive of cell proliferation). Changing the width of zone 3 had little effect on the compositions of zones 1 and 2 because the boundaries of these zones remained unchanged.
Dynamic blood vessel: Here, we considered the consequences of a dynamic vasculature. We assumed that the blood vessel has some probability of shifting location each generation. The rerouting of vasculature within tumors is typical as upstream occlusions of vessels or the production of growth factors such as VEG-F shifts blood flow within the tumor. We contrasted a low probability of shifting ( per generation) with a high probability (). These probabilities were 20 to 5 times slower, respectively, than the turnover rate of the cancer cells whose probability of death was When a shift occurred, the blood vessel disappeared from its current location and reappeared at a randomly selected location of the torus. In addition to considering a low and high probability of blood vessel shift, we considered cases where the width of each zone was either or 5 (narrow, intermediate or wide), and we contrasted the cases where neighborless cells could not () or could () divide. This created 12 combinations of factors: 2 shift rates × 3 zone widths × 2 neighborless cell proliferation rates. We ran each combination five times.
The shifting of the blood vessel represented a disturbance regime for its associated population of cancer cells. A random shift in the blood vessel’s location meant that most of the cancer cells that had been in zones 1–3 were now in zone 4 and incapable of proliferating. Persistence of the cancer cell population required that a sufficient number of cells coincidentally fell into the three proliferative zones of the new blood vessel. Such cells could come from persister cells in zone 4, cells from zone 3, and less likely from zones 1 and 2 due to their smaller areas. Thus, the population that recovered might start from a composition that more resembles the ESS of zone 3 than the other zone-specific ESSs. Recovery of the population was more likely if neighborless cells could proliferate, zone widths were larger, and blood vessel shifts were less common.
When the zone widths were 1 or 3 units, the cancer cell population always died out within 5000 generations. Extirpation occurred for all runs. With widths of 1 and the proliferative population formed a circle with a diameter of 8 or 20, respectively. Furthermore, zone 4 cells extended this to 10 and 22 spatial units, since the dispersal radius was Thus, for zone widths of 1, there was about a % chance that the new blood vessel had parts of zone 3 overlapping with cells that were in the zones 1–4 of the old vessel. This increased to about a 41% chance of overlap when the zone widths were 3 and a near 100% chance when the zone widths were
When zone widths were 5 units, no extirpations occurred for any of the five runs as long as either the rate of blood vessel shift was low () or the neighborless cells could proliferate (). For the five runs where blood vessels shifted at a high rate () and neighborless cells could not proliferate (), extirpation always occurred. This was because a high turnover of blood vessels created sparse populations of often neighborless cells (see simulation in Figure 10). If neighborless cells could proliferate, then extirpation did not occur because even sparse populations could recover. If turnover rates were slower, then residual populations remained less sparse and cell populations could recover as most cells had neighbors (see simulation in Figure 11). However, in all five runs of the simulation (high vessel turnover and ), one of the cell types went extinct and only two cell types persisted; and this persistence seemed durable for the 5000 generations. Which cell type experienced extinction was stochastic and we saw simulations where , or went extinct. This happened because, when a blood vessel died at a given position, cells that populate the new set of three zones began as sparse cell populations. When neighborless, there were no game dynamics and all cell types had the same fitness of As neighbors accrued one-type aggregations of cells became common, the two-cell type aggregations became less, and three-cell type aggregations became very rare. While the blood vessel persisted, cells in two-cell type aggregations had higher fitness due to the frequency-dependent interactions than single cell type aggregations. The extinction of a cell type meant that zone specific cell compositions rarely if ever achieved a composition near their ESS.
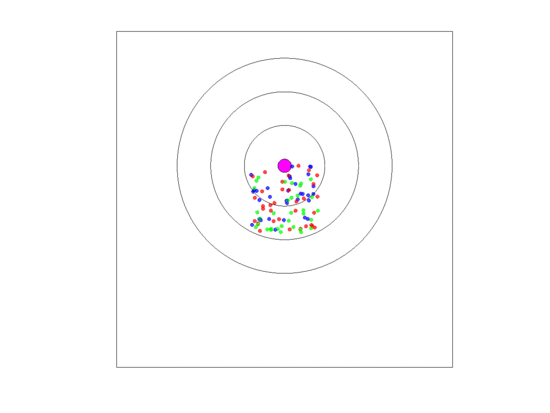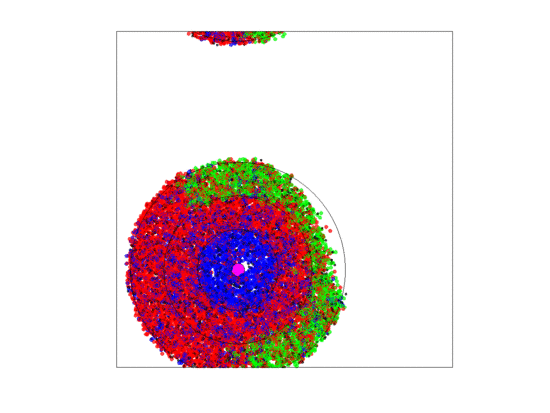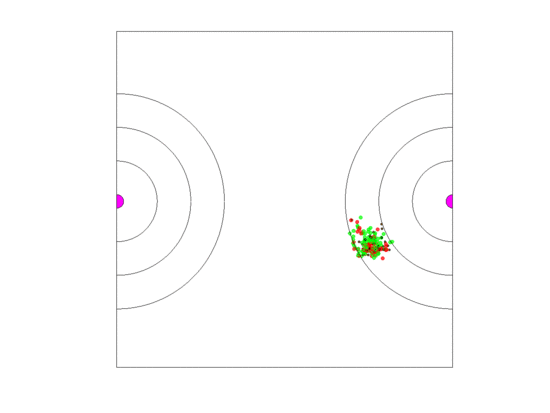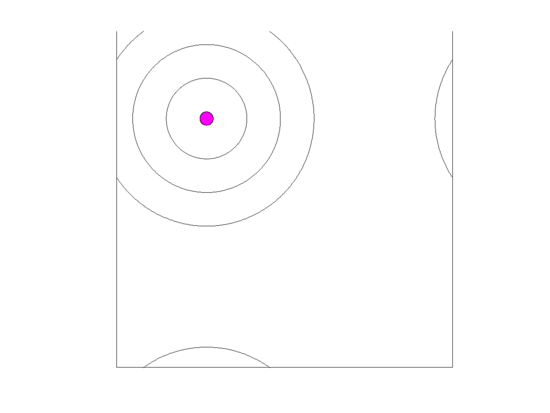
Figure 10.
Video of the game when the blood vessel has a high probability of per generation of dying and re-merging elsewhere. Even though the zone widths are large (5 units each), extinction always occurs within 5000 generations when neighborless cells cannot proliferate: This simulation pauses upon extinction.
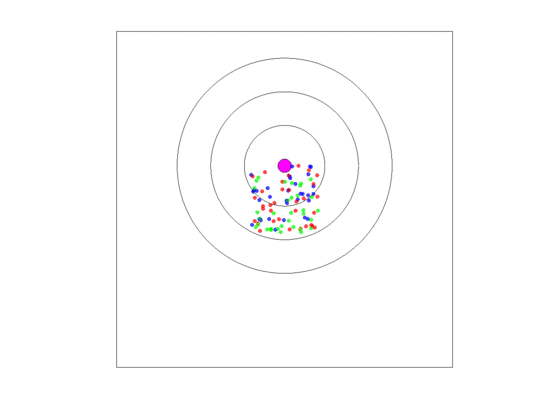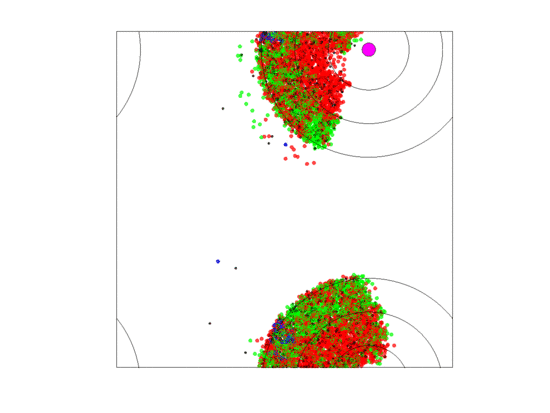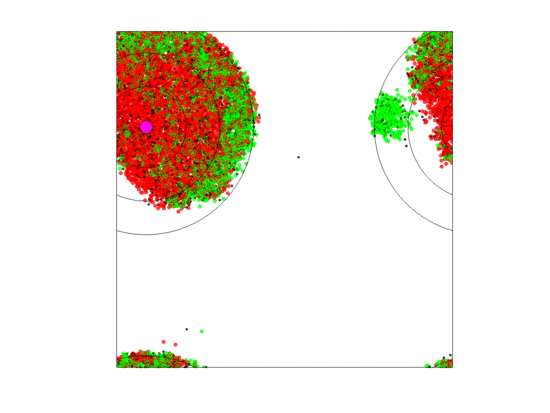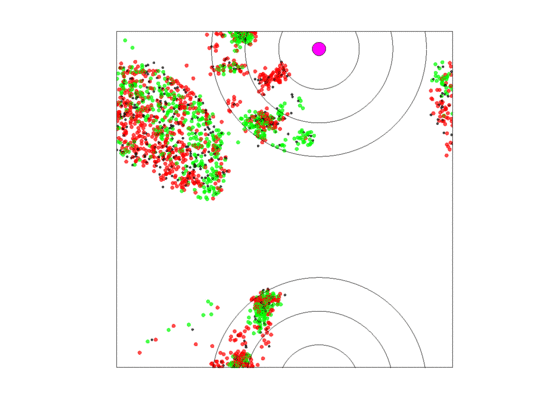
Figure 11.
Video of the game when the blood vessel has a high probability of per generation of dying and re-merging elsewhere. When neighborless cells can proliferate () and with large zone widths (5 units), extinction never occurred within 5000 generations for any of our replicate runs. The cancer cell populations collapses with the shift in blood vessel location, but quickly recovers. For all replicate runs, one of the cell types would rapidly go extinct (it could be any of the three) while the remaining two would persist through the 5000 generations.
With broad zone widths (5 units) and low blood vessel turnover (), all three cell types persisted. The five runs of a case yielded remarkably similar patterns of population and frequency dynamics. Whether neighborless cells could divide or not had little effect. With a shift in blood vessel, there was a sharp drop in the torus-wide population sizes of the three cell types. Population sizes of all cell types tended to recover swiftly (Figure 12). Thus, the pattern of population sizes exhibited periods of relative steady state punctuated by catastrophic declines. The dynamics of cell-type frequencies in the three zones also showed steady states punctuated by abrupt shifts in frequencies (Figure 13).
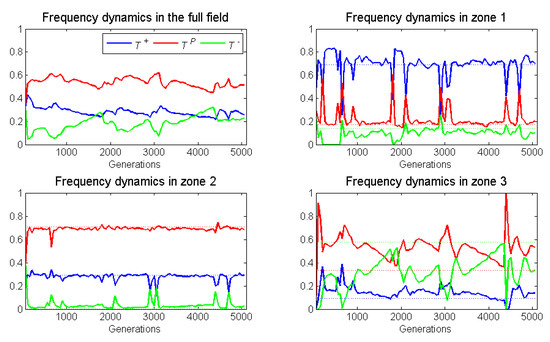
Figure 12.
For dynamic blood vessels, frequency dynamics (of one run) of the spatial game for each of the three cell types: across the whole space (top left); in zone 1 (top right); in zone 2 (bottom left); and in zone 3 (bottom right). The blood vessel switches location with a low probability of per generation, neighborless cells can proliferate (), and the zones have a broad width (). Frequency dynamics are much sharper in zones 1 and 3 than in zone 2 because the overall frequency of cell types matches more closely that of zone
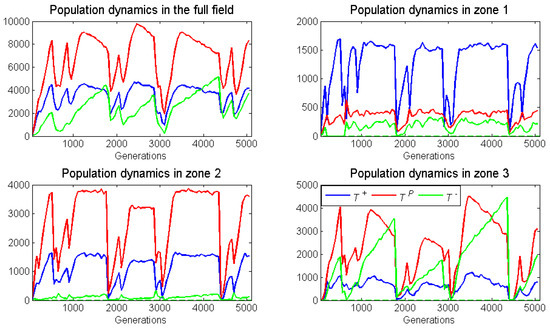
Figure 13.
For dynamic blood vessels, population dynamics (same run as Figure 12) of the spatial game for each of the three cell types: across the whole space (top left); in zone 1 (top right); in zone 2 (bottom left); and in zone 3 (bottom right). The blood vessel switches location with a low probability of per generation, neighborless cells can proliferate (), and the zones have a broad width (). With each blood vessel switch, populations crash and then quickly recover.
For zones 1 and 2, the relative steady state frequencies conformed even more closely to their static ESSs than when the blood vessel never shifted. The abrupt shifts in cell-type frequencies following a blood vessel disappearance and reappearance was most extreme in zone 1 and least for zone In all runs and following all blood vessel shifts, zone 1 experienced an abrupt rise in frequencies at the expense of This was because each zone of the new blood vessel became seeded with a frequency of cell types matching that of the overall torus. The overall frequency of and cells in the whole torus was much lower and higher, respectively, than those of zone 1 at steady state. The frequencies of cell types in the whole torus coincidently matched closely the steady state frequencies of zone Hence, there were much fewer abrupt shifts in frequency when the blood vessel moved. frequencies briefly shot up but then declined back towards near zero, consistent with the ESS of zone When zone 3 reappeared because of a new blood vessel, the “inherited” population tended to have an over-representation of both and Both tended to decline as the community moved toward the zone 3 equilibrium with a much higher frequency of However, a new disturbance tended to occur prior to reaching this steady state. Unlike zones 1 and zone 3 seemed to remain as a disturbance community with well below and well above their zone 3 ESS frequencies.
The simulation shown in Figure 12 and Figure 13 was representative for the dynamic blood vessel when the blood vessel died with probability and neighborless cells proliferated with probability Over the five separate runs, we observed only small variation in the mean cell type frequencies and mean cell numbers over the last 1000 generations per run (see Appendix B).
6. Discussion
Spatial heterogeneity in the physical properties of the tumor and a diversity of cancer cell types is the norm for cancers, particularly when the disease is disseminated and metastatic. At the largest scale, there can be tissue specific differences between, e.g., a primary tumor in the breast and a secondary tumor that has metastized and formed in the liver [37]. Within tumor heterogeneity may include areas on the edge of the tumor, areas within the tumor that are thriving but not near an edge, and necrotic regions where the physical environment can support few to no cancer cells. Heterogeneity from the edge to the interior of the tumor can promote quite different cell types [17]. Finally, at a very small spatial scale, distance from a blood vessel creates a gradient of oxygen, glucose and other resources; rich near the vessel and eventually insufficient at some distance [16]. This too can lead to the coexistence of different cell types based on proximity to blood vessels [17].
Each of these scales of heterogeneity offer different opportunities and hazards to the cancer cells. Most importantly, they represent scales of macrohabitats (tumors within a patient occupying different tissues), mesohabitats (edge versus interior of the tumor) and microhabitats (distance from a blood vessel). These scales matter. At the macroscale, there are little to no meaningful interactions between cells in one tumor and tumors at a metastatic site. Each tumor may influence the whole host physiology in a manner that feeds back on the other tumor (e.g., abscopal effects [38,39]), but these links will be highly indirect and likely quite damped. At the mesoscale, cells may migrate at a higher rate from mesohabitat to mesohabitat than would occur between distant tumors. However, a given cell likely proliferates, lives and then dies within the same mesohabitat. The bulk of cells will never, in their lifetimes, experience a different mesohabitat. Although the fraction that does migrate may have outsized effects, relative to their numbers, on tumor growth and the formation of metastases.
Thus, if the cancer cells at these scales are engaging in evolutionary games, we would expect each macrohabitat and mesohabitat to largely be at its ESS. Not so at the small spatial scale of distance from the blood vessel. Our agent-based model is intended to explore how gradient effects might shift the expected composition of cells away from their microhabitat-specific ESS. We explored this by imagining four zones (microhabitats), each successively farther from the blood vessel and each involving a distinct evolutionary game and ESS. In our model, we imagined zone 4 as a sink microhabitat, too distant from the blood vessel to permit cancer cell proliferation but still able to contain living cancer cells. For illustration, our model considered the three cell types (testosterone requiring), (testosterone producing) and (independent of testosterone) associated with men having castrate resistant metastatic prostate cancer [13,14,15].
Our model considers interactions within and between tumor microhabitats by extending the agent-based continuous-space model of You et al. [13] to include blood vessels. To illustrate the model’s application, we created payoff matrices that: (1) favored the dominance of , and cells in going from close to far from the blood vessel (zones 1–3); and (2) incorporated the beneficial effect of cells on cells via the public goods release of testosterone by cells. A unique feature of our model includes the ability to track cancer cells that disperse into the blood vessel itself. In cancer biology, these are the circulating tumor cells (CTCs), critical for the metastatic process [36]. Since the blood vessel is surrounded by zone the expected composition of circulating tumor cells resembled most the composition of cells in zone Dispersal into the blood vessel happened at a slow trickle, and if this were magnified over all of the vessels in the tumor, one could begin to model the total population of CTCs within the blood.
As expected, frequency-dependent interactions and dispersal across microhabitat boundaries shifted cell-type compositions from their zone-specific ESSs. For instance, the composition of zone 1 was altered by both cross-boundary interactions with cells as well as the influx of cells from zone 2. These effects doubly benefited cells and elevated their frequency. Dispersal dynamics resulted in a net loss of cells to zone 2 where they then fare poorly. In the end, the community in zone 1 resembled even less that of zone 2 because of strong cross-boundary frequency interactions. In contrast, the composition of zone 2 became more similar to that of zone 1 because of dispersal. Dispersal from zone 3 had negligible effects on zone 2 because of the low density of cells in zone 3 (a consequence of distance from the blood vessel). Zone 3, by virtue of being more isolated, achieved a community that most closely resembled its ESS but with deviations towards the ESS of zone 2 because of dispersal. The model can be modified to consider any number of zones, cell cancer types and payoff matrices that vary along the gradient of zones.
The size of microhabitats should matter as shown in the model by varying the width of the zones. The likelihood of cross-boundary interactions and dispersal decline as zone width increases. As the width of a zone increased, its composition of cell types converged on its ESS. With very large widths, the zones behave less like microhabitats and more like mesohabitats. For example, increasing the width of zone 2 while holding other zone widths constant amplifies zone 2’s spill-over effects onto the other zones while damping spillover effects into zone The already dominant cells of zone 1 increase further in frequency because of beneficial cross boundary interactions with the cells that predominate in zone Because of inter-zone dispersal effects, the composition of cell types in zone 3 diverges from its ESS and converges on the composition of zone
Our model also includes blood vessel dynamics where a vessel may become occluded or die leaving the surrounding cells without resources. The loss of a blood vessel leaves all or most of the cells in zone 4, the place of no proliferation and a steady mortality rate. Obviously, if a vessel dies and no new vessels form nearby, this subpopulation of cancer cells will die off in this necrotic space. However, new blood vessels likely appear nearby, either because the occluded blood vessel now flows along another nearby vessel, or because the cancer cells produce growth factors (VEG-F for example) that recruit vessels. We only considered a single vessel at a time. When it died with some probability, another appeared at a random location within the torus. This creates boom–bust cycles for the cancer subpopulation. To recover from the death and birth of a blood vessel, there must be some living cancer cells that find themselves coincidently within the proliferation zones (zone 1, 2 or 3 in the case of our example) of the new vessel. The source of these will most likely be from zones 3 and 4 because they occupy the largest space. As expected, with dynamic blood vessels the reconstituting subpopulation of cancer cells around a new blood vessel most resembled zone 3’s ESS. Furthermore, if the frequency of blood vessel mortality is high and the width of zones small, then the extirpation of the cancer subpopulation is highly likely. If zone widths are large and blood vessel death infrequent, then following “catastrophes” the cancer subpopulation returns to its dynamic steady state within each of the zones surrounding the new vessel. In this way, our model can explore the “ecological succession” of cancer cells following a shift in vasculature.
Our model complements existing models that include vasculature and the coexistence or evolution of different cancer cell types [40,41,42]. Most other models consider larger spatial scales than ours. They are often meant to mimic the whole tumor, whereas ours examined mere subpopulations of cancer cells within a tumor. Some models are spatially implicit and explore the evolution of VEG-F production to recruit blood vessels and increase the tumor’s supply of nutrients [43]. Here, the production of VEG-F by cancer cells or associated normal cells is seen as a public goods game where there may be producers and cheaters. In other spatial models, the tumor is seen as populated by a large number of blood vessels presented as mere points [44]. These can be modeled as hybrid models where the nutrients from the blood vessels diffuse across the space (modeled as partial differential equations), while individual cancer cells are agents occupying space on the landscape, similar to more general agent-based models approximating reaction–diffusion equations [45,46]. Other models that consider nutrients surrounding a particular blood vessel are not game-theoretic. However, they offer important insights into drug delivery, nutrient dynamics and gradients of resources, toxins, pH, etc. [36,47,48].
Future extensions of our model could incorporate a larger number of blood vessels. These vessels could vary in size (the width of zones around each), distribution in the space, and in the covariance between their appearance and disappearance. In some cases, the density or frequency of cancer cell types around the blood vessel may hasten its demise or prolong its presence. Our model can be extended to include frequency-dependent and density-dependent interactions between cancer cells in the presence or absence of cancer therapy, or fluctuations in drug delivery. For the present example, we set the dispersal, density-dependence and frequency-dependence radii equal to each other. More realistically, these could be varied independently. For instance, a more migratory cancer cell phenotype would have a higher dispersal radius. If the depletion radius of nutrients around a cell is larger or smaller than frequency-dependent interactions, then these radii can be set accordingly.
In the model presented here, we assumed that there are three distinct proliferation zones around the blood vessel, which differ in their carrying capacities and payoff matrices. We assumed discrete jumps in conditions. To render a more realistic continuum, one could either increase the number of zones, or create a matrix of interactions, carrying capacities and density limitations that change continuously with distance. In addition, in our model, a given cell had its frequency-dependent interactions determined from selecting a single cell at random from its neighborhood. Alternatively, one could let some linear or nonlinear combination of individuals within the frequency-dependence radius determine the outcome. Conversely, the number and frequency of cells within the neighborhood could determine a focal cell’s payoff. Finally, our approach and model lack explicit considerations of nutrients, oxygen and Ph, all known to be important and varying with distance from vessels. For such cases, a hybrid model or nutrient PDEs and discrete agent-based cells might be more appropriate. Our model will be most applicable to situations where much of the complexity can be distilled into a matrix game with two, three or perhaps more different cell types. In this way, any novel or existing matrix game model of cancer can be embedded into a spatial landscape of blood vasculature by extending and applying the approach developed here.
Author Contributions
Conceptualization, L.Y., M.v.K., T.L., V.P., S.R., P.K.S., F.T., K.S., J.S.B.; methodology, L.Y., M.v.K., T.L., V.P., S.R., P.K.S., F.T., K.S., J.S.B.; software, L.Y., M.v.K., T.L., V.P., S.R., P.K.S.; validation, L.Y., M.v.K., T.L., V.P., S.R., P.K.S.; formal analysis, F.T., K.S., J.S.B.; investigation, L.Y., M.v.K., T.L., V.P., S.R., P.K.S., F.T., K.S., J.S.B.; resources, F.T., K.S., J.S.B.; data curation, L.Y.; writing—original draft preparation, M.v.K., T.L., V.P., S.R., P.K.S.; writing—review and editing, L.Y., K.S., J.S.B.; visualization, L.Y., M.v.K., T.L., V.P., S.R., P.K.S.; supervision, F.T., K.S., J.S.B.; project administration, F.T., K.S., J.S.B.; funding acquisition, F.T., K.S., J.S.B.
Funding
This research was funded by the European Union’s Horizon 2020 research and innovation program (Marie Skłodowska-Curie grant agreement No 690817), the James S. McDonnell Foundation grant, “Cancer therapy: Perturbing a complex adaptive system”, a V Foundation grant, NIH/National Cancer Institute (NCI) R01CA170595, Application of Evolutionary Principles to Maintain Cancer Control (PQ21), and NIH/NCI U54CA143970-05 (Physical Science Oncology Network (PSON)) “Cancer as a complex adaptive system.”
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Parametrization of the Payoff Matrix in Each Zone
Our selection of payoff matrices for the three zones is based on the three cell types, , and , that form the basis for Zhang et al.’s model and clinical trial on castrate resistant metastatic prostate cancer mCRPC [14]. While recognizing that distance to blood vessels likely influences the success of the three cell types, You et al. [13], Zhang et al. [14], and Cunningham et al. [15] assumed that the interactions between the three prostate-cancer cell types (, and ) are represented by a single fitness matrix where
with zero diagonals. In this matrix, coefficients a–f were distinct values from the set satisfying , , , , , (see [13,14] for the cancer biology behind these rankings), where element of this matrix represents the payoff to a cell of type i when interacting with a cell of type j. In [14,15] these formed the basis for the competition coefficients in a Lotka-Volterra model of competition. Subtracting each element from 1 gave the competition coefficients. You et al. [13] in a continuous space, agent-based model equated the payoff matrix to the probability that a cell of type i can proliferate when it interacts with a cell of type
Like You et al. [13] we interpret the payoffs as the probabilities that the focal cell can proliferate (given that the density threshold has not been exceeded), but with two important deviations. First, we explicitly consider distance from a blood vessel and define a separate payoff matrix for the three zones within which cancer cells can proliferate: . Second, we give each of these matrices a diagonal element of by adding to all elements. This means that two interacting cells will have the opportunity to proliferate whether they are of the same or different type, and this sets a lower bound of and an upper bound of on the off-diagonal elements. Therefore, for our variant of the mCRPC game our matrices have the following structure:
Here the element on the ith row and jth column represents the probability that a cell of type will produce a daughter cell of the same type when interacting with a cell of type . Note that the ESSs of the original and our matrix are the same for the same a–f values.
Moreover, there is no reason to expect that all three matrices will satisfy the inequalities of [13] as they were imagining some integration across the spatial heterogeneity of a tumor with specific reference to distance from blood vessels. Instead we have constructed the matrices to (1) match the presumed biology, (2) create ESSs where , and predominate in zones 1, and respectively, (3) have three matrices that when combined as a weighted average recover the original inequalities of [13], (4) have off-diagonal elements greater than , and where (5) zone 2 has an absence of at its ESS. This last requirement is to enhance our ability to observe how cross-boundary dispersal and interactions skew a zone’s cell-type composition away from its ESS. Beyond satisfying these conditions, the selection of matrix values can be somewhat arbitrary.
Zone 1 matrix: This zone is closest to the blood supply and receives the most nutrients as well as any testosterone present in the blood. We require meaning a focal cell does better when interacting with a testosterone producing than a . We require indicating that a focal does better when competing with a than a (presumed to be the strongest competitor when resources are rich). We require indicating that a focal does better than a focal when interacting with a . Finally, indicates that a focal does better than a focal when interacting with a as the is starved for testosterone. This allows a number of different rankings but we elected for
Zone 2 matrix: This zone would be more depleted in resources as well as blood borne testosterone and we assume it most favors over the other cell types. This means indicating that a focal does better when interacting with a now less competitive than a . Similarly shows a focal doing better when competing with a than a We require indicating that a focal does better than a focal when interacting with a Finally, indicates that a focal does better than a focal when interacting with a as the is starved for testosterone. This allows a number of different rankings but we elected for to satisfy our other criteria.
Zone 3 matrix: This zone would be most depleted in resources and perhaps even harshly hypoxic and acidic. We assume that cells are more adapted than the other types for this microhabitat, though empirical evidence is sparse. Like zone 2, this means meaning a focal does better when interacting with a than a ; and shows a focal doing better when competing with a than a We require as requires for testosterone, and does poorly against Furthermore, indicates that a focal does better than a focal when interacting with a ; and indicates that a focal does better than a focal when interacting with a as the is starved for testosterone. This allows many fewer options for ranking parameters than zones 1 and and we elected for to satisfy our criteria.
In general as we go from to we see doing progressively more poorly, doing progressively better, cells doing progressively better against , and doing progressively worse against In all cases, does better or the same against than
Appendix B. Standard Deviation of Equilibrium Frequencies Per Case Study
A single fixed blood vessel: For the standard deviations of frequencies of , and in the entire torus and in zones 0–4 are , , , , and respectively. The corresponding standard deviations among the population sizes are , , , , and respectively. When , the standard deviations of frequencies of , and in the entire torus and in zones 0–4 are , , , , and respectively. The corresponding standard deviations of population sizes in the entire torus and in zones 0–4 are , , , , and , respectively. We observe even smaller standard deviations of the mean frequencies and cell numbers among the 5 runs.
Dynamic blood vessel: The standard deviations of , and in the entire torus and in zones 0–4 are and respectively. The corresponding standard deviations among the population sizes are , and respectively. Compared to the case studies of static blood vessels, we observe fewer cells landing inside the blood vessel as circulating cancer cells (CTCs), as the blood vessel position in the torus changes relatively often.
References
- Gatenby, R.A.; Cunningham, J.J.; Brown, J.S. Evolutionary triage governs fitness in driver and passenger mutations and suggests targeting never mutations. Nat. Commun. 2014, 5, 5499. [Google Scholar] [CrossRef] [PubMed]
- Merlo, L.M.; Pepper, J.W.; Reid, B.J.; Maley, C.C. Cancer as an evolutionary and ecological process. Nat. Rev. Cancer 2006, 6, 924–935. [Google Scholar] [CrossRef]
- Orlando, P.A.; Gatenby, R.A.; Brown, J.S. Cancer treatment as a game: Integrating evolutionary game theory into the optimal control of chemotherapy. Phys. Biol. 2012, 9, 065007. [Google Scholar] [CrossRef]
- Egeblad, M.; Nakasone, E.S.; Werb, Z. Tumors as organs: Complex tissues that interface with the entire organism. Dev. Cell 2010, 18, 884–901. [Google Scholar] [CrossRef]
- Basanta, D.; Scott, J.G.; Fishman, M.N.; Ayala, G.; Hayward, S.W.; Anderson, A.R.A. Investigating prostate cancer tumour–stroma interactions: Clinical and biological insights from an evolutionary game. Br. J. Cancer 2012, 106, 174. [Google Scholar] [CrossRef]
- Marusyk, A.; Almendro, V.; Polyak, K. Intra-tumour heterogeneity: A looking glass for cancer? Nat. Rev. Cancer 2012, 12, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.P.; Tirosh, I.; Trombetta, J.J.; Shalek, A.K.; Gillespie, S.M.; Wakimoto, H.; Cahill, D.P.; Nahed, B.V.; Curry, W.T.; Martuza, R.L. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science 2014, 344, 1396–1401. [Google Scholar] [CrossRef]
- Sottoriva, A.; Spiteri, I.; Piccirillo, S.G.; Touloumis, A.; Collins, V.P.; Marioni, J.C.; Curtis, C.; Watts, C.; Tavaré, S. Intratumor heterogeneity in human glioblastoma reflects cancer evolutionary dynamics. Proc. Natl. Acad. Sci. USA 2013, 110, 4009–4014. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Fujimoto, J.; Zhang, J.; Wedge, D.C.; Song, X.; Zhang, J.; Seth, S.; Chow, C.W.; Cao, Y.; Gumbs, C. Intratumor heterogeneity in localized lung adenocarcinomas delineated by multiregion sequencing. Science 2014, 346, 256–259. [Google Scholar] [CrossRef]
- Swanton, C. Intratumor heterogeneity: Evolution through space and time. Cancer Res. 2012, 72, 4875–4882. [Google Scholar] [CrossRef]
- Staňková, K.; Brown, J.; Dalton, W.; Gatenby, R.A. Optimizing Cancer Treatment Using Game Theory. JAMA Oncol. 2019, 5, 96–103. [Google Scholar] [CrossRef]
- Bayer, P.; Brown, J.; Staňková, K. A Two-Phenotype Model of Immune Evasion by Cancer Cells. J. Theor. Biol. 2018, 455, 191–204. [Google Scholar] [CrossRef]
- You, L.; Brown, J.S.; Thuijsman, F.; Cunningham, J.J.; Gatenby, R.A.; Zhang, J.; Staňková, K. Spatial vs. non-spatial eco-evolutionary dynamics in a tumor growth model. J. Theor. Biol. 2017, 435, 78–97. [Google Scholar] [CrossRef]
- Zhang, J.; Cunningham, J.J.; Brown, J.S.; Gatenby, R.A. Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nat. Commun. 2017, 8, 1816. [Google Scholar] [CrossRef]
- Cunningham, J.J.; Brown, J.S.; Gatenby, R.A.; Staňková, K. Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer. J. Theor. Biol. 2018, 459, 67–78. [Google Scholar] [CrossRef]
- Alfarouk, K.; Ibrahim, M.; Gatenby, R.; Brown, J. Riparian ecosystems in human cancers. Evol. Appl. 2013, 6, 46–53. [Google Scholar] [CrossRef]
- Lloyd, M.C.; Alfarouk, A.O.; Verduzzo, D.; Bui, M.M.; Gillies, R.J.; Ibrahim, M.E.; Brown, J.S.; Gatenby, R.A. Vascular measurements correlate with estrogen receptor status. BMC Cancer 2014, 14, 279–286. [Google Scholar] [CrossRef]
- Carmeliet, P. VEGF as a Key Mediator of Angiogenesis in Cancer. Oncology 2005, 69, 4–10. [Google Scholar] [CrossRef]
- Anderson, A.R.A.; Chaplain, M.A.J. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull. Math. Biol. 1998, 857–899. [Google Scholar] [CrossRef]
- Peirce, S.M. Computational and Mathematical Modeling of Angiogenesis. Microcirculation 2008, 15, 739–751. [Google Scholar] [CrossRef]
- Dingli, D.; Chalub, F.; Santos, F.; Van Segbroeck, S.; Pacheco, J. Cancer phenotype as the outcome of an evolutionary game between normal and malignant cells. Br. J. Cancer 2009, 101, 1130–1136. [Google Scholar] [CrossRef]
- Rak, J.; Croix, B.S.; Kerbel, R. Consequences of angiogenesis for tumor progression, metastasis and cancer therapy. Anticancer Drugs 1995, 6, 3–18. [Google Scholar] [CrossRef]
- Shirinifard, A.; Gens, J.S.; Zaitlen, B.L.; Popławski, N.J.; Swat, M.; Glazier, J.A. 3D Multi-Cell Simulation of Tumor Growth and Angiogenesis. PLoS ONE 2009, 4, 1–11. [Google Scholar] [CrossRef]
- Gerlee, P.; Anderson, A. An Evolutionary Hybrid Cellular Automaton Model of Solid Tumour Growth. J. Theor. Biol. 2007, 246, 583–603. [Google Scholar] [CrossRef]
- Bauer, A.L.; Jackson, T.L.; Jiang, Y. A Cell-Based Model Exhibiting Branching and Anastomosis during Tumor-Induced Angiogenesis. Biophys. J. 2007, 92, 3105–3121. [Google Scholar] [CrossRef]
- Axelrod, R.; Axelrod, D.E.; Pienta, K.J. Evolution of cooperation among tumor cells. Proc. Natl. Acad. Sci. USA 2006, 103, 13474–13479. [Google Scholar] [CrossRef]
- Pienta, K.J.; McGregor, N.; Axelrod, R.; Axelrod, D.E. Ecological Therapy for Cancer: Defining Tumors Using an Ecosystem Paradigm Suggests New Opportunities for Novel Cancer Treatments. Transl. Oncol. 2008, 158–164. [Google Scholar] [CrossRef]
- Archetti, M.; Pienta, K.J. Cooperation among cancer cells: Applying game theory to cancer. Nat. Rev. Cancer 2018. [Google Scholar] [CrossRef]
- Altrock, P.M.; Liu, L.L.; Michor, F. The mathematics of cancer: Integrating quantitative models. Nat. Rev. Cancer 2015, 15, 730–745. [Google Scholar] [CrossRef]
- Basanta, D.; Hatzikirou, H.; Deutsch, A. Studying the emergence of invasiveness in tumours using game theory. Eur. Phys. J. B 2008, 63, 393–397. [Google Scholar] [CrossRef]
- Hurlbut, E.; Ortega, E.; Erovenko, I.V.; Rowell, J.T. Game Theoretical Model of Cancer Dynamics with Four Cell Phenotypes. Games 2018, 9. [Google Scholar] [CrossRef]
- Hussain, M.; Tangen, C.M.; Berry, D.L.; Higano, C.S.; Crawford, E.D.; Liu, G.; Wilding, G.; Prescott, S.; Kanaga Sundaram, S.; Small, E.J. Intermittent versus continuous androgen deprivation in prostate cancer. N. Engl. J. Med. 2013, 368, 1314–1325. [Google Scholar] [CrossRef]
- Tsai, H.; Penson, D.F.; Makambi, K.H.; Lynch, J.H.; Van Den Eeden, S.K.; Potosky, A.L. Efficacy of intermittent androgen deprivation therapy vs conventional continuous androgen deprivation therapy for advanced prostate cancer: A meta-analysis. Urology 2013, 82, 327–334. [Google Scholar] [CrossRef]
- Lu-Yao, G.L.; Albertsen, P.C.; Moore, D.F.; Shih, W.; Lin, Y.; DiPaola, R.S.; Yao, S.L. Survival following primary androgen deprivation therapy among men with localized prostate cancer. JAMA 2008, 300, 173–181. [Google Scholar] [CrossRef]
- Mostaghel, E.A.; Marck, B.T.; Plymate, S.R.; Vessella, R.L.; Balk, S.; Matsumoto, A.M.; Nelson, P.S.; Montgomery, R.B. Resistance to CYP17A1 inhibition with abiraterone in castration-resistant prostate cancer: Induction of steroidogenesis and androgen receptor splice variants. Clin. Cancer Res. 2011, 17, 5913–5925. [Google Scholar] [CrossRef]
- Rejniak, K.A. Circulating Tumor Cells: When a Solid Tumor Meets a Fluid Microenvironment. Adv. Exp. Med. Biol. 2016, 936, 93–106. [Google Scholar] [CrossRef]
- Gerlinger, M.; Rowan, A.; Horswell, S.; Larkin, J.; Endesfelder, D.; Gronroos, E.; Martinez, P.; Matthews, N.; Stewart, A.; Tarpey, P.; et al. Intratumor Heterogeneity and Branched Evolution Revealed by Multiregion Sequencing. N. Engl. J. Med. 2012, 366, 883–892. [Google Scholar] [CrossRef]
- Demaria, S.; Formenti, S.C. Can abscopal effects of local radiotherapy be predicted by modeling T cell trafficking? J. Immunother. Cancer 2016, 29. [Google Scholar] [CrossRef]
- Poleszczuk, J.; Luddy, K.A.; Prokopiou, S.; Robertson-Tessi, M.; Moros, E.G.; Fishman, M.N.; Djeu, J.Y.; Finkelstein, S.E.; Enderling, H. Abscopal Benefits of Localized Radiotherapy Depend on Activated T-cell Trafficking and Distribution between Metastatic Lesions. Cancer Res. 2016, 76, 1009–1018. [Google Scholar] [CrossRef]
- Szabó, A.; Merks, R.M.H. Blood vessel tortuosity selects against evolution of aggressive tumor cells in confined tissue environments: A modeling approach. PLoS Comput. Biol. 2017, 13, e1005635. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, S.; Wu, J.; Long, Q. Coupled modelling of tumour angiogenesis, tumour growth and blood perfusion. Biochem. Cell Biol. 2011, 279, 90–101. [Google Scholar] [CrossRef]
- Gallaher, J.; Brown, J.; Anderson, A.R.A. The dynamic tumor ecosystem: How cell turnover and trade-offs affect cancer evolution. bioRxiv 2018. [Google Scholar] [CrossRef]
- Alarcón, T.; Page, K.M. Mathematical models of the VEGF receptor and its role in cancer therapy. J. R. Soc. Interface 2006, 4, 283–304. [Google Scholar] [CrossRef]
- Kuang, Y.; Nagy, J.; Eikenberry, S.E. Introduction to Mathematical Oncology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Avelino, P.; Bazeia, D.; Losano, L.; Menezes, J.; Oliveira, B. Junctions and spiral patterns in generalized rock-paper-scissors models. Phys. Rev. E 2012, 86, 036112. [Google Scholar] [CrossRef]
- Avelino, P.P.; Bazeia, D.; Losano, L.; Menezes, J.; de Oliveira, B.F. Spatial patterns and biodiversity in off-lattice simulations of a cyclic three-species Lotka-Volterra model. Europhys. Lett. 2018, 121, 48003. [Google Scholar] [CrossRef]
- Shah, A.; Rejniak, K.; Gevertz, J. Limiting the development of anti-cancer drug resistance in a spatial model of micrometastases. Math. Biosci. Eng. 2016, 13, 1185–1206. [Google Scholar] [CrossRef]
- Stefanini, M.O.; Qutub, A.A.; Mac Gabhann, F.; Popel, A.S. Computational models of VEGF-associated angiogenic processes in cancer. Math. Med. Biol. 2011, 29, 85–94. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).