Generating Trees for Comparison
Abstract
1. Introduction
2. Preliminaries
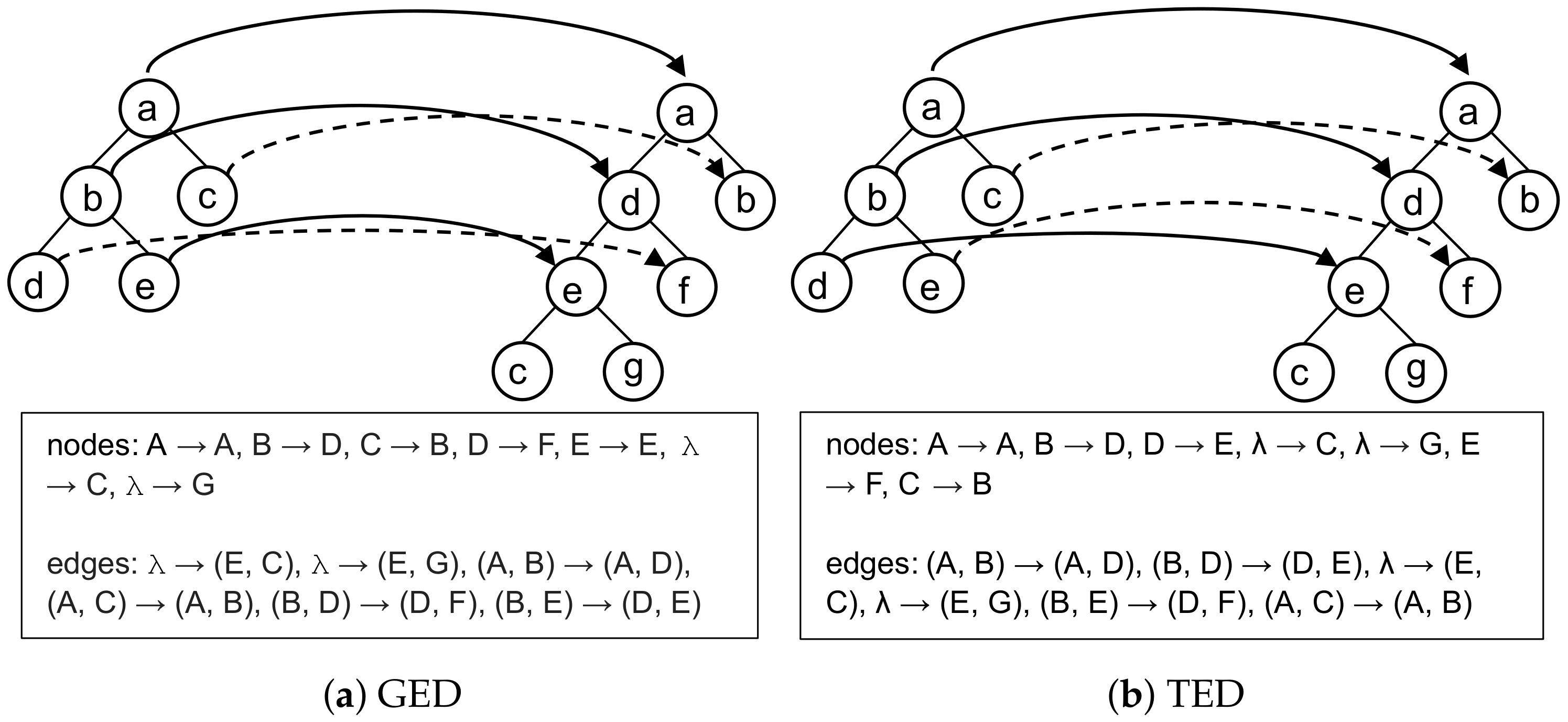
2.1. Dissimilarity Measures
2.2. Statistical Measures
3. Generating Trees
3.1. Random Variants
| Algorithm 1: Random tree algorithm |
| input: the number of nodes n. output: Tree
|
3.2. Generating Trees by Node Distribution
| Algorithm 2: Random tree by node distribution. |
| input: the number of nodes n and node distribution per level D (expressed as percentages) output: Tree
|
3.3. Distorted Tree
| Algorithm 3: Tree generated by given source tree and distortion parameters. |
| input: Tree , distortion parameters a, d, output: Tree
|
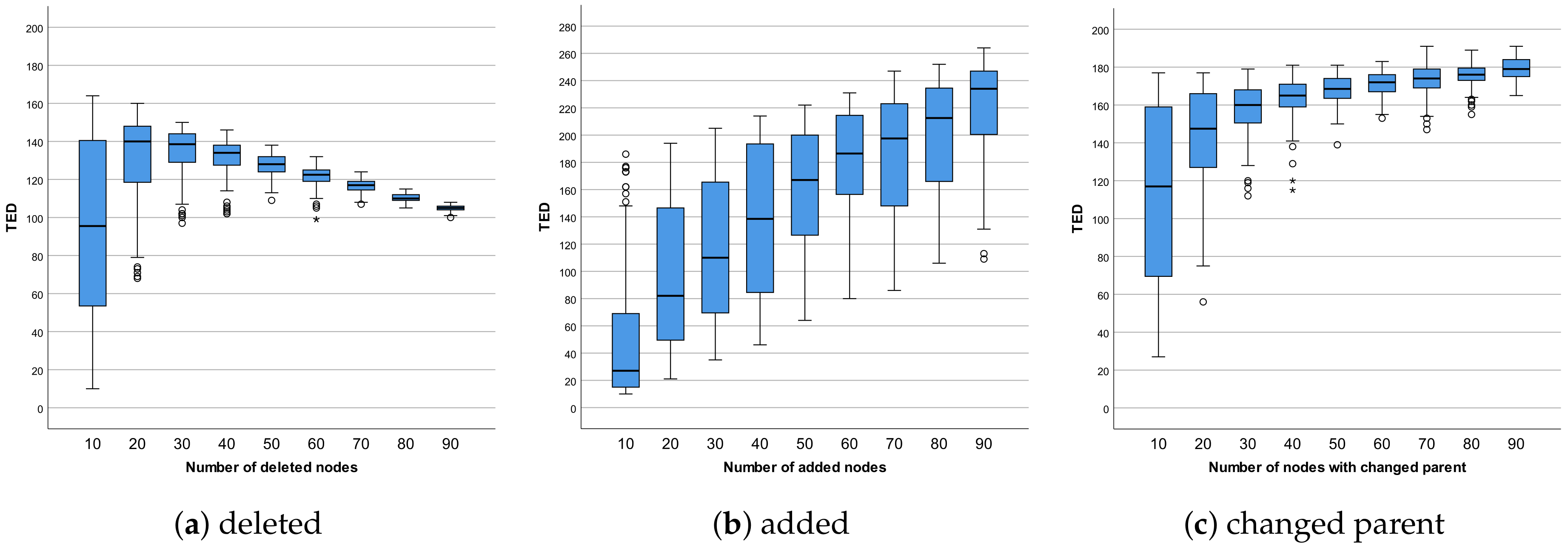
4. Experiments
4.1. Statistical and Edit Distance Measurements
4.2. Distortion Parameters
4.3. Node Distribution
5. Related Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Shasha, D.; Wang, J.T.; Kaizhong, Z.; Shih, F.Y. Exact and approximate algorithms for unordered tree matching. IEEE Trans. Syst. Man Cybern. 1994, 24, 668–678. [Google Scholar] [CrossRef]
- Shapiro, B.A.; Zhang, K. Comparing multiple RNA secondary structures using tree comparisons. Bioinformatics 1990, 6, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Mori, A. Diff/TS: A Tool for Fine-Grained Structural Change Analysis. In Proceedings of the 2008 15th Working Conference on Reverse Engineering, Antwerp, Belgium, 15–18 October 2008; pp. 279–288. [Google Scholar] [CrossRef]
- Chawathe, S.S.; Rajaraman, A.; Garcia-Molina, H.; Widom, J. Change Detection in Hierarchically Structured Information. SIGMOD Rec. 1996, 25, 493–504. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Valiente, G. Algorithms on Trees and Graphs; Springer-Verlag: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Mlinarić, D.; Milašinović, B.; Mornar, V. Tree Inheritance Distance. IEEE Access 2020, 8, 52489–52504. [Google Scholar] [CrossRef]
- Selkow, S.M. The tree-to-tree editing problem. Inf. Process. Lett. 1977, 6, 184–186. [Google Scholar] [CrossRef]
- Zhang, K.; Shasha, D. Simple Fast Algorithms for the Editing Distance Between Trees and Related Problems. SIAM J. Comput. 1989, 18, 1245–1262. [Google Scholar] [CrossRef]
- Gao, X.; Xiao, B.; Tao, D.; Li, X. A survey of graph edit distance. Pattern Anal. Appl. 2010, 13, 113–129. [Google Scholar] [CrossRef]
- Riesen, K. Structural Pattern Recognition with Graph Edit Distance: Approximation Algorithms and Applications, 1st ed.; Springer Publishing Company: Cham, Switzerland, 2016. [Google Scholar]
- A Libre Lightweight Streaming Front-End for Android.: TeamNewPipe/NewPipe. Available online: https://github.com/TeamNewPipe/NewPipe (accessed on 24 July 2019).
- Graphviz—Graph Visualization Software. Available online: https://www.graphviz.org/ (accessed on 9 October 2019).
- Meir, A.; Moon, J.W. Cutting down recursive trees. Math. Biosci. 1974, 21, 173–181. [Google Scholar] [CrossRef]
- Hibbard, T.N. Some Combinatorial Properties of Certain Trees With Applications to Searching and Sorting. J. ACM 1962, 9, 13–28. [Google Scholar] [CrossRef]
- Knuth, D.E. Art of Computer Programming, Volume 4, Fascicle 4, The: Generating All Trees–History of Combinatorial Generation; Addison-Wesley Professional: Boston, MA, USA, 2013. [Google Scholar]
- Aragon, C.R.; Seidel, R.G. Randomized Search Trees. In Proceedings of the 30th Annual Symposium on Foundations of Computer Science (SFCS’89), Research Triangle Park, NC, USA, 30 October–1 November 1989; IEEE Computer Society: Washington, DC, USA, 1989; pp. 540–545. [Google Scholar] [CrossRef]
- Martínez, C.; Roura, S. Randomized Binary Search Trees. J. ACM 1998, 45, 288–323. [Google Scholar] [CrossRef]
- Frieze, A.; Karoński, M. Introduction to Random Graphs; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Bollobás, B. Random Graphs, 2nd ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
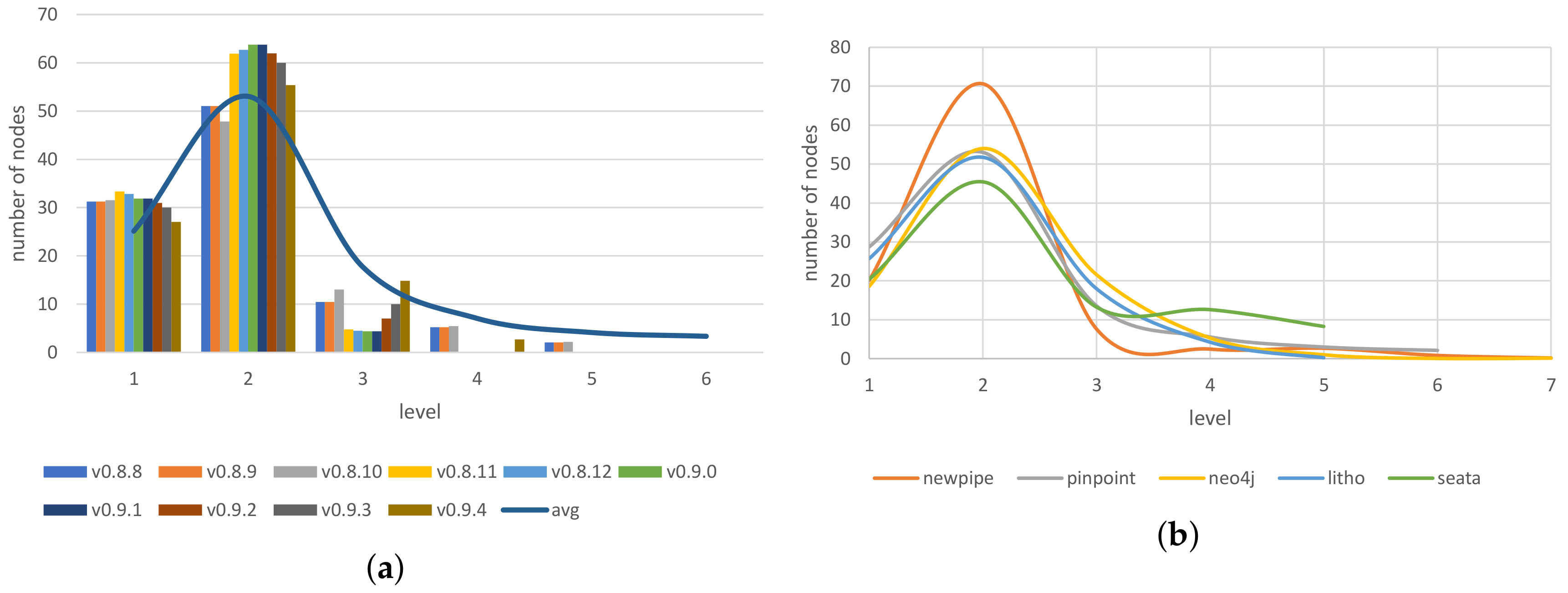

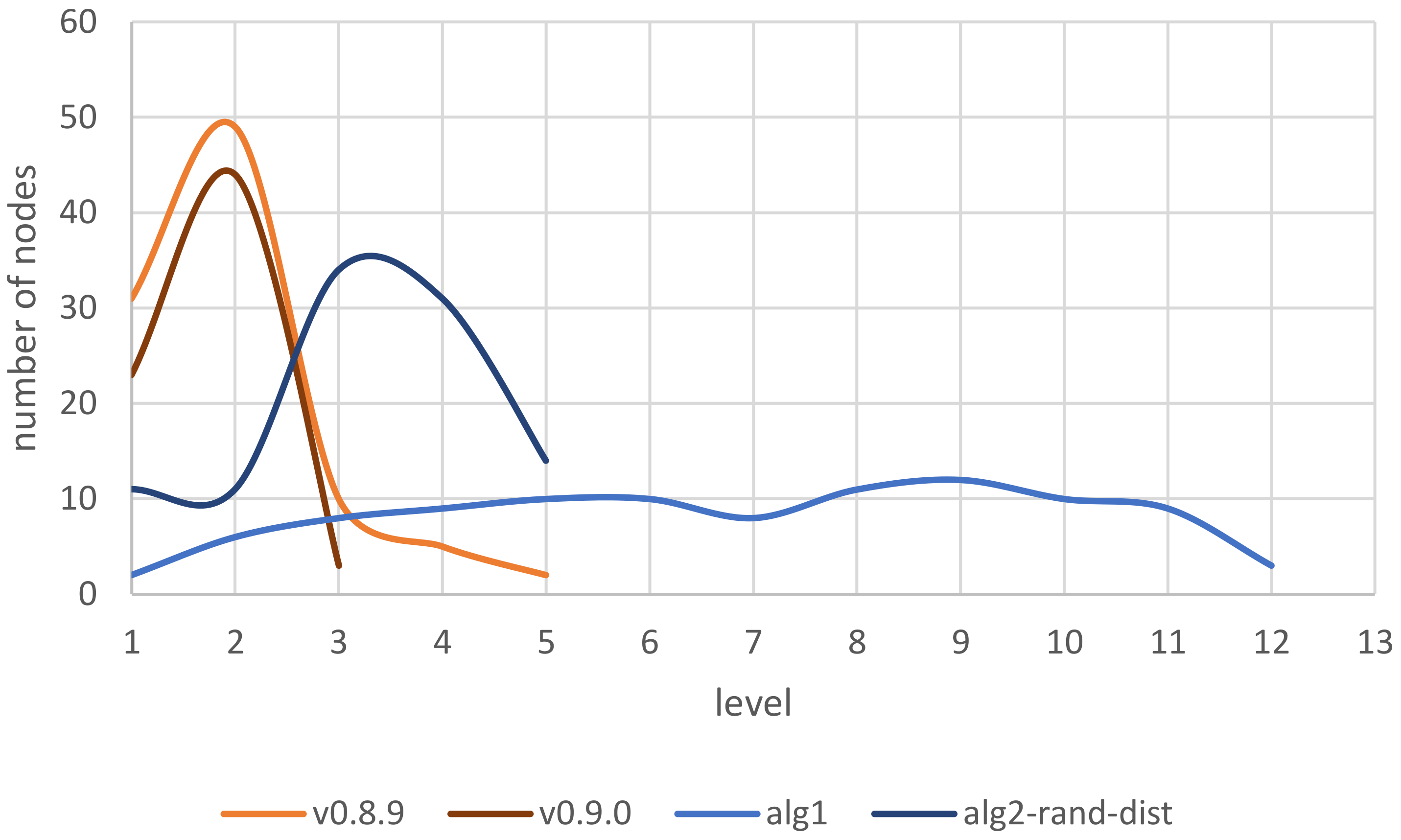
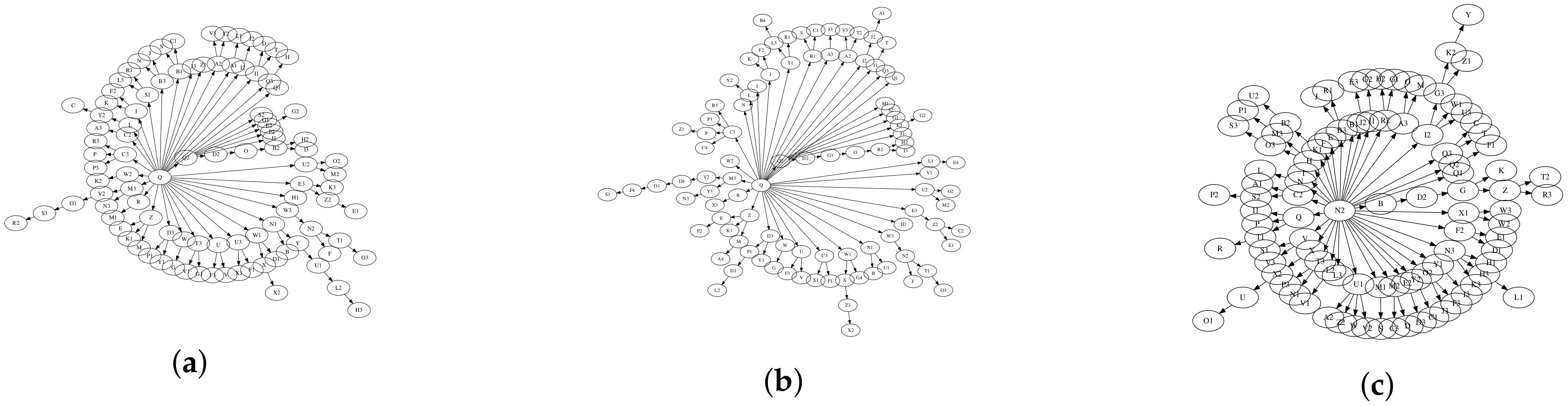
| v0.8.9 | v0.9.0 | |
|---|---|---|
| n | 97 | 70 |
| h | 5 | 3 |
| 1/30/49/10/5/2 | 1/22/44/3 | |
| 30/1.63/0.2/0.5/0.4/0 | 22/2/0.07/ 0 | |
| 31.25/51.04/10.42/5.21/2.08 | 31.88/63.77/4.35 |
| Step | Random P-C | Random P-C with | Random P Iterative C | Random P-C with / |
|---|---|---|---|---|
| [initialize] | ⌀ | ; | getRandomNode(V); | getRandomNode(V); |
| ; | ||||
| ; | ||||
| [parent] | getRandomNode(V); | getRandomNode(V); | getRandomNode(V); | getRandomNode(); |
| [child] | getRandomNode(V); | getRandomNode(); | getNextNode(V); | getRandomNode(); |
| [condition] | ⌀ | |||
| getPreds() | getPreds() | getPreds() | ||
| getPreds() | ||||
| [adjust] | ⌀ | ⌀ | ||
| Algorithm Variant | Avg. Height | Avg. EH |
|---|---|---|
| rand. P-C | 21.802 | 1.029 |
| [±4.979] | [±1.017] | |
| rand. P-C with Un | 21.746 | 1.045 |
| [±4.951] | [±1.035] | |
| rand. P iterative C | 24.590 | 1.530 |
| [±5.294] | [±1.487] | |
| rand. P-C with Un/Us | 8.471 | 0.000 |
| [±1.312] | [±0.000] |
| GED | TED | ||||
|---|---|---|---|---|---|
| 1/1/3/2/1/2 | 1/4/3/1/1 | 1/3/0.67/0.50/2/0 | 4/0.75/0.33/1/0 | 12 | 14 |
| 1/2/2/3/1/1 | 1/4/2/2/1 | 2/1/1.50/0.33/1/0 | 4/0.50/1/0.50/0 | 10 | 12 |
| 1/1/3/3/2 | 1/3/3/2/1 | 1/3/1/0,67/0 | 3/1/0.67/0.50/0 | 9 | 10 |
| 1/2/3/2/1/1 | 1/3/4/1/1 | 2/1.50/0.67/0.50/1/0 | 3/1.33/0.25/1/0 | 9 | 12 |
| 1/1/2/1/1/2/1/1 | 1/1/2/4/1/1 | 1/2/0.50/1/2/0.50/1/0 | 1/2/2/0.25/1/0 | 11 | 10 |
| 1/2/2/2/2/1 | 1/3/3/2/1 | 2/1/1/1/0.50/0 | 3/1/0.67/0,50/0 | 10 | 13 |
| 1/2/1/2/1/2/1 | 1/2/4/1/2 | 2/0.50/2/0.50/2/0.50/0 | 2/2/0.25/2/0 | 12 | 14 |
| 1/1/4/3/1 | 1/5/3/1 | 1/4/0.75/0.33/0 | 5/0.60/0.33/0 | 10 | 15 |
| 1/1/1/1/1/2/1/1/1 | 1/2/2/1/3/1 | 1/1/1/1/2/0.50/1/1/0 | 2/1/0.50/3/0.33/0 | 9 | 13 |
| 1/1/2/3/2/1 | 1/2/2/3/2 | 1/2/1.50/0.67/0.50/0 | 2/1/1.50/0.67/0 | 10 | 14 |
| 1/1.77/2.03/2.03/1.83/ 1.41/1.25/1 | 1/2.40/2.47/2.23/ 1.52/1.33/1 | 1.77/1.15/1/0.87/0.58/ 0.32/0.10/0 | 2.40/1.03/0.91/ 0.57/0.42/0.19/0 | 9.6 ±1.1 | 11.13 ±2.24 |
| Input Distribution | Output | Output by Distortion Parameters | |||
|---|---|---|---|---|---|
| (10, 10, 0.1) | (50, 0, 0) | (0, 50, 0) | (0, 0, 0.5) | ||
| 22.77%, 48.04%, 16.05%, 6.38%, 3.74%, 3.02% |  |  |  |  |  |
| 20%, …, 20% |  |  | 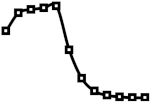 |  |  |
| 10%, …, 10% |  |  |  |  |  |
| 10%, 20%, 30%, 40% | 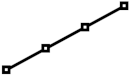 | 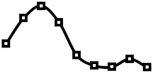 |  |  |  |
| 40%, 30%, 20%, 10% | 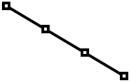 |  | 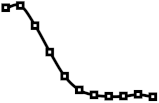 |  |  |
| 6.25%, 12.5%, 18.75%, 25%, 18.75%, 12.5%, 6.25% 3.9%, 6.3%, 7.8%, 8.75%, 9.15%, 9.35%, 9.5 | 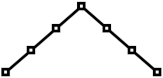 |  |  |  | 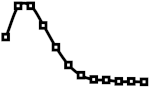 |
| 9.35%, 9.15%, 8.75%, 7.8%, 6.3%, 3.9% |  | 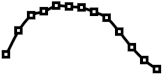 |  |  |  |
| Structure | Nodes Connection | Specifics | Structure Type | Usage |
|---|---|---|---|---|
| recursive tree [14] | from root | integer labels | unordered | * |
| random binary tree [15,16] | random insert | two child nodes | ordered | binary search |
| treap/randomized BST [17,18] | add/delete ops | two child nodes | ordered | binary search |
| random graphs [19,20] | probability of connection | ** | graph | * |
| Algorithm | Similarity | Differences |
|---|---|---|
| random (Algorithm 1) | binary trees | unordered, arbitrary number of child nodes |
| random (Algorithm 1) * | recursive trees | arbitrary labels |
| node distribution (Algorithm 2) | graphs | distribution of nodes, unordered trees |
| distort (Algorithm 3) | treap/randomized BST | unordered, arbitrary number of child nodes, |
| parent change operation |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlinarić, D.; Mornar, V.; Milašinović, B. Generating Trees for Comparison. Computers 2020, 9, 35. https://doi.org/10.3390/computers9020035
Mlinarić D, Mornar V, Milašinović B. Generating Trees for Comparison. Computers. 2020; 9(2):35. https://doi.org/10.3390/computers9020035
Chicago/Turabian StyleMlinarić, Danijel, Vedran Mornar, and Boris Milašinović. 2020. "Generating Trees for Comparison" Computers 9, no. 2: 35. https://doi.org/10.3390/computers9020035
APA StyleMlinarić, D., Mornar, V., & Milašinović, B. (2020). Generating Trees for Comparison. Computers, 9(2), 35. https://doi.org/10.3390/computers9020035





