Abstract
Online social network users share their information in different social sites to establish connections with individuals with whom they want to be a friend. While users share all their information to connect to other individuals, they need to hide the information that can bring about privacy risks for them. As user participation in social networking sites rises, the possibility of sharing information with unknown users increases, and the probability of privacy breaches for the user mounts. This work addresses the challenges of sharing information in a safe manner with unknown individuals. Currently, there are a number of available methods for preserving privacy in order to friending (the act of adding someone as a friend), but they only consider a single source of data and are more focused on users’ security rather than privacy. Consequently, a privacy-preserving friending mechanism should be considered for information shared in multiple online social network sites. In this paper, we propose a new privacy-preserving friending method that helps users decide what to share with other individuals with the reduced risk of being exploited or re-identified. In this regard, the first step is to calculate the sensitivity score for individuals using Bernstein’s polynomial theorem to understand what sort of information can influence a user’s privacy. Next, a new model is applied to anonymise the data of users who participate in multiple social networks. Anonymisation helps to understand to what extent a piece of information can be shared, which allows information sharing with reduced risks in privacy. Evaluation indicates that measuring the sensitivity of information besides anonymisation provides a more accurate outcome for the purpose of friending, in a computationally efficient manner.
1. Introduction
Online social networking sites are attractive to individuals due to their affordability and accessibility. These sites let users create semi- or fully public profiles to communicate and share information with others [1,2], as well as to see other individuals’ activities regarding the defined restrictions for their profile [3]. Most users disclose some of their information publicly to other individuals [4]. Evidences show that people are keen on swapping their private information for comparatively insignificant rewards [5]. This digital presence of users in online social networks has led to a massive quantity of data, both structured or unstructured [6].
While these social network sites provide the aforementioned features, users can also send private messages, create and post comments, as well as accept and request friendships [7]. One of the main features of these sites is friending (Merriam-Webster defines friending as “[including] (someone) in a list of designated friends on a person’s social networking site”). Lewis and West [8] define the friending process as the likelihood of a social contact increase where individuals gather and add other individuals (friends) on a mutual basis. Friending helps users to establish links with other users who may be unknown or unmet to the user and allow them to access the content of user’s profiles. Friending in social network sites typically provides that individual with particular rights [9] besides access to other users’ information. Providing access to the shared information to these individuals may lead to the misuse of user’s information and brings several privacy risks and vulnerabilities for the user. As more information is shared, the probability of privacy risks elevates [10,11]. Hence, users need an appropriate system to help them decide what and how information should, or should not, be shared publicly prior to friending, which in turn can preserve their online privacy.
Recent research has investigated a number of friending methods in online social networks. Different scholars [12,13,14] have investigated privacy preservation mechanisms for friending, which are more focused on secure communication channels for data transmission to achieve data security, while they do not concentrate on the data privacy of users in the process of friending. Although there are various definitions for privacy, a single precise explanation of privacy does not exist. In this study, we principally concentrate on the information privacy of users. Kang defined privacy as follows: “an individual’s claim to control the terms under which personal information identifiable to the individual is acquired, disclosed or used. User’s information privacy concept is intensely connected to the notation of confidentiality, which is one of the main attributes of information security, but not to be used in an interchangeable manner”. Confidentiality itself addresses the revealing information of an individual, while the privacy of data considers the ownership of information and the influences that information revelation has on data access permissions and privileges of the individual and his/her connections (friends) [2]. Other authors [15,16,17] have proposed privacy scoring systems without considering mitigation methods to preserve the privacy across multiple sources of data. Since online social networks provide an environment to share an individual’s information with other users for the purpose of befriending, these current methods cannot be applied for the process of friending with a reduced risk in privacy. Additionally, current methods do not take into consideration what should be shared in multiple online social network sites to meet users’ online privacy needs and what types of information should be preserved.
One of the main factors to mitigate the privacy risks and improve the friending process is to understand what types of information are more sensitive and have more impact on privacy for users and differentiate this information from non-sensitive information. This can provide more insight on what users can, while maintaining sufficient privacy, safely share prior to friending in online social networks. As sharing information in multiple sites elevates the probability of user’s information being exploited [11], our method reduces users’ privacy risks for the purpose of friending considering multiple online social networking sites.
To achieve this, we propose a sensitivity calculation scheme to decide what types of information (i.e., attributes) can bring about privacy threats for users. This is done by the evaluation of risks that users may be exposed to, which is accomplished by the proposed Bernstein polynomial function. Additionally, we develop a new anonymisation method based on the sensitivity of users’ information in multiple online social networking sites, which help users to decrease their privacy risks in cyberspace as well as the privacy of the information they share in order to achieve friending with others, solicited or unsolicited.
The principal contribution of this paper is to introduce an automated model for privacy-preserved friending for users concentrating on multiple online social networking sites based on the sensitivity of information.
The rest of this paper is organised as follows. Section 2 provides a review of current literature on preserving privacy friending and information sharing privacy on social networking sites. Section 3 defines the problem and details the methodology of the study. Section 4 describes the privacy-preservation framework, while Section 5 presents the experimental evaluation of the proposed method. The final section includes a discussion and future direction for the research.
2. Related Work
While users share information on social networks with friends and even with potential friends in a safe manner, there is a need to present a model to provide users their information secrecy and privacy. Information disclosure may lead to privacy risks for the user’s friends as well [18]. Sharing personally identifiable information (PII) (typically, an identifying variable is one that defines an attribute of an individual that is visible and evident, is recorded [such as social security number, employee ID, patient ID, etc.], and is something with which other people can identify) can result in several privacy issues for the users such as fraud, stalking, identity theft, or possibly even harassment. One way to tackle this issue is to score the privacy of users. Pensa and Blasi [15] proposed a self-assessment framework to derive a privacy score in a single source (i.e., a social network). Xu et al. [16] proposed a system which helps users to control the sharing of pictures in online social networking sites. Veiga and Eickhoff [17] measured the information leakage of information without considering mitigating methods to preserve privacy. Srivastava [19] proposed a naive approach to measure the privacy leak of users in social networking sites. To measure the sensitivity of information, they have only considered the status of shared information, whether it is publicly available or private. In this case, they determine the sensitivity of that information, ignoring the fact that sharing information even with friends can cause a privacy risk for users. Although the proposed naive approach is impartially simple, the gained values are considerably influenced by the population of users and the approach is very poor in estimation. Srivastava also mentioned that item response theory proposed by Liu and Terzi [20] to measure privacy risk could be biased in the estimation of privacy. Others have suggested the use of the Bernstein polynomial in the estimation problem. Nava et al. [21] proved that the Bernstein polynomial is more efficient in a computational manner, is universal, and is dominant in computation time compared with traditional polynomials. Hence, this approach has been applied to measure the sensitivity of information in the study and works well in approximation.
On the other hand, privacy preserving friending schemes that are mostly cryptographic are applied for preserving information security, neglecting the privacy of users’ context in social networks sites. Zhang et al. [12,13] proposed a secure mechanism for profile matching for the participants who want to be friend. The concentration of their mechanism is on communication security between the friend’s request sender and potential users with whom the user wants to connect. Preibusch and Beresford [14] investigated the friendship’s nature and applied hash identifiers to create a hidden friendship between users. Baden et al. [22] proposed the Persona system. This system lets individuals have personalised privacy by applying attribute-based encryption. Guha et al. [23] proposed a novel approach for preserving data privacy,neglecting the fact that the privacy of users is not assured in this system.
Despite various research studies on privacy calculation or privacy preservation, a technique with satisfactory privacy preservation for multiple sources of social data considering measurement of highly sensitive information has not been considered and developed. It is essential to measure the privacy when it gets distributed across multiple online social networking sites as more sensitive information of an individual is shared compared to a single source of data. This can help to perceive which sensitive information should be considered as private (does not go online publicly) when individuals want to have an active online presence, find friends, and safely share their information with those they want to befriend.
3. Problem Definition and Methodology
Sharing information in online social networks for the purpose of friending causes various privacy risks for users who participate in such sites and want to connect with each other. In order to reduce the privacy risks for users in such conditions, there is a need to understand which information is more sensitive and can mitigate the privacy risks for them in their online presence. As users participate in various social network sites, connect with more different individuals, and share more information compared to a single source of online social networking site, more sensitive information of a user is being shared. Hence, there is a need for techniques that consider which sorts of information can lead to privacy risks for users in the friending process and how to provide privacy preservation for them in the case of friending.
Figure 1 presents the overall framework for the privacy-enhanced friending technique for online social network users. The framework consists of three main phases: data preparation, sensitivity calculation and the anonymisation process, and finally the mechanism output. In the data preparation phase, 20 attributes of users are considered to be gathered from social networking sites—these attributes are the most common attributes considered in previous studies related to privacy measurement in online social networking sites and are also the compulsory attributes which a user should provide before creating an account in such sites. Compulsory attributes include name, surname, date of birth, gender and joined date and the rest of attributes gathered from historical studies include college name, company name, school, university, city, state, language, qualification, job position, phone number, email, religious views, political views, interests, and postcode. The values for the attributes are obtained from synthetic data, generated using Mockaroo (https://www.mockaroo.com/), which randomly generates test data with requested characteristics. The software creates realistic-looking data which is close to the real shared information on online social sites. Moreover, using testing data makes the results more robust as it provides fewer errors compared with the real data. The level of sensitivity of attributes is obtained from the user’s perspective and indicates how concerned a user is about his or her information being shared publicly. Regarding a user’s attributes, there are various classifications by different authors [24,25,26]. Arnes et al. [24] classified users’ profile data into three categories consisting of mandatory, extended, and personal data. Ritcthammer et al. [26] extended the Arnes classification by covering more attributes on social networking sites to classify the data. Ho et al. [25] proposed five different groups to classify users’ data. Based on the different methods for classifying the users’ data on social networking sites, we categorise the information of users in three different ways: personal information, compulsory information, and sensitive information.
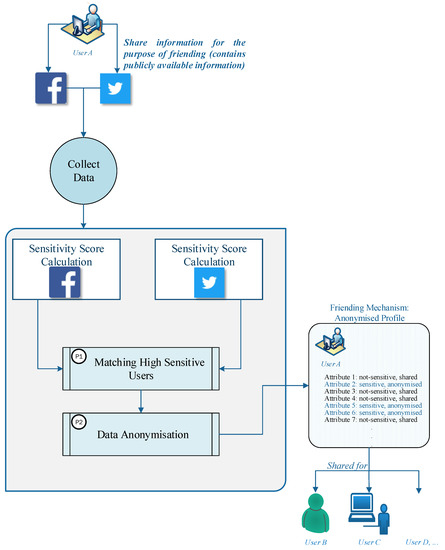
Figure 1.
Overall framework of the privacy-enhanced friending technique.
In the second phase, first, we calculate the sensitivity score of users’ profiles on two online social network sites, Facebook and Twitter. The sensitivity calculation can show which attributes are more sensitive compared to other attributes. Then, two different processes are identified to reduce the privacy risk of users, labelled P1 and P2. In the P1 phase, we recognise the sensitive information in both social networks and the importance of information for users. In this phase, we find users who share sensitive data in both social networks, i.e., users who are more susceptible to privacy risk. The aggregation of profiles can help to gain more data as we deal with multiple sources of data rather than a single source, while matching the sensitivity results can verify that the social media profile is real. After finding users who share sensitive information on both social networking sites, in P2, the anonymisation method will be applied to the obtained dataset from P1 to help users preserve their privacy prior to sharing their information for the purpose of friending. In the last phase, based on the sensitivity result, each attribute that may lead to the identification of an individual directly or is considered as highly sensitive will be detached. Other attributes that have less sensitivity based on the user’s perspective are replaced with less semantic values to decrease the privacy risks for users. In this phase, an anonymised profile of a user is obtained where the user can securely share information publicly to other users to achieve friending.
4. Privacy-Enhanced Friending Framework
4.1. Sensitivity Score Calculation
As mentioned, sensitivity is defined as the amount of potential privacy risks for users when sharing information in their online presence. Calculating the sensitivity level could help users to have a better understanding of the importance of shared information and assist them in deciding what to share with others. Here, we categorise five different levels for users’ information sensitivity. The users’ information can be (a) extremely sensitive, (b) very sensitive, (c) moderately sensitive, (d) low sensitive, and (e) very low sensitive. For measuring the sensitivity to each profile item, we assume that each user participates in k different online social networking sites. To achieve sensitivity calculation, a new method based on a Bernstein polynomial [27] has been proposed. By applying this model, the sensitivity score of social network profiles can be calculated. The response matrix for sensitivity calculation contains the sensitivity of attributes for each user profile. Users’ preferences for the sensitivity of their data are aggregated into this matrix. The value differs based on the nature of attributes, whether the attribute is sensitive, compulsory, or personal (how much it is considered sensitive for users). The first step is to compute the sensitivity for each profile item i using the following formula:
where is the sensitivity score of profile item i, N is the number of users, l is equal to the number of rows, is the summation of each attribute score in the response matrix, is the sum of sensitivity score of each of the response matrix, and m is equal to the scale of the sensitivity ().
At the next step, the sensitivity of each profile for each attribute is calculated based on the information sensitivity of each user by the following formula:
where j indicates the scale of the sensitivity of each attribute for each user, which is between , and m is equal to (). indicates the individual sensitivity score in the response matrix (from ,..,) and e is Euler’s number. This formula is derived from the polytomous Rasch partial credit score [28]. After calculating the response matrix of each value in the defined scale, each item has the profile sensitivity value in the response matrix R. The final sensitivity score for each user profile is derived from a linear combination of a linear basic Bernstein polynomial [27]. The basic Bernstein polynomial formula is given by
where n indicates the degree of polynomial and coefficient is called the Bernstein (Bezier) coefficient. Here, we use this formula as a base formula for computing the sensitivity score of each user. The value is formulated to the sensitivity of each user, and the value is formulated to the incremental polynomial of the value of sensitivity for the scale range . Hence, we are formulating this Bernstein formula to calculate the sensitivity score value as
After calculating the sensitivity of users’ profiles on each social network site, we should understand which users share sensitive information on both social networking sites to meet our assumption. For doing so, we calculate the average sensitivity score of all users who have shared their information in social networks.
where indicates the average score of sensitivity for each online social network site. Then, we match the users who share their sensitive information in both sites—users who have a sensitivity score higher than the average on both online social networking sites. In this case, the credibility of the users’ information can be guaranteed as well.
4.2. Data Anonymisation
To achieve users’ privacy, the sensitive information of users should be preserved. In the friending process, we are answering the question of whether a user’s information is shared publicly available or not. Generalisation and suppression can assure the suitable level of privacy for individuals as they diversify values and can help improve friending results. For P2, we developed an anonymisation model that can provide online privacy for users in terms of friending. Our proposed method contains the following steps. Initially, a table that comprises sensitive profiles on both social network sites is considered as an input for anonymisation. This table is denoted by a matrix. Then, we consider which attributes have a high or very high sensitivity based on the users’ perspective.
In the proposed method, based on the sensitivity of attributes, different techniques such as suppression, generalisation (which replaces the value with a less specific semantically consistent value), fuzzy-based rule generalisation, and binarisation are applied to provide a consistent anonymised table. For example, in our proposed model, age is generalised based on the fuzzy-based rule, while qualification is binarised based on true and false criteria. University is followed by a grouping model which shows a specific user to a particular university, whereas job is the outcome of specialisation and generalisation.
4.3. Time Complexity Comparison
Table 1 compares the computation cost of our proposed method with the most well-known anonymisation methods. Among all anonymisation methods, Le Fevre’s Mondrian algorithm [29] is the fastest local method among these approaches without considering sensitivity of information and multiple sources of information. However, our proposed method applies to both the sensitivity calculation and the anonymisation technique. In our model, looking for users to see who obtain highly sensitive profiles in both social networks or not is . The anonymisation process that contains fuzzy rules, generalisation, and suppression has complexity. Hence, the aggregated complexity for our proposed method has complexity. While the bottom-up method has the same order compared with our proposed method, it only focuses on data anonymisation (k-anonymity) in a single source without calculating the sensitivity of the attributes.

Table 1.
Algorithmic complexity comparison.
5. Experimental Evaluation
In this section, we present an assessment of our proposed privacy-enhanced friending framework. First, we present the results of the sensitivity score. Then, we show the results obtained from the proposed anonymisation method.
5.1. Sensitivity Score
In this section, we provide the sensitivity score of 100 users in two different online social networks, Facebook and Twitter. The selected quantity of individuals covers a variety of values from users’ social profiles that is desirable to confirm the utility of the proposed privacy-enhanced friending model. Based on the categorisation and the sensitivity of attributes from the literature, we assign a random number for the attributes between 1 and 5 considering the discrete uniform distribution. In this case, a random number between 3 and 5 is assigned to the attributes, which are more sensitive; for the rest of attributes which are compulsory or personal, a value between 1 and 5 would be assigned.
Figure 2 and Figure 3 show the comparison of the sensitivity scores of users in three different categories (very high to very low) for these synthetic users. Table 2 shows the bounds of sensitivity for each category and the final sensitivity score to determine the level of sensitivity. As mentioned before, three different categories were considered for the attributes. To define the lower and upper bounds of each category, we applied the mean function for the attributes related to each category in each social networks. Next, we calculated the difference of the obtained result and divided it to five equal bounds to determine the five different scales for the categories. At the next stage, we calculated the overall sensitivity for each category and compared it with the combined dataset which contains the information of users who have a high sensitivity score with respect to both social networking sites. As can be seen from Figure 2 and Figure 3, analyses of synthetic data show that nearly 53% of users do not desire to share their information in online social networks publicly, while the rest of the users see a trade-off between their information shared and their privacy in social media. It can be seen that nearly 22% of users do share their information or they may have accidentally shared information in such social sites publicly available.
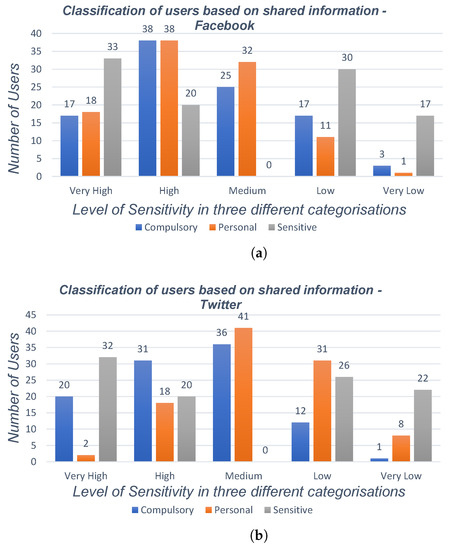
Figure 2.
Percentage of users who have shared information in three different categories of users’ data type in online social networks. (a) Percentage of users who have shared information in three different categories of users’ data type in online social networks—the Facebook case; (b) percentage of users who have shared information in three different categories of users’ data type in online social networks—the Twitter case.
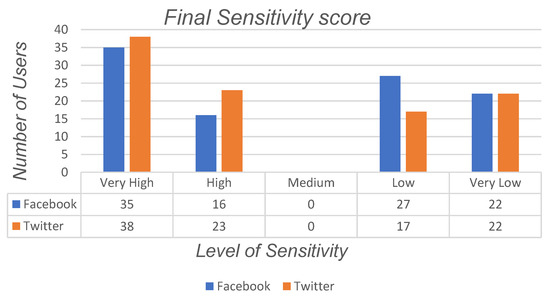
Figure 3.
Final sensitivity score, for synthetic user data.

Table 2.
Sensitivity of information bounds. Risk categories are very low (VL), (L)ow, (M)edium, (H)igh, and very high (VH). Information categories are (C)ompulsory, (P)ersonal, and (S)ensitive; F is the final sensitivity score.
Note: In this study, we only measure how sensitive the values of attributes for the users are when they share their information in online social networks. Measuring the level of users’ knowledge about privacy is beyond the scope of this study.
The sensitivity score of synthetic data of users on social networking sites indicates that the number of users who share sensitive information on social networking sites publicly is almost equal with the final result. As mentioned, the provided test data is robust, so it can be concluded that sensitive information plays a critical role in determining whether a user is really in privacy risks or not. Meanwhile, other categories and attributes of users that are shared cannot be neglected.
5.2. Anonymisation Output
In the P2 phase, the data from matched users obtained from the Bernstein model is anonymised. Table 3, Table 4 and Table 5 show examples of anonymisation output of our model from a set of raw (synthesised) data. By comparing the results of two tables, users can understand what they can share publicly to other users, what type of information should be shared with less semantic values, and what type of information should not be accessible to others because of its importance. Hence, the online privacy of users can be met while they can have an active presence on social networking sites. As a case in point, the automated system can help users to achieve friending with other individuals in online social networks with a mitigated risk of privacy.

Table 3.
Raw data vs. anonymised data publishing: raw data case.

Table 4.
Raw data vs. anonymised data publishing: anonymised data case.

Table 5.
Applied data disclosure method—sample.
6. Conclusions and Future Work
Sharing information for the purpose of friending on different online social network sites brings about several privacy concerns and risks for users. An identity breach can have several consequences for individuals. Hence, there is a need to protect the privacy of individuals in such networks as well as to increase users’ understanding of their privacy and sensitive information. Providing only a single method of anonymisation for users’ data considering a single social network site is not sufficient to preserve individuals’ sensitive information when they want to connect with other individuals. Additionally, it will not help users to have a clear understanding of what they can share with other individuals when they want to be friends with them. In this regard, we have demonstrated our friending model using a mixture of different statistical (Bernstein theorem) and anonymisation techniques (k-anonymity) considering multiple online social network sites. The proposed model has been applied to synthetic data to show the effectiveness and generality of the method. The result of the study indicates that many online social network users share their sensitive information. Our model can help users to see the level of sensitivity of their information and then provide an anonymised profile of social networks users which can provide a more accurate idea of their sharing information behaviour by the privacy-enhanced friending technique prior to friending other users. In the future, we can focus on personalisation in privacy preservation to increase the data utility of the shared information of individuals. This can help users to benefit from a model that matches their privacy perspective. The sorts of attacks that can be achieved on the anonymised data can also be investigated. Measuring users’ knowledge about privacy and achieving privacy settings on social networking sites and the trade-off between privacy and online presence can be considered in future studies.
References
Author Contributions
Conceptualization, E.A.; Methodology, E.A., S.G. & J.M.; Software, E.A.; Validation, E.A., S.G. & J.M.; Formal Analysis, E.A.; Data Curation, E.A.; Writing-Original Draft Preparation, E.A.; Writing-Review & Editing, E.A., S.G. & J.M.; Supervision, S.G. & J.M.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boyd, D.M.; Ellison, N.B. Social network sites: Definition, history, and scholarship. J. Comput. Med. Commun. 2007, 13, 210–230. [Google Scholar] [CrossRef]
- Aghasian, E.; Garg, S.; Montgomery, J. User’s Privacy in Recommendation Systems Applying Online Social Network Data, A Survey and Taxonomy. arXiv, 2018; arXiv:1806.07629. [Google Scholar]
- Zlatolas, L.N.; Welzer, T.; Heričko, M.; Hölbl, M. Privacy antecedents for SNS self-disclosure: The case of Facebook. Comput. Hum. Behav. 2015, 45, 158–167. [Google Scholar] [CrossRef]
- Gross, R.; Acquisti, A. Information revelation and privacy in online social networks. In Proceedings of the 2005 ACM Workshop on Privacy in the Electronic Society, Alexandria, VA, USA, 7 November 2005; pp. 71–80. [Google Scholar]
- Kokolakis, S. Privacy attitudes and privacy behaviour: A review of current research on the privacy paradox phenomenon. Comput. Secur. 2017, 64, 122–134. [Google Scholar] [CrossRef]
- Sharma, S.; Gupta, B. Information Privacy on Online Social Networks: Illusion-in-Progress in the Age of Big Data. In Analytics and Data Science; Springer: Berlin, Germany, 2018; pp. 179–196. [Google Scholar]
- Sahinoglu, M.; Akkaya, A.D.; Ang, D. Can We Assess and Monitor Privacy and Security Risk for Social Networks? Procedia Soc. Behav. Sci. 2012, 57, 163–169. [Google Scholar] [CrossRef]
- Lewis, J.; West, A. ‘Friending’: London-based undergraduates’ experience of Facebook. New Med. Soc. 2009, 11, 1209–1229. [Google Scholar] [CrossRef]
- Thelwall, M. Social networks, gender, and friending: An analysis of MySpace member profiles. J. Assoc. Inform. Sci. Technol. 2008, 59, 1321–1330. [Google Scholar] [CrossRef]
- Houghton, D.J.; Joinson, A.N. Privacy, social network sites, and social relations. J. Technol. Hum. Serv. 2010, 28, 74–94. [Google Scholar] [CrossRef]
- Aghasian, E.; Garg, S.; Gao, L.; Yu, S.; Montgomery, J. Scoring Users’ Privacy Disclosure Across Multiple Online Social Networks. IEEE Access 2017, 5, 13118–13130. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.Y.; Liu, Y. Message in a sealed bottle: Privacy preserving friending in social networks. In Proceedings of the 2013 IEEE 33rd International Conference on Distributed Computing Systems (ICDCS), Philadelphia, PA, USA, 8–11 July 2013; pp. 327–336. [Google Scholar]
- Zhang, L.; Li, X.Y.; Liu, K.; Jung, T.; Liu, Y. Message in a sealed bottle: Privacy preserving friending in mobile social networks. IEEE Trans. Mob. Comput. 2015, 14, 1888–1902. [Google Scholar] [CrossRef]
- Preibusch, S.; Beresford, A.R. Privacy-Preserving Friendship Relations for Mobile Social Networking. Available online: https://www.w3.org/2008/09/msnws/papers/Preibusch-BeresfordPrivacy-Preserving-Friendship-Relations.pdf (accessed on 5 August 2018).
- Pensa, R.G.; Di Blasi, G. A privacy self-assessment framework for online social networks. Expert Syst. Appl. 2017, 86, 18–31. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.; Guo, L.; Fang, Y.; Li, X. My privacy my decision: Control of photo sharing on online social networks. IEEE Trans. Dependable Secure Comput. 2017, 14, 199–210. [Google Scholar] [CrossRef]
- Veiga, M.H.; Eickhoff, C. Privacy leakage through innocent content sharing in online social networks. arXiv, 2016; arXiv:1607.02714. [Google Scholar]
- Alsarkal, Y.; Zhang, N.; Xu, H. Your Privacy Is Your Friend’s Privacy: Examining Interdependent Information Disclosure on Online Social Networks. In Proceedings of the 51st Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 3–6 January 2018; pp. 892–901. [Google Scholar]
- Srivastava, A.; Geethakumari, G. Measuring privacy leaks in online social networks. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 2095–2100. [Google Scholar]
- Liu, K.; Terzi, E. A framework for computing the privacy scores of users in online social networks. ACM Trans. Knowl. Discov. Data 2010, 5, 6. [Google Scholar] [CrossRef]
- Nava, J.; Kosheleva, O.; Kreinovich, V. Why Bernstein polynomials are better: fuzzy-inspired justification. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Brisbane, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar]
- Baden, R.; Bender, A.; Spring, N.; Bhattacharjee, B.; Starin, D. Persona: an online social network with user-defined privacy. In Proceedings of the ACM SIGCOMM Computer Communication Review, Barcelona, Spain, 17–21 August 2009; Volume 39, pp. 135–146. [Google Scholar]
- Guha, S.; Tang, K.; Francis, P. NOYB: Privacy in online social networks. In Proceedings of the First Workshop on Online Social Networks, Seattle, WA, USA, 17–22 August 2008; pp. 49–54. [Google Scholar]
- Årnes, A.; Skorstad, J.; Michelsen, L. Social network services and privacy. Available online: http://www.jukkarannila.fi/docs/11-00643-5-Part-I-RapportFacebook2011april2011.pdf (accessed on 5 August 2018).
- Ho, A.; Maiga, A.; Aïmeur, E. Privacy protection issues in social networking sites. In Proceedings of the International Conference on Computer Systems and Applications, Rabat, Morocco, 10–13 May 2009; pp. 271–278. [Google Scholar]
- Richthammer, C.; Netter, M.; Riesner, M.; Sänger, J.; Pernul, G. Taxonomy of social network data types. EURASIP J. Inf. Secur. 2014, 1, 11. [Google Scholar] [CrossRef]
- Schilling, R.L.; Song, R.; Vondracek, Z. Bernstein Functions: Theory and Applications; Walter de Gruyter: Berlin, Germany, 2012; Volume 37. [Google Scholar]
- Masters, G.N. A Rasch model for partial credit scoring. Psychometrika 1982, 47, 149–174. [Google Scholar] [CrossRef]
- LeFevre, K.; DeWitt, D.J.; Ramakrishnan, R. Mondrian multidimensional k-anonymity. In Proceedings of the 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 25. [Google Scholar]
- Xu, J.; Wang, W.; Pei, J.; Wang, X.; Shi, B.; Fu, A.W.C. Utility-based anonymization using local recoding. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 785–790. [Google Scholar]
- Lin, J.L.; Wei, M.C. An efficient clustering method for k-anonymization. In Proceedings of the 2008 International Workshop on Privacy and Anonymity in Information Society, Nantes, France, 29 March 2008; pp. 46–50. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).